Selection of Effective GCM Bias Correction Methods and Evaluation of Hydrological Response under Future Climate Scenarios
Abstract
1. Introduction
2. Materials and Methods
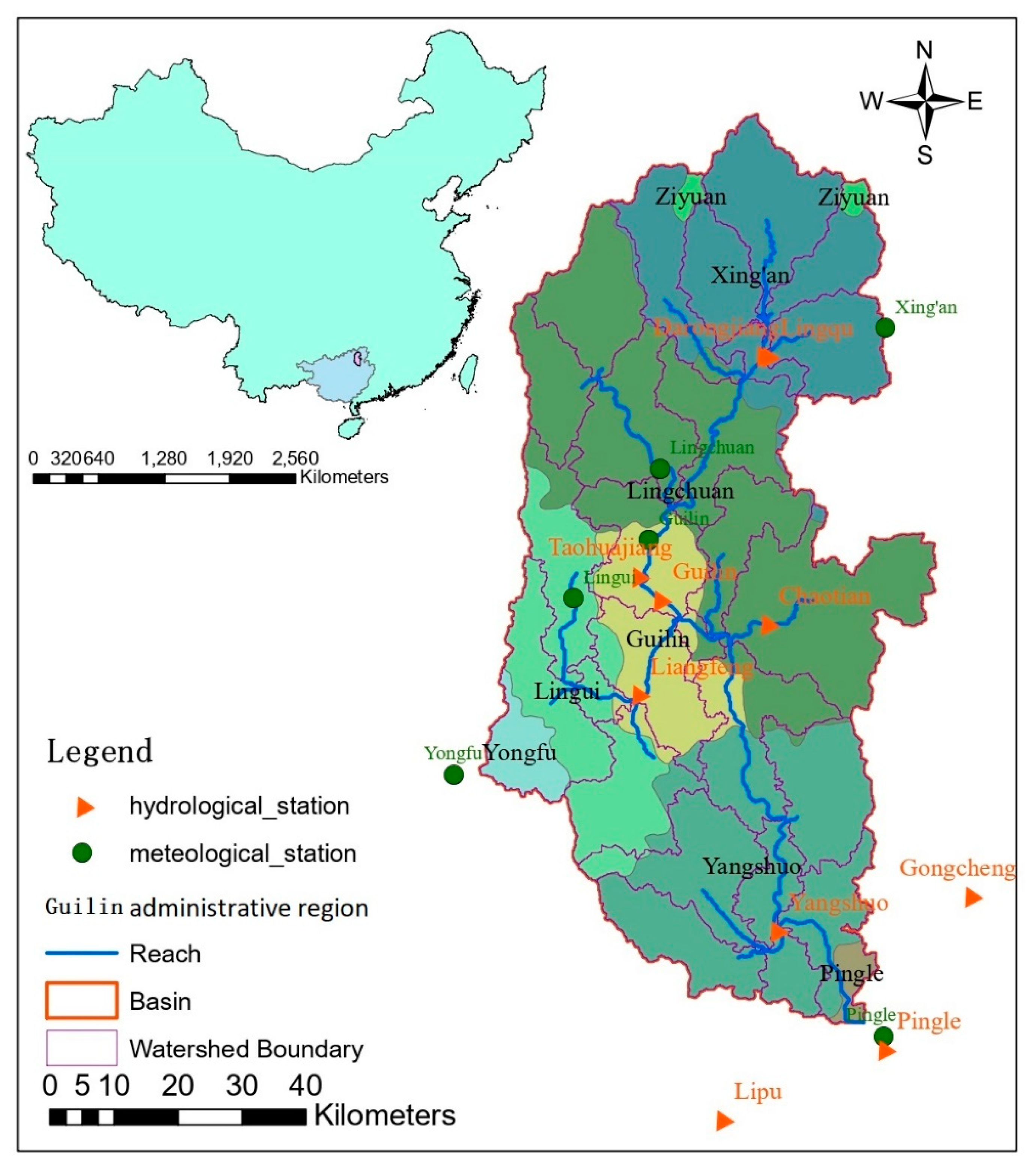
2.1. Study area and data
2.2. Bias correction and Evaluation of GCM Outputs
2.2.1. Overview of Bias Correction Methods
2.2.2. Hybrid Method
2.3. Description and Development of the SWAT Model
2.3.1. A brief Description of SWAT Model
2.3.2. SWAT Model Setup
2.3.3. Model Performance Assessment
3. Results
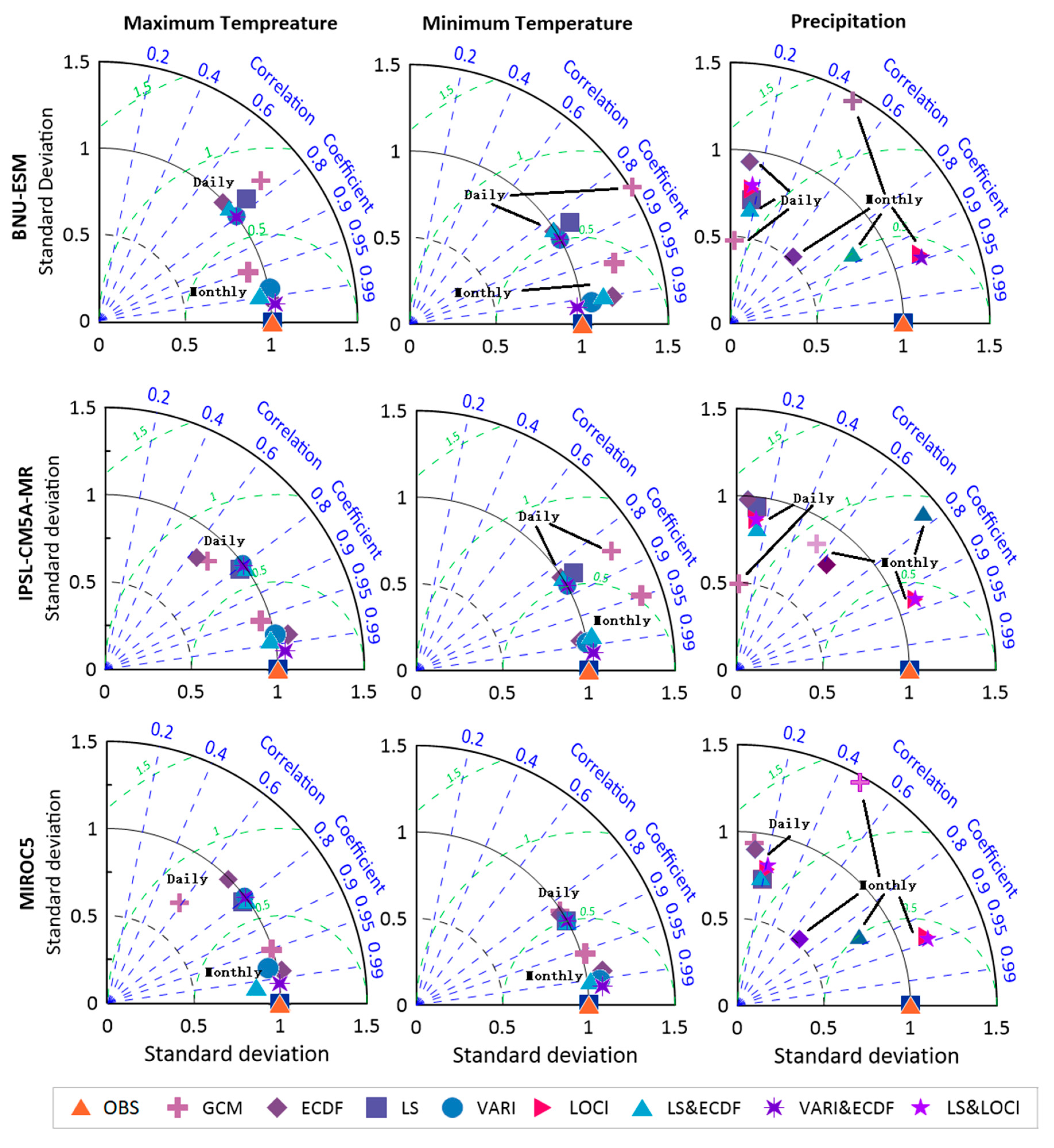
3.1. Assessment of the GCM Outputs Using Multiple Bias Correction Methods
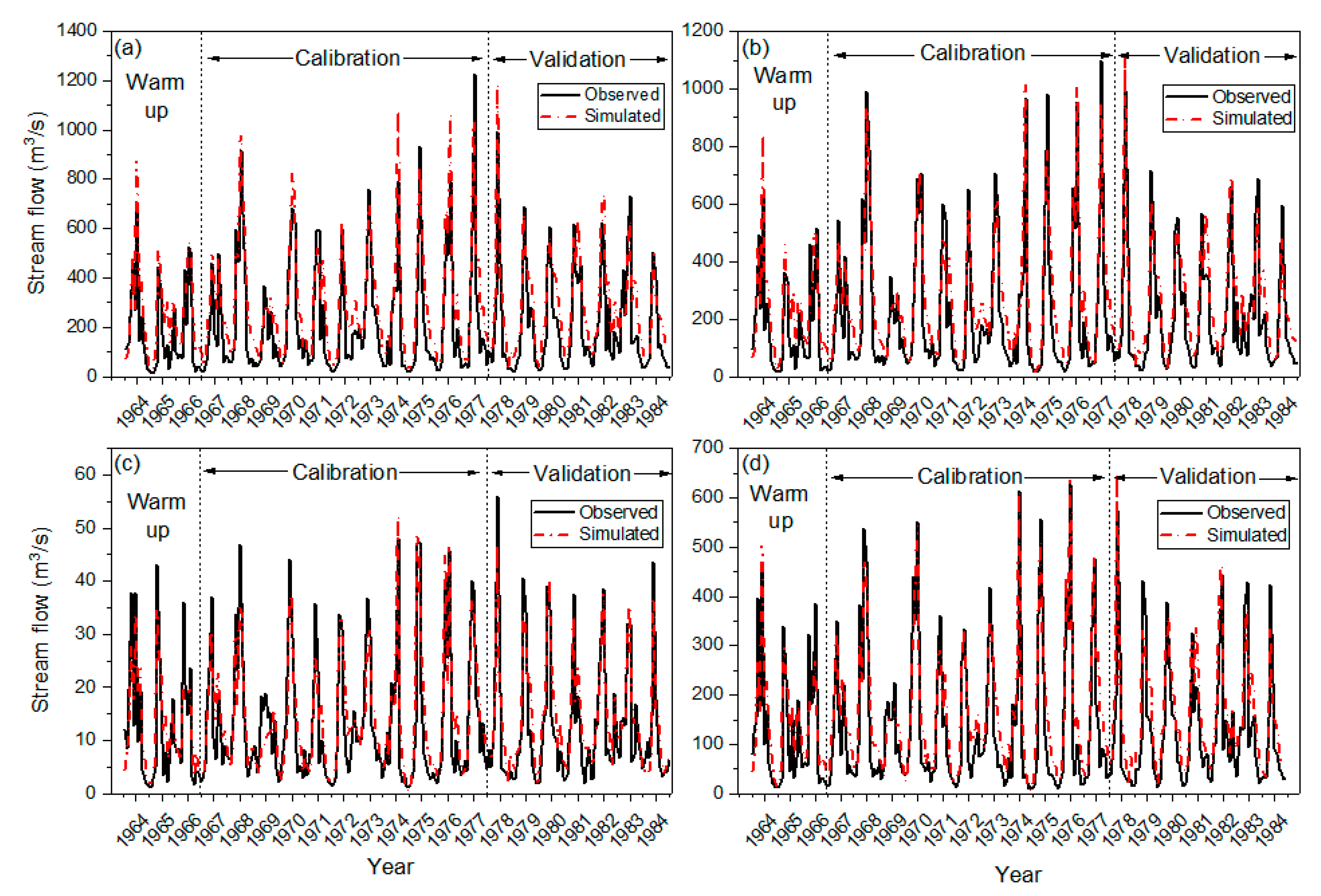
3.2. Calibration and Validation of the SWAT Model
3.3. Projected Climate Change Response to Hydrological Systems
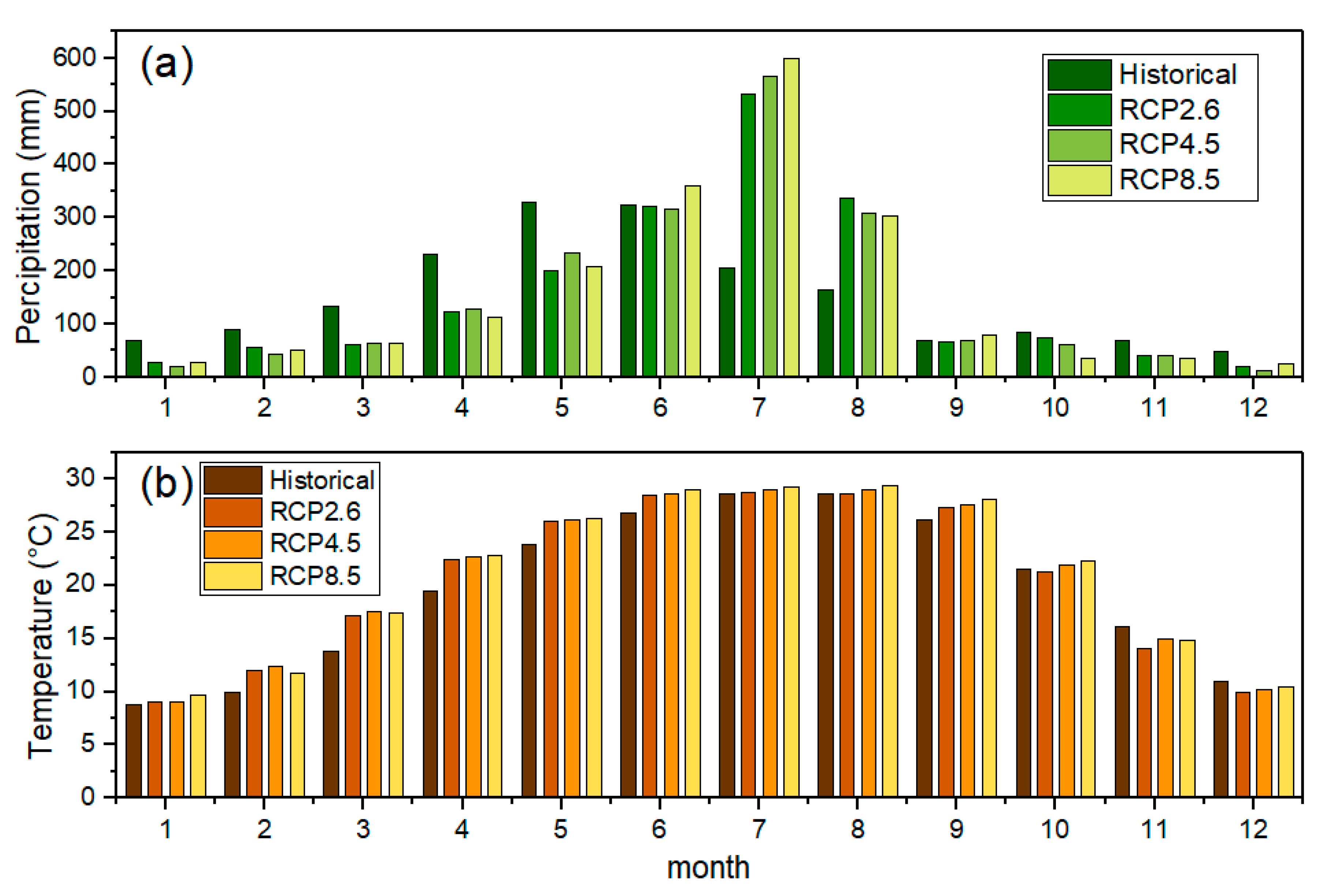
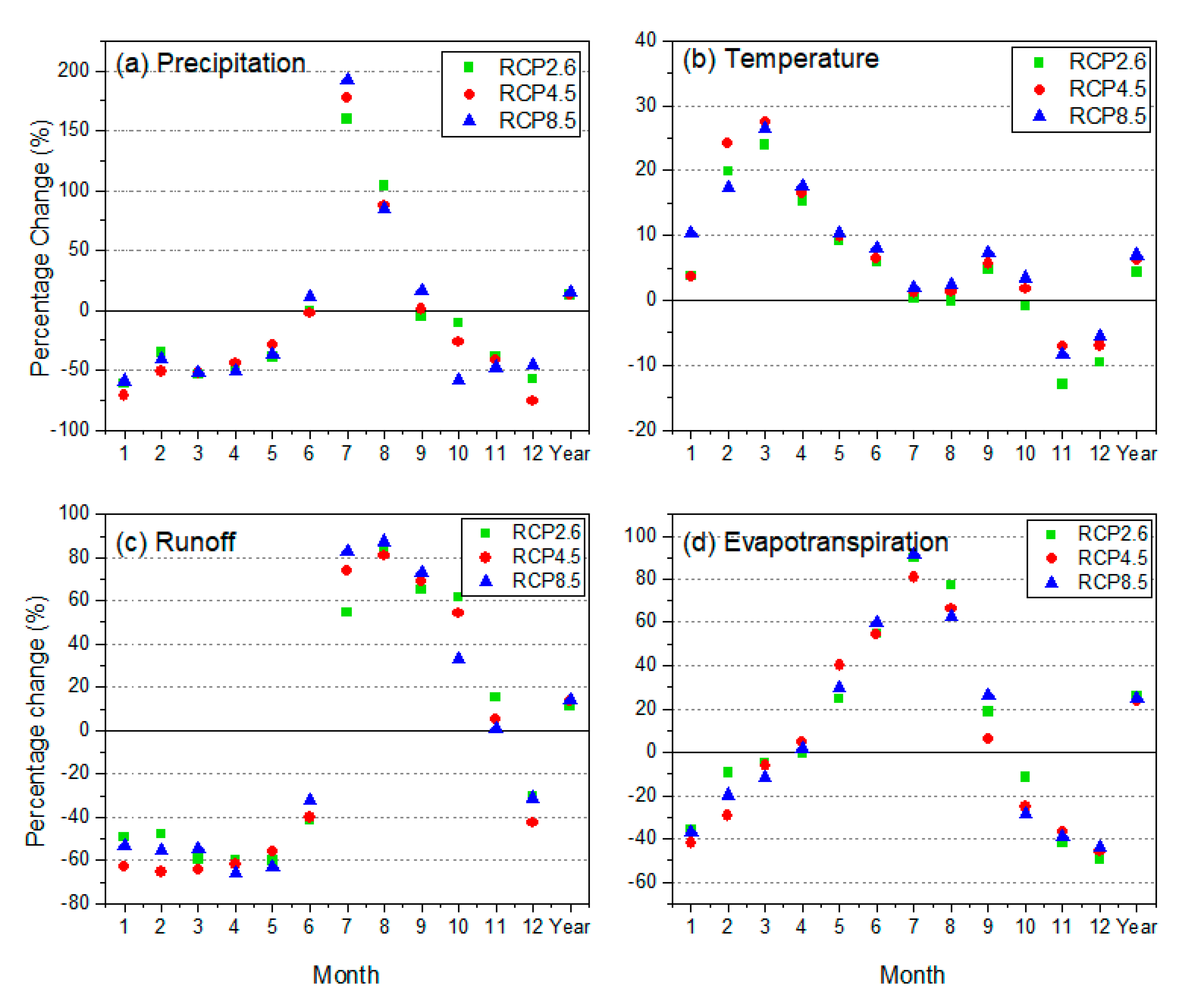
3.3.1. Changes in Projected Precipitation and Temperature
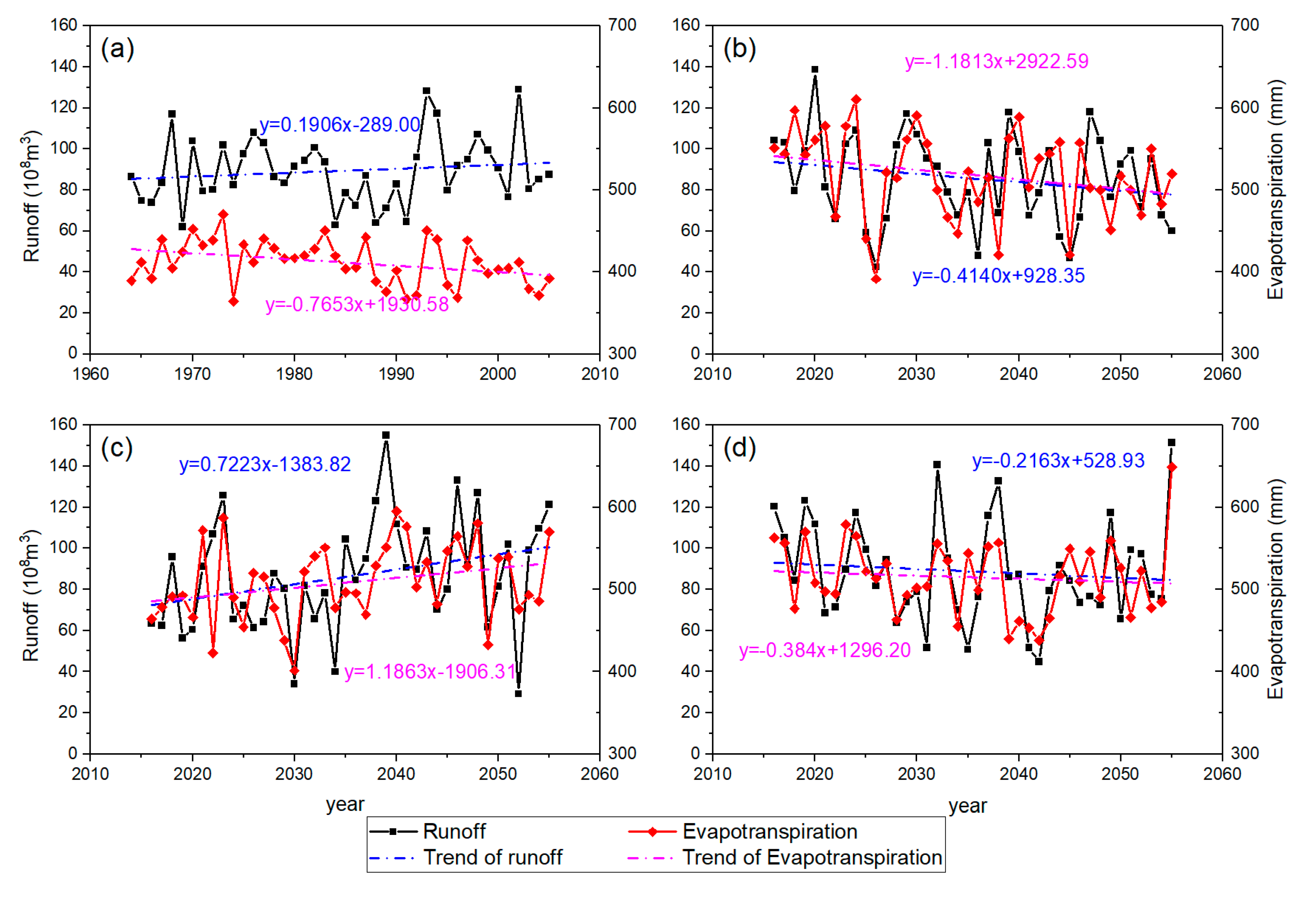
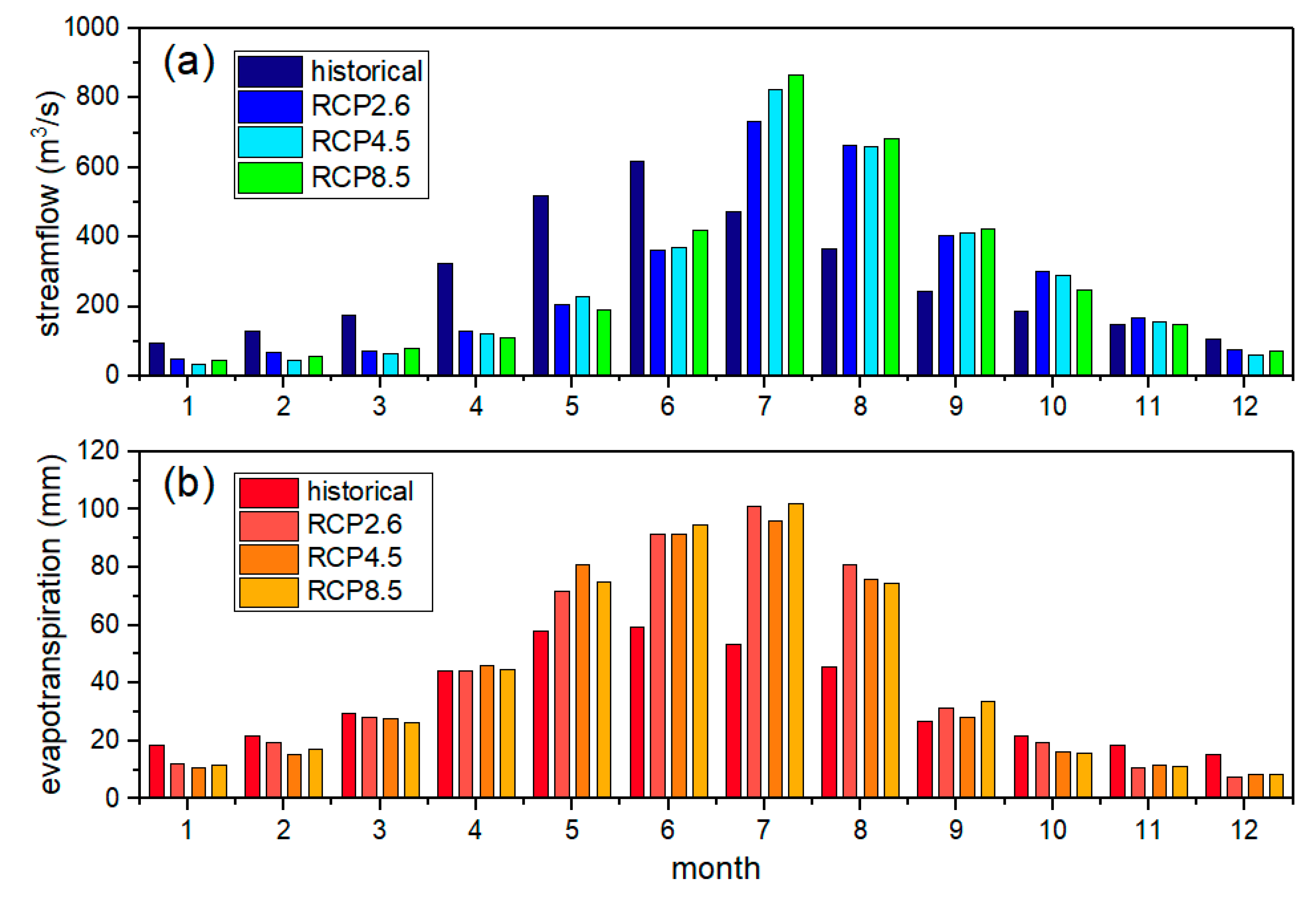
3.3.2. Changes in Future Runoff and Evapotranspiration
4. Discussion
4.1. Comparison of Different Bias Correction Methods
4.2. Variations of Hydrological Variables Caused by the Impacts of Climate Change
4.3. Changing Hydrological Variables Compared with Other Areas
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luo, M.; Liu, T.; Meng, F.; Duan, Y.; Bao, A.; Xing, W.; Feng, X.; de Maeyer, P.; Frankl, A. Identifying climate change impacts on water resources in Xinjiang, China. Sci. Total Environ. 2019, 676, 613–626. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). AR5 Synthesis Report: Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Li, F.; Zhang, Y.; Xu, Z.; Teng, J.; Liu, C.; Liu, W.; Mpelasoka, F. The impact of climate change on runoff in the southeastern Tibetan Plateau. J. Hydrol. 2013, 505, 188–201. [Google Scholar] [CrossRef]
- Ruelland, D.; Ardoin-Bardin, S.; Collet, L.; Roucou, P. Simulating future trends in hydrological regime of a large Sudano-Sahelian catchment under climate change. J. Hydrol. 2012, 424, 207–216. [Google Scholar] [CrossRef]
- Lin, Q.X.; Wu, Z.Y.; Singh, V.P.; Sadeghi, S.H.R.; He, H.; Lu, G. Correlation between hydrological drought, climatic factors, reservoir operation, and vegetation cover in the Xijiang Basin, South China. J. Hydrol. 2017, 549, 512–524. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Saeed, F.; Alkhalaf, A.K.; Dambul, R. Assessing the robustness and uncertainties of projected changes in temperature and precipitation in AR5 Global Climate Models over the Arabian Peninsula. Atmos. Res. 2017, 194, 202–213. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.; Lamarque, J.; Matsumoto, K.; Montzka, S.; Raper, S.; Riahi, K. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 2011, 109, 213–241. [Google Scholar] [CrossRef]
- Xin, X.; Zhang, L.; Zhang, J.; Wu, T.; Fang, Y. Climate change projections over East Asia with BCC-CSM1.1 climate model under RCP scenarios. J. Meteorol. Soc. Jpn. 2013, 91, 413–429. [Google Scholar] [CrossRef]
- Chen, J.; Frauenfeld, O.W. Surface air temperature changes over the twentieth and twenty-first centuries in China simulated by 20 CMIP5 models. J. Clim. 2014, 27, 3920–3937. [Google Scholar] [CrossRef]
- Siew, J.H.; Tangang, F.T.; Juneng, L. Evaluation of CMIP5 coupled atmosphere-ocean general circulation models and projection of the Southeast Asian winter monsoon in the 21th century. Int. J. Climatol. 2014, 34, 2872–2884. [Google Scholar] [CrossRef]
- Fonseca, A.R.; Santos, J.A. Predicting hydrological flows under climate change: The Tamega Basin as an analog for the Mediterranean region. Sci. Total Environ. 2019, 668, 1013–1024. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Ahmad, I.; Ijaz, M.W.; Farid, H.U.; Yagoub, Y.E.; Zaman, M.; Adnan, M. Performance evaluation of latest integrated multi-satellite retrievals for Global Precipitation Measurement (IMERG) over the northern highlands of Pakistan. Atmos. Res. 2018, 205, 134–146. [Google Scholar] [CrossRef]
- Chu, J.T.; Xia, J.; Xu, C.Y.; Singh, V.P. Statistical downscaling of daily mean temperature, pan evaporation and precipitation for climate change scenarios in Haihe River of China. Theor. Appl. Climatol. 2010, 99, 149–161. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Guerreiro, S.B.; Nicholson, A.; Liang, Q.; Quinn, P.; Zhang, L.; He, B.; Yin, J.; Fowle, H.J. Climate change impacts on Yangtze River discharge at the Three Gorges Dam. Hydrol. Earth Syst. Sci. 2017, 21, 1911–1927. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Luo, M.; Liu, T.; Meng, F.; Duan, Y.; Frankl, A.; Bao, A.; De Maeyer, P. Comparing bias correction methods used in downscaling precipitation and temperature from regional climate models: A case study from the Kaidu river basin in Western China. Water 2018, 10, 1046. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Hashino, M.; Yao, H.; Yoshida, H. Studies and evaluations on interception processes during rainfall based on a tank model. J. Hydrol. 2002, 255, 1–11. [Google Scholar] [CrossRef]
- Steele-Dunne, S.; Lynch, P.; McGrath, R.; Semmler, T.; Wang, S.; Hanafin, J.; Nolan, P. The impacts of climate change on hydrology in Ireland. J. Hydrol. 2008, 356, 28–45. [Google Scholar] [CrossRef]
- Gao, C.; Liu, L.; Ma, D.; He, K.; Xu, Y.P. Assessing responses of hydrological processes to climate change over the southeastern Tibetan Plateau based on resampling of future climate scenarios. Sci. Total Environ. 2019, 664, 737–752. [Google Scholar] [CrossRef]
- Gao, J.; Holden, J.; Kirkby, M. Modelling impacts of agricultural practice on flood peaks in upland catchments: An application of the distributed TOPMODEL. Hydrol. Process. 2017, 31, 4206–4216. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Siriwardena, L. Estimation of SIMHYD Parameter Values for Application in Ungauged Catchments 1; University of Melbourne: Melbourne, Australia, 2005. [Google Scholar]
- Harlan, D.; Wangsadipura, M.; Munajat, C.M. Rainfall-runoff modeling of Citarum Hulu River basin by using GR4J. Proc. World Congr. Eng. 2010, 2, 1–5. [Google Scholar]
- Martina, M.L.V.; Todini, E.; Liu, Z. Preserving the dominant physical processes in a lumped hydrological model. J. Hydrol. 2011, 399, 121–131. [Google Scholar] [CrossRef]
- Wi, S.; Ray, P.; Demaria, E.M.C.; Steinschneider, S.; Brown, C. A user-friendly software package for VIC hydrologic model development. Environ. Model. Softw. 2017, 98, 35–53. [Google Scholar] [CrossRef]
- Wang, Z.G.; Liu, C.M.; Wu, X.F. A review of the studies on distributed hydrological model based on DEM. J. Nat. Resour. 2003, 18, 168–173. [Google Scholar]
- Zhang, Y.; You, Q.; Che, C.; Ge, J. Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China. Atmos. Res. 2016, 178–179, 521–534. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Edwards, D.R.; Yu, Y.; Hamidisepehr, A. An Assessment of Climate Change Impacts on Future Water Availability and Droughts in the Kentucky River Basin. Environ. Process. 2017, 4, 477–507. [Google Scholar] [CrossRef]
- Xu, Y.-P.; Zhang, X.; Ran, Q.; Tian, Y. Impact of climate change on hydrology of upper reaches of Qiantang River basin, East China. J. Hydrol. 2013, 483, 51–60. [Google Scholar] [CrossRef]
- Christensen, J.H.; Boberg, F.; Christensen, O.B.; Lucas-Picher, P. On the need for bias correction of regional climate change projections of temperature and precipitation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. J. R. Meteorol. Soc. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.H.; Wang, D.; Zhang, X. Multi-period calibration of a semi-distributed hydrological model based on hydroclimatic clustering. Adv. Water Resour. 2011, 34, 1292–1303. [Google Scholar] [CrossRef]
- Soil Conservation Service (SCS). National Engineering Handbook, Hydrology, Section 4; Soil Conservation Service; US Department of Agriculture: Washington, DC, USA, 1956. [Google Scholar]
- Rallison, R.E.; Miller, N. Past, present, and future SCS runoff procedure. In Rainfall-Runoff Relationship/Proceedings, Proceedings of the International Symposium on Rainfall-Runoff Modeling, Starkville, MS, USA, 18–21 May 1981; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1982. [Google Scholar]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute, Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Naz, B.S.; Kao, S.C.; Ashfaq, M.; Rastogi, D.; Mei, R.; Bowling, L.C. Regional hydrologic response to climate change in the conterminous United States using high-resolution hydroclimate simulations. Glob. Planet. Chang. 2016, 143, 100–117. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J.; Chen, Y.; Zhang, S.; Deng, H.; Liu, H.; De Maeyer, P. Climate change impact on the hydrology of a typical watershed in the Tianshan Mountains. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]
- Stagge, J.H.; Moglen, G.E. A nonparametric stochastic method for generating daily climate-adjusted streamflows. Water Resour. Res. 2013, 49, 6179–6193. [Google Scholar] [CrossRef]
- Gao, G.; Chen, D.; Xu, C.Y.; Simelton, E. Trend of estimated actual evapotranspiration over China during 1960–2002. J. Geophys. Res. 2007. [Google Scholar] [CrossRef]

| Correction Methods | Mathematical Equations | Coverage | References | |
|---|---|---|---|---|
| Linear Scaling (LS) | Precipitation and Temperature | [17] | ||
| Local Intensity Scaling (LOCI) | Precipitation | [17,31] | ||
| Empirical Cumulative Distribution Function (ECDF) | Precipitation and temperature | [15,32] | ||
| Variance Scaling (VARI) | Temperature | [33,34] | ||
| Symbols | ||||
| P | Precipitation | |||
| μ() | Mean value | |||
| T | Temperature | |||
| s | Scaling factor | |||
| μ(A|B) | The mean value of A that satisfies the condition of B | |||
| F(x), f(t|α,β) | Cumulative distribution function and probability density function of Gamma distribution with two parameters α and β. Precipitation variable obey this distribution | |||
| G(x), g(t|μ,σ2) | Cumulative distribution function and probability density function of normal distribution with two parameters μ andσ2. Temperature variable obey this distribution | |||
| ecdf | Empirical cumulative distribution function | |||
| σ() | Standard deviation | |||
| Subscripts | ||||
| cor | Corrected variables | |||
| obs | Observed variables | |||
| GCM | Original GCM variables | |||
| m | Monthly interval | |||
| thres | Threshold | |||
| Predictions | Correcting Methods | CC | RMSE | ||||
|---|---|---|---|---|---|---|---|
| BNU-ESM | IPSL-CM5A-MR | MIROC5 | BNU-ESM | IPSL-CM5A-MR | MIROC5 | ||
| Precipitation | LS | 115.34 | 174.44 | 154.82 | −6.70 | −17.23 | 12.94 |
| ECDF | 17.93 | 53.92 | 62.64 | 1.36 | 2.21 | 19.10 | |
| LOCI | 120.99 | 224.29 | 163.86 | −9.47 | −12.51 | 10.80 | |
| LS&ECDF | 154.53 | 351.29 | 87.03 | −3.66 | −8.17 | 21.19 | |
| LS&LOCI | 119.55 | 223.67 | 155.84 | −10.66 | −12.59 | 19.67 | |
| Maximum temperature | LS | 10.31 | 22.55 | 38.93 | 12.32 | 14.09 | 16.69 |
| ECDF | 2.90 | 4.65 | 5.20 | 11.36 | 6.39 | 4.08 | |
| VARI | 24.10 | 18.65 | 34.04 | 23.59 | 10.42 | 12.92 | |
| LS&ECDF | 12.09 | 24.20 | 40.46 | 16.61 | 14.65 | 17.01 | |
| VARI&ECDF | 24.88 | 20.03 | 35.54 | 24.13 | 15.51 | 18.91 | |
| Minimum temperature | LS | 1.41 | 1.19 | 8.61 | 24.04 | 16.81 | 11.58 |
| ECDF | 1.19 | 1.20 | 2.79 | 26.00 | 18.72 | 3.96 | |
| VARI | 8.50 | 8.56 | 8.81 | 35.94 | 26.77 | 11.77 | |
| LS&ECDF | 2.26 | 2.30 | 9.43 | 27.53 | 19.81 | 12.77 | |
| VARI&ECDF | 8.96 | 8.92 | 8.99 | 36.02 | 26.86 | 11.91 | |
| Correcting Methods | Precipitation | Maximum Temperature | Minimum Temperature | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BNU-ESM | IPSL-CM5A-MR | MIROC5 | BNU-ESM | IPSL-CM5A-MR | MIROC5 | BNU-ESM | IPSL-CM5A-MR | MIROC5 | |
| GCM | −0.64 | −0.69 | −0.67 | 0.31 | 0.50 | 0.45 | 0.38 | 0.53 | 0.68 |
| LS | −0.30 | −0.63 | −0.27 | 0.47 | 0.63 | 0.62 | 0.72 | 0.75 | 0.81 |
| ECDF | −0.15 | −0.14 | −0.10 | 0.45 | 0.43 | 0.41 | 0.69 | 0.69 | 0.70 |
| LOCI | −0.36 | −0.25 | −0.33 | / | / | / | / | / | / |
| VARI | / | / | / | 0.59 | 0.60 | 0.59 | 0.80 | 0.80 | 0.81 |
| LS&ECDF | −0.12 | −0.09 | −0.32 | 0.52 | 0.65 | 0.63 | 0.67 | 0.69 | 0.76 |
| LS&LOCI | −0.27 | −0.15 | −0.37 | / | / | / | / | / | / |
| VARI&ECDF | / | / | / | 0.60 | 0.61 | 0.59 | 0.75 | 0.75 | 0.75 |
| Hydrological Station | Calibration Period | Validation Period | ||||
|---|---|---|---|---|---|---|
| R2 | MSE | NSE | R2 | MSE | NSE | |
| Pingle | 0.87 | 0.23 | 0.77 | 0.82 | 0.25 | 0.71 |
| Yangshuo | 0.89 | 0.16 | 0.85 | 0.86 | 0.16 | 0.81 |
| Lingqu | 0.87 | 0.15 | 0.76 | 0.85 | 0.26 | 0.77 |
| Guilin | 0.87 | 0.16 | 0.82 | 0.86 | 0.20 | 0.82 |
| Hydrological Variables | Scenarios | |||
|---|---|---|---|---|
| Historical | RCP2.6 | RCP4.5 | RCP8.5 | |
| Precipitation(mm) | 1814.41 | 1860.18 | 1864.76 | 1904.89 |
| Temperature(°C) | 19.56 | 20.41 | 20.76 | 20.92 |
| Hydrological Variables | Scenarios | |||
|---|---|---|---|---|
| Historical | RCP2.6 | RCP4.5 | RCP8.5 | |
| Runoff (108 m3) | 85.26 | 90.61 | 92.48 | 94.64 |
| Evapotranspiration (mm) | 411.83 | 508.45 | 514.57 | 518.15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Guzman, S.M.; Dong, Z.; Tan, L. Selection of Effective GCM Bias Correction Methods and Evaluation of Hydrological Response under Future Climate Scenarios. Climate 2020, 8, 108. https://doi.org/10.3390/cli8100108
Tan Y, Guzman SM, Dong Z, Tan L. Selection of Effective GCM Bias Correction Methods and Evaluation of Hydrological Response under Future Climate Scenarios. Climate. 2020; 8(10):108. https://doi.org/10.3390/cli8100108
Chicago/Turabian StyleTan, Yaogeng, Sandra M. Guzman, Zengchuan Dong, and Liang Tan. 2020. "Selection of Effective GCM Bias Correction Methods and Evaluation of Hydrological Response under Future Climate Scenarios" Climate 8, no. 10: 108. https://doi.org/10.3390/cli8100108
APA StyleTan, Y., Guzman, S. M., Dong, Z., & Tan, L. (2020). Selection of Effective GCM Bias Correction Methods and Evaluation of Hydrological Response under Future Climate Scenarios. Climate, 8(10), 108. https://doi.org/10.3390/cli8100108







