What Do Global Climate Models Tell Us about Future Arctic Sea Ice Coverage Changes?
Abstract
1. Introduction
2. Datasets
2.1. Climate Model Sea Ice Data
2.2. Observed Sea Ice Data
2.3. The Study Area and Analysis Methods
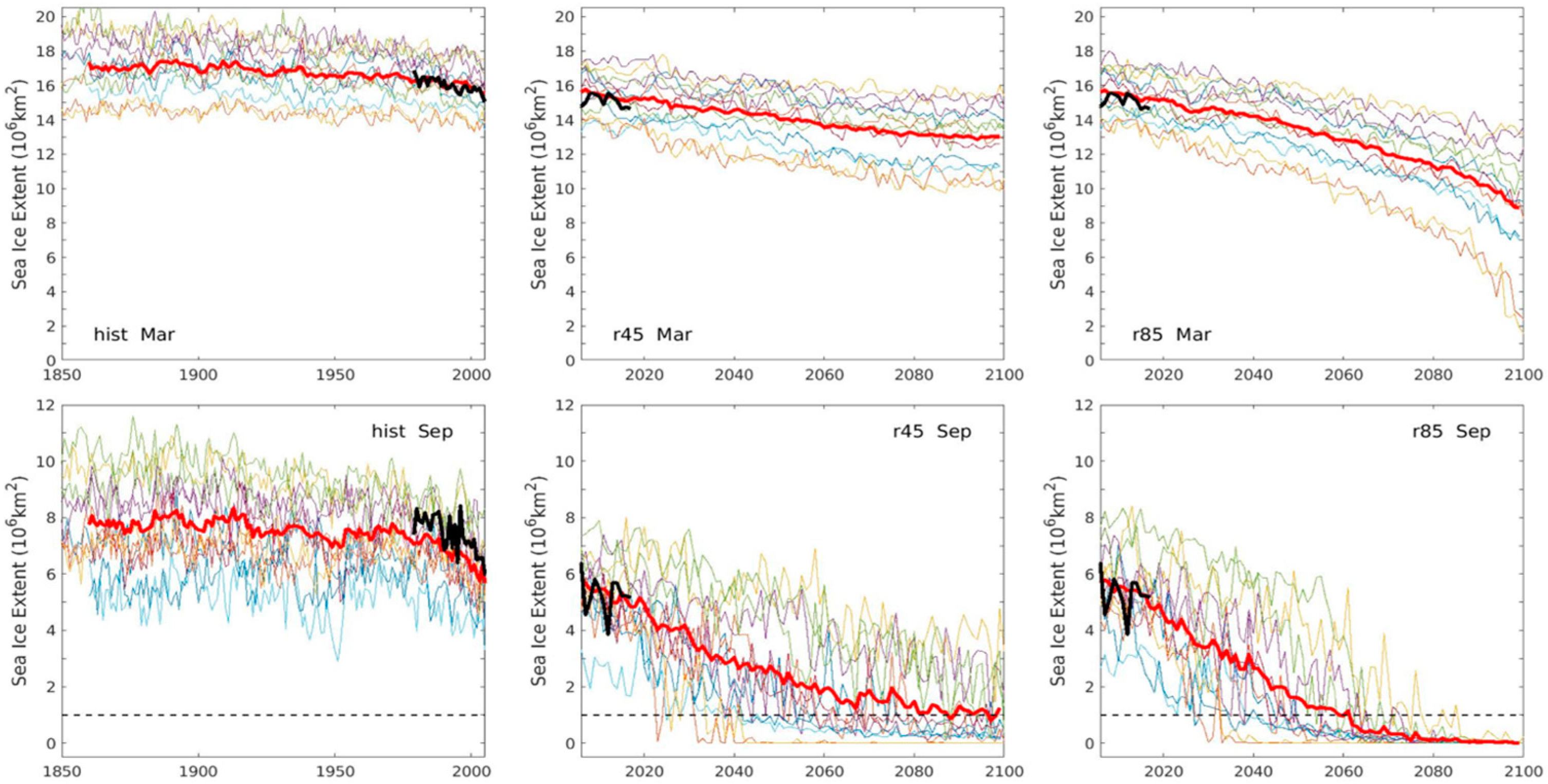
3. Results
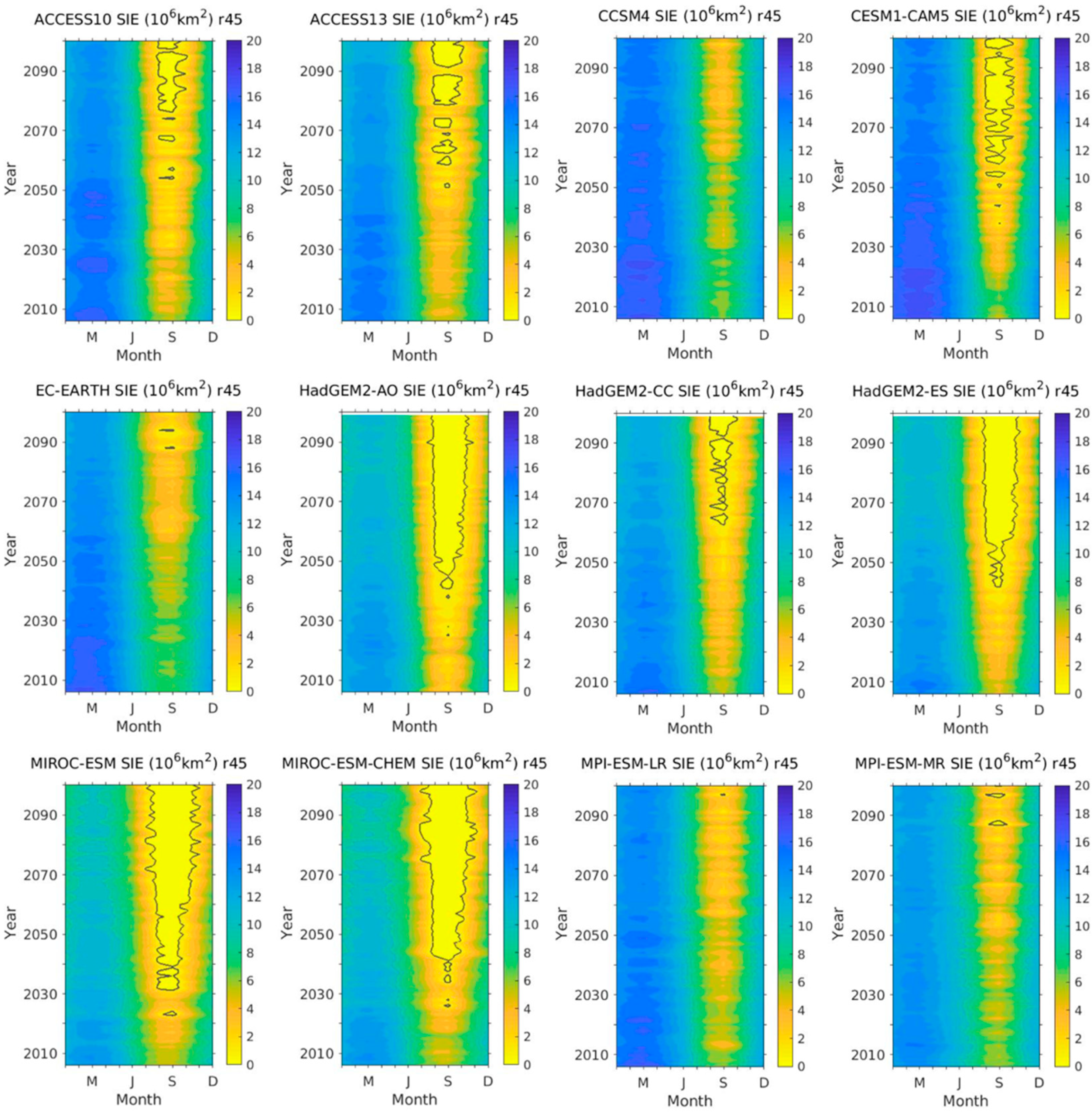
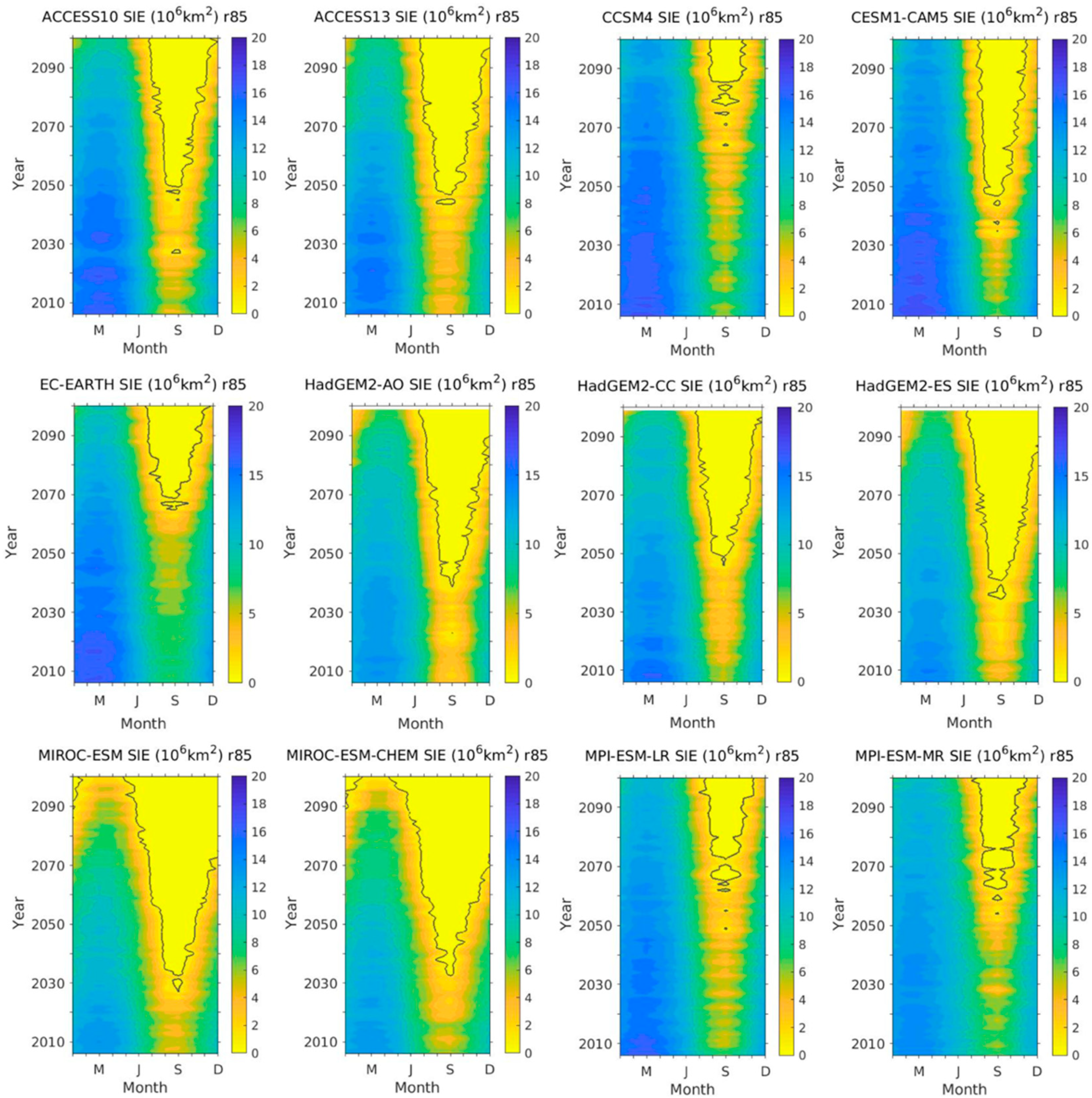
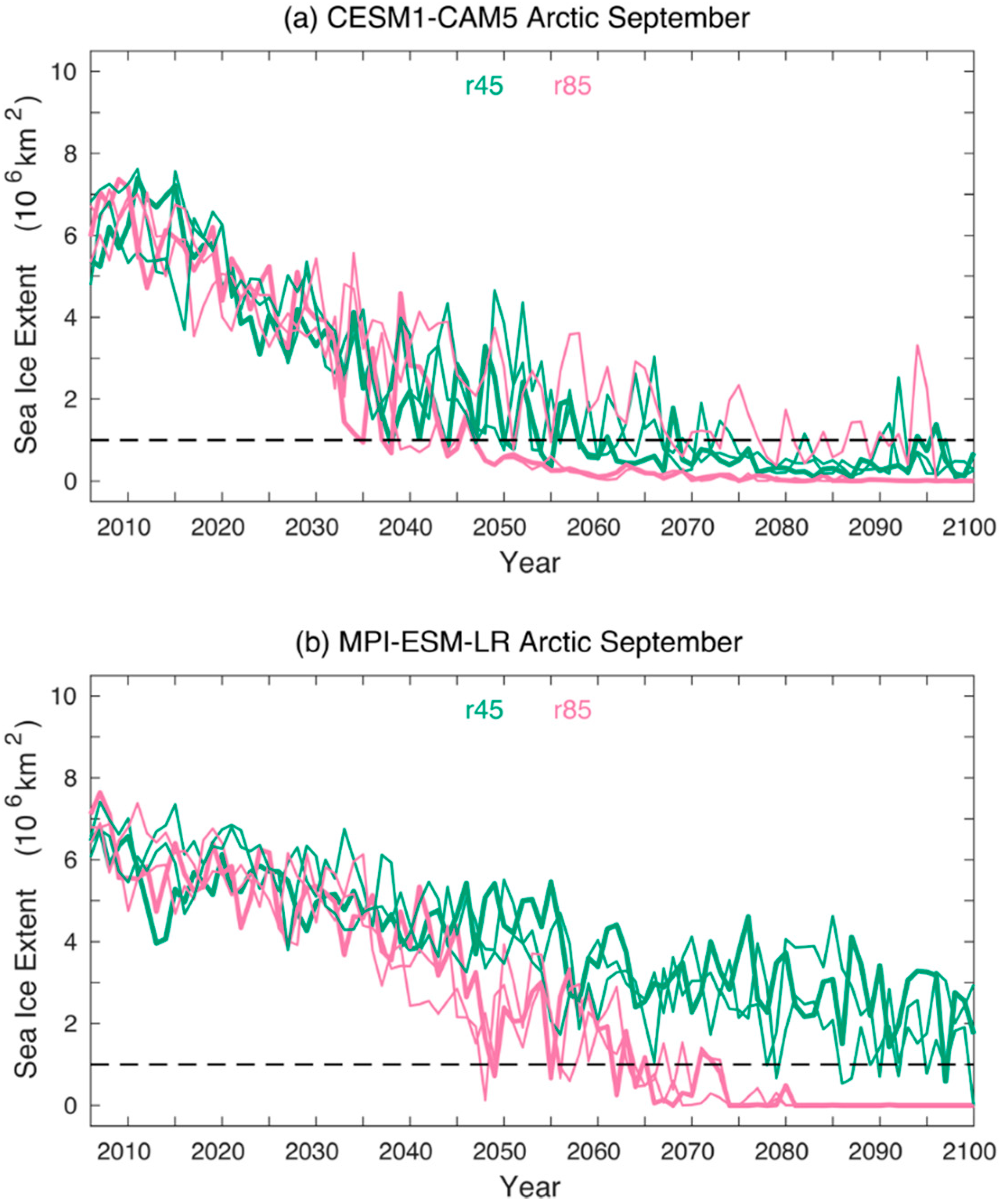
3.1. Temporal Characteristics of Model Historical Simulations and Projections
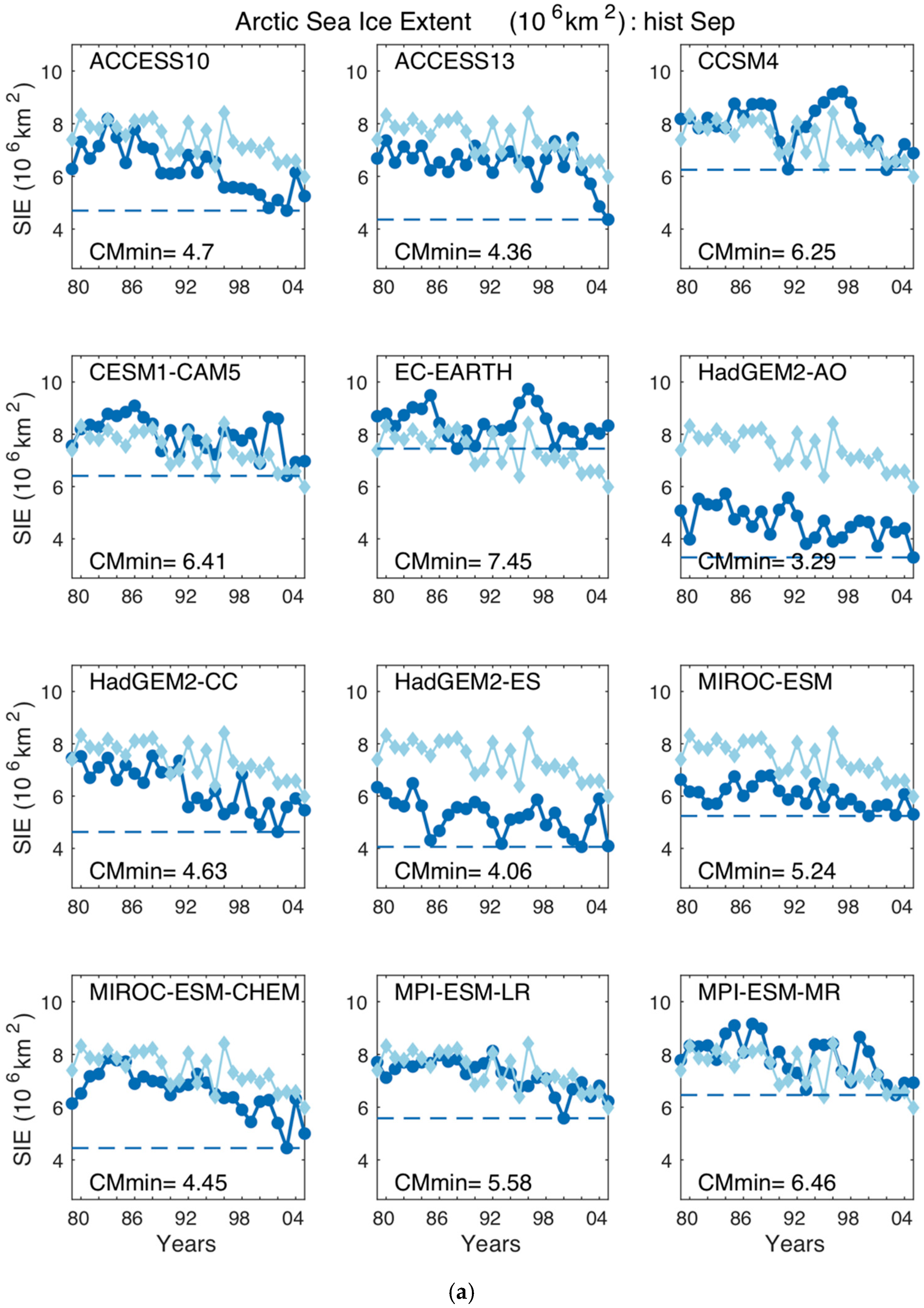
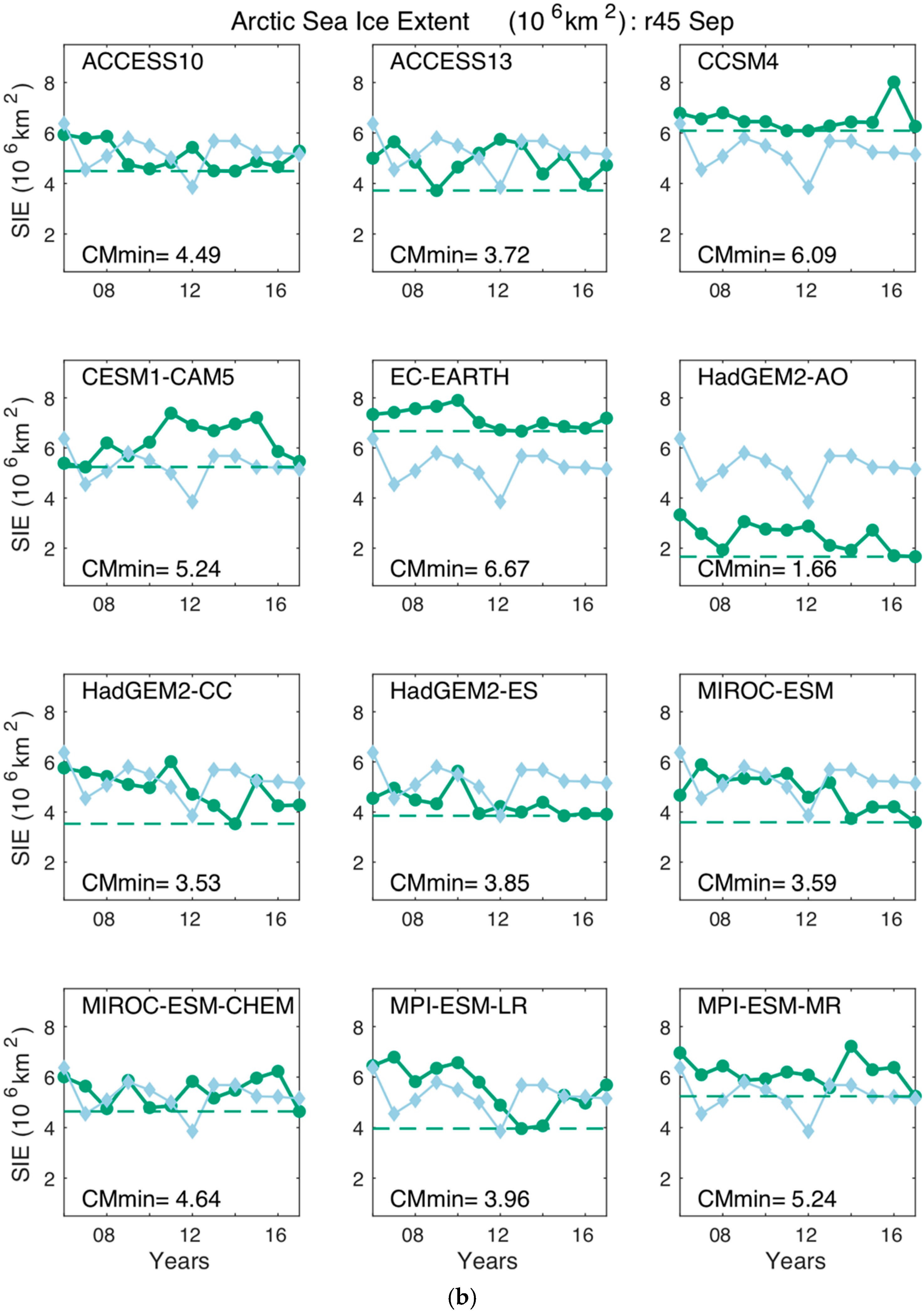
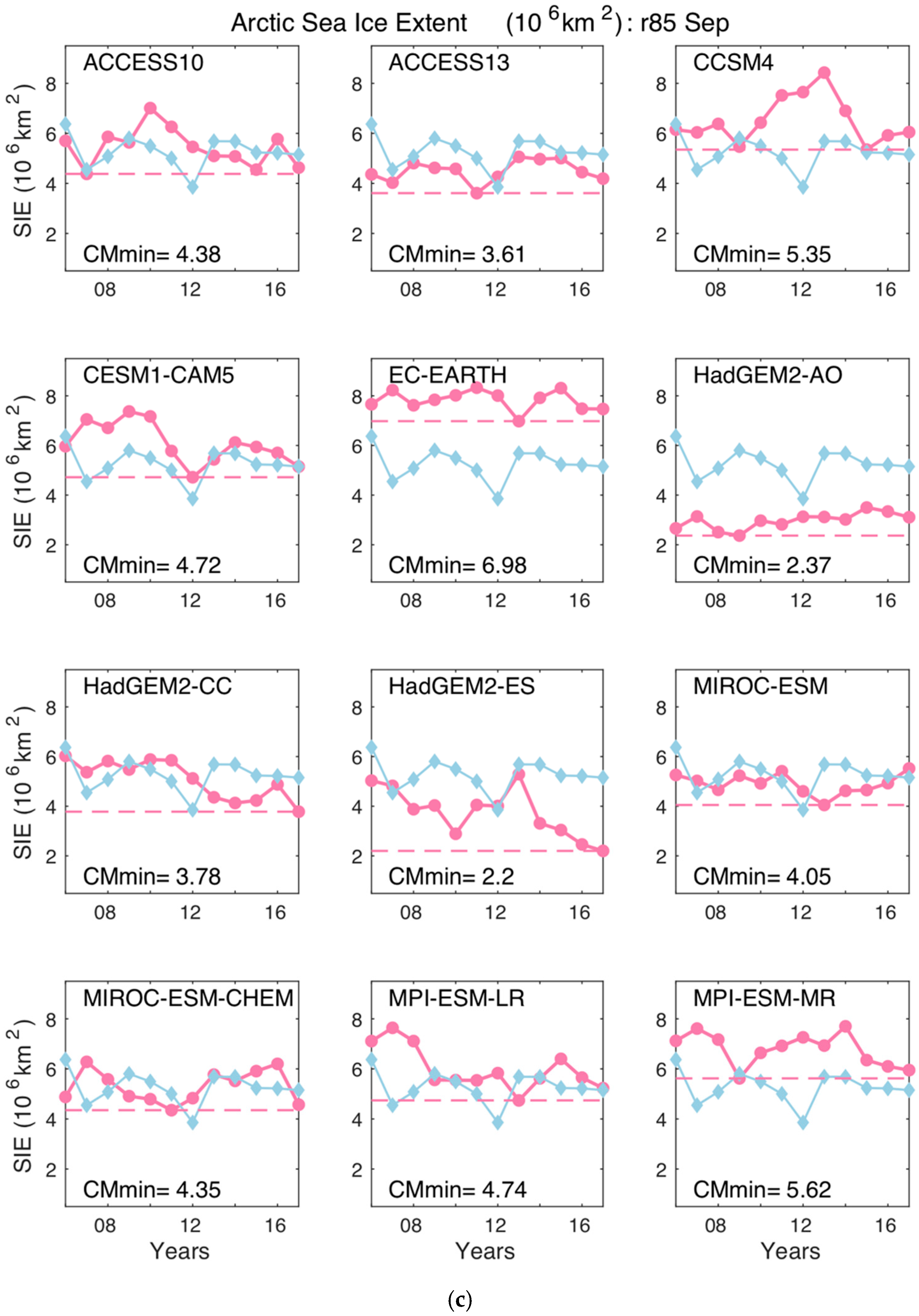
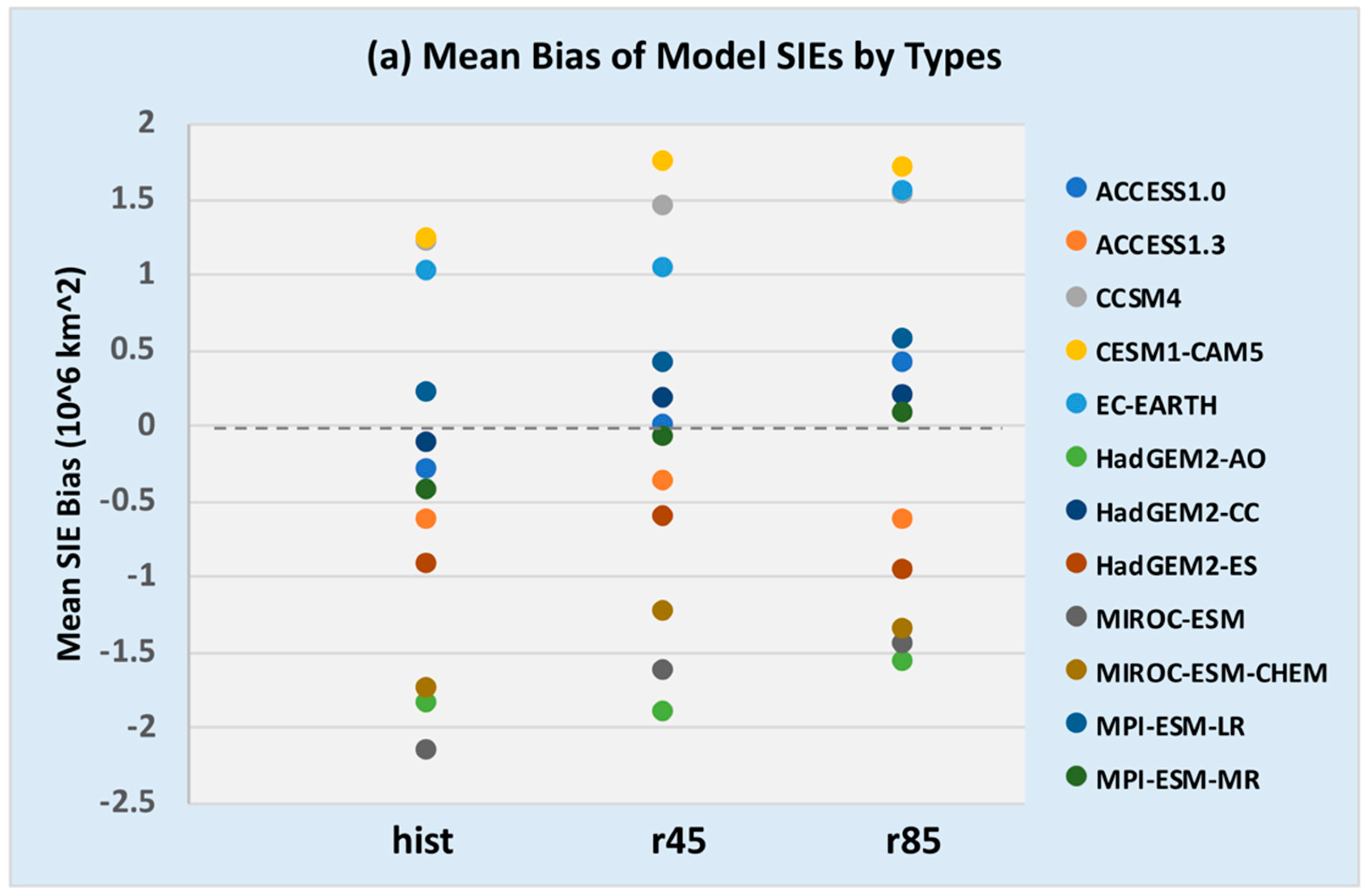
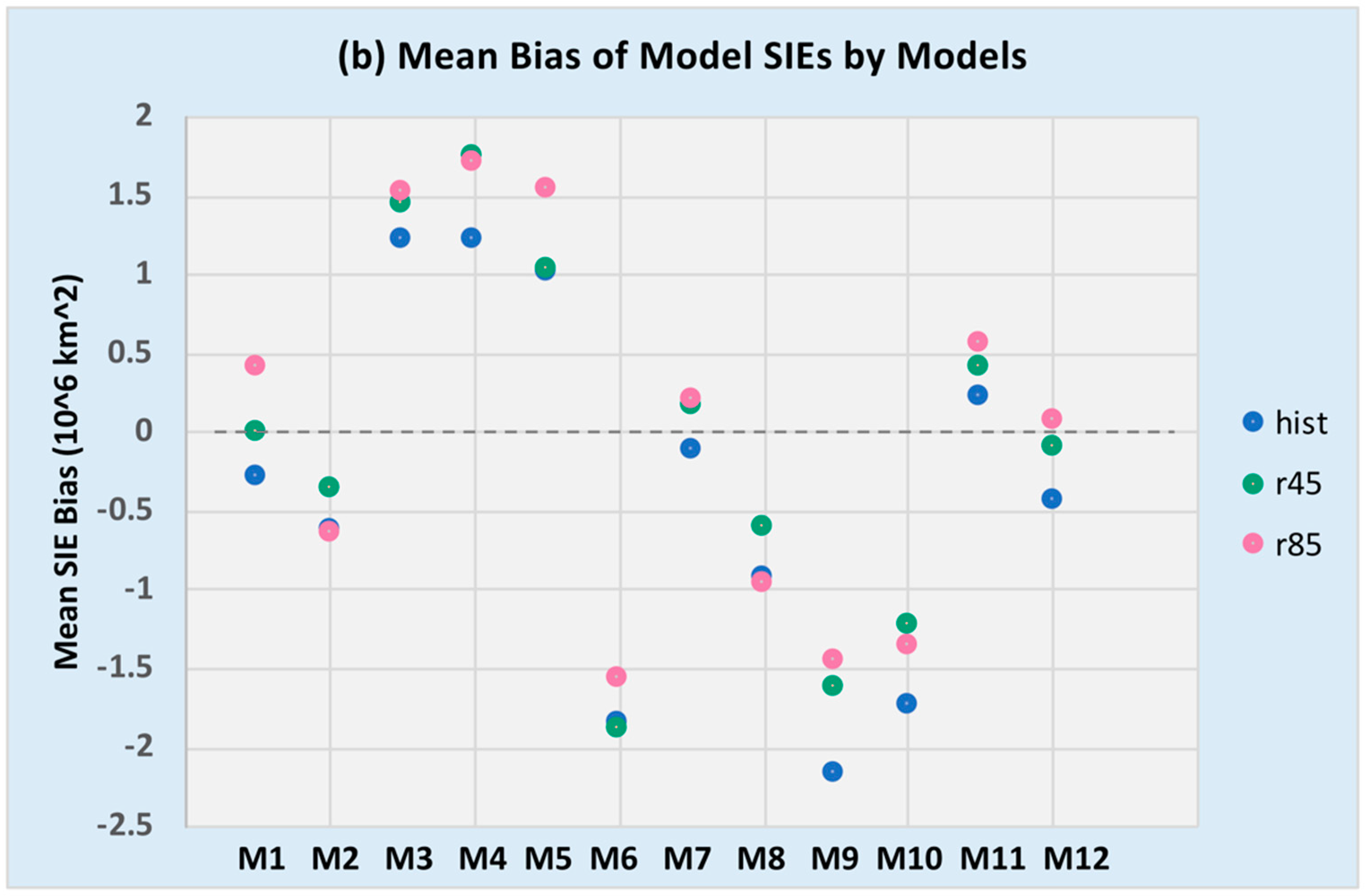
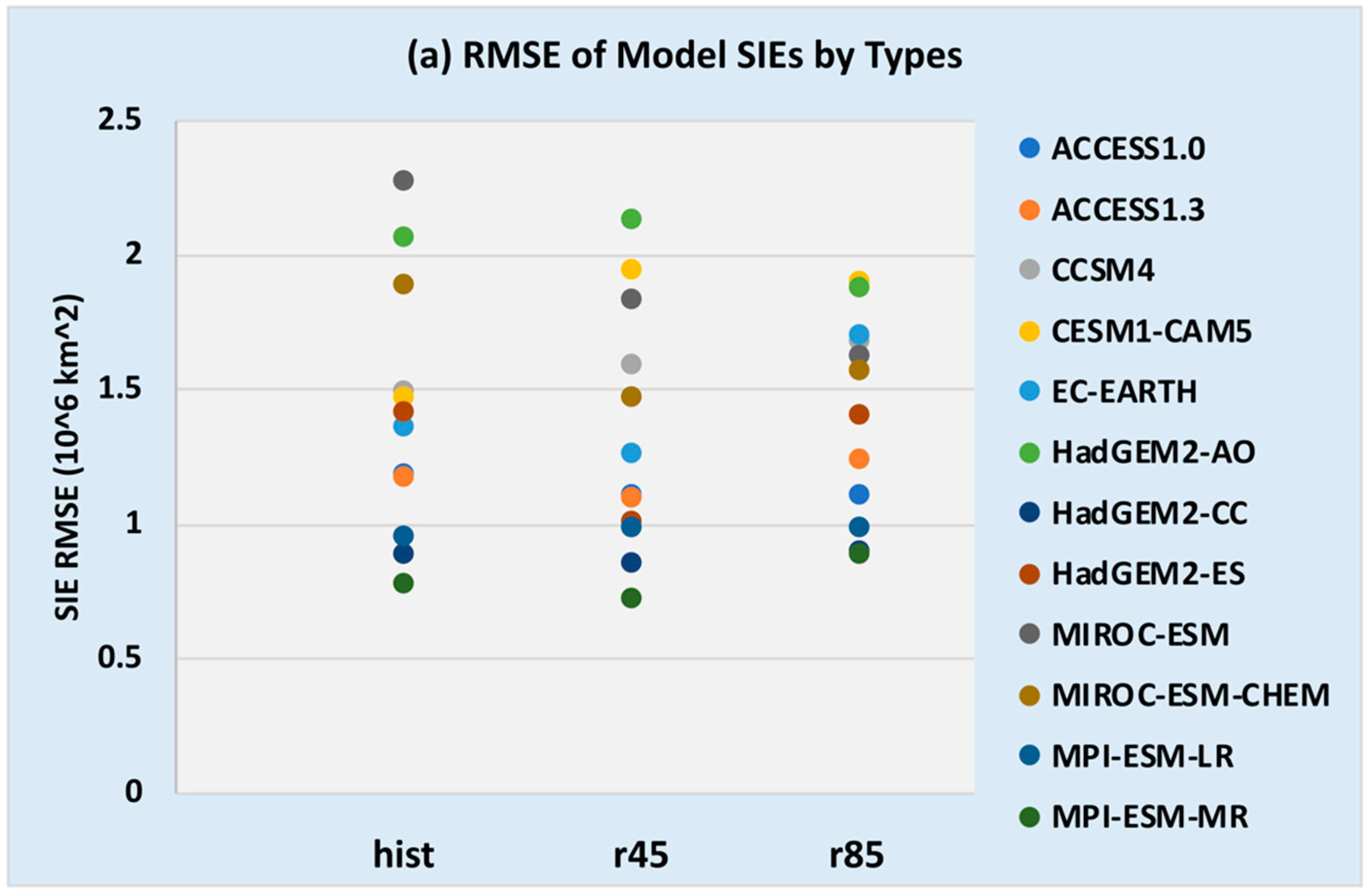
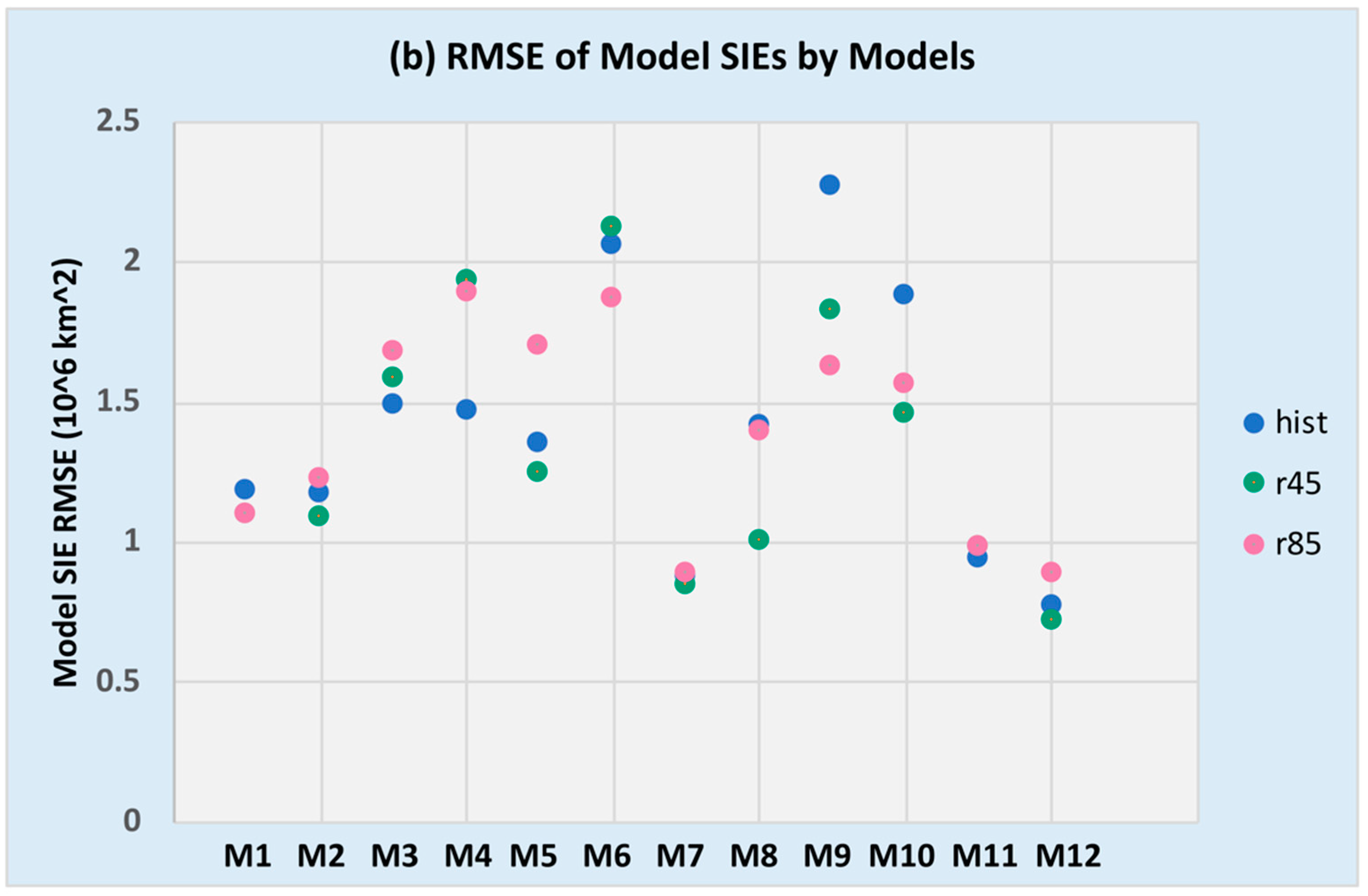
3.2. Statistical Characteristics
3.3. Evaluation of Climate Model Simulations and Projections
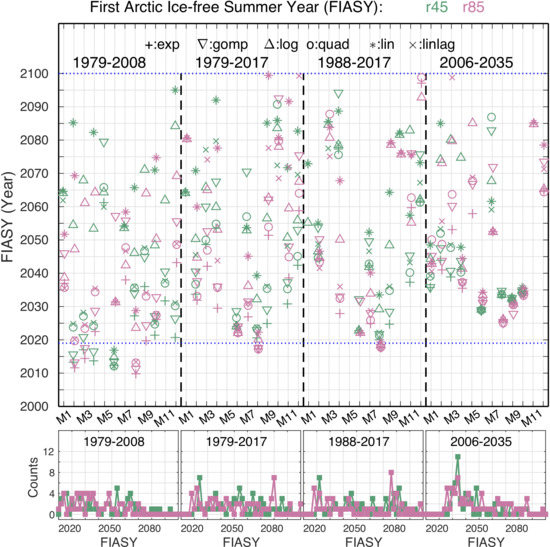
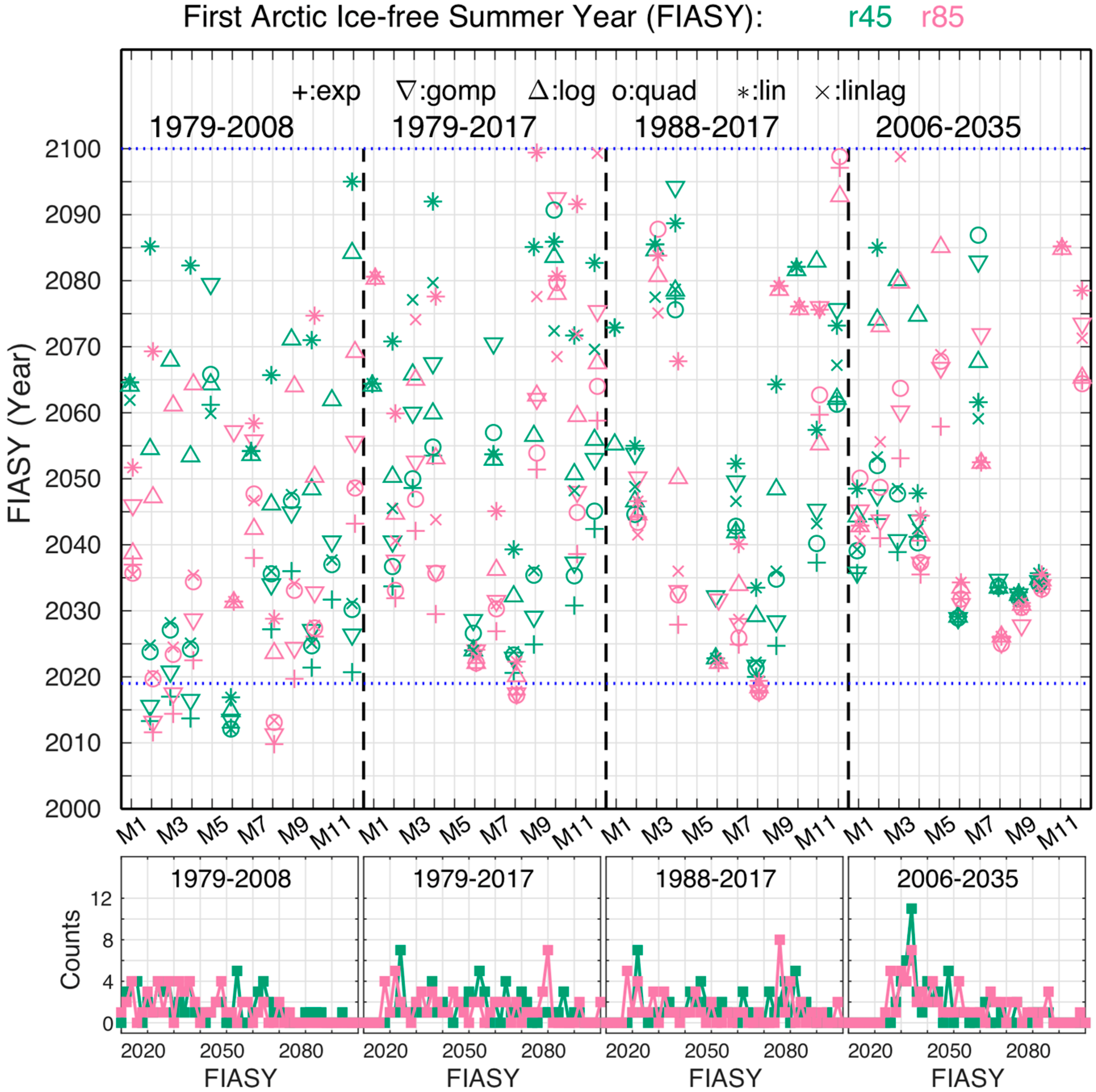
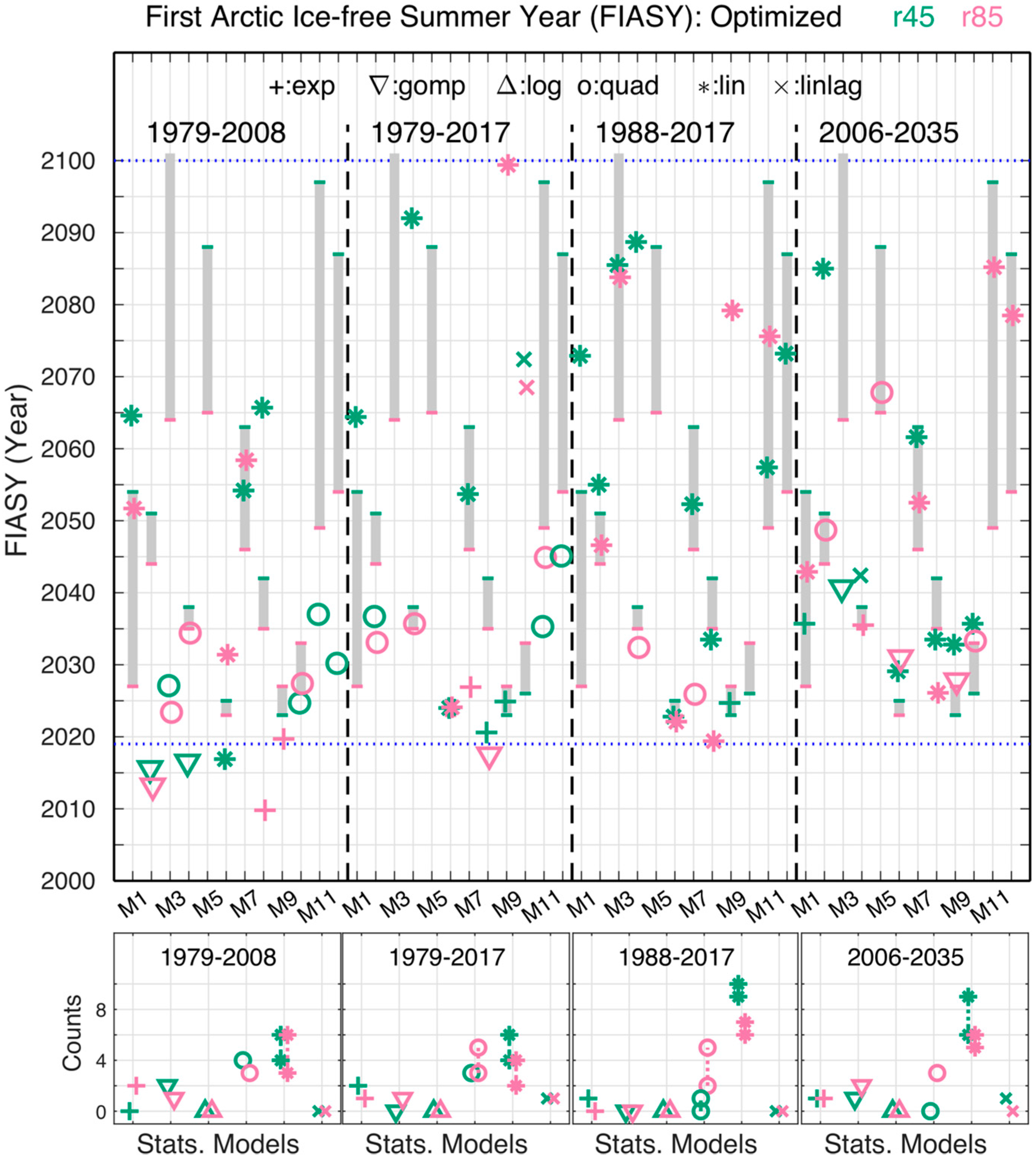
3.4. First Ice-Free Arctic Summer Year (FIASY)
3.5. Sensitivity of Different Statistical Curve-Fitting Functions
4. Discussion
5. Summary
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, M.; Overland, J.E. A sea ice free summer Arctic within 30 years? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Wang, M.; Overland, J.E. A sea ice free summer Arctic within 30 years: An update from CMIP5 models. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Kattsov, V.; Barrett, A.; Serreze, M.; Pavlova, T.; Holland, M.; Meier, W.N. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Peng, G.; Matthews, J.L.; Yu, J.T. Sensitivity analysis of Arctic sea ice extent trends and statistical projections using satellite data. Remote Sens. 2018, 10, 230. [Google Scholar] [CrossRef]
- ACIA. Impacts of a Warming Arctic—Arctic Climate Impact Assessment; ACIA Overview Report; Cambridge University Press: Cambridge, UK, 2004; p. 140. [Google Scholar]
- AMAP. Snow, Water, Ice and Permafrost in the Arctic (SWIPA) 2017; AMAP: Oslo, Norway, 2017; p. 288. [Google Scholar]
- IPCC. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Wang, L.; Derksen, C.; Brown, R.; Markus, T. Recent changes in pan-Arctic melt onset from satellite passive microwave measurements. Geophys. Res. Lett. 2013, 40, 522–528. [Google Scholar] [CrossRef]
- NSIDC. Arctic Sea Ice at Minimum Extent for 2019. Available online: https://nsidc.org/news/newsroom/arctic-sea-ice-minimum-extent-2019 (accessed on 10 April 2019).
- Wang, M.; Overland, J.E. Projected future duration of the sea-ice-free season in the Alaskan Arctic. Prog. Oceanogr. 2015, 136. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Sci. 2012, 485–497. [Google Scholar] [CrossRef]
- Hunke, E.C.; Lipscomb, W.H. CICE: The Los Alamos Sea Ice Model Documentation and Software User’s Manual, Version 4.1; Tech. Rep. LA-CC-06-012; Los Alamos National Laboratory: Los Alamos, NM, USA, 2010; p. 76.
- Bi, D.; Dix, M.; Marsland, S.J.; O’Farrell, S.; Rashid, H.A.; Uotila, P.; Hirst, A.C.; Golebiewski, E.K.M.; Sullivan, A.; Yan, H.; et al. The ACCESS coupled model: Description, control climate and evaluation. Aust. Meteorol. Ocean. J. 2013, 63, 41–64. [Google Scholar] [CrossRef]
- Collier, M.; Uhe, P. CMIP5 Datasets from the ACCESS1.0 and ACCESS1.3 Coupled Climate Models; CAWCR Technical Report No. 059; The Centre for Australian Weather and Climate Research: Melbourne, VIC, Australia, December 2012; p. 32. [Google Scholar]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Neale, R.B.; Chen, C.-C.; Gettelman, A.; Lauritzen, P.H.; Park, S.; Williamson, D.L.; Conley, A.; Garcia, R.; Kinnison, D.; Lamarque, J.-F.; et al. Description of the NCAR Community Atmosphere Model (CAM5.0); NCAR Tech. Rep. NCAR/TN-4861STR; The National Center for Atmospheric Research: Boulder, CO, USA, 2012; p. 268. [Google Scholar]
- Hazeleger, W.; Wang, X.; Severijns, C.; Ştefănescu, S.; Bintanja, R.; Sterl, A.; Wyser, K.; Semmler, T.; Yang, S.; Van Den Hurk, B.; et al. EC-Earth V2.2: Description and validation of a new seamless earth system prediction model. Clim. Dyn. 2012, 39, 2611–2629. [Google Scholar] [CrossRef]
- Collins, W.J.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Halloran, P.; Hinton, T.; Hughes, J.; Jones, C.D.; Joshi, M.; Liddicoat, S.; et al. Development and evaluation of an Earth-system model HadGEM2. Geosci. Model Dev. 2011, 4, 997–1062. [Google Scholar] [CrossRef]
- Watanabe, S.; Hajima, T.; Sudo, K.; Nagashima, T.; Takemura, T.; Okajima, H.; Nozawa, T.; Kawase, H.; Abe, M.; Yokohata, T.; et al. MIROC-ESM 2010: Model description and basic results of CMIP5-20c3m experiments. Geosci. Model Dev. 2011, 4, 845–872. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Jungclaus, J.; Reick, C.H.; Legutke, S.; Bader, J.; Böttinger, M.; Brovkin, V.; Crueger, T.; Esch, M.; Fieg, K.; et al. Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J. Adv. Model. Earth Syst. 2013, 5, 572–597. [Google Scholar] [CrossRef]
- Meier, W.N.; Fetterer, F.; Savoie, M.; Mallory, S.; Duerr, R.; Stroeve, J. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 3; National Snow and Ice Data Center: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 1996. [CrossRef]
- Comiso, J.J. Large decadal decline of the Arctic multiyear ice cover. J. Clim. 2012, 25, 1176–1193. [Google Scholar] [CrossRef]
- Peng, G.; Meier, W.N.; Scott, D.J.; Savoie, M. A long-term and reproducible passive microwave sea ice concentration data record for climate studies and monitoring. Earth Syst. Sci. Data 2013, 5, 311–318. [Google Scholar] [CrossRef]
- Meier, W.N.; Peng, G.; Scott, D.J.; Savoie, M.H. Verification of a new NOAA/NSIDC passive microwave sea-ice concentration climate record. Polar Res. 2014, 33. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K.; Ficklin, D.L. Assessment of three dimensionless measures of model performance. Environ. Model. Softw. 2015, 73, 167–174. [Google Scholar] [CrossRef]
- Overland, J.E.; Wang, M.; Bond, N.A.; Walsh, J.E.; Kattsov, V.M.; Chapman, W.L. Considerations in the selection of global climate models for regional climate projections: The Arctic as a case study. J. Clim. 2011, 24, 1583–1597. [Google Scholar] [CrossRef]
- Jahn, A.; Kay, J.E.; Holland, M.M.; Hall, D.M. How predictable is the timing of a summer ice-free Arctic? Geophys. Res. Lett. 2016, 43, 9113–9120. [Google Scholar] [CrossRef]
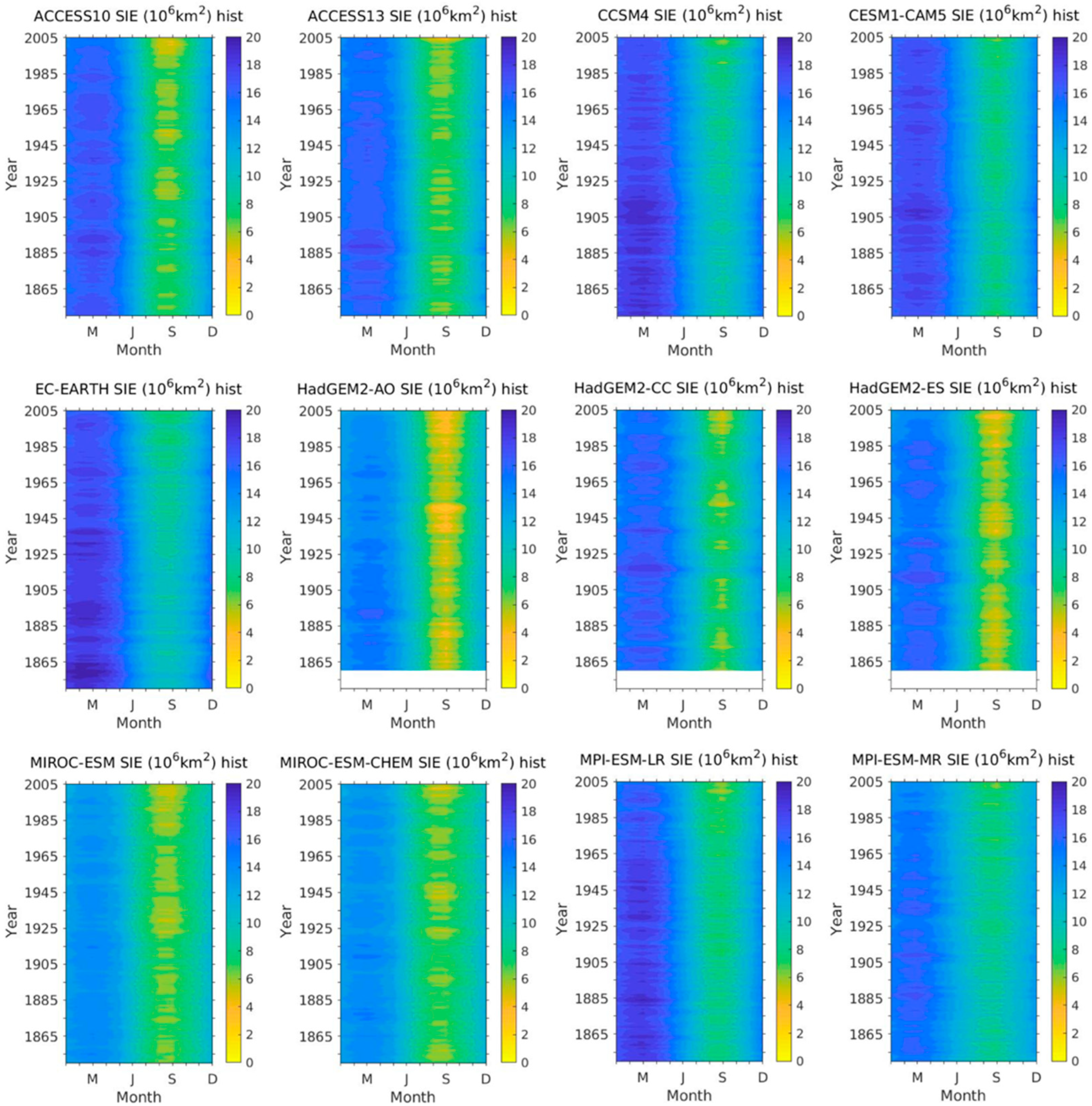
| Model ID | Models Short Name | Country | Institute ID * | Sea Ice Model | Modeling Center/Group [Reference] |
|---|---|---|---|---|---|
| M1 | ACCESS10 | Australia | CSIRO-BOM | CICE, v4.1 | Commonwealth Scientific and Industrial Research Organization (CSIRO) and the Bureau of Meteorology (BOM) [13,14] |
| M2 | ACCESS13 | Australia | CSIRO-BOM | CICE, v4.1 | |
| M3 | CCSM4 | USA | NCAR | CICE, v4 | National Center for Atmospheric Research (NCAR) [15] |
| M4 | CESM1-CAM5 | USA | NSF-DOE-NCAR | CICE, v4 | Community Earth System Model Contributors [16] |
| M5 | EC-EARTH | European Center | EC-EARTH | LM2 | EC-EARTH consortium [17] |
| M6 | HadGEM2-AO | S. Korea | NIMR/KMA | Sea ice component of HadGOM2 | National Institute of Meteorological Research/Korea Meteorological Administration [18] |
| M7 | HadGEM2-CC | UK | MOHC | Inspired from CICE | Met Office Hadley Centre (additional HadGEM2-ES realizations contributed by Instituto Nacional de Pesquisas Espaciais) [18] |
| M8 | HadGEM2-ES | UK | MOHC | Inspired from CICE | |
| M9 | MIROC-ESM | Japan | MIROC | COCO v3.4 | Japan Agency for Marine-Earth Science and Technology (JAMEST), Atmosphere and Ocean Research Institute (AORI) of the University of Tokyo, and National Institute for Environmental Studies (NIES) [19] |
| M10 | MIROC-ESM-CHEM | Japan | MIROC | COCO v3.4 | |
| M11 | MPI-ESM-LR | Germany | MPI-M | Sea ice component of MPI-OM | Max Planck Institute for Meteorology [20] |
| M12 | MPI-ESM-MR | Germany | MPI-M | Sea ice component of MPI-OM |
| Model Short Name. (Case Type—Hist) | Mean | Min | Max | STD | Bias | RMSE | MAE |
|---|---|---|---|---|---|---|---|
| ACCESS10 | 12.1277 | 4.7 | 17.6 | 3.8415 | −0.2878 | 1.1802 | 0.9682 |
| ACCESS13 | 11.7885 | 4.36 | 16.6 | 3.5165 | −0.6269 | 1.1695 | 0.9434 |
| CCSM4 | 13.6377 | 6.25 | 18.7 | 3.4672 | 1.2208 | 1.4853 | 1.2707 |
| CESM1-CAM5 | 13.6405 | 6.41 | 18.4 | 3.3861 | 1.2244 | 1.4697 | 1.2671 |
| EC-EARTH | 13.4292 | 7.45 | 18.5 | 3.4406 | 1.0153 | 1.3501 | 1.1484 |
| HadGEM2-AO | 10.5722 | 3.29 | 15.2 | 3.4767 | −1.8427 | 2.0633 | 1.8474 |
| HadGEM2-CC | 12.2978 | 4.63 | 17.2 | 3.3891 | −0.1166 b | 0.8826 | 0.7012 |
| HadGEM2-ES | 11.4869 | 4.06 | 16.9 | 3.6571 | −0.9289 | 1.4122 | 1.1515 |
| MIROC-ESM | 10.2487 | 5.24 | 14.6 | 2.8756 | −2.1654 a | 2.2661 a | 2.1654 a |
| MIROC-ESM-CHEM | 10.6744 | 4.45 | 15.1 | 2.8706 | −1.7389 | 1.8838 | 1.7428 |
| MPI-ESM-LR | 12.6344 | 5.58 | 18.3 | 3.5578 | 0.2177 | 0.9427 | 0.7762 |
| MPI-ESM-MR | 11.9817 | 6.46 | 16.4 | 2.5929 | −0.4315 | 0.7699 b | 0.661 b |
| Model Means | 12.043 | 5.240 | 16.958 | 3.339 | −0.372 | 1.406 | 1.22 |
| OBSERVATIONS | 12.403 | 5.981 | 16.878 | 2.923 | 0 | 0 | 0 |
| Model Short Name (Case Type—r45) | Mean | Min | Max | STD | Bias | RMSE | MAE |
|---|---|---|---|---|---|---|---|
| ACCESS10 | 11.2194 | 4.40 | 16.9 | 4.0652 | 0.0019 b | 1.0963 | 0.925 |
| ACCESS13 | 10.8473 | 3.72 | 15.9 | 3.942 | −0.3702 | 1.0917 | 0.8939 |
| CCSM4 | 12.6624 | 6.09 | 17.5 | 3.596 | 1.4450 | 1.5885 | 1.4659 |
| CESM1-CAM5 | 12.9672 | 5.24 | 17.7 | 3.7989 | 1.7498 | 1.9341 | 1.7741 |
| EC-EARTH | 12.2539 | 6.67 | 17.4 | 3.4701 | 1.0364 | 1.2502 | 1.0607 |
| HadGEM2-AO | 9.3219 | 1.66 | 14.0 | 3.8858 | −1.8955 a | 2.1257 a | 1.8980 a |
| HadGEM2-CC | 11.3904 | 3.53 | 16.4 | 3.6622 | 0.1730 | 0.8474 | 0.6553 |
| HadGEM2-ES | 10.6139 | 3.85 | 15.4 | 3.5950 | −0.6036 | 1.0035 | 0.8032 |
| MIROC-ESM | 9.5925 | 3.59 | 14.2 | 3.224 | −1.6249 | 1.8261 | 1.6669 |
| MIROC-ESM-CHEM | 9.9883 | 4.64 | 14.3 | 3.0575 | −1.2292 | 1.4597 | 1.3302 |
| MPI-ESM-LR | 11.6303 | 3.96 | 17.1 | 3.8053 | 0.4129 | 0.9854 | 0.7947 |
| MPI-ESM-MR | 11.1275 | 5.24 | 15.2 | 2.9418 | −0.0899 | 0.7175 b | 0.574 b |
| Model Means | 11.135 | 4.383 | 16.000 | 3.587 | −0.083 | 1.327 | 1.153 |
| OBSERVATIONS | 11.217 | 3.857 | 15.554 | 3.290 | 0 | 0 | 0 |
| Model Short Name (Case Type—r85) | Mean | Min | Max | STD | Bias | RMSE | MAE |
|---|---|---|---|---|---|---|---|
| ACCESS1.0 | 11.6199 | 4.38 | 17.0 | 3.9881 | 0.4024 | 1.1024 | 0.9252 |
| ACCESS1.3 | 10.5794 | 3.61 | 16.0 | 4.0235 | −0.6381 | 1.2294 | 1.0295 |
| CCSM4 | 12.7355 | 5.35 | 17.5 | 3.5848 | 1.5180 | 1.6782 | 1.5487 |
| CESM1-CAM5 | 12.9202 | 4.72 | 18.0 | 3.8224 | 1.7028 a | 1.8891 a | 1.7312 a |
| EC-EARTH | 12.7568 | 6.98 | 17.2 | 3.3331 | 1.5394 | 1.6994 | 1.5398 |
| HadGEM2-AO | 9.6455 | 2.37 | 14.7 | 3.8748 | −1.5720 | 1.8671 | 1.5960 |
| HadGEM2-CC | 11.4117 | 3.78 | 16.4 | 3.6287 | 0.1943 | 0.8935 | 0.7128 |
| HadGEM2-ES | 10.2462 | 2.20 | 15.4 | 3.8743 | −0.9712 | 1.3984 | 1.0759 |
| MIROC-ESM | 9.7631 | 4.05 | 14.1 | 3.1855 | −1.4543 | 1.6223 | 1.482 |
| MIROC-ESM-CHEM | 9.8586 | 4.35 | 14.1 | 3.0014 | −1.3588 | 1.5678 | 1.4382 |
| MPI-ESM-LR | 11.7807 | 4.74 | 16.9 | 3.6386 | 0.5632 | 0.9848 | 0.8099 |
| MPI-ESM-MR | 11.2946 | 5.62 | 15.0 | 2.6567 | 0.0771 b | 0.8848 b | 0.6726 b |
| Model Means | 11.218 | 4.346 | 16.025 | 3.551 | 0.0 | 1.401 | 1.213 |
| OBSERVATIONS | 11.217 | 3.857 | 15.554 | 3.290 | 0 | 0 | 0 |
| Models Short Name /Basic Statistics | FIASY for RCP4.5 (Case r45; Unit: Year) | FIASY for RCP8.5 (Case r85; Unit: Year) | RCP8.5–4.5 (Unit: Year) |
|---|---|---|---|
| ACCESS10 | 2054 | 2027 | −27 |
| ACCESS13 | 2051 | 2044 | −7 |
| CCSM4 | >2100 | 2064 | <−36 |
| CESM1-CAM5 | 2038 | 2035 | −3 |
| EC-EARTH | 2088 | 2065 | −23 |
| HadGEM2-AO | 2025 | 2023 | −2 |
| HadGEM2-CC | 2063 | 2046 | −17 |
| HadGEM2-ES | 2042 | 2035 | −7 |
| MIROC-ESM | 2023 | 2027 | 4 |
| MIROC-ESM-CHEM | 2026 | 2033 | 7 |
| MPI-ESM-LR | 2097 | 2049 | −48 |
| MPI-ESM-MR | 2087 | 2054 | −33 |
| Mean | 2054 | 2042 | −14 |
| Min (Absolute Value) | 2023 | 2023 | 2 |
| Max (Absolute Value) | >2100 | 2065 | 48 |
| Spread | >77 | 42 | 55 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Matthews, J.L.; Wang, M.; Vose, R.; Sun, L. What Do Global Climate Models Tell Us about Future Arctic Sea Ice Coverage Changes? Climate 2020, 8, 15. https://doi.org/10.3390/cli8010015
Peng G, Matthews JL, Wang M, Vose R, Sun L. What Do Global Climate Models Tell Us about Future Arctic Sea Ice Coverage Changes? Climate. 2020; 8(1):15. https://doi.org/10.3390/cli8010015
Chicago/Turabian StylePeng, Ge, Jessica L. Matthews, Muyin Wang, Russell Vose, and Liqiang Sun. 2020. "What Do Global Climate Models Tell Us about Future Arctic Sea Ice Coverage Changes?" Climate 8, no. 1: 15. https://doi.org/10.3390/cli8010015
APA StylePeng, G., Matthews, J. L., Wang, M., Vose, R., & Sun, L. (2020). What Do Global Climate Models Tell Us about Future Arctic Sea Ice Coverage Changes? Climate, 8(1), 15. https://doi.org/10.3390/cli8010015