A Physical–Mathematical Approach to Climate Change Effects through Stochastic Resonance
Abstract
1. Introduction
2. Methodology
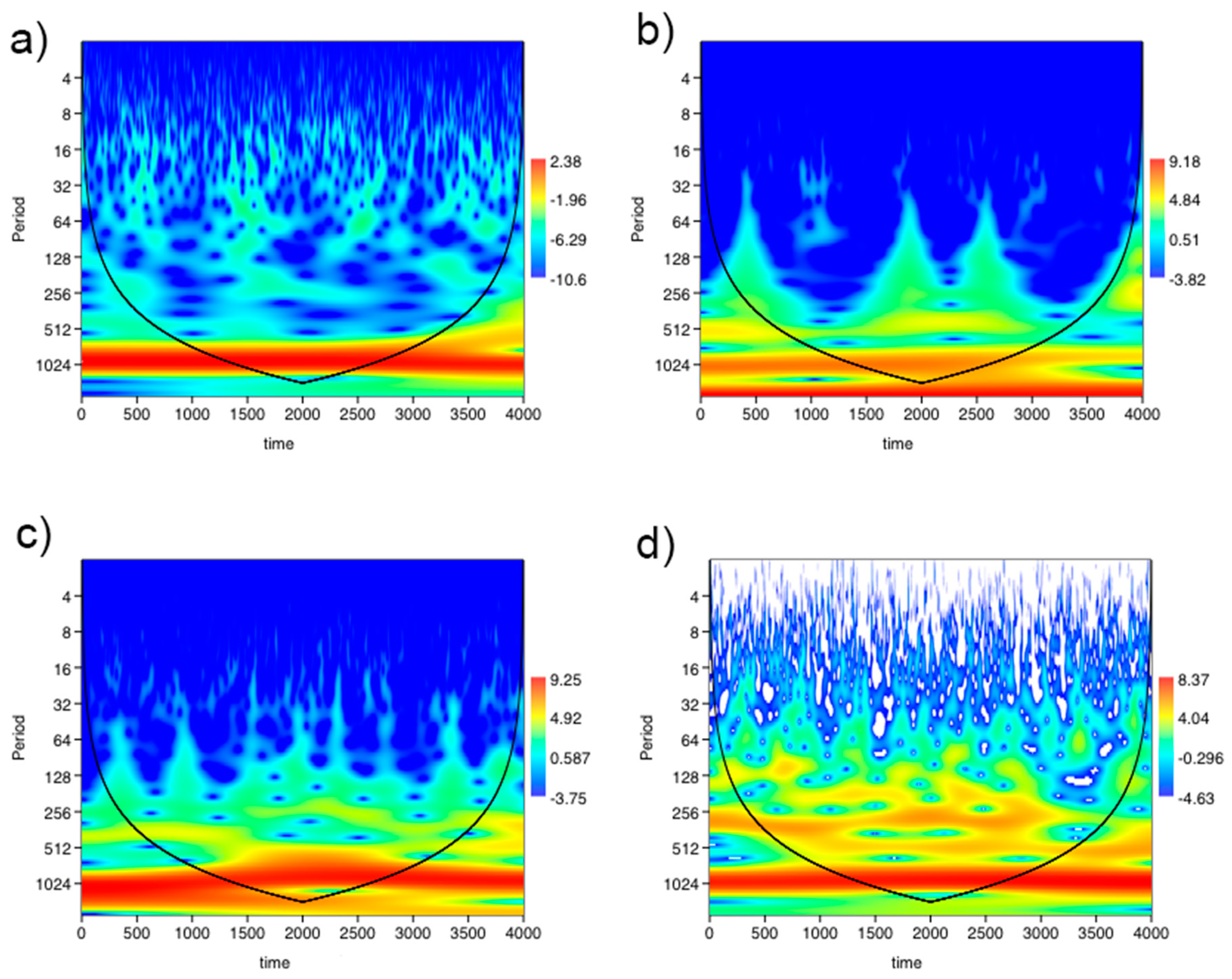
2.1. Wavelet Analysis
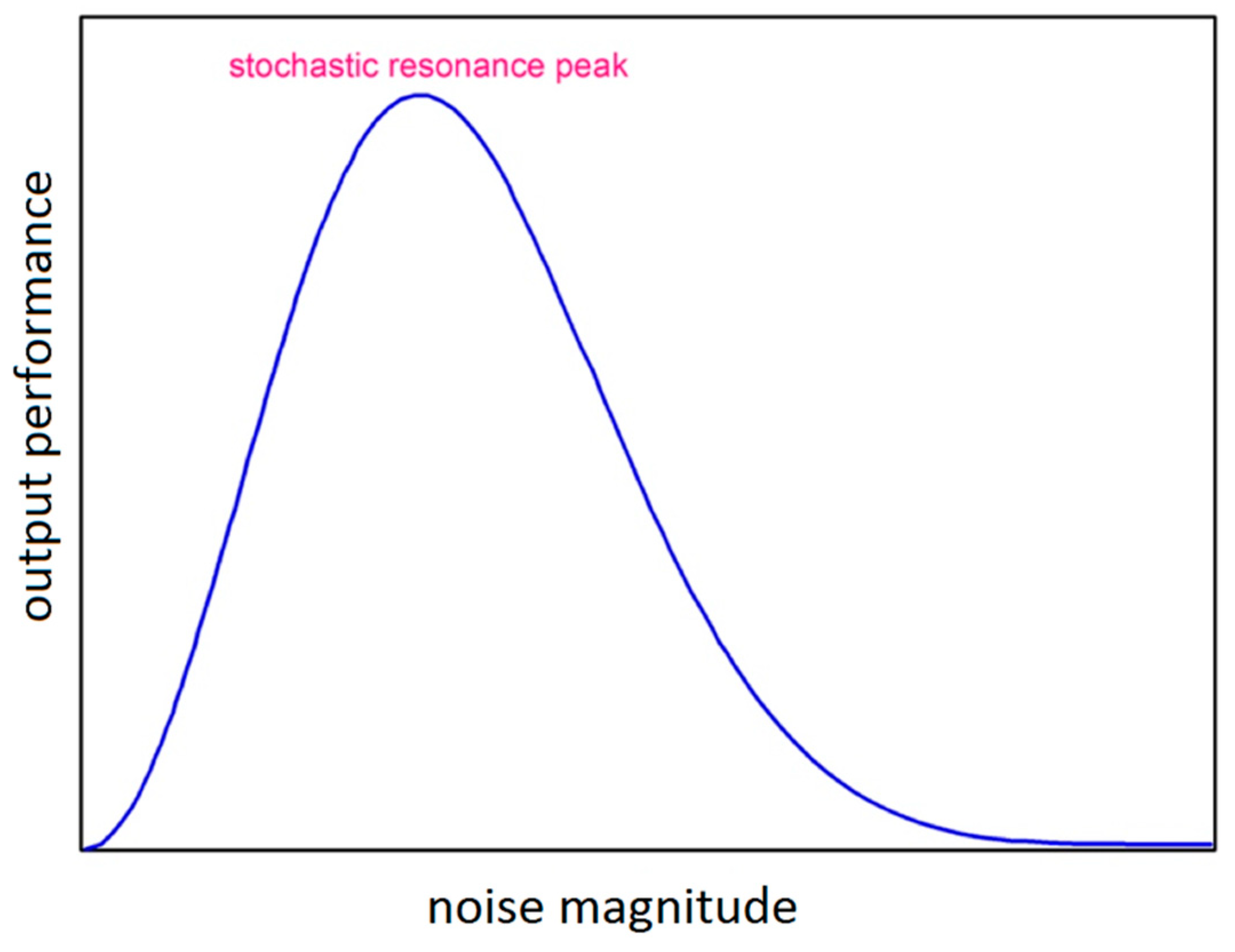
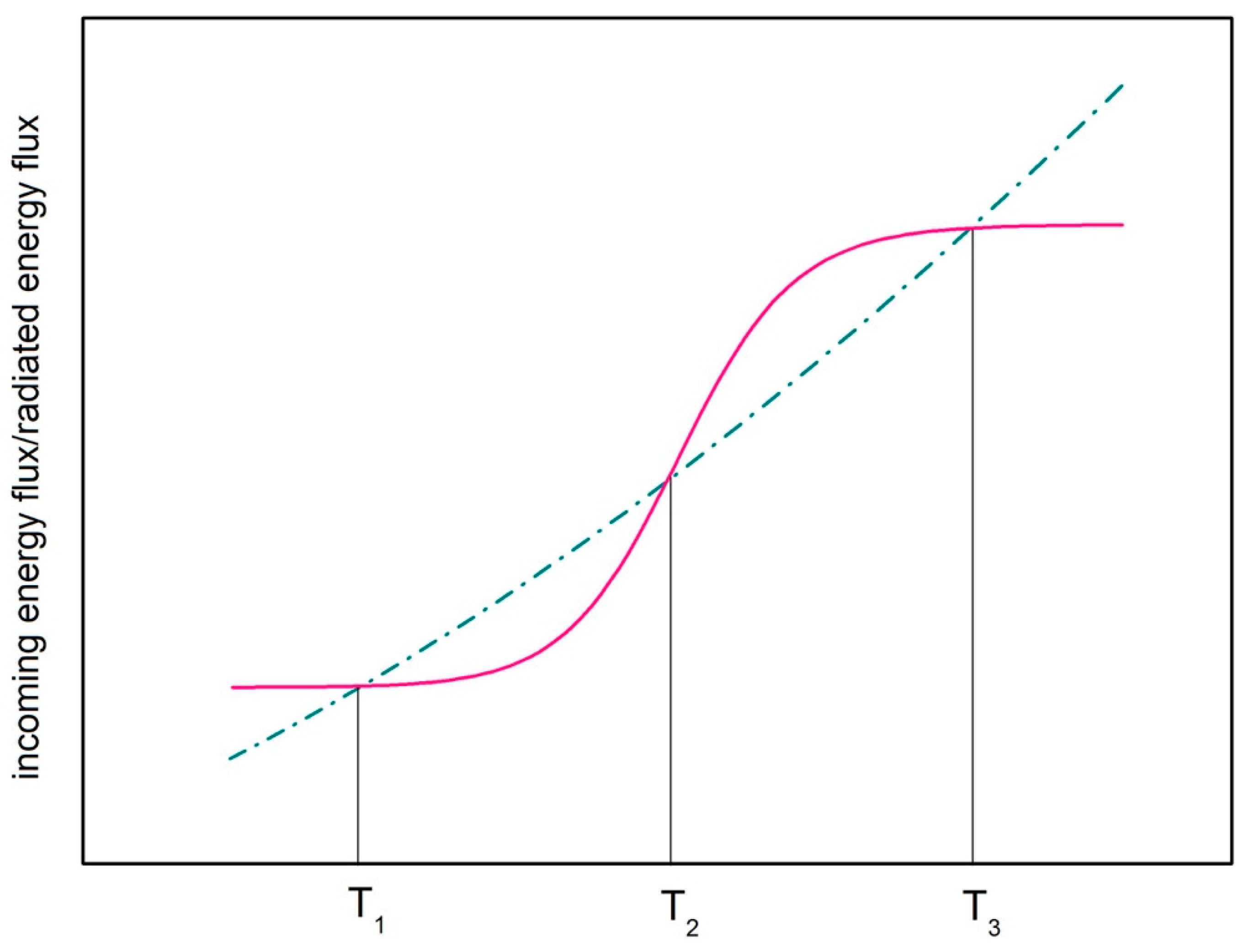
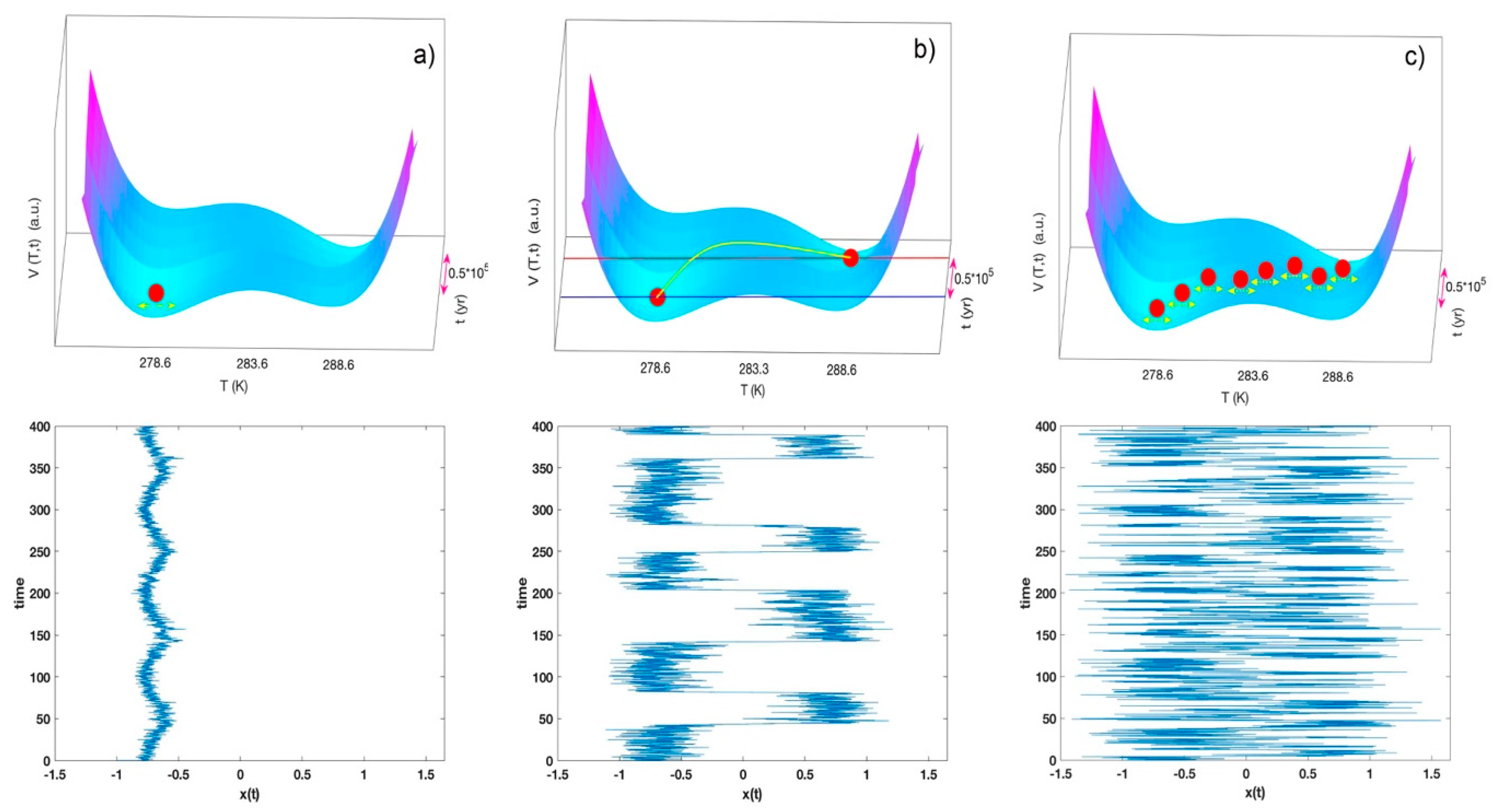
2.2. Stochastic Resonance
- (1)
- a non-linear system characterized by an energetic activation barrier or, more generally, by a form of threshold;
- (2)
- a weak input;
- (3)
- a source of noise that is inherent in the system, or that adds to the input.
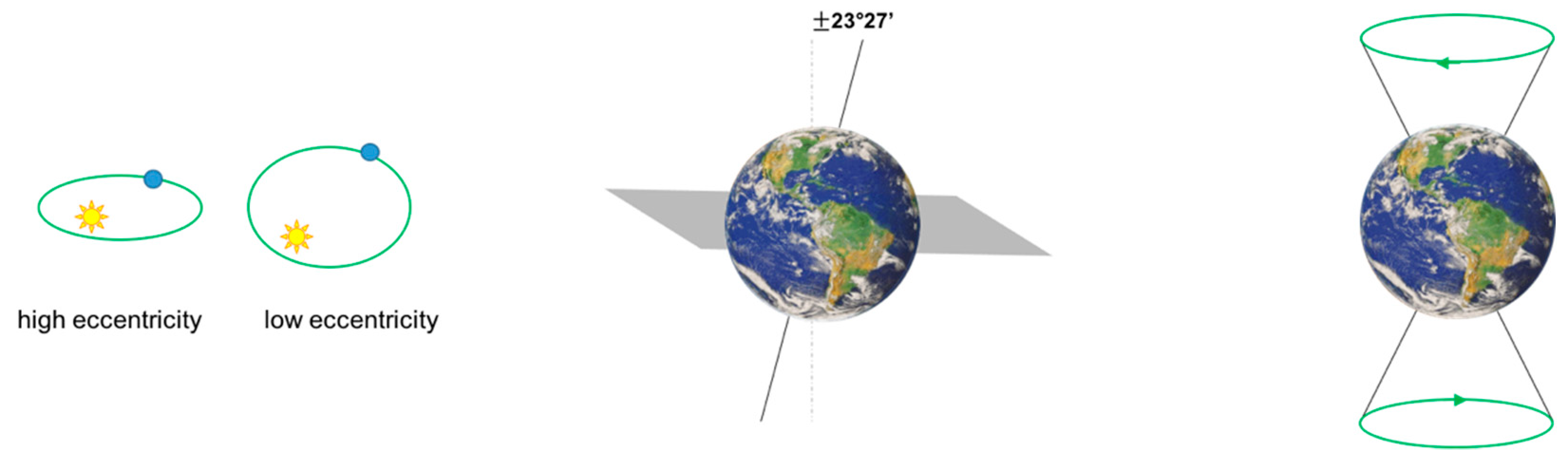
2.3. Slow and Fast Processes of Earth’s Energy Balance
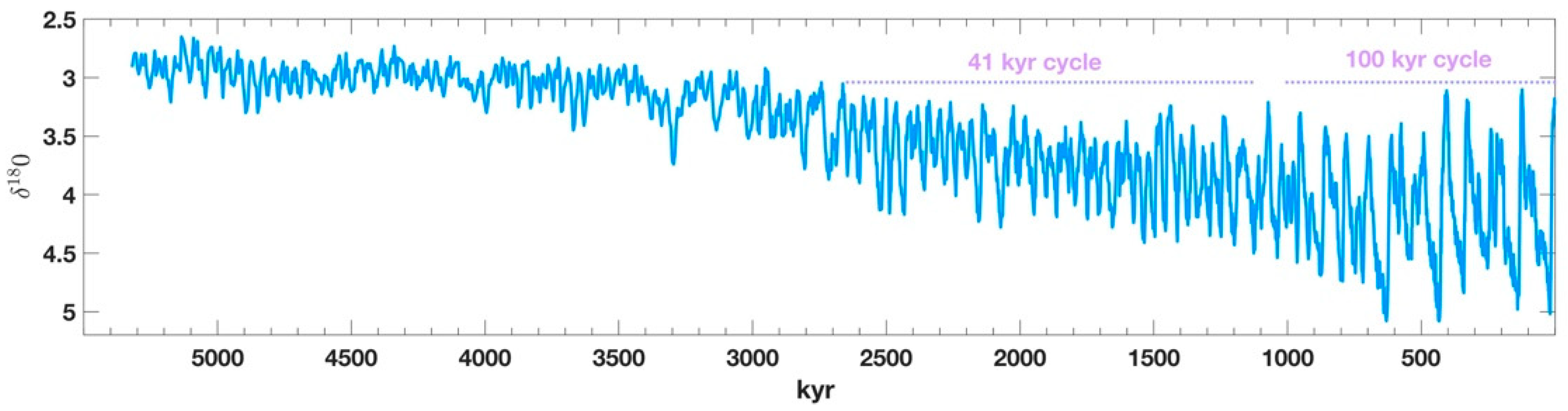
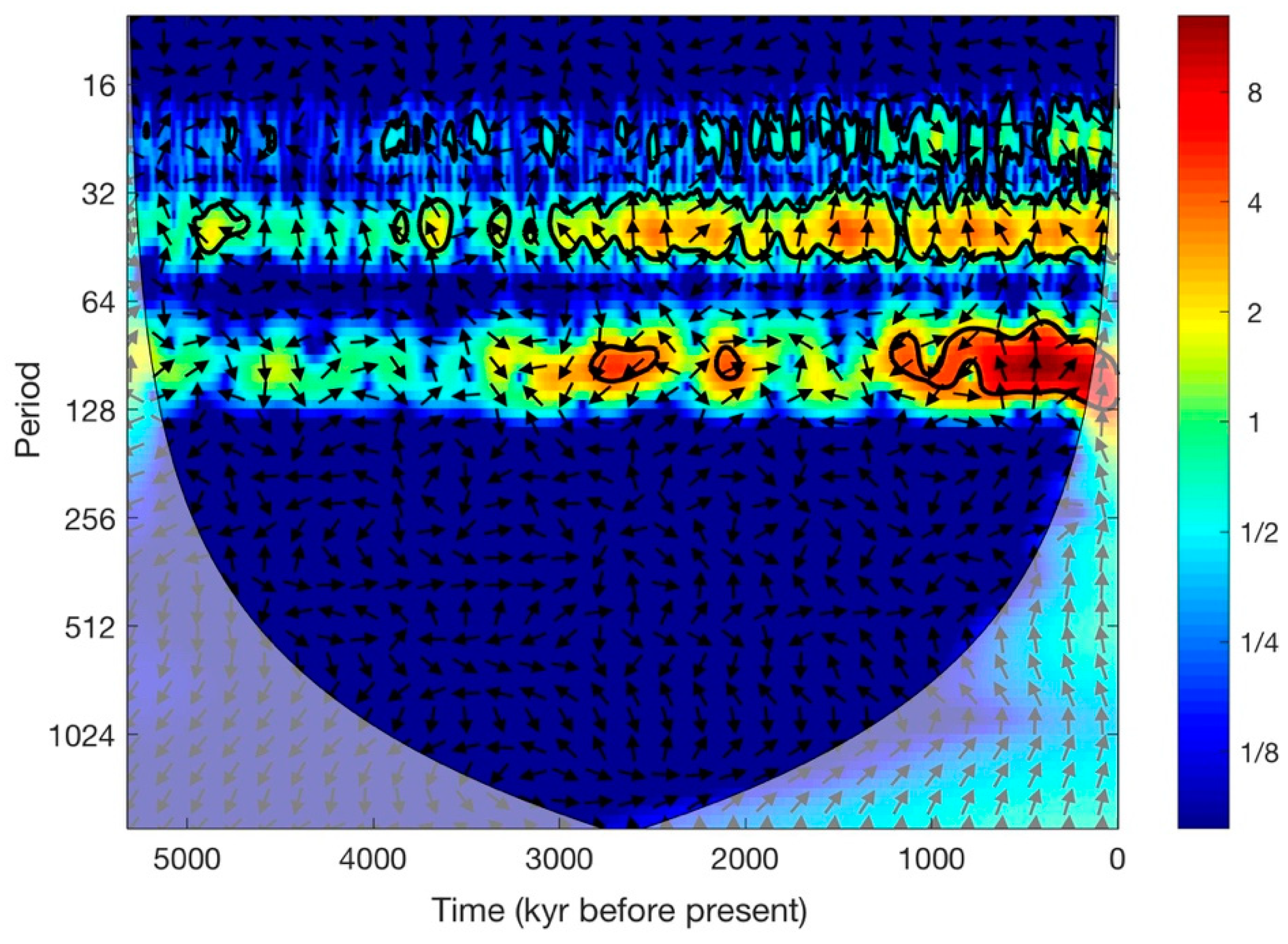
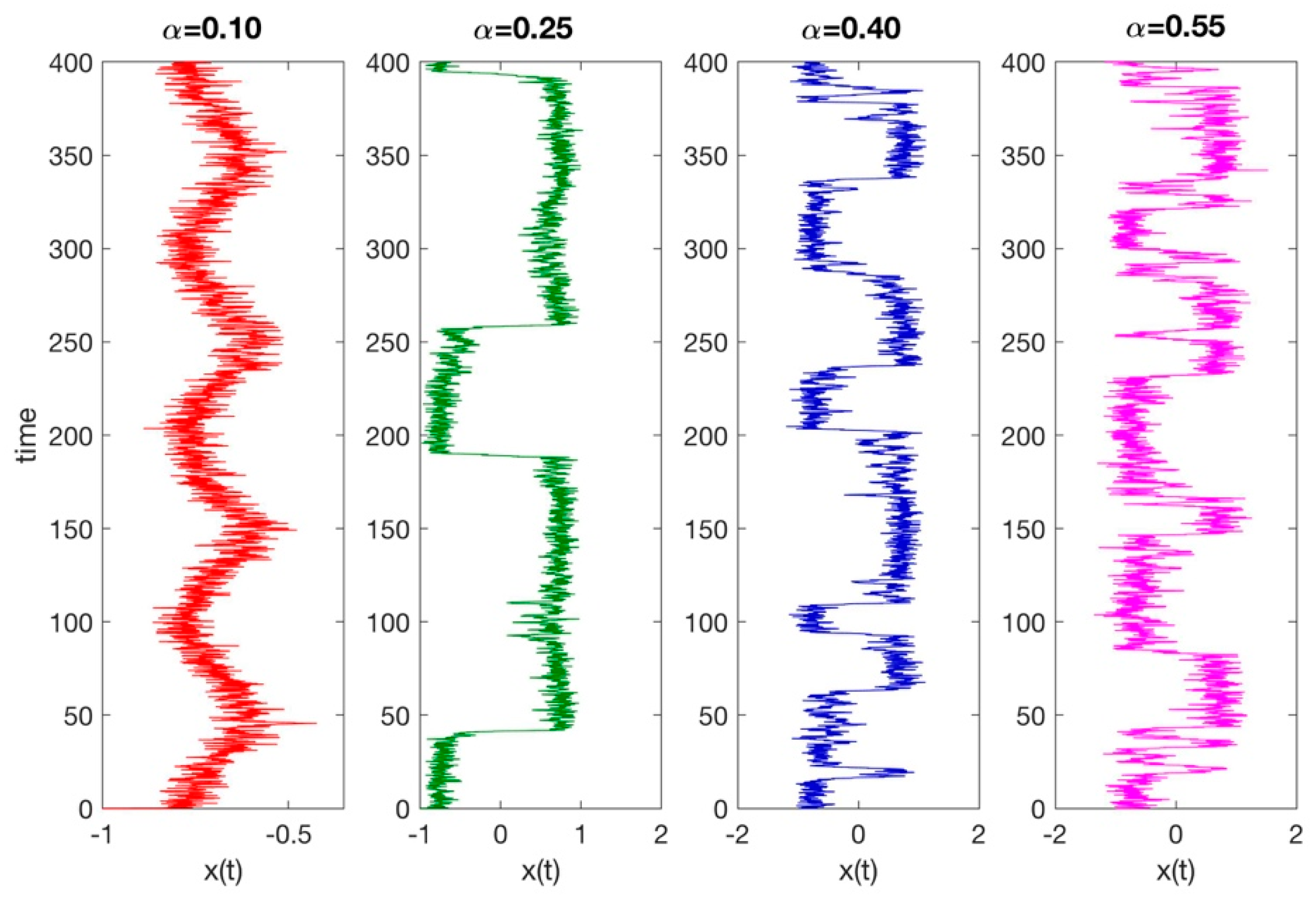
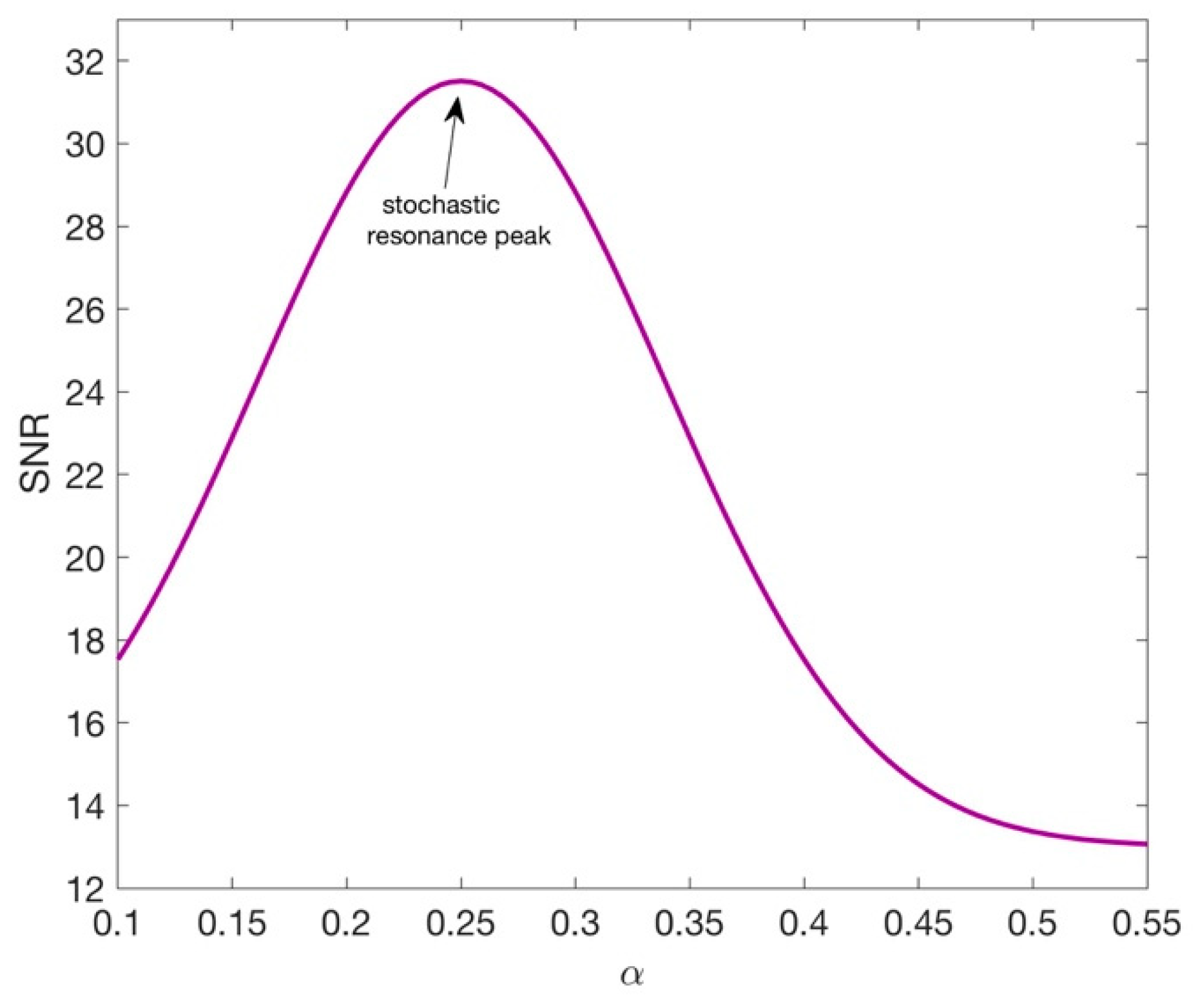
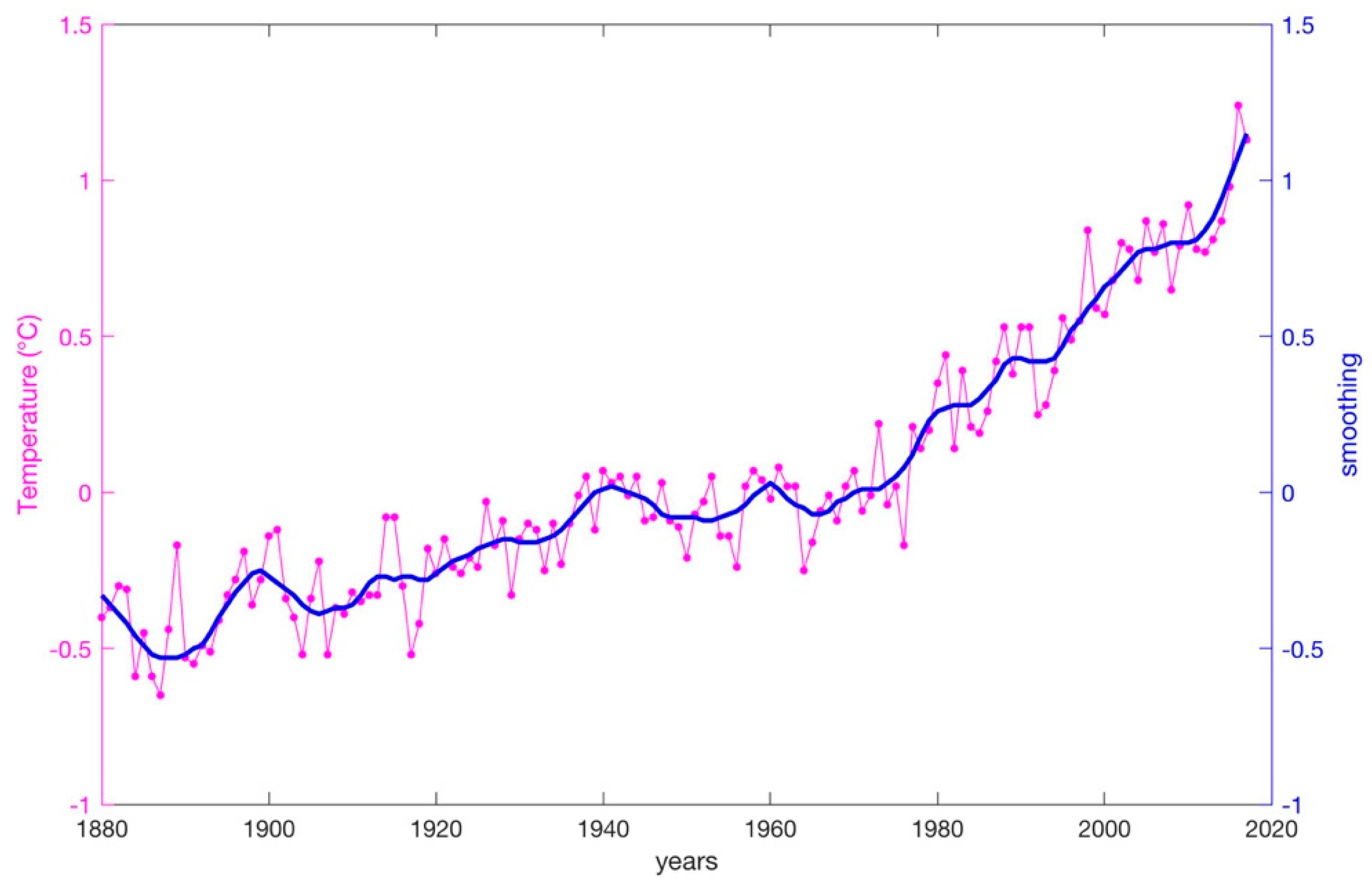
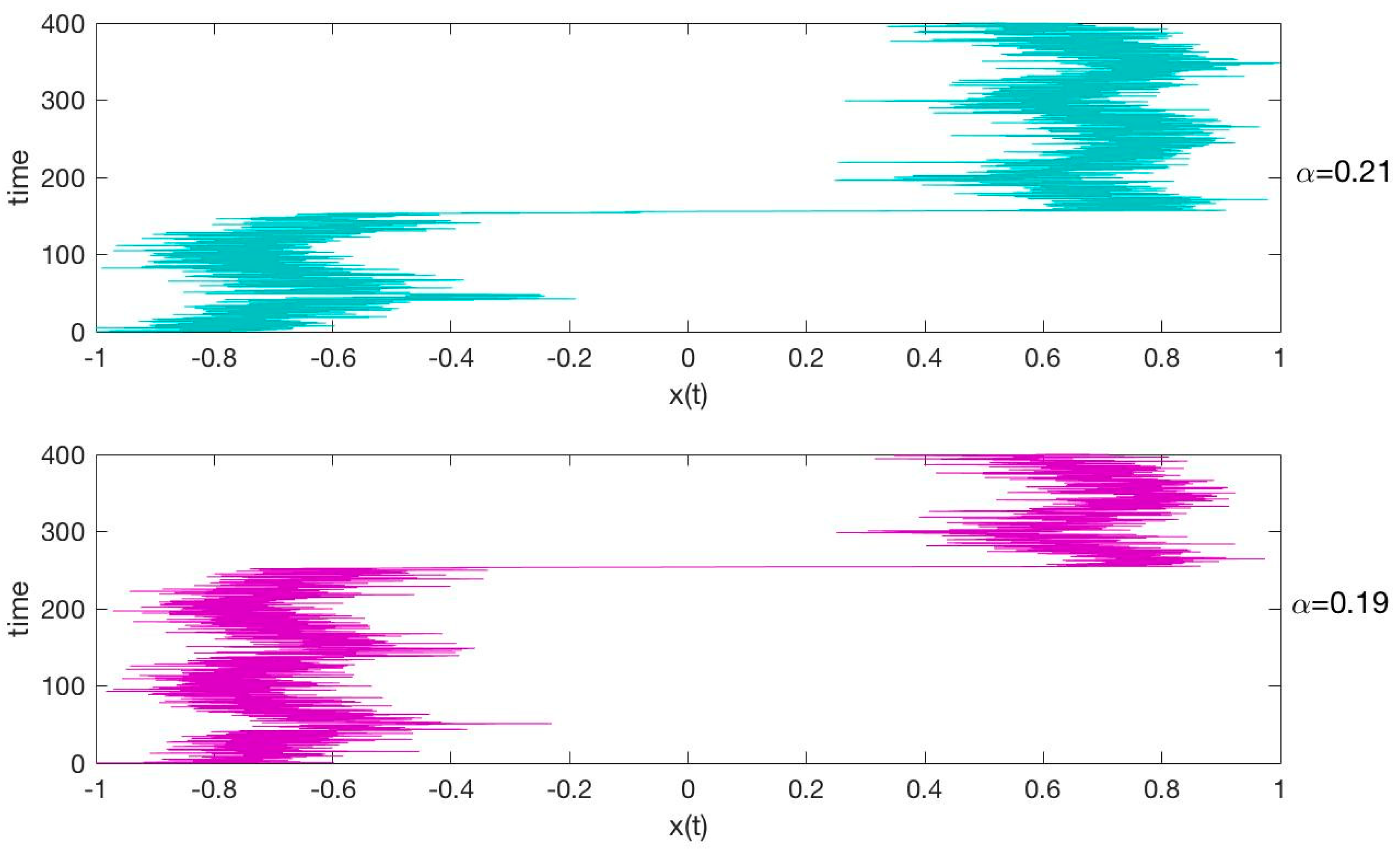
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Benzi, R. Stochastic resonance: From climate to biology. Nonlinear Proc. Geophs. 2010, 17, 431–441. [Google Scholar] [CrossRef]
- Jacka, T.H.; Budd, W.F. Detection of temperature and sea-ice-extent changes in the Antarctic and Southern Ocean, 1949–1996. Ann. Glaciol. 1998, 27, 553–559. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Castorina, G.; Colombo, F.; Insinga, V.; Maiorana, E.; Magazù, S. Weather forecast performances for complex orographic areas: Impact of different grid resolutions and of geographic data on heavy rainfall event simulations in Sicily. Atmos. Res. 2017, 198, 22–33. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Reconstructing sea level from paleo and projected temperatures 200 to 2100 AD. Clim. Dyn. 2010, 34, 461–472. [Google Scholar] [CrossRef]
- Calabrò, E.; Magazù, S. Correlation between increases of the annual global solar radiation and the ground albedo solar radiation due to desertification-A possible factor contributing to climatic change. Climate 2016, 4, 64. [Google Scholar] [CrossRef]
- Monnin, E.; Indermuhle, A.; Dallenbach, A.; Fluckiger, J.; Stauffer, B.; Stocker, T.F.; Raynaud, D.; Barnola, J.-M. Atmospheric CO2 Concentrations over the Last Glacial Termination. Science 2001, 291, 112–114. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Doi, K.; Shibuya, K. Estimation of seasonal changes in the flow of Shirase Glacier using JERS-1/SAR image correlation. Polar Sci. 2007, 1, 73–84. [Google Scholar] [CrossRef]
- Davey, M.C. Effects of continuous and repeated dehydration on carbon fixation by bryophytes from the maritime Antarctic. Oecologia 1997, 110, 25–31. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Calabrò, E.; Cannuli, A.; Magazù, S. Wavelet Study of Meteorological Data Collected by Arduino-Weather Station: Impact on Solar Energy Collection Technology”. MATEC Web Conf. 2016, 55, 02004. [Google Scholar] [CrossRef]
- Raper, S.C.; Wigley, T.M.; Jones, P.D.; Salinger, M.J. Variations in surface air temperatures: Part 3. The Antarctic, 1957–1982. Mon. Weather Rev. 1984, 112, 1341–1353. [Google Scholar] [CrossRef]
- Babalola, O.O.; Kirby, B.M.; Le Roes-Hill, M.; Cook, A.E.; Cary, S.C.; Burton, S.G.; Cowan, D.A. Phylogenetic analysis of actinobacterial populations associated with Antarctic Dry Valley mineral soils. Environ. Microb. 2009, 11, 566–576. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.D. Recent variations in mean temperature and the diurnal temperature range in the Antarctic. Geophys. Res. Lett. 1995, 22, 1345–1348. [Google Scholar] [CrossRef]
- Jones, P.D.; Mann, M.E. Climate Over Past Millennia. Rev. Geophys. 2004, 42, RG2002. [Google Scholar] [CrossRef]
- Bailey, D.M.; Johnston, I.A.; Peck, L.S. Invertebrate muscle performance at high latitude: Swimming activity in the Antarctic scallop Adamussium colbecki. Polar Biol. 2005, 28, 464–469. [Google Scholar] [CrossRef]
- Stark, J.S.; Snape, I.; Riddle, M.J. Abandoned Antarctic waste disposal sites: Monitoring remediation outcomes and limitations at Casey Station. Ecol. Manag. Restor. 2006, 7, 21–31. [Google Scholar] [CrossRef]
- Moberg, A.; Sonechkin, D.M.; Holmgren, K.; Datsenko, N.M.; Karlén, W. Highly variable Northern Hemisphere temperatures reconstructed from low- and high-resolution proxy data. Nature 2005, 433, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Azam, F.; Beers, J.R.; Campbell, L.; Carlucci, A.F.; Holm-Hansen, O.; Reis, F.M.H.; Karl, D.M. Occurrence and metabolic activity of organisms under the Ross Ice Shelf, Antarctica, at station J9. Science 1979, 203, 451–453. [Google Scholar] [CrossRef] [PubMed]
- Colombo, F.; Caccamo, M.T.; Magazù, S. Trehalose Based Extremophiles in Harsh Environments. In Trehalose: Sources, Chemistry and Applications; Nova Publishers: New York, NY, USA, 2019. [Google Scholar]
- Lokotosh, T.V.; Magazù, S.; Maisano, G.; Malomuzh, N.P. Nature of Self-Diffusion and Viscosity in Supercooled Liquid Water. Phys. Rev. E 2000, 62, 3572–3580. [Google Scholar] [CrossRef]
- Magazù, S.; Migliardo, F.; Telling, M.T.F. Structural and dynamical properties of water in sugar mixtures. Food Chem. 2008, 106, 1460–1466. [Google Scholar] [CrossRef]
- Migliardo, F.; Caccamo, M.T.; Magazù, S. Elastic Incoherent Neutron Scatterings Wavevector and Thermal Analysis on Glass-forming Homologous Disaccharides. J. Non-Cryst. Solids 2013, 378, 144–151. [Google Scholar] [CrossRef]
- Magazù, S.; Migliardo, F.; Caccamo, M.T. Innovative Wavelet Protocols in Analyzing Elastic Incoherent Neutron Scattering. J. Phys. Chem. B 2012, 116, 9417–9423. [Google Scholar] [CrossRef] [PubMed]
- Barnola, J.-M.; Raynaud, D.; Korotkevich, Y.S.; Lorius, C. Vostok ice core provides 160,000-year record of atmospheric CO2. Nature 1987, 329, 408–441. [Google Scholar] [CrossRef]
- Jouzel, J.; Lorius, C.; Petit, J.R.; Genthon, C.; Barkov, N.I.; Kotlyakov, V.M.; Petrov, V.M. Vostok ice core: A continuous isotopic temperature record over the last climatic cycle (160,000 years). Nature 1987, 329, 403–408. [Google Scholar] [CrossRef]
- Pepin, L.; Raynaud, D.; Barnola, J.-M.; Loutre, M.F. Hemispheric roles of climate forcings during glacial-interglacial transitions as deduced from the Vostok record and LLN-2D model experiments. J. Geophys. Res. 2001, 106, 31:885–31:892. [Google Scholar] [CrossRef]
- Petit, J.R.; Basile, I.; Leruyuet, A.; Raynaud, D.; Lorius, C.; Jouzel, J.; Stievenard, M.; Lipenkov, V.Y.; Barkov, N.I.; Kudryashov, B.B.; et al. Four climate cycles in Vostok ice core. Nature 1997, 387, 359–360. [Google Scholar] [CrossRef]
- Basile, I.; Grousset, F.E.; Revel, M.; Petit, J.R.; Biscaye, P.E.; Barkovd, N.I. Patagonian origin dust deposited in East Antarctica (Vostok and Dome C) during glacial stages 2, 4 and 6. Earth Planet. Sci. Lett. 1997, 146, 573–589. [Google Scholar] [CrossRef]
- Becker, J.; Lourens, L.J.; Hilgen, F.J.; van der Laan, E.; Kouwenhoven, T.J.; Reichart, G.J. Late Pliocene climate variability on Milankovitch to millennial time scales: A high-resolution study of MIS100 from the Mediterranean. Palaeogeogr. Palaeocl. 2005, 228, 338–360. [Google Scholar] [CrossRef]
- Lachniet, M.; Asmerom, Y.; Polyak, V.; Denniston, R. Arctic cryosphere and Milankovitch forcing of Great Basin paleoclimate. Sci. Rep. 2017, 7, 12955. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.-M.; Basile, I.; Benders, M.; Chappellaz, J.; Davis, M.; Delayque, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core. Antarctica. Nat. 1999, 399, 429–436. [Google Scholar]
- Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic d18O records. Paleoceanography 2005, 20, PA1003. [Google Scholar]
- Milankovitch, M. Canon of Insolation and the Ice Age Problem; Zavod za Udz benike i Nastavna Sredstva: Belgrade, Serbia, 1941. [Google Scholar]
- Petit, J.R.; Mounier, L.; Jouzel, J.; Korotkevitch, Y.S.; Kotlyakov, V.I.; Lorius, C. Paleoclimatological implications of the Vostok core dust record. Nature 1990, 343, 56–58. [Google Scholar] [CrossRef]
- Waelbroeck, C.; Jouzel, J.; Labeyrie, L.; Lorius, C.; Labracherie, M.; Stiévenard, N.; Barkov, N.I. A comparison of the Vostok ice deuterium record and series from Southern Ocean core MD 88-770 over the last two glacial-interglacial cycles. Clim. Dyn. 1995, 12, 113–123. [Google Scholar] [CrossRef]
- Suwa, M.; Bender, M.L. Chronology of the Vostok ice core constrained by O2/N2 ratios of occluded air, and its implication for the Vostok climate records. Quaternary Sci. Rev. 2008, 27, 1093–1106. [Google Scholar] [CrossRef]
- Landais, A.; Barkan, E.; Luz, B. Record of delta δ18O and 17O-excess in ice from Vostok Antarctica during the last 150,000 years. Geophys. Res. Lett. 2008, 35, L02709. [Google Scholar]
- Bopp, L.; Kohfeld, K.E.; Le Quere, C.; Aumont, O. Dust impact on marine biota and atmospheric CO2 during glacial periods. Paleoceanography 2003, 18, 1046. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Lloyd, J.; Taylor, J.A.; Flanagan, L.B.; Syvertsen, J.P.; Hubick, K.T.; Wong, S.C.; Ehleringer, J.R. Vegetation effects on the isotope composition of oxygen in atmospheric CO2. Nature 1993, 363, 439–442. [Google Scholar] [CrossRef]
- Bargagli, R.; Agnorelli, C.; Borghini, F.; Monaci, F. Enhanced deposition and bioaccumulation of mercury in Antarctic terrestrial ecosystems facing a coastal polynya. Environ. Sci. Technol. 2005, 39, 8150–8155. [Google Scholar] [CrossRef]
- Richardson, A.J.; Schoeman, D.S. Climate impact on ecosystems in the northeast Atlantic. Science 2004, 305, 1609–1612. [Google Scholar] [CrossRef]
- Imbrie, J.; Boyle, E.A.; Clemens, S.C.; Duffy, A.; Howard, W.R.; Kukla, G.; Toggweiler, J.R. On the Structure and Origin of Major Glaciation Cycles 1. Linear Responses to Milankovitch Forcing. PALOC 1992, 7, 701–738. [Google Scholar] [CrossRef]
- Li, H.; Nozaki, T. Wavelet cross-correlation analysis and its application to a plane turbulent jet. Int. J. Ser. B 1997, 40, 58–66. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Magazù, S. Ethylene Glycol—Polyethylene Glycol (EG-PEG) Mixtures: Infrared Spectra Wavelet Cross-Correlation Analysis. Appl. Spectrosc. 2017, 71, 401–409. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geoph. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A 1981, 14, L453–L457. [Google Scholar] [CrossRef]
- Bulsara, A.R.; Dari, A.; Ditto, W.L.; Murali, K.; Sinha, S. Logical stochastic resonance. Chem. Phys. 2010, 375, 424–434. [Google Scholar] [CrossRef]
- Benzi, R.; Parisi, G.; Sutera, A.; Vulpiani, A. Stochastic resonance in climatic change. Tellus 1982, 34, 10–16. [Google Scholar] [CrossRef]
- Hänggi, P.; Inchiosa, M.E.; Fogliatti, D.; Bulsara, A.R. Nonlinear stochastic resonance: The saga of anomalous output-input gain. Phys. Rev. E 2000, 62, 6155–6163. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance: A remarkable idea that changed our perception of noise. Eur. Phys. J. B 2009, 69, 1–3. [Google Scholar] [CrossRef]
- Berdichevsky, V.; Gitterman, M. Stochastic resonance in linear systems subject to multiplicative and additive noise. Phys. Rev. E 1999, 60, 1494–1499. [Google Scholar] [CrossRef]
- Li, J.H.; Han, Y.X. Phenomenon of stochastic resonance caused by multiplicative asymmetric dichotomous noise. Phys. Rev. E 2006, 74, 051115. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Bulsara, A.R. Nonlinear sensors activated by noise. Phys. A 2003, 325, 152–164. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Magazù, S. Variable mass pendulum behaviour processed by wavelet analysis. Eur. J. Phys. 2017, 38, 15804. [Google Scholar] [CrossRef]
- Prokoph, A.; Patterson, R.T. Application of wavelet and discontinuity analysis to trace temperature changes: Eastern Ontario as a case study. Atmos. Ocean 2004, 42, 201–212. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Cannuli, A.; Magazù, S. Wavelet analysis of near-resonant series RLC circuit with time-dependent forcing frequency. Eur. J. Phys. 2017, 38, 015804. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory; Part I, Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Magazù, S. Variable length pendulum analyzed by a comparative Fourier and wavelet approach. Revista Mexicana de Fisica E 2018, 64, 81–86. [Google Scholar]
- Kronland-Martinet, R.; Morlet, J.; Grossmann, A. Analysis of sound patterns through wavelet transform. Int. J. Pattern Recogn. 1987, 1, 97–126. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Magazù, S. Thermal restraint on PEG-EG mixtures by FTIR investigations and wavelet cross-correlation analysis. Polym. Test. 2017, 62, 311–318. [Google Scholar] [CrossRef]
- Crucifix, M. Oscillators and relaxation phenomena in Pleistocene climate theory. Philosoph. Trans. R. Soc. A 2012, 370, 1140–1165. [Google Scholar] [CrossRef]
- Razdan, A. Wavelet Correlation Coefficient of ‘strongly correlated’ financial time series. Phys. A 2004, 333, 335–342. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Magazù, S. Tagging the oligomer-to-polymer crossover on EG and PEGs by infrared and Raman spectroscopies and by wavelet cross-correlation spectral analysis. Vib. Spectrosc. 2016, 85, 222–227. [Google Scholar] [CrossRef]
- Veleda, D.; Montagne, R.; Araujo, M. Cross-wavelet bias corrected by normalizing scales. J. Atmos. Ocean. Technol. 2012, 29, 1401–1408. [Google Scholar] [CrossRef]
- Gitterman, M. Harmonic oscillator with fluctuating damping parameter. Phys. Rev. E 2004, 69, 041101. [Google Scholar] [CrossRef] [PubMed]
- Wellens, T.; Shatokhin, V.; Buchleitner, A. Stochastic resonance. Rep. Prog. Phys. 2004, 67, 45–105. [Google Scholar] [CrossRef]
- Douglass, J.K.; Wilkens, L.; Pantazelou, E.; Moss, F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 1993, 365, 337–340. [Google Scholar] [CrossRef] [PubMed]
- Wiesenfeld, K.; Moss, F. Stochastic resonance and the benefits of noise: From ice ages to crayfish and SQUIDs. Nature 1995, 373, 33–36. [Google Scholar] [CrossRef]
- McNamara, B.; Wiesenfeld, K. Theory of stochastic resonance. Phys. Rev. A 1989, 39, 4854–4869. [Google Scholar] [CrossRef]
- Walsh, J.; Rackauckas, C. On the Budyko-Sellers Energy Balance Climate Model with Ice Line Coupling. Discrete Cont. Dyn. B 2015, 20, 10–20. [Google Scholar] [CrossRef]
- Widiasih, E. Dynamics of the Budyko energy balance model. SIAM J. Appl. Dyn. Syst. 2013, 12, 2068–2092. [Google Scholar] [CrossRef]
- McGehee, R.; Widiasih, E. A quadratic approximation to Budyko’s ice-albedo feedback model with ice line dynamics. SIAM J. Appl. Dyn. Syst. 2014, 13, 518–536. [Google Scholar] [CrossRef]
- Walsh, J.A.; Widiasih, E. A dynamics approach to a low-order climate model. Disc. Cont. Dyn. Syst. B 2014, 19, 257–279. [Google Scholar] [CrossRef]
- Budyko, I. The effect of solar radiation variation on the climate of the Earth. Tellus 1969, 5, 611–619. [Google Scholar]
- Luterbacher, J.; Dietrich, D.; Xoplaki, E.; Grosjean, M.; Wanner, H. European seasonal and annual temperature variability, trends, and extremes since 1500. Science 2004, 303, 1499–1503. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caccamo, M.T.; Magazù, S. A Physical–Mathematical Approach to Climate Change Effects through Stochastic Resonance. Climate 2019, 7, 21. https://doi.org/10.3390/cli7020021
Caccamo MT, Magazù S. A Physical–Mathematical Approach to Climate Change Effects through Stochastic Resonance. Climate. 2019; 7(2):21. https://doi.org/10.3390/cli7020021
Chicago/Turabian StyleCaccamo, Maria Teresa, and Salvatore Magazù. 2019. "A Physical–Mathematical Approach to Climate Change Effects through Stochastic Resonance" Climate 7, no. 2: 21. https://doi.org/10.3390/cli7020021
APA StyleCaccamo, M. T., & Magazù, S. (2019). A Physical–Mathematical Approach to Climate Change Effects through Stochastic Resonance. Climate, 7(2), 21. https://doi.org/10.3390/cli7020021





