An Innovative Damage Model for Crop Insurance, Combining Two Hazards into a Single Climatic Index
Abstract
1. Introduction
1.1. Context and Objectives
1.2. A Review of Climatic Indices
1.3. Synthesis
2. Materials and Methods
2.1. Input Data
2.1.1. Meteorological Data
2.1.2. Yield Data and Yield Anomaly Computing
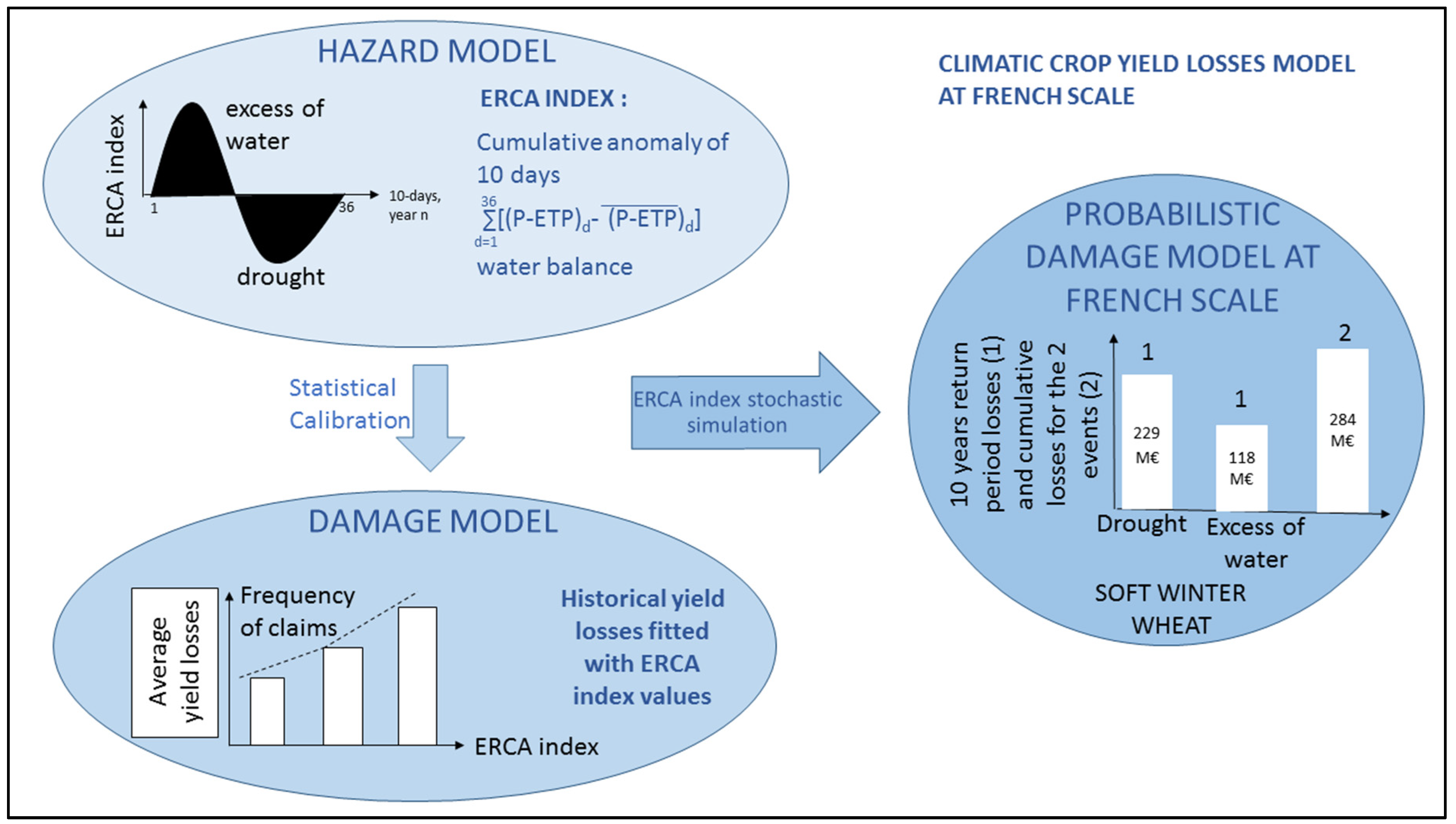
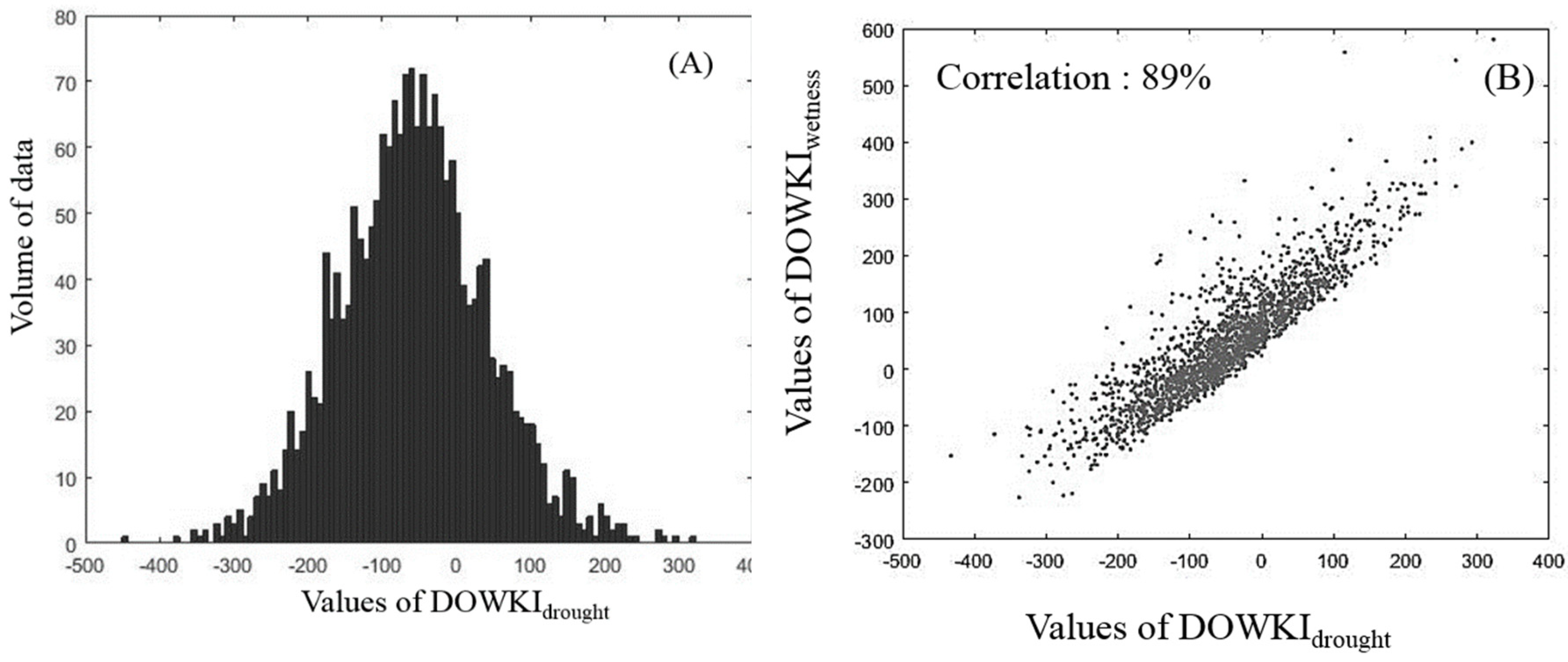
2.2. Computing the DOWKI Index
2.3. Statistical Analysis/Experimental Design
- The first 10 days of the vulnerability period of the crop: 1 (1–10 January) to 15 (20–30 May);
- The last 10 days of the vulnerability period of the crop: 18 (20–30 June) to 30 (20–30 October);
- Two extreme event definition thresholds (for drought and excess of water) computed as a percentile of the whole DOWKI distribution for all departments and years: 2nd percentile to 30th percentile;
- Two minimum number of departments concerned by extreme DOWKI values (above threshold) for systemic extreme event definition.
- Average error and percentiles;
- Number of drought and excess of water events;
- Maximum number of true positive (TP);
- Maximum value of the ratio TP/false positive (FP);
- Maximum value of the ratio (sum of anomalies of TP/sum of anomalies of false negative (FN));
- Maximum value of the ratio (average anomaly of TP/ average anomaly of FN);
- Frequency of claims;
- Yield anomalies percentile 90 for the higher class of DOWKIwetness and lower class of the DOWKIdrought;
- Yield anomalies average for the higher class of DOWKIwetness and lower class of the DOWKIdrought;
2.4. Calibration of the Damage Models
- Frequency of claim: (number of years with a yield anomaly above the threshold/total number of years);
- Average value of the yield anomalies above the threshold;
- Distribution of yield anomalies characterized by percentile values (10th, 25th, 50th, 75th, 90th).
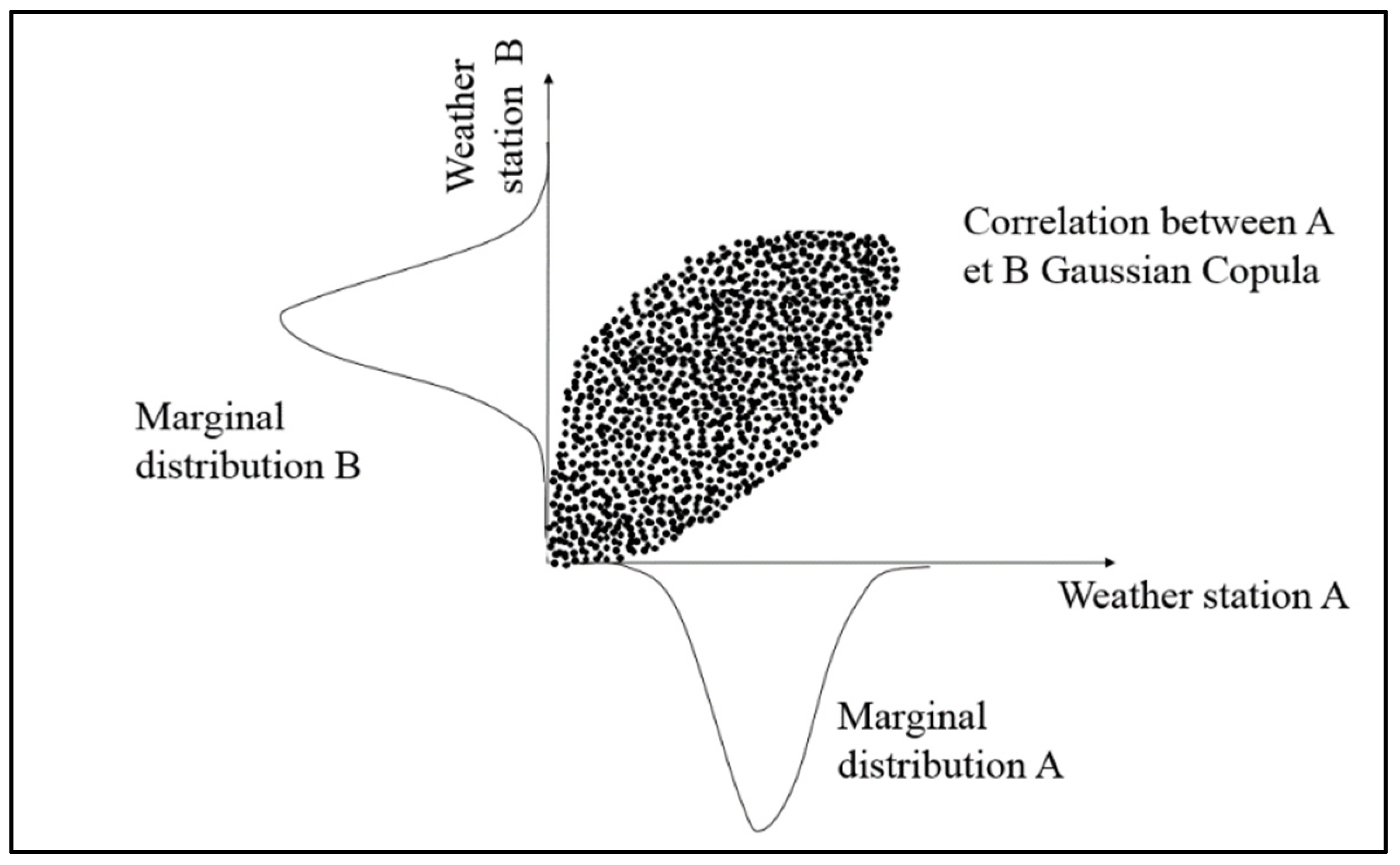
2.5. Stochastic Simulations of Yield Anomalies Based on the DOWKI Indices
3. Results
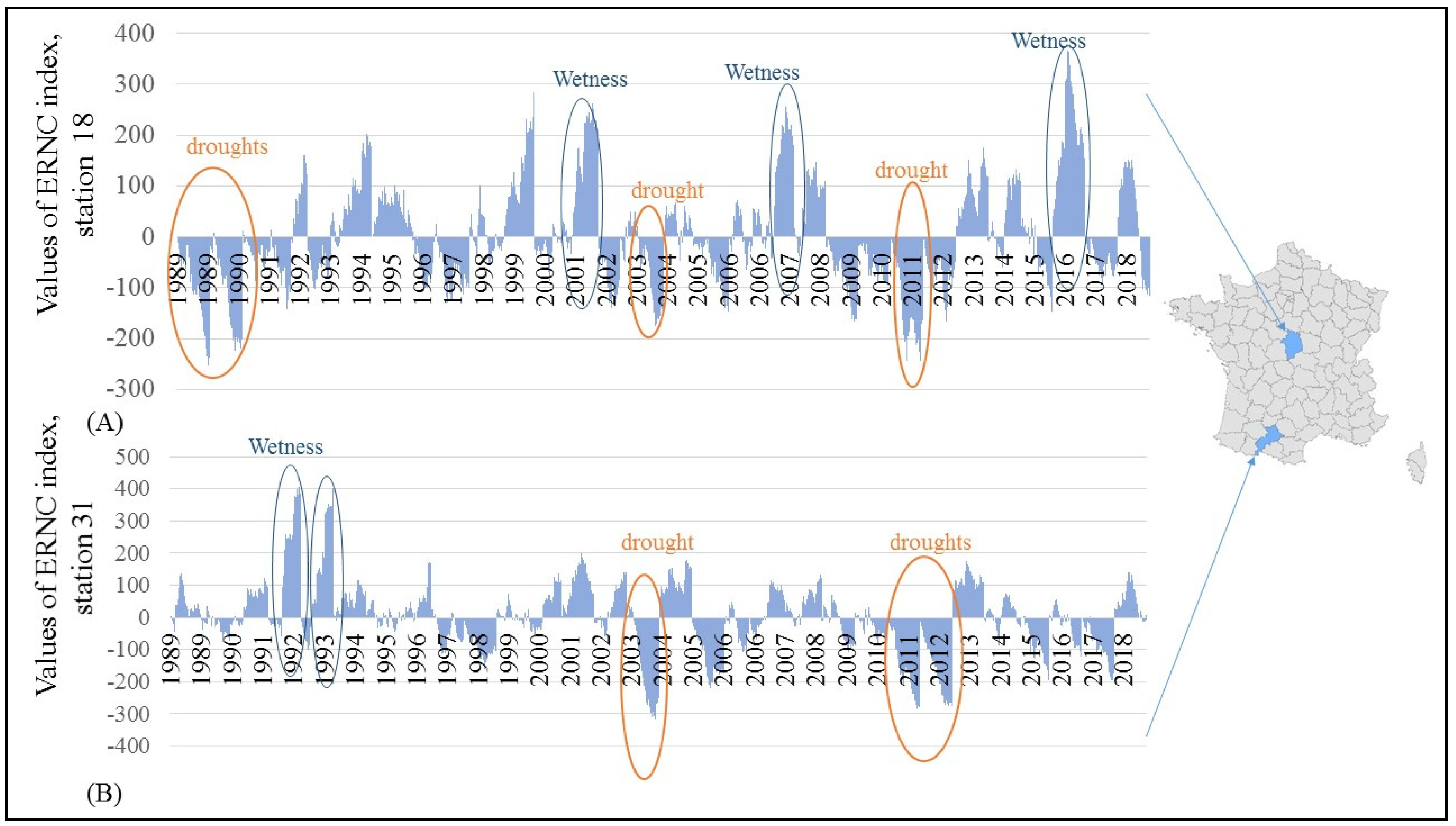
3.1. Multi-year ERNC Values for a 10-day Time Step
- The number of departments concerned by extreme values of DOWKI index;
- The threshold defining extreme values of DOWKI index (a quantile on the global DOWKI distribution for France for the historical period).
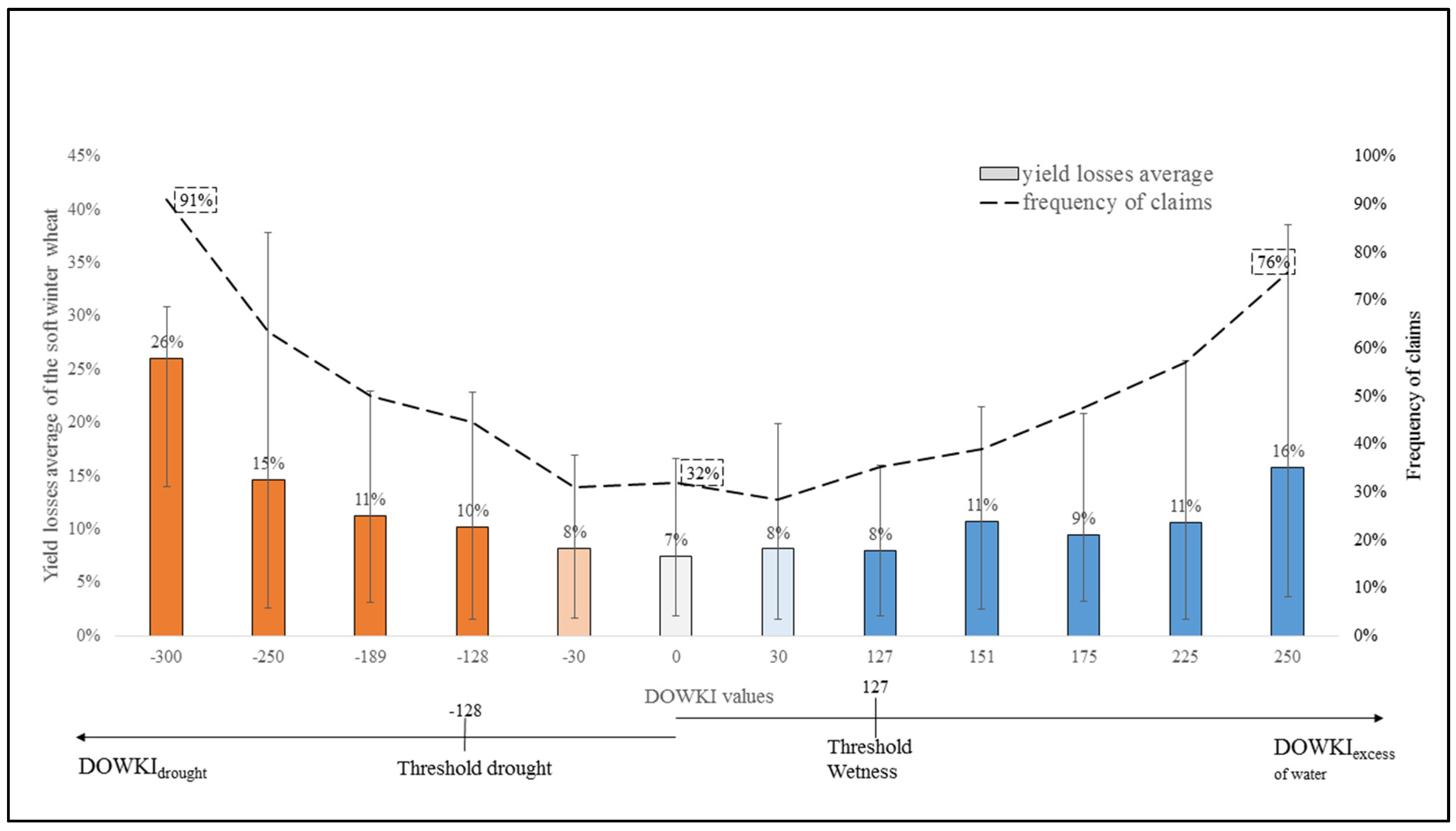
3.2. Calibration of the Damage Models
- One for drought events (defined by the index threshold and the number of departments concerned);
- One for excess of water events;
- One for the attritional years (no drought and no excess of water).
- A parameter was not included in the DOWKI calculation (e.g., temperature, soil water content);
- Adaptation of the agricultural practices (modifying the sowing period and harvest period, choice of varieties);
- Protection measures: the irrigation information was not provided in the AGRESTE database and can significantly change yield anomalies in case of extreme drought.
- An average yield prediction error (and error quantiles 10:25:75:90): 0.039 (−0.33:−0.11:0.25:0.34) for drought;
- For excess of water: 0.077 (−0.35:−0.14:0.29:0.33).
3.3. Experimental Design Results and Parameters Sensitivity
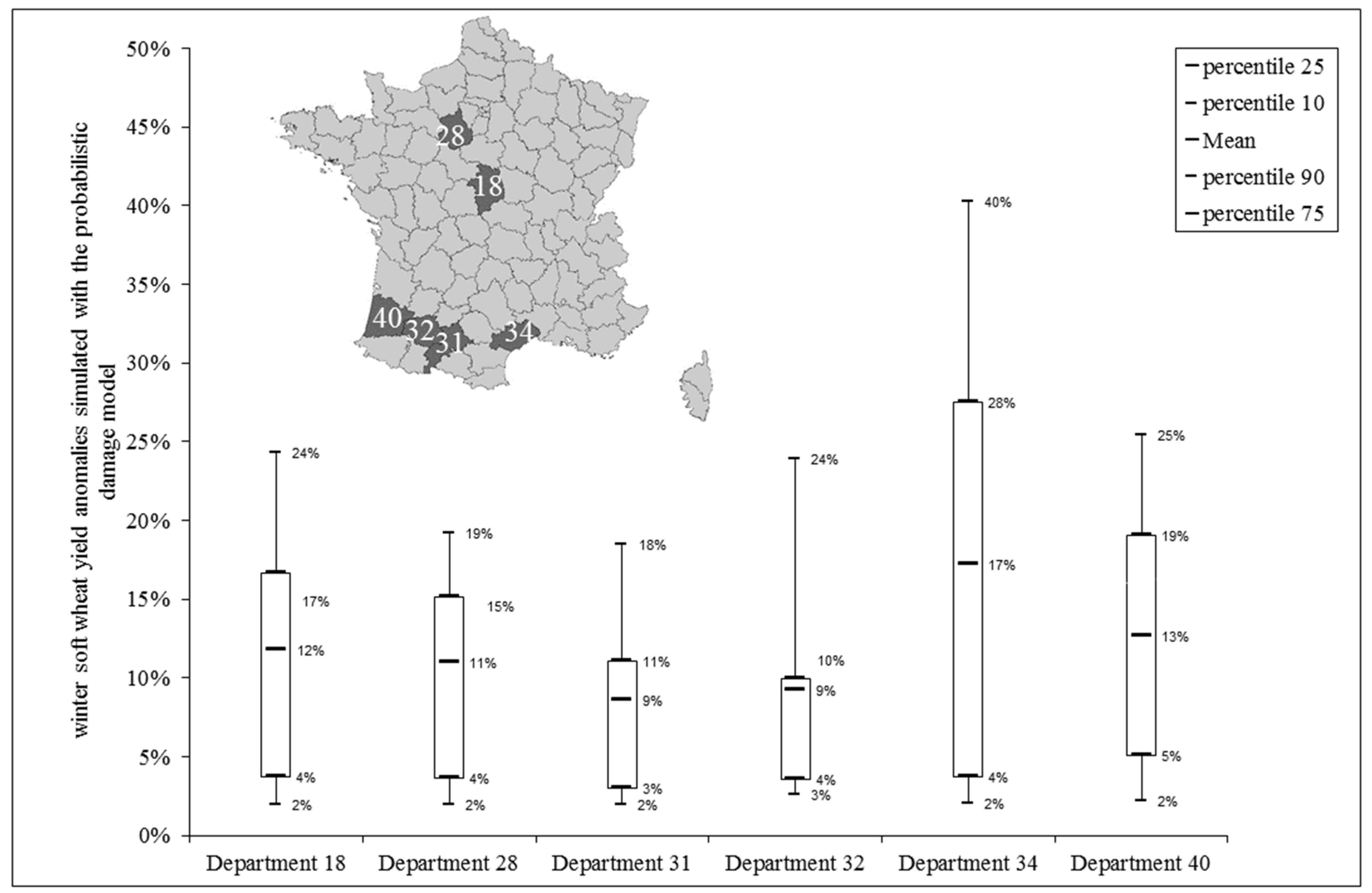
3.4. Stochastic Simulations and Extreme Value Analysis
4. Discussion
- Human decisions: irrigation, sowing dates, alternative crops, cultivation methods and options, all preventive measures taken by the farmer with the objective to reduce the impact of the climatic events during the season;
- Non meteorological natural factors: soil nature, micro-relief (slopes, depressions, exposition);
- Not modeled climatic perils: frost, hail.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; p. 582. [Google Scholar]
- Van der Velde, M.; Tubiello, F.N.; Vrieling, A.; Bouraoui, F. Impacts of extreme weather on wheat and maize in France: Evaluating regional crop simulations against observed data. Clim. Chang. 2012, 113, 751–765. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A.; et al. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- COPA-COGECA. Assessment of the Impact of the Heat Wave and Drought of the Summer 2003 on Agriculture and Forestry; Committee of Agricultural Organisations in the European Union and General Committee for Agricultural cooperation in the European Union: Brussels, Belgium, 2003; pp. 1–15. [Google Scholar]
- Bazzaz, F.; Sombroek, W. Changements du Climat et Production Agricole; FAO: Rome, Italy, 1997; ISBN 92-5-203987-2. [Google Scholar]
- Lobell, D.B.; Schlenker, W.; Costa-Roberts, J. Climate Trends and Global Crop Production Since 1980. Science 2011, 333, 616–620. [Google Scholar] [CrossRef] [PubMed]
- Olesen, J.E.; Trnka, M.; Kersebaum, K.C.; Skjelvag, A.O.; Seguin, B.; Peltonen-Sainio, P.; Rossi, F.; Kozyra, J.; Micale, F. Impacts and adaptation of European crop production systems to climate change. Eur. J. Agron. 2011, 34, 96–112. [Google Scholar] [CrossRef]
- Challinor, A.J.; Watson, J.; Lobell, D.B.; Howden, S.M.; Smith, D.R.; Chhetri, N. A meta-analysis of crop yield under climate change and adaptation. Nat. Clim. Chang. 2014, 4, 287–291. [Google Scholar] [CrossRef]
- Gouache, D.; Bouchon, A.-S.; Jouanneau, E.; Le Bris, X. Agrometeorological analysis and prection of wheat yield at the departmental level in France. Agric. For. Meteorol. 2015, 209–210, 1–10. [Google Scholar] [CrossRef]
- Mathieu, J.A.; Aires, F. Assessment of the agro-climatic indices to improve crop yield forecasting. Agric. For. Meteorol. 2018, 253–254, 15–30. [Google Scholar] [CrossRef]
- Ben-Ari, T.; Adrian, J.; Klein, T.; Calanca, P.; Van der Velde, M.; Makowski, D. Identifying indicators of extreme wheat and maize yield losses. Agric. For. Meteorol. 2016, 220, 130–140. [Google Scholar] [CrossRef]
- Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef]
- Amigues, J.P.; Debaeke, P.; Itier, B.; Lemaire, G.; Seguin, B.; Tardieu, F.; Thomas, A. Sécheresse et Agriculture. Réduire la Vulnérabilité de L’agriculture à un Risque Accru du Manque D’eau; INRA: Paris, France, 2006; p. 72. [Google Scholar]
- Bourcier, V.; Carrega, M.; Corona, C.; Degache-Masperi, A.; Duvernoy, J.; Eckert, N.; Etchevers, P.; Faug, T.; Habets, F.; Giacona, F.; et al. Les Événements Météorologiques Extrêmes Dans un Contexte de Changement Climatique; La documentation Française; ONERC: Paris, France, 2019; p. 200. [Google Scholar]
- IPCC. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; p. 976. [Google Scholar]
- COM. Proposal for a Regulation of the European Parliament and of the Council Establishing Rules on Support Ofr Strategic Plans to Be Drawn up by Member States under the Common Agricultural Policy (CAP Strategic Plans) and Financed by the European Agricultural Guarantee Fund (EAGF) and by the European Agricultural Fund for Rural Development (EAFRD) and Repealing Regulation (EU) No 1305/2013 of the European Parliament and of the Council and Regulation (EU) No 1307/2013 of the European Parliament and of the Council. 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2018%3A392%3AFIN (accessed on 24 October 2019).
- Moncoulon, D.; Labat, D.; Ardon, J.; Leblois, E.; Onfroy, T.; Poulard, C.; Aji, S.; Rémy, A.; Quantin, A. Analysis of the French insurance market exposure to floods: A stochastic model combining river overflow and surface runoff. Nat. Hazards Earth Syst. Sci. 2013, 1, 3217–3261. [Google Scholar] [CrossRef]
- Naulin, J.P.; Moncoulon, D.; Le Roy, S.; Pedreros, R.; Idier, D.; Oliveros, C. Estimation of insurance-related losses resulting from coastal flooding in France. Nat. Hazards Earth Syst. Sci. 2016, 16, 195–207. [Google Scholar] [CrossRef]
- Moncoulon, D.; Veysseire, M.; Naulin, J.-P.; Wang, Z.-X.; Tinard, P.; Desarthe, J.; Hajji, C.; Onfroy, T.; Regimbeau, F.; Déqué, M. Modelling the evolution of the financial impacts of flood and storm surge between 2015 and 2050 in France. Int. J. Saf. Secur. Eng. 2016, 6, 141–149. [Google Scholar] [CrossRef][Green Version]
- Kapsambelis, D.; Moncoulon, D.; Veysseire, M.; Cordier, J. Impact of Climate Change on Agricultural Economic Losses in France: Modelling Drought and Frost Events in 2050 and Their Impact on Agricultural Yield Loss Rates; European Meteorological Society, Berlin: Lyngby, Denmark, 2019; Volume 16, p. 130. [Google Scholar]
- OMM; GWP. Programme de Gestion Intégrée des Sécheresses. In Manuel des Indicateurs et Indices de Sécheresse; Svoboda, M., Fuchs, B.A., Eds.; OMM: Genève, Switzerland, 2016. [Google Scholar]
- Banimahd, S.A.; Khalili, D. Factors Influencing Markov Chains Predictability Characteristics, Utilizing SPI, RDI, EDI, and SPEI Drought Indices in Different Climatic Zones. Water Resour. Manag. 2013, 27, 3911–3928. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Droughts; Weather Bureau Research Paper; U.S. Department of Commerce: Washington, DC, USA, 1965; p. 58.
- Karl, T.R. Some spatial characteristics of drought duration in the United States. J. Clim. Appl. Meteorol. 1983, 22, 1356–1366. [Google Scholar] [CrossRef]
- Karl, T.R. The sensitivity of the Palmer Drought Severity Index and Palmer’s Z-Index to their calibration coefficients including Potential Evapotranspiration. J. Clim. Appl. Meteorol. 1986, 25, 77–86. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer Drought Severity Index: Limitationd and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Guttman, N.B. Comparing the palmer drought index and the standardized precipitation index1. J. Am. Water Resour. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-Calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–184. [Google Scholar]
- Byun, H.R.; Wilhite, D.A. Daily quantification of drought severity and duration. J. Clim. 1996, 5, 1181–1201. [Google Scholar]
- Lobell, D.B.; Hammer, G.L.; McLean, G.; Messina, C.; Roberts, M.J.; Schlenker, W. The critical role of extreme heat for maize production in the United States. Nat. Clim. Chang. Lett. 2013, 3, 497–501. [Google Scholar] [CrossRef]
- Iizumi, T.; Ramankutty, N. Changes in yield variability of major crops for 1981–2010 explained by climate change. Environ. Res. Lett. 2016, 11, 34003. [Google Scholar] [CrossRef]
- Teixeira, E.I.; Fischer, G.; van Velthuizen, H.; Walter, C.; Ewert, F. Global hot-spots of heat stress on agricultural crops due to climate change. Agric. For. Meteorol. 2013, 170, 206–215. [Google Scholar] [CrossRef]
- Ray, D.K.; Gerber, J.S.; MacDonald, G.K.; West, P.C. Climate variation explains a third of global crop yield variability. Nat. Commun. 2015, 6, 5989. [Google Scholar] [CrossRef] [PubMed]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Ayanlade, A.; Radeny, M.; Morton, J.F.; Muchaba, T. Rainfall variability and drought characteristics in two agro-climatic zones: An assessment of climate change challenges in Africa. Sci. Total Environ. 2018, 630, 728–737. [Google Scholar] [CrossRef]
- Rebetez, M.; Mayer, H.; Dupont, O.; Schindler, D.; Gartner, K.; Kropp, J.P.; Menzel, A. Heat and drought 2003 in Europe: A climate synthetis. Ann. For. Sci. 2006, 63, 569–577. [Google Scholar] [CrossRef]
- Potop, V.; Možný, M.; Soukup, J. Drought evolution at various time scales in the lowland regions and their impact on vegetable crops in the Czech Republic. Agric. For. Meteorol. 2012, 156, 121–133. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Donohue, R.; McVicar, T.; Roderick, M. Assessing the ability of potential evaporation formulations to capture the dynamics in evaporative demand within a changing climate. J. Hydrol. 2010, 386, 186–197. [Google Scholar] [CrossRef]
- Tsakiris, G.; Vangelis, H. Establishing a Drought Index Incorporating Evapotranspiration. Eur. Water 2005, 9/10, 3–11. [Google Scholar]
- Woli, P.; Jones, J.W.; Ingram, K.T.; Fraisse, C.W. Agricultural reference index for drought (ARID). Agron. J. 2012, 104, 287–300. [Google Scholar] [CrossRef]
- Fu, B.P. On the calculation of the evaporation from and surface. Chin. J. Atmos. Sci. 1981, 5, 23–31. (In Chinese) [Google Scholar]
- Pagani, V.; Guarneri, T.; Fumagalli, D.; Movedi, E.; Testi, L.; Klein, T.; Calanca, P.; Villalobos, F.; Lopez-Bernal, A.; Niemeyer, S.; et al. Improving cereal yield forecasts in Europe—The impact of weather extremes. Eur. J. Agron. 2017, 89, 97–106. [Google Scholar] [CrossRef]
- Sepulcre-Canto, G.; Horion, S.; Singleton, A.; Carrao, H.; Vogt, J. Development of a Combined Drought Indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef]
- Anderson, M.C.; Hain, C.; Wardlow, B.; Pimstein, A.; Mecikalski, J.R.; Kustas, W.P. Evaluation of drought indices based on hermal Remote Sensing of evapotranspiration over the continental United States. J. Clim. 2011, 24, 2025–2044. [Google Scholar] [CrossRef]
- Huete, A.R.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A Normalized Difference Water Index for Remote Sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Brown, J.F.; Wardlow, B.D.; Tadesse, T.; Hayes, M.J.; Reed, B.C. The Vegetation Drought Response Index (VegDRI): A new integrated approach for monitoring drought stress in vegetation. GISci. Remote Sens. 2008, 45, 16–46. [Google Scholar] [CrossRef]
- Roumiguié, A.; Jacquin, A.; Sigel, G.; Hervé, P.; Lepoivre, B.; Hagolle, O. Development of an index-based insurance product: Validation of a forage production index derived from medium spatial resolution fCover time series. GISci. Remote Sens. 2015, 52, 94–113. [Google Scholar] [CrossRef]
- Ministère de l’Agriculture, de l’Agroalimentaire et de la Foret, Ministère de l’Economie et des Finances Cahier des charges applicable aux entreprises d’assurance pour la prise en charge partielle de primes et cotisations d’assurance récolte 2016. Pris en application des articles 1, 2 et 10 du décret fixant pour les années 2016-2020 les modalités d’application de l’article L. 361-4 du code rural et de la pêche maritime en vue de favoriser le développement de l’assurance contre certains risques agricoles. 2016. Available online: https://www.legifrance.gouv.fr/affichTexte.do?cidTexte=JORFTEXT000037330968&categorieLien=id (accessed on 24 October 2019).
- Sklar, A. Fonctions de repartition à n dimensions et leurs marges. Institut Statistique de l’Université de Paris 1959, 8, 229–231. [Google Scholar]
- Moncoulon, D.; Desarthe, J.; Naulin, J.-P.; Onfroy, T.; Tinard, P.; Wang, Z.-X.; Hajji, C.; Veysseire, M.; Dequé, M.; Régimbeau, F. Conséquences du Changement Climatique sur le Coût des Catastrophes Naturelles en France à L’horizon 2050; Caisse Centrale de Réassurance & Météo: Paris, France, 2018; p. 31. [Google Scholar]
- Caisse Centrale de Réassurance. Modélisation de L’impact du Changement Climatique sur les Dommages Assurés Dans le Cadre du Régime Catastrophes Naturelles; Caisse Centrale de Réassurance: Paris, France, 2015. [Google Scholar]

| Crop | Simulated Average Annual Losses (10th Percentile–90th Percentile) | Historical Average Annual Losses (Extreme Losses) | Simulated Maximum Claim (10th Percentile–90th Percentile) | Estimated Historical Maximum Claim |
|---|---|---|---|---|
| Soft winter wheat | 82.0 (71.5–98.8) | 111.4 | 1403.2 (783.1–1735.0) | 846.9 |
| Winter barley | 18.5 (16.0–22.8) | 25.0 | 262.6 (140.3–310.7) | 178.2 |
| Sunflower | 19.7 (16.3–24.0) | 20.1 | 253.3 (130.8–380.5) | 139.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapsambelis, D.; Moncoulon, D.; Cordier, J. An Innovative Damage Model for Crop Insurance, Combining Two Hazards into a Single Climatic Index. Climate 2019, 7, 125. https://doi.org/10.3390/cli7110125
Kapsambelis D, Moncoulon D, Cordier J. An Innovative Damage Model for Crop Insurance, Combining Two Hazards into a Single Climatic Index. Climate. 2019; 7(11):125. https://doi.org/10.3390/cli7110125
Chicago/Turabian StyleKapsambelis, Dorothée, David Moncoulon, and Jean Cordier. 2019. "An Innovative Damage Model for Crop Insurance, Combining Two Hazards into a Single Climatic Index" Climate 7, no. 11: 125. https://doi.org/10.3390/cli7110125
APA StyleKapsambelis, D., Moncoulon, D., & Cordier, J. (2019). An Innovative Damage Model for Crop Insurance, Combining Two Hazards into a Single Climatic Index. Climate, 7(11), 125. https://doi.org/10.3390/cli7110125





