Central Asia’s Changing Climate: How Temperature and Precipitation Have Changed across Time, Space, and Altitude
Abstract
1. Introduction
2. Materials and Methods
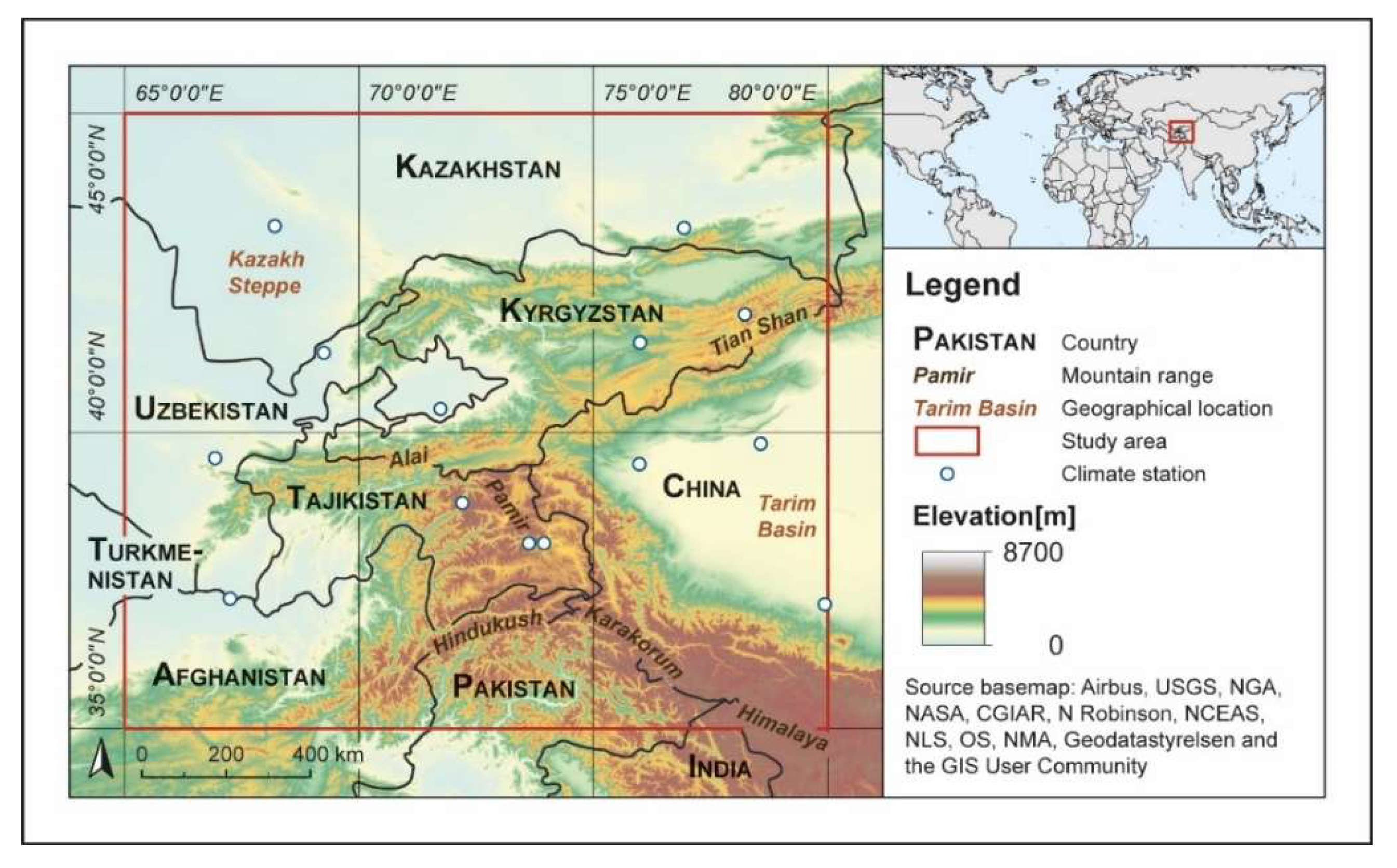
2.1. Study Area
2.2. Data
2.2.1. CRU TS v. 4.01
2.2.2. TRMM 3B43 v.7
2.3. Methods
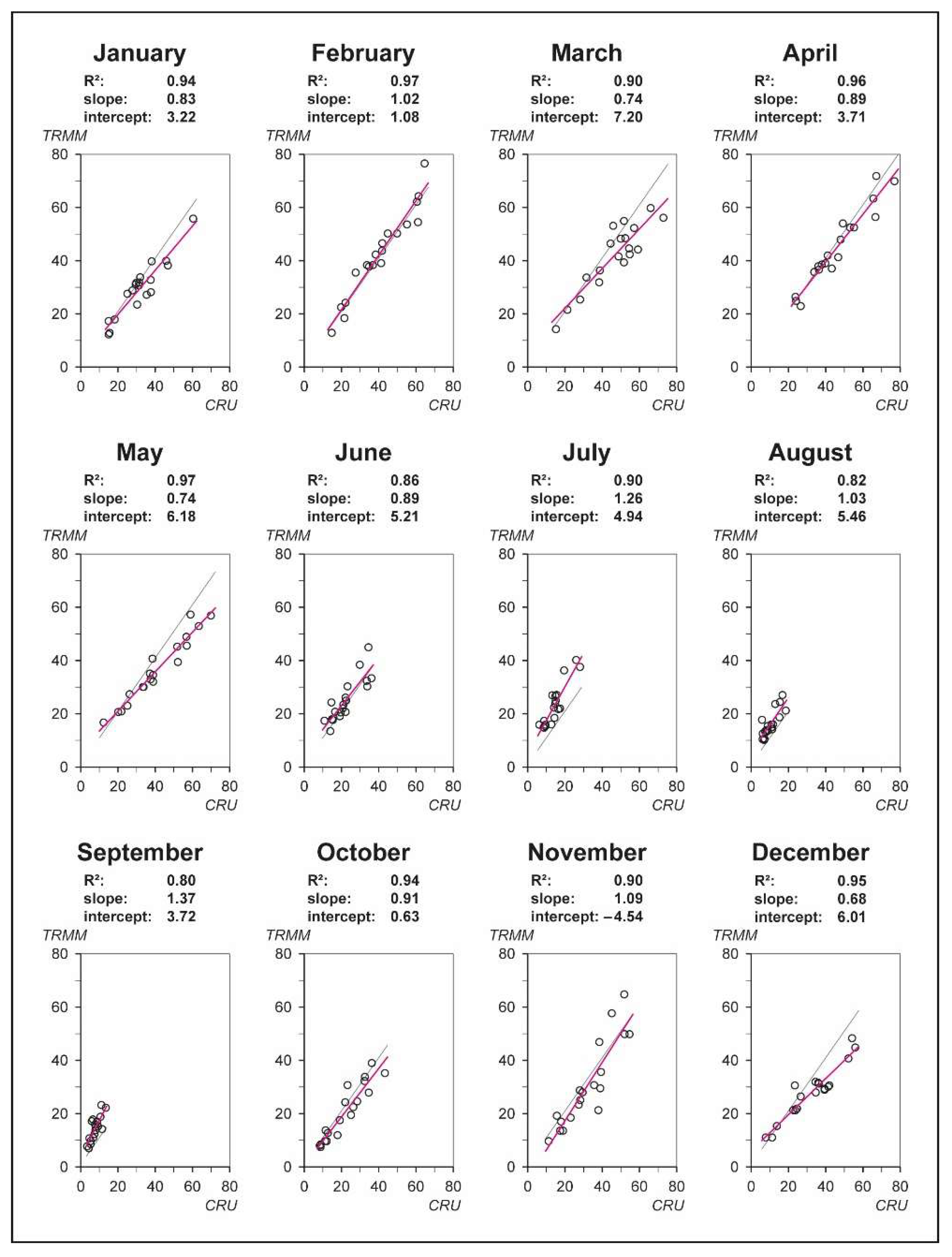
2.3.1. Linear Merging of the CRU TS and TRMM 3B43 Datasets
2.3.2. Temporal Trend Analysis
2.3.3. Spatial Trend Analysis
Mann–Kendall Test
Theil and Sen’s Slope Estimator
3. Results
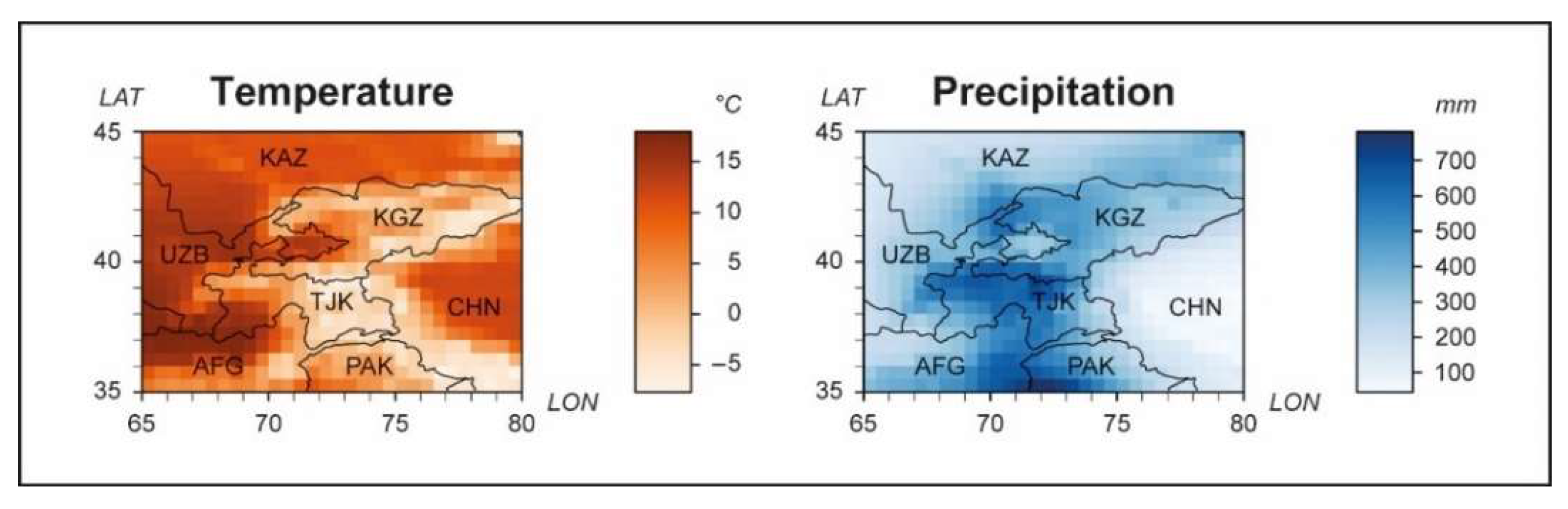
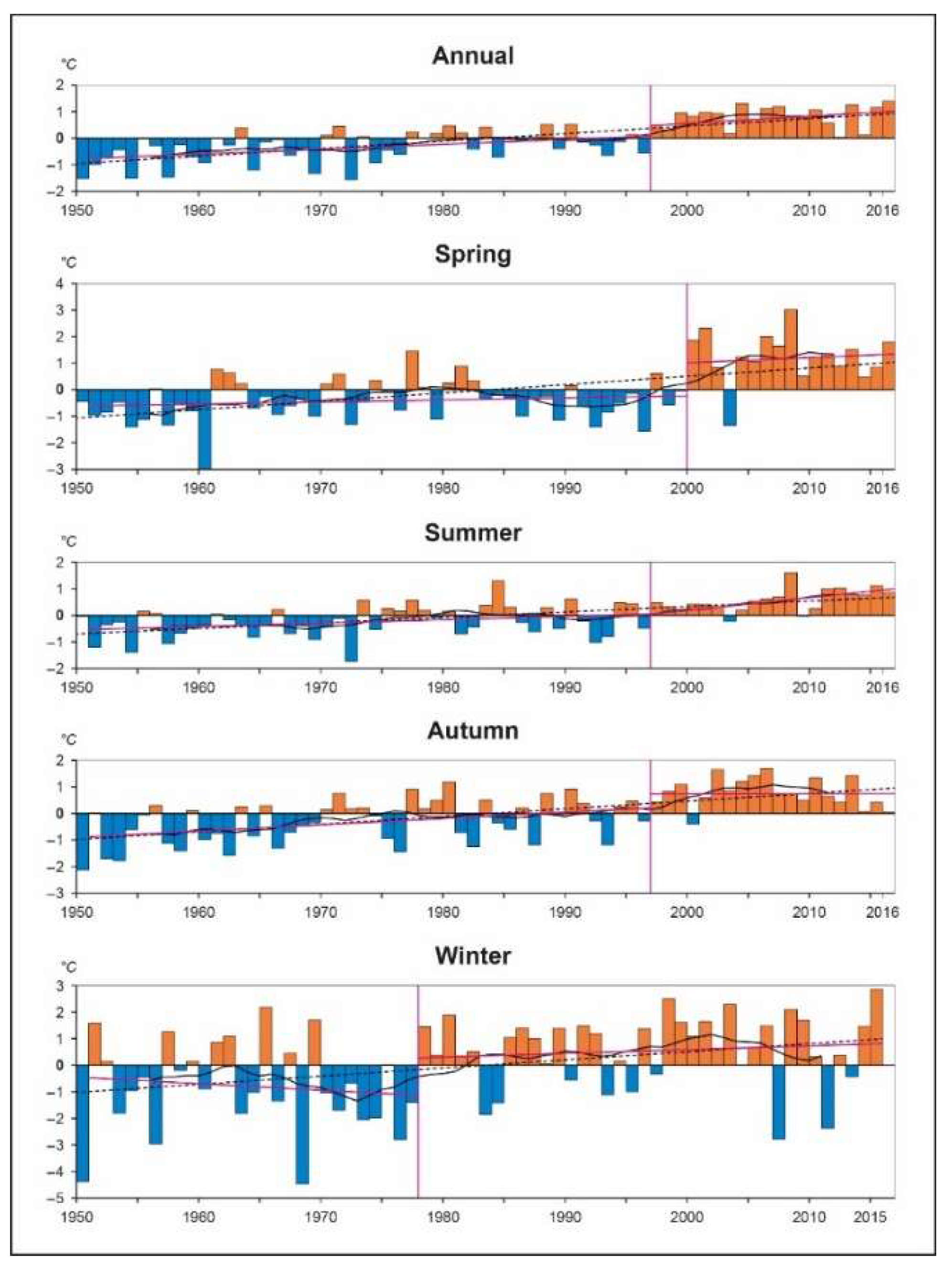
3.1. Temporal Changes in Air Temperature
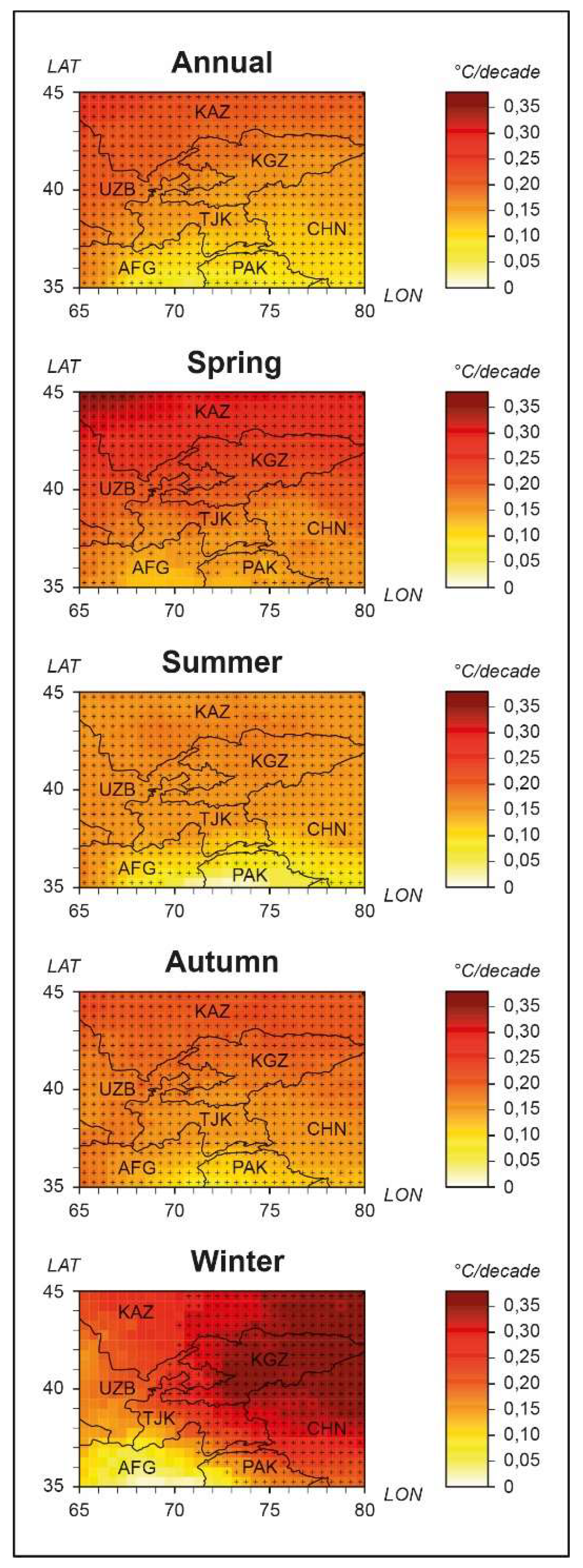
3.2. Spatial Changes in Air Temperature
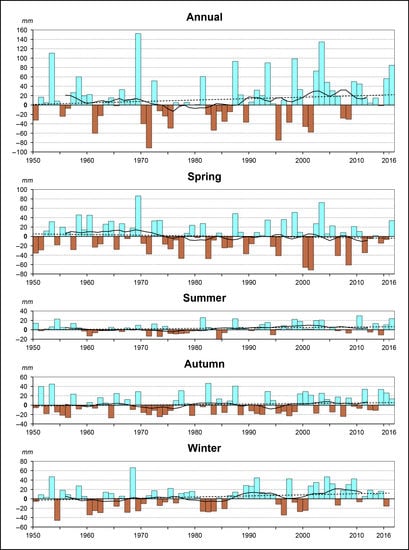
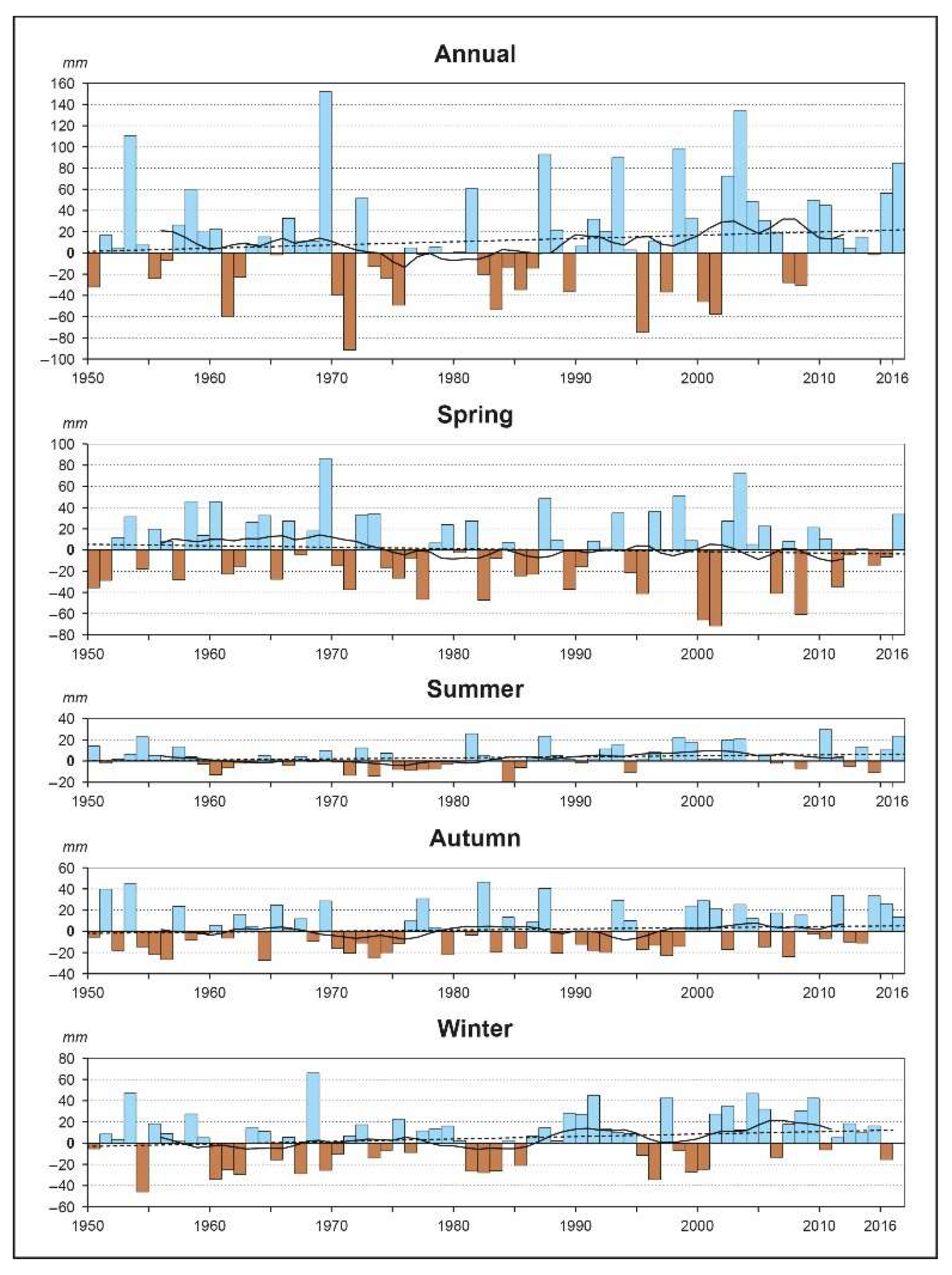
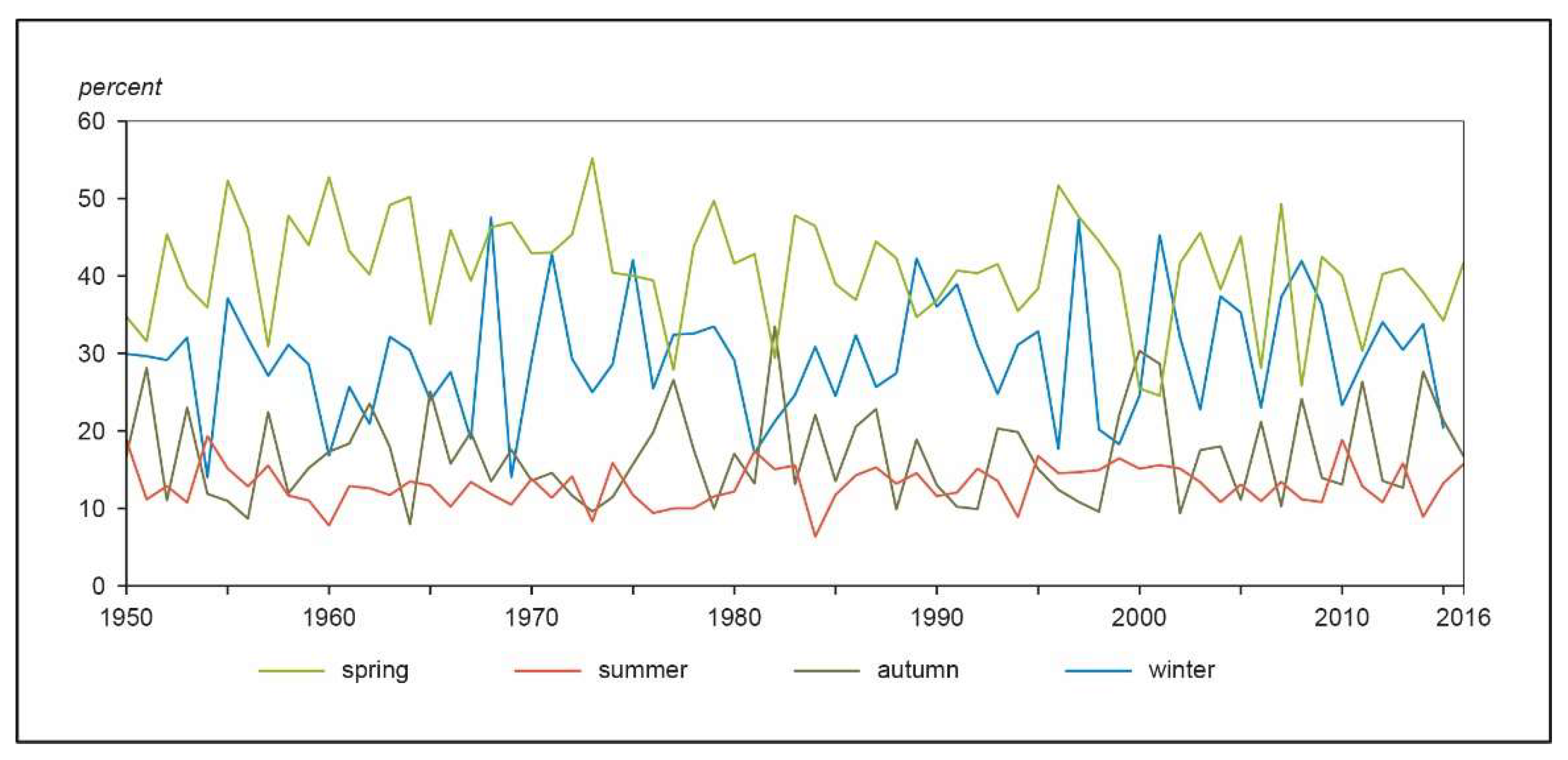
3.3. Temporal Changes in Precipitation
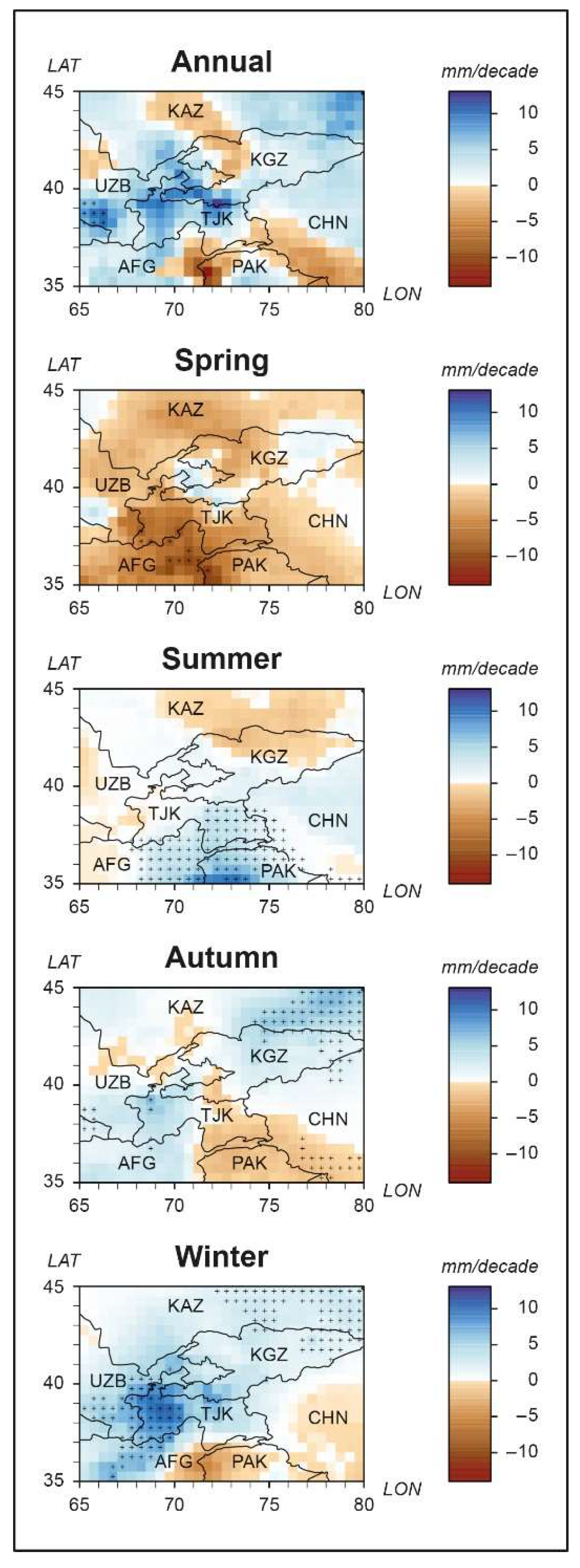
3.4. Spatial Changes in Precipitation
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Henebry, G.M.; Owsley, B.C.; Sokolik, I.N. Large scale climate oscillation impacts on temperature, precipitation and land surface phenology in Central Asia. Environ. Res. Lett. 2018, 13, 65018. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, C.; Hu, Q.; Tian, H. Temperature changes in Central Asia from 1979 to 2011 based on multiple datasets. J. Clim. 2014, 27, 1143–1167. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Shen, Y.; Li, B. Tracking climate change in Central Asia through temperature and precipitation extremes. J. Geogr. Sci. 2019, 29, 3–28. [Google Scholar] [CrossRef]
- Chen, F.; Huang, W.; Jin, L.; Chen, J.; Wang, J. Spatiotemporal precipitation variations in the arid Central Asia in the context of global warming. Sci. China Earth Sci. 2011, 54, 1812–1821. [Google Scholar] [CrossRef]
- Hu, Z.; Zhou, Q.; Chen, X.; Qian, C.; Wang, S.; Li, J. Variations and changes of annual precipitation in Central Asia over the last century. Int. J. Climatol. 2017, 37, 157–170. [Google Scholar] [CrossRef]
- Reyer, C.P.O.; Otto, I.M.; Adams, S.; Albrecht, T.; Baarsch, F.; Cartsburg, M.; Coumou, D.; Eden, A.; Ludi, E.; Marcus, R.; et al. Climate change impacts in Central Asia and their implications for development. Reg. Environ. Chang. 2015. [Google Scholar] [CrossRef]
- Seim, A.; Schultz, J.A.; Leland, C.; Davi, N.; Byambasuren, O.; Liang, E.; Wang, X.; Beck, C.; Linderholm, H.W.; Pederson, N. Synoptic-scale circulation patterns during summer derived from tree rings in mid-latitude Asia. Clim. Dyn. 2016, 49, 1917–1931. [Google Scholar] [CrossRef]
- Siegfried, T.; Bernauer, T.; Guiennet, R.; Sellars, S.; Robertson, A.W.; Mankin, J.; Bauer-Gottwein, P.; Yakovlev, A. Will climate change exacerbate water stress in Central Asia? Clim. Chang. 2012, 112, 881–899. [Google Scholar] [CrossRef]
- Yin, G.; Hu, Z.; Chen, X.; Tiyip, T. Vegetation dynamics and its response to climate change in Central Asia. J. Arid Land 2016, 8, 375–388. [Google Scholar] [CrossRef]
- Xenarios, S.; Gafurov, A.; Schmidt-Vogt, D.; Sehring, J.; Manandhar, S.; Hergarten, C.; Shigaeva, J.; Foggin, M. Climate change and adaptation of mountain societies in Central Asia: Uncertainties, knowledge gaps, and data constraints. Reg. Environ. Change 2019, 19, 1339–1352. [Google Scholar] [CrossRef]
- Hijioka, Y.; Lin, E.; Pereira, J.J.; Corlett, R.T.; Gui, X.; Insarov, G.E.; Lasco, R.D.; Lindgren, E.; Surjan, A. Asia. In Climate Change 2014: Impacrs, Adaptation, and Vulnerability. Part B: Regional Aspects. Contributions of Working Group II to the Fith Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Lioubimtseva, E.; Henebry, G.M. Climate and environmental change in arid Central Asia: Impacts, vulnerability, and adaptations. J. Arid Environ. 2009, 73, 963–977. [Google Scholar] [CrossRef]
- Bhutiyani, M.R.; Kale, V.S.; Pawar, N.J. Climate change and the precipitation variations in the northwestern Himalaya: 1866–2006. Int. J. Climatol. 2010, 85. [Google Scholar] [CrossRef]
- Liu, X.; Chen, B. Climatic warming in the Tibetan Plateau during recent decades. Int. J. Climatol. 2000, 20, 1729–1742. [Google Scholar] [CrossRef]
- Shekhar, M.S.; Chand, H.; Kumar, S.; Srinivasan, K.; Ganju, A. Climate-change studies in the western Himalaya. Ann. Glaciol. 2010, 51, 105–112. [Google Scholar] [CrossRef]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Glob. Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Q.; Chen, X.; Teng, Z.; Chen, C.; Yin, G.; Zhang, Y. Climate changes in temperature and precipitation extremes in an alpine grassland of Central Asia. Theor. Appl. Climatol. 2016, 126, 519–531. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Hartmann, H.; Buchanan, H. Trends in extreme precipitation events in the Indus river basin and flooding in Pakistan. Atmos. Ocean 2014, 52, 77–91. [Google Scholar] [CrossRef]
- Palazzi, E.; von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Ren, Y.-Y.; Ren, G.-Y.; Sun, X.-B.; Shrestha, A.B.; You, Q.-L.; Zhan, Y.-J.; Rajbhandari, R.; Zhang, P.-F.; Wen, K.-M. Observed changes in surface air temperature and precipitation in the Hindu Kush Himalayan region over the last 100-plus years. Adv. Clim. Change Res. 2017, 8, 148–156. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beck, L.P.H.; Bierkens, M.F.P. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Wang, J.; Jin, L.; Zhang, Q.; Li, J.; Chen, J. Rapid warming in mid-latitude central Asia for the past 100 years. Front. Earth Sci. China 2009, 3, 42–50. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Bai, L.; Xu, J. Multiscale evolution of surface air temperature in the arid region of Northwest China and its linkages to ocean oscillations. Theor. Appl. Climatol. 2017, 128, 945–958. [Google Scholar] [CrossRef]
- Feng, R.; Yu, R.; Zheng, H.; Gan, M. Spatial and temporal variations in extreme temperature in Central Asia. Int. J. Climatol. 2018, 38, e388–e400. [Google Scholar] [CrossRef]
- Aizen, E.M.; Aizen, V.B.; Melack, J.M.; Nakamura, T.; Ohta, T. Precipitation and atmospheric circulation patterns at mid-latitudes of Asia. Int. J. Climatol. 2001, 21, 535–556. [Google Scholar] [CrossRef]
- Song, S.; Bai, J. Increasing winter precipitation over arid Central Asia under global warming. Atmosphere 2016, 7, 139. [Google Scholar] [CrossRef]
- Chen, X.; Wang, S.; Hu, Z.; Zhou, Q.; Hu, Q. Spatiotemporal characteristics of seasonal precipitation and their relationships with ENSO in Central Asia during 1901–2013. J. Geogr. Sci. 2018, 28, 1341–1368. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Peterson, T.C.; Quadir, D.A.; Dorji, S.; Zou, X.; Tang, H.; Santhosh, K.; Joshi, U.R.; Jaswal, A.K.; Kolli, R.K.; et al. Changes in daily temperature and precipitation extremes in Central and South Asia. J. Geophys. Res. 2006, 111, D23107. [Google Scholar] [CrossRef]
- Yao, J.; Chen, Y. Trend analysis of temperature and precipitation in the Syr Darya Basin in Central Asia. Theor. Appl. Climatol. 2015, 120, 521–531. [Google Scholar] [CrossRef]
- Hu, Z.; Hu, Q.; Zhang, C.; Chen, X.; Li, Q. Evaluation of reanalysis, spatially interpolated and satellite remotely sensed precipitation data sets in central Asia. J. Geophys. Res. Atmos. 2016, 121, 5648–5663. [Google Scholar] [CrossRef]
- Pohl, E.; Knoche, M.; Gloaguen, R.; Andermann, C.; Krause, P. The hydrological cycle in the high Pamir Mountains: How temperature and seasonal precipitation distribution influence stream flow in the Gunt catchment, Tajikistan. Earth Surf. Dynam. Discuss. 2014, 2, 1155–1215. [Google Scholar] [CrossRef]
- Schiemann, R.; Lüthi, D.; Vidale, P.L.; Schär, C. The precipitation climate of Central Asia—Intercomparison of observational and numerical data sources in a remote semiarid region. Int. J. Climatol. 2008, 28, 295–314. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Raykova, K.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U. GPCC Full Data Daily Version 1.0 at 1.0: Daily Land-Surface Precipitation from Rain-Gauges built on GTS-based and Historic Data. Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory. Available online: https://doi.org/10.5065/D6V69GRT (accessed on 1 March 2017).
- Willmott, C.J.; Matsuura, K. Terrestrial Air Temperature: 1900–2010 Gridded Monthly Time Series (1900–2010): Version 3.01. Available online: http://climate.geog.udel.edu/~climate/html_pages/README.ghcn_ts2.html (accessed on 1 March 2018).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-Global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Tropical Rainfall Measuring Mission (TRMM). TRMM 2011 (TMPA/3B43) Rainfall Estimate L3 1 Month 0.25 Degree × 0.25 Degree V7, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://disc.gsfc.nasa.gov/datacollection/TRMM_3B43_7.html (accessed on 1 March 2018).
- Karaseva, M.O.; Prakash, S.; Gairola, R.M. Validation of high-resolution TRMM-3B43 precipitation product using rain gauge measurements over Kyrgyzstan. Theor. Appl. Climatol. 2012, 108, 147–157. [Google Scholar] [CrossRef]
- Rana, S.; McGregor, J.; Renwick, J. Wintertime precipitation climatology and ENSO sensitivity over central southwest Asia. Int. J. Climatol. 2017, 37, 1494–1509. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, Y. Evaluating the performance of remote sensing precipitation products CMORPH, PERSIANN, and TMPA, in the arid region of northwest China. Theor. Appl. Climatol. 2014, 118, 429–445. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.; Xue, X.; Zhang, X. Inter-Comparison of high-resolution satellite precipitation products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef]
- Zhao, W.; Yu, X.; Ma, H.; Zhu, Q.; Zhang, Y.; Qin, W.; Ai, N.; Wang, Y. Analysis of precipitation characteristics during 1957–2012 in the Semi-Arid Loess Plateau, China. PLoS ONE 2015, 10, 1–13. [Google Scholar] [CrossRef]
- Huang, A.; Zhou, Y.; Zhang, Y.; Huang, D.; Zhao, Y.; Wu, H. Changes of the annual precipitation over Central Asia in the twenty-first century projected by multimodels of CMIP5. J. Clim. 2014, 27, 6627–6646. [Google Scholar] [CrossRef]
- Small, E.E.; Giorgi, F.; Sloan, L.C. Regional climate model simulation of precipitation in central Asia: Mean and interannual variability. J. Geophys. Res. 1999, 104, 6563–6582. [Google Scholar] [CrossRef]
- Böhner, J. General climatic controls and topoclimatic variations in Central and High Asia. Boreas 2006, 35, 279–295. [Google Scholar] [CrossRef]
- National Centers for Environmental Information (NCEI). Climate Data Online (CDO)—The National Climatic Data Center’s (NCDC) Climate Data Online (CDO) Provides Free Access to NCDC’s Archive of Historical Weather and Climate Data in Addition to Station History Information. National Climatic Data Center (NCDC). Available online: https://www.ncdc.noaa.gov/cdo-web/ (accessed on 22 August 2019).
- Huang, J.; Guan, X.; Ji, F. Enhanced cold-season warming in semi-arid regions. Atmos. Chem. Phys. 2012, 12, 5391–5398. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, H. Impacts of SST warming in tropical Indian Ocean on CMIP5 model-projected summer rainfall changes over Central Asia. Clim. Dyn. 2016, 46, 3223–3238. [Google Scholar] [CrossRef]
- Mao, J.; Wu, G. Diurnal variations of summer precipitation over the Asian monsoon region as revealed by TRMM satellite data. Sci. China Earth Sci. 2012, 55, 554–566. [Google Scholar] [CrossRef]
- Shrestha, D.; Singh, P.; Nakamura, K. Spatiotemporal variation of rainfall over the central Himalayan region revealed by TRMM precipitation radar. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- RStudio: Integrated Development Environment for R; RStudio, Inc.: Boston, MA, USA, 2012.
- Hyndman, R.J.; Athanasopoulos, G.; Bergmeir, C.; Caceres, G.; Chhay, L.; O’Hara-Wild, M.; Petropoulos, F.; Razbash, S.; Wang, E.; Yasmeen, F. Forecast: Forecasting functions for time series and linear models. R package. 2019. [Google Scholar]
- Ross, G.J. Parametric and nonparametric sequential change detection in R: The cpm package. J. Stat. Softw. 2015, 66. [Google Scholar] [CrossRef]
- Blyth, S.; Groombridge, B.; Lysenko, I.; Miles, L.; Newton, A. Mountain Watch; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Patakamuri, S.K. Modifiedmk: Modified Mann Kendall Trend Tests. R package version. 2017. [Google Scholar]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann–Kendall test. Water Resour. Res. 2002, 38, 41–47. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Charles Griffin & Company LTD: London/High Wycombe, UK, 1975. [Google Scholar]
- Blain, G.C. Removing the influence of the serial correlation on the Mann–Kendall test. Rev. Bras. Meteorol. 2014, 29, 161–170. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. Ј. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Part 3. Ned. Akad. Wet. 1950, 53, 1397–1412. [Google Scholar]
- Bhutiyani, M.R.; Kale, V.S.; Pawar, N.J. Long-term trends in maximum, minimum and mean annual air temperatures across the Northwestern Himalaya during the twentieth century. Clim. Change 2007, 85, 159–177. [Google Scholar] [CrossRef]
- Geng, Q.; Wu, P.; Zhao, X. Spatial and temporal trends in climatic variables in arid areas of northwest China. Int. J. Climatol. 2016, 36, 4118–4129. [Google Scholar] [CrossRef]
- Jones, P.D.; Harpham, C.; Harris, I.; Goodess, C.M.; Burton, A.; Centella-Artola, A.; Taylor, M.A.; Bezanilla-Morlot, A.; Campbell, J.D.; Stephenson, T.S.; et al. Long-term trends in precipitation and temperature across the Caribbean. Int. J. Climatol. 2016, 36, 3314–3333. [Google Scholar] [CrossRef]
- Syed, F.S.; Giorgi, F.; Pal, J.S.; Keay, K. Regional climate model simulation of winter climate over Central-Southwest Asia, with emphasis on NAO and ENSO effects. Int. J. Climatol. 2010, 30, 220–235. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Wang, H.; Liu, X. A comparative study on precipitation climatology and interannual variability in the lower midlatitude East Asia and Central Asia. J. Clim. 2014, 27, 7830–7848. [Google Scholar] [CrossRef]
- Viviroli, D.; Archer, D.R.; Buytaert, W.; Fowler, H.J.; Greenwood, G.B.; Hamlet, A.F.; Huang, Y.; Koboltschnig, G.; Litaor, M.I.; López-Moreno, J.I.; et al. Climate change and mountain water resources: Overview and recommendations for research, management and policy. Hydrol. Earth Syst. Sci. 2011, 15, 471–504. [Google Scholar] [CrossRef]
- Rangwala, I.; Miller, J.R. Climate change in mountains: A review of elevation-dependent warming and its possible causes. Clim. Change 2012, 114, 527–547. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 2011, 34, 448–467. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. A new scheme for multivariate, multisite weather generator with inter-variable, inter-site dependence and inter-annual variability based on empirical copula approach. Clim. Dyn. 2019, 52, 2247–2267. [Google Scholar] [CrossRef]
- Paschalis, A.; Molnar, P.; Fatichi, S.; Burlando, P. A stochastic model for high-resolution space-time precipitation simulation. Water Resour. Res. 2013, 49, 8400–8417. [Google Scholar] [CrossRef]
| (A) | |||||
|---|---|---|---|---|---|
| Abbr. | Name | Variables | Spatial Resolution | Temporal Resolution | Source |
| OBS | Observations meteorological stations | Temperature Precipitation | Point data | Monthly | [48] |
| CRU TS | CRU TS v. 4.01 Climatic Research Unit | Temperature Precipitation | 0.5° × 0.5° | Monthly 1901–2016 | [35] |
| TRMM 3B43 | TRMM 3B43 v. 7 Tropical Rainfall Measuring Mission | Precipitation | 0.25° × 0.25° | Three-hourly since 1998 | [39] |
| (B) | |||||
|---|---|---|---|---|---|
| Number | WMO Code | Name | Latitude (°N) | Longitude (°E) | Elevation (masl) |
| 1 | 36870 | Almaty | 43.23 | 76.93 | 847 |
| 2 | 51716 | Bachu | 39.80 | 78.57 | 1117 |
| 3 | 38618 | Fergana | 40.37 | 71.75 | 578 |
| 4 | 51828 | Hotan | 37.13 | 79.93 | 1375 |
| 5 | no code | Irkht | 38.16 | 72.63 | 3276 |
| 6 | 51709 | Kashi | 39.44 | 75.98 | 1291 |
| 7 | no code | Lednik Phedchenko | 38.83 | 72.22 | 4169 |
| 8 | no code | Murghab | 38.16 | 73.96 | 3576 |
| 9 | 36974 | Naryn | 41.43 | 76.00 | 2039 |
| 10 | 38696 | Samarkand | 39.57 | 66.95 | 726 |
| 11 | 38457 | Tashkent | 41.27 | 69.27 | 477 |
| 12 | 38927 | Termez | 37.23 | 67.27 | 309 |
| 13 | 36982 | Tian Shan | 41.88 | 78.23 | 3639 |
| 14 | 38198 | Turkestan | 43.27 | 68.22 | 206 |
| N° | Station | CRU TS 4.01 (Temperature) | CRU TS/TRMM 3B43 (Precipitation) | TRMM 3B43 (Precipitation) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (°C/month) | MAE (°C/month) | R2 | RMSE (mm/month) | MAE (mm/month) | R2 | RMSE (mm/month) | MAE (mm/month) | ||
| 1 | Almaty | 0.96 * | 0.62 | 0.46 | 0.64 * | 10.29 | 8.05 | 0.28 * | 11.77 | 9.67 |
| 2 | Bachu | 0.94 * | 0.84 | 0.63 | 0.70 * | 4.71 | 3.10 | −0.04 | 28.40 | 21.70 |
| 3 | Fergana | 0.97 * | 0.51 | 0.37 | 0.74 * | 9.37 | 7.19 | 0.43 * | 11.40 | 8.29 |
| 4 | Hotan | 0.97 * | 0.51 | 0.36 | 0.64 * | 4.58 | 3.57 | −0.04 | 34.80 | 29.20 |
| 5 | Irkht + | no data | no data | no data | 0.87 * | 14.38 | 10.32 | no data | no data | no data |
| 6 | Kashi | 0.95 * | 0.78 | 0.58 | 0.71 * | 7.48 | 5.06 | −0.07 | 20.70 | 16.10 |
| 7 | Lednik Phedchenko + | no data | no data | no data | 0.88 * | 23.62 | 17.34 | no data | no data | no data |
| 8 | Murghab + | no data | no data | no data | 0.39 * | 24.04 | 18.39 | no data | no data | no data |
| 9 | Naryn | 0.94 * | 1.16 | 0.84 | 0.59 * | 10.34 | 7.60 | 0.43 * | 15.26 | 10.72 |
| 10 | Samarkand | 0.97 * | 0.54 | 0.41 | 0.83 * | 10.60 | 7.93 | 0.53 * | 13.60 | 10.50 |
| 11 | Tashkent | 0.97 * | 0.56 | 0.42 | 0.84 * | 8.66 | 6.53 | 0.24 * | 15.64 | 11.56 |
| 12 | Termez | 0.96 * | 0.68 | 0.50 | 0.82 * | 9.84 | 6.44 | 0.75 * | 16.10 | 12.10 |
| 13 | Tian Shan + | no data | no data | no data | 0.83 * | 10.33 | 7.66 | no data | no data | no data |
| 14 | Turkestan | 0.97 * | 0.71 | 0.50 | 0.94 * | 6.37 | 4.46 | no data | no data | no data |
| A | Temperature (°C/decade) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Season | Full | z-value | Confidence Interval | Mnt | z-value | Confidence Interval | Pln | z-value | Confidence Interval |
| Annual | 0.28 * | 6.47 | 0.22–0.35 | 0.13 * | 3.40 | 0.07–0.21 | 0.18 * | 3.84 | 0.11–0.29 |
| MAM | 0.30 * | 4.31 | 0.18–0.41 | 0.15 * | 3.36 | 0.00–0.20 | 0.17 * | 3.39 | 0.00–0.23 |
| JJA | 0.20 * | 5.31 | 0.14–0.27 | 0.07 * | 4.22 | 0.02–0.09 | 0.09 * | 5.28 | 0.05–0.12 |
| SON | 0.28 * | 5.26 | 0.18–0.39 | 0.12 * | 4.49 | 0.00–0.15 | 0.15 * | 4.16 | 0.00–0.17 |
| DJF | 0.32 * | 2.88 | 0.13–0.54 | 0.11 * | 3.63 | 0.06–0.17 | 0.10 * | 2.84 | 0.05–0.19 |
| Season | Precipitation (mm/month) | ||||||||
| Full | z-value | Confidence Interval | Mnt | z-value | Confidence Interval | Pln | z-value | Confidence Interval | |
| Annual | 3.13 | 0.94 | −2.48–+8.21 | 2.22 | 0.73 | −3.36–+8.26 | 2.41 | 1.35 | −1.80–+9.33 |
| MAM | −0.87 | −0.35 | −5.30–+3.35 | −0.01 | −0.04 | −0.40–+0.30 | −0.16 | −0.69 | −0.58–+0.29 |
| JJA | 0.68 | 1.05 | −0.66–+2.12 | 0.00 | 0.02 | −0.23–+0.20 | 0.15* | 2.48 | −0.58–+0.29 |
| SON | 1.29 | 0.93 | −1.41–+3.78 | 0.14 | 1.12 | −0.13–+0.42 | 0.13 | 1.32 | −0.09–+0.33 |
| DJF | 2.48 | 1.98 | 0.01–4.87 | 0.28* | 2.06 | −0.03–+0.51 | 0.33 | 1.66 | −0.13–+0.65 |
| B | Temperature (°C/decade) | Precipitation (mm/month) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | Full | z-value | Mnt. | z-value | Pln. | z-value | Full | z-value | Mnt. | z-value | Pln. | z-value |
| Jan. | 0.40 | 2.95 | 0.37 | 3.25 | 0.37 | 2.35 | 0.12 | 0.19 | 0.21 | 0.43 | 0.56 | 0.54 |
| Feb. | 0.37 | 1.78 | 0.37 | 2.36 | 0.39 | 1.78 | 1.23 | 1.47 | 0.59 | 0.85 | 1.42 | 1.25 |
| Mar. | 0.38 * | 3.20 | 0.28 | 2.60 | 0.37 | 2.45 | −0.14 | −0.09 | −0.21 | −0.15 | −0.86 | −0.65 |
| Apr. | 0.31 * | 3.63 | 0.20 | 2.75 | 0.29 * | 2.91 | −0.64 | −0.76 | −0.67 | −0.70 | −0.95 | −0.98 |
| May | 0.20 | 2.59 | 0.18 | 2.19 | 0.22 | 2.58 | 0.04 | 0.04 | 0.16 | 0.13 | −0.49 | −0.48 |
| Jun. | 0.25 * | 4.29 | 0.20 * | 3.60 | 0.26 * | 3.73 | 0.19 | 0.48 | 0.02 | 0.07 | 0.46 | 1.18 |
| Jul. | 0.15 * | 3.24 | 0.15 * | 2.94 | 0.14 | 2.63 | 0.24 | 0.57 | 0.04 | 0.13 | 0.41 | 1.57 |
| Aug. | 0.22 * | 4.05 | 0.12 | 2.74 | 0.18 * | 3.02 | 0.22 | 0.02 | 0.20 | 0.75 | 0.45 * | 2.18 |
| Sep. | 0.23 * | 4.22 | 0.17 * | 2.96 | 0.20 * | 3.49 | 0.21 | 1.26 | 0.24 | 1.12 | 0.25 | 1.57 |
| Oct. | 0.26 * | 3.46 | 0.19 | 2.60 | 0.23 | 2.61 | 0.87 | 1.20 | 0.99 | 1.14 | 0.54 | 0.76 |
| Nov. | 0.39 * | 3.13 | 0.24 | 2.32 | 0.27 | 2.09 | 0.41 | 0.50 | 0.08 | 0.05 | 0.73 | 0.81 |
| Dec. | 0.28 | 2.14 | 0.21 | 1.88 | 0.25 | 1.69 | 1.06 | 1.32 | 1.07 | 1.43 | 0.63 | 0.59 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haag, I.; Jones, P.D.; Samimi, C. Central Asia’s Changing Climate: How Temperature and Precipitation Have Changed across Time, Space, and Altitude. Climate 2019, 7, 123. https://doi.org/10.3390/cli7100123
Haag I, Jones PD, Samimi C. Central Asia’s Changing Climate: How Temperature and Precipitation Have Changed across Time, Space, and Altitude. Climate. 2019; 7(10):123. https://doi.org/10.3390/cli7100123
Chicago/Turabian StyleHaag, Isabell, Philip D. Jones, and Cyrus Samimi. 2019. "Central Asia’s Changing Climate: How Temperature and Precipitation Have Changed across Time, Space, and Altitude" Climate 7, no. 10: 123. https://doi.org/10.3390/cli7100123
APA StyleHaag, I., Jones, P. D., & Samimi, C. (2019). Central Asia’s Changing Climate: How Temperature and Precipitation Have Changed across Time, Space, and Altitude. Climate, 7(10), 123. https://doi.org/10.3390/cli7100123