Precipitation Trends over the Indus Basin
Abstract
1. Introduction
2. Methods
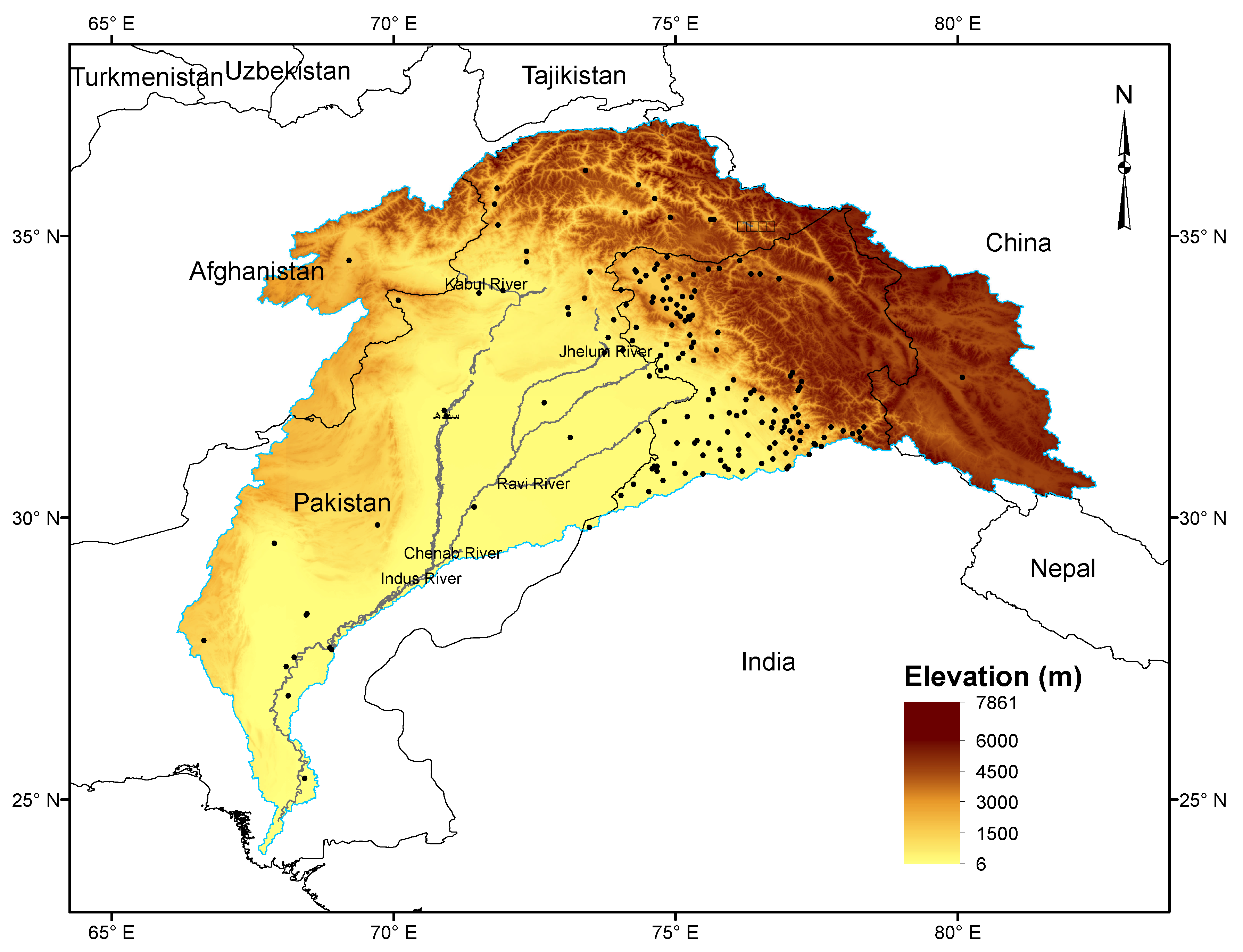
2.1. Basin Delineation
2.2. Station Precipitation Observations
- Precipitation up to the end of 2018 from all available stations ( 160) within the Indus basin were extracted from the Global Historical Climatology Network–Daily (GHCN) dataset [32]. The included stations were mostly in India, with some in Pakistan and Afghanistan. Observations went back as far as 1901, with the largest number before 1981. Observations flagged for quality concerns [33] were not used.
- Monthly precipitation for 35 stations in Pakistan, covering primarily the period 1980–2014, was obtained from the Pakistan Meteorological Department (PMD), Government of Pakistan.
- Monthly precipitation amounts for nine stations in Pakistan for 1997–2008 were obtained from the International Water Management Institute (IWMI) online Water Data Portal, with PMD also the ultimate source.
2.3. Gridded Precipitation Data Sets
2.3.1. Overview
2.3.2. Station-Based Gridded Data Sets
2.3.3. Satellite-Based Gridded Data Sets
2.3.4. Reanalyses
2.4. Evaluation of Gridded Precipitation Data Sets
2.5. Precipitation Trends
3. Results
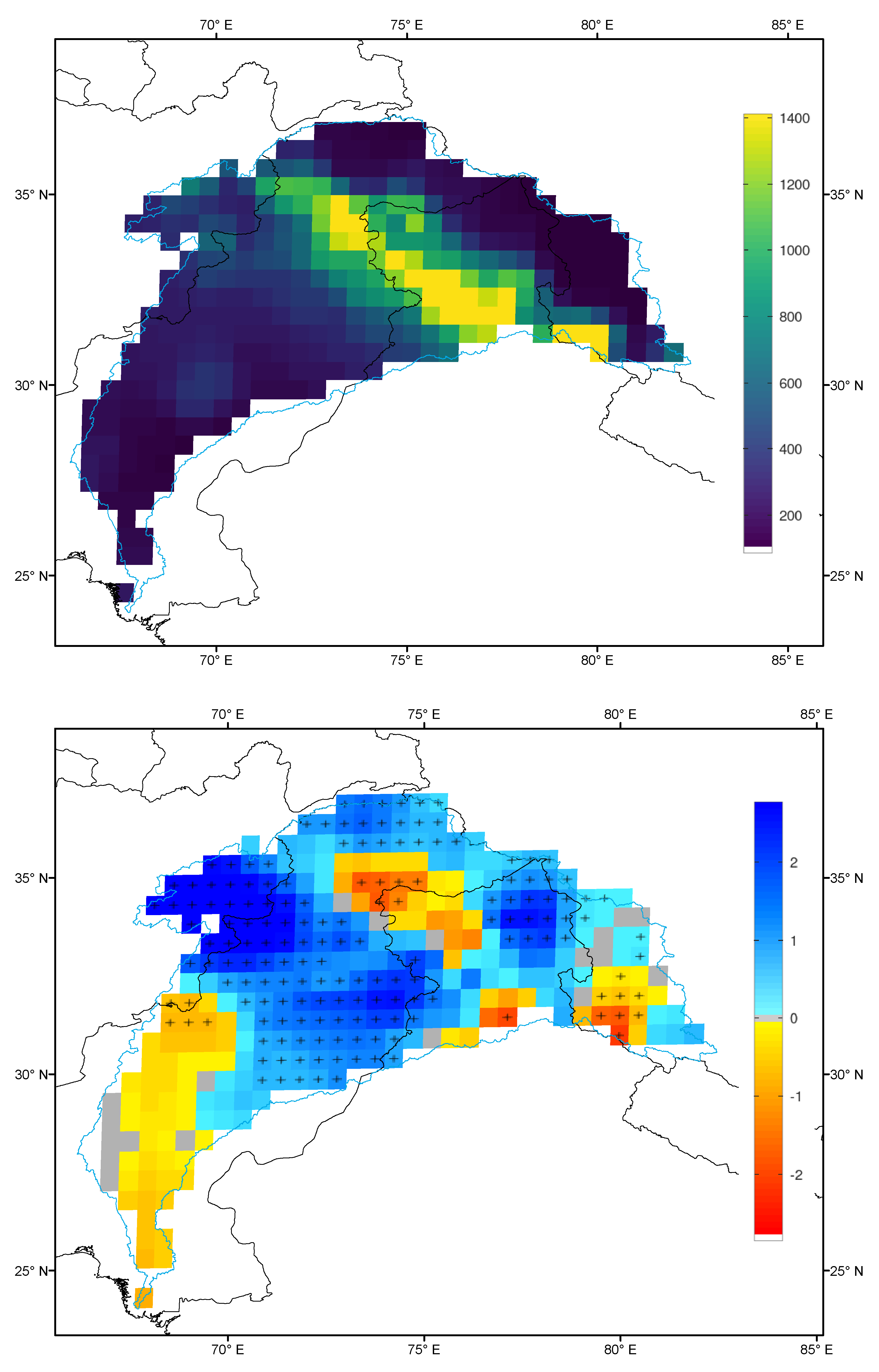
3.1. Comparison of Gridded Data Sets with Station Observations
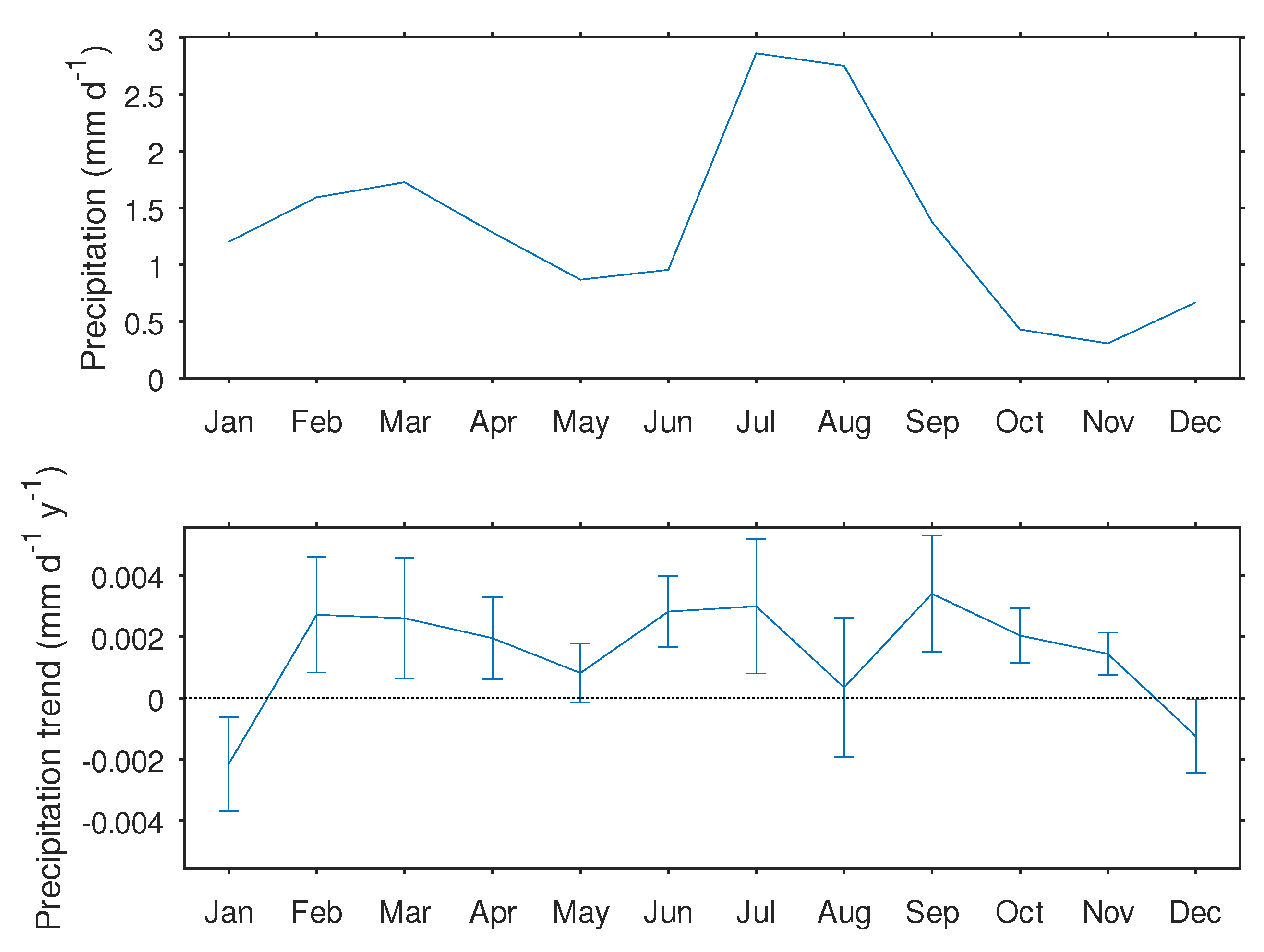
3.2. Trends in Basin Precipitation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frenken, K. Irrigation in Southern and Eastern Asia in Figures: AQUASTAT Survey—2011; Technical Report; Food and Agriculture Organization (FAO): Rome, Italy, 2012. [Google Scholar]
- Rajbhandari, R.; Shrestha, A.B.; Kulkarni, A.; Patwardhan, S.K.; Bajracharya, S.R. Projected changes in climate over the Indus river basin using a high resolution regional climate model (PRECIS). Clim. Dyn. 2015, 44, 339–357. [Google Scholar] [CrossRef]
- Zurick, D.; Pacheco, J.; Shreshta, B.; Bajracharya, B. Atlas of the Himalaya; International Centre for Integrated Mountain Development: Kathmandu, Nepal, 2005. [Google Scholar]
- Dimri, A.P.; Niyogi, D.; Barros, A.P.; Ridley, J.; Mohanty, U.C.; Yasunari, T.; Sikka, D.R. Western Disturbances: A review. Rev. Geophys. 2015, 53, 225–246. [Google Scholar] [CrossRef]
- Cannon, F.; Carvalho, L.M.V.; Jones, C.; Norris, J. Winter westerly disturbance dynamics and precipitation in the western Himalaya and Karakoram: A wave-tracking approach. Theor. Appl. Climatol. 2016, 125, 27–44. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Khan, A. A reevaluation of the snowmelt and glacial melt in river flows within Upper Indus basin and its significance in a changing climate. J. Hydrol. 2015, 527, 119–132. [Google Scholar] [CrossRef]
- Palazzi, E.; von Hardenberg, J.; Terzago, S.; Provenzale, A. Precipitation in the Karakoram-Himalaya: A CMIP5 view. Clim. Dyn. 2014. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Gemmer, M.; Jian, D.; Tao, H.; Jiang, T.; Zhao, C. Statistical downscaling of CMIP5 multi-model ensemble for projected changes of climate in the Indus River Basin. Atmos. Res. 2016, 178–179, 138–149. [Google Scholar] [CrossRef]
- Hasson, S. Seasonality of precipitation over Himalayan watersheds in CORDEX South Asia and their driving CMIP5 experiments. Atmosphere 2016, 7, 123. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shrestha, A.B.; Bierkens, M.F.P. Climate change impacts on the Upper Indus hydrology: Sources, shifts and extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef]
- Meher, J.K.; Das, L.; Akhter, J.; Benestad, R.E.; Mezghani, A. Performance of CMIP3 and CMIP5 GCMs to simulate observed rainfall characteristics over the western Himalayan region. J. Clim. 2017, 30, 7777–7799. [Google Scholar] [CrossRef]
- Panthi, J.; Krakauer, N.; Pradhanang, S. Sharing climate information in the Himalayas. Eos 2015, 96. [Google Scholar] [CrossRef]
- Christensen, M.F.; Heaton, M.J.; Rupper, S.; Reese, C.S.; Christensen, W.F. Bayesian multi-scale spatio-temporal modeling of precipitation in the Indus watershed. Front. Earth Sci. 2019, 7. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S. Evaluating changes and estimating seasonal precipitation for the Colorado River Basin using a stochastic nonparametric disaggregation technique. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Archer, D.; Fowler, H. Spatial and temporal variations in precipitation in the Upper Indus Basin, global teleconnections and hydrological implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef]
- Bhutiyani, M.R.; Kale, V.S.; Pawar, N.J. Climate change and the precipitation variations in the northwestern Himalaya: 1866–2006. Int. J. Climatol. 2010, 30, 535–548. [Google Scholar] [CrossRef]
- Khattak, M.S.; Babel, M.S.; Sharif, M. Hydro-meteorological trends in the upper Indus River basin in Pakistan. Clim. Res. 2011, 46, 103–119. [Google Scholar] [CrossRef]
- Ahmad, W.; Fatima, A.; Awan, U.K.; Anwar, A. Analysis of long term meteorological trends in the middle and lower Indus basin of Pakistan—A non-parametric statistical approach. Glob. Planet. Chang. 2014, 122, 282–291. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation trends over time using Mann-Kendall and Spearman’s rho tests in Swat river basin, Pakistan. Adv. Meteorol. 2015, 2015, 15. [Google Scholar] [CrossRef]
- Ullah, S.; You, Q.; Ullah, W.; Ali, A. Observed changes in precipitation in China–Pakistan economic corridor during 1980–2016. Atmos. Res. 2018, 210, 1–14. [Google Scholar] [CrossRef]
- Chevuturi, A.; Dimri, A.P.; Thayyen, R.J. Climate change over Leh (Ladakh), India. Theor. Appl. Climatol. 2018, 131, 531–545. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N. Spatial distribution of the trends in precipitation and precipitation extremes in the sub-Himalayan region of Pakistan. Theor. Appl. Climatol. 2019. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Chung, E.; Ismail, T.; Wang, X. Spatial distribution of secular trends in annual and seasonal precipitation over Pakistan. Clim. Res. 2017, 74, 95–107. [Google Scholar] [CrossRef]
- Hartmann, H.; Andresky, L. Flooding in the Indus River basin—A spatiotemporal analysis of precipitation records. Glob. Planet. Chang. 2013, 107, 25–35. [Google Scholar] [CrossRef]
- Wang, S. Abrupt climate change and collapse of ancient civilizations at 2200BC–2000BC. Prog. Nat. Sci. 2005, 15, 908–914. [Google Scholar] [CrossRef]
- Dixit, Y.; Tandon, S.K. Hydroclimatic variability on the Indian subcontinent in the past millennium: Review and assessment. Earth Sci. Rev. 2016, 161, 1–15. [Google Scholar] [CrossRef]
- Cook, E.R.; Palmer, J.G.; Ahmed, M.; Woodhouse, C.A.; Fenwick, P.; Zafar, M.U.; Wahab, M.; Khan, N. Five centuries of Upper Indus River flow from tree rings. J. Hydrol. 2013, 486, 365–375. [Google Scholar] [CrossRef]
- Hunt, K.M.R.; Turner, A.G. The role of the subtropical jet in deficient winter precipitation across the mid-Holocene Indus basin. Geophys. Res. Lett. 2019. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos Trans. Am. Geophys. Union 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Farr, T.G.; Kobrick, M. Shuttle radar topography mission produces a wealth of data. Eos Trans. AGU 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Khan, A.; Richards, K.S.; Parker, G.T.; McRobie, A.; Mukhopadhyay, B. How large is the Upper Indus basin? The pitfalls of auto-delineation using DEMs. J. Hydrol. 2014, 509, 442–453. [Google Scholar] [CrossRef]
- Menne, M.; Durre, I.; Vose, R.; Gleason, B.; Houston, T. An overview of the Global Historical Climatology Network-Daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive automated quality assurance of daily surface observations. J. Appl. Meteorol. Climatol. 2010, 49, 1615–1633. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Schneider, U.; Ziese, M.; Meyer-Christoffer, A.; Finger, P.; Rustemeier, E.; Becker, A. The new portfolio of global precipitation data products of the Global Precipitation Climatology Centre suitable to assess and quantify the global water cycle and resources. Proc. Int. Assoc. Hydrol. Sci. 2016, 374, 29–34. [Google Scholar] [CrossRef]
- Schneider, U.; Finger, P.; Meyer-Christoffer, A.; Rustemeier, E.; Ziese, M.; Becker, A. Evaluating the hydrological cycle over land using the newly-corrected precipitation climatology from the Global Precipitation Climatology Centre (GPCC). Atmosphere 2017, 8, 52. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901-present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.; Osborn, T.; Lister, D. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Adler, F.R.; Sapiano, R.M.; Huffman, J.G.; Wang, J.J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E.; et al. The Global Precipitation Climatology Project (GPCP) Monthly analysis (new Version 2.3) and a review of 2017 global precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.; Adler, R.; Bolvin, D.; Nelkin, E. The TRMM multi-satellite precipitation analysis (TMPA). In Satellite Rainfall Applications For Surface Hydrology; Gebremichael, M., Hossain, F., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar] [CrossRef]
- Yamamoto, M.K.; Ueno, K.; Nakamura, K. Comparison of satellite precipitation products with rain gauge data for the Khumb region, Nepal Himalayas. J. Meteorol. Soc. Japan. Ser. II 2011, 89, 597–610. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; et al. Similarity and difference of the two successive V6 and V7 TRMM multisatellite precipitation analysis performance over China. J. Geophys. Res. Atmos. 2013, 118, 13060–13074. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Pradhanang, S.M.; Panthi, J.; Lakhankar, T.; Jha, A.K. Probabilistic precipitation estimation with a satellite product. Climate 2015, 3, 329–348. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Ijaz, M.W.; Zhang, S. Evaluation of high-resolution satellite-based real-time and post-real-time precipitation estimates during 2010 extreme flood event in Swat River Basin, Hindukush region. Adv. Meteorol. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Wehbe, Y.; Ghebreyesus, D.; Temimi, M.; Milewski, A.; Mandous, A.A. Assessment of the consistency among global precipitation products over the United Arab Emirates. J. Hydrol. Reg. Stud. 2017, 12, 122–135. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Liu, J.; Ahmad, I.; Ijaz, M.W.; Khan, M.I. Quantification of spatial temporal variability of snow cover and hydro-climatic variables based on multi-source remote sensing data in the Swat watershed, Hindukush Mountains, Pakistan. Meteorol. Atmos. Phys. 2018, 131, 467–486. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Anjum, M.N.; Ding, Y.; Shangguan, D.; Ahmad, I.; Ijaz, M.W.; Farid, H.U.; Yagoub, Y.E.; Zaman, M.; Adnan, M. Performance evaluation of latest integrated multi-satellite retrievals for Global Precipitation Measurement (IMERG) over the northern highlands of Pakistan. Atmos. Res. 2018, 205, 134–146. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and hydrological comparisons between TRMM and GPM Level-3 products over a midlatitude basin: Is Day-1 IMERG a good successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Kirstetter, P.E.; Hong, Y.E.; Gourley, J.J.; Huffman, G.J.; Petersen, W.A.; Xue, X.; Schwaller, M.R. To what extent is the Day 1 GPM IMERG satellite precipitation estimate improved as compared to TRMM TMPA-RT? J. Geophys. Res. Atmos. 2018, 123, 1694–1707. [Google Scholar] [CrossRef]
- Kobayashi, S.; Yukinari, O.T.A.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Hirokazu, E.N.D.O.; et al. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Kang, S.; Ahn, J.B. Global energy and water balances in the latest reanalyses. Asia-Pac. J. Atmos. Sci. 2015, 51, 293–302. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24. [Google Scholar] [CrossRef]
- Randles, C.A.; da Silva, A.M.; Buchard, V.; Colarco, P.R.; Darmenov, A.; Govindaraju, R.; Smirnov, A.; Holben, B.; Ferrare, R.; Hair, J.; et al. The MERRA-2 aerosol reanalysis, 1980–Onward, Part I: System description and data assimilation evaluation. J. Clim. 2017. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Draper, C.S.; Mahanama, S.P.P.; Partyka, G.S. Land surface precipitation in MERRA-2. J. Clim. 2017. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Cohan, D.S. Interannual variability and seasonal predictability of wind and solar resources. Resources 2017, 6, 29. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Robertson, F.R.; Takacs, L.; Molod, A.; Mocko, D. Atmospheric water balance and variability in the MERRA-2 reanalysis. J. Clim. 2017. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Higgins, R.W.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.C.; Munoz-Sabater, J.; de Rosnay, P.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The Twentieth Century Reanalysis Project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Giese, B.S.; Brohan, P.; Slivinski, L. 20th Century reanalysis version “2c” (1851-2012) and prospects for 200 years of reanalysis. In Proceedings of the AGU Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Laloyaux, P.; de Boisseson, E.; Balmaseda, M.; Bidlot, J.R.; Broennimann, S.; Buizza, R.; Dalhgren, P.; Dee, D.; Haimberger, L.; Hersbach, H.; et al. CERA-20C: A coupled reanalysis of the twentieth century. J. Adv. Model. Earth Syst. 2018, 10, 1172–1195. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Pradhanang, S.M.; Lakhankar, T.; Jha, A.K. Evaluating satellite products for precipitation estimation in mountain regions: A case study for Nepal. Remote Sens. 2013, 5, 4107–4123. [Google Scholar] [CrossRef]
- Khan, A.D.; Ghoraba, S.; Arnold, J.G.; Luzio, M.D. Hydrological modeling of Upper Indus basin and assessment of deltaic ecology. Int. J. Mod. Eng. Res. 2014, 4, 73–85. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann–Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Shrestha, A.B.; Bierkens, M.F.P. Consistent increase in High Asia’s runoff due to increasing glacier melt and precipitation. Nat. Clim. Chang. 2014, 4, 587. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Wang, X.; Nawaz, N.; Khan, N. Evaluation of gridded precipitation datasets over arid regions of Pakistan. Water 2019, 11, 210. [Google Scholar] [CrossRef]
- Adnan, S.; Ullah, K.; Shouting, G. Investigations into precipitation and drought climatologies in south central Asia with special focus on Pakistan over the period 1951–2010. J. Clim. 2016, 29, 6019–6035. [Google Scholar] [CrossRef]
- Ferguson, C.R.; Villarini, G. An evaluation of the statistical homogeneity of the Twentieth Century Reanalysis. Clim. Dyn. 2014, 42, 2841–2866. [Google Scholar] [CrossRef]
- Giorgi, F.; Marinucci, M.R. A investigation of the sensitivity of simulated precipitation to model resolution and its implications for climate studies. Mon. Weather Rev. 1996, 124, 148–166. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; Clark, M.; Werner, K.; Brandon, D.; Rajagopalan, B. Effects of spatial and temporal aggregation on the accuracy of statistically downscaled precipitation estimates in the upper Colorado River basin. J. Hydrometeorol. 2004, 5, 1192–1206. [Google Scholar] [CrossRef]
- Pritchard, H.D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
- Dahri, Z.H.; Ludwig, F.; Moors, E.; Ahmad, B.; Khan, A.; Kabat, P. An appraisal of precipitation distribution in the high-altitude catchments of the Indus basin. Sci. Total Environ. 2016, 548–549, 289–306. [Google Scholar] [CrossRef]
- Dahri, Z.H.; Moors, E.; Ludwig, F.; Ahmad, S.; Khan, A.; Ali, I.; Kabat, P. Adjustment of measurement errors to reconcile precipitation distribution in the high-altitude Indus basin. Int. J. Climatol. 2018, 38, 3842–3860. [Google Scholar] [CrossRef]
- Khan, A.; Masud, T.; Attaullah, H.; Khan, M. Accuracy assessment of gridded precipitation datasets in the Upper Indus basin. In Proceedings of the EGU General Assembly Conference 2017, Vienna, Austria, 23–28 April 2017; Volume 19, p. 11897. [Google Scholar]
- Washington, R.; James, R.; Pearce, H.; Pokam, W.M.; Moufouma-Okia, W. Congo Basin rainfall climatology: Can we believe the climate models? Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20120296. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Klotter, D.; Dezfuli, A.K.; Zhou, L. New rainfall datasets for the Congo basin and surrounding regions. J. Hydrometeorol. 2018, 19, 1379–1396. [Google Scholar] [CrossRef]
- Vuille, M.; Bradley, R.S.; Werner, M.; Keimig, F. 20th Century climate change in the tropical Andes: Observations and model results. In Advances in Global Change Research; Springer: Dordrecht, The Netherlands, 2003; pp. 75–99. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust Responses of the Hydrological Cycle to Global Warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Lambert, F.H.; Stine, A.R.; Krakauer, N.Y.; Chiang, J.C.H. How much will precipitation increase with global warming? EOS Trans. Am. Geophys. Union 2008, 89, 193–194. [Google Scholar] [CrossRef]
- Preethi, B.; Mujumdar, M.; Kripalani, R.H.; Prabhu, A.; Krishnan, R. Recent trends and tele-connections among South and East Asian summer monsoons in a warming environment. Clim. Dyn. 2017, 48, 2489–2505. [Google Scholar] [CrossRef]
- Bollasina, M.A.; Ming, Y.; Ramaswamy, V. Anthropogenic aerosols and the weakening of the South Asian summer monsoon. Science 2011, 334, 502–505. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R.; Sabin, T.P.; Vellore, R.; Mujumdar, M.; Sanjay, J.; Goswami, B.N.; Hourdin, F.; Dufresne, J.L.; Terray, P. Deciphering the desiccation trend of the South Asian monsoon hydroclimate in a warming world. Clim. Dyn. 2016, 47, 1007–1027. [Google Scholar] [CrossRef]
- Wang, X.; Wang, T.; Liu, D.; Guo, H.; Huang, H.; Zhao, Y. Moisture-induced greening of the South Asia over the past three decades. Glob. Chang. Biol. 2017, 23, 4995–5005. [Google Scholar] [CrossRef] [PubMed]
- Krakauer, N.Y.; Lakhankar, T.; Anadón, J.D. Mapping and attributing Normalized Difference Vegetation Index trends for Nepal. Remote Sens. 2017, 9, 986. [Google Scholar] [CrossRef]
- Baniya, B.; Tang, Q.; Huang, Z.; Sun, S.; Techato, K. Spatial and temporal variation of NDVI in response to climate change and the implication for carbon dynamics in Nepal. Forests 2018, 9, 329. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Year-ahead predictability of South Asian Summer Monsoon precipitation. Environ. Res. Lett. 2019, 14, 044006. [Google Scholar] [CrossRef]
- Minallah, S.; Ivanov, V.Y. Interannual variability and seasonality of precipitation in the Indus River basin. J. Hydrometeorol. 2019, 20, 379–395. [Google Scholar] [CrossRef]
- Sorí, R.; Nieto, R.; Drumond, A.; Vicente-Serrano, S.M.; Gimeno, L. The atmospheric branch of the hydrological cycle over the Indus, Ganges, and Brahmaputra river basins. Hydrol. Earth Syst. Sci. 2017, 21, 6379–6399. [Google Scholar] [CrossRef]
- Afzal, M.; Haroon, M.A.; Rana, A.S.; Imran, A. Influence of North Atlantic Oscillations and Southern Oscillations on winter precipitation of northern Pakistan. Pak. J. Meteorol. 2013, 9, 1–8. [Google Scholar]
- Cannon, F.; Carvalho, L.M.V.; Jones, C.; Bookhagen, B. Multi-annual variations in winter westerly disturbance activity affecting the Himalaya. Clim. Dyn. 2015, 44, 441–455. [Google Scholar] [CrossRef]
- Greene, A.M.; Robertson, A.W. Interannual and low-frequency variability of Upper Indus basin winter/spring precipitation in observations and CMIP5 models. Clim. Dyn. 2017, 49, 4171–4188. [Google Scholar] [CrossRef]

| Data Set | Type | Resolution | Years |
|---|---|---|---|
| GPCC | G | 0.5 | 1891–2016 |
| CRU | G | 0.5 | 1901–2018 |
| APHRODITE V1101 | G | 0.25 | 1951–2007 |
| APHRODITE V1901 | G | 0.25 | 1998–2015 |
| GPCP | S | 2.5 | 1979–2018 |
| TMPA | S | 0.25 | 1998–2018 |
| IMERG | S | 0.1 | 2015–2018 |
| JRA-55 | R | 0.5625 | 1958–2013 |
| MERRA-2 | R | 0.625× 0.5 | 1980–2018 |
| ERA5 | R | 0.5 | 1979–2018 |
| 20CR-2c | R | 1.875 | 1851–2014 |
| CERA-20C | R | 1.125 | 1901–2010 |
| Data Set | (%) | ||||
|---|---|---|---|---|---|
| GPCC | 3 | 0.804 | 0.762 | 0.906 | 0.704 |
| CRU | −26 | 0.412 | 0.157 | 0.748 | 0.238 |
| APHRODITE V1101 | −14 | 0.799 | 0.744 | 0.941 | 0.659 |
| APHRODITE V1901 | −1 | 0.718 | 0.892 | 0.872 | 0.448 |
| GPCP | −11 | 0.610 | 0.597 | 0.831 | 0.464 |
| TMPA | 1 | 0.803 | 0.900 | 0.873 | 0.649 |
| IMERG | 12 | 0.766 | 0.626 | 0.515 | 0.431 |
| JRA-55 | 26 | 0.192 | −0.002 | 0.680 | −0.130 |
| MERRA-2 | −43 | 0.454 | 0.326 | 0.538 | 0.290 |
| ERA5 | 19 | 0.561 | 0.446 | 0.801 | 0.348 |
| 20CR-2c | −11 | 0.055 | 0.084 | 0.354 | −0.550 |
| CERA-20C | 9 | 0.349 | 0.236 | 0.655 | 0.020 |
| Data Set | Mean | Trend | Bias Trend | Trend (1958–2010) |
|---|---|---|---|---|
| GPCC | 488 | +0.53 ± 0.18 ** | −1.46 ± 0.80 | +0.66 ± 0.69 |
| CRU | 439 | +0.53 ± 0.16 ** | +1.85 ± 0.80 * | +0.54 ± 0.51 |
| APHRODITE V1101 | 382 | −0.31 ± 0.44 | +3.21 ± 3.39 | |
| APHRODITE V1901 | 493 | +24.45 ± 5.68 ** | +19.16 ± 6.07 ** | |
| GPCP | 580 | −0.68 ± 1.18 | +8.27 ± 1.14 ** | |
| TMPA | 503 | +6.03 ± 2.74 * | +3.49 ± 1.21 ** | |
| IMERG | 523 | −85.99 ± 34.69 | −7.72 ± 34.55 | |
| JRA-55 | 725 | +0.07 ± 0.91 | +1.52 ± 2.92 | −0.02 ± 1.00 |
| MERRA-2 | 280 | +1.28 ± 1.03 | +4.57 ± 1.44 ** | |
| ERA5 | 696 | −1.91 ± 1.03 | +4.71 ± 1.51 ** | |
| 20CR-2c | 749 | −1.94 ± 0.21 ** | −4.79 ± 1.10 ** | −3.89 ± 0.99 ** |
| CERA-20C | 585 | −2.57 ± 0.25 ** | −7.78 ± 1.06 ** | −0.92 ± 0.75 |
| GPCC | CRU | A V1101 | A V1901 | GPCP | TMPA | IMERG | JRA-55 | MERRA-2 | ERA5 | 20CR-2c | CERA-20C | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPCC | 1 | 0.881 | 0.919 | 0.872 | 0.937 | 0.978 | 1 | 0.661 | 0.656 | 0.765 | 0.220 | 0.360 |
| CRU | 1 | 0.822 | 0.783 | 0.831 | 0.900 | 0.939 | 0.702 | 0.557 | 0.838 | 0.168 | 0.262 | |
| A V1101 | 1 | 0.946 | 0.882 | 0.966 | - | 0.612 | 0.452 | 0.902 | 0.428 | 0.706 | ||
| A V1901 | 1 | 0.846 | 0.846 | - | 0.703 | 0.630 | 0.624 | 0.092 | 0.817 | |||
| GPCP | 1 | 0.984 | 0.974 | 0.642 | 0.560 | 0.843 | 0.236 | 0.840 | ||||
| TMPA | 1 | 0.990 | 0.842 | 0.741 | 0.875 | 0.223 | 0.865 | |||||
| IMERG | 1 | - | 0.925 | 0.790 | - | - | ||||||
| JRA-55 | 1 | 0.633 | 0.715 | 0.391 | 0.632 | |||||||
| MERRA-2 | 1 | 0.399 | 0.304 | 0.558 | ||||||||
| ERA5 | 1 | 0.315 | 0.858 | |||||||||
| 20CR-2c | 1 | 0.420 | ||||||||||
| CERA-20C | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krakauer, N.Y.; Lakhankar, T.; Dars, G.H. Precipitation Trends over the Indus Basin. Climate 2019, 7, 116. https://doi.org/10.3390/cli7100116
Krakauer NY, Lakhankar T, Dars GH. Precipitation Trends over the Indus Basin. Climate. 2019; 7(10):116. https://doi.org/10.3390/cli7100116
Chicago/Turabian StyleKrakauer, Nir Y., Tarendra Lakhankar, and Ghulam H. Dars. 2019. "Precipitation Trends over the Indus Basin" Climate 7, no. 10: 116. https://doi.org/10.3390/cli7100116
APA StyleKrakauer, N. Y., Lakhankar, T., & Dars, G. H. (2019). Precipitation Trends over the Indus Basin. Climate, 7(10), 116. https://doi.org/10.3390/cli7100116







