Spatial and Seasonal Variations and Inter-Relationship in Fitted Model Parameters for Rainfall Totals across Australia at Various Timescales
Abstract
1. Introduction
2. Material and Methods
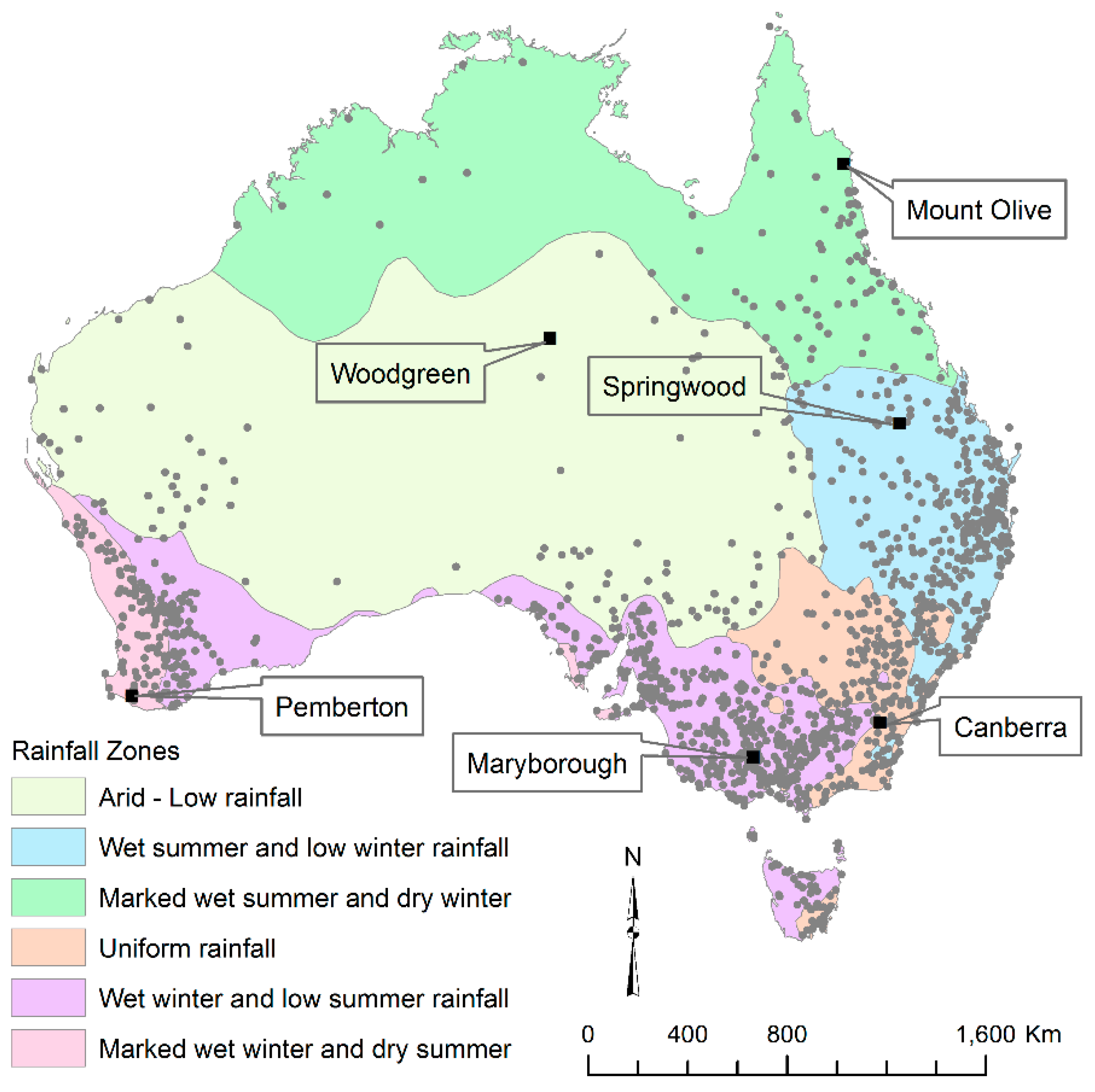
2.1. Data
2.2. Methods
3. Results
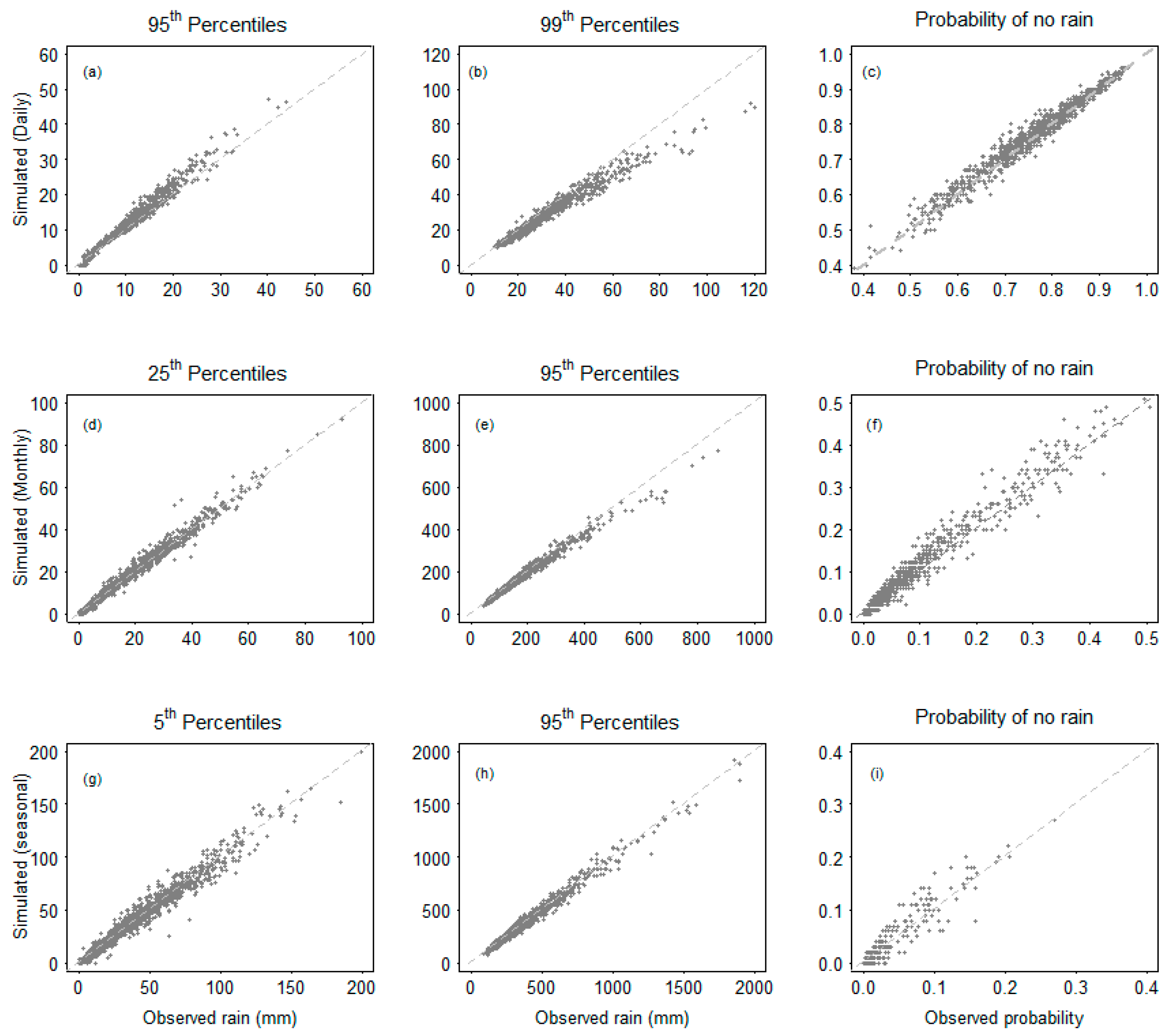
3.1. Comparing the Fit of the Model Using Tweedie Distributions
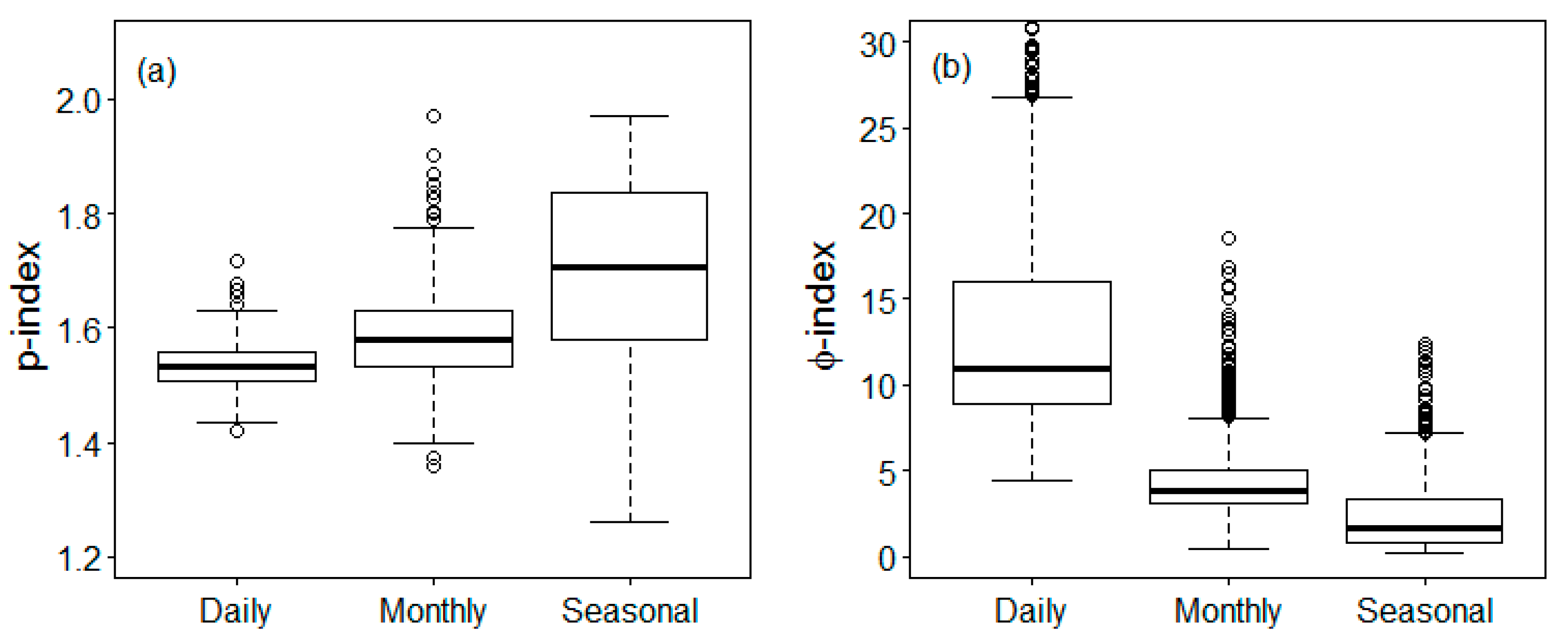
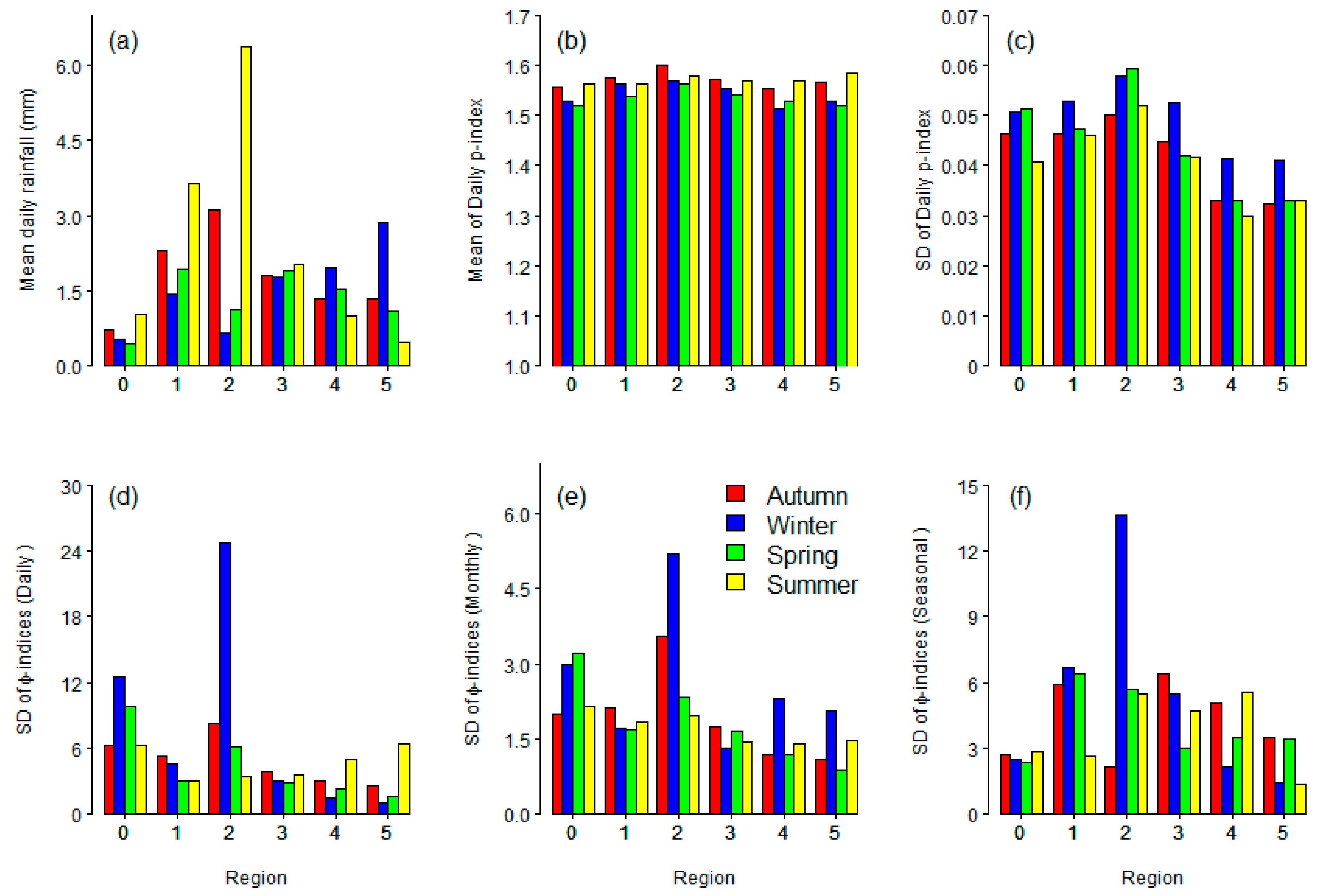
3.2. Spatial and Seasonal Variations of Parameters
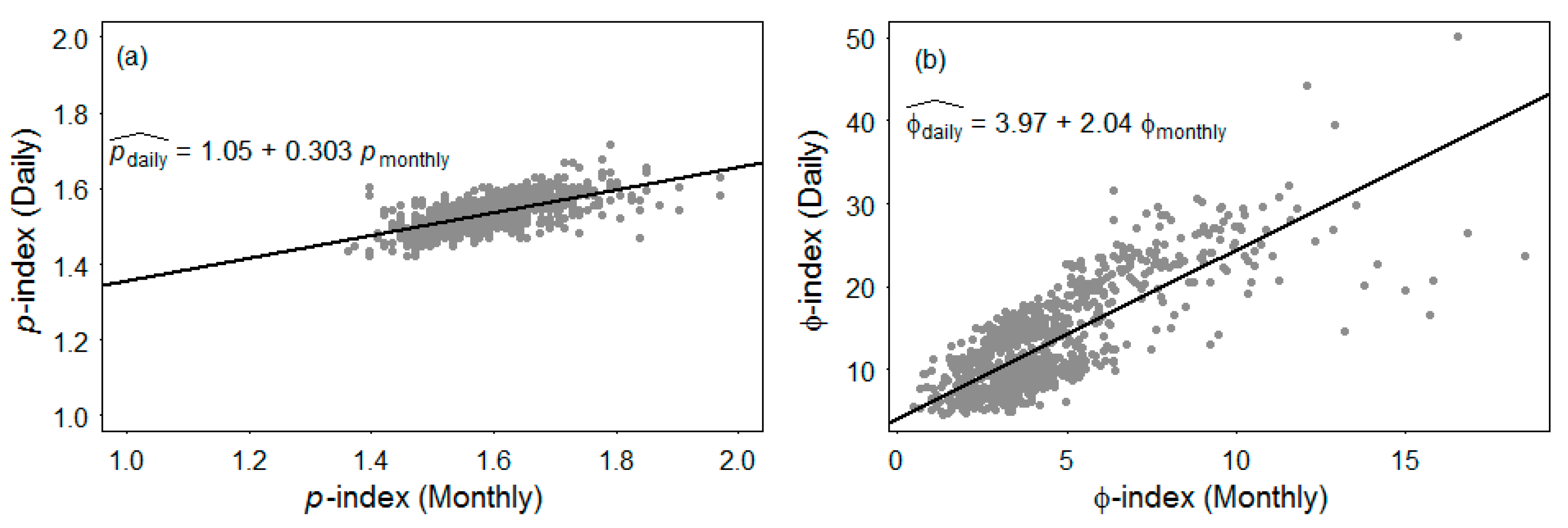
3.3. Estimating Parameters for Seasonal Models Using the Combined Model and Daily Timescales Form Monthly Timescale
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Beskow, S.; Caldeira, T.L.; de Mello, C.R.; Faria, L.C.; Guedes, H.A.S. Multiparameter probability distributions for heavy rainfall modeling in extreme Southern Brazil. J. Hydrol.-Reg. Stud. 2015, 4, 123–133. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Thorolfsson, S.T.; Alfredsen, K. Regional frequency analysis of extreme precipitation with consideration of uncertainties to update idf curves for the city of Trondheim. J. Hydrol. 2013, 498, 305–318. [Google Scholar] [CrossRef]
- Baigorria, G.A.; Jones, J.W. Gist: A stochastic model for generating spatially and temporally correlated daily rainfall data. J. Clim. 2010, 23, 5990–6008. [Google Scholar] [CrossRef]
- Hasan, M.M.; Dunn, P.K. Entropy, consistency in rainfall distribution and potential water resource availability in Australia. Hydrol. Processes 2011, 25, 2613–2622. [Google Scholar] [CrossRef]
- Nowak, G.; Welsh, A.; O’Neill, T.; Feng, L. Spatio-temporal modelling of rainfall in the murray-darling basin. J. Hydrol. 2018, 557, 522–538. [Google Scholar] [CrossRef]
- Shukla, S.; McNally, A.; Husak, G.; Funk, C. A seasonal agricultural drought forecast system for food-insecure regions of East Africa. Hydrol. Earth Syst. Sci. 2014, 18, 3907–3921. [Google Scholar] [CrossRef]
- Hasan, M.M.; Croke, B. Filling gaps in daily rainfall data: A statistical approach. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013. [Google Scholar]
- Rosenberg, K.; Boland, J.; Howlett, P.G. Simulation of monthly rainfall totals. ANZIAM J. 2008, 46, 85–104. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.; Jun, H. A study of the influence of the spatial distribution of rain gauge networks on areal average rainfall calculation. Water 2018, 10, 1635. [Google Scholar] [CrossRef]
- Camberlin, P.; Gitau, W.; Oettli, P.; Ogallo, L.; Bois, B. Spatial interpolation of daily rainfall stochastic generation parameters over East Africa. Clim. Res. 2014, 59, 39–60. [Google Scholar] [CrossRef]
- Chowdhury, A.; Lockart, N.; Willgoose, G.; Kuczera, G.; Kiem, A.S.; Manage, N.P. Modelling daily rainfall along the east coast of australia using a compound distribution markov chain model. In Proceedings of the 36th Hydrology and Water Resources Symposium: The Art and Science of Water, Hobart, Australia, 7–10 December 2015; Engineers Australia: Barton, Australia, 2015; p. 625. [Google Scholar]
- Rajah, K.; O’Leary, T.; Turner, A.; Petrakis, G.; Leonard, M.; Westra, S. Changes to the temporal distribution of daily precipitation. Geophys. Res. Lett. 2014, 41, 8887–8894. [Google Scholar] [CrossRef]
- Liang, L.; Zhao, L.; Gong, Y.; Tian, F.; Wang, Z. Probability distribution of summer daily precipitation in the huaihe basin of China based on gamma distribution. Acta Meteorol. Sin. 2012, 26, 72–84. [Google Scholar] [CrossRef]
- Piantadosi, J.; Boland, J.; Howlett, P. Generating synthetic rainfall on various timescales—Daily, monthly and yearly. Environ. Model. Assess. 2009, 14, 431–438. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. A global survey on the seasonal variation of the marginal distribution of daily precipitation. Adv. Water Resour. 2016, 94, 131–145. [Google Scholar] [CrossRef]
- Mandal, S.; Choudhury, B. Estimation and prediction of maximum daily rainfall at sagar island using best fit probability models. Theor. Appl. Climatol. 2015, 121, 87–97. [Google Scholar] [CrossRef]
- Li, Z.; Brissette, F.; Chen, J. Assessing the applicability of six precipitation probability distribution models on the loess plateau of China. Int. J. Climatol. 2014, 34, 462–471. [Google Scholar] [CrossRef]
- Suhaila, J.; Jemain, A. Fitting the statistical distribution for daily rainfall in peninsular malaysia based on aic criterion. J. Appl. Sci. Res. 2008, 4, 1846–1857. [Google Scholar]
- Borwein, J.; Howlett, P.; Piantadosi, J. Modelling and simulation of seasonal rainfall using the principle of maximum entropy. Entropy 2014, 16, 747–769. [Google Scholar] [CrossRef]
- Ghosh, S.; Roy, M.K.; Biswas, S.C. Determination of the best fit probability distribution for monthly rainfall data in Bangladesh. Am. J. Math. Stat. 2016, 6, 170–174. [Google Scholar]
- Kossieris, P.; Makropoulos, C.; Onof, C.; Koutsoyiannis, D. A rainfall disaggregation scheme for sub-hourly time scales: Coupling a bartlett-lewis based model with adjusting procedures. J. Hydrol. 2018, 556, 980–992. [Google Scholar] [CrossRef]
- Pal, S.; Mazumdar, D. Stochastic modelling of monthly rainfall volume during monsoon season over gangetic west Bengal, India. Nat. Environ. Pollut. Technol. 2015, 14, 951–956. [Google Scholar]
- Yue, S.; Hashino, M. Long term trends of annual and monthly precipitation in Japan. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 587–596. [Google Scholar] [CrossRef]
- Abtew, W.; Melesse, A.M.; Dessalegne, T. El niño southern oscillation link to the blue nile river basin hydrology. Hydrol. Processes 2009, 23, 3653–3660. [Google Scholar] [CrossRef]
- Husak, G.J.; Michaelsen, J.; Funk, C. Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications. Int. J. Climatol. 2007, 27, 935–944. [Google Scholar] [CrossRef]
- Rader, M.; Kirshen, P.; Roncoli, C.; Hoogenboom, G.; Ouattara, F. Agricultural risk decision support system for resource-poor farmers in Burkina Faso, West Africa. J. Water Resour. Plan. Manag. 2009, 135, 323–333. [Google Scholar] [CrossRef]
- Hasan, M.M.; Dunn, P.K. Two tweedie distributions that are near-optimal for modelling monthly rainfall in Australia. Int. J. Climatol. 2011, 31, 1389–1397. [Google Scholar] [CrossRef]
- Hasan, M.M.; Dunn, P.K. Seasonal rainfall totals of Australian stations can be modelled with distributions from the tweedie family. Int. J. Climatol. 2015, 35, 3093–3101. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A language for data analysis and graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar]
- Dunn, P. Tweedie: Tweedie Exponential Family Models; R Package Version 2.2.1; R Core Team: Vienna, Austria, 2014. [Google Scholar]
- McCullagh, P.; Nelder, J. Generalized Linear Models; Chapman & Hall: New York, NY, USA, 1989. [Google Scholar]
- Saha, K.; Hasan, M.; Quazi, A. Forecasting tropical cyclone-induced rainfall in coastal Australia: Implications for effective flood management. Australas. J. Environ. Manag. 2015, 22, 446–457. [Google Scholar] [CrossRef]
- Yunus, R.M.; Hasan, M.M.; Razak, N.A.; Zubairi, Y.Z.; Dunn, P.K. Modelling daily rainfall with climatological predictors: Poisson-gamma generalized linear modelling approach. Int. J. Climatol. 2017, 37, 1391–1399. [Google Scholar] [CrossRef]
- Dunn, P.K. Occurrence and quantity of precipitation can be modelled simultaneously. Int. J. Climatol. 2004, 24, 1231–1239. [Google Scholar] [CrossRef]
- Jiang, J. Linear and Generalized Linear Mixed Models and Their Applications; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Dunn, P.K.; Smyth, G.K. Series evaluation of tweedie exponential dispersion model densities. Stat. Comput. 2005, 15, 267–280. [Google Scholar] [CrossRef]
| Stations | Daily | Monthly | Seasonal | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean (mm) | CV * | % Zero | 95th Percentile | CV * | % Zero | 95th Percentile | CV * | % Zero | 95th Percentile | |
| Woodgreen | 0.80 | 619.64 | 93.05 | 3.0 | 174.28 | 37.86 | 96.0 | 114.20 | 9.26 | 208.85 |
| Mount Olive | 4.41 | 345.15 | 70.81 | 26.6 | 137.77 | 8.18 | 545.9 | 99.83 | 0.91 | 1176.73 |
| Springwood | 1.92 | 430.12 | 87.00 | 11.9 | 118.59 | 11.76 | 200.9 | 87.39 | 1.41 | 461.98 |
| Canberra | 1.69 | 331.57 | 70.03 | 10.2 | 76.89 | 0.35 | 125.7 | 48.65 | 0 | 275.60 |
| Maryborough | 1.42 | 312.53 | 68.93 | 8.1 | 73.47 | 0.92 | 97.7 | 49.30 | 0 | 248.69 |
| Pemberton | 3.18 | 212.14 | 51.81 | 17.8 | 84.15 | 0 | 240.7 | 67.90 | 0 | 631.56 |
| Stations | Daily | Monthly | Seasonal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| p Value | Distribution | ϕ | p | Distribution | ϕ | p | Distribution | ϕ | |
| Woodgreen | 1.46 | P-G | 26.87 | 1.49 | P-G | 10.86 | 1.56 | P-G | 6.70 |
| Springwood | 1.51 | P-G | 19.27 | 1.64 | P-G | 5.15 | 2.29 | Gamma | 0.17 |
| Mount Olive | 1.62 | P-G | 13.93 | 1.74 | P-G | 5.83 | 2.20 | Gamma | 0.45 |
| Canberra Airport Comparison | 1.63 | P-G | 8.72 | 1.67 | P-G | 2.04 | 1.87 | P-G | 0.45 |
| Maryborough | 1.54 | P-G | 7.99 | 1.58 | P-G | 2.76 | 2.10 | Gamma | 0.17 |
| Pemberton | 1.58 | P-G | 6.62 | 2.07 | Gamma | 0.73 | 2.13 | Gamma | 0.28 |
| p-Index | ϕ-Index | |||||
|---|---|---|---|---|---|---|
| Correlation Coefficient | Regression Coefficients | Correlation Coefficient | Regression Coefficients | |||
| Constant | Slope (SD *) | Constant | Slope (SD *) | |||
| Autumn | 0.76 | 0.38 | 0.75 (0.01) a | 0.91 | −0.61 | 0.99 (0.01) a |
| Winter | 0.70 | 0.60 | 0.63 (0.12) a | 0.39 | 10.80 | 0.40 (0.03) a |
| Spring | 0.81 | 0.35 | 0.79 (0.02) a | 0.94 | 0.87 | 1.04 (0.01) a |
| Summer | 0.77 | 0.12 | 0.92 (0.02) a | 0.72 | −5.67 | 1.39 (0.04) a |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.M.; Croke, B.F.W.; Karim, F. Spatial and Seasonal Variations and Inter-Relationship in Fitted Model Parameters for Rainfall Totals across Australia at Various Timescales. Climate 2019, 7, 4. https://doi.org/10.3390/cli7010004
Hasan MM, Croke BFW, Karim F. Spatial and Seasonal Variations and Inter-Relationship in Fitted Model Parameters for Rainfall Totals across Australia at Various Timescales. Climate. 2019; 7(1):4. https://doi.org/10.3390/cli7010004
Chicago/Turabian StyleHasan, Md Masud, Barry F. W. Croke, and Fazlul Karim. 2019. "Spatial and Seasonal Variations and Inter-Relationship in Fitted Model Parameters for Rainfall Totals across Australia at Various Timescales" Climate 7, no. 1: 4. https://doi.org/10.3390/cli7010004
APA StyleHasan, M. M., Croke, B. F. W., & Karim, F. (2019). Spatial and Seasonal Variations and Inter-Relationship in Fitted Model Parameters for Rainfall Totals across Australia at Various Timescales. Climate, 7(1), 4. https://doi.org/10.3390/cli7010004





