Dust Devils: Structural Features, Dynamics and Climate Impact
Abstract
1. Introduction
2. Main Features
2.1. Dust Devils—Columns of Rising Dust
2.2. Dust Devils: Typical Parameters
2.3. Saltation
2.4. The Electrification of Dust
2.5. Dust Devils as an Element of the Family of Concentrated Small-Scale Vortices in the Atmosphere
2.6. The Dustiness of the Atmosphere and Climate
3. Generation of Vertical Jets (Plumes) and Vortices in an Unstable Stratified Atmosphere
3.1. Convective Instability of the Near-Surface Atmospheric Layer
3.2. Generation of Vertical Jets (Plumes) in an Unstable Stratified Atmosphere
3.3. Generation Model of Dust Devils from Vertical Jets
4. Quasi-Stationary Models of Concentrated Vortices
4.1. Previous Models
4.2. Model of Concentrated Vortices in a Non-Dissipative Medium
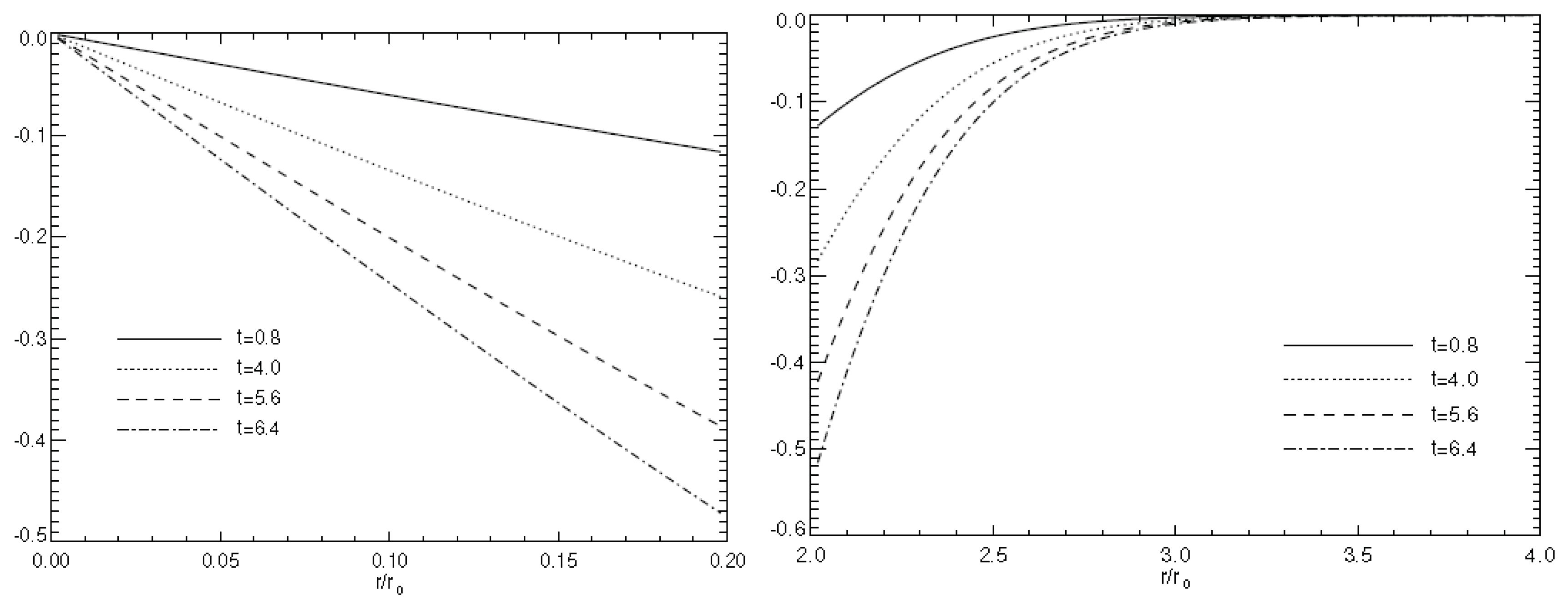
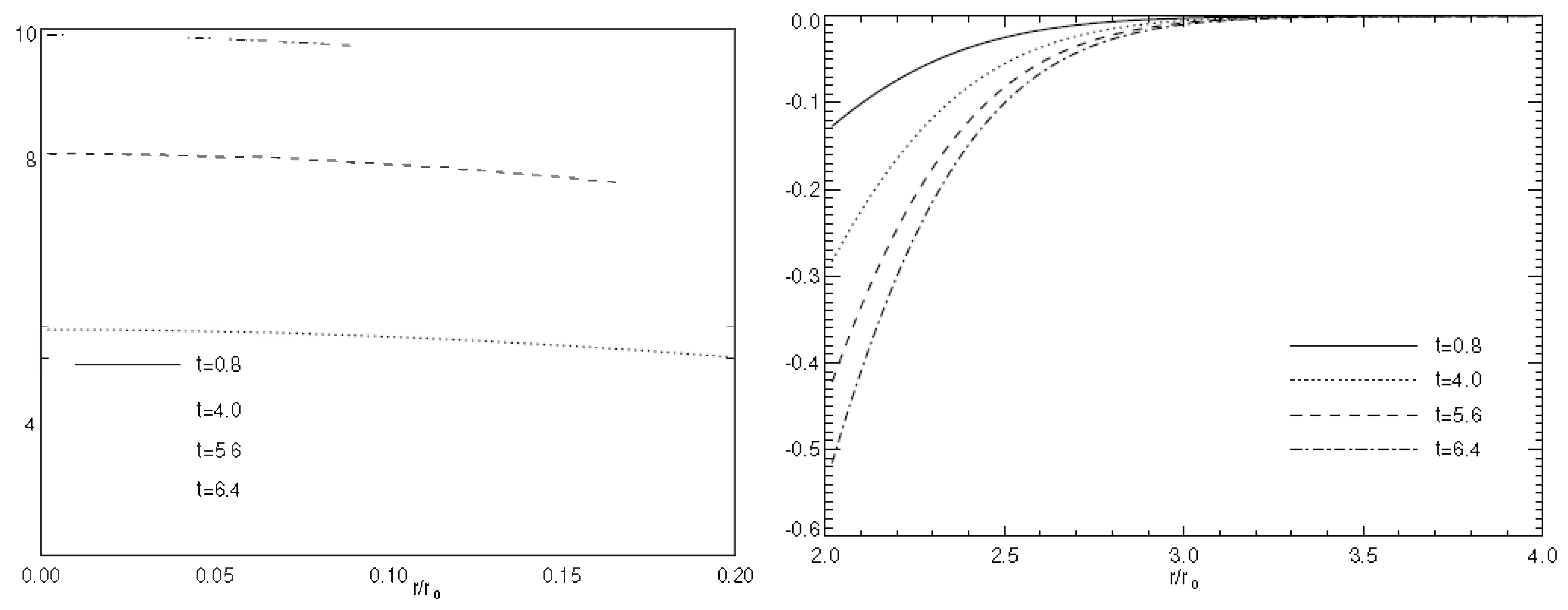
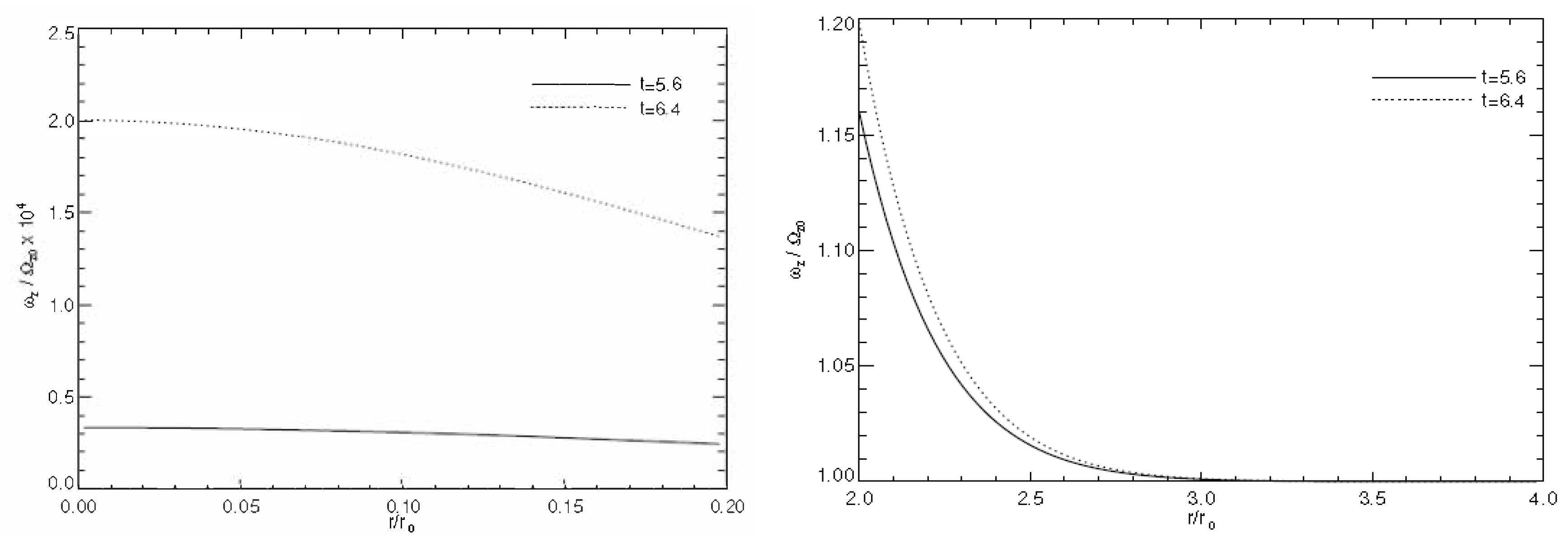
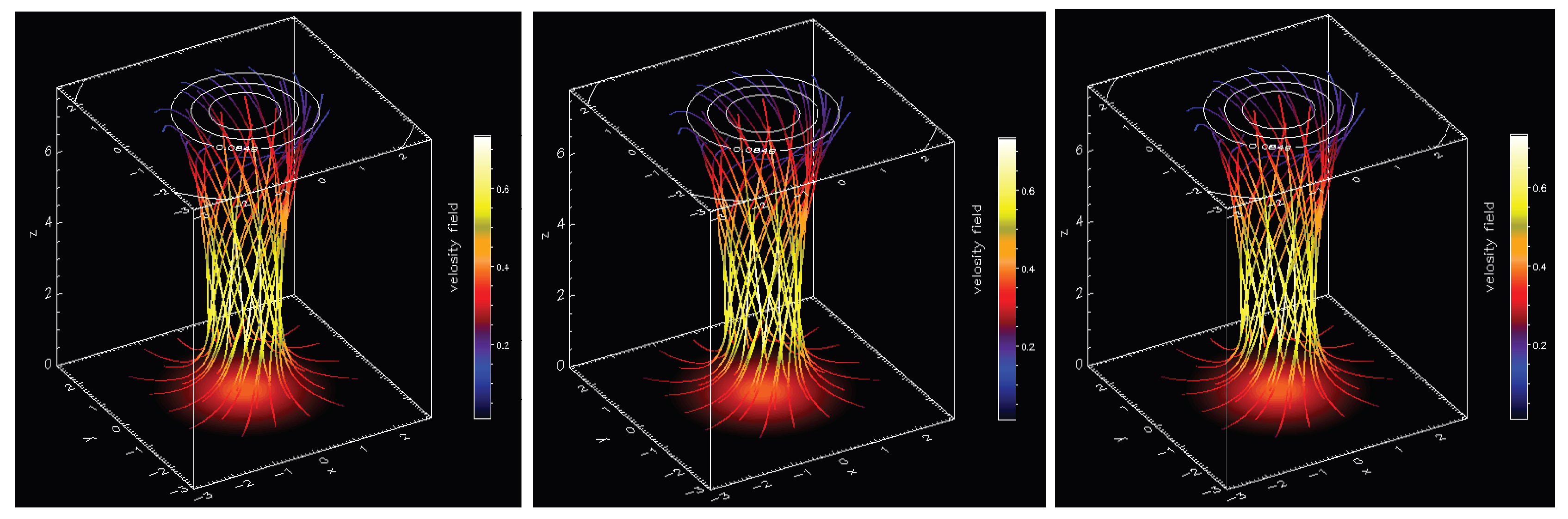
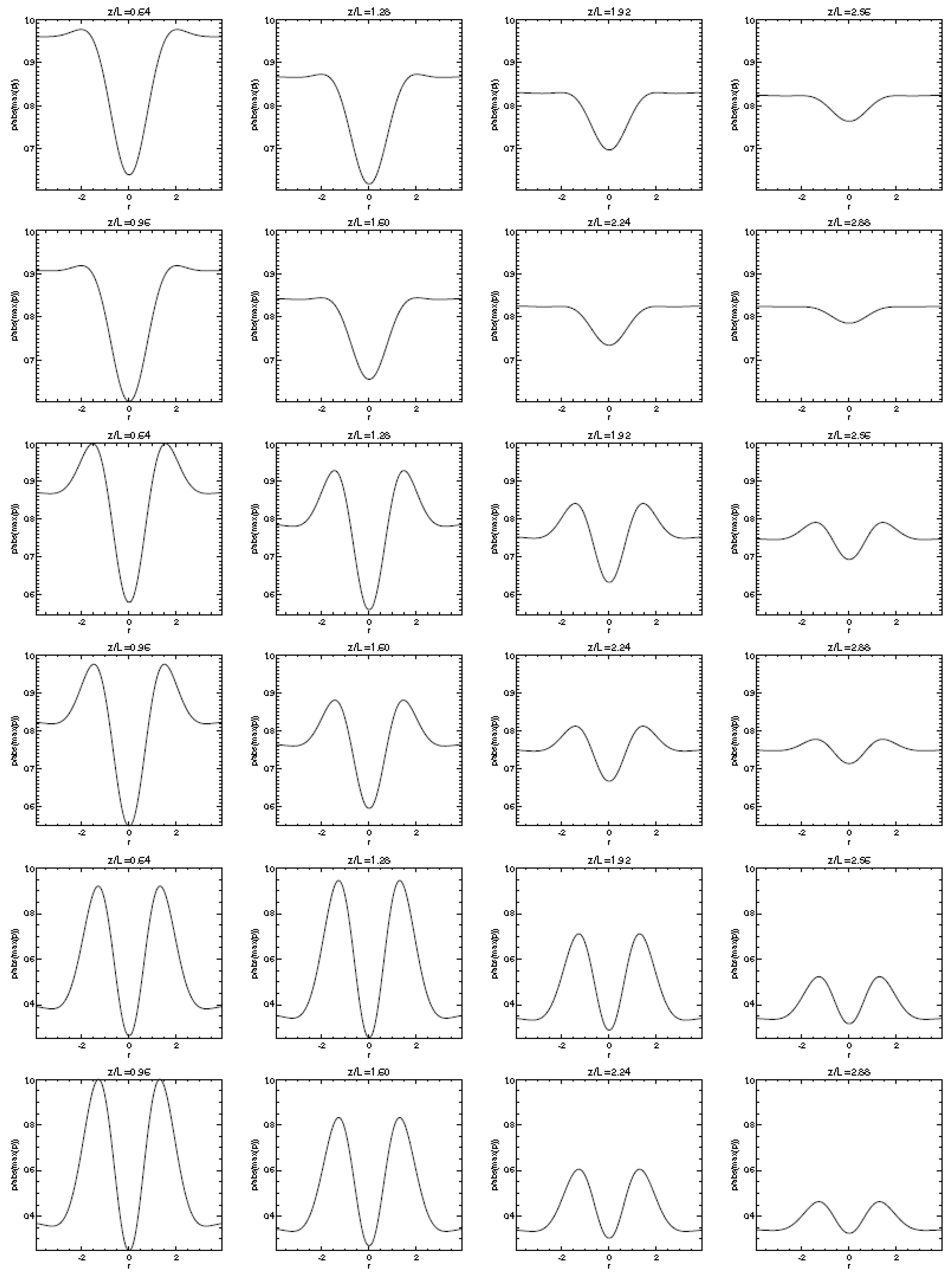
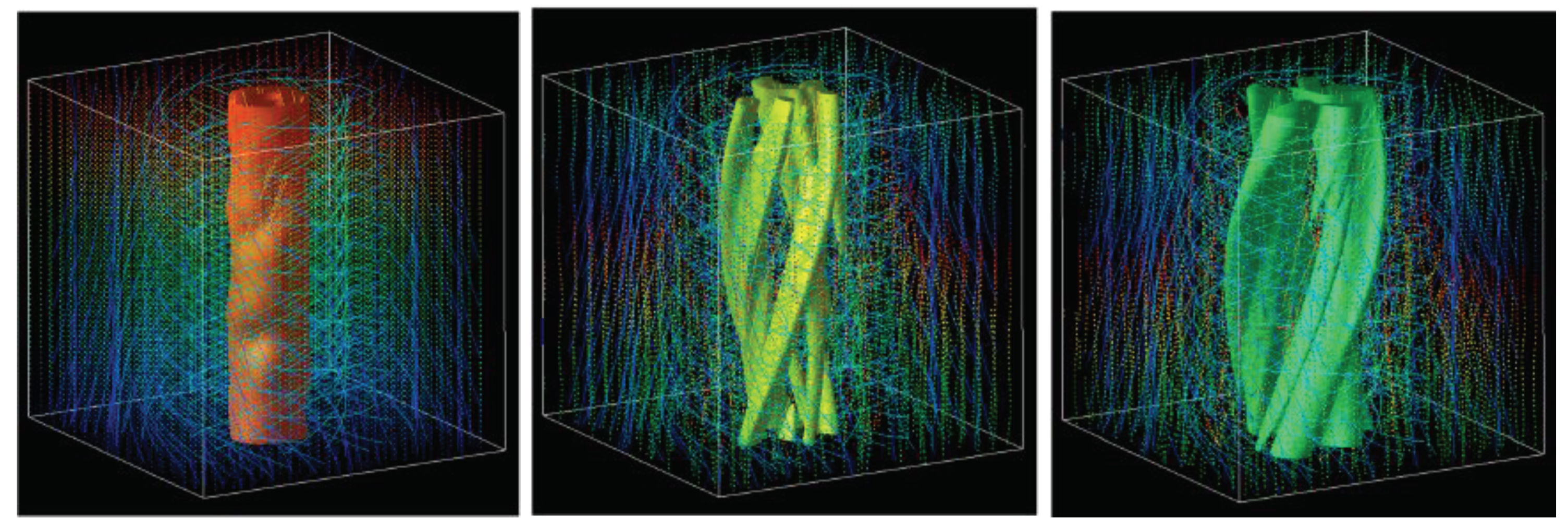
5. Numerical Simulations of Vortex Dynamics
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baddeley, P.F.H. Whirlwinds and Dust Storms of India; Bell & Daldy: London, UK, 1860. [Google Scholar]
- Bagnold, R.A. The Physics of Blown Sand and Desert Dunes; Chapman and Hall: London, UK, 1941. [Google Scholar]
- Lorenz, R.D.; Myers, M.J. Dust devil hazard to aviation. A review of United States Air accident reports. J. Meteorol. 2005, 30, 178–184. [Google Scholar]
- Ives, R.L. Behavior of dust devils. Bull. Am. Meteorol. Soc. 1947, 28, 168–174. [Google Scholar] [CrossRef]
- Grant, C.G. Dust devils in the sub-arctic. Weather 1949, 4, 402–403. [Google Scholar]
- Crozier, W.D. Dust devil properties. J. Geophys. Res. 1970, 75, 4583–4585. [Google Scholar] [CrossRef]
- Leovy, C.B. MarsThe devil is in the dust. Nature 2003, 424, 1008–1009. [Google Scholar] [CrossRef] [PubMed]
- Balme, M.; Greeley, R. Dust devils on Earth and Mars. Rev. Geophys. 2006, 44, RG3003. [Google Scholar] [CrossRef]
- Kok, J.F.; Parteli, E.J.R.; Michaels, T.I.; Karam, D.B. The physics of wind-blown sand and dust. Rep. Prog. Phys. 2012, 75, 106901. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Balme, M.R.; Gu, Z.; Kahanpää, H.; Klose, M.; Kurgansky, M.V.; Patel, M.R.; Reiss, D.; Rossi, A.P.; Spiga, A.; et al. History and Applications of Dust Devil Studies. Space Sci. Rev. 2016, 203, 5–37. [Google Scholar] [CrossRef]
- Sinclair, P.C. Some Preliminary Dust Devil MEASUREMENTS. Mon. Weather Rev. 1964, 92, 363. [Google Scholar] [CrossRef]
- Sinclair, P.C. On the rotation of dust devils. Bull. Am. Meteorol. Soc. 1965, 46, 388–391. [Google Scholar] [CrossRef]
- Sinclair, P.C. General Characteristics of Dust Devils. J. Appl. Meteorol. 1969, 8, 32–45. [Google Scholar] [CrossRef]
- Sinclair, P.C. The Lower Structure of Dust Devils. J. Atmos. Sci. 1973, 30, 1599–1619. [Google Scholar] [CrossRef]
- Idso, S.B. Tornado-Like Dust Devils. Weather 1975, 30, 115–117. [Google Scholar] [CrossRef]
- Rennó, N.O.; Bluestein, H.B. A Simple Theory for Waterspouts. J. Atmos. Sci. 2001, 58, 927–932. [Google Scholar] [CrossRef]
- Snow, J.T.; McClelland, T.M. Dust devils at White Sands Missile Range, New Mexico: 1. Temporal and spatial distributions. J. Geophys. Res. 1990, 95, 13. [Google Scholar] [CrossRef]
- Kurgansky, M.V. Steady-state properties and statistical distribution of atmospheric dust devils. Geophys. Res. Lett. 2006, 33, L19S06. [Google Scholar] [CrossRef]
- Ringrose, T.J. Dust devils: Inside dust devils. Astron. Geophys. 2005, 46, 5.16–5.19. [Google Scholar] [CrossRef]
- Carroll, J.J.; Ryan, J.A. Atmospheric vorticity and dust devil rotation. J. Geophys. Res. 1970, 75, 5179–5184. [Google Scholar] [CrossRef]
- Ryan, J.A.; Carroll, J.J. Dust devil wind velocities: Mature state. J. Geophys. Res. 1970, 75, 531–541. [Google Scholar] [CrossRef]
- Fitzjarrald, D.E. A Field Investigation of Dust Devils. J. Appl. Meteorol. 1973, 12, 808–813. [Google Scholar] [CrossRef]
- Hess, G.D.; Spillane, K.T. Characteristics of Dust Devils in Australia. J. Appl. Meteorol. 1990, 29, 498–507. [Google Scholar] [CrossRef]
- Metzger, S.M.; Carr, J.R.; Johnson, J.R.; Parker, T.J.; Lemmon, M.T. Dust devil vortices seen by the Mars Pathfinder Camera. Geophys. Res. Lett. 1999, 26, 2781–2784. [Google Scholar] [CrossRef]
- Renno, N.O.; Abreu, V.J.; Koch, J.; Smith, P.H.; Hartogensis, O.K.; De Bruin, H.A.R.; Burose, D.; Delory, G.T.; Farrell, W.M.; Watts, C.J.; et al. MATADOR 2002: A pilot field experiment on convective plumes and dust devils. J. Geophys. Res. (Planets) 2004, 109, E07001. [Google Scholar] [CrossRef]
- Lewellen, D.C.; Lewellen, W.S.; Xia, J. The Influence of a Local Swirl Ratio on Tornado Intensification near the Surface. J. Atmos. Sci. 2000, 57, 527–544. [Google Scholar] [CrossRef]
- Metzger, S.M. Dust Devils as Aeolian Transport Mechanisms in Southern Nevada And the Mars Pathfinder Landing Site. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 1999. [Google Scholar]
- Shao, Y. Physics and Modelling of Wind Erosion; Springer: Berlin, Germany, 2008. [Google Scholar]
- Iversen, J.D.; White, B.R. Saltation threshold on Earth, Mars and Venus. Sedimentology 1982, 29, 111–119. [Google Scholar] [CrossRef]
- Greeley, R.; Iversen, J.D. Wind As a Geological Process on Earth, Mars, Venus And Titan; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Neakrase, L.D.V.; Balme, M.R.; Esposito, F.; Kelling, T.; Klose, M.; Kok, J.F.; Marticorena, B.; Merrison, J.; Patel, M.; Wurm, G. Particle Lifting Processes in Dust Devils. Space Sci. Rev. 2016, 203, 347–376. [Google Scholar] [CrossRef]
- Almeida, M.P.; Parteli, E.J.R.; Andrade, J.S.; Herrmann, H.J. From the Cover: Giant saltation on Mars. Proc. Natl. Acad. Sci. USA 2008, 105, 6222–6226. [Google Scholar] [CrossRef]
- Balme, M.R.; Whelley, P.L.; Greeley, R. Mars: Dust devil track survey in Argyre Planitia and Hellas Basin. J. Geophys. Res. (Planets) 2003, 108, 5086. [Google Scholar] [CrossRef]
- Balme, M.; Metzger, S.; Towner, M.; Ringrose, T.; Greeley, R.; Iversen, J. Friction wind speeds in dust devils: A field study. Geophys. Res. Lett. 2003, 30, 1830. [Google Scholar] [CrossRef]
- Oke, A.M.C.; Dunkerley, D.; Tapper, N.J. Willy-willies in the Australian landscape: Sediment transport characteristics. J. Arid Environ. 2007, 71, 216–228. [Google Scholar] [CrossRef]
- Greeley, R.; Balme, M.R.; Iversen, J.D.; Metzger, S.; Mickelson, R.; Phoreman, J.; White, B. Martian dust devils: Laboratory simulations of particle threshold. J. Geophys. Res. (Planets) 2003, 108, 5041. [Google Scholar] [CrossRef]
- Neakrase, L.D.V.; Greeley, R.; Iversen, J.D.; Balme, M.R.; Eddlemon, E.E. Dust flux within dust devils: Preliminary laboratory simulations. Geophys. Res. Lett. 2006, 33, L19S09. [Google Scholar] [CrossRef]
- Twohy, C.H.; Kreidenweis, S.M.; Eidhammer, T.; Browell, E.V.; Heymsfield, A.J.; Bansemer, A.R.; Anderson, B.E.; Chen, G.; Ismail, S.; DeMott, P.J.; et al. Saharan dust particles nucleate droplets in eastern Atlantic clouds. Geophys. Res. Lett. 2009, 36, L01807. [Google Scholar] [CrossRef]
- Tegen, I.; Lacis, A.A.; Fung, I. The influence on climate forcing of mineral aerosols from disturbed soils. Nature 1996, 380, 419–422. [Google Scholar] [CrossRef]
- Renno, N.O.; Kok, J.F. Electrical Activity and Dust Lifting on Earth, Mars, and Beyond. Space Sci. Rev. 2008, 137, 419–434. [Google Scholar] [CrossRef]
- Freier, G.D. The Electric Field of a Large Dust Devil. J. Geophys. Res. 1960, 65, 3504. [Google Scholar] [CrossRef]
- Kok, J.F.; Renno, N.O. Enhancement of the emission of mineral dust aerosols by electric forces. Geophys. Res. Lett. 2006, 33, L19S10. [Google Scholar] [CrossRef]
- Kok, J.F.; Renno, N.O. Electrostatics in Wind-Blown Sand. Phys. Rev. Lett. 2008, 100, 014501. [Google Scholar] [CrossRef]
- Lacks, D.J.; Levandovsky, A. Effect of particle size distribution on the polarity of triboelectric charging in granular insulator systems. J. Electrost. 2007, 65, 107–112. [Google Scholar] [CrossRef]
- Schmidt, D.S.; Schmidt, R.A.; Dent, J.D. Electrostatic force on saltating sand. J. Geophys. Res. 1998, 103, 8997–9001. [Google Scholar] [CrossRef]
- Jackson, T.L.; Farrell, W.M. Electrostatic Fields in Dust Devils: An Analog to Mars. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2942–2949. [Google Scholar] [CrossRef]
- Stow, C.D. Dust and Sand Storm Electrification. Weather 1969, 24, 134–144. [Google Scholar] [CrossRef]
- Pähtz, T.; Herrmann, H.J.; Shinbrot, T. Why do particle clouds generate electric charges? Nat. Phys. 2010, 6, 364–368. [Google Scholar] [CrossRef]
- Mills, A.A. Dust clouds and frictional generation of glow discharges on Mars. Nature 1977, 268, 614. [Google Scholar] [CrossRef]
- Crozier, W.D. The Electrical Field of a New Mexico Dust Devil. J. Geophys. Res. 1964, 69, 5427–5429. [Google Scholar] [CrossRef]
- Williams, E.; Nathou, N.; Hicks, E.; Pontikis, C.; Russell, B.; Miller, M.; Bartholomew, M.J. The electrification of dust-lofting gust fronts (‘haboobs’) in the Sahel. Atmos. Res. 2009, 91, 292–298. [Google Scholar] [CrossRef]
- Rudge, W.A.D. Atmospheric electrification during South African dust storms. Nature 1913, 91, 31–32. [Google Scholar] [CrossRef]
- Farrell, W.M.; Smith, P.H.; Delory, G.T.; Hillard, G.B.; Marshall, J.R.; Catling, D.; Hecht, M.; Tratt, D.M.; Renno, N.; Desch, M.D.; et al. Electric and magnetic signatures of dust devils from the 2000–2001 MATADOR desert tests. J. Geophys. Res. (Planets) 2004, 109, E03004. [Google Scholar] [CrossRef]
- Farrell, W.M.; Delory, G.T.; Cummer, S.A.; Marshall, J.R. A simple electrodynamic model of a dust devil. Geophys. Res. Lett. 2003, 30, 2050. [Google Scholar] [CrossRef]
- Farrell, W.M.; Renno, N.; Delory, G.T.; Cummer, S.A.; Marshall, J.R. Integration of electrostatic and fluid dynamics within a dust devil. J. Geophys. Res. (Planets) 2006, 111, E01006. [Google Scholar] [CrossRef]
- Eden, H.F.; Vonnegut, B. Electrical Breakdown Caused by Dust Motion in Low-Pressure Atmospheres: Considerations for Mars. Science 1973, 180, 962–963. [Google Scholar] [CrossRef] [PubMed]
- Melnik, O.; Parrot, M. Electrostatic discharge in Martian dust storms. J. Geophys. Res. 1998, 103, 29107–29118. [Google Scholar] [CrossRef]
- Zheng, X.J.; Huang, N.; Zhou, Y.H. Laboratory measurement of electrification of wind-blown sands and simulation of its effect on sand saltation movement. J. Geophys. Res. (Atmos.) 2003, 108, 4322. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Guo, X.; Zheng, X.J. Experimental measurement of wind-sand flux and sand transport for naturally mixed sands. Phys. Rev. E 2002, 66, 021305. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.; Yue, G.; Zheng, X. Numerical simulations of a dust devil and the electric field in it. J. Geophys. Res. (Atmos.) 2008, 113, D20203. [Google Scholar] [CrossRef]
- Ireland, P.M. Triboelectrification of particulate flows on surfaces: Part I? Experiments. Powder Technol. 2010, 198, 189–198. [Google Scholar] [CrossRef]
- Ireland, P.M. Triboelectrification of particulate flows on surfaces: Part II? Mechanisms and models. Powder Technol. 2010, 198, 199–210. [Google Scholar] [CrossRef]
- Ireland, P.M.; Jameson, G.J. Particle dynamics in cyclone tribochargers. J. Electrost. 2013, 71, 449–455. [Google Scholar] [CrossRef]
- Lowell, J.; Truscott, W.S. Triboelectrification of identical insulators. II. Theory and further experiments. J. Phys. D Appl. Phys. 1986, 19, 1281–1298. [Google Scholar] [CrossRef]
- Lacks, D.J.; Duff, N.; Kumar, S.K. Nonequilibrium Accumulation of Surface Species and Triboelectric Charging in Single Component Particulate Systems. Phys. Rev. Lett. 2008, 100, 188305. [Google Scholar] [CrossRef]
- Lacks, D.J.; Mohan Sankaran, R. Contact electrification of insulating materials. J. Phys. D Appl. Phys. 2011, 44, 453001. [Google Scholar] [CrossRef]
- Matsusaka, S.; Masuda, H. Electrostatics of particles. Adv. Powder Technol. 2003, 14, 143–166. [Google Scholar] [CrossRef]
- Onishchenko, O.G.; Pokhotelov, O.A.; Astafieva, N.M. Reviews of topical problems: Generation of large-scale eddies and zonal winds in planetary atmospheres. Phys. Uspekhi 2008, 51, 577–589. [Google Scholar] [CrossRef]
- Mullen, J.B.; Maxworthy, T. A laboratory model of dust devil vortices. Dyn. Atmos. Oceans 1977, 1, 181–214. [Google Scholar] [CrossRef]
- Church, C.R.; Snow, J.T.; Baker, G.L.; Agee, E.M. Characteristics of Tornado-Like Vortices as a Function of Swirl Ratio: A Laboratory Investigation. J. Atmos. Sci. 1979, 36, 1755–1776. [Google Scholar] [CrossRef]
- Howells, P.A.C.; Rotunno, R.; Smith, R.K. A comparative study of atmospheric and laboratory-analogue numerical tornado-vortex models. Q. J. R. Meteorol. Soc. 1988, 114, 801–822. [Google Scholar] [CrossRef]
- Idso, S.B.; Kimball, B.A. Tornado or Dust Devil: The Enigma of Desert Whirlwinds. Am. Sci. 1974, 62, 530–541. [Google Scholar]
- Nolan, D.S.; Farrell, B.F. The Structure and Dynamics of Tornado-Like Vortices. J. Atmos. Sci. 1999, 56, 2908–2936. [Google Scholar] [CrossRef]
- Trapp, R.J.; Fiedler, B.H. Tornado-like Vortexgenesis in a Simplified Numerical Model. J. Atmos. Sci. 1995, 52, 3757–3778. [Google Scholar] [CrossRef]
- Mahowald, N. Aerosol Indirect Effect on Biogeochemical Cycles and Climate. Science 2011, 334, 794. [Google Scholar] [CrossRef]
- Mahowald, N.; Ward, D.S.; Kloster, S.; Flanner, M.G.; Heald, C.L.; Heavens, N.G.; Hess, P.G.; Lamarque, J.F.; Chuang, P.Y. Aerosol Impacts on Climate and Biogeochemistry. Ann. Rev. Environ. Resour. 2011, 36, 45–74. [Google Scholar] [CrossRef]
- Miller, R.L.; Knippertz, P.; Pérez Garcia-Pando, C.; Perlwitz, J.P.; Tegen, I. Impact of dust radiative forcing upon climate. In Mineral Dust; Knippertz, P., Stuut, J.-B.W., Eds.; Springer: Berlin, Germany, 2014; pp. 327–357. [Google Scholar]
- Yoshioka, M.; Mahowald, N.M.; Conley, A.J.; Collins, W.D.; Fillmore, D.W.; Zender, C.S.; Coleman, D.B. Impact of Desert Dust Radiative Forcing on Sahel Precipitation: Relative Importance of Dust Compared to Sea Surface Temperature Variations, Vegetation Changes, and Greenhouse Gas Warming. J. Clim. 2007, 20, 1445. [Google Scholar] [CrossRef]
- Pokharel, A.K.; Kaplan, M.L.; Fiedler, S. The Role of Jet Adjustment Processes in Subtropical Dust Storms. J. Geophys. Res. (Atmos.) 2017, 122, 12. [Google Scholar] [CrossRef]
- Pokharel, A.K.; Kaplan, M.L.; Fiedler, S. Subtropical Dust Storms and Downslope Wind Events. J. Geophys. Res. (Atmos.) 2017, 122, 10. [Google Scholar] [CrossRef]
- Ramanathan, V.; Crutzen, P.J.; Kiehl, J.T.; Rosenfeld, D. Aerosols, Climate, and the Hydrological Cycle. Science 2001, 294, 2119–2124. [Google Scholar] [CrossRef] [PubMed]
- Toon, O.B. African dust in Florida clouds. Nature 2003, 424, 623–624. [Google Scholar] [CrossRef] [PubMed]
- Twohy, C.H.; Anderson, B.E.; Ferrare, R.A.; Sauter, K.E.; L’Ecuyer, T.S.; van den Heever, S.C.; Heymsfield, A.J.; Ismail, S.; Diskin, G.S. Saharan dust, convective lofting, aerosol enhancement zones, and potential impacts on ice nucleation in the tropical upper troposphere. J. Geophys. Res. (Atmos.) 2017, 122, 8833–8851. [Google Scholar] [CrossRef]
- Kohfeld, K.E.; Harrison, S.P. DIRTMAP: The geological record of dust. Earth Sci. Rev. 2001, 54, 81–114. [Google Scholar] [CrossRef]
- Harrison, S.P.; Kohfeld, K.E.; Roelandt, C.; Claquin, T. The role of dust in climate changes today, at the last glacial maximum and in the future. Earth Sci. Rev. 2001, 54, 43–80. [Google Scholar] [CrossRef]
- Prospero, J.M.; Lamb, P.J. African Droughts and Dust Transport to the Caribbean: Climate Change Implications. Science 2003, 302, 1024–1027. [Google Scholar] [CrossRef]
- DeMott, P.J.; Sassen, K.; Poellot, M.R.; Baumgardner, D.; Rogers, D.C.; Brooks, S.D.; Prenni, A.J.; Kreidenweis, S.M. African dust aerosols as atmospheric ice nuclei. Geophys. Res. Lett. 2003, 30, 1732. [Google Scholar] [CrossRef]
- Zhao, Y.Z.; Gu, Z.L.; Yu, Y.Z.; Ge, Y.; Li, Y.; Feng, X. Mechanism and large eddy simulation of dust devils. Atmos.-Ocean 2004, 41, 61–84. [Google Scholar] [CrossRef]
- Rafkin, S.; Jemmett-Smith, B.; Fenton, L.; Lorenz, R.; Takemi, T.; Ito, J.; Tyler, D. Dust Devil Formation. Space Sci. Rev. 2016, 203, 183–207. [Google Scholar] [CrossRef]
- Raasch, S.; Franke, T. Structure and formation of dust devil-like vortices in the atmospheric boundary layer: A high-resolution numerical study. J. Geophys. Res. (Atmos.) 2011, 116, D16120. [Google Scholar] [CrossRef]
- Kurgansky, M.V. A simple model of dry convective helical vortices (with applications to the atmospheric dust devil). Dyn. Atmos. Oceans 2005, 40, 151–162. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Pazmany, A.L. Observations of Tornadoes and Other Convective Phenomena with a Mobile, 3-mm Wavelength, Doppler Radar: The Spring 1999 Field Experiment. Bull. Am. Meteorol. Soc. 2000, 81, 2939–2952. [Google Scholar] [CrossRef]
- Jackson, B.; Lorenz, R.; Davis, K.; Lipple, B. Using an Instrumented Drone to Probe Dust Devils on Oregon’s Alvord Desert. Remote Sens. 2018, 10, 65. [Google Scholar] [CrossRef]
- Rennó, N.O.; Burkett, M.L.; Larkin, M.P. A Simple Thermodynamical Theory for Dust Devils. J. Atmos. Sci. 1998, 55, 3244–3252. [Google Scholar] [CrossRef]
- Onishchenko, O.G.; Horton, W.; Pokhotelov, O.A.; Stenflo, L. Dust devil generation. Phys. Scr. 2014, 89, 075606. [Google Scholar] [CrossRef]
- Onishchenko, O.G.; Pokhotelov, O.A.; Horton, W. Dust devil dynamics in the internal vortex region. Phys. Scr. 2015, 90, 068004. [Google Scholar] [CrossRef]
- Onishchenko, O.; Pokhotelov, O.; Horton, W.; Fedun, V. Dust devil vortex generation from convective cells. Ann. Geophys. 2015, 33, 1343–1347. [Google Scholar] [CrossRef]
- Onishchenko, O.G.; Horton, W.; Pokhotelov, O.A.; Fedun, V. “Explosively growing” vortices of unstably stratified atmosphere. J. Geophys. Res. (Atmos.) 2016, 121, 11. [Google Scholar] [CrossRef]
- Rankine, W.J.M. A Manual of Applied Mechanics; C. Griffin and Co., Limited: London, UK, 1901. [Google Scholar]
- Battan, L.J. Energy of a Dust Devil. J. Atmos. Sci. 1958, 15, 235–236. [Google Scholar] [CrossRef]
- Toigo, A.D.; Richardson, M.I.; Ewald, S.P.; Gierasch, P.J. Numerical simulation of Martian dust devils. J. Geophys. Res. (Planets) 2003, 108, 5047. [Google Scholar] [CrossRef]
- Kurgansky, M.V.; Lorenz, R.D.; Renno, N.O.; Takemi, T.; Gu, Z.; Wei, W. Dust Devil Steady-State Structure from a Fluid Dynamics Perspective. Space Sci. Rev. 2016, 203, 209–244. [Google Scholar] [CrossRef]
- Vatistas, G.H.; Kozel, V.; Mih, W.C. A simpler model for concentrated vortices. Exp. Fluids 1991, 11, 73–76. [Google Scholar] [CrossRef]
- Burgers, J.M. A Mathematical Model Illustrating the Theory of Turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Rott, N. On the viscous core of a line vortex. Z. Angew. Math. Phys. 1958, 9, 543–553. [Google Scholar] [CrossRef]
- Sullivan, R.D. A two-cell vortex solution of the Navier-Stokes equations. J. Aerosp. Sci. 1959, 26, 767–768. [Google Scholar] [CrossRef]
- Gu, Z.; Qiu, J.; Zhao, Y.; Li, Y. Simulation of terrestrial dust devil patterns. Adv. Atmos. Sci. 2008, 25, 31–42. [Google Scholar] [CrossRef]
- Michaels, T.I.; Rafkin, S.C.R. Large-eddy simulation of atmospheric convection on Mars. Q. J. R. Meteorol. Soc. 2004, 130, 1251–1274. [Google Scholar] [CrossRef]
- Onishchenko, O.G.; Fedun, V.; Horton, W.; Pokhotelov, O.A.; Astafieva, N.M.; Verth, G. Stationary concentrated vortex model. Q. J. R. Meteorol. Soc. 2018. submitted. [Google Scholar]
- Onishchenko, O.G.; Pokhotelov, O.A.; Astafieva, N.M. A novel model of quasi-stationary vortices in the Earth’s atmosphere. Izv. Atmos. Ocean. Phys. 2018, 54, 130–134. [Google Scholar]
- Kamra, A.K. Measurements of the electrical properties of dust storms. J. Geophys. Res. 1972, 77, 5856–5869. [Google Scholar] [CrossRef]
- Perkins, S. Static electricity strengthens desert dust storms. Science 2016. [Google Scholar] [CrossRef]
- Izvekova, Y.N.; Popel, S.I. Nonlinear Wave Structures and Plasma-Dust Effects in the Earth’s Atmosphere. Plasma Phys. Rep. 2018, 44, 835–839. [Google Scholar] [CrossRef]
- Spiga, A.; Barth, E.; Gu, Z.; Hoffmann, F.; Ito, J.; Jemmett-Smith, B.; Klose, M.; Nishizawa, S.; Raasch, S.; Rafkin, S.; et al. Large-Eddy Simulations of Dust Devils and Convective Vortices. Space Sci. Rev. 2016, 203, 245–275. [Google Scholar] [CrossRef]
- Lorenz, R.D. Vortex Encounter Rates with Fixed Barometer Stations: Comparison with Visual Dust Devil Counts and Large-Eddy Simulations. J. Atmos. Sci. 2014, 71, 4461–4472. [Google Scholar] [CrossRef]
- Kanak, K.M. Numerical simulation of dust devil-scale vortices. Q. J. R. Meteorol. Soc. 2005, 131, 1271–1292. [Google Scholar] [CrossRef]
- Kanak, K.M.; Lilly, D.K.; Snow, J.T. The formation of vertical Vortices in the convective boundary layer. Q. J. R. Meteorol. Soc. 2000, 126, 2789–2810. [Google Scholar] [CrossRef]
- Leslie, L.M.; Smith, R.K. On the choice of radial boundary conditions for numerical models of sub-synoptic vortex flows in the atmosphere, with application to dust devils. Q. J. R. Meteorol. Soc. 1977, 103, 499–510. [Google Scholar] [CrossRef]
- Smith, R.K.; Leslie, L.M. Thermally driven vortices: A numerical study with application to dust-devil dynamics. Q. J. R. Meteorol. Soc. 1976, 102, 791–804. [Google Scholar] [CrossRef]
- Neves, T.; Fisch, G.; Raasch, S. Local Convection and Turbulence in the Amazonia Using Large Eddy Simulation Model. Atmosphere 2018, 9, 399. [Google Scholar] [CrossRef]
- Harrison, R.G.; Barth, E.; Esposito, F.; Merrison, J.; Montmessin, F.; Aplin, K.L.; Borlina, C.; Berthelier, J.J.; Déprez, G.; Farrell, W.M.; et al. Applications of Electrified Dust and Dust Devil Electrodynamics to Martian Atmospheric Electricity. Space Sci. Rev. 2016, 203, 299–345. [Google Scholar] [CrossRef]
- Barth, E.L.; Farrell, W.M.; Rafkin, S.C. The Electric Environment of Martian Dust Devils. AGU Fall Meeting Abstracts. 2017. Available online: http://adsabs.harvard.edu/abs/2017AGUFM.P33I..04B (accessed on 9 January 2019).
- Farrell, W.M.; McLain, J.L.; Collier, M.R.; Keller, J.W. The Martian dust devil electron avalanche: Laboratory measurements of the E-field fortifying effects of dust-electron absorption. Icarus 2017, 297, 90–96. [Google Scholar] [CrossRef]
- Zhai, Y.; Cummer, S.A.; Farrell, W.M. Quasi-electrostatic field analysis and simulation of Martian and terrestrial dust devils. J. Geophys. Res. (Planets) 2006, 111, E06016. [Google Scholar] [CrossRef]
- Horton, W.; Miura, H.; Onishchenko, O.; Couedel, L.; Arnas, C.; Escarguel, A.; Benkadda, S.; Fedun, V. Dust devil dynamics. J. Geophys. Res. (Atmos.) 2016, 121, 7197–7214. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onishchenko, O.; Fedun, V.; Horton, W.; Pokhotelov, O.; Verth, G. Dust Devils: Structural Features, Dynamics and Climate Impact. Climate 2019, 7, 12. https://doi.org/10.3390/cli7010012
Onishchenko O, Fedun V, Horton W, Pokhotelov O, Verth G. Dust Devils: Structural Features, Dynamics and Climate Impact. Climate. 2019; 7(1):12. https://doi.org/10.3390/cli7010012
Chicago/Turabian StyleOnishchenko, Oleg, Viktor Fedun, Wendell Horton, Oleg Pokhotelov, and Gary Verth. 2019. "Dust Devils: Structural Features, Dynamics and Climate Impact" Climate 7, no. 1: 12. https://doi.org/10.3390/cli7010012
APA StyleOnishchenko, O., Fedun, V., Horton, W., Pokhotelov, O., & Verth, G. (2019). Dust Devils: Structural Features, Dynamics and Climate Impact. Climate, 7(1), 12. https://doi.org/10.3390/cli7010012




