A Proposal to Evaluate Drought Characteristics Using Multiple Climate Models for Multiple Timescales
Abstract
1. Introduction
2. Materials and Methodology
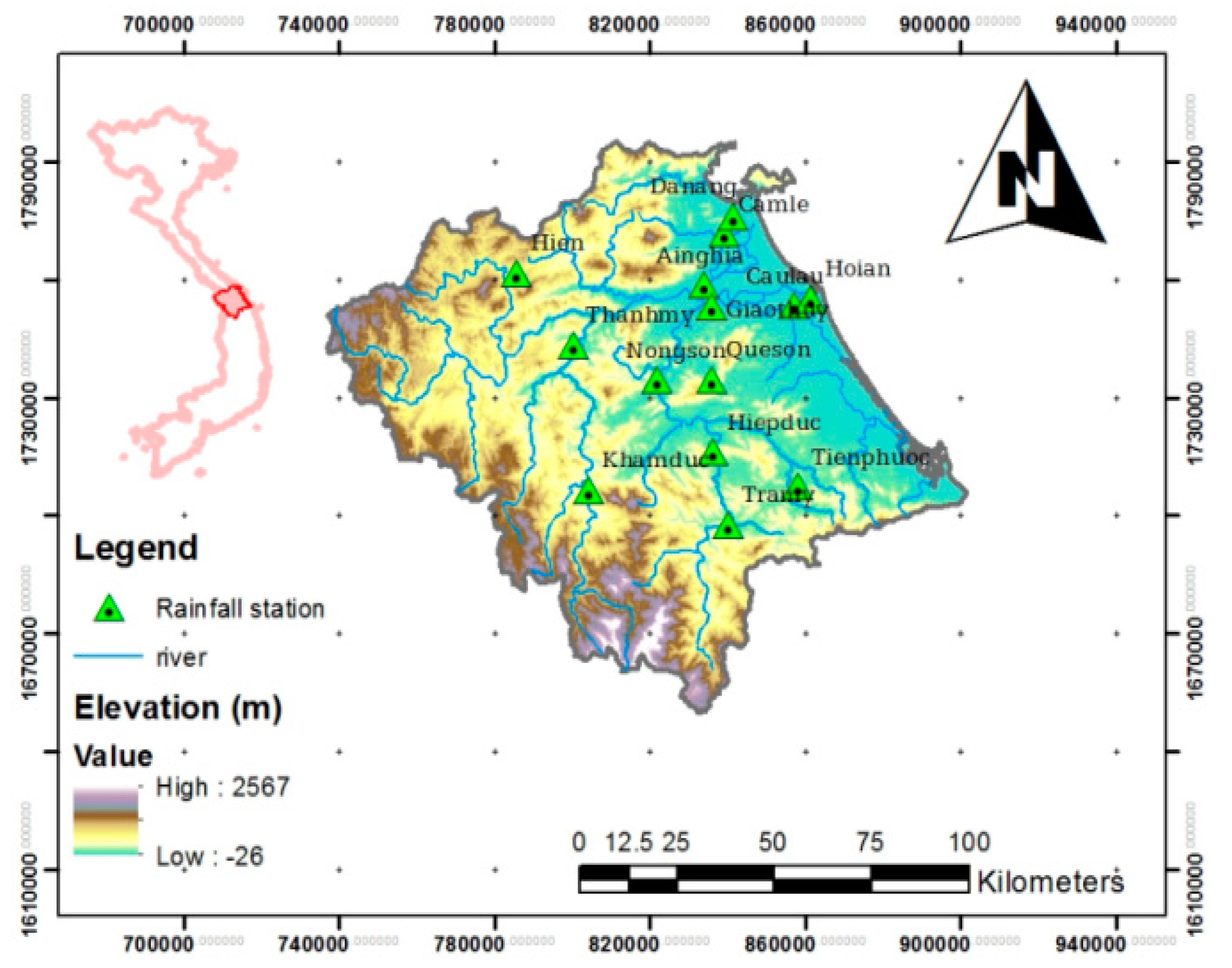
2.1. Description of the Case Study Area: Vu Gia-Thu Bon Basin
2.2. Data
2.2.1. Observational Data
2.2.2. Gridded Data
2.3. Methods
2.3.1. Delta Change Factor
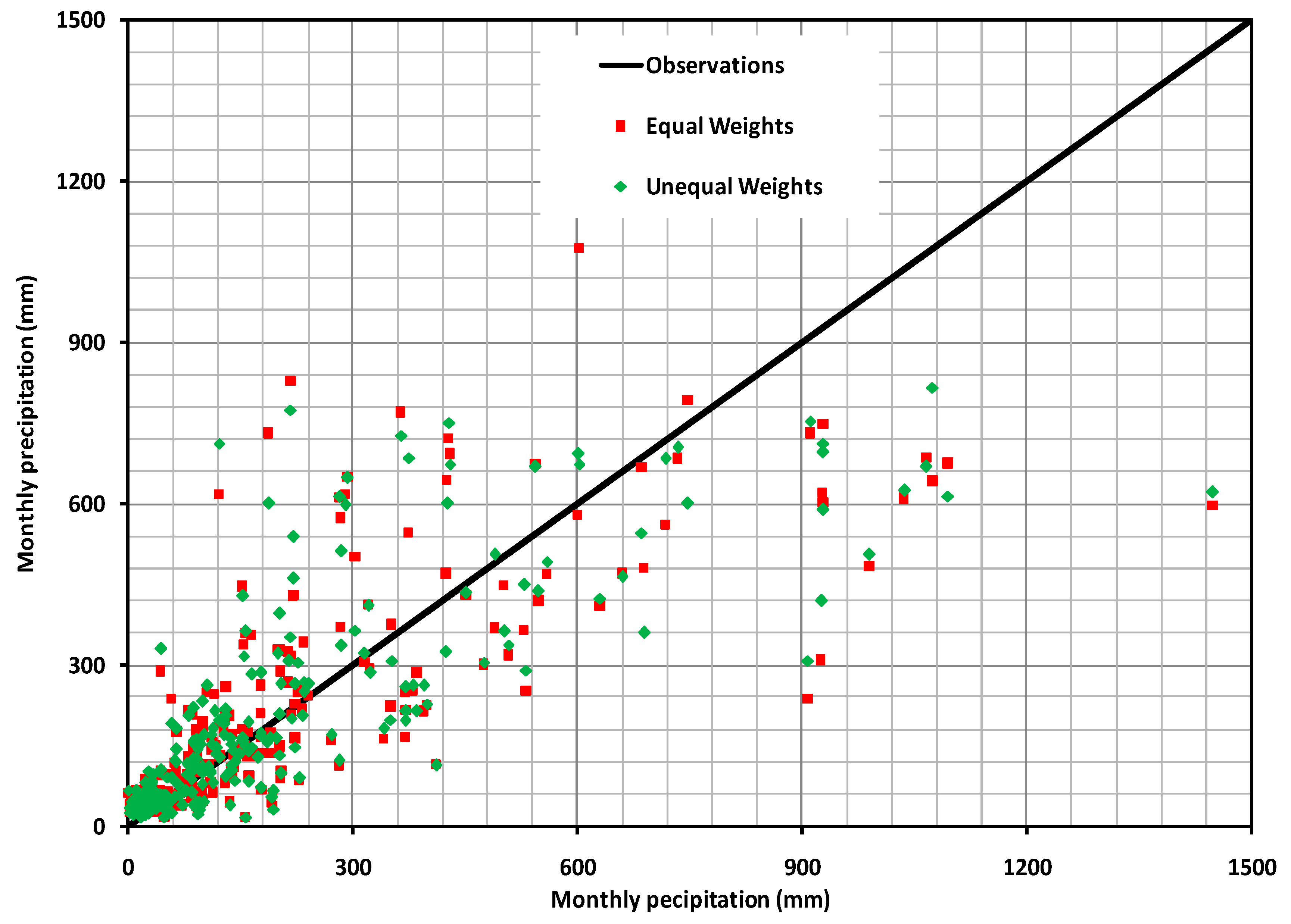
2.3.2. Unequal Weights
- (1)
- Calculation of the statistical indices on the basic of the historical observations and climate simulations from regional climate models forced by the reanalysis data of the European Centre for Medium-Range Weather Forecasts during 1989–2008. Each climate simulation receives a rank from 1 to N depending on the levels of perfect score for each statistical index, starting with the best as 1 and the worst is N. As an example, if the RMSE index of the ith climate model has the best score (the perfect score of RMSE is zero), the received rank is 1. Then, an ensemble rank order (r) as an integer number is calculated from the average of the ranks they span for each climate simulation.
- (2)
- Calculation of rank sum for each climate simulation by N-r + 1 with N is the number of climate simulations.
- (3)
- Establishing a reciprocal matrix between sets of models aij = 1/aji with i,j ranging from 1 corresponding to the best climate simulation which has the largest rank sum to N and aij = 1 as i = j. aij is determined by the difference of rank sum between sets of models plus 1.
- (4)
- Estimation of weights matrix wij = aij/ (i,j = 1, N)
- (5)
- Estimation of each weight for each climate simulation wi = (i = 1, N) with .
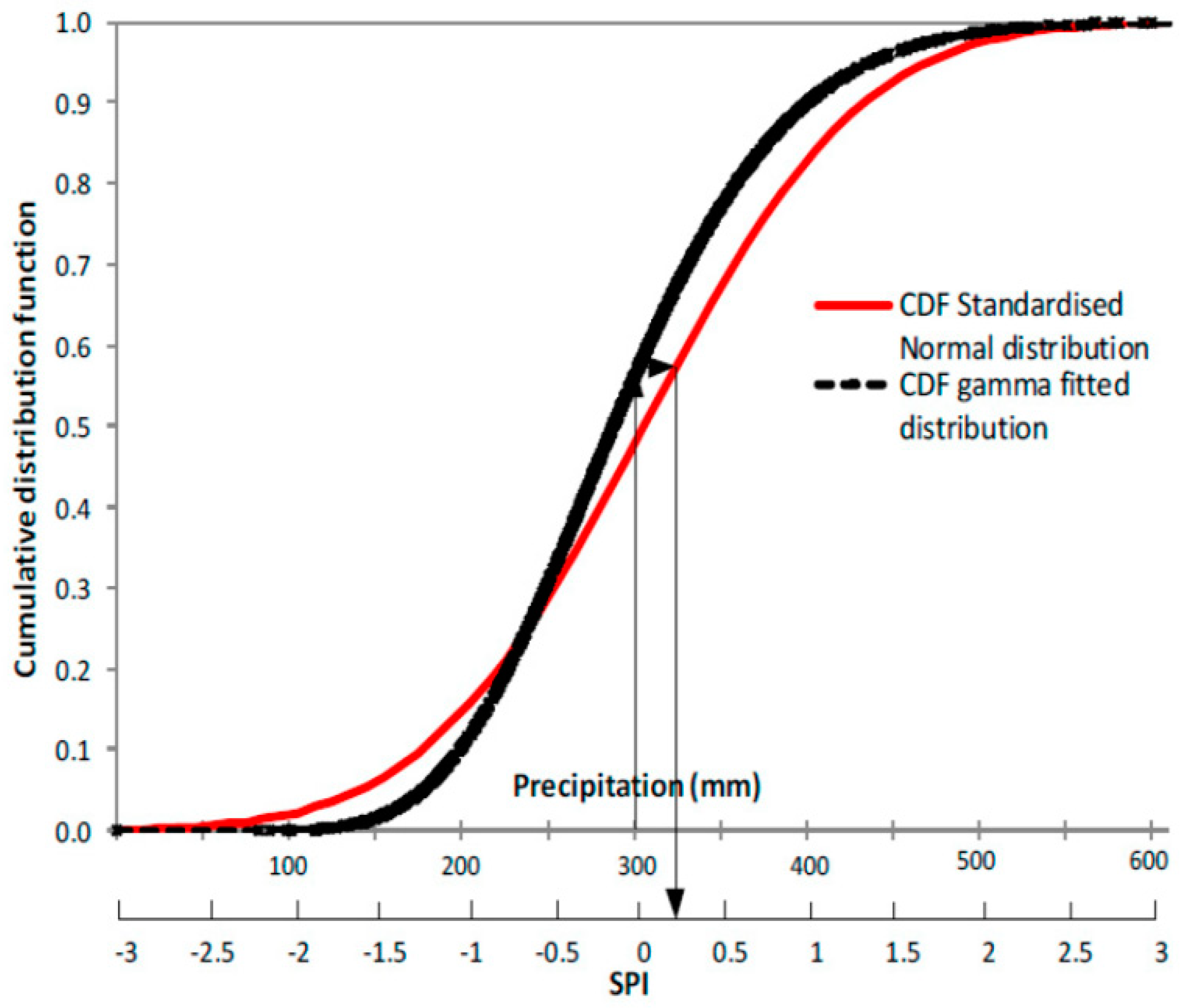
2.3.3. Standardized Precipitation Index (SPI)
2.3.4. Non-Parametric Mann–Kendall Test
2.3.5. The Sen’s Slope Estimator
3. Results and Discussions
3.1. Calculation of Weights for Each Climate Model
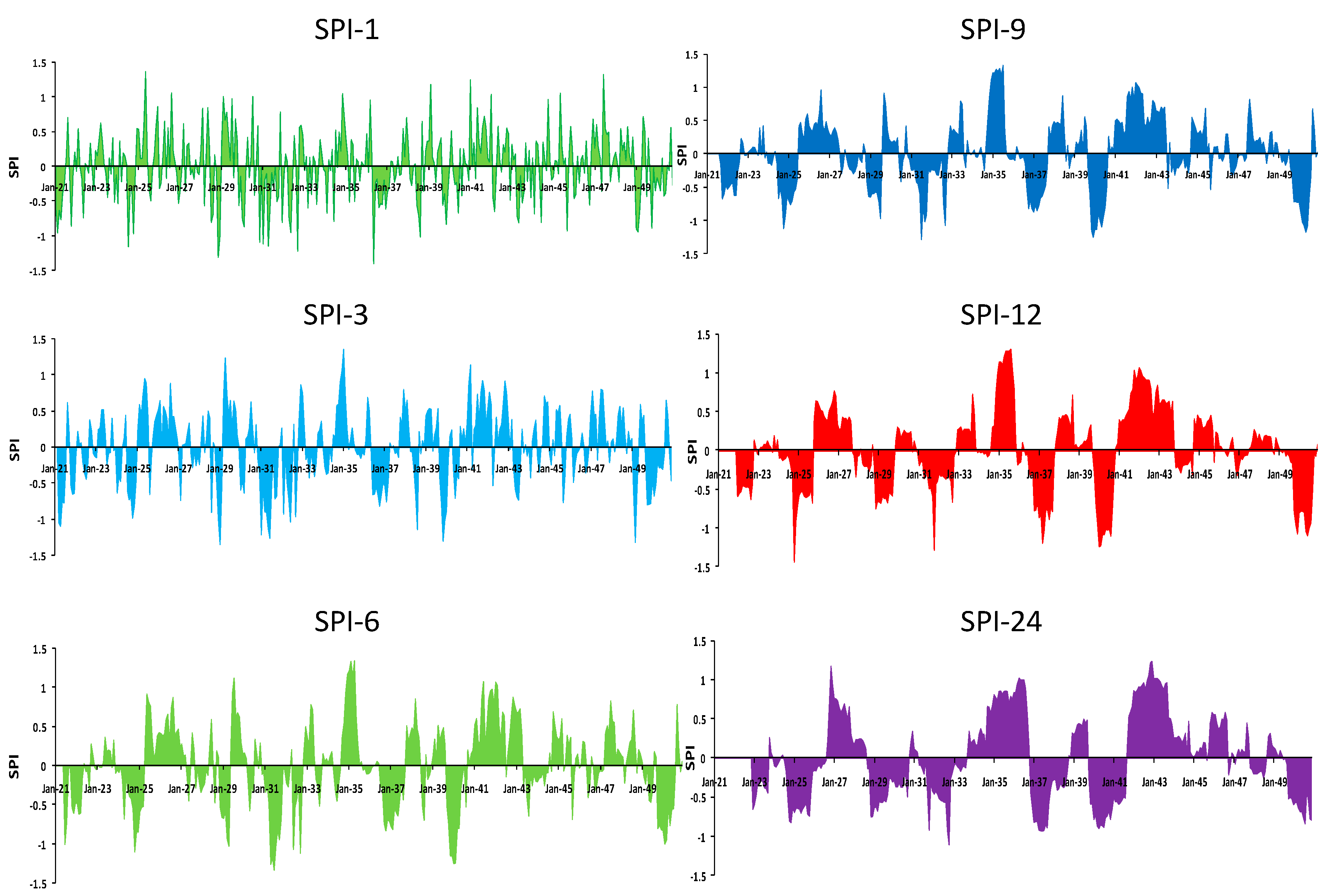
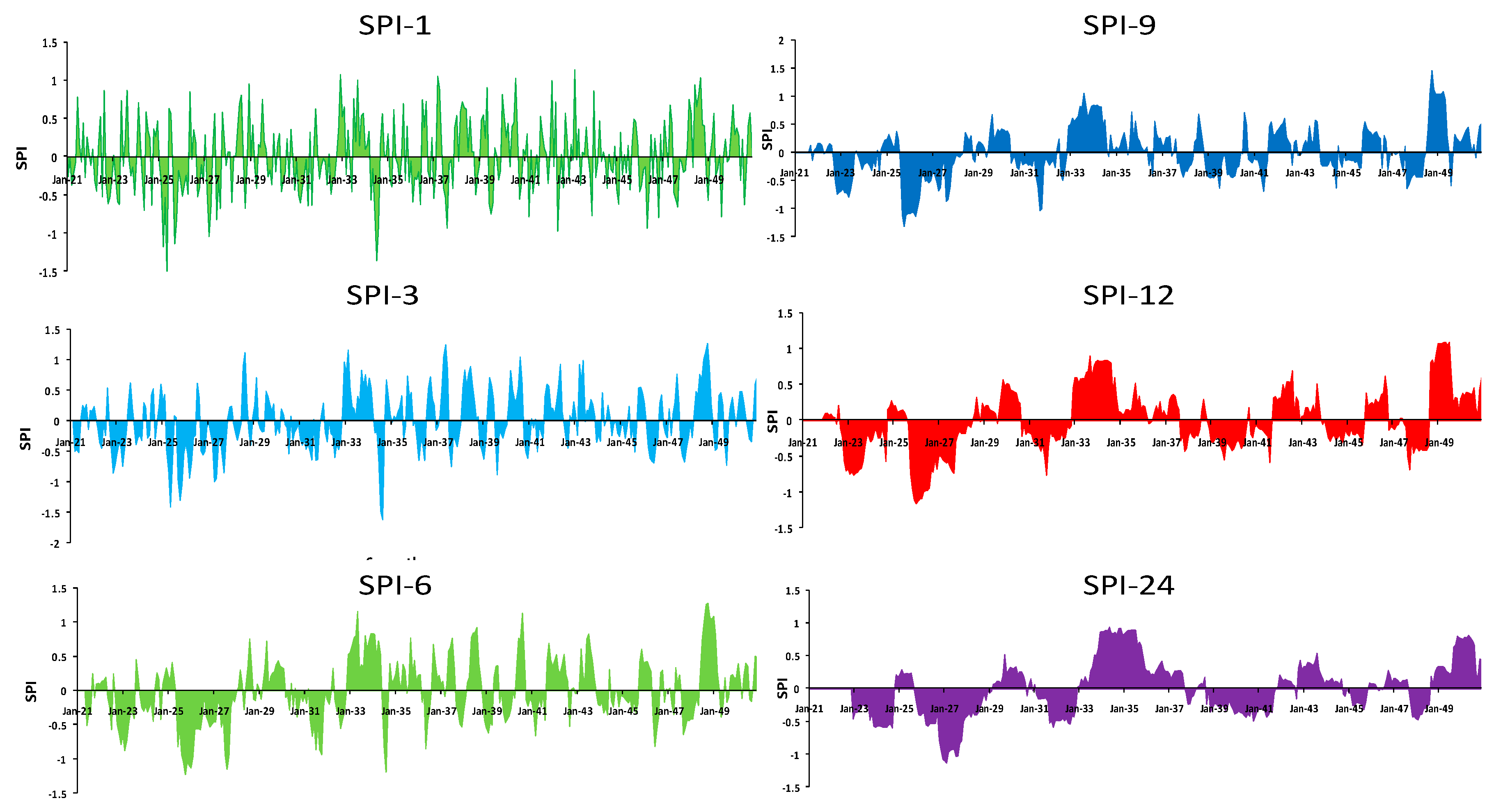
3.2. Calculation of SPI
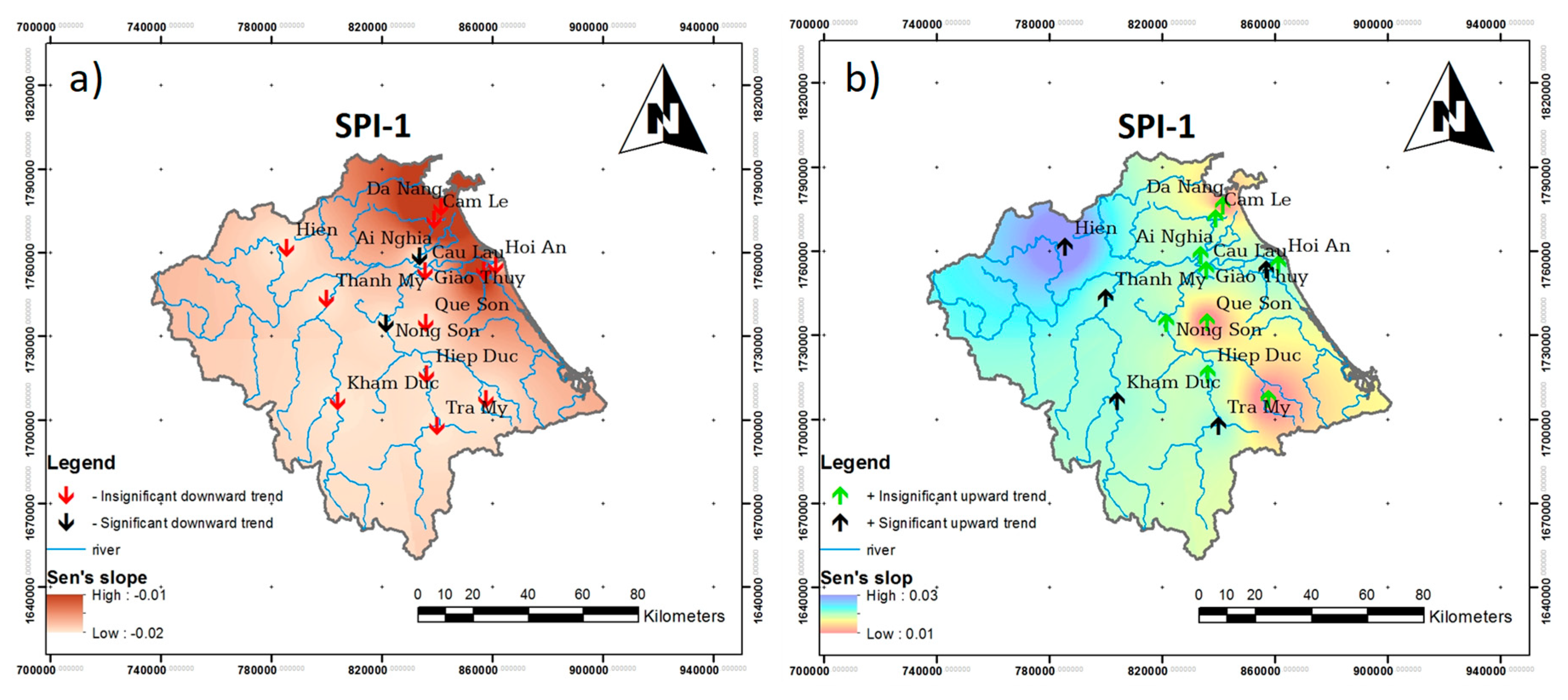
3.3. Projection Trends in SPI
4. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Weigel, A.P.; Knutti, R.; Liniger, M.A.; Appenzeller, C. Risks of model weighting in multimodel climate projections. J. Clim. 2010, 23, 4175–4191. [Google Scholar] [CrossRef]
- Moreland, J. Drought: Us Geological Survey Water Fact Sheet; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 1993; pp. 93–642.
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- WMO. Standardized Precipitation Index—User Guide; WMO-No. 1090; WMO: Geneva, Switzerland, 2012. [Google Scholar]
- IPCC. Climate Change 2007—The Physical Science Basis: Working Group I Contribution to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007; Volume 4. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Svoboda, M.; Fuchs, B. Handbook of Drought Indicators and Indices; WMO-No. 1173; WMO: Geneva, Switzerland, 2016. [Google Scholar]
- Svoboda, M.; LeComte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar] [CrossRef]
- Vogt, J.; Barbosa, P.; Hofer, B.; Magni, D.; Jager, A.; Singleton, A.; Horion, S.; Sepulcre, G.; Micale, F.; Sokolova, E. Developing a European Drought Observatory for Monitoring, Assessing and Forecasting Droughts across the European Continent; AGU Fall Meeting Abstracts; Copernicus Publications: Göttingen, Germany, 2011. [Google Scholar]
- Anctil, F.; Larouche, W.; Viau, A.; Parent, L.-E. Exploration of the standardized precipitation index with regional analysis. Can. J. Soil Sci. 2002, 82, 115–125. [Google Scholar] [CrossRef]
- Salehnia, N.; Alizadeh, A.; Sanaeinejad, H.; Bannayan, M.; Zarrin, A.; Hoogenboom, G. Estimation of meteorological drought indices based on agmerra precipitation data and station-observed precipitation data. J. Arid Land 2017, 9, 797–809. [Google Scholar] [CrossRef]
- Ntale, H.K.; Gan, T.Y. Drought indices and their application to East Africa. Int. J. Climatol. 2003, 23, 1335–1357. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Research Paper No. 45; US Department of Commerce Weather Bureau: Washington, DC, USA, 1965; p. 59.
- 1Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the reconnaissance drought index (rdi). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Carrao, H.; Barbosa, P.; Vogt, J. World drought frequency, duration, and severity for 1951–2010. Int. J. Climatol. 2014, 34, 2792–2804. [Google Scholar] [CrossRef]
- Weisheimer, A.; Doblas-Reyes, F.; Palmer, T.; Alessandri, A.; Arribas, A.; Déqué, M.; Keenlyside, N.; MacVean, M.; Navarra, A.; Rogel, P. Ensembles: A new multi-model ensemble for seasonal-to-annual predictions—Skill and progress beyond demeter in forecasting tropical pacific ssts. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- DelSole, T.; Yang, X.; Tippett, M.K. Is unequal weighting significantly better than equal weighting for multi-model forecasting? Q. J. R. Meteorol. Soc. 2013, 139, 176–183. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Wehner, M.; Knutti, R. Skill and independence weighting for multi-model assessments. Geosci. Model Dev. 2017. [Google Scholar] [CrossRef]
- Knutti, R.; Abramowitz, G.; Collins, M.; Eyering, V.; Gleckler, P.J.; Hewitson, B.; Mearns, L.O. Good Practice Guidance Paper on Assessing and Combining Multi Model Climate Projections. In Proceedings of the IPCC Expert Meeting on Assessing and Combining Multi Model Climate Projections, Boulder, CO, USA, 28–27 January 2010; p. 1. [Google Scholar]
- Krishnamurti, T.N.; Kishtawal, C.; Zhang, Z.; LaRow, T.; Bachiochi, D.; Williford, E.; Gadgil, S.; Surendran, S. Multimodel ensemble forecasts for weather and seasonal climate. J. Clim. 2000, 13, 4196–4216. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of cmip5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Publishing Co.: Oxford, UK, 1955. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econ. J. Econ. Soc. 1945, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Douglas, E.; Vogel, R.; Kroll, C. Trends in floods and low flows in the united states: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: New York, NY, USA, 1992; Volume 49. [Google Scholar]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Giorgi, F.; Coppola, E.; Solmon, F.; Mariotti, L.; Sylla, M.; Bi, X.; Elguindi, N.; Diro, G.; Nair, V.; Giuliani, G. Regcm4: Model description and preliminary tests over multiple cordex domains. Clim. Res. 2012, 52, 7–29. [Google Scholar] [CrossRef]
- Collins, W.; Bellouin, N.; Doutriaux-Boucher, M.; Gedney, N.; Halloran, P.; Hinton, T.; Hughes, J.; Jones, C.; Joshi, M.; Liddicoat, S. Development and evaluation of an earth-system model—Hadgem2. Geosci. Model Dev. 2011, 4, 1051–1075. [Google Scholar] [CrossRef]
- Lee, D.-K.; Cha, D.-H.; Kang, H.-S. Regional climate simulation of the 1998 summer flood over East Asia. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 1735–1753. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Park, H.; Cheong, H.-B.; Kim, J.-E.E.; Koo, M.-S.; Jang, J.; Ham, S.; Hwang, S.-O.; Park, B.-K.; Chang, E.-C. The global/regional integrated model system (grims). Asia-Pac. J. Atmos. Sci. 2013, 49, 219–243. [Google Scholar] [CrossRef]
- Maraun, D. Bias correcting climate change simulations—A critical review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (rcm) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef]
- Olsson, J.; Berggren, K.; Olofsson, M.; Viklander, M. Applying climate model precipitation scenarios for urban hydrological assessment: A case study in Kalmar City, Sweden. Atmos. Res. 2009, 92, 364–375. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Deursen, W.V. Estimates of future discharges of the river rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Sun, F.; Roderick, M.L.; Farquhar, G.D. Rainfall statistics, stationarity, and climate change. Proc. Natl. Acad. Sci. USA 2018, 115, 2305–2310. [Google Scholar] [CrossRef] [PubMed]
- Wilks, D.S.; Wilby, R.L. The weather generation game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Remo, L.D.A. Projected changes of precipitation idf curves for short duration under climate change in central Vietnam. Hydrology 2018, 5, 33. [Google Scholar]
- Choi, S.C.; Wette, R. Maximum likelihood estimation of the parameters of the gamma distribution and their bias. Technometrics 1969, 11, 683–690. [Google Scholar] [CrossRef]
- Thom, H.C. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Edwards, D.C. Characteristics of 20th Century Drought in the United States at Multiple Time Scales; Air Force Inst of Tech: Wright-Patterson AFB, OH, USA, 1997. [Google Scholar]
- Azam, M.; Maeng, S.; Kim, H.; Lee, S.; Lee, J. Spatial and temporal trend analysis of precipitation and drought in South Korea. Water 2018, 10, 765. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The mann-kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using mann-kendall and sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Blain, G.C. Removing the influence of the serial correlation on the mann-kendall test. Revista Brasileira de Meteorologia 2013, 29. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the mann-kendall and spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. In Henri Theil’s Contributions to Economics and Econometrics; Springer: Berlin, Germany, 1992; pp. 345–381. [Google Scholar]
- Grell, G.A.; Dudhia, J.; Stauffer, D.R. A Description of the Fifth-Generation Penn State/Ncar Mesoscale Model (mm5). 1994. Available online: http://danida.vnu.edu.vn/cpis/files/Books/MM5%20Discription%20-%201995.pdf (accessed on 23 August 2018).
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–183. [Google Scholar]
| Historical (1986–2005) | RCP4.5 (2021–2050) | RCP8.5 (2021–2050) | Spatial Resolution | Temporal Resolution | |
|---|---|---|---|---|---|
| RegCM4 forced by MPI-ESM-MR (REG/MPI) | 1 | 1 | 1 | 20 km | Monthly |
| RegCM4 forced by IPSL-CM5A-LR (REG /IPSL) | 1 | 1 | 1 | 20 km | Monthly |
| RegCM4 forced by ICHEC-EC-EARTH (REG/ICHEC) | 1 | 1 | 1 | 20 km | Monthly |
| RegCM4 forced by HadGEM2-AO (REG/HadGEM) | 1 | 1 | 1 | 20 km | Monthly |
| SNU-MM5 forced by HadGEM2-AO (SNU/HadGEM) | 1 | 1 | 1 | 20 km | Monthly |
| RSM forced by HadGEM2-AO (RSM/HadGEM) | 1 | 1 | 1 | 20 km | Monthly |
| ln(Nash) | RMSE | Nash | |
|---|---|---|---|
| REG/ICHEC | 0.935 | 170.67 | 0.523 |
| REG/IPSL | 0.941 | 157.44 | 0.594 |
| REG/MPI | 0.937 | 171.90 | 0.516 |
| REG/HadGEM | 0.891 | 256.72 | −0.079 |
| SNU/HadGEM | 0.913 | 252.75 | −0.046 |
| RSM/HadGEM | 0.880 | 278.93 | −0.274 |
| ln(Nash) | RMSE | Nash | Average | Ensemble Rank | Rank Sum | |
|---|---|---|---|---|---|---|
| REG/ICHEC | 3 | 2 | 2 | 2.3 | 2 | 5 |
| REG/IPSL | 1 | 1 | 1 | 1.0 | 1 | 6 |
| REG/MPI | 2 | 3 | 3 | 2.7 | 3 | 4 |
| REG/HadGEM | 5 | 5 | 4 | 4.7 | 5 | 2 |
| SNU/HadGEM | 4 | 4 | 5 | 4.3 | 4 | 3 |
| RSM/HadGEM | 6 | 6 | 6 | 6.0 | 6 | 1 |
| REG/IPSL | REG/ICHEC | REG/MPI | SNU/HadGEM | REG/HadGEM | RSM/HadGEM | Total | |
|---|---|---|---|---|---|---|---|
| REG/IPSL | 1 | 2 | 3 | 4 | 5 | 6 | 21 |
| REG/ICHEC | 1/2 | 1 | 2 | 3 | 4 | 5 | 15.5 |
| REG/MPI | 1/3 | 1/2 | 1 | 2 | 3 | 4 | 10.83 |
| SNU/HadGEM | 1/4 | 1/3 | 1/2 | 1 | 2 | 3 | 7.08 |
| REG/HadGEM | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 2 | 4.28 |
| RSM/HadGEM | 1/6 | 1/5 | 1/4 | 1/3 | 1/2 | 1 | 2.45 |
| Total | 61.15 |
| Classification | Min | 25% | Median | 75% | Max | |
|---|---|---|---|---|---|---|
| SPI-1 | Moderatelywet | 1.4 | 1.5 | 2.1 | 2.2 | 2.8 |
| Moderately dry | 1.4 | 1.7 | 2.1 | 2.2 | 3.1 | |
| SPI-3 | Moderatelywet | 0.8 | 1.2 | 1.4 | 1.9 | 2.2 |
| Moderately dry | 1.1 | 2.6 | 3.1 | 3.4 | 3.9 | |
| SPI-6 | Moderately wet | 0.6 | 1.1 | 1.3 | 1.9 | 2.5 |
| Moderately dry | 1.4 | 3.7 | 3.8 | 4.2 | 5.1 | |
| SPI-9 | Moderately wet | 0.3 | 0.3 | 1.3 | 2.4 | 3.4 |
| Moderately dry | 1.7 | 3.3 | 4.0 | 4.5 | 6.0 | |
| SPI-12 | Moderately wet | 0.0 | 0.3 | 0.7 | 1.8 | 3.7 |
| Moderately dry | 0.9 | 3.2 | 3.7 | 4.4 | 6.3 | |
| SPI-24 | Moderately wet | 0.3 | 1.8 | 2.4 | 3.5 | 5.9 |
| Moderately dry | 0.0 | 0.4 | 4.2 | 5.5 | 6.5 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tien Thanh, N. A Proposal to Evaluate Drought Characteristics Using Multiple Climate Models for Multiple Timescales. Climate 2018, 6, 79. https://doi.org/10.3390/cli6040079
Tien Thanh N. A Proposal to Evaluate Drought Characteristics Using Multiple Climate Models for Multiple Timescales. Climate. 2018; 6(4):79. https://doi.org/10.3390/cli6040079
Chicago/Turabian StyleTien Thanh, Nguyen. 2018. "A Proposal to Evaluate Drought Characteristics Using Multiple Climate Models for Multiple Timescales" Climate 6, no. 4: 79. https://doi.org/10.3390/cli6040079
APA StyleTien Thanh, N. (2018). A Proposal to Evaluate Drought Characteristics Using Multiple Climate Models for Multiple Timescales. Climate, 6(4), 79. https://doi.org/10.3390/cli6040079





