Decreasing Past and Mid-Century Rainfall Indices over the Ouémé River Basin, Benin (West Africa)
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.3. Extreme Precipitation Indices
2.4. Temporal Trend Analysis
3. Results
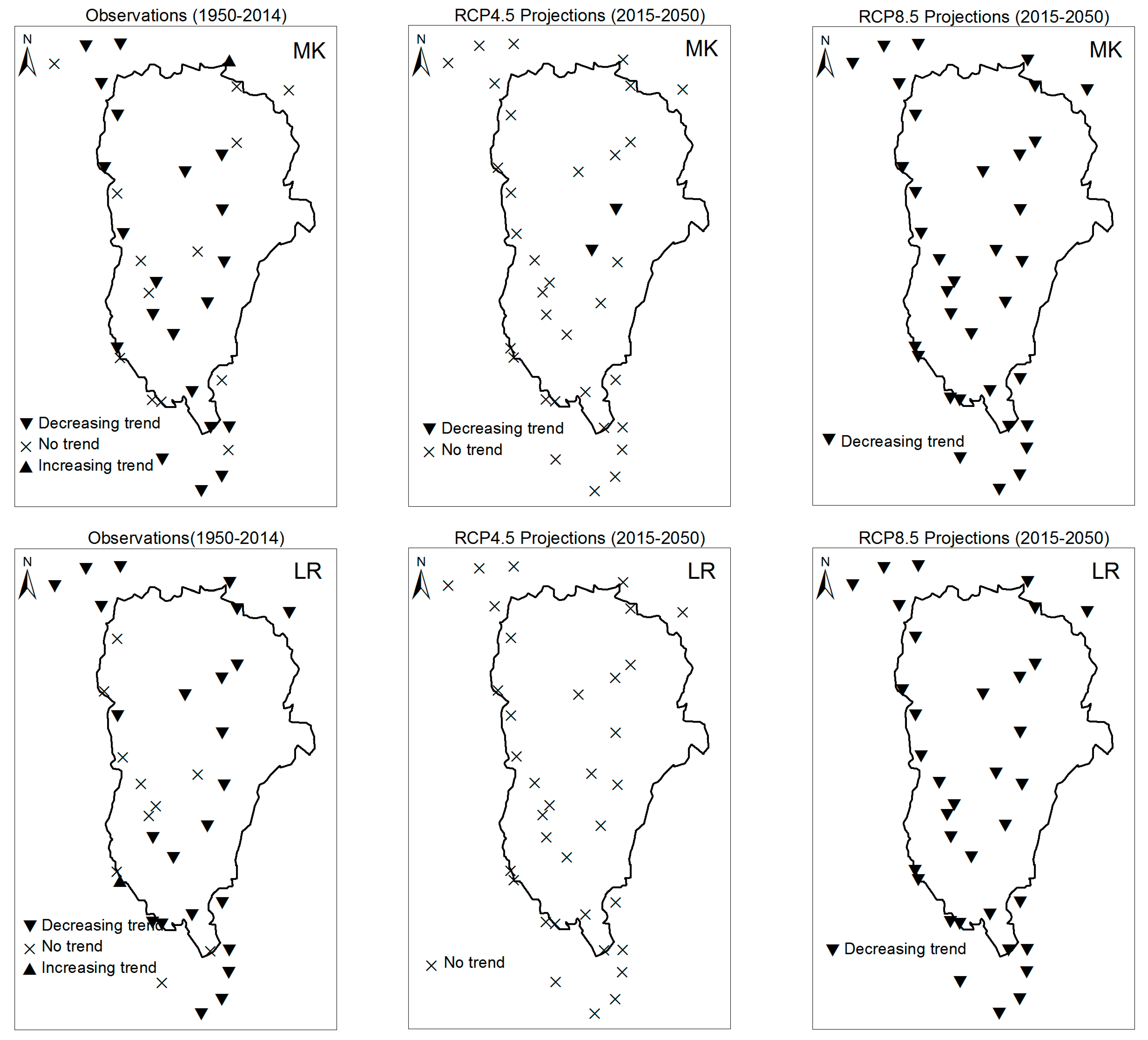
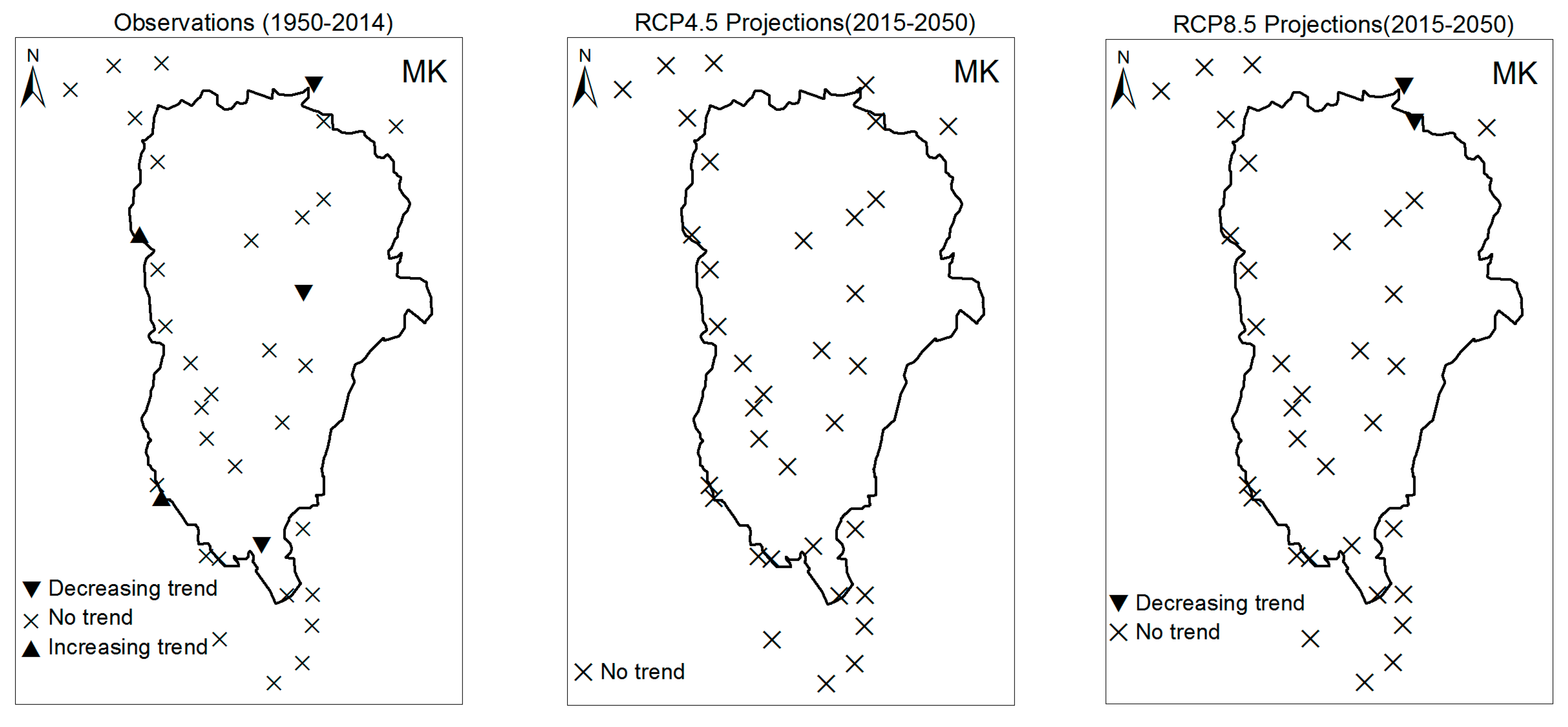
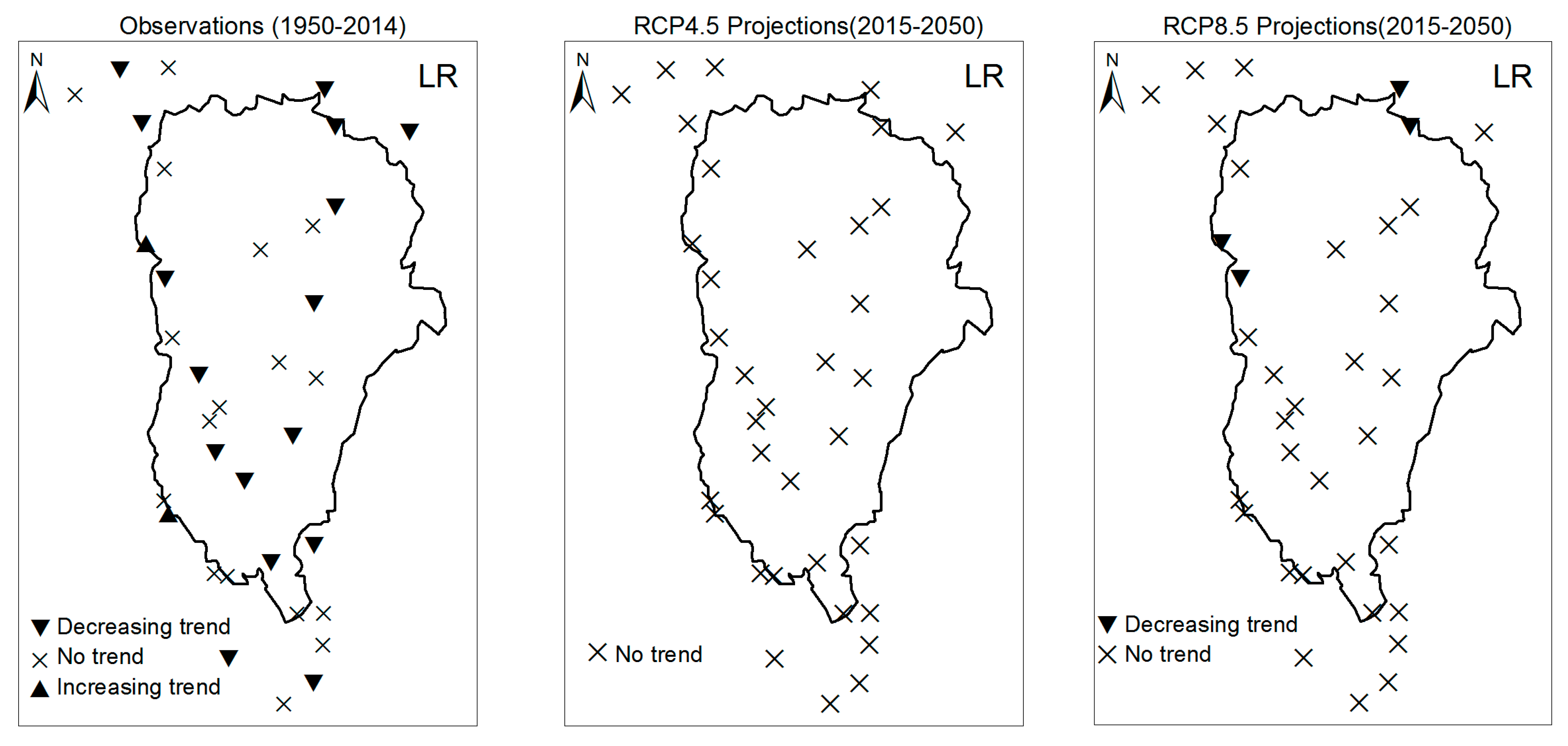
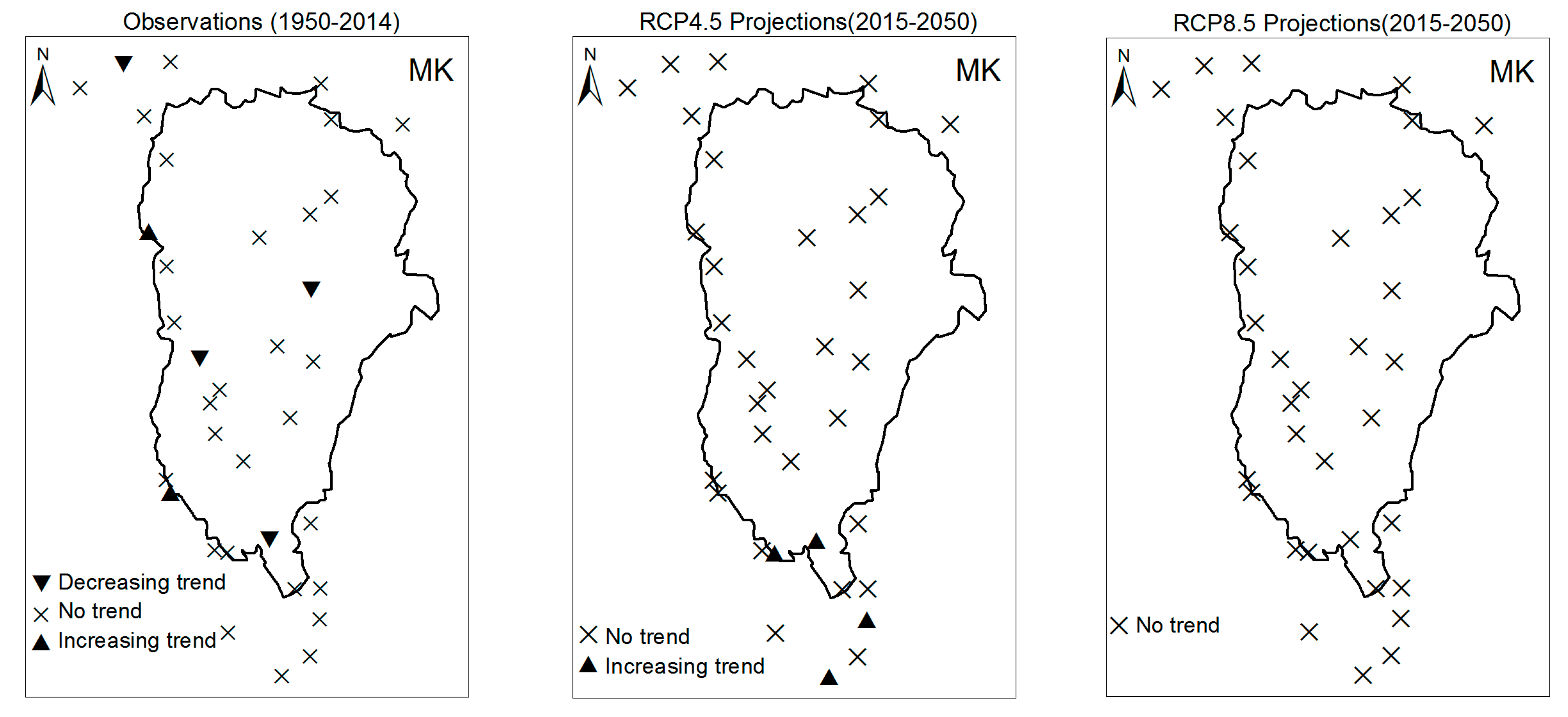
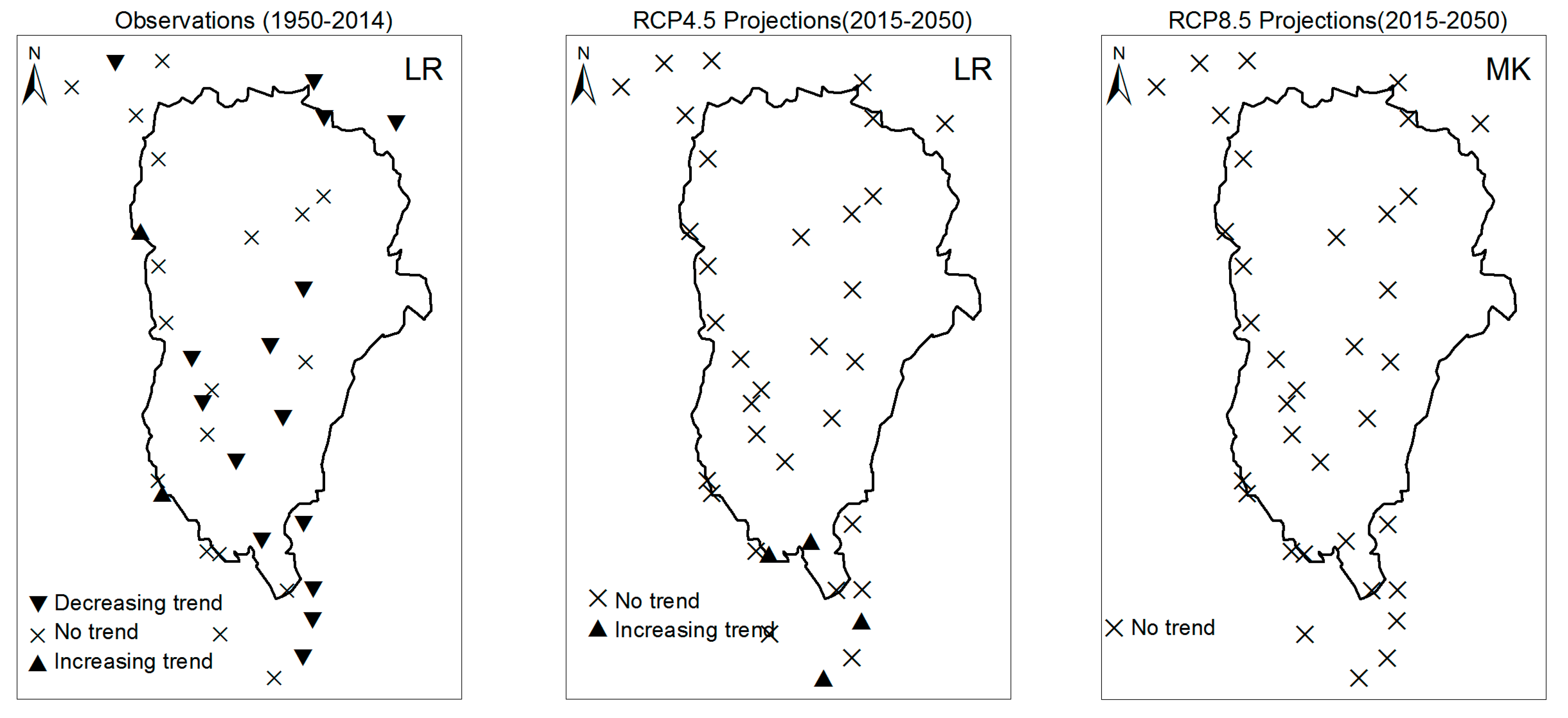
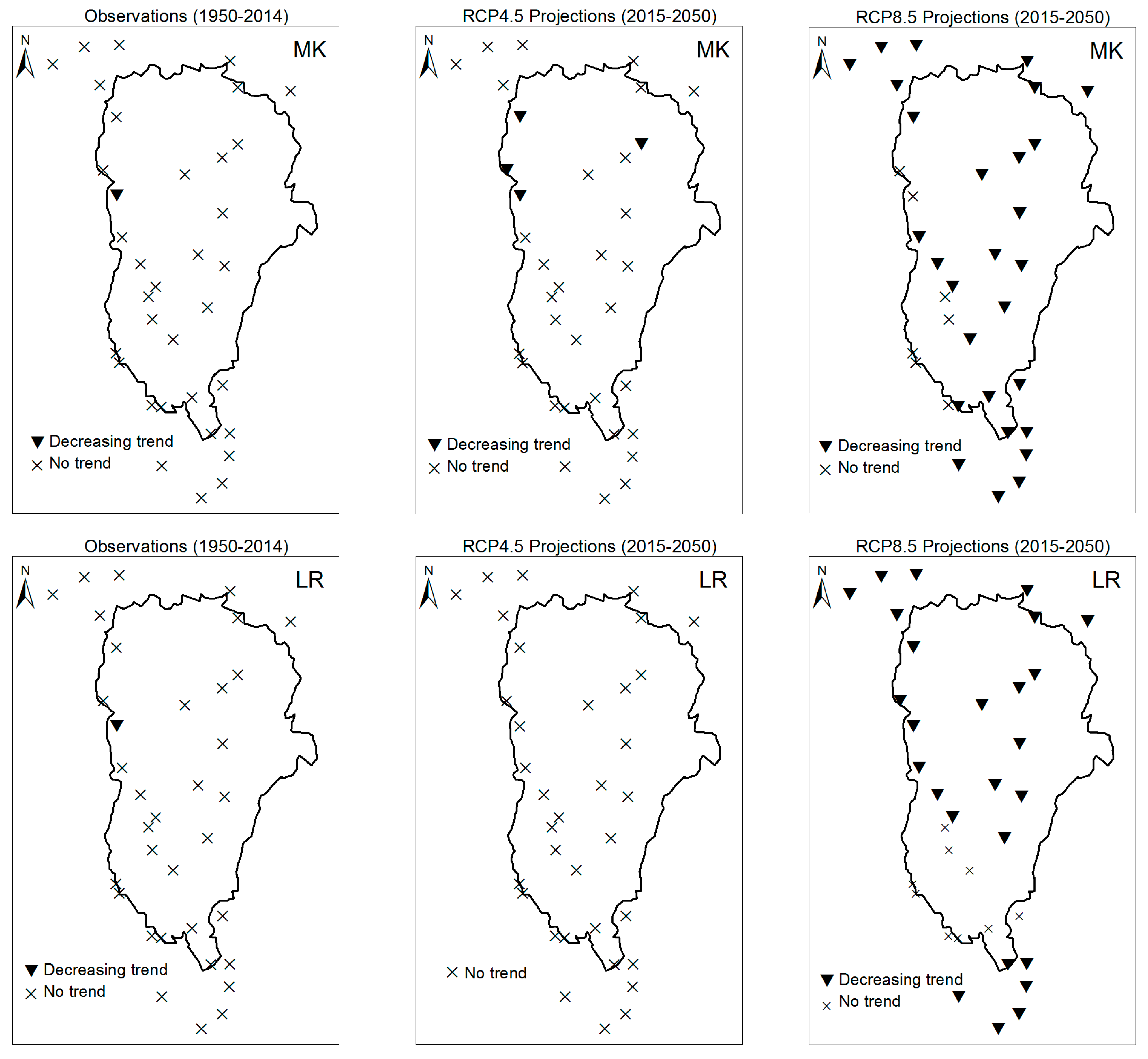
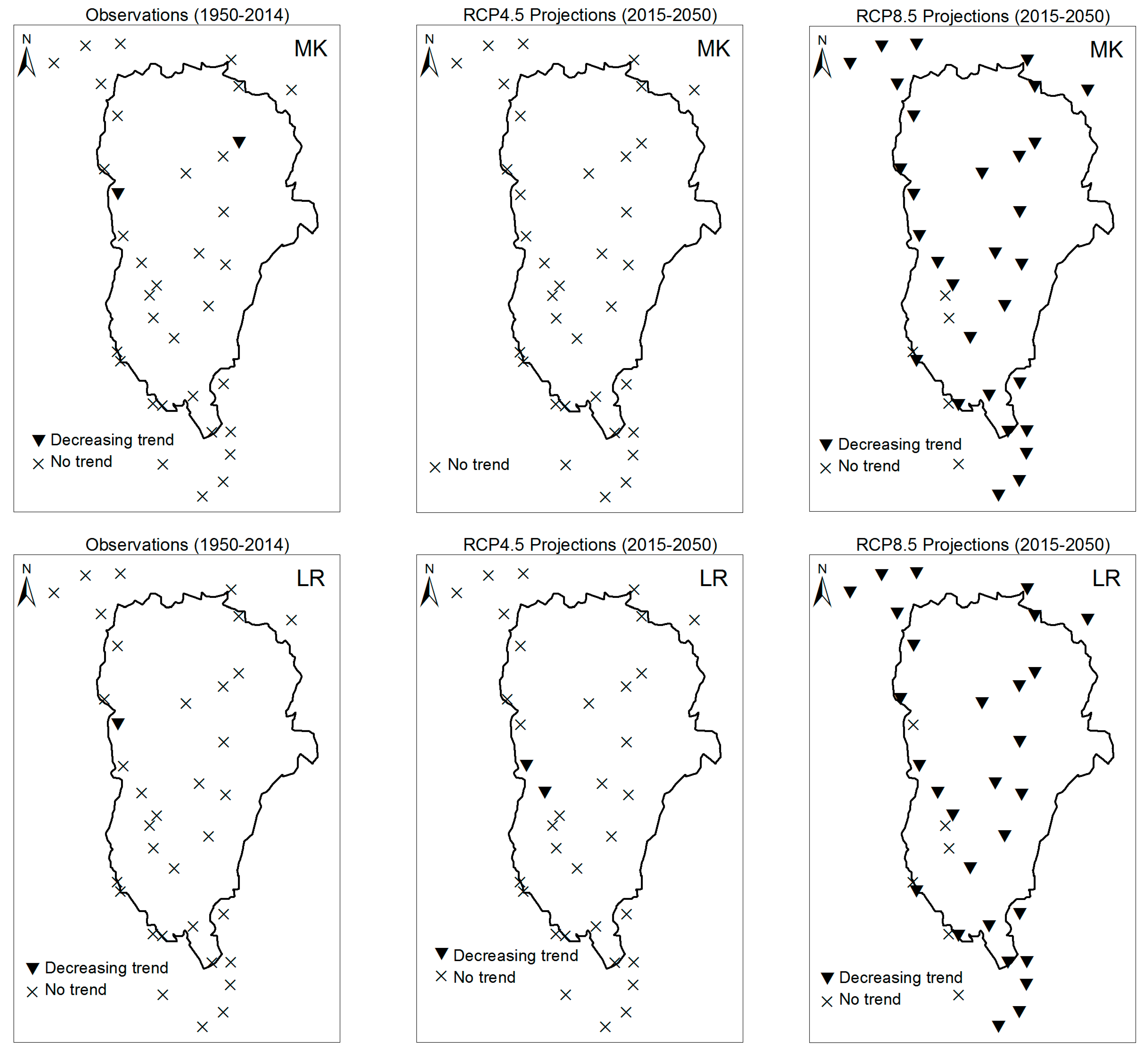
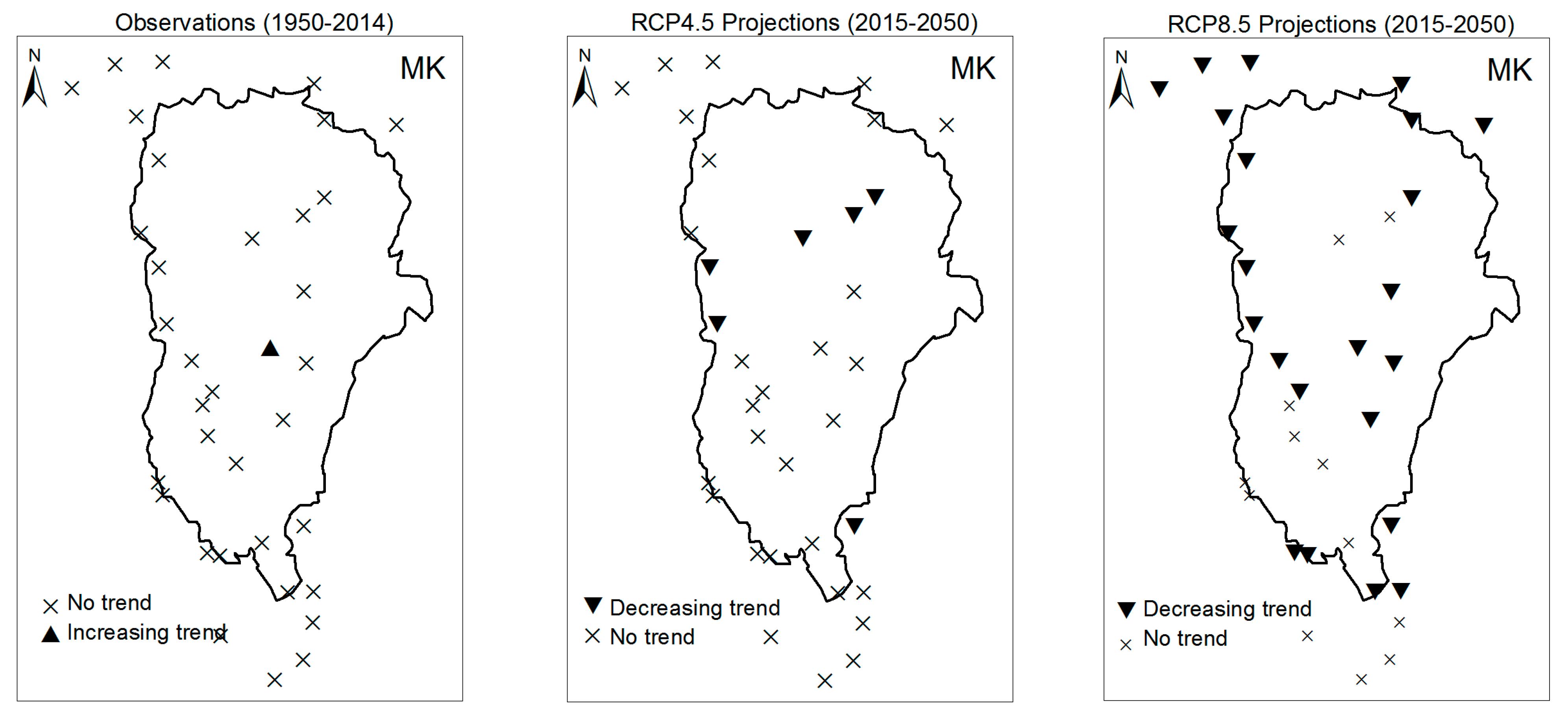
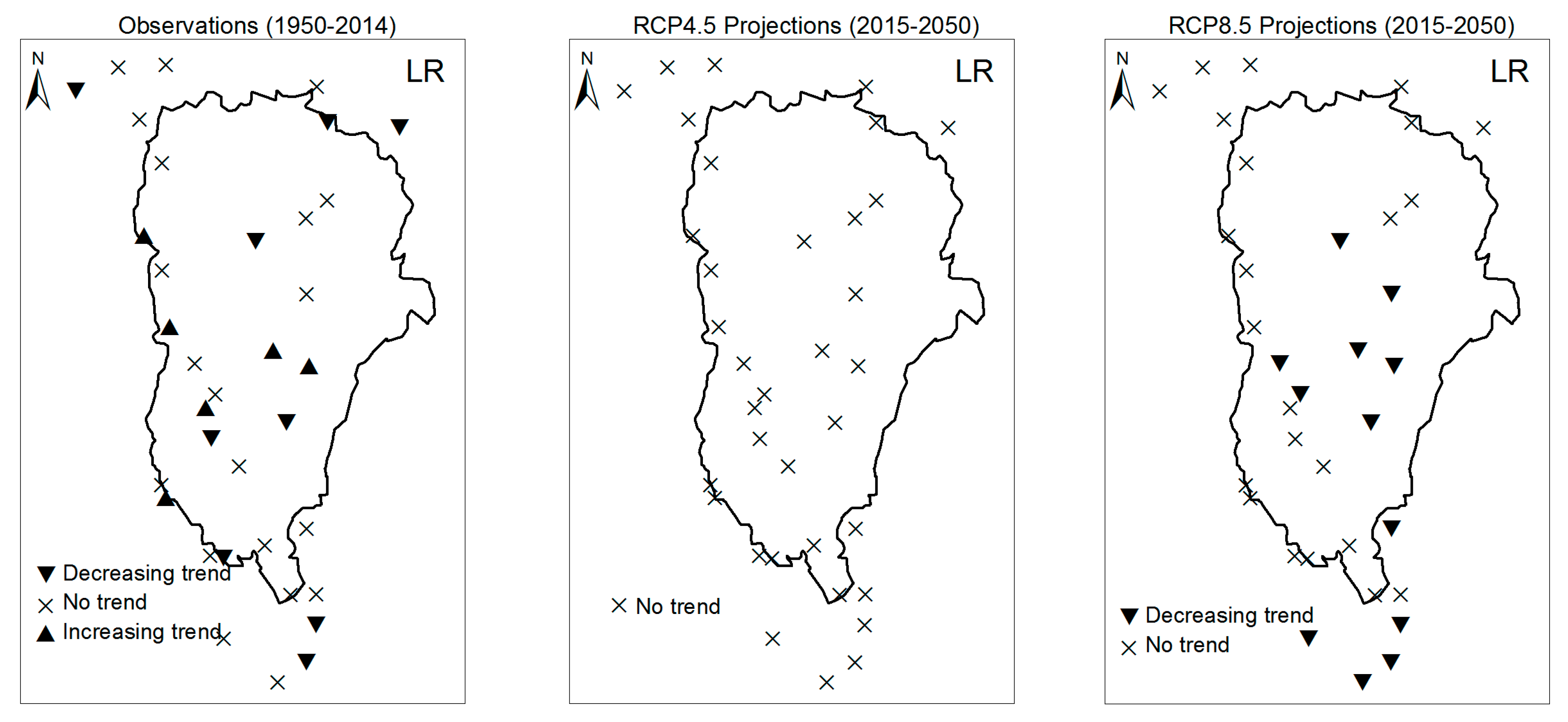
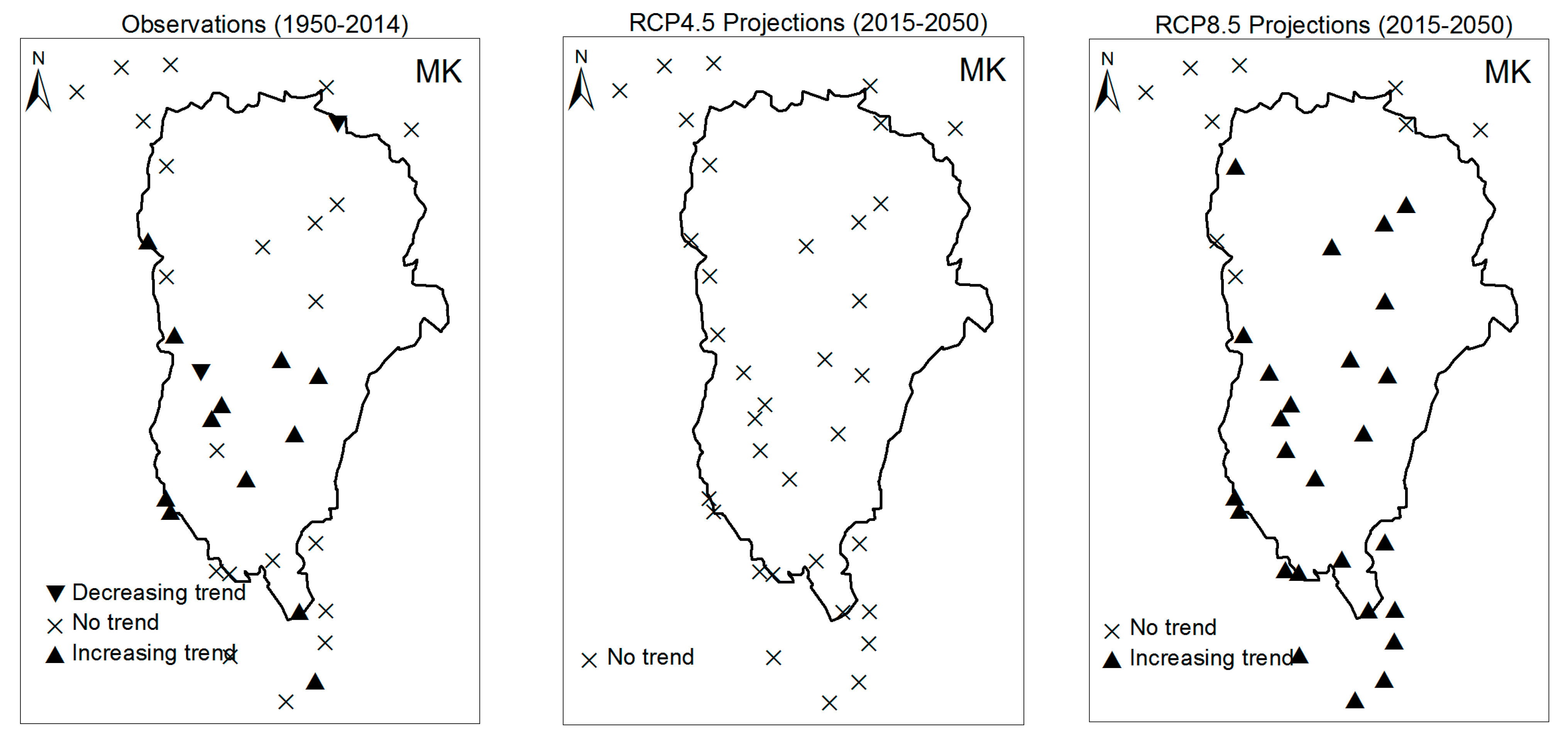
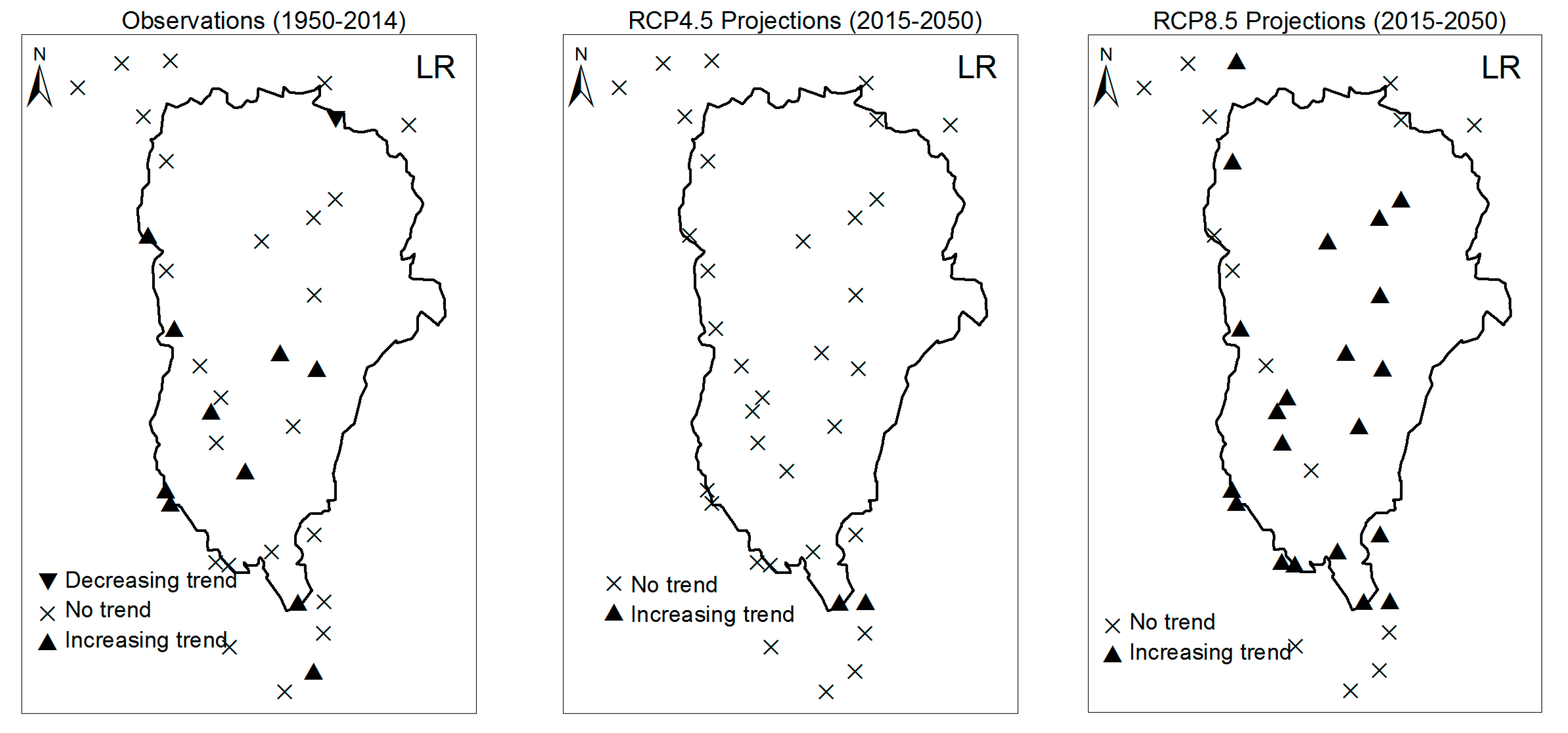
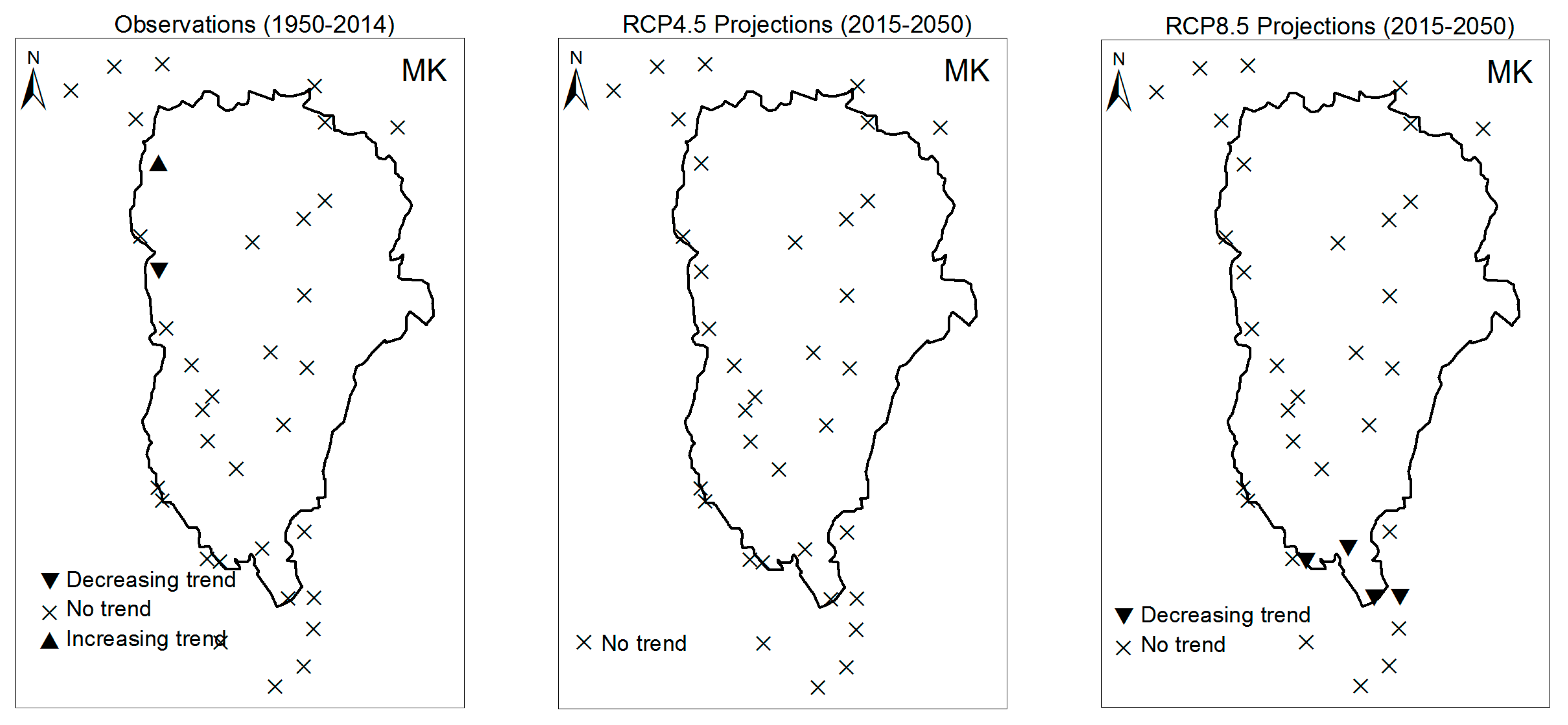
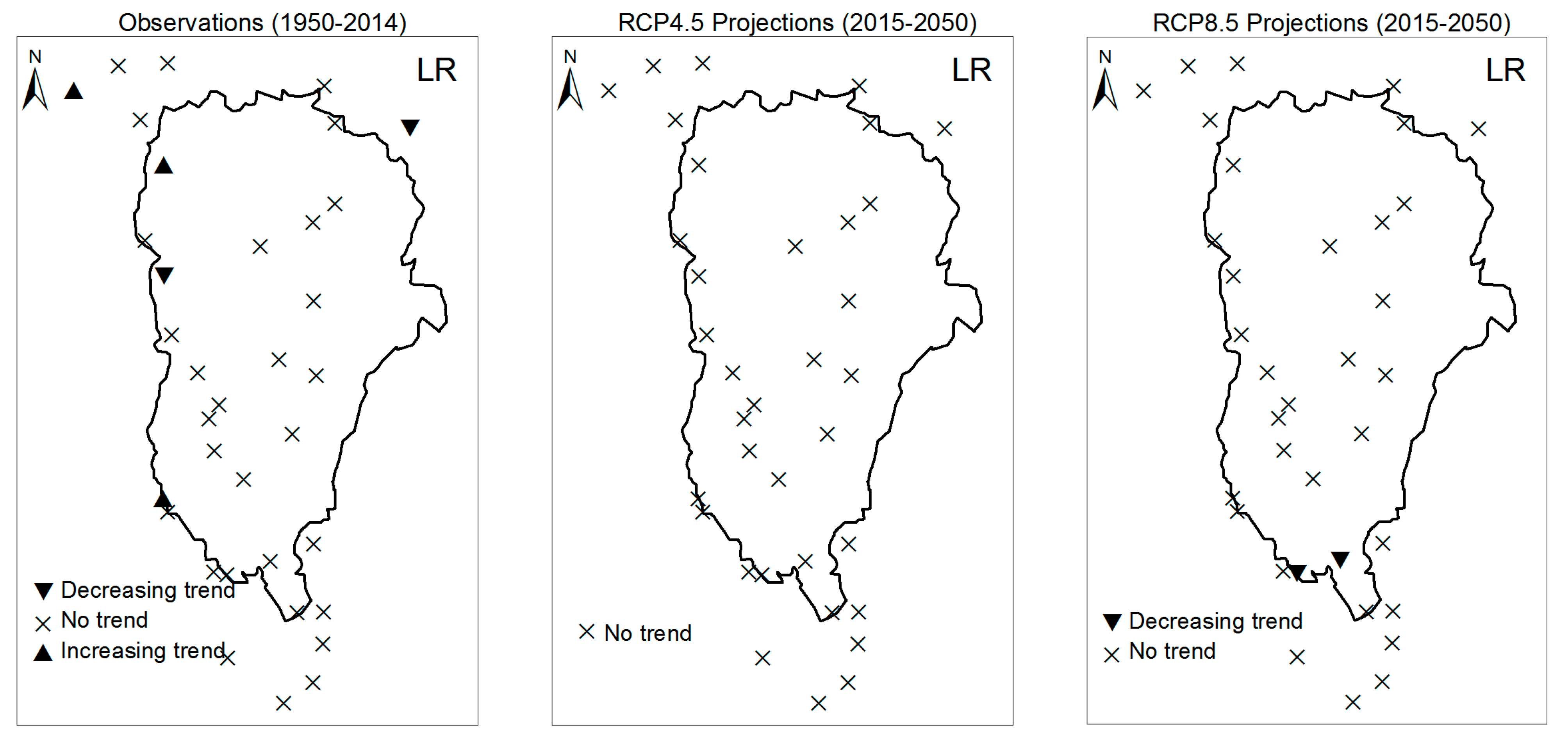
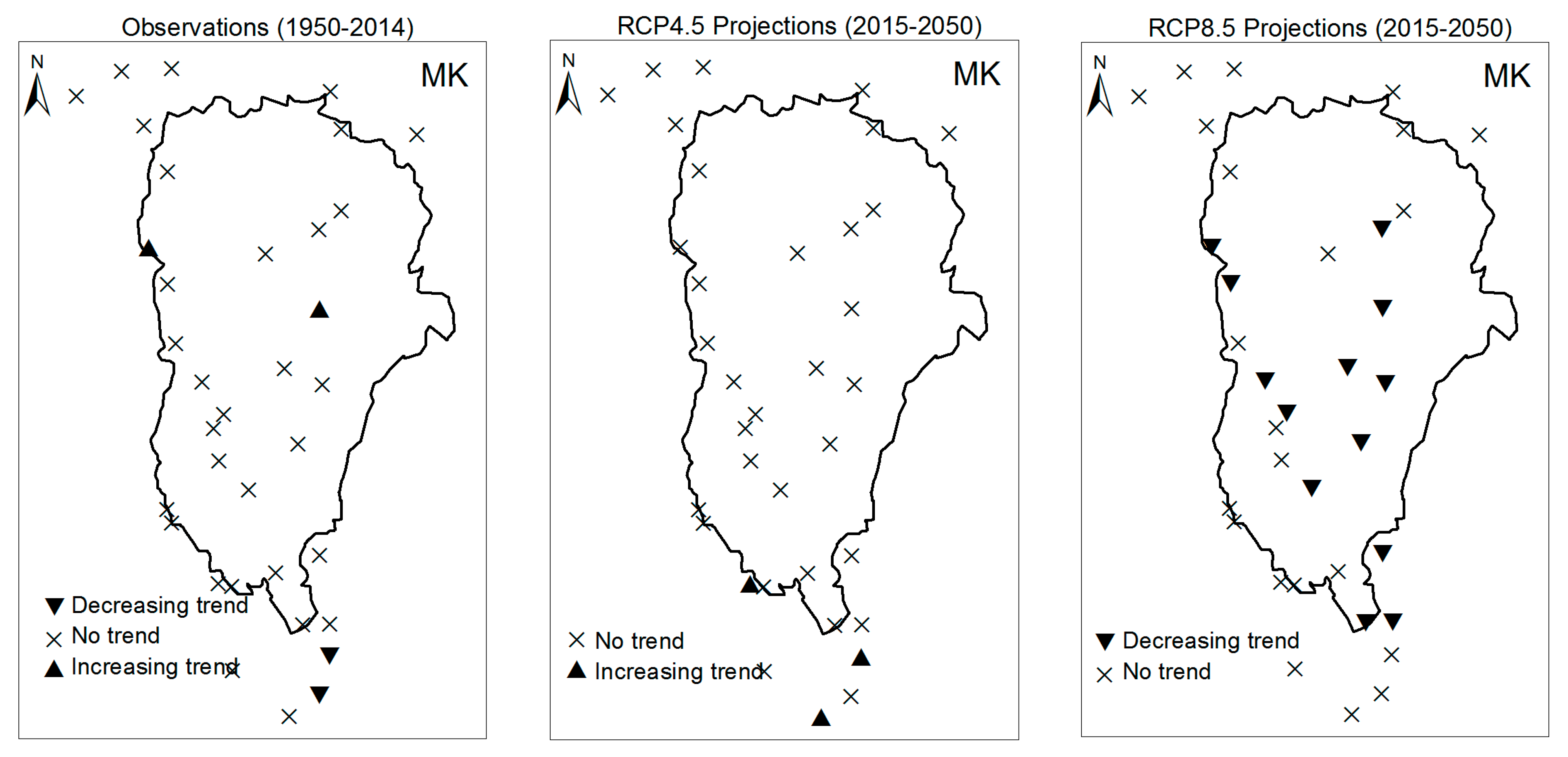
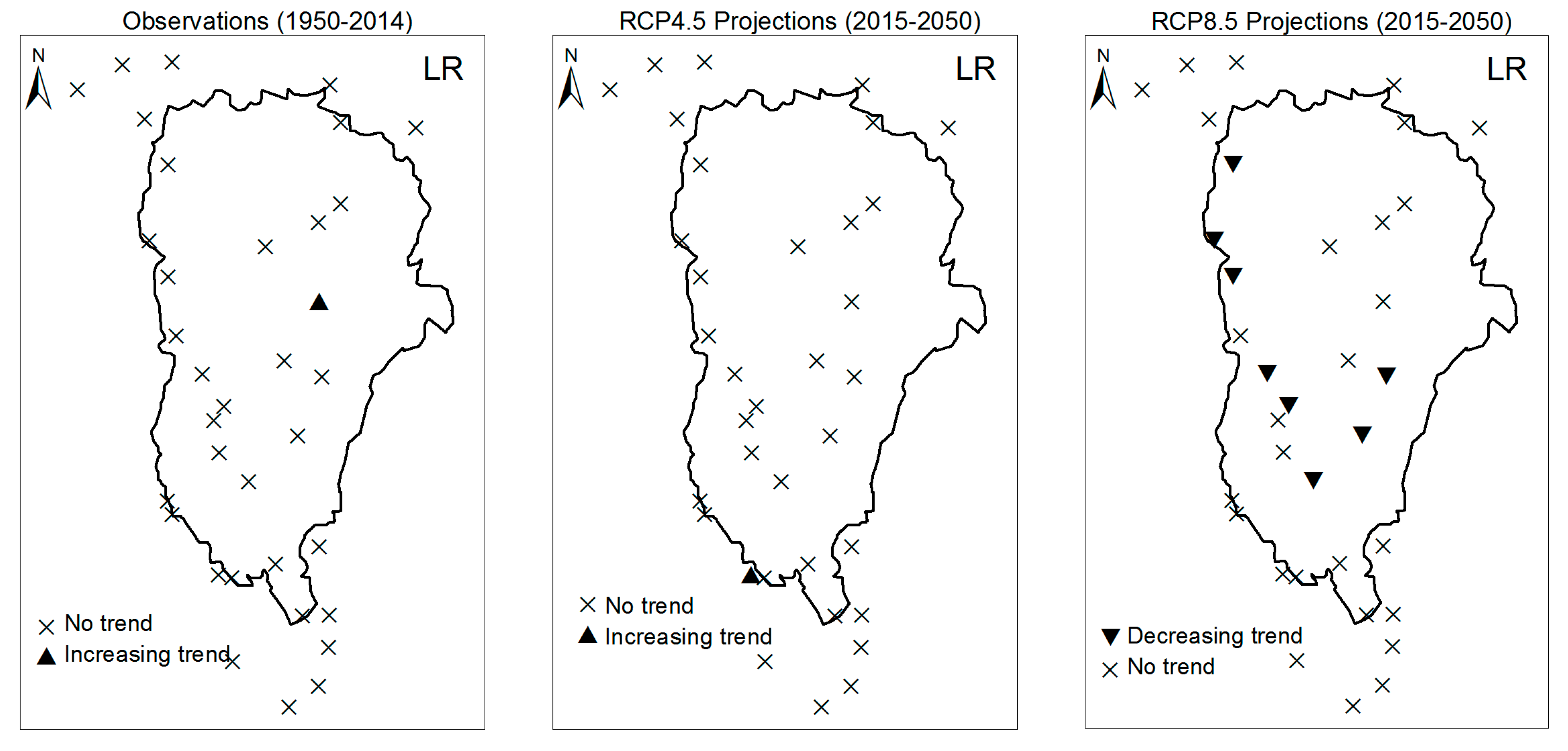
3.1. Annual Past and Future Climate Indices Trends
3.1.1. Annual Total Precipitation and Number of Wet Days
3.1.2. Consecutive Cumulative Wet Days and Heavy Precipitation
3.2. Rainy Season Past and Future Climate Index Trends
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Stations | R1mm | R10mm | R20mm | CDD | CWD | PRCPTOT | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | β | Z | β | Z | β | Z | β | Z | β | Z | β | |
| Abomey | −1.88 | −0.26 | −0.83 | −0.04 | −0.46 | 0.00 | 2.05 | 2.49 | −1.13 | 0.00 | −1.97 | −1.37 |
| Adjohoun | −1.98 | 0.00 | −1.96 | 0.00 | 0.54 | 0.00 | 1.33 | 0.22 | 0.77 | 0.00 | −1.96 | −1.16 |
| Agouna | −1.97 | −0.17 | 1.87 | 0.55 | 3.35 | 0.36 | 0.13 | 0.04 | −1.20 | −0.05 | 1.67 | 9.22 |
| Aklampa | −0.77 | −0.60 | −2.16 | −0.25 | 0.28 | 0.00 | 0.11 | 1.40 | −0.29 | 0.00 | −2.12 | −7.13 |
| Bantè | 0.74 | 0.06 | 0.86 | 0.05 | 1.47 | 0.06 | 1.95 | 0.61 | 1.11 | 0.00 | 0.30 | 0.53 |
| Bassila | −4.44 | −1.00 | −1.32 | −0.16 | 0.38 | 0.05 | 1.79 | 1.00 | −1.85 | −0.06 | −1.53 | −6.14 |
| Bembèrèkè | −1.65 | −0.24 | 1.98 | −0.14 | −2.73 | −0.10 | 1.73 | 0.41 | −2.33 | −0.02 | 1.96 | −4.45 |
| Beterou | −2.36 | 0.00 | −1.97 | −0.08 | −0.08 | 0.00 | 2.00 | 1.53 | −1.97 | 0.00 | −2.10 | −0.36 |
| Birni | −3.34 | −0.55 | −0.49 | −0.04 | 0.08 | 0.00 | 1.23 | 1.00 | −1.23 | −0.04 | −0.98 | −3.32 |
| Bohicon | −2.27 | −0.18 | −2.24 | 0.00 | 2.42 | 0.00 | 1.87 | 0.35 | −2.69 | −0.02 | −1.96 | −0.56 |
| Bonou | −1.08 | −0.71 | 1.78 | 0.31 | 1.90 | 0.28 | 2.18 | 0.33 | −1.38 | 0.00 | 1.27 | 7.13 |
| Boukombé | −4.61 | −0.86 | −1.98 | −0.09 | −0.21 | 0.00 | 1.88 | 0.79 | −2.43 | −0.04 | −2.10 | −3.11 |
| Cotonou | −2.13 | 0.00 | −2.10 | 0.00 | −0.20 | 0.00 | 0.95 | 0.16 | −2.80 | −0.02 | −1.99 | −0.05 |
| Dassa | −2.00 | −0.27 | −1.97 | −0.09 | 0.95 | 0.05 | 0.87 | 0.25 | −2.21 | 0.00 | −2.30 | −1.97 |
| Djougou | −1.98 | 0.00 | −2.31 | 0.00 | 0.52 | 0.00 | 1.29 | 0.53 | −1.98 | 0.00 | −1.96 | −0.95 |
| Gouka | 1.34 | 0.42 | 1.08 | 0.17 | 2.07 | 0.30 | −1.39 | −0.97 | 1.08 | 0.00 | −1.41 | −9.81 |
| Ina | −1.75 | −0.46 | −1.78 | −0.22 | −1.78 | −0.11 | 2.69 | 1.13 | −1.80 | −0.03 | −1.95 | −6.95 |
| Ketou | −2.30 | 0.00 | −2.69 | −0.10 | 0.40 | 0.00 | 1.78 | 0.88 | −2.15 | 0.00 | −1.98 | −1.81 |
| Kokoro | −1.98 | −0.04 | −1.97 | −0.04 | −2.01 | 0.00 | 1.67 | 0.81 | −1.97 | 0.00 | −2.17 | −3.35 |
| Kouandé | −2.10 | −0.09 | −1.05 | −0.13 | −1.87 | −0.11 | 1.97 | 0.58 | −1.96 | 0.00 | −1.98 | −2.89 |
| Natitingou | −3.21 | −0.10 | −1.99 | −0.07 | −0.32 | 0.00 | −0.56 | −0.10 | −2.49 | −0.03 | −2.10 | −2.16 |
| Nikki | −2.30 | −0.11 | −1.77 | −0.18 | −2.30 | −0.13 | 1.44 | 0.53 | −1.35 | 0.00 | −1.89 | −4.81 |
| Okpara | −4.10 | −0.16 | −1.46 | −0.10 | −0.50 | 0.00 | 0.59 | 0.18 | −0.43 | 0.00 | −0.72 | −1.47 |
| Ouèssè | −0.89 | −0.08 | 0.51 | 0.03 | 0.75 | 0.03 | 1.32 | 0.57 | 0.61 | 0.00 | −0.29 | −0.87 |
| Parakou | −1.99 | −0.06 | −2.49 | −0.08 | −0.02 | 0.00 | 1.64 | 0.33 | −2.27 | 0.00 | −2.30 | −0.39 |
| Pénéssoulou | −3.22 | −1.00 | −1.98 | −0.29 | −0.11 | 0.00 | 0.76 | 1.33 | −2.70 | 0.00 | −1.97 | −3.72 |
| Pira | −2.04 | 0.00 | −2.10 | 0.00 | 1.17 | 0.10 | −0.25 | −0.13 | −3.22 | 0.00 | 0.33 | 1.50 |
| Pobè | −2.17 | −0.07 | −1.96 | −0.03 | −1.31 | −0.06 | 0.78 | 0.10 | −2.10 | 0.00 | −2.08 | −1.59 |
| Porto-Novo | −5.93 | −0.82 | −3.39 | −0.23 | −2.00 | −0.08 | 1.96 | 0.32 | −1.95 | −0.06 | −1.93 | −6.67 |
| Sakété | −2.39 | −0.18 | −1.90 | −0.13 | −0.66 | −0.03 | 0.78 | 0.14 | −2.11 | 0.00 | −0.93 | −1.86 |
| Savalou | −1.98 | −0.03 | −2.28 | −0.07 | −1.11 | −0.04 | 0.83 | 0.20 | −1.96 | 0.00 | −1.96 | −1.85 |
| Savè | −2.52 | −0.20 | −2.13 | −0.02 | 0.59 | 0.00 | 1.16 | 0.21 | −1.30 | 0.00 | −2.14 | −1.09 |
| Tchaourou | −1.28 | −0.46 | −1.96 | −0.10 | −0.07 | 0.00 | −1.96 | 0.00 | −2.03 | 0.00 | −3.20 | −2.30 |
| Tchètti | −4.30 | −1.92 | −2.30 | −0.08 | 0.35 | 0.08 | 1.10 | 1.50 | −3.45 | −0.17 | −0.63 | −4.07 |
| Zagnanando | 1.31 | 0.17 | −3.10 | −0.08 | −2.70 | −0.05 | 1.70 | 0.50 | −3.14 | −0.30 | −1.15 | −2.83 |
| Stations | SDII | RX1day | RX5day | R95pSUM | R99pSUM | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Z | β | Z | β | Z | β | Z | β | Z | β | |
| Abomey | 1.35 | 0.02 | 0.99 | 0.15 | −0.60 | −0.16 | 0.03 | 0.05 | 0.98 | 0.00 |
| Adjohoun | 0.27 | 0.01 | 0.63 | 0.09 | 0.42 | 0.08 | −0.11 | −0.10 | 0.85 | 0.00 |
| Agouna | 4.21 | 0.29 | 2.71 | 1.74 | 2.36 | 2.25 | 2.09 | 3.04 | 2.69 | 4.34 |
| Aklampa | −0.27 | −0.10 | −0.99 | −2.12 | −0.77 | −2.96 | −1.04 | −6.33 | −0.74 | 0.00 |
| Bantè | −1.15 | −0.02 | −2.13 | −0.39 | −0.57 | −0.14 | −1.51 | −1.89 | −2.91 | −1.48 |
| Bassila | 3.13 | 0.15 | −0.23 | −0.08 | −2.01 | −0.84 | −0.29 | −1.01 | 0.03 | 0.00 |
| Bembèrèkè | −0.70 | −0.01 | −1.96 | −0.30 | −2.35 | −0.59 | −2.47 | −2.08 | −1.29 | 0.00 |
| Beterou | 1.97 | 0.02 | 0.94 | 0.28 | 0.05 | 0.03 | 0.19 | 0.33 | 0.90 | 0.00 |
| Birni | 2.32 | 0.09 | −0.50 | −0.14 | −0.66 | −0.33 | −0.41 | −0.44 | 0.23 | 0.00 |
| Bohicon | 2.77 | 0.03 | 0.96 | 0.14 | 1.04 | 0.20 | 1.43 | 1.38 | 0.79 | 0.00 |
| Bonou | 4.76 | 0.26 | −0.12 | −0.03 | −0.19 | −0.07 | 0.82 | 1.74 | −0.21 | 0.00 |
| Boukombé | 1.87 | 0.11 | 1.01 | 0.28 | −0.59 | −0.28 | −0.03 | 0.00 | 1.43 | 0.00 |
| Cotonou | 0.06 | 0.00 | −0.95 | −0.24 | −1.28 | −0.66 | 0.38 | 0.45 | −0.28 | 0.00 |
| Dassa | 1.35 | 0.04 | −0.32 | −0.08 | −0.65 | −0.19 | 0.08 | 0.17 | −0.34 | 0.00 |
| Djougou | 0.33 | 0.01 | 0.72 | 0.14 | 0.92 | 0.22 | 0.61 | 0.81 | 0.52 | 0.00 |
| Gouka | 0.82 | 0.06 | 0.67 | 0.57 | 1.61 | 1.90 | 1.22 | 6.84 | 0.64 | 0.00 |
| Ina | −0.33 | −0.01 | −1.05 | −0.27 | −2.00 | −0.54 | −1.05 | −1.85 | −0.51 | 0.00 |
| Ketou | −0.66 | −0.01 | −1.04 | −0.17 | −0.45 | −0.11 | −0.55 | −0.61 | −1.27 | 0.00 |
| Kokoro | −0.03 | 0.00 | 0.95 | 0.51 | 1.67 | 0.94 | 1.02 | 3.34 | 0.45 | 0.00 |
| Kouandé | −0.98 | −0.02 | 0.03 | 0.00 | 0.21 | 0.07 | 0.55 | 0.68 | 0.43 | 0.00 |
| Natitingou | −0.71 | −0.01 | −1.10 | −0.12 | −1.43 | −0.15 | −1.58 | −1.55 | −1.98 | 0.00 |
| Nikki | −1.03 | −0.04 | −0.67 | −0.16 | −0.30 | −0.13 | −1.54 | −2.26 | −0.64 | 0.00 |
| Okpara | 0.72 | 0.02 | 0.90 | 0.23 | −0.68 | −0.14 | 0.08 | 0.08 | 0.83 | 0.00 |
| Ouèssè | 1.20 | 0.03 | −0.04 | −0.01 | −0.06 | −0.04 | −0.23 | −0.23 | −0.39 | 0.00 |
| Parakou | −0.81 | −0.01 | 1.92 | 0.29 | −0.01 | 0.00 | 1.00 | 0.85 | 1.62 | 0.00 |
| Pénéssoulou | 2.54 | 0.35 | 2.88 | 3.04 | 1.52 | 2.71 | 2.24 | 4.83 | 3.01 | 10.28 |
| Pira | 0.70 | 0.03 | 0.40 | 0.14 | 0.95 | 0.69 | −0.09 | −0.16 | 0.97 | 0.00 |
| Pobè | −0.12 | 0.00 | −0.75 | −0.14 | −1.25 | −0.30 | −0.47 | −0.47 | −0.84 | 0.00 |
| Porto-Novo | 3.76 | 0.10 | −1.41 | −0.34 | −1.67 | −0.70 | −0.64 | −1.29 | −1.37 | 0.00 |
| Sakété | 0.44 | 0.01 | −0.40 | −0.08 | −1.11 | −0.30 | 0.12 | 0.25 | −0.65 | 0.00 |
| Savalou | −1.14 | −0.02 | 0.68 | 0.24 | 0.93 | 0.23 | −0.36 | −0.76 | 0.64 | 0.00 |
| Savè | 1.61 | 0.02 | −0.10 | −0.02 | −1.36 | −0.27 | −0.85 | −0.71 | 0.03 | 0.00 |
| Tchaourou | 1.71 | 0.04 | −0.08 | −0.03 | −1.98 | −0.48 | −2.02 | −1.64 | −1.98 | 0.00 |
| Tchètti | 3.08 | 0.39 | 0.07 | 0.06 | 0.35 | 0.29 | −0.49 | −1.78 | 0.13 | 0.00 |
| Zagnanando | −2.19 | −0.08 | −2.13 | −0.22 | −1.97 | −0.30 | −2.10 | −1.06 | −2.03 | 0.00 |
| Stations | R1 | R10 | R20 | CWD | PRCPTOT | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Z | β | Z | β | Z | β | Z | β | Z | β | |
| Abomey | −1.97 | −2.00 | −4.05 | −0.06 | −2.62 | −2.95 | −0.30 | −0.40 | 2.30 | −9.06 |
| Adjohoun | −2.36 | −12.96 | −3.09 | −0.45 | −2.84 | −3.17 | −2.33 | −3.37 | 1.98 | −9.11 |
| Agouna | −2.30 | −2.92 | −3.00 | −1.25 | −1.95 | −1.70 | −1.98 | −0.90 | 1.98 | −8.25 |
| Aklampa | −1.96 | −10.78 | −1.96 | −5.69 | −2.15 | −2.48 | 1.10 | 0.23 | 4.65 | −15.38 |
| Bantè | −3.00 | −10.76 | −5.25 | −6.41 | −2.15 | −2.48 | 0.30 | 0.00 | 2.87 | −14.83 |
| Bassila | −1.96 | −1.82 | −5.21 | −8.46 | −1.96 | −2.29 | 0.80 | 0.08 | 1.96 | −20.92 |
| Bembèrèkè | −1.17 | −8.89 | −2.00 | −3.29 | −3.01 | −3.34 | −1.25 | −0.50 | 1.97 | −5.58 |
| Bétérou | −4.32 | −9.91 | −4.18 | −8.25 | −1.97 | −2.30 | −1.80 | 0.17 | 2.19 | −20.50 |
| Birni | −2.50 | −9.93 | −2.22 | −5.47 | −2.31 | −2.64 | 0.08 | 0.00 | 2.27 | −14.94 |
| Bohicon | −2.30 | −11.00 | −2.09 | −1.02 | −1.80 | −3.10 | −1.96 | −1.03 | 2.20 | −13.02 |
| Bonou | −1.99 | −7.00 | −6.23 | −0.74 | −3.00 | −3.33 | −2.07 | −2.80 | 2.70 | −9.74 |
| Boukombé | −2.80 | −5.98 | −2.17 | −4.66 | −2.62 | −2.95 | −1.90 | −0.34 | 2.10 | −13.32 |
| Cotonou | −4.20 | −3.87 | −4.09 | −2.49 | −1.05 | −2.50 | −3.02 | −5.12 | 3.45 | −2.99 |
| Dassa-Zoumè | −1.98 | −9.79 | −2.07 | −3.89 | −3.08 | −3.41 | −1.97 | −0.90 | 1.99 | −8.79 |
| Djougou | −2.00 | −15.94 | −3.12 | −9.38 | −1.98 | −2.31 | −1.23 | −0.10 | 2.52 | −18.77 |
| Gouka | −3.22 | −7.86 | −2.10 | −5.72 | −1.70 | −1.02 | −0.90 | 0.00 | 2.57 | −14.43 |
| Ina | −1.98 | −2.88 | −4.00 | −3.39 | −1.96 | −2.29 | 1.23 | 0.00 | 2.13 | −5.78 |
| Kétou | −2.01 | −10.00 | −2.06 | −0.81 | −2.80 | −3.13 | 1.20 | 0.10 | 3.10 | −7.39 |
| Kokoro | −3.20 | −13.89 | −6.14 | −3.22 | −2.20 | −2.53 | −0.50 | 0.30 | 3.01 | −9.44 |
| Kouandé | −5.60 | −15.97 | −2.25 | −6.46 | −2.45 | −2.78 | −2.17 | −3.20 | 1.96 | −12.92 |
| Natitingou | −3.10 | −2.92 | −5.21 | −5.35 | −2.54 | −2.87 | −1.40 | −0.17 | 2.27 | −14.69 |
| Nikki | −2.10 | −15.85 | −3.14 | −4.16 | −3.12 | −3.45 | 0.30 | −3.00 | 3.43 | −11.31 |
| Okpara | −4.05 | −2.83 | −2.15 | −6.23 | −1.96 | −2.29 | 1.80 | 0.13 | 4.25 | −14.46 |
| Ouèssè | −1.97 | −8.00 | −3.33 | −5.83 | −2.30 | −2.63 | −0.60 | −0.01 | 1.96 | −14.67 |
| Parakou | −3.00 | −3.93 | −3.23 | −6.26 | −2.28 | −2.61 | −0.98 | −0.20 | 2.83 | −11.52 |
| Pénéssoulou | −1.96 | −11.79 | −2.20 | −9.58 | −2.06 | −2.39 | −0.04 | −0.09 | 1.96 | −23.16 |
| Pira | −4.03 | −7.75 | −3.27 | −6.00 | −2.51 | −2.84 | −0.21 | −2.00 | 3.14 | −12.00 |
| Pobè | −2.37 | −7.00 | −1.89 | −0.74 | −2.07 | −2.40 | −3.60 | −1.24 | 3.15 | −7.74 |
| Porto-Novo | −2.33 | −12.95 | −2.30 | −0.52 | −2.80 | −3.13 | −1.97 | −0.02 | 4.36 | −4.95 |
| Sakété | −2.01 | −10.91 | −2.10 | −2.31 | −1.88 | −0.50 | −2.30 | 0.00 | 3.45 | −6.61 |
| Savalou | −4.77 | −13.84 | −3.10 | −5.83 | −1.40 | −1.20 | −1.97 | −2.30 | 1.97 | −13.67 |
| Savè | −5.22 | −13.87 | −1.97 | −5.95 | −1.12 | −0.80 | −2.47 | −4.60 | 2.22 | −13.89 |
| Tchaourou | −4.17 | −7.00 | −1.99 | −6.34 | −1.99 | −2.32 | −3.90 | −0.20 | 1.98 | −11.67 |
| Tchetti | −2.44 | −15.83 | −1.98 | −5.91 | −1.94 | −1.33 | 0.80 | 0.20 | 2.57 | −15.83 |
| Zagnanando | −2.35 | −16.04 | −1.97 | −0.93 | −1.06 | −0.77 | −1.98 | −0.05 | 5.20 | −11.93 |
| 1950−2014 | 2015−2050 | |||||||
|---|---|---|---|---|---|---|---|---|
| Significative Negative Trends (%) | Significative Positive Trends (%) | Significative Negative Trends (%) | Significative Positive Trends (%) | |||||
| LR | MK | LR | MK | LR | MK | LR | MK | |
| RX1day | 11 | 9 | 6 | 6 | 0 | 11 | 6 | 0 |
| RX5day | 17 | 14 | 3 | 3 | 0 | 6 | 0 | 0 |
| SDII | 31 | 0 | 26 | 26 | 11 | 6 | 0 | 0 |
| R10mm | 69 | 60 | 3 | 3 | 100 | 100 | 0 | 0 |
| R20mm | 45 | 11 | 6 | 9 | 71 | 71 | 0 | 0 |
| R1mm | 74 | 71 | 0 | 0 | 100 | 94 | 0 | 0 |
| CDD | 68 | 57 | 6 | 17 | 2 | 0 | 14 | 20 |
| CWD | 69 | 57 | 0 | 0 | 29 | 40 | 0 | 0 |
| R95p | 45 | 11 | 6 | 6 | 11 | 6 | 0 | 0 |
| R99p | 44 | 11 | 6 | 6 | 0 | 0 | 0 | 0 |
| PRCPTOT | 63 | 52 | 3 | 3 | 100 | 100 | 0 | 0 |
References
- Ogountundé, P.G.; Friesen, J.; van de Giesen, N.; Savenije, H.H.G. Hydroclimatology of the Volta River Basin in West Africa: Trends and variability from 1901 to 2002. Phys. Chem. Earth 2006, 31, 1180–1188. [Google Scholar] [CrossRef]
- Houghton, J.T.; Meira Filho, L.G.; Callander, B.A.; Harris, N.; Kattenberg, A.; Maskell, K. Climate Change. The IPCC Second Assessment Report; Cambridge University Press: New York, NY, USA, 1996; p. 572. [Google Scholar]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over southern and west Africa. J. Geophys. Res. 2006, 111, D14102. [Google Scholar] [CrossRef]
- Oguntundé, P.G.; Abiodunb, B.J.; Lischeid, G. Rainfall trends in Nigeria, 1901–2000. J. Hydrol. 2011, 411, 207–218. [Google Scholar] [CrossRef]
- Powell, E.J.; Keim, B.D. Trends in daily temperature and precipitation extremes for the Southeastern United States: 1948–2012. J. Clim. 2015, 28, 1592–1612. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Andsager, K.; Easterling, D.R. Long-term trends in extreme precipitation events over the conterminous United States and Canada. J. Clim. 1999, 12, 2515–2527. [Google Scholar] [CrossRef]
- Suppiah, R.; Hennessy, K.J. Trend in total rainfall, heavy rain events and number of dry days in Australia, 1910–1990. Int. J. Climatol. 1998, 10, 1141–1164. [Google Scholar] [CrossRef]
- Zhai, P.M.; Zhang, X.B.; Wan, H.; Pan, X.H. Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Tomassini, L.; Jacob, D. Spatial analysis of trends in extreme precipitation events in high-resolution climate model results and observations for Germany. J. Geophys. Res. 2009, 114, D12113. [Google Scholar] [CrossRef]
- Rajeevan, M.; Bhate, J.; Jaswal, A.K. Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Cantet, P. Impacts du Changement Climatique sur les Pluies Extrêmes par l’utilisation d’un Générateur Stochastique de Pluies. Ph.D. Thesis, Université Montpellier II, Montpellier, France, 2009. [Google Scholar]
- Yazid, M.; Humphries, U. Regional Observed Trends in Daily Rainfall Indices of Extremes over the Indochina Peninsula fro m 1960 to 2007. Climate 2015, 3, 168–192. [Google Scholar] [CrossRef]
- Bielec, Z. Long terme variability of thunderstorms and thunderstorms precipitation occurrence in Cracow, Poland, in the period 1896–1995. Atmos. Res. 2001, 56, 161–170. [Google Scholar] [CrossRef]
- Donat, M.G.; Peterson, T.C.; Brunet, M.; King, A.D.; Almazroui, M.; Kolli, R.K.; Boucherf, D.; Al-Mulla, A.Y.; Nour, A.Y.; Aly, A.A.; et al. Changes in extreme temperature and precipitation in the Arab region: Long-term trends and variability related to ENSO and NAO. Int. J. Climatol. 2013. [Google Scholar] [CrossRef]
- Ozer, A.; Ozer, P. Désertification au Sahel: Crise climatique ou anthropique? Bull. Séances l’Acad. R. Sci. d’Outre-Mer 2005, 51, 395–423. [Google Scholar]
- Easterling, D.R.; Evans, J.L.; Groisman, P.Y.; Karl, T.R.; Kunkel, K.E.; Ambenye, P. Observed variability and trends in extreme climate events: A brief review. Bull. Am. Meteorol. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- Aguilar, E.; Aziz Barry, A.; Brunet, M.; Ekang, L.; Fernandes, A.; Massoukina, M.; Mbah, J.; Mhanda, A.; do Nascimento, D.J.; Peterson, T.C.; et al. Changes in temperature and precipitation extremes in western central Africa, Guinea Conakry, and Zimbabwe, 1955–2006. J. Geophys. Res. 2009, 114, D02115. [Google Scholar] [CrossRef]
- Ozer, P.; Hountondji, Y.C.; Laminou Manzo, O. Evolution des caractéristiques pluviométriques dans l’est du Niger de 1940 à 2007. GEO-ECO-Trop 2009, 33, 11–30. [Google Scholar]
- Soro, G.E.; Noufé, D.; Goula Bi, T.A.; Shorohou, B. Trend Analysis for Extreme Rainfall at Sub-Daily and Daily Timescales in Côte d’Ivoire. Climate 2016, 4, 37. [Google Scholar] [CrossRef]
- Mason, S.J.; Waylen, P.R.; Mimmack, G.M.; Rajaratnam, B.; Harrison, J.M. Changes in extreme rainfall events in South Africa. Clim. Chang. 1999, 41, 249–257. [Google Scholar] [CrossRef]
- Hountondji, Y.-C.; De Longueville, F.; Ozer, P. Trends in extreme rainfall events in Benin (West Africa), 1960–2000. In Proceedings of the 1st International Conference on Energy, Environment and Climate Changes, Ho Chi Minh City, Vietnam, 26–27 August 2011. [Google Scholar]
- Hounkpè, J.; Diekkrüger, B.; Badou, D.F.; Afouda, A.A. Change in Heavy Rainfall Characteristics over the Ouémé River Basin, Benin Republic, West Africa. Climate 2016, 4, 15. [Google Scholar]
- Nicholson, S.E. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. ISRN Meteorol. 2013, 2013, 32. [Google Scholar] [CrossRef]
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Morcrette, J.J.; Smith, L.; Fourquart, Y. Pressure and temperature dependance of the absorption in longwave radiation parameterizations. Beitr. Phys. Atmos. 1986, 59, 455–469. [Google Scholar]
- Giorgetta, M.; Wild, M. The Water Vapour Continuum and Its Representation in ECHAM4; Max-Planck Institut für Meteorologie: Hamburg, Germany, 1995. [Google Scholar]
- Louis, J.-F. A parametric model of vertical eddy fluxes in the atmosphere. Bound.-Layer Meteor. 1979, 17, 187–202. [Google Scholar] [CrossRef]
- Lohmann, U.; Roeckner, E. Design and performance of a new cloud microphysics scheme developed for the ECHAM4 general circulation model. Clim. Dyn. 1996, 12, 557–572. [Google Scholar] [CrossRef]
- Hagemann, S. An Improved Land Surface Parameter Dataset for Global and Regional Climate Models; Max-Planck-Institute for Meteorology: Hamburg, Germany, 2002. [Google Scholar]
- Rechid, D.; Raddatz, T.; Jacob, D. Parameterization of snow-free land surface albedo as a function of vegetation phenology based on MODIS data and applied in climate modelling. Theor. Appl. Climatol. 2009, 95, 245–255. [Google Scholar] [CrossRef]
- The REMO Model. Available online: http://www.remo-rcm.de/059966/index.php.en#tab-10 (accessed on 18 September 2017).
- Giorgi, F.; Jones, C.; Asrar, G. Addressing climate information needs at the regional level: The CORDEX framework. World Meteorol. Org. Bull. 2009, 58, 175–183. [Google Scholar]
- Haensler, A.; Saeed, F.; Jacob, D. Assessing the robustness of projected precipitation changes over central Africa on the basis of a multitude of global and regional climate projections. Clim. Chang. 2013, 121, 349–363. [Google Scholar] [CrossRef]
- Kaboré, E.; Nikiema, M.; Ibrahim, B.; Helmschrot, J. Merging historical data records with MPI-ESM-LR, CanESM2, AFR MPI and AFR 44 scenarios to assess long-term climate trends for the Massili Basin in central Burkina Faso. Int. J. Curr. Eng. Technol. 2015, 5, 1846–1852. [Google Scholar]
- Sarr, M.A.; Seidou, O.; Tramblay, Y.; El Adlouni, S. Comparison of downscaling methods for mean and extreme precipitation in Senegal. J. Hydrol. Reg. Stud. 2015, 4, 369–385. [Google Scholar] [CrossRef]
- Mbaye, M.L.; Hagemann, S.; Haensler, A.; Gaye, A.T.; Afouda, A. Assessment of Climate Change Impact on Water Resources in the Upper Senegal Basin(West Africa). Am. J. Clim. Chang. 2015, 4, 77–93. [Google Scholar] [CrossRef]
- Giertz, S.; Höllermann, B.; Diekkrüger, B. An interdisciplinary scenario analysis to assess the water availability and water consumption in the Upper Ouémé catchment in Benin. Adv. Geosci. 2006, 9, 3–13. [Google Scholar] [CrossRef]
- Nikulin, G.; Jones, C.; Giorgi, F.; Asrar, G.; Cerezo-Mota, M.; Christensen, O.B.; Déqué, M.; Fernandez, J.; Hänsler, A.; Meijgaard, E.V.; et al. Precipitation climatology in an ensemble of CORDEX-Africa regional climate simulations. J. Clim. 2012, 25, 6057–6078. [Google Scholar] [CrossRef]
- N’Tcha M’Po, Y.; Lawin, A.E.; Oyerinde, G.T.; Yao, K.B.; Afouda, A.A. Comparison of Daily Precipitation Bias Correction Methods Based on Four Regional Climate Model Outputs in Ouémé Basin, Benin. Hydrology 2017, 4, 58–71. [Google Scholar] [CrossRef]
- Paeth, H.; Born, K.; Podzun, R.; Jacob, D. Regional dynamic downscaling over Westafrica: Model evaluation and comparison of wet and dry years. Meteorol. Z. 2005, 143, 349–367. [Google Scholar] [CrossRef]
- CORDEX Database. Available online: https://www.cordex.org (accessed on 18 September 2017).
- Hagemann, S.; Chen, C.; Haerter, J.O.; Heinke, J.; Gerten, D.; Piani, C. Impact of a statistical bias correction on the projected hydrological changes obtained from three GCMs and two hydrology models. J. Hydrometeorol. 2011, 12, 556–578. [Google Scholar] [CrossRef]
- Gutjahr, O.; Heinemann, G. Comparing precipitation bias correction methods for high-resolution regional climate simulations using COSMO-CLM. Effects on extreme values and climate change signal. Theor. Appl. Climatol. 2013, 114, 511–529. [Google Scholar] [CrossRef]
- Amengual, A.; Homar, V.; Romero, R.; Alonso, S.; Ramis, C. A Statistical Adjustment of Regional Climate Model Outputs to Local Scales: Application to Platja de Palma, Spain. J. Clim. 2012, 25, 939–957. [Google Scholar] [CrossRef]
- Obada, E.; Alamou, A.E.; Zandagba, E.J.; Biao, I.E.; Chabi, A.; Afouda, A.A. Comparative study of seven bias correction methods applied to three Regional Climate Models in Mekrou catchment (Benin, West Africa). Int. J. Curr. Eng. Technol. 2016, 6, 1831–1840. [Google Scholar]
- Dai, A. Precipitation Characteristics in Eighteen Coupled Climate Models. J. Clim. 2006, 19, 4605–4630. [Google Scholar] [CrossRef]
- Yazid, M.; Humphries, U.; Sudarmadji, T. Spatiotemporal of extreme rainfall events in the Indochina peninsula. In Proceedings of the International Conference on Applied Statistics, Khon Kaen, Thailand, 21–24 May 2014; pp. 238–245. [Google Scholar]
- Zhang, X.; Hogg, W.D.; Mekis, E. Spatial and temporal characteristics of heavy precipitation events over Canada. Am. Meteorol. Soc. 2001, 14, 1923–1936. [Google Scholar] [CrossRef]
- Tabari, H.; Somee, B.S.; Zadeh, M.R. Testing for long-term trends in climatic variables in Iran. Atmos. Res. 2011, 100, 132–140. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zhou, L. Observed trends in extreme precipitation events in China during 1961–2001 and the associated changes in large-scale circulation. Geophys. Res. Lett. 2005, 32, L09707. [Google Scholar] [CrossRef]
- Ozer, P.; Mahamoud, A. Recent Extreme Precipitation and Temperature Changes in Djibouti City (1966–2011). J. Climatol. 2013, 2013. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Muhlbauer, A.; Spichtinger, P.; Lohmann, U. Application and Comparison of Robust Linear Regression Methods for Trend Estimation. J. Appl. Meteorol. Climatol. 2007, 48, 1961–1970. [Google Scholar] [CrossRef]
- Odekunle, O.T.; Adejuwon, A.S. Assessing changes in the rainfall regime in Nigeria between 1961 and 2004. GeoJournal 2007, 70, 145–159. [Google Scholar] [CrossRef]
- Dosio, A.; Panitz, H.-J. Climate change projections for CORDEX Africa with COSMO-CLM regional climate model and differences with the driving global climate models. Clim. Dyn. 2016, 46, 1599–1625. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Summary for Policymakers. Climate Change 2014: Impacts, Adaptation, and Vulnerability; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Diekkrüger, B.; Diederich, M.; Giertz, S.; Höllermann, B.; Kocher, A.; Reichert, B.; Steup, G. Water availability and water demand under Global Change in Benin, West Africa. In Global Change and Water Resources in West Africa the German-African GLOWA Projects; Bundesministerium fur Bildung und Forschung: Ouagadougou, Burkina Faso, 2008. [Google Scholar]
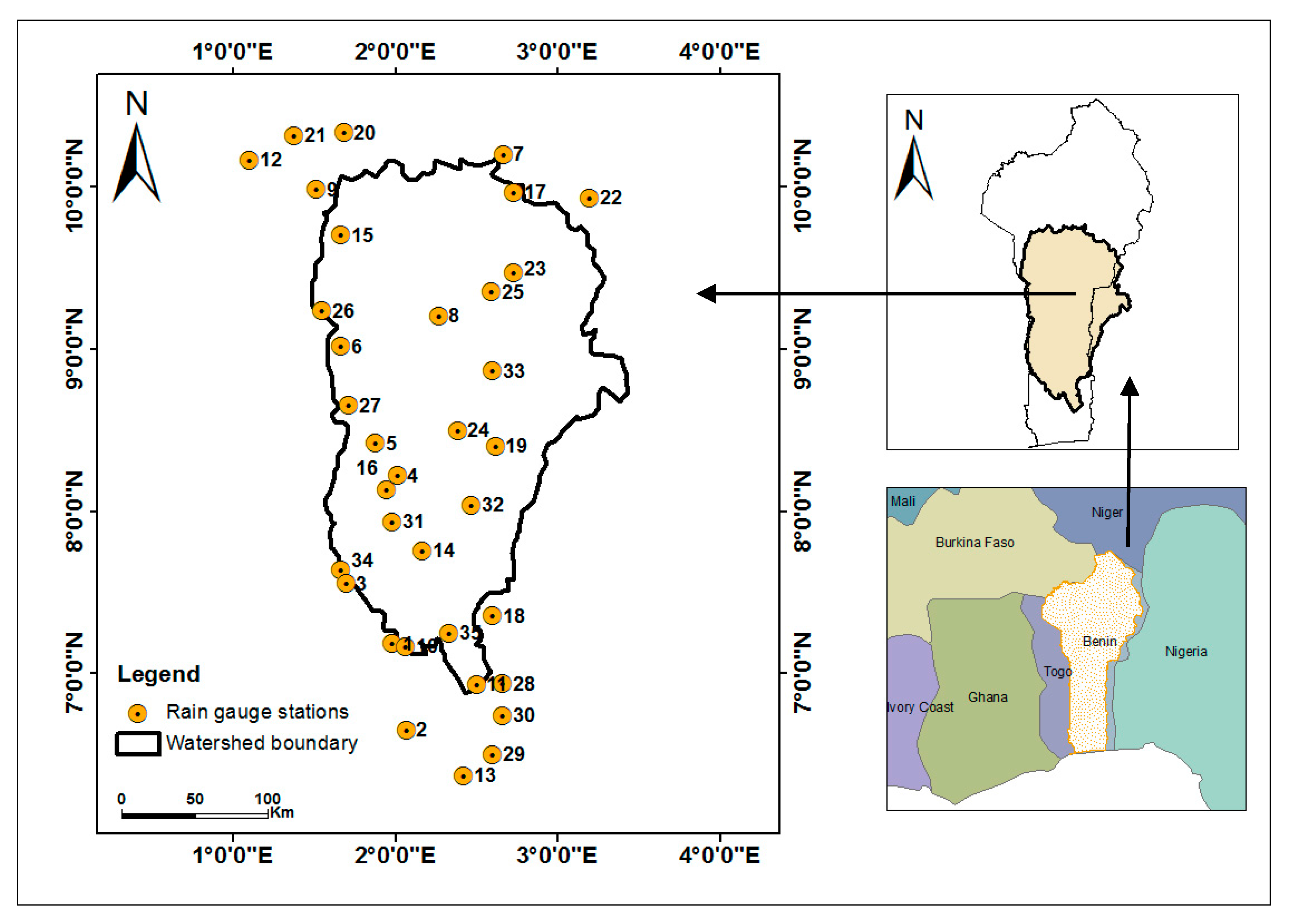
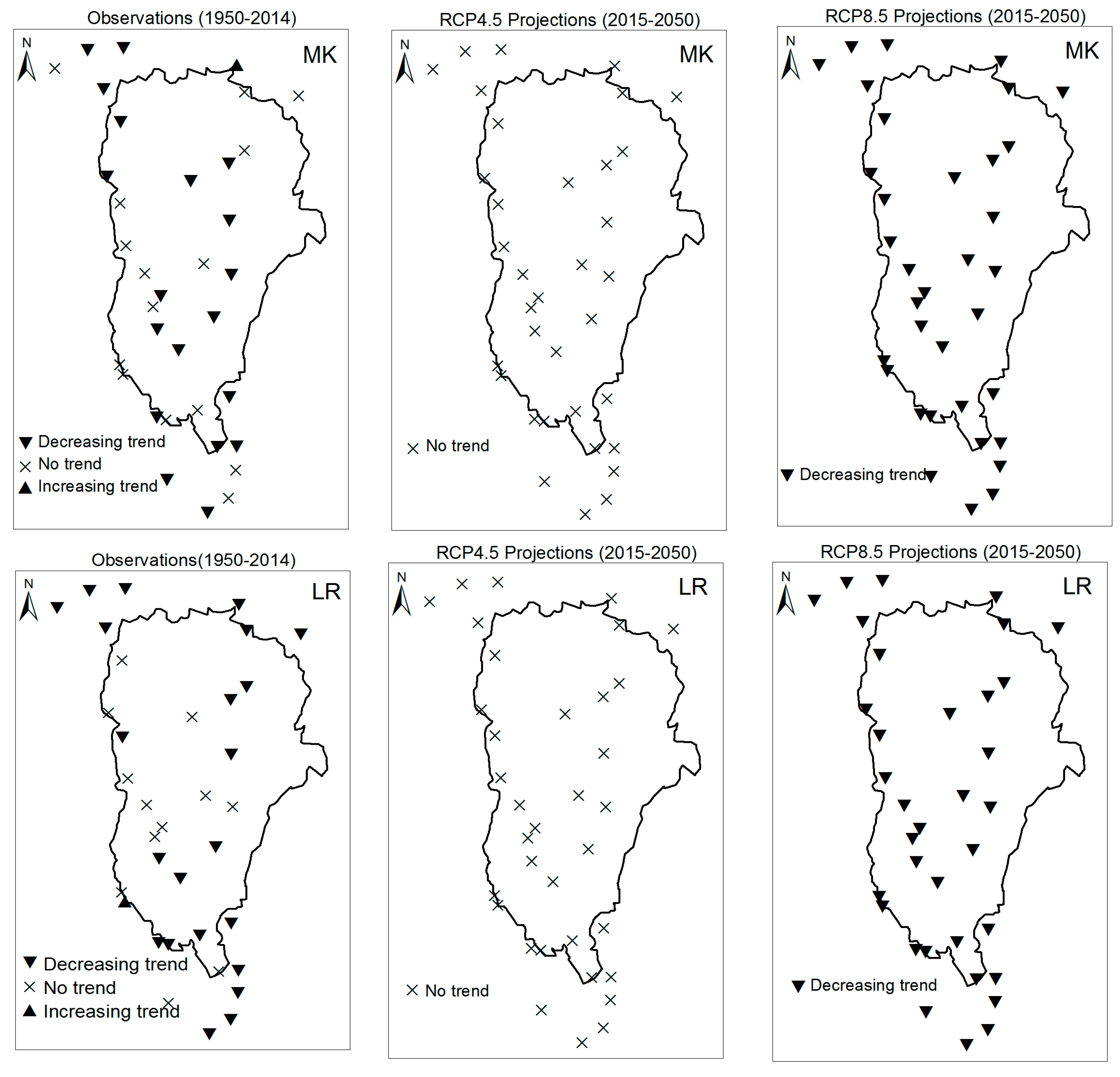
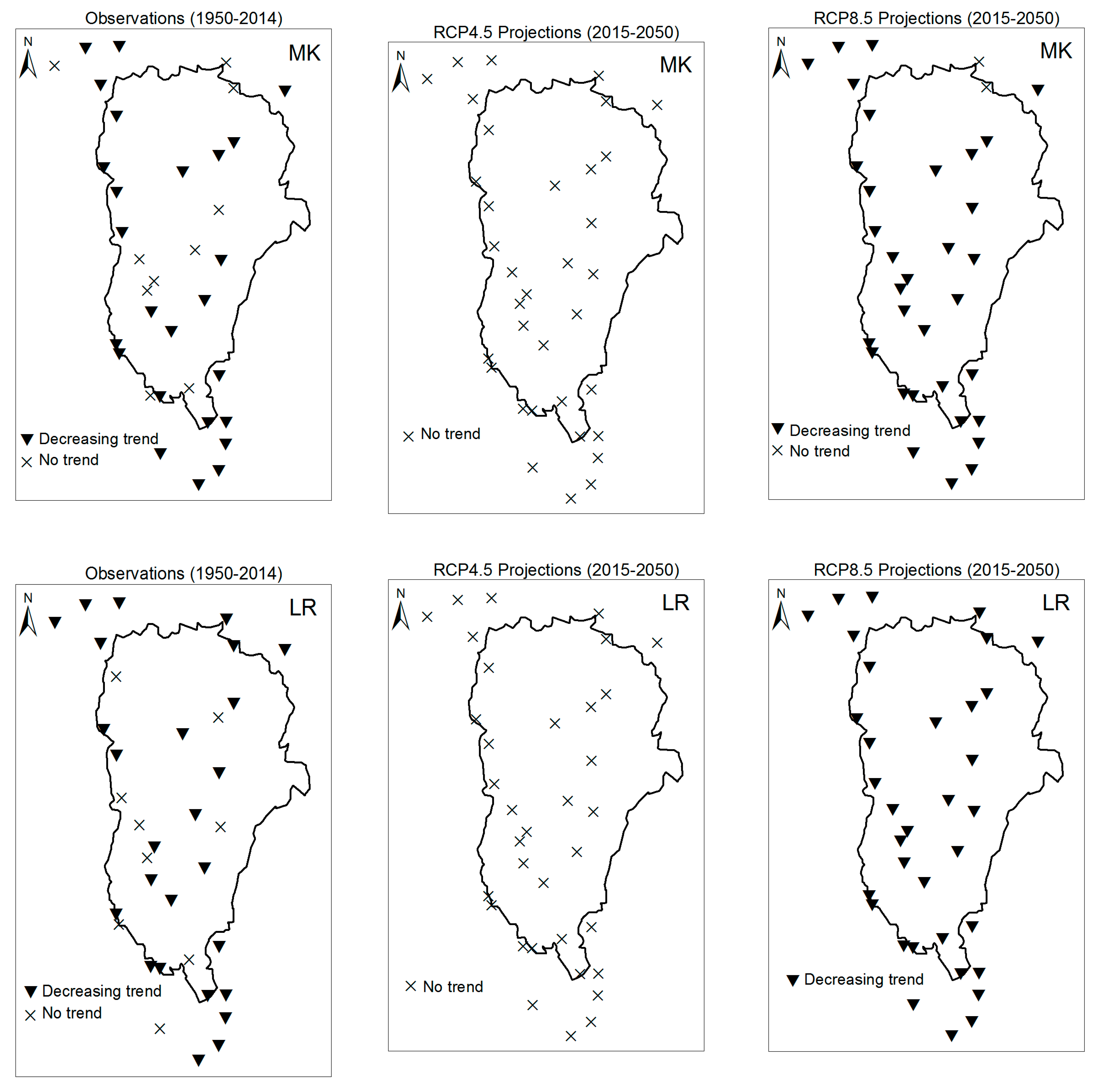
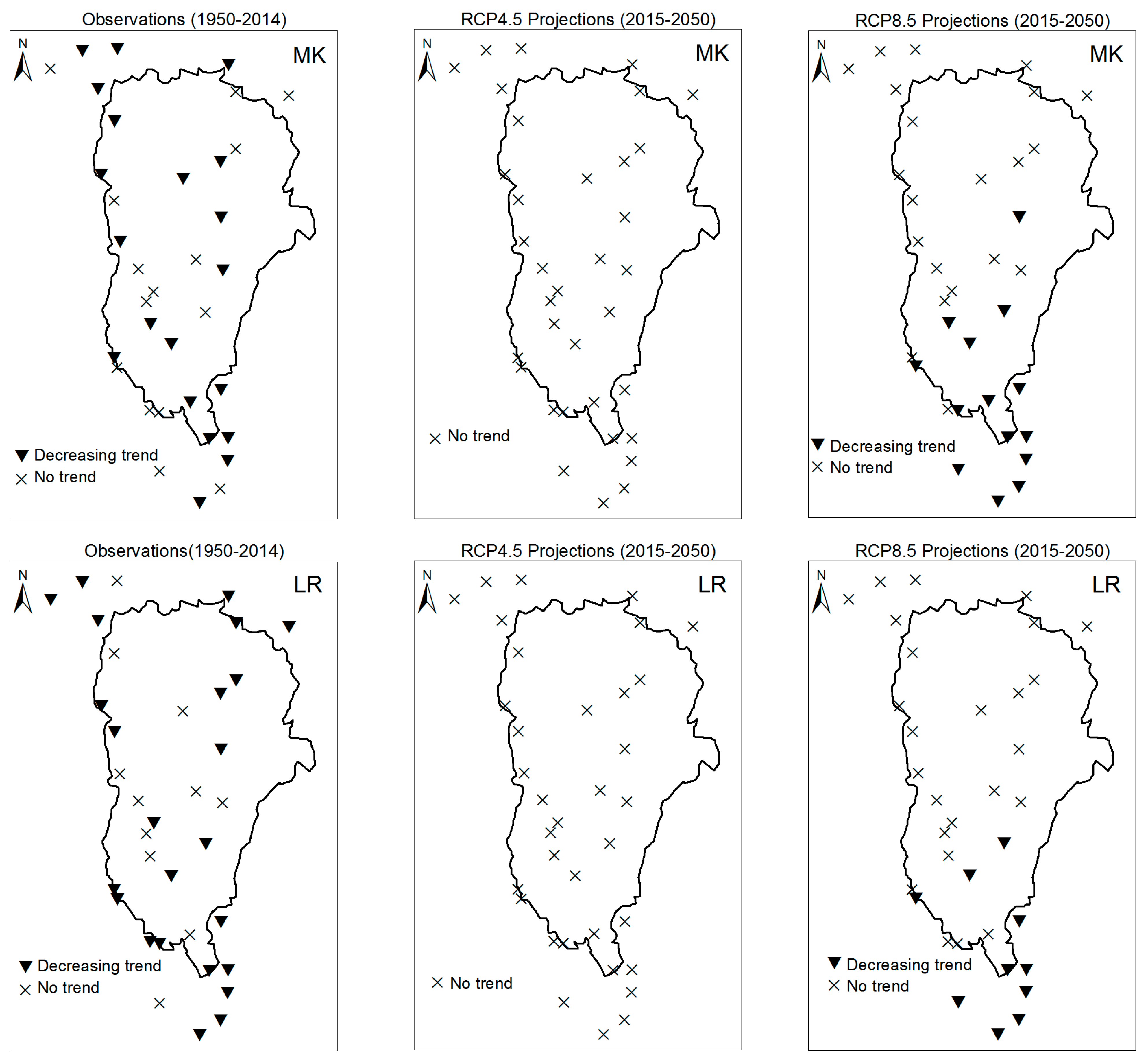




| No. | Stations Name | Long. (deg.) | Lat. (deg.) | Creation Year | Missing Rate (%) | No. | Stations Name | Long. (deg.) | Lat. (deg.) | Creation Year | Missing Rate (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Abomey | 1.98 | 7.18 | 1921 | 2.0 | 19 | Kokoro | 2.62 | 8.40 | 1969 | 5.0 |
| 2 | Adjohoun | 2.48 | 6.70 | 1921 | 3.3 | 20 | Kouandé | 1.68 | 10.33 | 1931 | 4.0 |
| 3 | Agouna | 1.70 | 7.55 | 1968 | 12.0 | 21 | Natitingou | 1.38 | 10.32 | 1921 | 0.0 |
| 4 | Aklampa | 2.02 | 8.55 | 1968 | 4.0 | 22 | Nikki | 3.20 | 9.93 | 1921 | 10.0 |
| 5 | Bantè | 1.88 | 8.42 | 1942 | 8.0 | 23 | Okpara | 2.73 | 9.47 | 1956 | 4.0 |
| 6 | Bassila | 1.67 | 9.02 | 1950 | 12.0 | 24 | Ouèssè | 2.60 | 8.67 | 1964 | 1.4 |
| 7 | Bembèrèkè | 2.67 | 10.20 | 1921 | 0.0 | 25 | Parakou | 2.60 | 9.35 | 1921 | 1.0 |
| 8 | Bétérou | 2.27 | 9.20 | 1953 | 7.0 | 26 | Pénéssoulou | 1.55 | 9.23 | 1969 | 20.0 |
| 9 | Birni | 1.52 | 9.98 | 1953 | 10.0 | 27 | Pira | 1.72 | 8.65 | 1968 | 6.0 |
| 10 | Bohicon | 2.07 | 7.17 | 1940 | 0.2 | 28 | Pobè | 2.67 | 6.93 | 1926 | 7.0 |
| 11 | Bonou | 2.50 | 6.93 | 1946 | 7.0 | 29 | Porto-Novo | 2.61 | 6.48 | 1921 | 3.0 |
| 12 | Boukombé | 1.10 | 10.16 | 1952 | 11.0 | 30 | Sakété | 2.07 | 6.72 | 1921 | 10.0 |
| 13 | Cotonou | 2.38 | 6.35 | 1921 | 0.0 | 31 | Savalou | 1.98 | 7.93 | 1921 | 17.0 |
| 14 | Dassa-Zoumè | 2.17 | 7.75 | 1941 | 0.0 | 32 | Savè | 2.47 | 8.03 | 1921 | 16.0 |
| 15 | Djougou | 1.67 | 9.70 | 1921 | 5.0 | 33 | Tchaourou | 2.60 | 8.87 | 1937 | 13.0 |
| 16 | Gouka | 1.95 | 8.13 | 1968 | 6.0 | 34 | Tchetti | 1.67 | 7.82 | 1964 | 17.0 |
| 17 | Ina | 2.73 | 9.97 | 1947 | 6.0 | 35 | Zagnanando | 2.33 | 7.25 | 1921 | 0.1 |
| 18 | Kétou | 2.60 | 7.35 | 1950 | 5.0 |
| Institute | Climate Service Centre, Hamburg, Germany |
|---|---|
| Main driving Model | MPI-ESM-LR |
| Projection | Rotated spherical grid |
| Resolution | 0.44 degree |
| Vertical coordinates | Hybrid |
| Vertical levels | 27 |
| Advection | Semi-lagrangian |
| Time step | 240 s |
| Convection Scheme | Tiedke [24] |
| Radiation Scheme | Morcrette et al. [25]; Giorgetta and Wild [26] |
| Turbulence vertical diffusion | Louis [27] |
| Cloud Microphysics Scheme | Lohmann and Roeckner [28] |
| Land Surface Scheme | Hagemann [29]; Rechid et al. [30] |
| ID | Indicator Name | Definitions | Units |
|---|---|---|---|
| RX1day | Max 1-day precipitation amount | Annual maximum 1-day precipitation | mm |
| RX5day | Max 5-day precipitation amount | Annual maximum consecutive 5-day precipitation | mm |
| SDII | Simple daily intensity index | Annual total precipitation divided by the number of wet days (defined as PRCP ≥1 mm) in the year | mm/day |
| R10mm | Number of heavy precipitation days | Annual count of days when PRCP ≥10 mm | days |
| R20mm | Number of very heavy precipitation days | Annual count of days when PRCP ≥20 mm | days |
| R1mm | Number of days wet days | Annual count of days when PRCP ≥1 mm | days |
| CDD | Consecutive dry days | Maximum number of consecutive days with PRCP <1 mm | days |
| CWD | Consecutive wet days | Maximum number of consecutive days with PRCP ≥1 mm | days |
| R95pSUM | Very wet days | Annual total precipitation when PRCP >95th percentile of period 1981–2010 | mm |
| R99pSUM | Extremely wet days | Annual total precipitation when PRCP >99th percentile of period 1981–2010 | mm |
| PRCPTOT | Annual total wet-day precipitation | Annual total precipitation in wet days (PRCP ≥ 1 mm) | mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
N’Tcha M’Po, Y.; Lawin, E.A.; Yao, B.K.; Oyerinde, G.T.; Attogouinon, A.; Afouda, A.A. Decreasing Past and Mid-Century Rainfall Indices over the Ouémé River Basin, Benin (West Africa). Climate 2017, 5, 74. https://doi.org/10.3390/cli5030074
N’Tcha M’Po Y, Lawin EA, Yao BK, Oyerinde GT, Attogouinon A, Afouda AA. Decreasing Past and Mid-Century Rainfall Indices over the Ouémé River Basin, Benin (West Africa). Climate. 2017; 5(3):74. https://doi.org/10.3390/cli5030074
Chicago/Turabian StyleN’Tcha M’Po, Yèkambèssoun, Emmanuel Agnidé Lawin, Benjamin Kouassi Yao, Ganiyu Titilope Oyerinde, André Attogouinon, and Abel Akambi Afouda. 2017. "Decreasing Past and Mid-Century Rainfall Indices over the Ouémé River Basin, Benin (West Africa)" Climate 5, no. 3: 74. https://doi.org/10.3390/cli5030074
APA StyleN’Tcha M’Po, Y., Lawin, E. A., Yao, B. K., Oyerinde, G. T., Attogouinon, A., & Afouda, A. A. (2017). Decreasing Past and Mid-Century Rainfall Indices over the Ouémé River Basin, Benin (West Africa). Climate, 5(3), 74. https://doi.org/10.3390/cli5030074





