Should We Use Quantile-Mapping-Based Methods in a Climate Change Context? A “Perfect Model” Experiment
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Downscaling Methodologies
3. Experimental Design
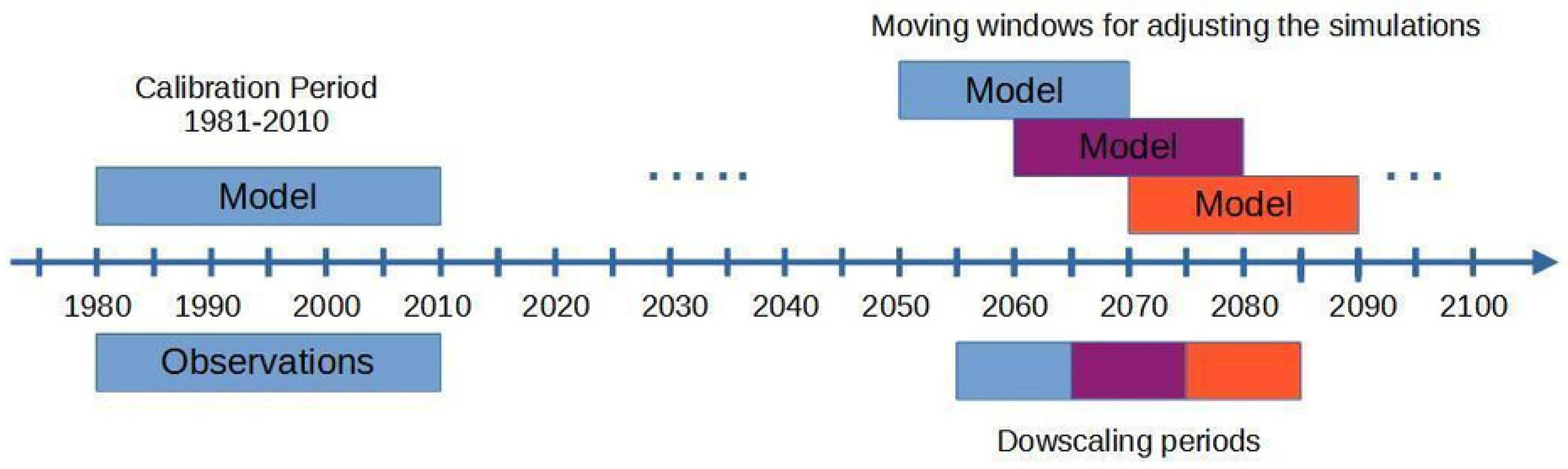
3.1. Calibration and Validation Setup
3.2. Experiments
- The third experiment, called LAN, is the CDF-t method with a modification of the treatment of the extreme quantiles, as described by Lanzante et al. [35]. This modification involves two parameters, aiming at correcting the tail of the distribution:
- –
- TLN (meaning “Tail length”), defined as the “number of tail points to be adjusted”;
- –
- NPT (meaning “lastN-points”), defined as “the number of ‘good points’ (i.e., those adjacent to the portion of a tail to be adjusted) averaged to determine the tail adjustment factor”.
Here, in order to avoid potential instabilities in the tails of the corrected distribution (i.e., in the few smallest or highest downscaled values), the lowest and the highest TLN = 10 values of the data are all adjusted by the value , corresponding to the mean correction of the NPT = 10 values preceding the highest TLN values or following the lowest TLN values. In a more mathematical formulation, if is the model data to be downscaled ranked in increasing order and if is the value of (i.e., the lowest value of ) and is the downscaled value obtained within the projection period (p), then for the adjustment of the lowest (i.e., left) tail of the distribution,while for the highest (i.e., right) tail of the distribution,The downscaled values for the first TLN points () and the last TLN points (, where N is the total number of data points) are then obtained asbased on the appropriate value. This corresponds to a safeguard to prevent the most extreme points of the distribution from becoming numerical outliers. Figure 2 illustrates the procedure used in the LAN experiment for the upper tail of temperature in October and for the grid cell containing the city of Paris, with TLN = 5 data points and NPT = 10 data points for computing . - The fourth experiment, called NPAS, is based on the LAN experiment by changing only the number of cuts of the quantiles and setting the variable to 100 (i.e., instead of 1000 for temperature and 5000 for precipitation for the CDF-t and LAN experiments). This experiment is conducted to explore the sensitivity of the results to low values.
- The fifth experiment, called MW, is also based on the LAN experiment but changes only the parameters of the moving window to 30–10 (instead of 20–10). This is done to test the effect of a longer (external) window period.
- Finally, the sixth and last experiment, called TLN, is also based on the LAN experiment, but the parameter TLN is set to 5. This is to test a smaller number of tail points to limit the change to 1% of the available data (900 data points; thus, five points for each tail) at the tails of the distribution.
3.3. Metrics
4. Results
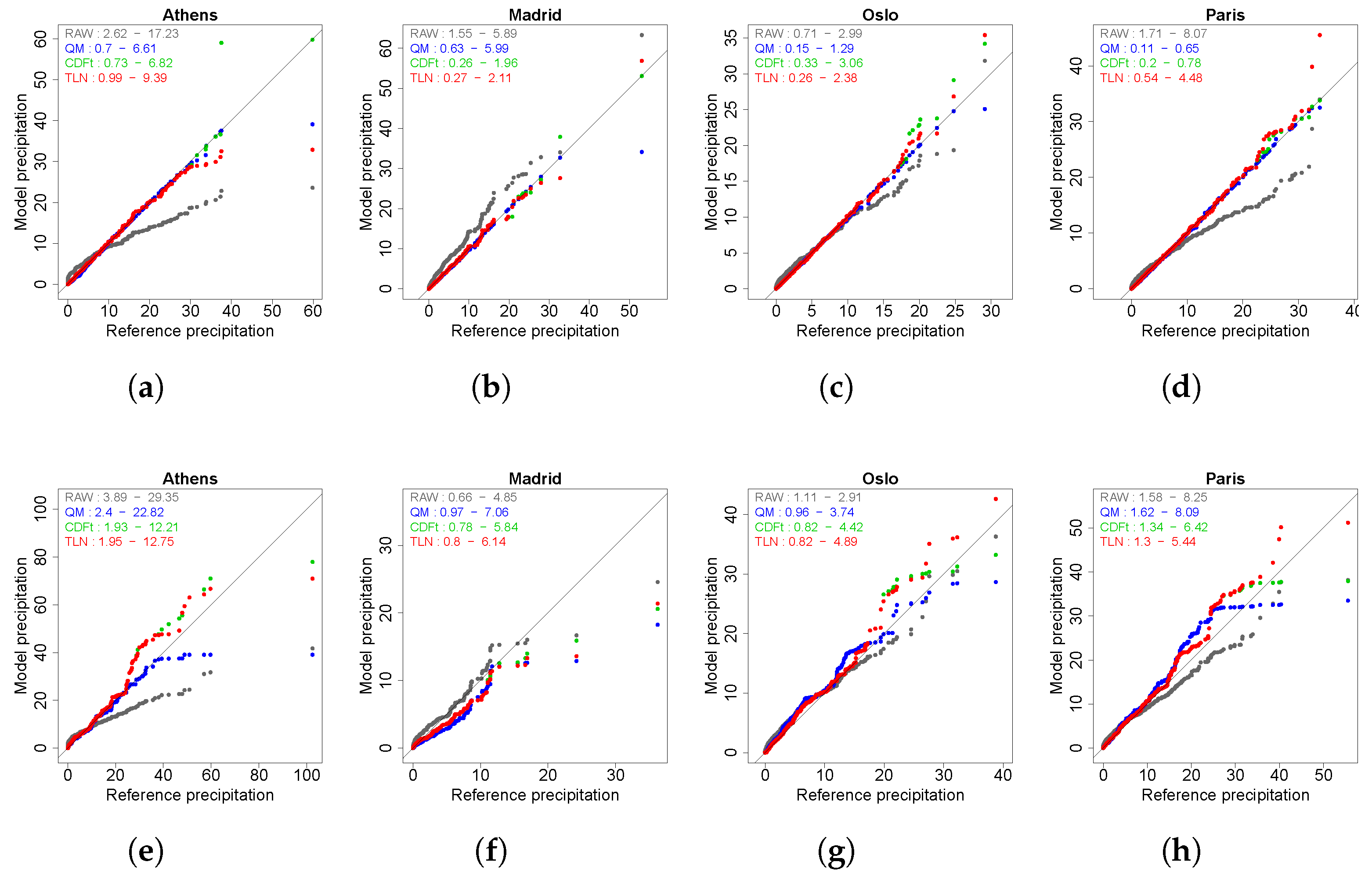
4.1. Evaluation of Marginal Distributions
4.2. Evaluation of Extremes
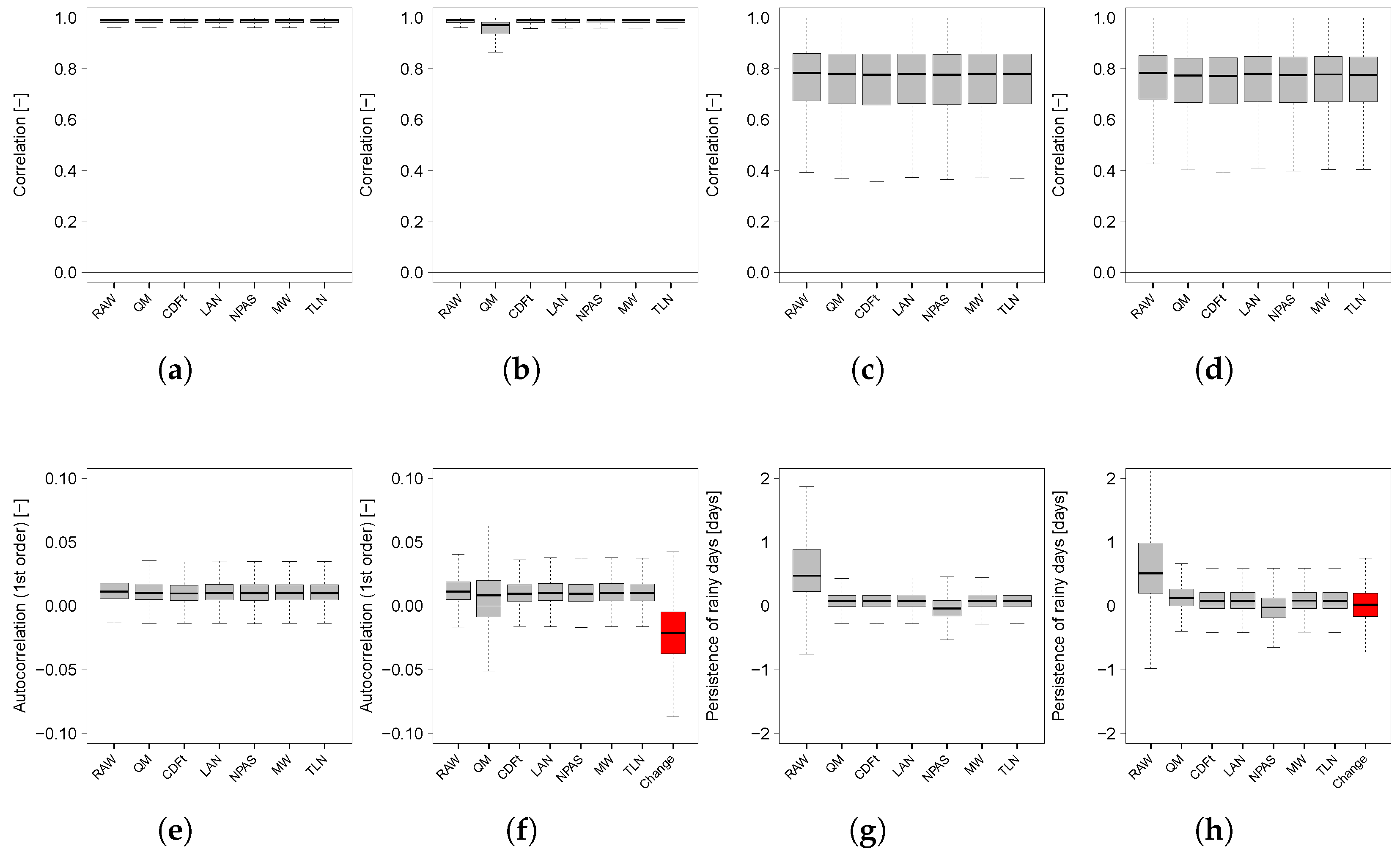
4.3. Evaluations of Temporal Properties
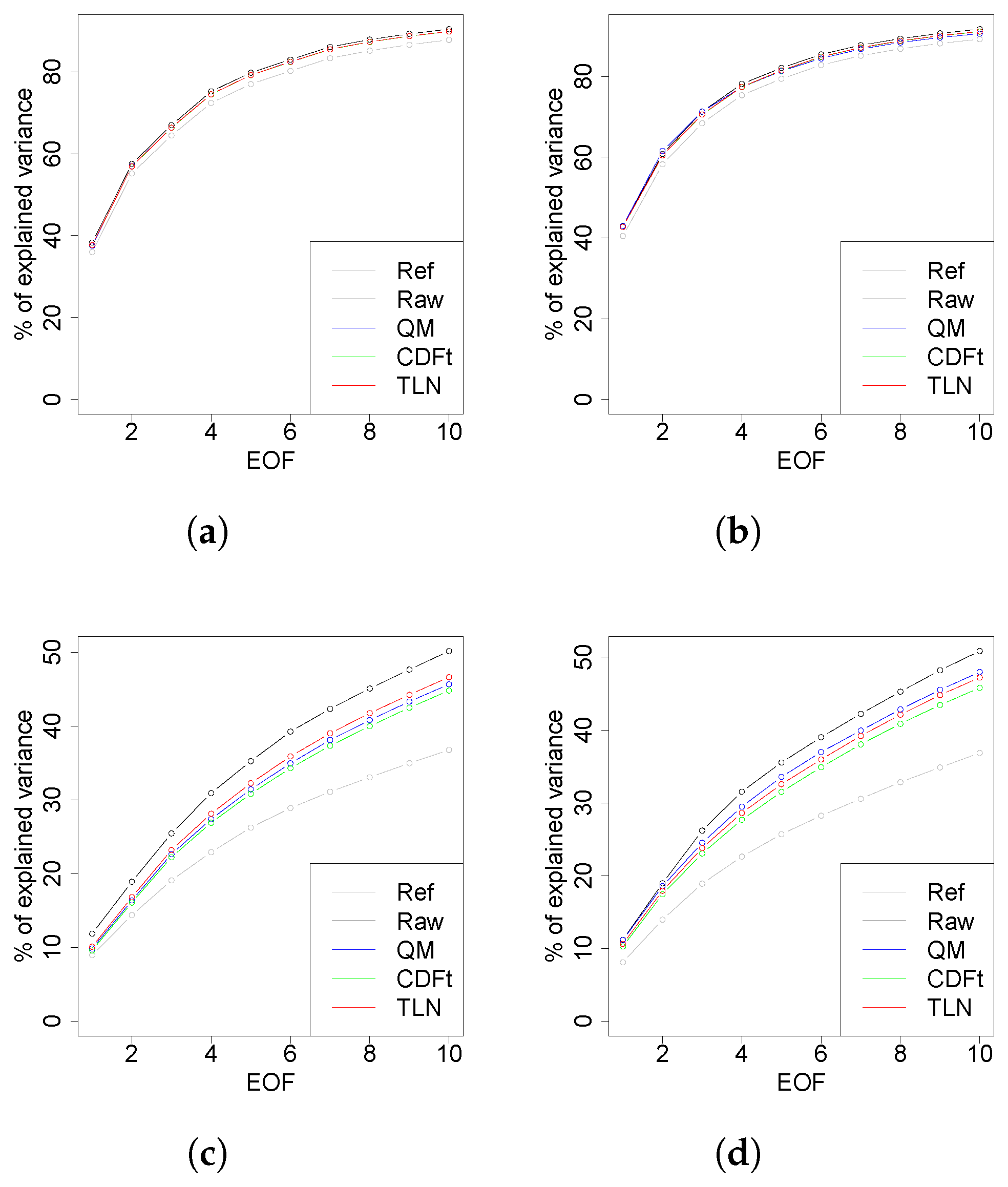
4.4. Multivariate Analysis: Inter-Variable & Spatial Properties
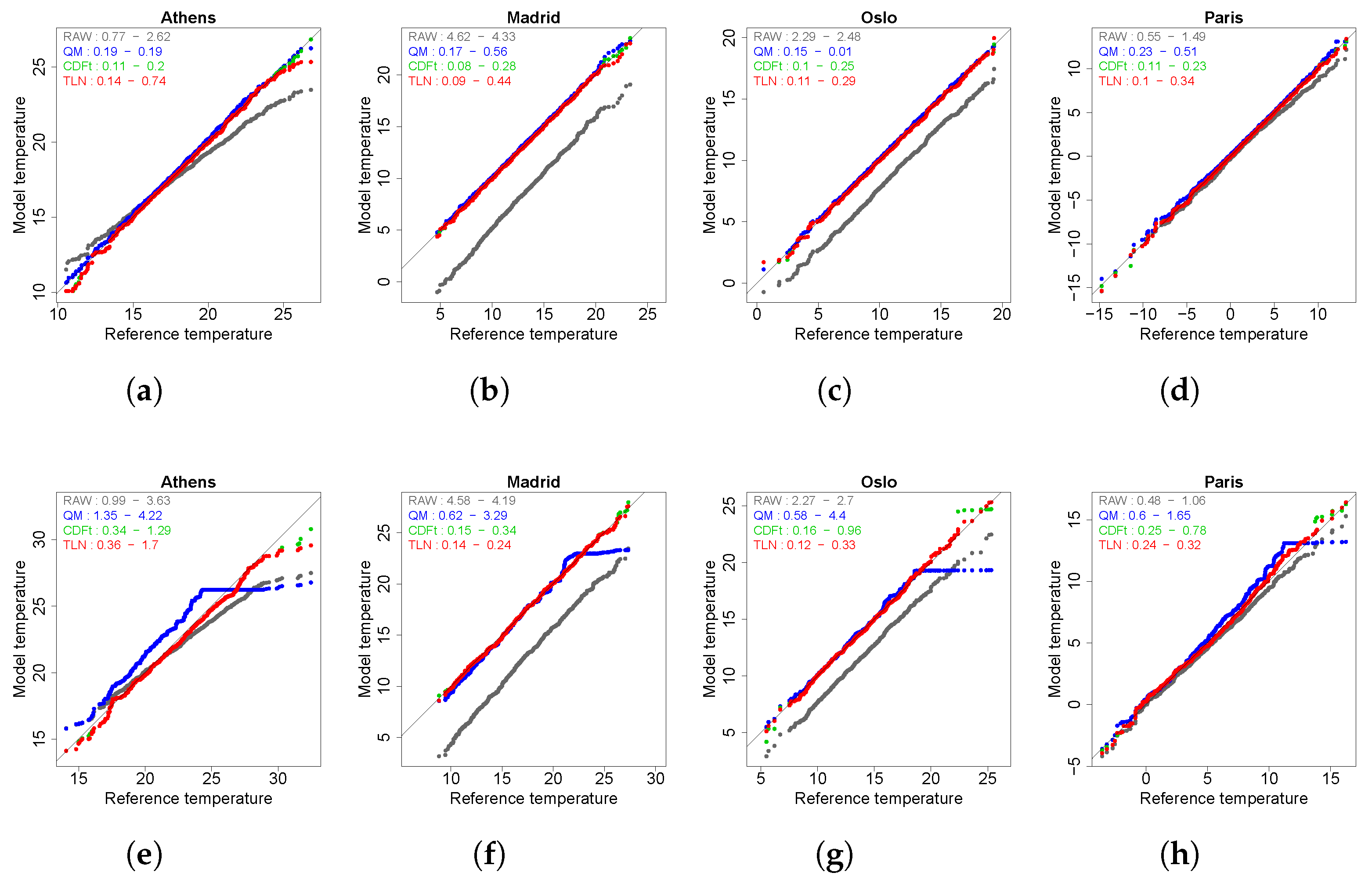
4.5. Evaluation at Local Scale
5. Conclusions and Discussion
5.1. Conclusions
5.2. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chokkavarapu, N.; Mandla, V.R. Comparative study of GCMs, RCMs, downscaling and hydrological models: A review toward future climate change impact estimation. SN Appl. Sci. 2019, 1, 1698. [Google Scholar] [CrossRef]
- Müller, C.; Franke, J.; Jägermeyr, J.; Ruane, A.C.; Elliott, J.; Moyer, E.; Heinke, J.; Falloon, P.D.; Folberth, C.; Francois, L.; et al. Exploring uncertainties in global crop yield projections in a large ensemble of crop models and CMIP5 and CMIP6 climate scenarios. Environ. Res. Lett. 2021, 16, 034040. [Google Scholar] [CrossRef]
- Laux, P.; Rötter, R.P.; Webber, H.; Dieng, D.; Rahimi, J.; Wei, J.; Faye, B.; Srivastava, A.K.; Bliefernicht, J.; Adeyeri, O.; et al. To bias correct or not to bias correct? An agricultural impact modelers’ perspective on regional climate model data. Agric. For. Meteorol. 2021, 304–305, 108406. [Google Scholar] [CrossRef]
- Baron, C.; Sultan, B.; Balme, M.; Sarr, B.; Traore, S.; Lebel, T.; Janicot, S.; Dingkuhn, M. From GCM grid cell to agricultural plot: Scale issues affecting modelling of climate impact. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 2095–2108. [Google Scholar] [CrossRef] [PubMed]
- Challinor, A.J.; Osborne, T.; Morse, A.; Shaffrey, L.; Wheeler, T.; Weller, H.; Vidale, P.L. Methods and Resources for Climate Impacts Research. Bull. Am. Meteorol. Soc. 2009, 90, 836–848. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Navarro, A.; Moreno, R.; Sánchez, J.L.; García-Ortega, E. Regional climate models: 30 years of dynamical downscaling. Atmos. Res. 2020, 235, 104785. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M. Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Ayar, P.V.; Vrac, M.; Bastin, S.; Carreau, J.; Déqué, M.; Gallardo, C. Intercomparison of statistical and dynamical downscaling models under the EURO- and MED-CORDEX initiative framework: Present climate evaluations. Clim. Dyn. 2016, 46, 1301–1329. [Google Scholar] [CrossRef]
- Gaitan, C.; Hsieh, W.; Cannon, A.; Gachon, P. Evaluation of Linear and Non-Linear Downscaling Methods in Terms of Daily Variability and Climate Indices: Surface Temperature in Southern Ontario and Quebec, Canada. Atmos.-Ocean 2014, 52, 211–221. [Google Scholar] [CrossRef]
- Baño-Medina, J.; Manzanas, R.; Gutiérrez, J.M. Configuration and intercomparison of deep learning neural models for statistical downscaling. Geosci. Model Dev. 2020, 13, 2109–2124. [Google Scholar] [CrossRef]
- Terzago, S.; Palazzi, E.; von Hardenberg, J. Stochastic downscaling of precipitation in complex orography: A simple method to reproduce a realistic fine-scale climatology. Nat. Hazards Earth Syst. Sci. 2018, 18, 2825–2840. [Google Scholar] [CrossRef]
- Harris, L.; McRae, A.T.T.; Chantry, M.; Dueben, P.D.; Palmer, T.N. A Generative Deep Learning Approach to Stochastic Downscaling of Precipitation Forecasts. J. Adv. Model. Earth Syst. 2022, 14, e2022MS003120. [Google Scholar] [CrossRef]
- Legasa, M.N.; Manzanas, R.; Calviño, A.; Gutiérrez, J.M. A Posteriori Random Forests for Stochastic Downscaling of Precipitation by Predicting Probability Distributions. Water Resour. Res. 2022, 58, e2021WR030272. [Google Scholar] [CrossRef]
- Uytven, E.V.; Niel, J.D.; Willems, P. Uncovering the shortcomings of a weather typing method. Hydrol. Earth Syst. Sci. 2020, 24, 2671–2686. [Google Scholar] [CrossRef]
- François, B.; Thao, S.; Vrac, M. Adjusting spatial dependence of climate model outputs with cycle-consistent adversarial networks. Clim. Dyn. 2021, 57, 3323–3353. [Google Scholar] [CrossRef]
- Haddad, Z.S.; Rosenfeld, D. Optimality of empirical Z-R relations. Q. J. R. Meteorol. Soc. 1997, 123, 1283–1293. [Google Scholar] [CrossRef]
- Déqué, M. Frequency of precipitation and temperature extremes over France in an anthropogenic scenario: Model results and statistical correction according to observed values. Glob. Planet. Change 2007, 57, 16–26. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Galmarini, S.; Cannon, A.; Ceglar, A.; Christensen, O.; de Noblet-Ducoudré, N.; Dentener, F.; Doblas-Reyes, F.; Dosio, A.; Gutierrez, J.; Iturbide, M.; et al. Adjusting climate model bias for agricultural impact assessment: How to cut the mustard. Clim. Serv. 2019, 13, 65–69. [Google Scholar] [CrossRef]
- Galmarini, S.; Solazzo, E.; Ferrise, R.; Srivastava, A.K.; Ahmed, M.; Asseng, S.; Cannon, A.; Dentener, F.; Sanctis, G.D.; Gaiser, T.; et al. Assessing the impact on crop modelling of multi- and uni-variate climate model bias adjustments. Agric. Syst. 2024, 215, 103846. [Google Scholar] [CrossRef]
- Michelangeli, P.; Vrac, M.; Loukos, H. Probabilistic downscaling approaches: Application to wind cumulative distribution functions. Geophys. Res. Lett. 2009, 36, L11708. [Google Scholar] [CrossRef]
- Vrac, M.; Drobinski, P.; Merlo, A.; Herrmann, M.; Lavaysse, C.; Li, L.; Somot, S. Dynamical and statistical downscaling of the French Mediterranean climate: Uncertainty assessment. Nat. Hazards Earth Syst. Sci. 2012, 12, 2769–2784. [Google Scholar] [CrossRef]
- Kallache, M.; Vrac, M.; Naveau, P.; Michelangeli, P.A. Nonstationary probabilistic downscaling of extreme precipitation. J. Geophys. Res. 2011, 116, D05113. [Google Scholar] [CrossRef]
- Vrac, M.; Noël, T.; Vautard, R. Bias correction of precipitation through Singularity Stochastic Removal: Because occurrences matter. J. Geophys. Res. Atmos. 2016, 121, 5237–5258. [Google Scholar] [CrossRef]
- Oettli, P.; Sultan, B.; Baron, C.; Vrac, M. Are regional climate models relevant for crop yield prediction in West Africa? Environ. Res. Lett. 2011, 6, 014008. [Google Scholar] [CrossRef]
- Colette, A.; Vautard, R.; Vrac, M. Regional climate downscaling with prior statistical correction of the global climate forcing. Geophys. Res. Lett. 2012, 39, L13707. [Google Scholar] [CrossRef]
- Tisseuil, C.; Vrac, M.; Grenouillet, G.; Wade, A.; Gevrey, M.; Oberdorff, T.; Grodwohl, J.B.; Lek, S. Strengthening the link between climate, hydrological and species distribution modeling to assess the impacts of climate change on freshwater biodiversity. Sci. Total Environ. 2012, 424, 193–201. [Google Scholar] [CrossRef]
- Tramblay, Y.; Neppel, L.; Carreau, J.; Sanchez-Gomez, E. Extreme value modelling of daily areal rainfall over Mediterranean catchments in a changing climate. Hydrol. Processes 2012, 26, 3934–3944. [Google Scholar] [CrossRef]
- Defrance, D.; Ramstein, G.; Charbit, S.; Vrac, M.; Famien, A.M.; Sultan, B.; Swingedouw, D.; Dumas, C.; Gemenne, F.; Alvarez-Solas, J.; et al. Consequences of rapid ice sheet melting on the Sahelian population vulnerability. Proc. Natl. Acad. Sci. USA 2017, 114, 6533–6538. [Google Scholar] [CrossRef]
- Defrance, D.; Sultan, B.; Castets, M.; Famien, A.M.; Baron, C. Impact of climate change in West Africa on cereal production per capita in 2050. Sustainability 2020, 12, 7585. [Google Scholar] [CrossRef]
- Famien, A.M.; Janicot, S.; Ochou, A.D.; Vrac, M.; Defrance, D.; Sultan, B.; Noël, T. A bias-corrected CMIP5 dataset for Africa using the CDF-t method – a contribution to agricultural impact studies. Earth Syst. Dyn. 2018, 9, 313–338. [Google Scholar] [CrossRef]
- Bartók, B.; Tobin, I.; Vautard, R.; Vrac, M.; Jin, X.; Levavasseur, G.; Denvil, S.; Dubus, L.; Parey, S.; Michelangeli, P.A.; et al. A climate projection dataset tailored for the European energy sector. Clim. Serv. 2019, 16, 100138. [Google Scholar] [CrossRef]
- Noël, T.; Loukos, H.; Defrance, D.; Vrac, M.; Levavasseur, G. A high-resolution downscaled CMIP5 projections dataset of essential surface climate variables over the globe coherent with the ERA5 reanalysis for climate change impact assessments. Data Brief 2021, 35, 106900. [Google Scholar] [CrossRef] [PubMed]
- Lanzante, J.R.; Nath, M.J.; Whitlock, C.E.; Dixon, K.W.; Adams-Smith, D. Evaluation and improvement of tail behaviour in the cumulative distribution function transform downscaling method. Int. J. Climatol. 2019, 39, 2449–2460. [Google Scholar] [CrossRef]
- Noël, T.; Loukos, H.; Defrance, D.; Vrac, M.; Levavasseur, G. Extending the global high-resolution downscaled projections dataset to include CMIP6 projections at increased resolution coherent with the ERA5-Land reanalysis. Data Brief 2022, 45, 108669. [Google Scholar] [CrossRef] [PubMed]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Change 2012, 112, 449–468. [Google Scholar] [CrossRef]
- de Ela, R.; Laprise, R.; Denis, B. Forecasting Skill Limits of Nested, Limited-Area Models: A Perfect-Model Approach. Mon. Weather Rev. 2002, 130, 2006–2023. [Google Scholar] [CrossRef]
- Vrac, M.; Marbaix, P.; Paillard, D.; Naveau, P. Non-linear statistical downscaling of present and LGM precipitation and temperatures over Europe. Clim. Past 2007, 3, 669–682. [Google Scholar] [CrossRef]
- Dixon, K.W.; Lanzante, J.R.; Nath, M.J.; Hayhoe, K.; Stoner, A.; Radhakrishnan, A.; Balaji, V.; Gaitán, C.F. Evaluating the stationarity assumption in statistically downscaled climate projections: Is past performance an indicator of future results? Clim. Change 2016, 135, 395–408. [Google Scholar] [CrossRef]
- Chen, F.; Gao, Y.; Wang, Y.; Li, X. A downscaling-merging method for high-resolution daily precipitation estimation. J. Hydrol. 2020, 581, 124414. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Change 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Jones, C.; Giorgi, F.; Asrar, G. The coordinated regional downscaling experiment (CORDEX). An international downscaling link to CMIP5. CLIVAR Exch. 2011, 56, 1797680. [Google Scholar]
- Dufresne, J.L.; Foujols, M.A.; Denvil, S.; Caubel, A.; Marti, O.; Aumont, O.; Balkanski, Y.; Bekki, S.; Bellenger, H.; Benshila, R.; et al. Climate change projections using the IPSL-CM5 Earth System Model: From CMIP3 to CMIP5. Clim. Dyn. 2013, 40, 2123–2165. [Google Scholar] [CrossRef]
- Schulzweida, U. CDO User Guide (2.3.0). Zenodo 2023. [Google Scholar] [CrossRef]
- Vrac, M.; Vaittinada Ayar, P. Influence of Bias Correcting Predictors on Statistical Downscaling Models. J. Appl. Meteorol. Climatol. 2017, 56, 5–26. [Google Scholar] [CrossRef]
- Maraun, D.; Widmann, M.; Gutiérrez, J.M.; Kotlarski, S.; Chandler, R.E.; Hertig, E.; Wibig, J.; Huth, R.; Wilcke, R.A. VALUE: A framework to validate downscaling approaches for climate change studies. Earth’s Future 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Vrac, M. Multivariate bias adjustment of high-dimensional climate simulations: The Rank Resampling for Distributions and Dependences (R2 D2) bias correction. Hydrol. Earth Syst. Sci. 2018, 22, 3175–3196. [Google Scholar] [CrossRef]
- Cannon, A.J. Multivariate Bias Correction of Climate Model Output: Matching Marginal Distributions and Intervariable Dependence Structure. J. Clim. 2016, 29, 7045–7064. [Google Scholar] [CrossRef]
- Vrac, M.; Thao, S. R2 D2 v2.0: Accounting for temporal dependences in multivariate bias correction via analogue rank resampling. Geosci. Model Dev. 2020, 13, 5367–5387. [Google Scholar] [CrossRef]
- Robin, Y.; Vrac, M. Is time a variable like the others in multivariate statistical downscaling and bias correction? Earth Syst. Dyn. 2021, 12, 1253–1273. [Google Scholar] [CrossRef]
- François, B.; Vrac, M.; Cannon, A.J.; Robin, Y.; Allard, D. Multivariate bias corrections of climate simulations: Which benefits for which losses? Earth Syst. Dyn. 2020, 11, 537–562. [Google Scholar] [CrossRef]
- Iturbide, M.; Casanueva, A.; Bedia, J.; Herrera, S.; Milovac, J.; Gutiérrez, J.M. On the need of bias adjustment for more plausible climate change projections of extreme heat. Atmos. Sci. Lett. 2022, 23, e1072. [Google Scholar] [CrossRef]
- Abdelmoaty, H.M.; Rajulapati, C.R.; Nerantzaki, S.D.; Papalexiou, S.M. Bias-corrected high-resolution temperature and precipitation projections for Canada. Sci. Data 2025, 12, 191. [Google Scholar] [CrossRef] [PubMed]




| Experiment | Double-Moving-Window (Ext.-Int. in Years) | NPAS (Temp–Prec) | TLN/NPT |
|---|---|---|---|
| QM | 20–10 | 1000–5000 | –/– |
| CDF-t | 20–10 | 1000–5000 | –/– |
| LAN | 20–10 | 1000–5000 | 10/10 |
| NPAS | 20–10 | 100–100 | 10/10 |
| MW | 30–10 | 1000–5000 | 10/10 |
| TLN | 20–10 | 1000–5000 | 5/10 |
| Metric | Unit | Variable | Type | Calculation | Definition |
|---|---|---|---|---|---|
| Bias in the Mean | [°C, mm] | T&P | MD | ; m is the mean over 30 years; For precipitation, dry days < 1 mm/d are excluded. | Difference in mean value over a 30-year period per grid cell, ref. the minus experiment. For P, dry days are excluded. |
| Bias in the Std. Dev. | [°C, mm] | T&P | MD | ; dry days < 1 mm/d excluded. | Difference in standard deviation over a 30-year period per grid cell. Dry days excluded for P. |
| Bias in Rainy Days | [days] | P | MD | ; D is the # of days with Pr > 1 mm. | Difference in the # of rainy days over a 30-year period per grid cell. |
| Root Mean Squared Error | [°C, mm] | T&P | MD | Root Mean Squared Error on daily values over a 30-year period. | |
| Bias in Q98 | [°C, mm] | T&P | Ext | ; for P, dry days excluded. | Difference in the 98th percentile per grid cell. Dry days excluded for precipitation. |
| Bias in Q02 | [°C, mm] | T&P | Ext | ; dry days excluded. | Difference in the 2nd percentile per grid cell. Dry days excluded for P. |
| Bias in Warm Days | [days] | T | Ext | where D is the # of days with T > 20 °C (spring/fall), 25 °C (summer), and 15 °C (winter). | Difference in the # of warm days per 30-year period. |
| Bias in Heavy Precip. Days | [days] | P | Ext | where D is the # of days with Pr > 20 mm. | Difference in the # of very heavy precipitation days over 30 years. |
| Pearson Corr. | [−] | T&P | TP | Pearson correlation per grid cell over 30 years between the model and reference. | |
| Bias in Lag-1 Autocorrelation | [−] | T | TP | ; with as the 1 day-lag autocorrelation. | Difference in 1-day lag autocorrelation per grid cell. |
| Bias in Persistence | [days] | P | TP | ; S = the mean wet spell duration. | Difference in mean wet spell duration over a 30-year period. |
| Bias in T-P Corr. | [−] | T&P | InterVar | per grid cell. | Difference in Pearson correlation between T and P over 30 years. |
| Explained Variance | [%] | T&P | Sp | PCA on experiment results and PCA on references. | Comparison of explained variance from PCA. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrac, M.; Loukos, H.; Noël, T.; Defrance, D. Should We Use Quantile-Mapping-Based Methods in a Climate Change Context? A “Perfect Model” Experiment. Climate 2025, 13, 137. https://doi.org/10.3390/cli13070137
Vrac M, Loukos H, Noël T, Defrance D. Should We Use Quantile-Mapping-Based Methods in a Climate Change Context? A “Perfect Model” Experiment. Climate. 2025; 13(7):137. https://doi.org/10.3390/cli13070137
Chicago/Turabian StyleVrac, Mathieu, Harilaos Loukos, Thomas Noël, and Dimitri Defrance. 2025. "Should We Use Quantile-Mapping-Based Methods in a Climate Change Context? A “Perfect Model” Experiment" Climate 13, no. 7: 137. https://doi.org/10.3390/cli13070137
APA StyleVrac, M., Loukos, H., Noël, T., & Defrance, D. (2025). Should We Use Quantile-Mapping-Based Methods in a Climate Change Context? A “Perfect Model” Experiment. Climate, 13(7), 137. https://doi.org/10.3390/cli13070137






