Recovery and Reconstructions of 18th Century Precipitation Records in Italy: Problems and Analyses
Abstract
1. Introduction
2. Materials and Methods
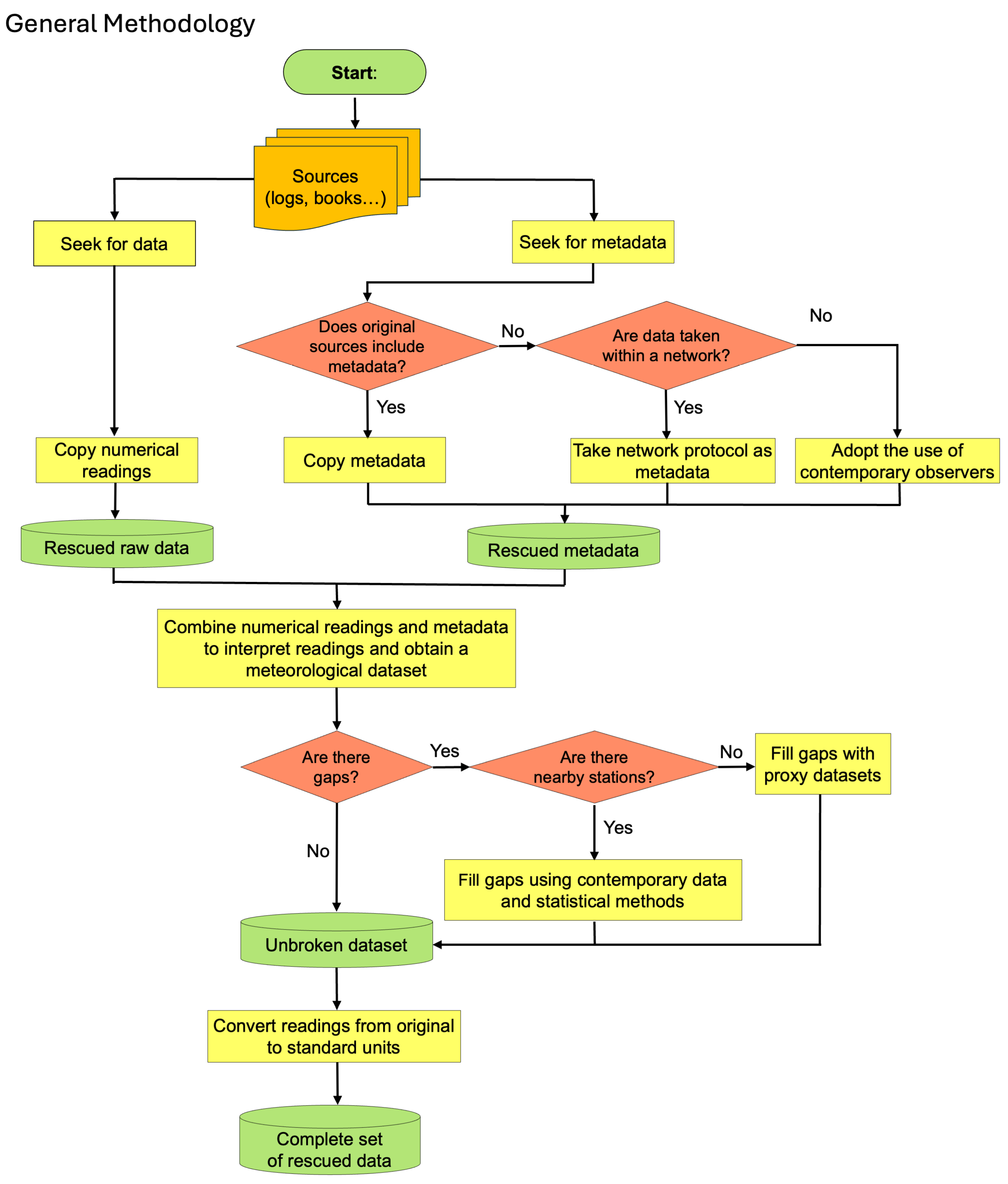
2.1. Methodology
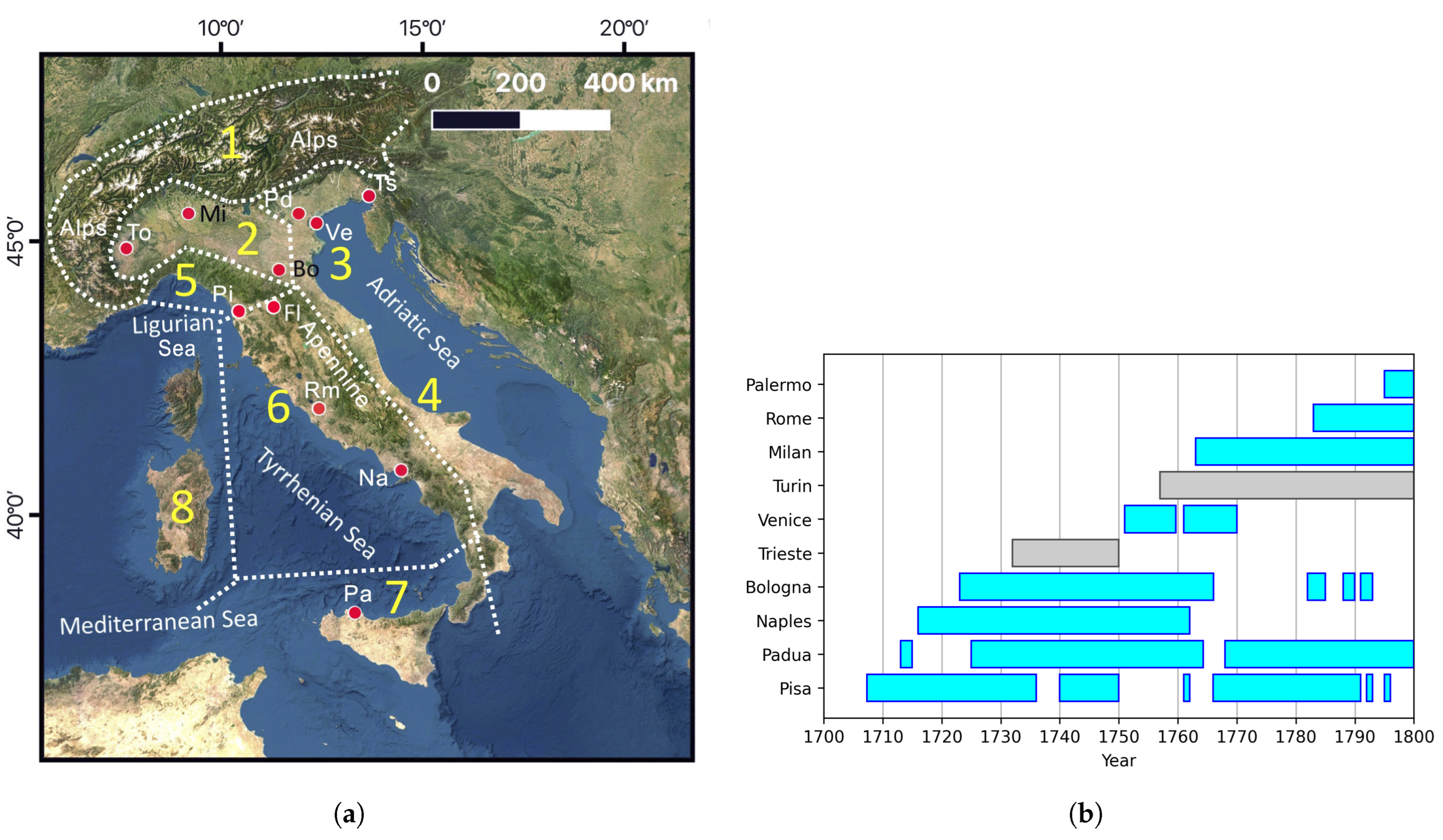
2.2. Overview of the Earliest Italian Precipitation Series
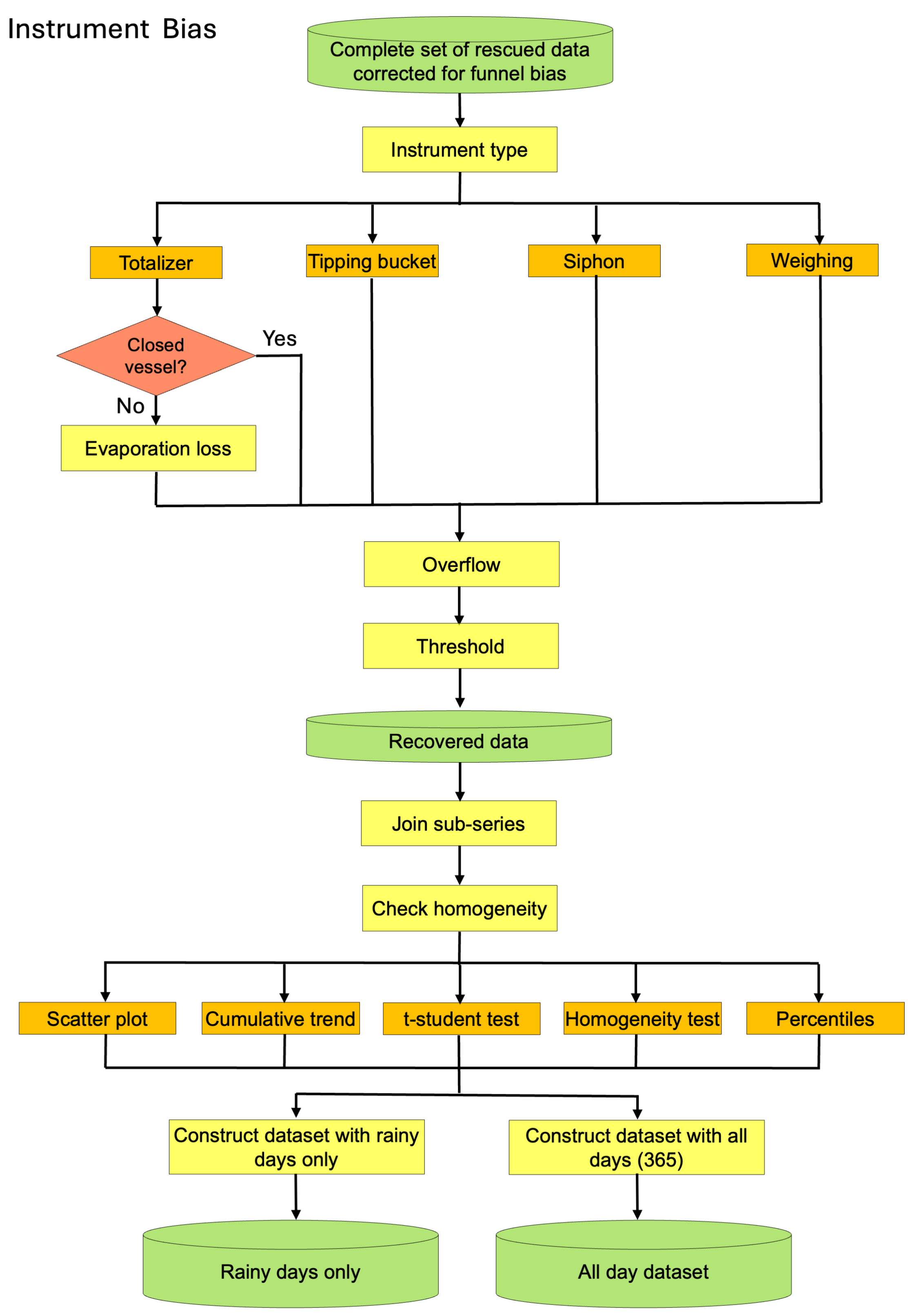
2.3. Instruments
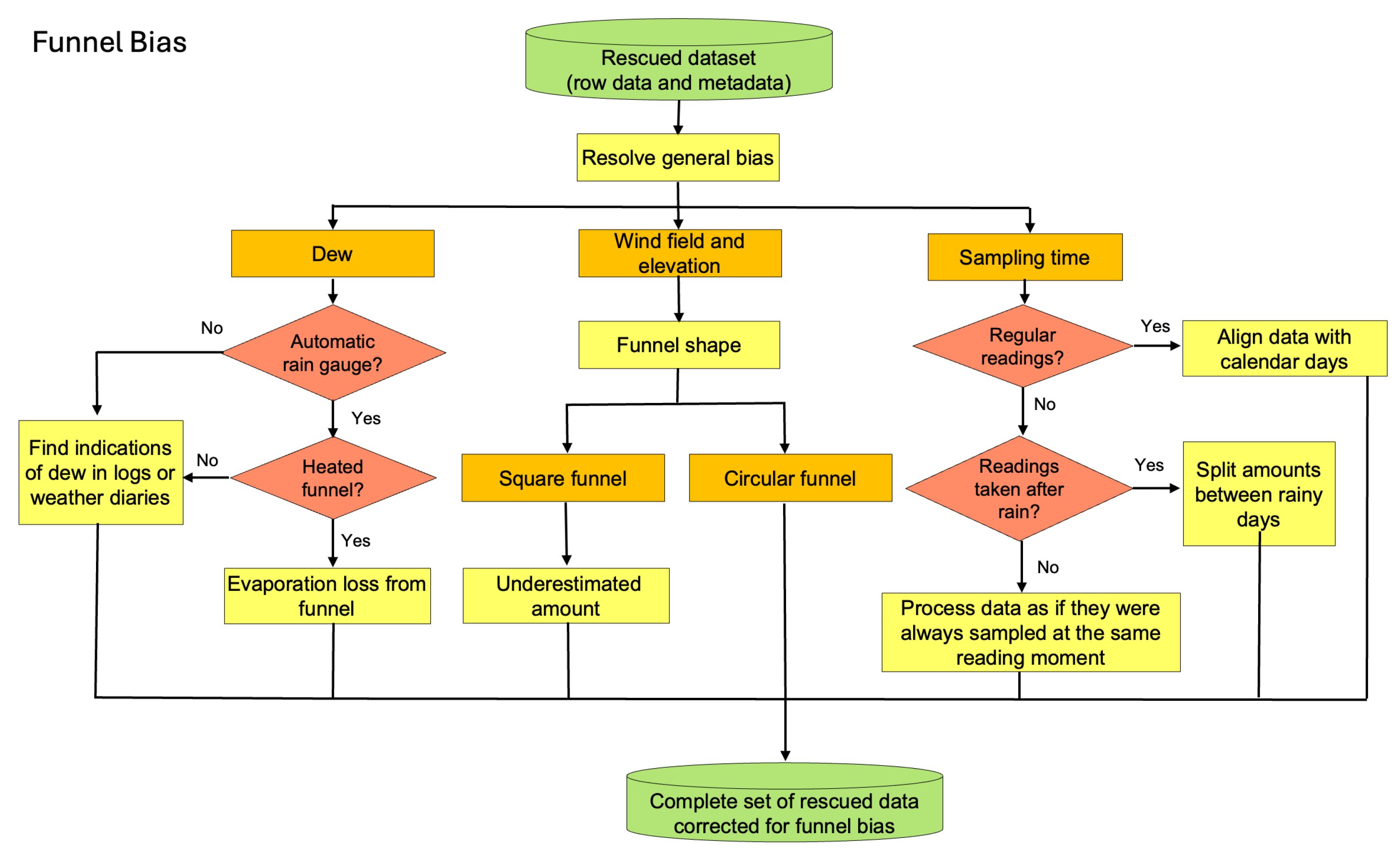
3. Main Biases Affecting Precipitation Series and Their Solution
3.1. Gaps and Missing Data
3.2. Missing Original Logs
3.3. Evaporation
3.4. Wind Field and Instrument Elevation Above the Ground
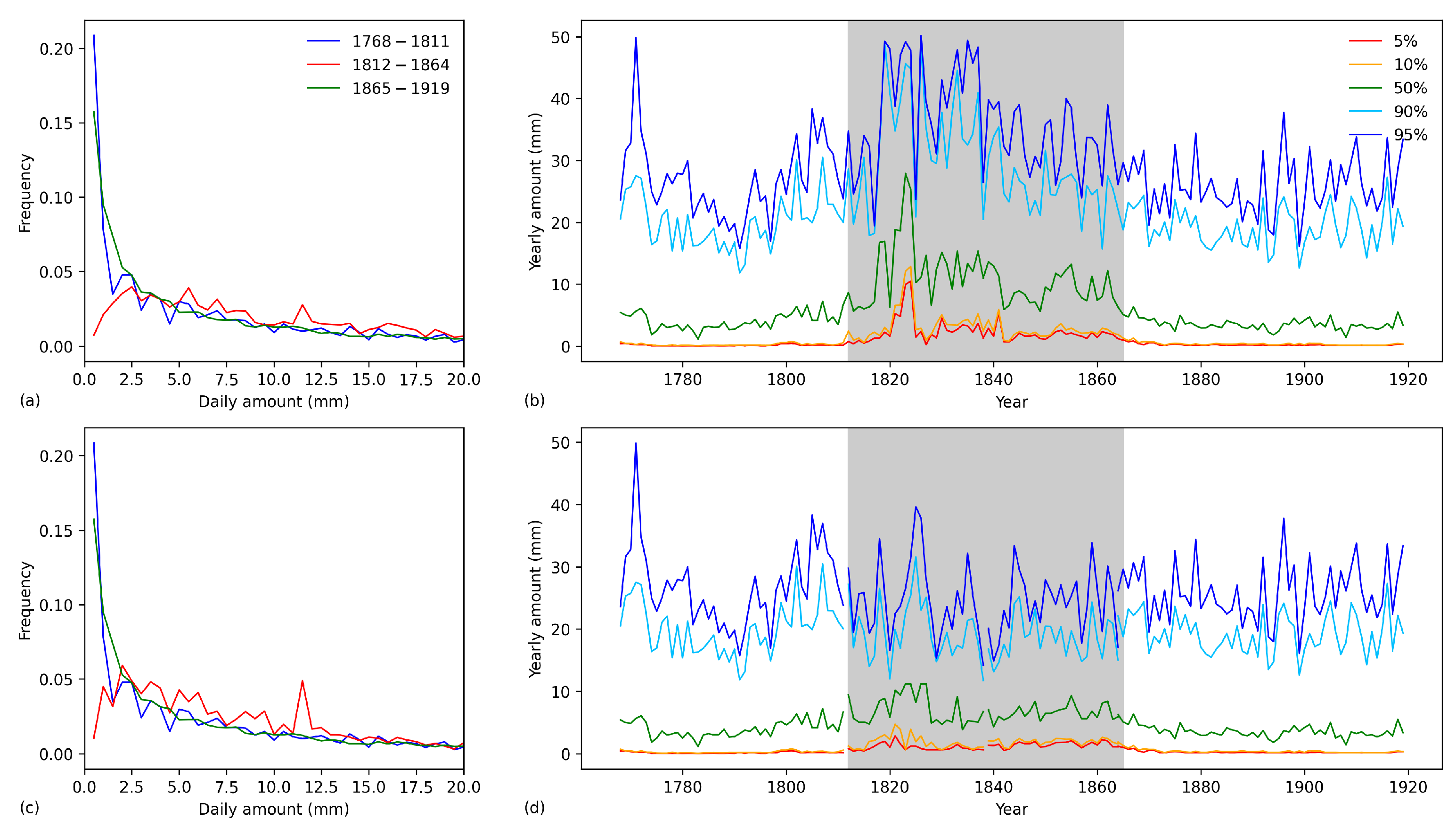
3.5. Threshold
3.6. Observational Protocol
3.7. Dew
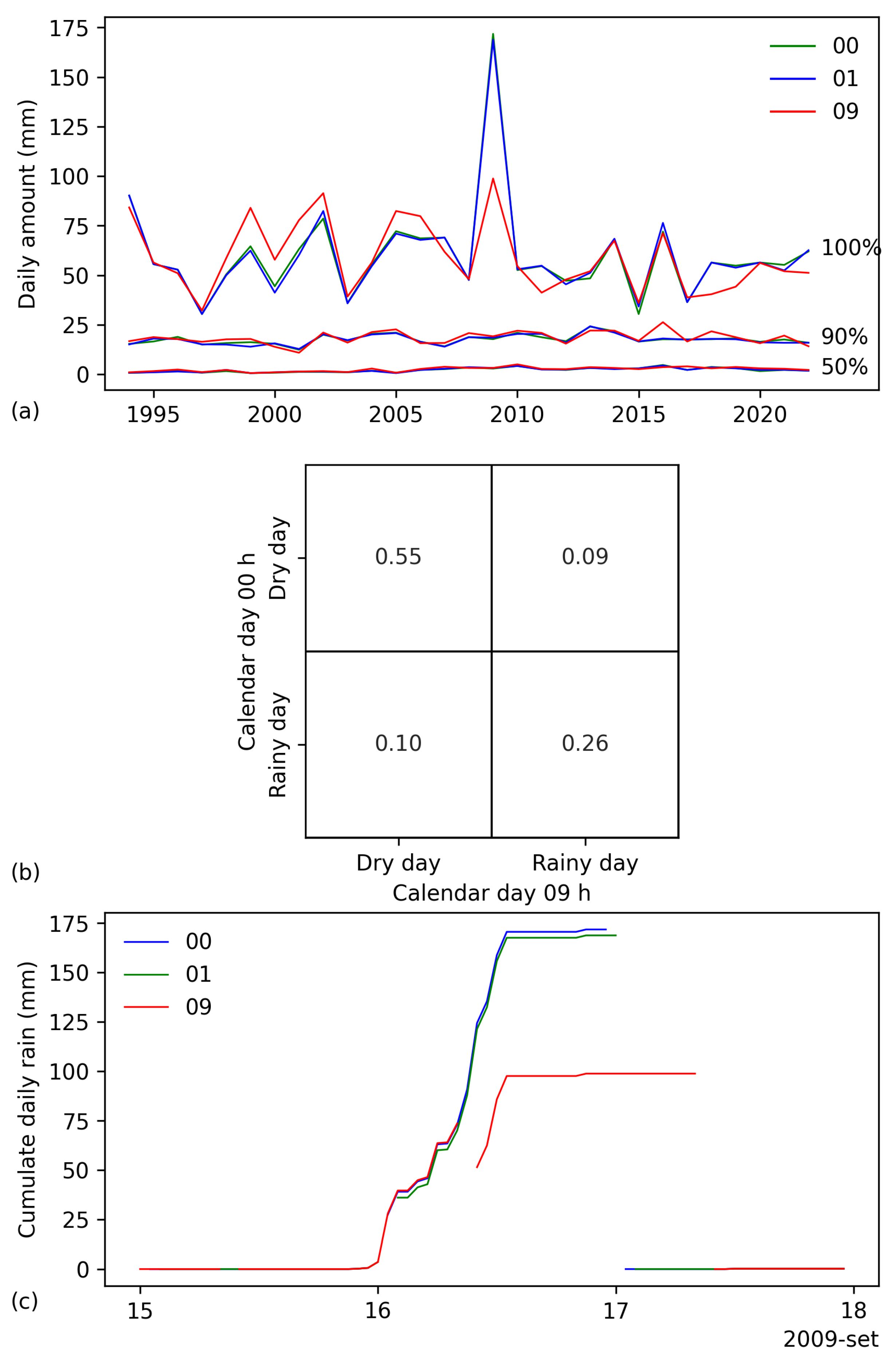
3.8. Sampling Time
3.9. Full Vessel
4. Compatibility Between Subseries
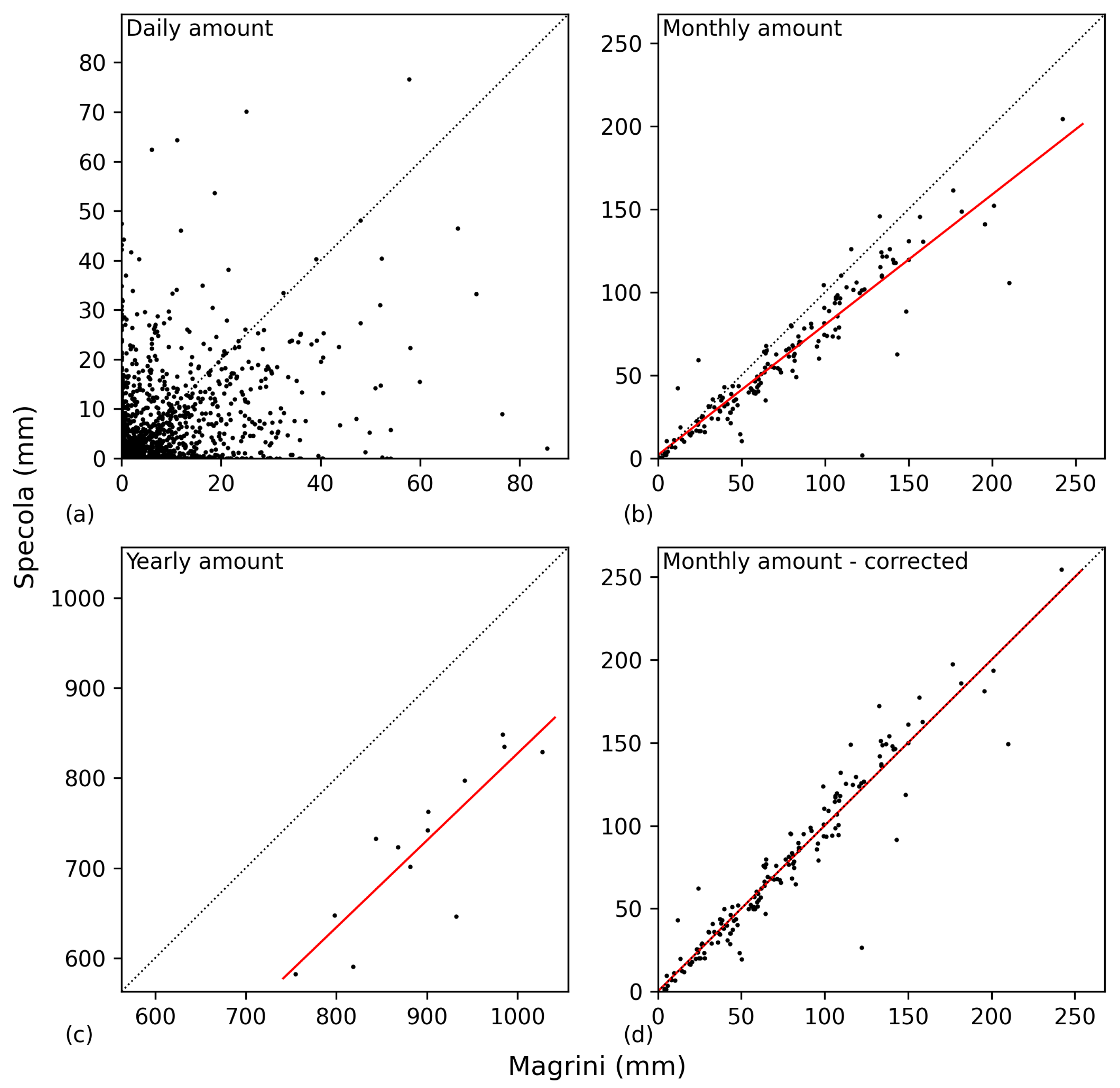
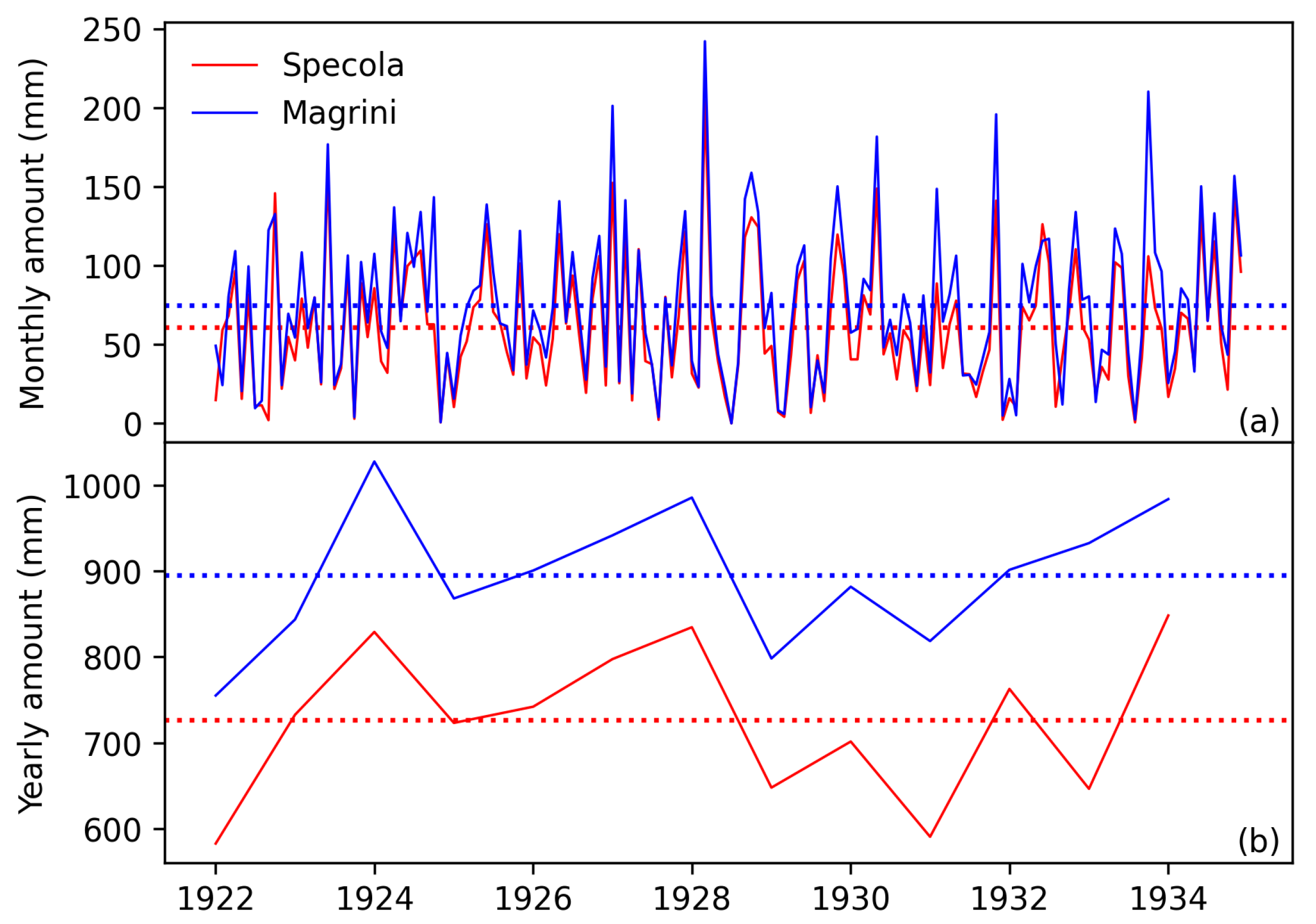
4.1. Direct Comparison of Overlapping Periods
4.2. Cumulate Method
4.3. Student’s t-Test
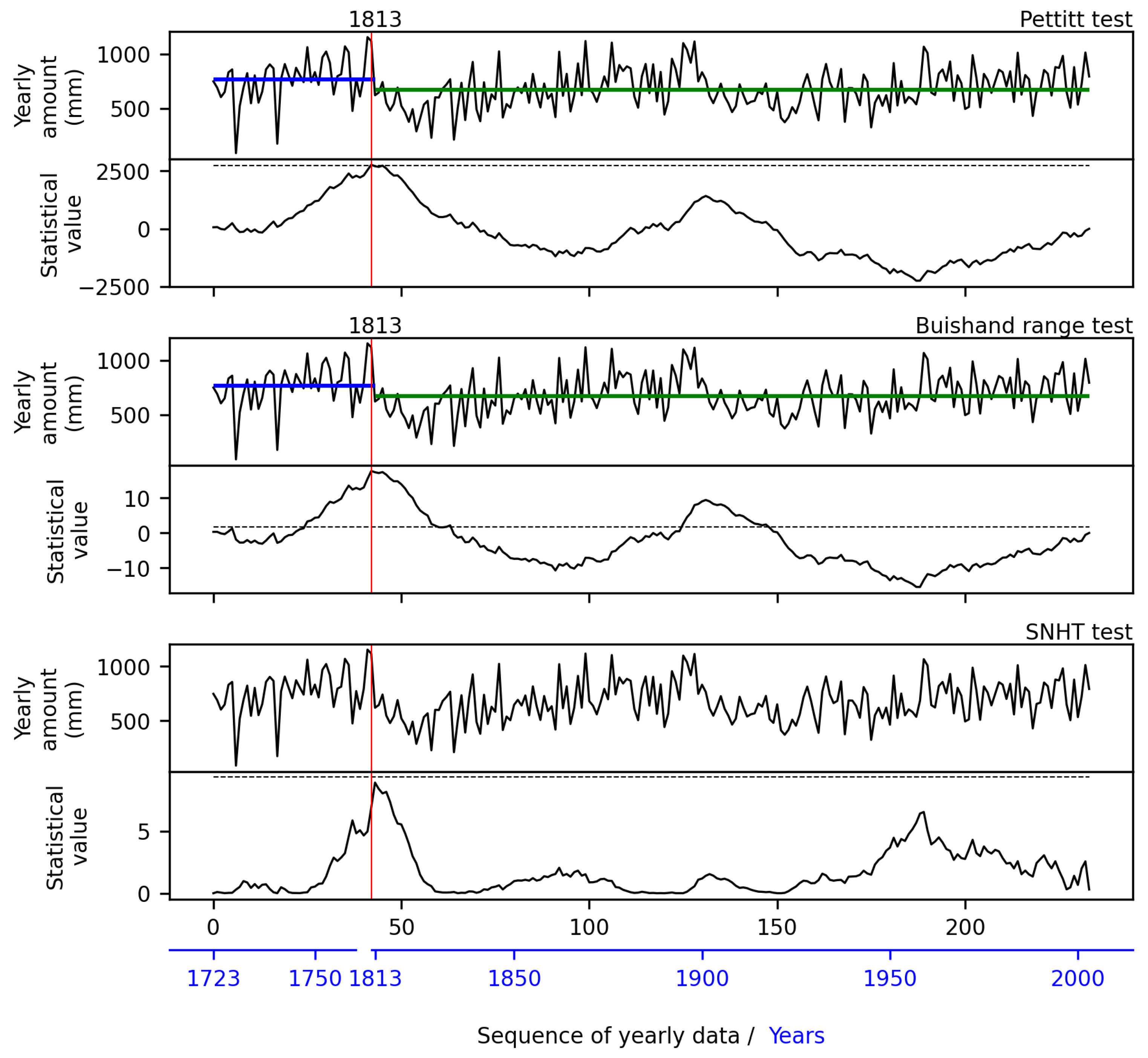
4.4. Homogeneity Tests
- Useful: one or zero tests reject the null hypothesis;
- Doubtful: two tests reject the null hypothesis;
- Suspect: three or four tests reject the null hypothesis.
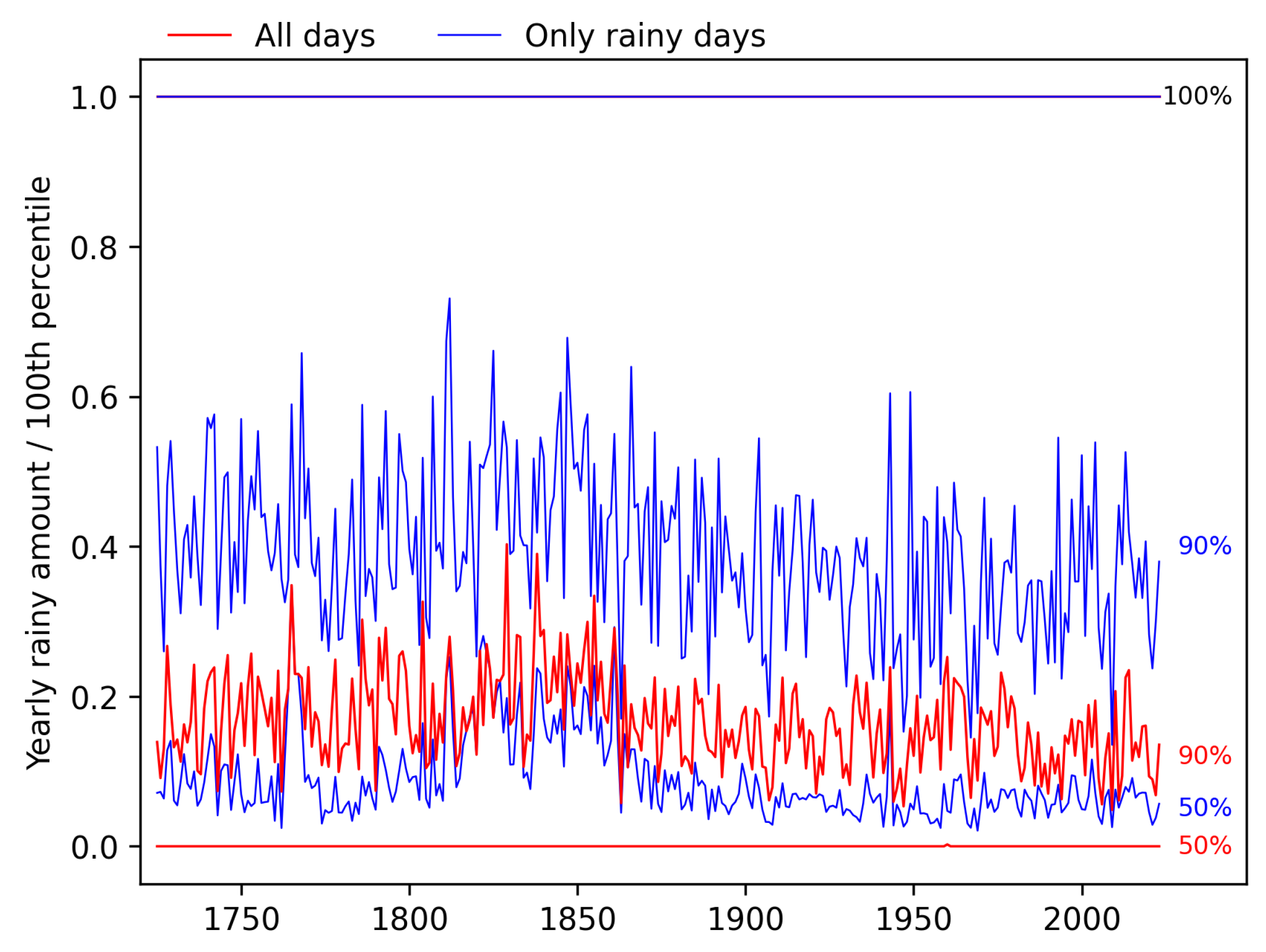
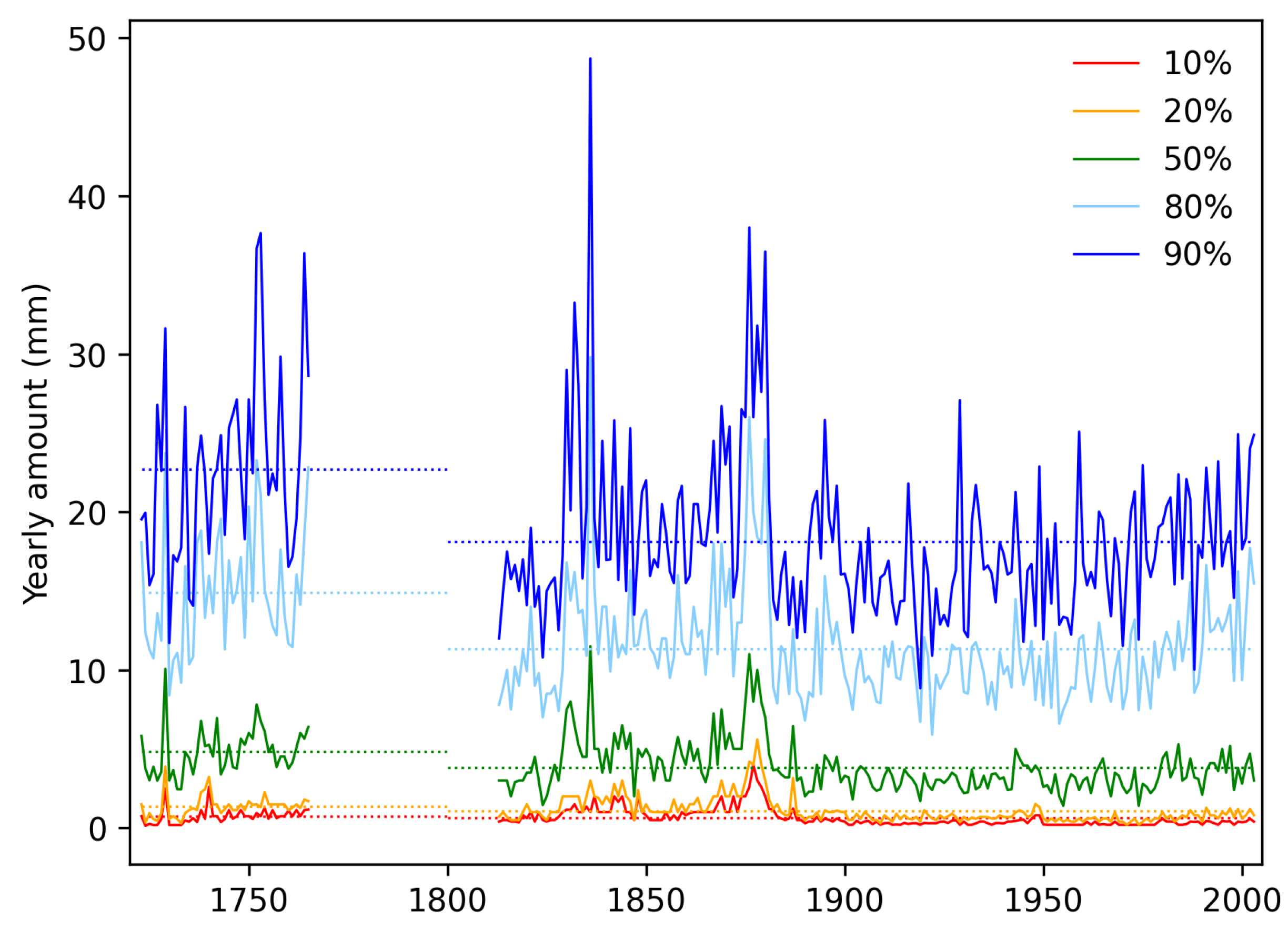
4.5. Percentiles
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | “Aeronautica Militare” (Italian Air Force) |
| ARPA | “Agenzia regionale per la protezione ambientale” (Regional Environmental Protection Agency) |
| BU | Buishand U test |
| CIMO | Commission for Instruments and Methods of Observation |
| IMC | International Meteorological Committee |
| IMO | International Meteorological Organization |
| SNHT | Standard Normal Homogeneity Test |
| VN | von Neumann ratio |
| WMO | World Meteorological Organization |
Appendix A
References
- Marchi, M.; Castellanos-Acuña, D.; Hamann, A.; Wang, T.; Ray, D.; Menzel, A. ClimateEU, scale-free climate normals, historical time series, and future projections for Europe. Sci. Data 2020, 7, 428. [Google Scholar] [CrossRef]
- Lundstad, E.; Brugnara, Y.; Pappert, D.; Kopp, J.; Samakinwa, E.; Hürzeler, A.; Andersson, A.; Chimani, B.; Cornes, R.; Demarée, G.; et al. The global historical climate database HCLIM. Sci. Data 2023, 10, 44. [Google Scholar] [CrossRef] [PubMed]
- Flaounas, E.; Davolio, S.; Raveh-Rubin, S.; Pantillon, F.; Miglietta, M.M.; Gaertner, M.A.; Hatzaki, M.; Homar, V.; Khodayar, S.; Korres, G.; et al. Mediterranean cyclones: Current knowledge and open questions on dynamics, prediction, climatology and impacts. Weather Clim. Dyn. 2022, 3, 173–208. [Google Scholar] [CrossRef]
- Authority of the Meteorological Committee. Protocols and and Appendices. In Report of the Proceedings of the Meteorological Congress at Leipzig in 1783; Her Majesty’s Stationary Office: London, UK, 1873. [Google Scholar]
- Camuffo, D.; della Valle, A.; Becherini, F. Instrumental and Observational Problems of the Earliest Temperature Records in Italy: A Methodology for Data Recovery and Correction. Climate 2023, 11, 178. [Google Scholar] [CrossRef]
- Sevruk, B.; Hamon, W. Operational Hydrology. Report No. 21. Methods of Correction for Systematic Error in Point Precipitation Measurement for Operational Use; Vol. WMO No 589; World Meteorological Organization: Geneva, Switzerland, 1982; Available online: https://library.wmo.int/idurl/4/33639 (accessed on 15 April 2025).
- World Meteorological Organization. Instruments and Observing Methods Report No. 39; Vol. WMO/TD-No. 313; World Meteorological Organization: Geneva, Switzerland, 1989; Available online: https://library.wmo.int/idurl/4/41708 (accessed on 15 April 2025).
- World Meteorological Organization. Guide to Instruments and Methods of Observation; Vol. WMO-No. 8, I; World Meteorological Organization: Geneva, Switzerland, 2023; Available online: https://library.wmo.int/idurl/4/68695 (accessed on 15 April 2025).
- Toaldo, G. Della Vera Influenza degli Astri, delle Stagioni e delle Mutazioni di Tempo, Saggio Meteorologico; Manfré: Padua, Italy, 1770. [Google Scholar]
- Heberden, W. Of the quantities of rain which appear to fall at different heights over the same spot of ground. Philos. Trans. 1769, 59, 359–362. [Google Scholar]
- Crestani, G. Studio Storico Critico. In Le Precipitazioni Atmosferiche a Padova; Ministero dei Lavori Pubblici, Ufficio Idrografico: Rome, Italy, 1935. [Google Scholar]
- World Meteorological Organization. Manual on the WMO Integrated Global Observing System. Annex VIII to the WMO Technical Regulations; Vol. WMO-No. 1160; World Meteorological Organization: Geneva, Switzerland, 2024; Available online: https://library.wmo.int/idurl/4/55063 (accessed on 6 June 2025).
- World Meteorological Organization. Guide to the Global Observing System; Vol. WMO-No. 488; World Meteorological Organization: Geneva, Switzerland, 2017; Available online: https://library.wmo.int/idurl/4/35699 (accessed on 6 June 2025).
- Cantù, V. The Climate of Italy. In World Survey of Climatology—Climates of Central and Southern Europe; Landsberg, H., Ed.; Elsevier: Amsterdam, The Netherlands, 1977; Volume 7, pp. 127–183. [Google Scholar]
- Tilli, G.L. Acqua di Pioggia passata per la Pevera del Giardino dei Semplici in quest’Anno 1775. Mag. Toscano 1776, 26, 138–139. [Google Scholar]
- Vallisneri, A. Lezione Accademica Intorno all’Origine delle Fontane, 2nd ed.; Pietro Poletti: Venice, Italy, 1726; pp. 1–365. [Google Scholar]
- Rapetti, F.; Ruschi, M. Osservazioni botanico-meteorologiche condotte da Giovanni Lorenzo Tilli presso il Giardino dei Semplici di Pisa (1775–1780). Atti Soc. Toscana Sci. Nat. Mem. 2009, 114, 45–59. Available online: http://www.stsn.it/images/pdf/serA114/Rapetti%20Ruschi%202009.pdf (accessed on 15 April 2025).
- Camuffo, D. Analysis of the series of precipitation at Padova, Italy. Clim. Change 1984, 6, 57–77. [Google Scholar] [CrossRef]
- Camuffo, D.; Becherini, F.; della Valle, A.; Zanini, V. Three centuries of daily precipitation in Padua, Italy, 1713–2018: History, relocations, gaps, homogeneity and raw data. Clim. Change 2020, 162, 923–942. [Google Scholar] [CrossRef]
- Camuffo, D.; Becherini, F.; della Valle, A. The Beccari series of precipitation in Bologna, Italy, from 1723 to 1765. Clim. Change 2019, 155, 359–376. [Google Scholar] [CrossRef]
- Camuffo, D.; Becherini, F.; della Valle, A.; Zanini, V. A comparison between different methods to fill gaps in early precipitation series. Environ. Earth Sci. 2022, 81, 345. [Google Scholar] [CrossRef]
- Jurin, J. Invitatio ad observationes Meteorologicas communi consilio instituendas a Jacobo Jurin M. D. Soc. Reg Secr et Colleg Med Lond Socio. Philos. Trans. 1723, 379, 422–427. [Google Scholar]
- Hemmer, J. Descriptio instrumentorum meteorologicorum, tam eorum, quam Societas distribuit, quam quibus praeter haec Manheimii utitur. Ephemer. Soc. Meteorol. Palatinae 1783, 1, 57–90. [Google Scholar]
- Cotte, L. Mémoires sur la Météorologie pour Servir de Suite et de Supplément au Traité de Météorologie Publié en 1774; Imprimerie Royale: Paris, France, 1774. [Google Scholar]
- Leutmann, J. Instrumenta Meteorognosiae Inservientia; Zimmermann: Wittemberg, Germany, 1725. [Google Scholar]
- Poleni, G. Johannis Poleni Miscellanea hoc est: I Dissertatio de Barometris et Termometris; Aloysium Pavinum: Venice, Italy, 1709. [Google Scholar]
- Burnings, C. Bericht wegens een’ nieuwen hyethometer. In Vederhandelingen uitgegeeven door de Hollandsche Maatschappye der Weetenschappen; Walré: Haarlem, The Netherlands, 1789; pp. 317–323. [Google Scholar]
- Camuffo, D.; Becherini, F.; della Valle, A. How the rain-gauge threshold affects the precipitation frequency and amount. Clim. Change 2022, 170, 7. [Google Scholar] [CrossRef]
- Buchardat, A. Fisica Elementare; Filiatre Sebezio: Naples, Italy, 1814. [Google Scholar]
- Marvin, C. Measurement of Precipitation; US Department of Agricolture, Weather Bureau. Government Printing Office: Washington, DC, USA, 1913. [Google Scholar]
- Eredia, F. Gli Strumenti di Meteorologia ed Aerologia; Bardi: Rome, Italy, 1936. [Google Scholar]
- Caldera, H.P.G.M.; Piyathisse, V.R.P.C.; Nandalal, K.D.W. A Comparison of Methods of Estimating Missing Daily Rainfall Data. Eng. J. Inst. Eng. Sri Lanka 2016, 49, 1–8. [Google Scholar] [CrossRef]
- Longman, R.J.; Newman, A.J.; Giambelluca, T.W.; Lucas, M. Characterizing the Uncertainty and Assessing the Value of Gap-Filled Daily Rainfall Data in Hawaii. J. Appl. Meteorol. Climatol. 2020, 59, 1261–1276. [Google Scholar] [CrossRef]
- Aieb, A.; Madani, K.; Scarpa, M.; Bonaccorso, B.; Lefsih, K. A new approach for processing climate missing databases applied to daily rainfall data in Soummam watershed, Algeria. Heliyon 2019, 5, e01247. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Gualda, J.E.; Garcìa-Marìn, A.P. Assessing Machine Learning Models for Gap Filling Daily Rainfall Series in a Semiarid Region of Spain. Atmosphere 2021, 12, 1158. [Google Scholar] [CrossRef]
- Pfister, L.; Brönnimann, S.; Schwander, M.; Isotta, F.A.; Horton, P.; Rohr, C. Statistical reconstruction of daily precipitation and temperature fields in Switzerland back to 1864. Clim. Past 2020, 16, 663–678. [Google Scholar] [CrossRef]
- Crestani, G. L’inizio delle osservazioni meteorologiche a Padova. Il contributo di Giovanni Poleni alla meteorologia. In Memorie della R. Accademia di Scienze Lettere ed Arti; Rondi, G. B.: Padua, Italy, 1926; Volume XLII, pp. 19–83. [Google Scholar]
- Crestani, G. Le osservazioni meteorologiche—I fenomeni meteorologici. In La laguna di Venezia; Magrini, G., Ed.; Ferrari: Venice, Italy, 1933; Volume I, Part II, Tomo III, pp. 1–203. [Google Scholar]
- Rodrigo, F.S.; Esteban-Parra, M.J.; Castro-Diez, Y. An attempt to reconstruct the rainfall regime of andalusia (southern Spain) from 1601 A.D. to 1650 A.D. using historical documents. Clim. Change 1994, 27, 397–418. [Google Scholar] [CrossRef]
- Dominguez-Castro, F.; Garcìa-Herrera, R.; Vaquero, J.M. An early weather diary from Iberia (Lisbon, 1631–1632). Weather 2015, 70, 20–24. [Google Scholar] [CrossRef]
- Fernández-Fernández, M.I.; Gallego, M.C.; Domínguez-Castro, F.; Trigo, R.M.; Vaquero, J.M. The climate in Zafra from 1750 to 1840: Precipitation. Clim. Change 2015, 129, 267–280. [Google Scholar] [CrossRef]
- Santos, J.A.; Carneiro, M.F.; Alcoforado, M.J.; Leal, S.; Luz, A.L.; Camuffo, D.; Zorita, E. Calibration and multi-source consistency analysis of reconstructed precipitation series in Portugal since the early 17th century. Holocene 2015, 25, 663–676. [Google Scholar] [CrossRef]
- Alcoforado, M.J.; de Fátima Nunes, M.; Garcia, J.C.; Taborda, J.P. Temperature and precipitation reconstruction in southern Portugal during the late Maunder Minimum (AD 1675–1715). Holocene 2000, 10, 333–340. [Google Scholar] [CrossRef]
- Gimmi, U.; Luterbacher, J.; Pfister, C.; Wanner, H. A method to reconstruct long precipitation series using systematic descriptive observations in weather diaries: The example of the precipitation series for Bern, Switzerland (1760–2003). Theor. Appl. Climatol. 2007, 87, 185–199. [Google Scholar] [CrossRef]
- Ge, Q.S.; Zheng, J.Y.; Hao, Z.X.; Zhang, P.Y.; Wang, W.C. Reconstruction of historical climate in China: High-Resolution Precipitation Data from Qing Dynasty Archives. Bull. Am. Meteorol. Soc. 2005, 86, 671–680. [Google Scholar] [CrossRef]
- Brázdil, R.; Chromá, K.; Valášek, H.; Dolák, L. Hydrometeorological extremes derived from taxation records for south-eastern Moravia, Czech Republic, 1751–1900 AD. Clim. Past 2012, 8, 467–481. [Google Scholar] [CrossRef]
- Harvey-Fishenden, A.; Macdonald, N. Evaluating the utility of qualitative personal diaries in precipitation reconstruction in the eighteenth and nineteenth centuries. Clim. Past 2021, 17, 133–149. [Google Scholar] [CrossRef]
- Diodato, N. Climatic fluctuations in southern Italy since the 17th century: Reconstruction with precipitation records at Benevento. Clim. Change 2007, 80, 411–431. [Google Scholar] [CrossRef]
- Raicich, F. Some features of Trieste climate from an eighteenth century diary (1732–1749). Clim. Change 2008, 86, 211–226. [Google Scholar] [CrossRef]
- Derham, W. Tables of the barometrical altitudes at Zuerich in Switzerland in the year 1708, observed by John James Scheuchzer, F.R.S. and at Upminster in England, observed at the same time by Mr W. Derham, F.R.S., and also the Rain at Pisa in Italy in 1707 and 1708 observed there by Dr Michael Angelo Tilli, F.R.S., and at Zurich in 1708 and at Upminster in all that time. Philos. Trans. 1710, 26, 342–366. [Google Scholar]
- Derham, W. Physico-Theology: Or, a Demonstration of the Being and Attributes of God, from His Works of Creation; Innys: London, UK, 1713. [Google Scholar]
- Winkler, P. The early meteorological network of the Societas Meteorologica Palatina (1781–1792): Foundation, organization, and reception. Hist. Geo- Space Sci. 2023, 14, 93–120. [Google Scholar] [CrossRef]
- Pietropoli, G. Relazione meteorologica dell’anno 1838. In Giornale Astro-Meteorologico per l’anno 1840; Tipografia del Seminario: Padua, Italy, 1839; pp. 41–54. [Google Scholar]
- della Valle, A.; Camuffo, D.; Becherini, F.; Zanini, V. Recovering, correcting, and reconstructing precipitation data affected by gaps and irregular readings: The Padua series from 1812 to 1864. Clim. Change 2023, 176, 9. [Google Scholar] [CrossRef]
- Goodison, B.; Ferguson, H.; McKay, G. Comparison of point snowfall measurement techniques. In Handbook of Snow; Gray, D., Male, M., Eds.; Pergamon: Tarrytown, NY, USA, 1981; pp. 200–210. [Google Scholar]
- Sevruk, B.; Hamon, W. Instrument and Observing Methods. Report No. 17. International Comparison of National Precipitation Gauges with a Reference pit Gauge; Vol. WMO/TD No. 38; World Meteorological Organization: Geneva, Switzerland, 1984; Available online: https://library.wmo.int/idurl/4/41740 (accessed on 15 April 2025).
- Lanza, L.; Leroy, M.; Alexadropoulos, C.; Stagi, L.; Wauben, W. Instruments and Observing Methods. Report No. 84. The WMO Laboratory Intercomparison of Rainfall Intensity Gauges: Final Report; Vol. WMO/TD No. 1304; World Meteorological Organization: Geneva, Switzerland, 2006; Available online: https://library.wmo.int/idurl/4/35348 (accessed on 15 April 2025).
- Mariotte, M. Traité du Mouvement des Eaux et des Autres Corps Fluides; Chez Estienne Michallet: Paris, France, 1686. [Google Scholar]
- Sevruk, B. Evaporation losses from containers of Hellmann precipitation gauges. Hydrol. Sci. Bull. 1974, 19, 231–236. [Google Scholar] [CrossRef]
- Leeper, R.D.; Kochendorfer, J. Evaporation from weighing precipitation gauges: Impacts on automated gauge measurements and quality assurance methods. Atmos. Meas. Tech. 2015, 8, 2291–2300. [Google Scholar] [CrossRef]
- Camuffo, D. Microclimate for Cultural Heritage, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Hutchinson, G. A Treatise on the Causes and Principles of Meteorological Phenomena; Fullarton and Co: Glasgow, UK, 1835. [Google Scholar]
- Cauteruccio, A.; Colli, M.; Freda, A.; Stagnaro, M.; Lanza, L.G. The role of free-stream turbulence in attenuating the wind updraft above the collector of precipitation gauges. J. Atmos. Ocean. Technol. 2020, 37, 103–113. [Google Scholar] [CrossRef]
- Subbaramayya, I.; Rao, N. The Frequency Distribution of Rainfall of Different Intensities. J. Meteorol. Soc. Jpn. Ser. II 1964, 42, 277–284. [Google Scholar] [CrossRef]
- Ho, M.K.; Yusof, F. Determination of Best-fit Distribution and Rainfall Events in Damansara and Kelantan, Malaysia. MATEMATIKA Malays. J. Ind. Appl. Math. 2013, 29, 43–52. [Google Scholar]
- Drufuca, G.; Zawadzki, I.I. Statistics of Raingage Data. J. Appl. Meteorol. (1962–1982) 1975, 14, 1419–1429. [Google Scholar] [CrossRef]
- Wilks, D. Statistical Methods in the Atmospheric Sciences, 3rd ed.; International Geophysics, Academic Press: Oxford, UK, 2011. [Google Scholar]
- Zhan, C.; Cao, W.; Fan, J.; Tse, C. Impulse Weibull distribution for daily precipitation and climate change in China during 1961–2011. Phys. A Stat. Mech. Its Appl. 2018, 512, 57–67. [Google Scholar] [CrossRef]
- Camuffo, D.; Becherini, F.; della Valle, A. Relationship between selected percentiles and return periods of extreme events. Acta Geophys. 2020, 68, 1201–1211. [Google Scholar] [CrossRef]
- Mach, K.; Meyer, L.; Pachauri, R.; Planton, S.; von Stechow, C. Annex II: Glossary. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2014: Synthesis Report; IPCC: Geneva, Switzerland, 2014; Available online: https://www.ipcc.ch/report/ar5/syr/ (accessed on 15 April 2025).
- World Meteorological Organization. WMO Guidelines on the Calculation of Climate Normals; Vol. WMO-No. 1203; World Meteorological Organization: Geneva, Switzerland, 2017; Available online: https://library.wmo.int/idurl/4/55797 (accessed on 15 April 2025).
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Holder, C.; Boyles, R.; Syed, A.; Niyogi, D.; Raman, S. Comparison of Collocated Automated (NCECONet) and Manual (COOP) Climate Observations in North Carolina. J. Atmos. Ocean. Technol. 2006, 23, 671–682. [Google Scholar] [CrossRef]
- Oyler, J.W.; Nicholas, R.E. Time of observation adjustments to daily station precipitation may introduce undesired statistical issues. Int. J. Climatol. 2018, 38, e364–e377. [Google Scholar] [CrossRef]
- Maurer, E.P.; Wood, A.W.; Adam, J.C.; Lettenmaier, D.P.; Nijssen, B. A Long-Term Hydrologically Based Dataset of Land Surface Fluxes and States for the Conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar] [CrossRef]
- Kim, J.W.; Pachepsky, Y.A. Reconstructing missing daily precipitation data using regression trees and artificial neural networks for SWAT streamflow simulation. J. Hydrol. 2010, 394, 305–314. [Google Scholar] [CrossRef]
- Becherini, F.; Stefanini, C.; della Valle, A.; Rech, F.; Zecchini, F.; Camuffo, D. Adjustment Methods Applied to Precipitation Series with Different Starting Times of the Observation Day. Atmosphere 2024, 15, 412. [Google Scholar] [CrossRef]
- Whitley, E.; Ball, J. Statistics review 5: Comparison of means. Crit. Care 2002, 6, 1–5. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. J. R. Meteorol. Soc. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Von Neumann, J. Distribution of the ratio of the mean square successive difference to the variance. Ann. Math. Stat. 1941, 12, 367–395. [Google Scholar] [CrossRef]
- Wijngaard, J.; Klein Tank, A.; Können, G. Homogeneity of 20th century European daily temperature and precipitation series. Int. J. Climatol. J. R. Meteorol. Soc. 2003, 23, 679–692. [Google Scholar] [CrossRef]
- Kocsis, T.; Kovács-Székely, I.; Anda, A. Homogeneity tests and non-parametric analyses of tendencies in precipitation time series in Keszthely, Western Hungary. Theor. Appl. Climatol. 2020, 139, 849–859. [Google Scholar] [CrossRef]
- Kang, H.M.; Yusof, F. Homogeneity tests on daily rainfall series. Int. J. Contemp. Math. Sci. 2012, 7, 9–22. [Google Scholar]
- Verstraeten, G.; Poesen, J.; Demarée, G.; Salles, C. Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Moonen, C.; Masoni, A.; Ercoli, L.; Mariotti, M.; Bonari, E. Long-term changes in rainfall and temperature in Pisa, Italy. Agric. Mediterr. 2001, 131, 66–76. [Google Scholar]
- Rapetti, F. Dall’archivio meteorologico del Seminario Arcivescovile Santa Caterina d’Alessandria di Pisa un contributo alla conoscenza della storia pluviometrica della cittá dall’inizio del settecento ad oggi. Atti Soc. Toscana Sci. Nat. Mem. 2015, 122, 63–73. [Google Scholar] [CrossRef]
- Camuffo, D.; Becherini, F.; della Valle, A. Recovery of the Long Series of Precipitation in Pisa, Italy: Trend, Anomaly and Extreme Events. Climate 2025, 13, 73. [Google Scholar] [CrossRef]
- Mecatti, G. Continuazione delle Osservazioni Sopra Diverse Eruzioni del Vesuvio; Giovanni di Simone: Naples, Italy, 1761. [Google Scholar]
- Camuffo, D.; Diodato, N.; Bellocchi, G.; Bertolin, C. Mixed nonlinear regression for modelling historical temperatures in Central—Southern Italy. Theor. Appl. Climatol. 2013, 113, 187–196. [Google Scholar] [CrossRef]
- Derham, W. An Abstract of the Meteorological Diaries, communicated to the Royal Society, with Remarks upon them. Philos. Trans. 1734, 38, 405–412. [Google Scholar]
- Serao, F. Storia dell’Incendio del Vesuvio Accaduto nel Mese di Maggio 1737; De Bonis: Naples, Italy, 1738. [Google Scholar]
- Marani, M.; Zanetti, S. Long-term oscillations in rainfall extremes in a 268 year daily time series. Water Resour. Res. 2015, 51, 639–647. [Google Scholar] [CrossRef]
- Brunetti, M.; Buffoni, L.; Lo Vecchio, G.; Maugeri, M.; Nanni, T. Tre Secoli di Meteorologia a Bologna; CUSL: Milan, Italy, 2001. [Google Scholar]
- Giuliani, C. Memorie Sopra la Fisica e Istoria Naturale di Diversi Valentuomini; Salani e Giuntini: Lucca, Italy, 1744; Volume 2. [Google Scholar]
- Chlistovsky, F.; Buffoni, L.; Maugeri, M. La Precipitazione a Milano-Brera; CUSL: Milan, Italy, 1999. [Google Scholar]
- Carlini, C. Riassunti Mensili ed Annuali delle Osservazioni Meteorologiche di Milano. Dal 1763 al 1840 Compilati nell’imp. Regia Specola di Brera; Guglielmini e Readelli: Milan, Italy, 1841. [Google Scholar]
- Pappert, D.; Brugnara, Y.; Jourdain, S.; Pospieszyńska, A.; Przybylak, R.; Rohr, C.; Brönnimann, S. Unlocking weather observations from the Societas Meteorologica Palatina (1781–1792). Clim. Past 2021, 17, 2361–2379. [Google Scholar] [CrossRef]
- Chinnici, I.; Foderà; Serio, G.; Granata, L. Duecento anni di Meteorologia all’Osservatorio Astronomico di Palermo; Osservatorio Astronomico G.S.: Palermo, Italy, 2000. [Google Scholar]
- Domenico, R. Giornale Astronomico e Meteorologico del Reale Osservatorio di Palermo; R. Pagano e C. Piola: Palermo, Italy, 1855; Volume 1. [Google Scholar]
- Vassalli-Eandi, A.M. La Meteorologia Torinese, ossia risultamenti delle Osservazioni fatti dal 1757 al 1817. In Memorie della Società Italiana delle Scienze; Accademia nazionale dei Lincei: Rome, Italy, 1815; Volume 17, pp. 1–26. [Google Scholar]
- Rossetti, D. La Figura Della Neve; Vedova Gianelli e Domenico Paulino: Turin, Italy, 1681. [Google Scholar]
- Leporati, E.; Mercalli, L. Snowfall series of Turin, 1784–1992: Climatological analysis and action on structures. Ann. Glaciol. 1994, 19, 77–84. [Google Scholar] [CrossRef]
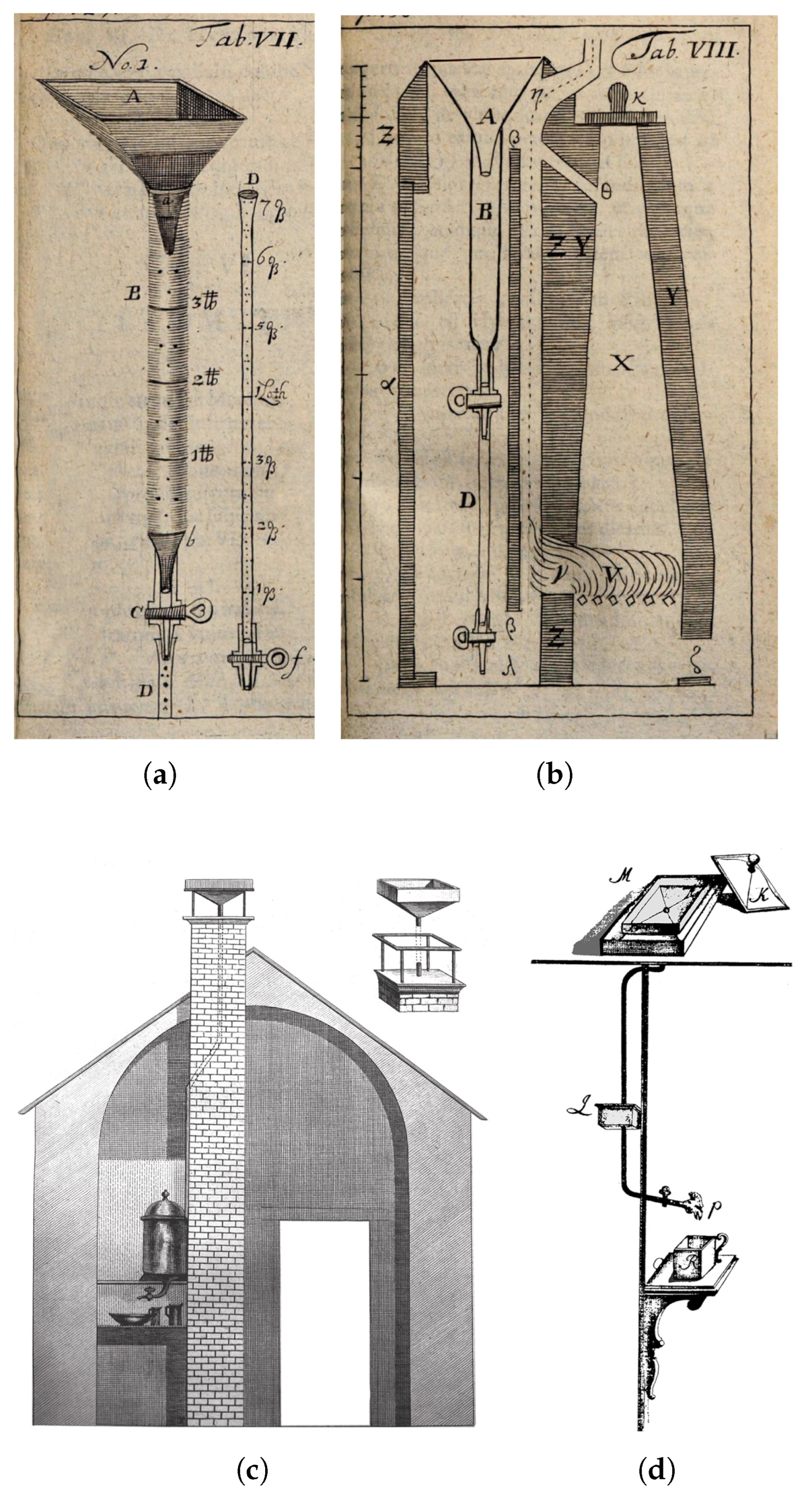


| Name | Period | Starting Time (LT) |
|---|---|---|
| Italian Hydrographic Service | 1917–1998 | 09 |
| Meteorological Service of the Italian Air Force (AM) | 1951–present | 01 |
| Regional Environmental Protection Agency (ARPA) | 1993–present | 00 |
| Leave measurements unchanged | |
|---|---|
| Shift morning observations back to one calendar day [73,74] | |
| Moving average with a window of two days around the target day [75] | |
| Disaggregation of daily precipitation amounts to hourly and then aggregation back at a different definition of the climatological day | using actual hourly observations [73] |
| assuming that daily amount is uniformly distributed across the whole day [74,76]; | |
| using reanalysis models to split daily precipitation to hourly [77] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
della Valle, A.; Becherini, F.; Camuffo, D. Recovery and Reconstructions of 18th Century Precipitation Records in Italy: Problems and Analyses. Climate 2025, 13, 131. https://doi.org/10.3390/cli13060131
della Valle A, Becherini F, Camuffo D. Recovery and Reconstructions of 18th Century Precipitation Records in Italy: Problems and Analyses. Climate. 2025; 13(6):131. https://doi.org/10.3390/cli13060131
Chicago/Turabian Styledella Valle, Antonio, Francesca Becherini, and Dario Camuffo. 2025. "Recovery and Reconstructions of 18th Century Precipitation Records in Italy: Problems and Analyses" Climate 13, no. 6: 131. https://doi.org/10.3390/cli13060131
APA Styledella Valle, A., Becherini, F., & Camuffo, D. (2025). Recovery and Reconstructions of 18th Century Precipitation Records in Italy: Problems and Analyses. Climate, 13(6), 131. https://doi.org/10.3390/cli13060131








