Scaling Properties of Rainfall as a Basis for Intensity–Duration–Frequency Relationships and Their Spatial Distribution in Catalunya, NE Spain
Abstract
1. Introduction
2. Materials and Methods
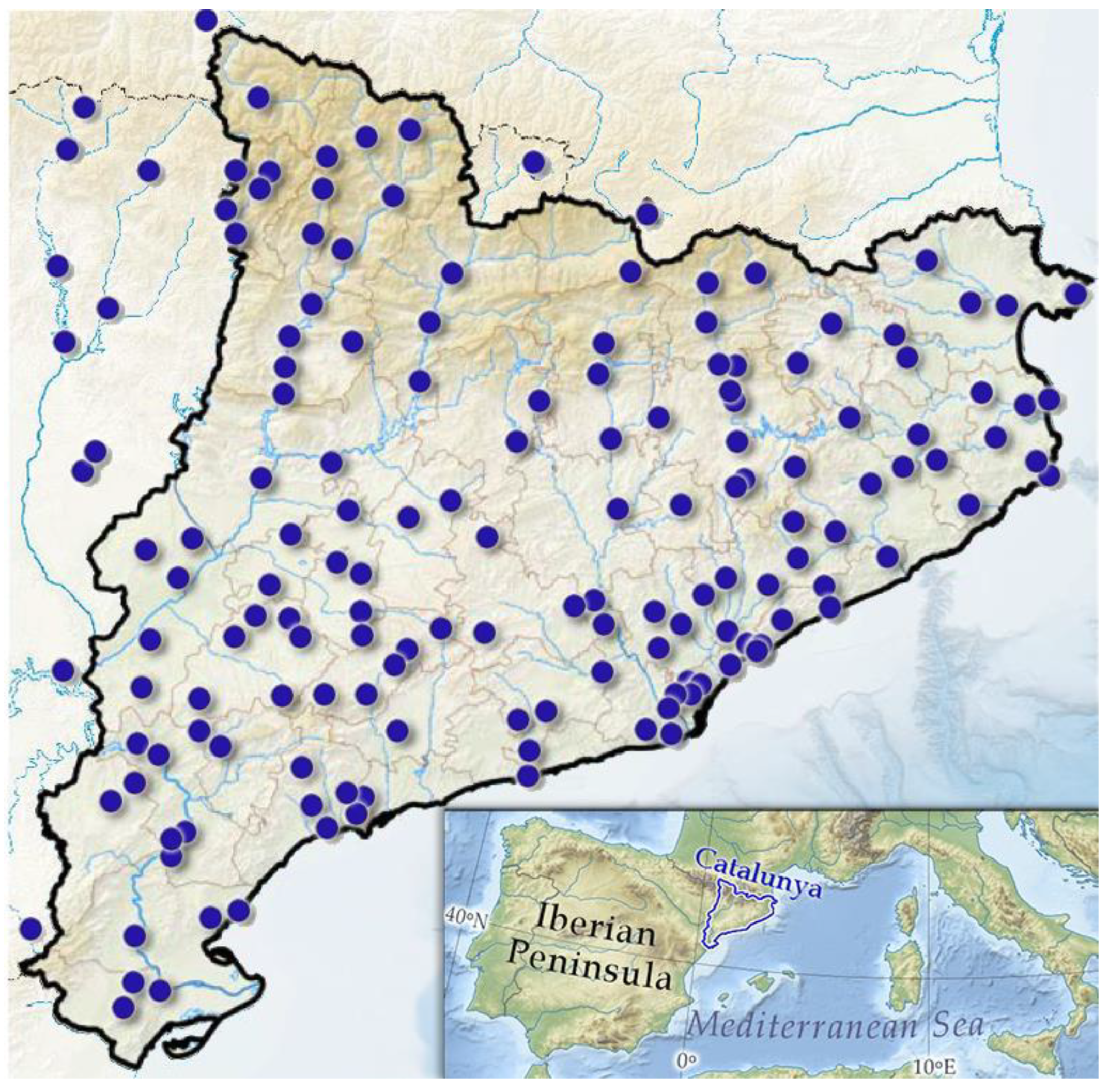
2.1. Rainfall Data
2.2. Statistical Analysis of the Daily Maximum Intensity Series
2.3. Simple Scaling Methodology
2.4. Downscaling for Sub-Daily Intensity Estimations
3. Results
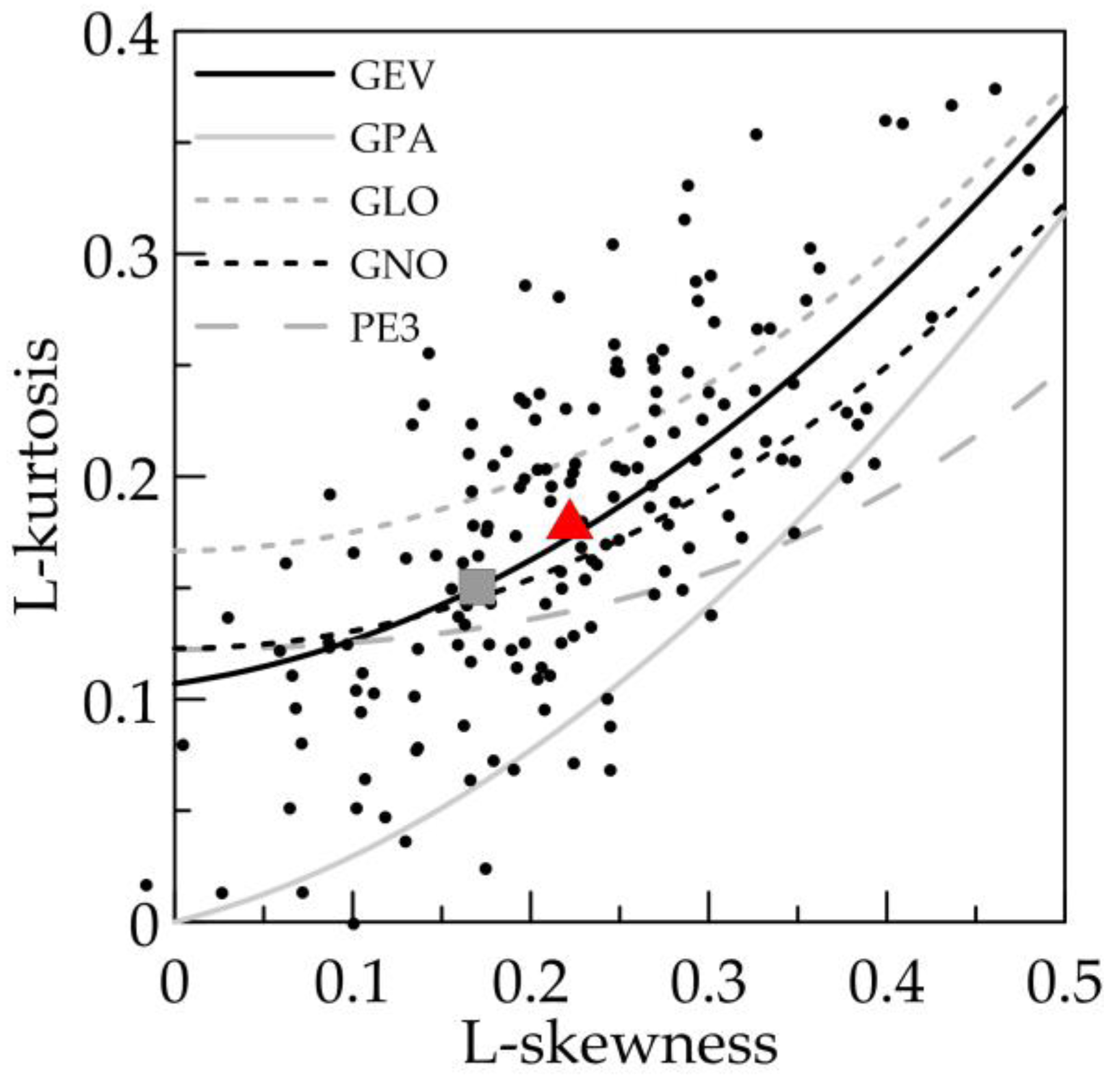
3.1. Statistical Analysis of the Daily Maximum Intensity Series
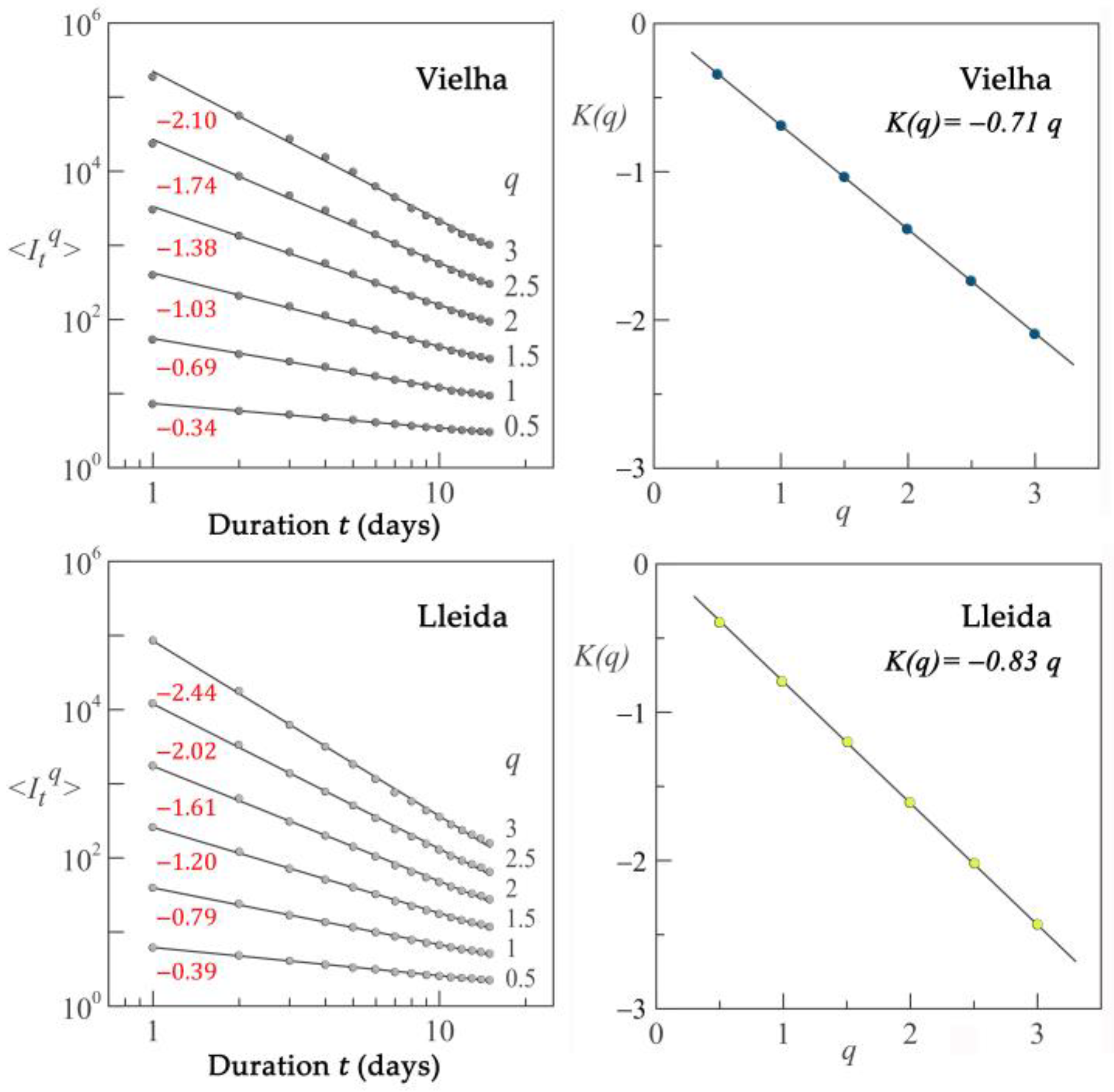
3.2. Simple Scaling Analysis
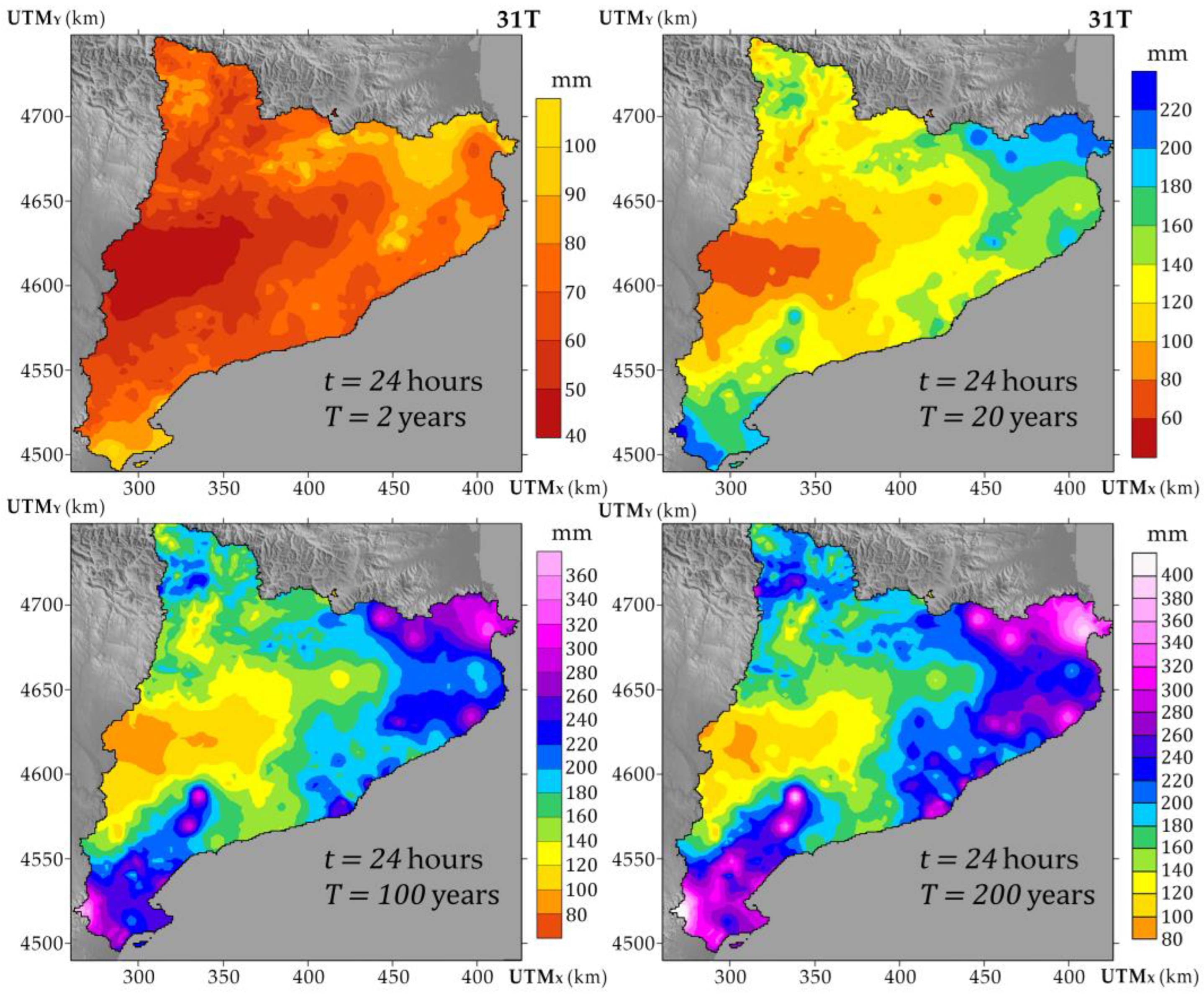
3.3. Downscaling the Intensity–Frequency for 24 h to Sub-Daily Durations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, International ed.; McGraw-Hill Book Company: New York, NY, USA, 1988; Available online: https://ponce.sdsu.edu/Applied_Hydrology_Chow_1988.pdf (accessed on 4 December 2024).
- Willems, P. Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Mays, L.W. Water Resources Engineering, 3rd ed.; John and Wiley & Sons: Hoboken, NJ, USA, 2019; Available online: http://dl.watereng.ir/doc/Larry%20W.%20Mays%20-%20Water%20Resources%20Engineering%20_2010,%20Wiley_.pdf (accessed on 2 December 2024).
- Sherman, C.W. Frequency and Intensity of Excessive Rainfall at Boston. Mass. Trans. Am. Soc. Civil Eng. 1931, 95, 951–960. [Google Scholar] [CrossRef]
- Bernard, M.M. Formulas for rainfall intensities of long duration. Trans. Am. Soc. Civ. Eng. 1932, 96, 592–606. [Google Scholar] [CrossRef]
- Hershfield, D.M. Extreme Rainfall Relationships. J. Hydraul. Div. 1962, 88, 73–92. [Google Scholar] [CrossRef]
- Bell, F.C. Generalized Rainfall-Duration-Frequency Relationships. J. Hydraul. Div. 1969, 95, 311–327. [Google Scholar] [CrossRef]
- Chen, C.L. Rainfall intensity–duration–frequency formulas. J. Hydraul. Div. 1983, 109, 1603–1621. [Google Scholar] [CrossRef]
- Harremoës, P.; Mikkelsen, P. Properties of extreme point rainfall I: Results from a rain gauge system in Denmark. Atmos. Res. 1995, 37, 277–286. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Yu, P.; Cheng, C. Incorporating uncertainty analysis into a regional IDF formula. Hydrol. Process. 1998, 12, 713–726. [Google Scholar] [CrossRef]
- Salas, L.; Fernandez, J. “In-site” regionalization to estimate an intensity—Duration—Frequency law: A solution to scarce spatial data in Spain. Hydrol. Process. 2007, 21, 3507–3513. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K.L. Developing Intensity-Duration-Frequency (IDF) Curves from Satellite-Based Precipitation: Methodology and Evaluation. Water Resour. Res. 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
- Gutiérrez-López, A.; Jiménez-Hernández, S.B.; Escalante-Sandoval, C. Physical Parameterization of IDF Curves Based on Short-Duration Storms. Water 2019, 11, 1813. [Google Scholar] [CrossRef]
- García-Bartual, R.; Schneider, M. Estimating maximum expected short-duration rainfall intensities from extreme convective storms. Phys. Chem. Earth Part B 2001, 26, 675–681. [Google Scholar] [CrossRef]
- Aronica, G.T.; Freni, G. Estimation of sub-hourly DDF curves using scaling properties of hourly and sub-hourly data at partially gauged site. Atmos. Res. 2005, 77, 114–123. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Brath, A.; Montanari, A. Reliability of different depth-duration-frequency equations for estimating short-duration design storms. Water Resour. Res. 2006, 42, W12501. [Google Scholar] [CrossRef]
- Willems, P.; Arnbjerg-Nielsen, K.; Olsson, J.; Nguyen, V. Climate change impact assessment on urban rainfall extremes and urban drainage: Methods and shortcomings. Atmos. Res. 2012, 103, 106–118. [Google Scholar] [CrossRef]
- Nwaogazie, I.L.; Sam, M.G. A review study on stationary and non-stationary IDF models used in rainfall data analysis around the world from 1951–2020. Int. J. Environ. Clim. Change 2020, 10, 465–482. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Update of intensity-duration-frequency (IDF) curves under climate change: A review. Water Supply 2022, 22, 4951–4974. [Google Scholar] [CrossRef]
- Yan, H.; Sun, N.; Chen, X.; Wigmosta, M.S. Next-Generation Intensity-Duration-Frequency Curves for Climate-Resilient Infrastructure Design: Advances and Opportunities. Front. Water 2020, 2, 545051. [Google Scholar] [CrossRef]
- Lanciotti, S.; Ridolfi, E.; Russo, F.; Napolitano, F. Intensity–Duration–Frequency Curves in a Data-Rich Era: A Review. Water 2022, 14, 3705. [Google Scholar] [CrossRef]
- Casas, M.C.; Codina, B.; Redaño, Á.; Lorente, J. A methodology to classify extreme rainfall events in the western Mediterranean area. Theor. Appl. Climatol. 2004, 77, 139–150. [Google Scholar] [CrossRef]
- Pérez-Zanón, N.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Peña, J.C.; Rius, A.; Solé, J.G.; Redaño, À. Analysis of extreme rainfall in the Ebre Observatory (Spain). Theor. Appl. Climatol. 2016, 124, 935–944. [Google Scholar] [CrossRef]
- Casas-Castillo, M.C.; Rodríguez-Solà, R.; Navarro, X.; Russo, B.; Lastra, A.; González, P.; Redaño, À. On the consideration of scaling properties of extreme rainfall in Madrid (Spain) for developing a generalized intensity-duration-frequency equation and assessing probable maximum precipitation estimates. Theor. Appl. Climatol. 2018, 131, 573–580. [Google Scholar] [CrossRef]
- Olsson, J.; Niemczynowicz, J.; Berndtsson, R.; Larson, M. An analysis of the rainfall time structure by box counting—Some practical implications. J. Hydrol. 1992, 137, 261–277. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R. Scaling and muitiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Multifractality of rainfall and scaling of intensity-duration-frequency curves. Water Resour. Res. 2002, 38, 1306. [Google Scholar] [CrossRef]
- Menabde, M.; Seed, A.; Pegram, G. A simple scaling model for extreme rainfall. Water Resour. Res. 1999, 35, 335–340. [Google Scholar] [CrossRef]
- Rodríguez-Solà, R.; Casas-Castillo, M.C.; Navarro, X.; Redaño, À. A study of the scaling properties of rainfall in Spain and its appropriateness to generate intensity-duration-frequency curves from daily records. Int. J. Climatol. 2017, 37, 770–780. [Google Scholar] [CrossRef]
- Innocenti, S.; Mailhot, A.; Frigon, A. Simple scaling of extreme precipitation in North America. Hydrol. Earth Syst. Sci. 2017, 21, 5823–5846. [Google Scholar] [CrossRef]
- Casas-Castillo, M.C.; Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Navarro, X. A single scaling parameter as a first approximation to describe the rainfall pattern of a place: Application on Catalonia. Acta Geophys. 2018, 66, 415–424. [Google Scholar] [CrossRef]
- Bara, M.; Kohnová, S.; Gaál, L.; Szolgay, J.; Hlavčová, K. Estimation of IDF Curves of Extreme Rainfall by Simple Scaling in Slovakia. Contrib. Geophys. Geod. 2009, 39, 187–206. Available online: https://www.sav.sk/journals/uploads/11270958Bara-et-al_CGG-39-3.pdf (accessed on 4 December 2014).
- Casas-Castillo, M.C.; Rodríguez-Solà, R.; Llabrés-Brustenga, A.; García-Marín, A.P.; Estévez, J.; Navarro, X. A Simple Scaling Analysis of Rainfall in Andalusia (Spain) under Different Precipitation Regimes. Water 2022, 14, 1303. [Google Scholar] [CrossRef]
- Creaco, E. Scaling models of intensity–duration–frequency (IDF) curves based on adjusted design event durations. J. Hydrol. 2024, 632, 130847. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, À. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef]
- Huo, R.; Li, L.; Chen, H.; Xu, C.; Chen, J.; Guo, S. Extreme Precipitation Changes in Europe from the Last Millennium to the End of the Twenty-First Century. J. Clim. 2021, 34, 567–588. [Google Scholar] [CrossRef]
- Kahraman, A.; Kendon, E.J.; Chan, S.C.; Fowler, H.J. Quasi-Stationary Intense Rainstorms Spread Across Europe Under Climate Change. Geophys. Res. Lett. 2021, 48, e2020GL092361. [Google Scholar] [CrossRef]
- Amiri, A.; Gumiere, S.J.; Gharabaghi, B.; Bonakdari, H. From warm seas to flooded streets: The impact of sea surface temperature on cutoff low and extreme rainfall in Valencia, Spain. J. Flood Risk Manag. 2025, 18, e13055. [Google Scholar] [CrossRef]
- Moustakis, Y.; Papalexiou, S.M.; Onof, C.J.; Paschalis, A. Seasonality, intensity, and duration of rainfall extremes change in a warmer climate. Earth Future 2021, 9, e2020EF001824. [Google Scholar] [CrossRef]
- Llasat, M.C.; Marcos, R.; Turco, M.; Gilabert, J.; Llasat-Botija, M. Trends in flash flood events versus convective precipitation in the Mediterranean region: The case of Catalonia. J. Hydrol. 2016, 541, 24–37. [Google Scholar] [CrossRef]
- Van den Besselaar, E.J.M.; Klein-Tank, A.M.G.; Buishand, T.A. Trends in European precipitation extremes over 1951-2010. Int. J. Climatol. 2013, 33, 2682–2689. [Google Scholar] [CrossRef]
- Casanueva, A.; Rodríguez-Puebla, C.; Frías, M.D.; González-Reviriego, N. Variability of extreme precipitation over Europe and its relationships with teleconnection patterns. Hydrol. Earth Syst. Sci. 2014, 18, 709–725. [Google Scholar] [CrossRef]
- Cardoso-Pereira, S.; Marta-Almeida, M.; Carvalho, A.C.; Rocha, A. Extreme precipitation events under climate change in the Iberian Peninsula. Int. J. Climatol. 2020, 40, 1255–1278. [Google Scholar] [CrossRef]
- Lana, X.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Serra, C.; Martínez, M.D.; Kirchner, R. Rainfall regime trends at annual and monthly scales in Catalonia (NE Spain) and indications of CO2 emissions effects. Theor. Appl. Climatol. 2021, 146, 981–996. [Google Scholar] [CrossRef]
- Servei Meteorològic de Catalunya: Climatologia/Dades i Productes Climàtics/Corbes IDF. Available online: https://www.meteo.cat/wpweb/climatologia/dades-i-productes-climatics/corbes-idf/ (accessed on 4 December 2024).
- Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Casas-Castillo, M.C.; Redaño, À. Quality control process of the daily rainfall series available in Catalonia from 1855 to the present. Theor. Appl. Climatol. 2019, 137, 2715–2729. [Google Scholar] [CrossRef]
- Llabrés-Brustenga, A. Intensity-Duration-Frequency of Rainfall in Catalunya: Maximum Expected Precipitation and IDF Relationships at High Temporal and Spatial Resolution. Ph.D. Thesis, Universitat de Barcelona, Barcelona, Spain, 14 January 2020. Available online: http://hdl.handle.net/10803/668777 (accessed on 4 December 2024).
- Domonkos, P.; Coll, J. Homogenisation of temperature and precipitation time series with ACMANT3: Method description and efficiency tests. Int. J. Climatol. 2016, 37, 1910–1921. [Google Scholar] [CrossRef]
- Hershfield, D.M. Rainfall Frequency Atlas of the United States for Durations from 30 Minutes to 24 Hours and Return Periods from 1 to 100 Years; Weather Bureau Technical Paper 40; U.S. Weather Bureau: Washington, DC, USA, 1961; p. 115. Available online: https://reduceflooding.com/wp-content/uploads/2018/09/TechnicalPaper_No40.pdf (accessed on 5 December 2024).
- Weiss, L.L. Ratio of true to fixed-interval maximum rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar] [CrossRef]
- Dwyer, I.J.; Reed, D.W. Allowance for Discretization in Hydrological and Environmental Risk Estimation; Report 123; Institute of Hydrology: Wallingford, UK, 1995; p. 51. Available online: https://nora.nerc.ac.uk/7366/1/IH_123.pdf (accessed on 5 December 2024).
- Young, C.B.; McEnroe, B.M. Sampling adjustment factors for rainfall recorded at fixed time intervals. J. Hydrol. Eng. 2003, 8, 294–296. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Dialynas, Y.G.; Grimaldi, S. Hershfield factor revisited: Correcting annual maximum precipitation. J. Hydrol. 2016, 542, 884–895. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Cifrodelli, M.; Picciafuoco, T.; Corradini, C.; Casas-Castillo, M.C.; Fowler, J.H.; Wilkinson, S.M. Effect of temporal aggregation on the estimate of annual maximum rainfall depths for the design of hydraulic infrastructure systems. J. Hydrol. 2017, 554, 710–720. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Picciafuoco, T.; Dari, J.; Corradini, C. Characteristics of the underestimation error of annual maximum rainfall depth due to coarse temporal aggregation. Atmosphere 2018, 9, 303. [Google Scholar] [CrossRef]
- Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Casas-Castillo, M.C. Influence of regional and seasonal rainfall patterns on the ratio between fixed and unrestricted measured intervals of rainfall amounts. Theor. Appl. Climatol. 2020, 140, 389–399. [Google Scholar] [CrossRef]
- DelSole, T.; Tippett, M. Extreme Value Theory. In Statistical Methods for Climate Scientists; Cambridge University Press: Cambridge, MA, USA, 2022; pp. 446–467. [Google Scholar] [CrossRef]
- Ragulina, G.; Reitan, T. Generalized extreme value shape parameter and its nature for extreme precipitation using long time series and the Bayesian approach. Hydrolog. Sci. J. 2017, 62, 863–879. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments, lmom. R Package, Version 3.2. 2019. Available online: https://cran.r-project.org/web/packages/lmom/ (accessed on 6 December 2024).
- Hosking, J.R.M. Regional Frequency Analysis Using L-Moments, lmomRFA R Package, Version 3.3. 2019. Available online: https://cran.r-project.org/web/packages/lmomRFA/ (accessed on 6 December 2024).
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B Stat. Method. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Esri. Geographically Weighted Regression (GWR) and Kriging. ArcGIS Pro Documentation. 2024. Available online: https://pro.arcgis.com (accessed on 6 December 2024).
- Rodríguez, R.; Casas, M.C.; Redaño, À. Multifractal analysis of the rainfall time distribution on the metropolitan area of Barcelona (Spain). Meteorol. Atmos. Phys. 2013, 121, 181–187. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. Multiscaling properties of spatial rainfall and river flow distributions. J. Geophys. Res. Atmos. 1990, 95, 1999–2009. [Google Scholar] [CrossRef]
- Montanari, A.; Merz, B.; Blöschl, G. HESS Opinions: The sword of Damocles of the impossible flood. Hydrol. Earth Syst. Sci. 2024, 28, 2603–2615. [Google Scholar] [CrossRef]
- Casas, M.C.; Rodríguez, R.; Nieto, R.; Redaño, À. The estimation of probable maximum precipitation: The case of Catalonia. Ann. N. Y. Acad. Sci. 2008, 1146, 291–302. [Google Scholar] [CrossRef]
- Martín-Vide, J.; Lopez-Bustins, J.A.; Lemus, M.; Moreno-García, M.C.; Balagué, X.; González-Hidalgo, J.C.; Beguería, S.; Peña-Angulo, D.; Trullenque, V. The consecutive disparity of precipitation in conterminous Spain. Theor. Appl. Climatol. 2022, 147, 1151–1161. [Google Scholar] [CrossRef]
- Lana, X.; Serra, C.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Prohom, M. Two centuries of monthly rainfall in Barcelona (NE Spain): Disparity trends, correlation of autumnal rainfall with the WeMO index and its contribution to annual amounts. Climate 2024, 12, 166. [Google Scholar] [CrossRef]
- Lana, X.; Rodríguez-Solà, R.; Casas-Castillo, M.C.; Serra, C.; Kirchner, R.; Martínez, M.D. Rainfall disparity at monthly scale on Catalonia (NE Spain): Dependence on geographic coordinates, altitude and distance to the Mediterranean coast. Theor. Appl. Climatol. 2023, 153, 1293–1306. [Google Scholar] [CrossRef]
- Boisvert, J.B.; Manchuk, J.G.; Deutsch, C.V. Kriging in the Presence of Locally Varying Anisotropy Using Non-Euclidean Distances. Math. Geosci. 2009, 41, 585–601. [Google Scholar] [CrossRef]
- Casas, M.C.; Herrero, M.; Ninyerola, M.; Pons, X.; Rodríguez, R.; Rius, A.; Redaño, À. Analysis and objective mapping of extreme daily rainfall in Catalonia. Int. J. Climatol. 2007, 27, 399–409. [Google Scholar] [CrossRef]
- Servei Meteorològic de Catalunya: Divulgacio/La Predicció Meteorològica/Predicció/. Available online: https://www.meteo.cat/wpweb/divulgacio/la-prediccio-meteorologica/prediccio/ (accessed on 9 December 2024).
- Martín-Vide, J.; Raso-Nadal, J.M. Atles Climàtic de Catalunya: Període 1961–1990; Institut Cartogràfic de Catalunya & Servei Meteorològic de Catalunya: Barcelona, Spain, 2008. [Google Scholar]
- Anghel, C.G. Revisiting the Use of the Gumbel Distribution: A Comprehensive Statistical Analysis Regarding Modeling Extremes and Rare Events. Mathematics 2024, 12, 2466. [Google Scholar] [CrossRef]
- Meseguer-Ruiz, O.; Martín-Vide, J. Análisis de la fractalidad temporal de la precipitación en Cataluña, España (2010). Investig. Geográficas Una Mirada Desde El Sur 2014, 47, 41–52. [Google Scholar] [CrossRef][Green Version]
- Cortès, M.; Turco, M.; Llasat-Botija, M.; Llasat, M.C. The relationship between precipitation and insurance data for floods in a Mediterranean region (northeast Spain). Nat. Hazards Earth Syst. Sci. 2018, 18, 857–868. [Google Scholar] [CrossRef]
- Servei Meteorològic de Catalunya: Serveis/Formularis/Petició d’Informes i Dades Meteorològiques. Available online: https://www.meteo.cat/wpweb/serveis/formularis/ (accessed on 11 December 2024).
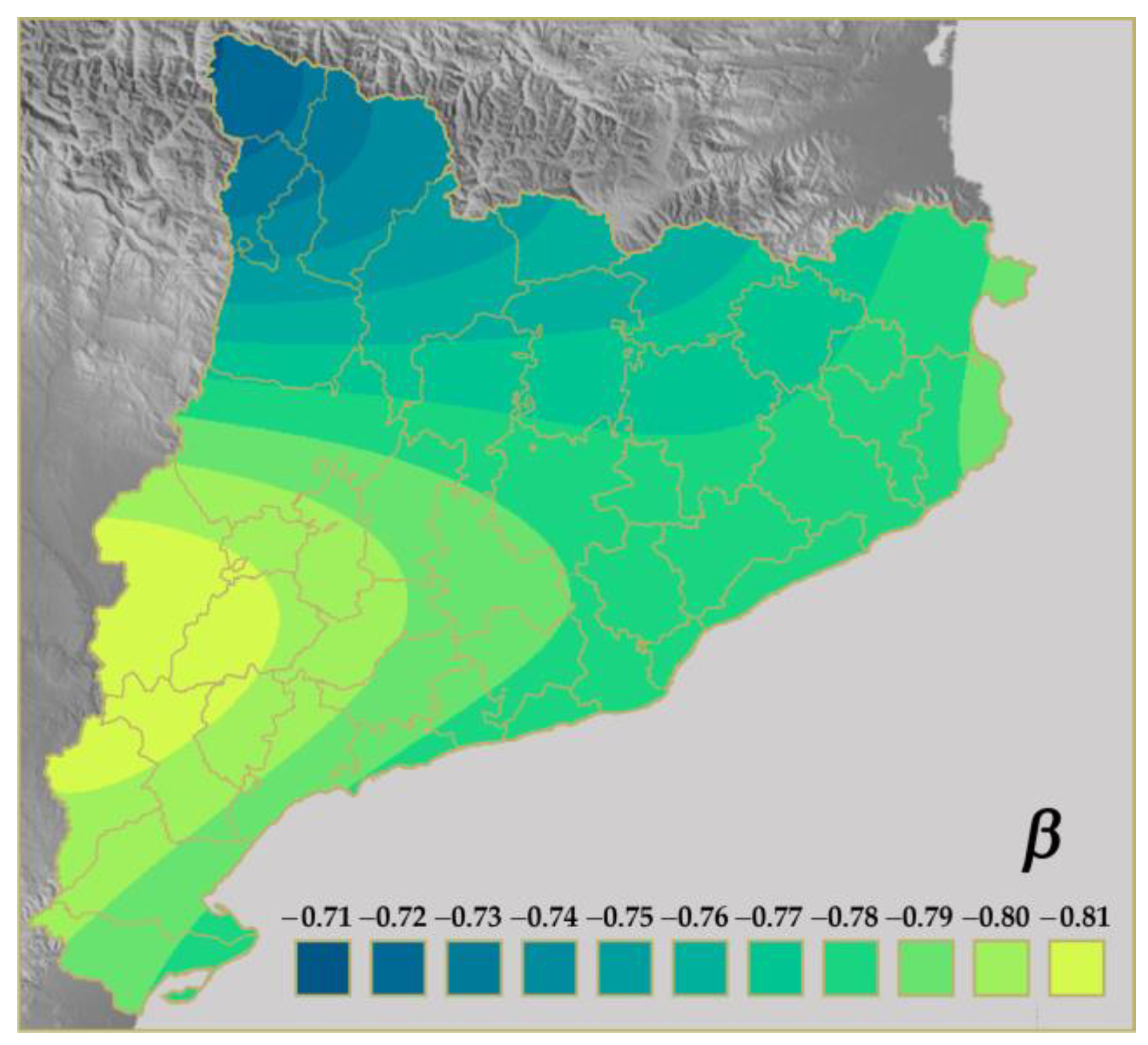
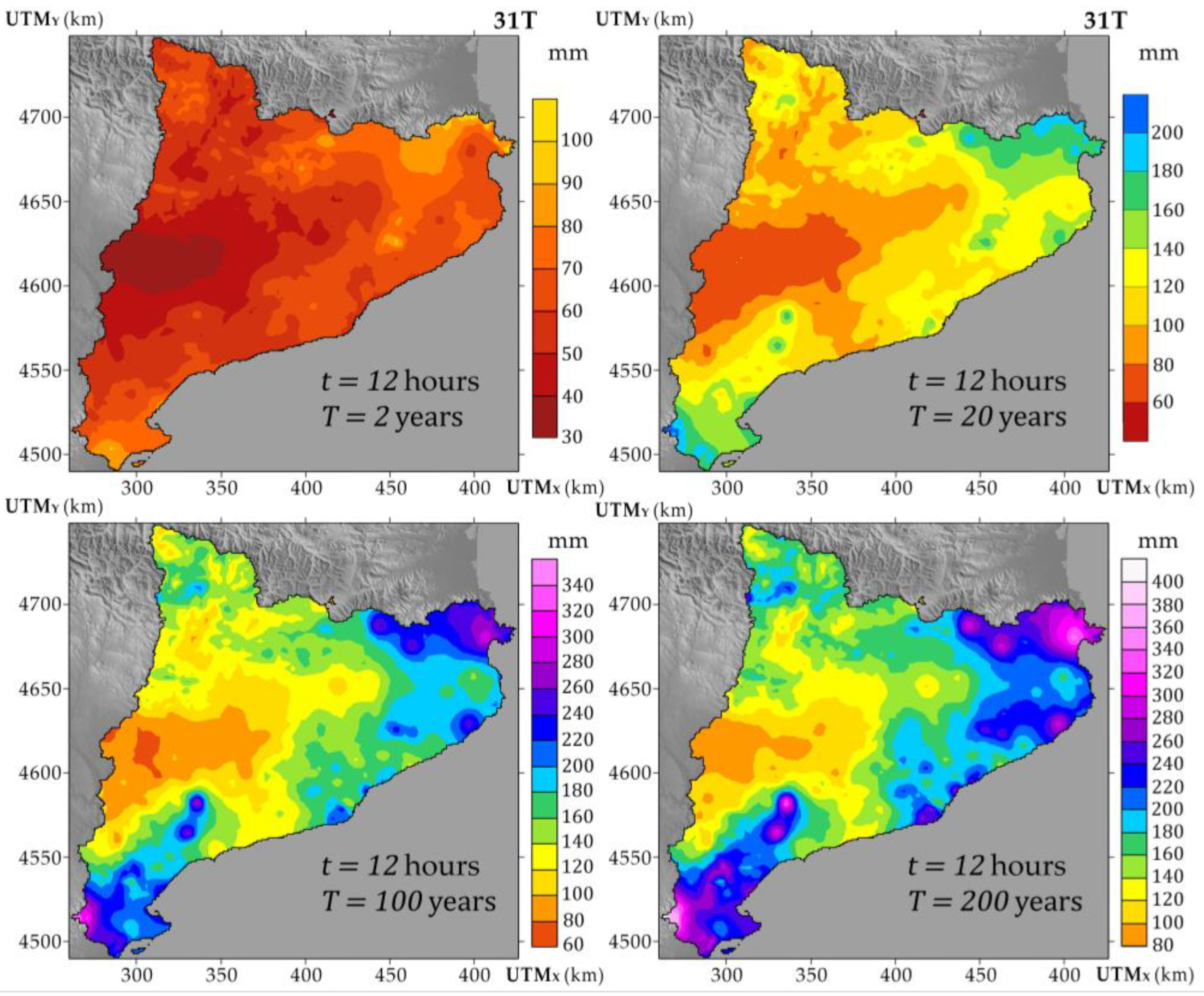
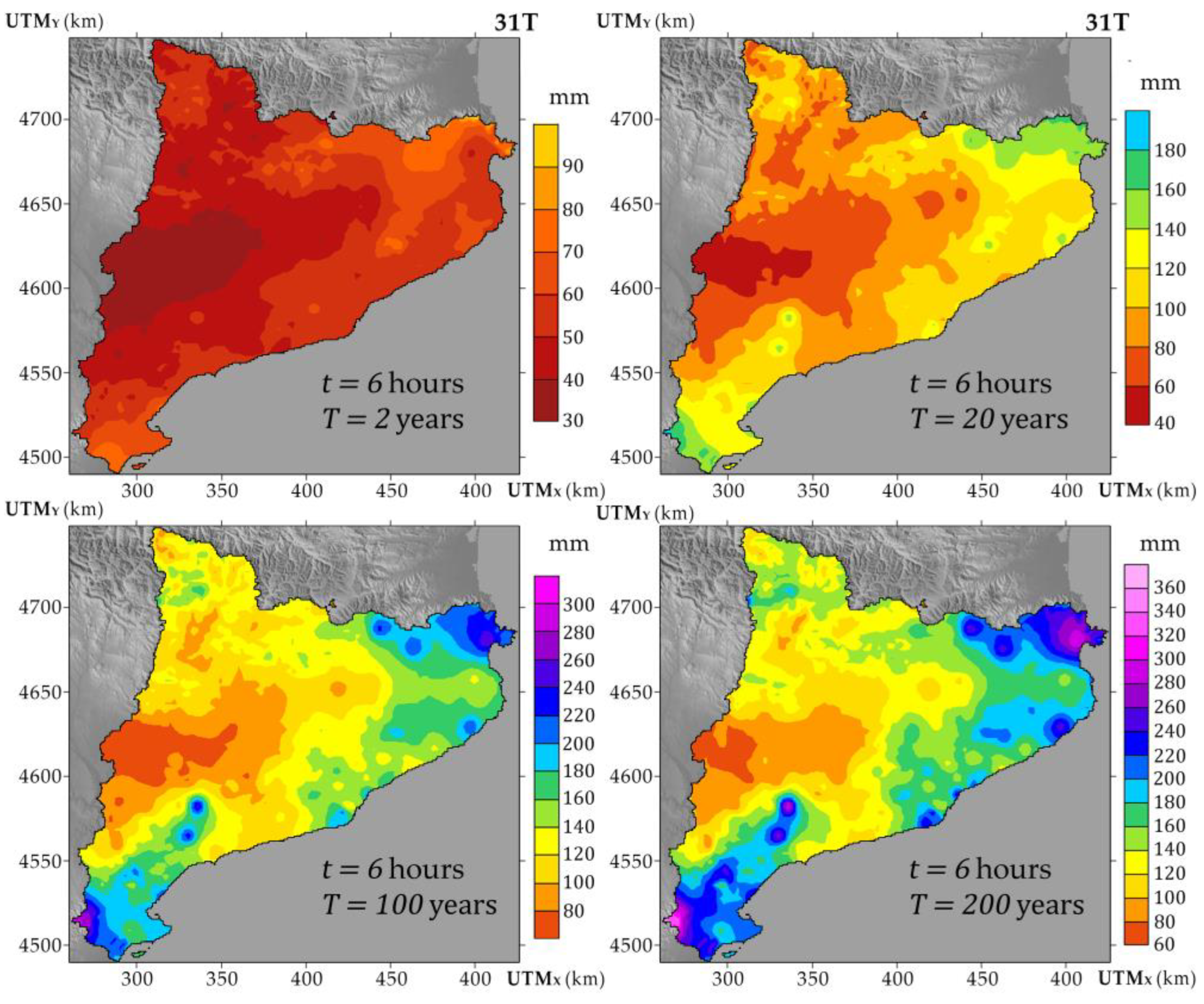

| Return Period (Years) | Intensity Threshold 40 mm/h | Accumulation Threshold 100 mm/24 h | Accumulation Threshold 200 mm/24 h |
|---|---|---|---|
| 2 | 19.1% | 1.2% | 0.0% |
| 5 | 72.0% | 36.0% | 0.0% |
| 10 | 90.5% | 65.4% | 0.0% |
| 20 | 97.5% | 81.8% | 3.6% |
| 50 | 100% | 90.9% | 15.4% |
| 100 | 100% | 96.2% | 30.6% |
| 200 | 100% | 98.7% | 47.3% |
| 500 | 100% | 100% | 65.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casas-Castillo, M.d.C.; Llabrés-Brustenga, A.; Rodríguez-Solà, R.; Rius, A.; Redaño, À. Scaling Properties of Rainfall as a Basis for Intensity–Duration–Frequency Relationships and Their Spatial Distribution in Catalunya, NE Spain. Climate 2025, 13, 37. https://doi.org/10.3390/cli13020037
Casas-Castillo MdC, Llabrés-Brustenga A, Rodríguez-Solà R, Rius A, Redaño À. Scaling Properties of Rainfall as a Basis for Intensity–Duration–Frequency Relationships and Their Spatial Distribution in Catalunya, NE Spain. Climate. 2025; 13(2):37. https://doi.org/10.3390/cli13020037
Chicago/Turabian StyleCasas-Castillo, María del Carmen, Alba Llabrés-Brustenga, Raül Rodríguez-Solà, Anna Rius, and Àngel Redaño. 2025. "Scaling Properties of Rainfall as a Basis for Intensity–Duration–Frequency Relationships and Their Spatial Distribution in Catalunya, NE Spain" Climate 13, no. 2: 37. https://doi.org/10.3390/cli13020037
APA StyleCasas-Castillo, M. d. C., Llabrés-Brustenga, A., Rodríguez-Solà, R., Rius, A., & Redaño, À. (2025). Scaling Properties of Rainfall as a Basis for Intensity–Duration–Frequency Relationships and Their Spatial Distribution in Catalunya, NE Spain. Climate, 13(2), 37. https://doi.org/10.3390/cli13020037








