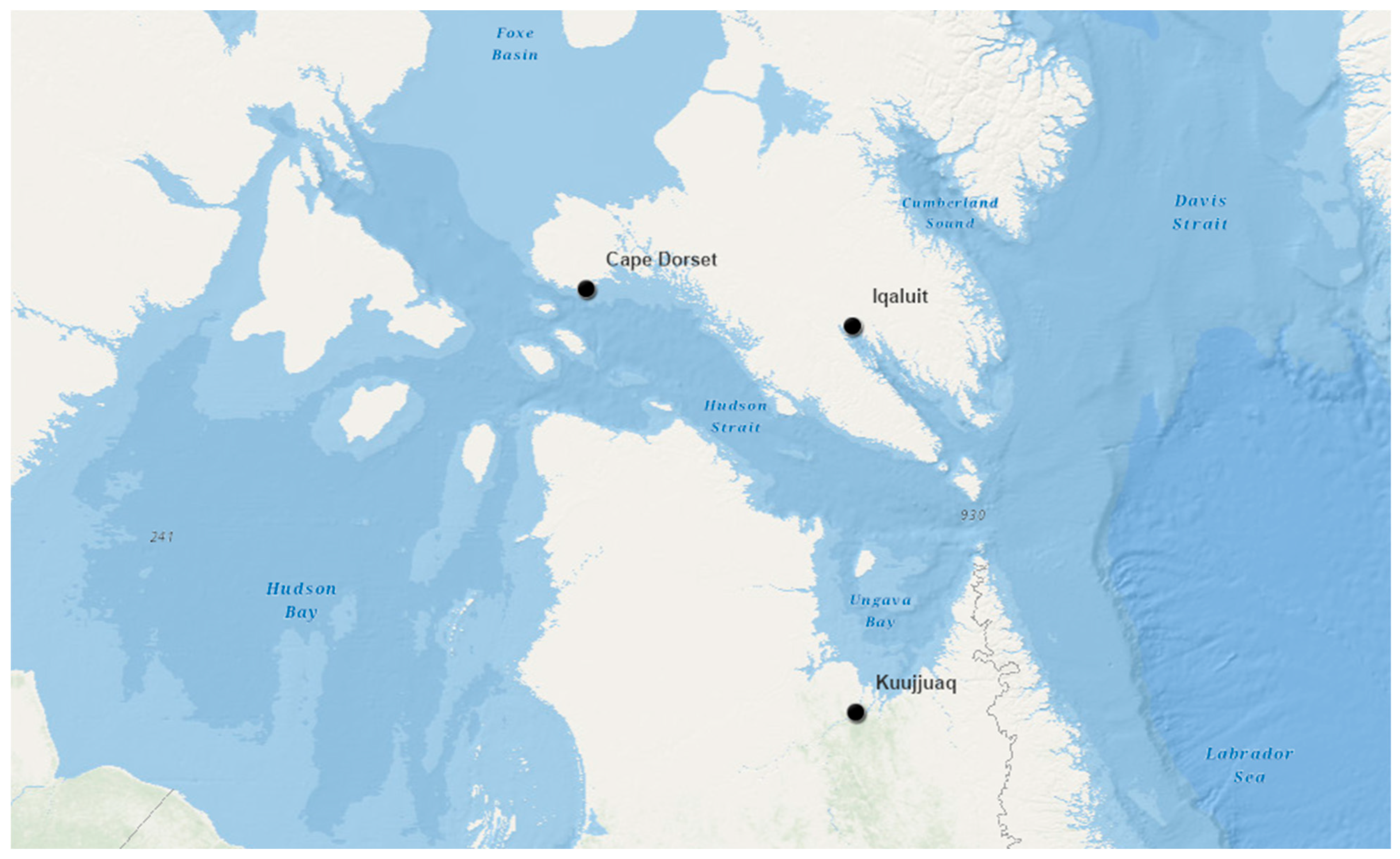
Spatial and Temporal Evolution of Seasonal Sea Ice Extent of Hudson Strait, Canada, 1971–2018
Abstract
1. Introduction
Research Objectives
- How statistically significant are the temporal changes in the breakup, freeze-up, and ice-free seasons for the 24 grid points representing Hudson Strait for three time periods, 1971–2018, 1971–1994, 1995–2018, and the relationship to concurrent temperature change?
- Using a spatial cluster analysis, how coherent is the nature of breakup, freeze-up, and ice-free season spatially, using the three time periods?
2. Materials and Methods
2.1. Surface Air Temperature Data
2.2. Sea Ice Data
2.3. Time Series Analysis
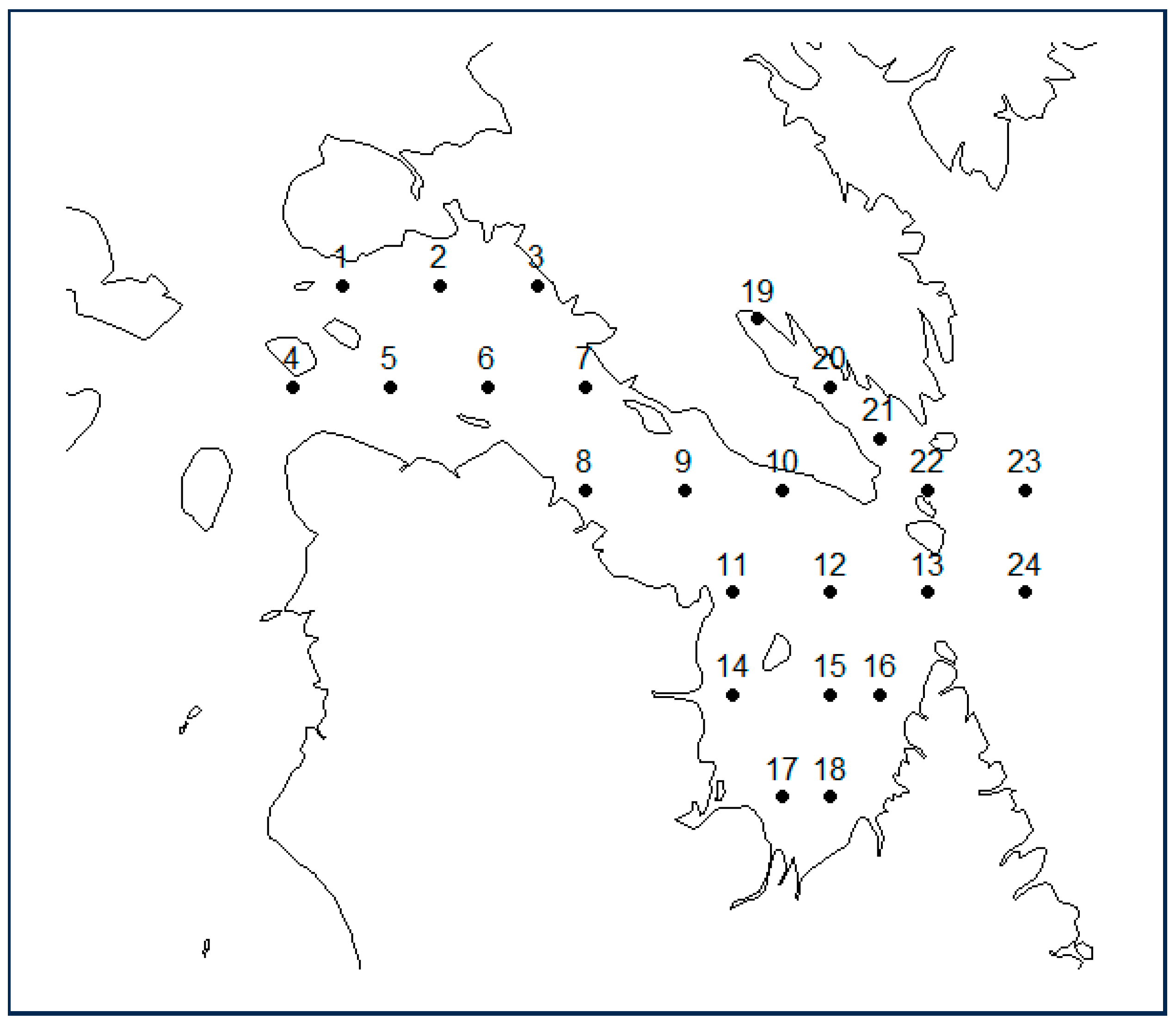
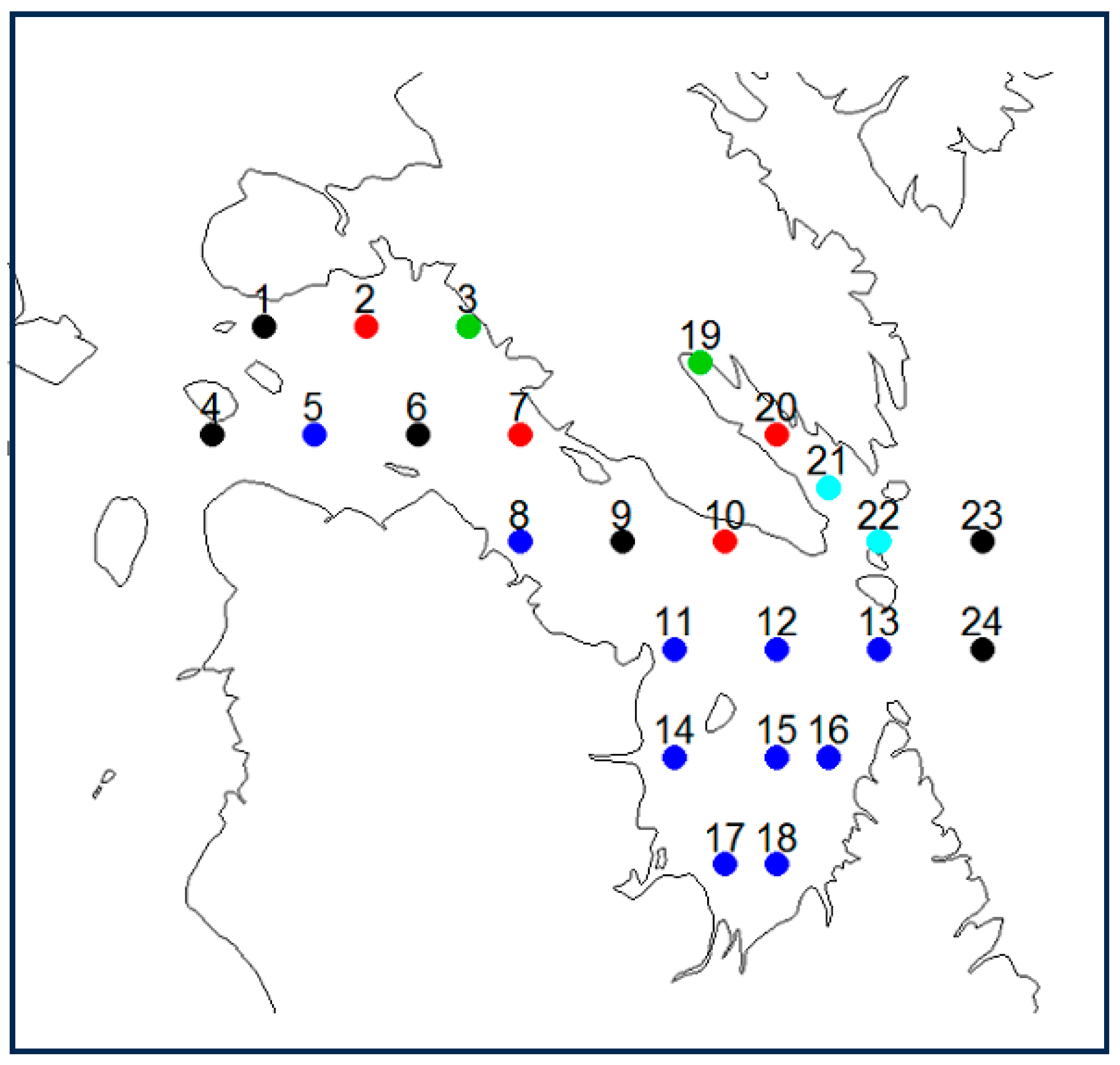
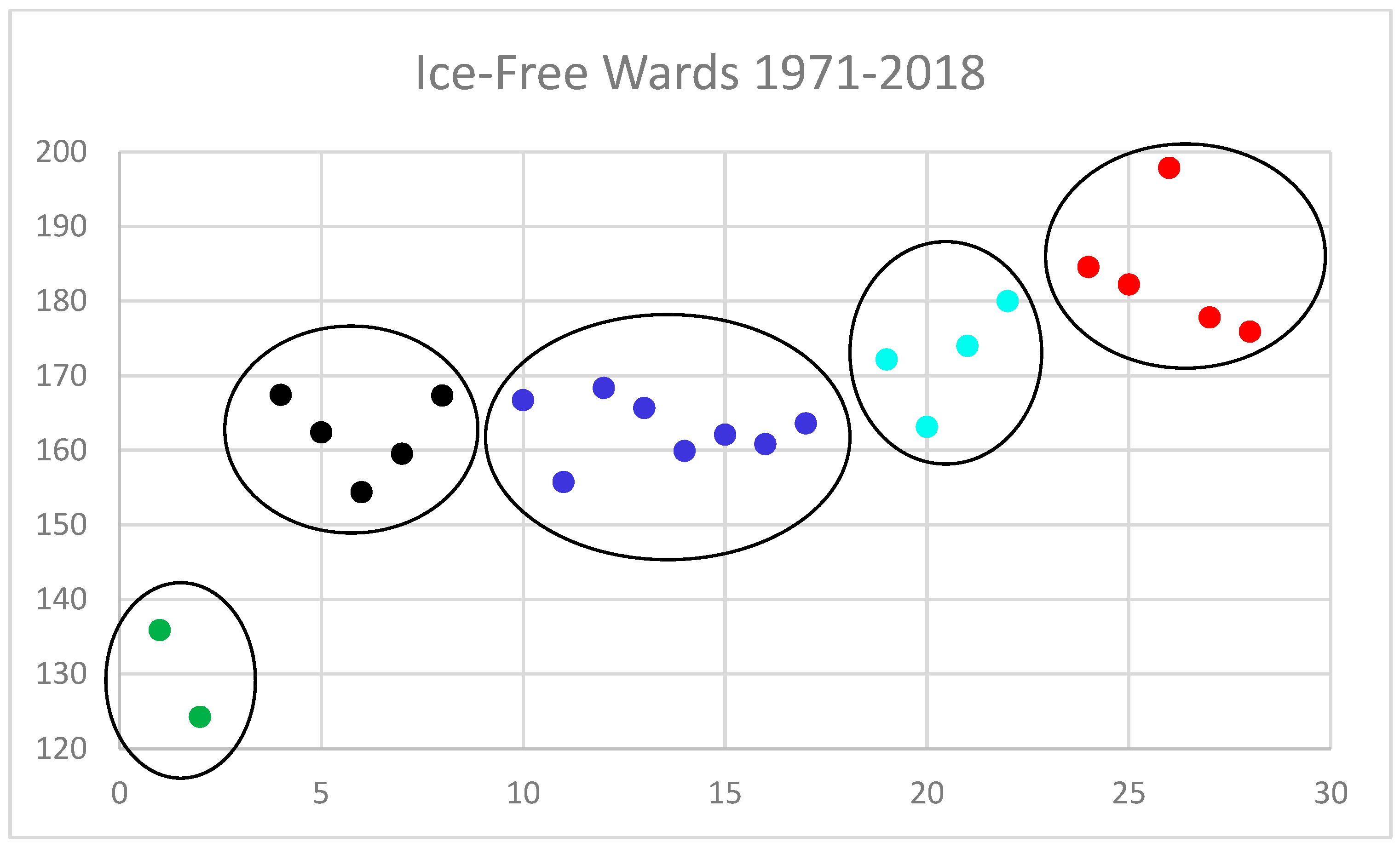
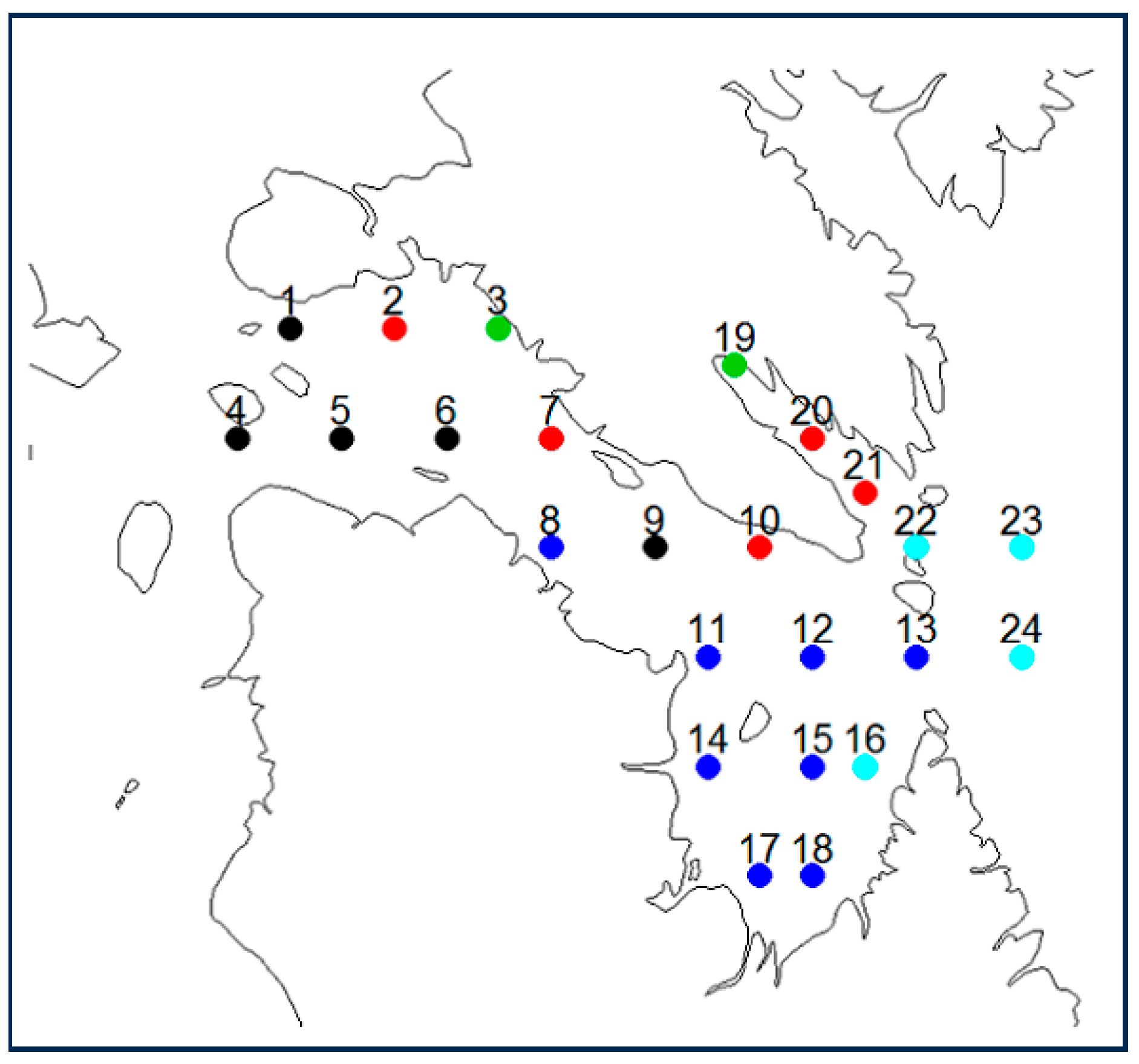
2.4. Spatial Analysis
- Each point begins in a cluster by itself.
- Merge two clusters in order to produce the smallest increase in the sum of squares (merging cost). The merging cost is the increase in sum of squares when two clusters are merged.
- Keep merging until k clusters are reached.
3. Results
3.1. Temperature Analysis
3.2. Sea Ice Time Series Analysis
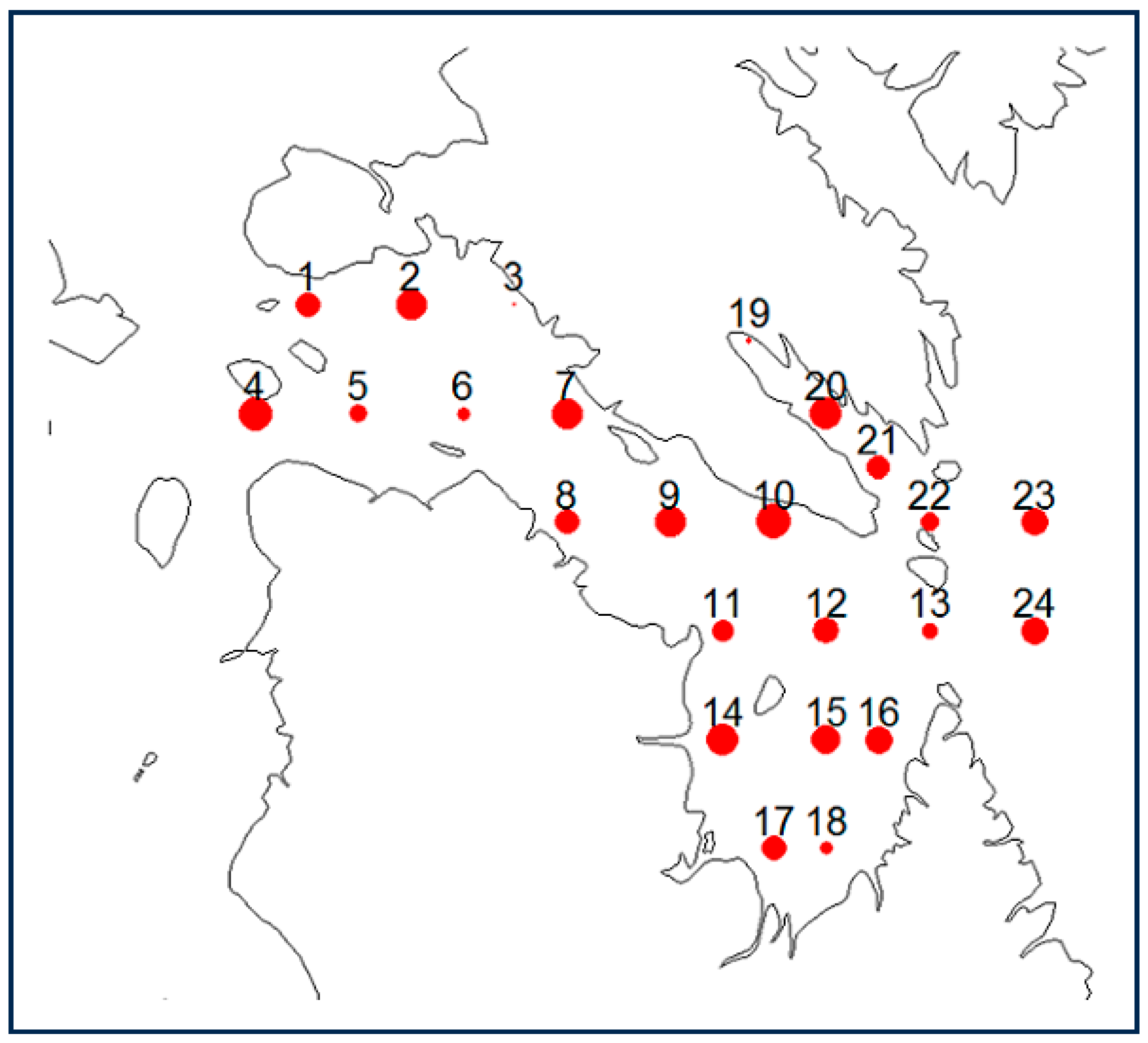
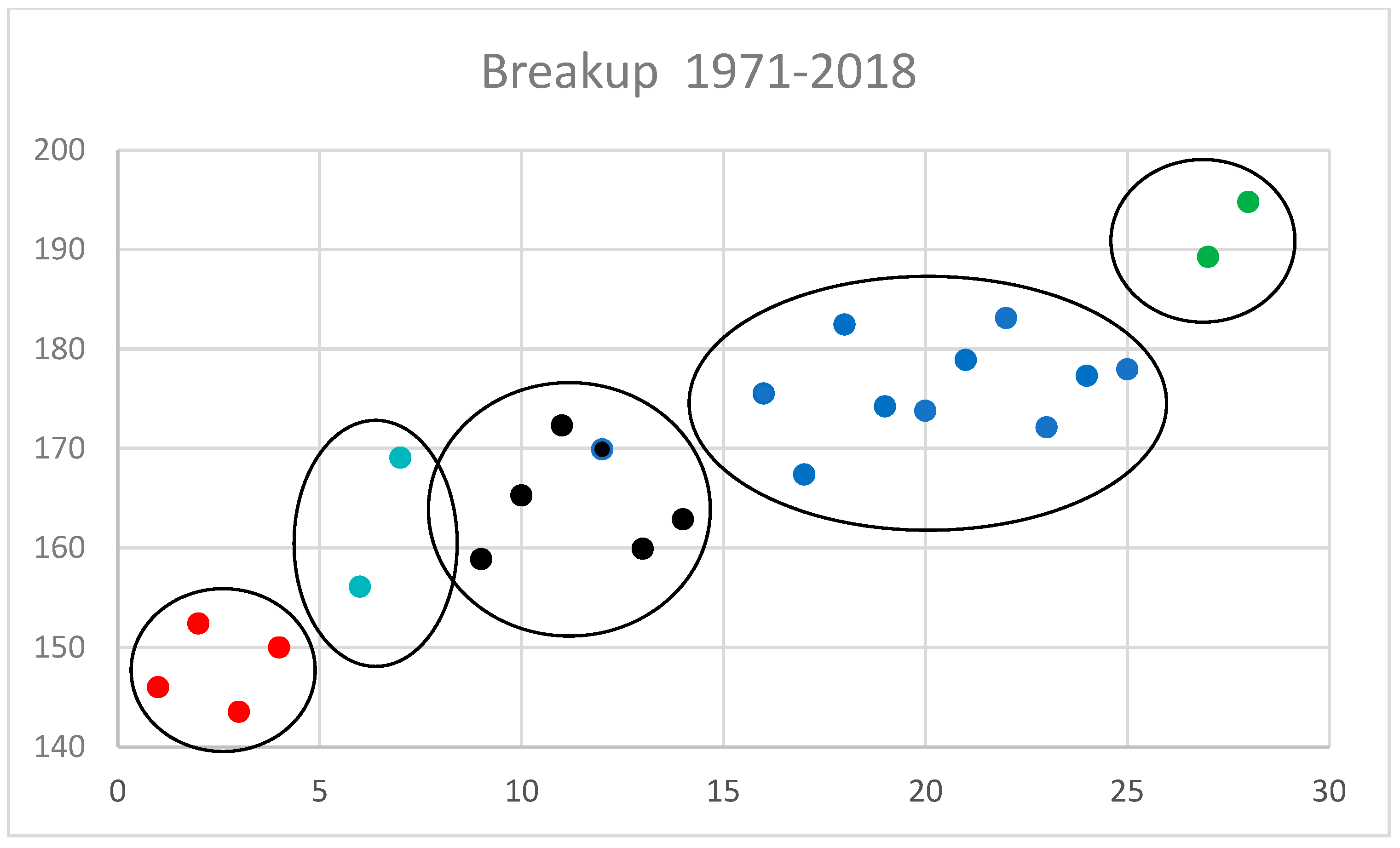
3.3. Spatial Analysis
4. Discussion
How statistically significant are the temporal changes in the breakup, freeze-up, and ice-free season for the 24 grid points representing Hudson Strait for three time periods, 1971–2018, 1971–1994, 1995–2018, and the relationship to concurrent temperature change?
Using a spatial cluster analysis, how coherent is the nature of breakup, freeze-up, and ice-free season spatially using three time periods?
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rantanen, M.; Karpechko, A.Y.; Lipponen, A.; Nordling, K.; Hyvärinen, O.; Ruosteenoja, K.; Vihma, T.; Laaksonen, A. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ. 2022, 3, 168. [Google Scholar] [CrossRef]
- Tivy, A.; Howell, S.E.L.; Alt, B.; McCourt, S.; Chagnon, R.; Crocker, G.; Carrieres, T.; Yackel, J.J. Trends and variability in summer sea ice cover in the Canadian Arctic based on the Canadian Ice Service Digital Archive, 1960–2008 and 1968–2008. J. Geophys. Res. 2011, 116, C03007. [Google Scholar] [CrossRef]
- Andrews, J.; Babb, D.; Barber, D.G. Climate change and sea ice: Shipping accessibility on the marine transportation corridor through Hudson Bay and Hudson Strait (1980–2014). Elem. Sci. Anthr. 2017, 5, 15. [Google Scholar] [CrossRef]
- Andrews, J.; Babb, D.; Barber, D.G. Climate change and sea ice: Shipping in Hudson Bay, Hudson Strait, and Foxe Basin (1980–2016). Elem. Sci. Anthr. 2018, 6, 19. [Google Scholar] [CrossRef]
- Babb, D.G.; Kirillov, S.; Galley, R.J.; Straneo, F.; Ehn, J.K.; Howell, S.E.L.; Brady, M.; Ridenour, N.A.; Barber, D.G. Sea Ice Dynamics in Hudson Strait and Its Impact on Winter Shipping Operations. J. Geophys. Res. Oceans 2021, 126, e2021JC018024. [Google Scholar] [CrossRef]
- Laidler, G.J.; Elee, P. Human geographies of sea ice: Freeze/thaw processes around Cape Dorset, Nunavut, Canada. Polar Rec. 2008, 44, 51–76. [Google Scholar] [CrossRef]
- Ford, J.D.; McDowell, G.; Shirley, J.; Pitre, M.; Siewierski, R.; Gough, W.; Duerden, F.; Pearce, T.; Adams, P.; Statham, S. The Dynamic Multiscale Nature of Climate Change Vulnerability: An Inuit Harvesting Example. Ann. Assoc. Am. Geogr. 2013, 103, 1193–1211. [Google Scholar] [CrossRef]
- Crane, R.G. Seasonal variations of sea ice extent in the Davis Strait–Labrador Sea area and relationship with syn-optic-scale atmospheric circulation. Arctic 1978, 31, 434–447. [Google Scholar] [CrossRef]
- Houser, C.; Gough, W.A. Variations in Sea Ice in the Hudson Strait: 1971–1999. Polar Geogr. 2003, 27, 1–14. [Google Scholar] [CrossRef]
- Galbraith, P.S.; Larouche, P. Sea-surface temperature in Hudson Bay and Hudson Strait in relation to air temperature and ice cover breakup, 1985–2009. J. Mar. Syst. 2011, 87, 463–475. [Google Scholar] [CrossRef]
- Ridenour, N.A.; Straneo, F.; Holte, J.; Gratton, Y.; Myers, P.G.; Barber, D.G. Hudson Strait Inflow: Structure and Variability. J. Geophys. Res. Oceans 2021, 126, e2020JC017089. [Google Scholar] [CrossRef]
- Statham, S.; Ford, J.; Berrang-Ford, L.; Gough, W.; Siewierski, R.; Lardeau, M.P. Anomalous climatic conditions during winter 2010/11 and vulnerability of the traditional Inuit food system in Iqaluit, Nunavut. Polar Rec. 2015, 51, 301–317. [Google Scholar] [CrossRef]
- Gough, W.A.; Houser, C. Climate Memory and Long-Range Forecasting of Sea Ice Conditions in Hudson Strait. Polar Geogr. 2005, 29, 17–26. [Google Scholar] [CrossRef]
- Kowal, S.; Gough, W.A.; Butler, K. Temporal and Spatial Evolution of Seasonal Sea Ice of Arctic Bay, Nunavut. Coasts 2023, 3, 113–124. [Google Scholar] [CrossRef]
- Gagnon, A.S.; Gough, W.A. Trends in the Dates of Ice Freeze-up and Breakup over Hudson Bay, Canada. Arctic 2005, 58, 370–382. [Google Scholar] [CrossRef]
- Kowal, S.; Gough, W.A.; Butler, K. Temporal evolution of Hudson Bay Sea Ice (1971–2011). Theor. Appl. Clim. 2017, 127, 753–760. [Google Scholar] [CrossRef]
- Archer, L.; Ford, J.; Pearce, T.; Kowal, S.; Gough, W.A.; Allurut, M. Longitudinal assessment of climate vulner-ability: A case study from the Canadian Arctic. Sustain. Sci. 2017, 12, 15–29. [Google Scholar] [CrossRef]
- Etkin, D.A. Break-up in Hudson Strait: Its sensitivity to air temperatures and implications for climate warming. Climatol. Bull. 1991, 25, 21–34. [Google Scholar]
- Stirling, I.; Derocher, A.E. Possible Impacts of Climatic Warming on Polar Bears. Arctic 1993, 46, 240–245. [Google Scholar] [CrossRef]
- Neave, H.R.; Worthington, P.L. Distribution-Free Tests; Unwin Hyman Limited: London, UK, 1988. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 5th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Hochheim, K.P.; Barber, D.G. An Update on the Ice Climatology of the Hudson Bay System. Arct. Antarct. Alp. Res. 2014, 46, 66–83. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Crawford, A.D.; Stammerjohn, S. Using timing of ice retreat to predict timing of fall freeze-up in the Arctic. Geophys. Res. Lett. 2016, 43, 6332–6340. [Google Scholar] [CrossRef]




| Points | Significance | Slope (Days per Year) | Significance | Slope (Days per Year) | Significance | Slope (Days per Year) |
|---|---|---|---|---|---|---|
| 1971–2018 | 1971–2018 | 1971–1994 | 1971–1994 | 1995–2018 | 1995–2018 | |
| 1 | ***§ | −0.851 | NS | 0.024 | * | −1.000 |
| 2 | *** | −1.073 | * | −1.112 | NS | −0.410 |
| 3 | NS | 0.113 | NS | 0.639 | NS | 0.091 |
| 4 | ***§ | −1.160 | NS | −0.423 | *** | −2.463 |
| 5 | ** | −0.636 | NS | −0.286 | NS | −0.286 |
| 6 | ***§ | −0.447 | NS | 0.500 | ** | −1.186 |
| 7 | *** | −1.080 | NS | −0.721 | ** | −1.826 |
| 8 | **§ | −0.899 | NS | −1.056 | NS | 0.642 |
| 9 | ***§ | −1.074 | NS | −0.567 | NS | 0.000 |
| 10 | *** | −1.241 | ** | −1.290 | * | −1.233 |
| 11 | *** | −0.772 | NS | −0.422 | NS | −0.121 |
| 12 | ***§ | −0.915 | NS | −0.775 | NS | −0.472 |
| 13 | *** | −0.547 | NS | −0.367 | NS | −0.375 |
| 14 | ***§ | −1.156 | NS | −0.268 | NS | −1.250 |
| 15 | *** | −1.033 | *** | −1.442 | NS | −0.310 |
| 16 | *** | −1.000 | NS | −0.286 | NS | −0.390 |
| 17 | *** | −0.853 | NS | −0.662 | * | −1.243 |
| 18 | ***§ | −0.469 | NS | 0.396 | NS | −0.375 |
| 19 | ***§ | −0.198 | NS | 0.067 | NS | 0.321 |
| 20 | **§ | −1.143 | NS | −0.085 | NS | −1.225 |
| 21 | ***§ | −0.848 | NS | −0.787 | NS | −0.812 |
| 22 | ***§ | −0.667 | NS | −0.312 | NS | −0.642 |
| 23 | ***§ | −1.000 | * | −0.633 | NS | −0.214 |
| 24 | ***§ | −0.961 | NS | −0.636 | NS | −0.523 |
| Points | Significance | Slope (Days per Year) | Significance | Slope (Days per Year) | Significance | Slope (Days per Year) |
|---|---|---|---|---|---|---|
| 1971–2018 | 1971–2018 | 1971–1994 | 1971–1994 | 1995–2018 | 1995–2018 | |
| 1 | ***§ | 1.135 | NS | 0.400 | NS | 0.533 |
| 2 | ***§ | 0.667 | NS | 0.467 | NS | −0.385 |
| 3 | ***§ | 0.636 | NS | −0.167 | NS | −0.286 |
| 4 | *** | 0.587 | NS | 0.611 | NS | 0.000 |
| 5 | *** | 0.507 | NS | 0.250 | NS | −0.357 |
| 6 | *** | 0.588 | NS | 0.500 | NS | −0.100 |
| 7 | ***§ | 0.645 | NS | 0.000 | NS | −0.500 |
| 8 | *** | 0.417 | NS | 0.122 | NS | −0.091 |
| 9 | *** | 0.474 | NS | 0.100 | NS | 0.000 |
| 10 | *** | 0.500 | NS | 0.000 | NS | −0.571 |
| 11 | *** | 0.500 | NS | 0.667 | NS | 0.088 |
| 12 | *** | 0.545 | NS | 0.222 | NS | −0.261 |
| 13 | ** | 0.429 | NS | 0.333 | NS | −0.350 |
| 14 | *** | 0.526 | NS | 0.308 | NS | 0.033 |
| 15 | ** | 0.500 | NS | 0.000 | NS | −0.236 |
| 16 | ** | 0.571 | NS | 0.000 | NS | −0.095 |
| 17 | ** | 0.385 | NS | −0.231 | NS | −0.167 |
| 18 | ** | 0.389 | NS | 0.000 | NS | 0.000 |
| 19 | ***§ | 0.486 | NS | −0.200 | NS | −0.556 |
| 20 | *** | 0.634 | NS | 0.429 | NS | 0.000 |
| 21 | *** | 0.611 | NS | 0.250 | NS | 0.114 |
| 22 | ***§ | 0.500 | NS | 0.026 | NS | −0.581 |
| 23 | *** | 0.500 | NS | 0.067 | NS | 0.058 |
| 24 | ** | 0.667 | NS | 0.000 | NS | −0.367 |
| Points | Significance | Slope (Days per Year) | Significance | Slope (Days per Year) | Significance | Slope (Days per Year) |
|---|---|---|---|---|---|---|
| 1971–2018 | 1971–2018 | 1971–1994 | 1971–1994 | 1995–2018 | 1995–2018 | |
| 1 | *** | 2.000 | NS | 0.000 | *** | 2.059 |
| 2 | ***§ | 1.652 | NS | 0.750 | NS | −0.429 |
| 3 | ** | 0.525 | NS | −0.778 | NS | 0.000 |
| 4 | ***§ | 1.645 | NS | 0.000 | *** | 2.278 |
| 5 | *** | 1.077 | NS | 0.000 | NS | 0.000 |
| 6 | **§ | 0.913 | NS | −0.875 | NS | 0.931 |
| 7 | *** | 1.802 | NS | 0.636 | NS | 1.077 |
| 8 | *** | 1.217 | NS | 1.167 | NS | −1.136 |
| 9 | ***§ | 1.500 | NS | 0.000 | NS | 0.000 |
| 10 | *** | 1.778 | NS | 0.000 | NS | 0.080 |
| 11 | ***§ | 1.346 | NS | 1.400 | NS | 0.000 |
| 12 | *** | 1.400 | NS | 0.000 | NS | 1.167 |
| 13 | *** | 0.909 | NS | 1.167 | NS | 0.700 |
| 14 | ***§ | 1.826 | NS | 0.000 | NS | 1.856 |
| 15 | *** | 1.909 | *** | 2.100 | NS | −0.273 |
| 16 | ***§ | 1.923 | NS | 0.000 | NS | −0.214 |
| 17 | *** | 1.400 | NS | 0.000 | NS | 0.583 |
| 18 | * | 0.875 | NS | −1.000 | * | −1.235 |
| 19 | ***§ | 0.700 | NS | 0.000 | * | −0.947 |
| 20 | *** | 1.620 | NS | −0.700 | NS | 0.500 |
| 21 | *** | 1.200 | NS | 0.000 | NS | 0.319 |
| 22 | *** | 1.167 | NS | 0.000 | NS | 0.000 |
| 23 | ***§ | 1.470 | NS | 0.801 | NS | 0.500 |
| 24 | *** | 2.500 | NS | 1.273 | NS | 0.556 |
| Point | Cor | Det | Point | Cor | Det | Point | Cor | Det | Point | Cor | Det |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.37 | −0.07 | 7 | −0.42 | −0.13 | 13 | −0.15 | 0.00 | 19 | −0.41 | −0.30 |
| 2 | −0.34 | −0.09 | 8 | −0.48 | −0.34 | 14 | −0.41 | −0.22 | 20 | −0.32 | −0.11 |
| 3 | −0.12 | −0.23 | 9 | −0.40 | −0.16 | 15 | −0.43 | −0.26 | 21 | −0.23 | −0.12 |
| 4 | −0.40 | −0.09 | 10 | −0.40 | −0.22 | 16 | −0.28 | −0.03 | 22 | −0.34 | −0.23 |
| 5 | −0.63 | −0.43 | 11 | −0.47 | −0.25 | 17 | −0.30 | −0.18 | 23 | −0.42 | −0.20 |
| 6 | −0.49 | −0.16 | 12 | −0.15 | 0.11 | 18 | −0.09 | 0.02 | 24 | −0.32 | −0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowal, S.; Gough, W.A.; Butler, K. Spatial and Temporal Evolution of Seasonal Sea Ice Extent of Hudson Strait, Canada, 1971–2018. Climate 2024, 12, 103. https://doi.org/10.3390/cli12070103
Kowal S, Gough WA, Butler K. Spatial and Temporal Evolution of Seasonal Sea Ice Extent of Hudson Strait, Canada, 1971–2018. Climate. 2024; 12(7):103. https://doi.org/10.3390/cli12070103
Chicago/Turabian StyleKowal, Slawomir, William A. Gough, and Kenneth Butler. 2024. "Spatial and Temporal Evolution of Seasonal Sea Ice Extent of Hudson Strait, Canada, 1971–2018" Climate 12, no. 7: 103. https://doi.org/10.3390/cli12070103
APA StyleKowal, S., Gough, W. A., & Butler, K. (2024). Spatial and Temporal Evolution of Seasonal Sea Ice Extent of Hudson Strait, Canada, 1971–2018. Climate, 12(7), 103. https://doi.org/10.3390/cli12070103







