Impacts of Climate Variability and Change on Sorghum Crop Yield in the Babile District of Eastern Ethiopia
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.1.1. Climate
2.1.2. Topography and Land Features
2.2. Sources and Types of Data
2.3. Climate Models
2.4. Statistical Downscaling of Simple Delta Approach Technique for Future Climate
2.4.1. Analysis of Seasonal Rainfall Contribution
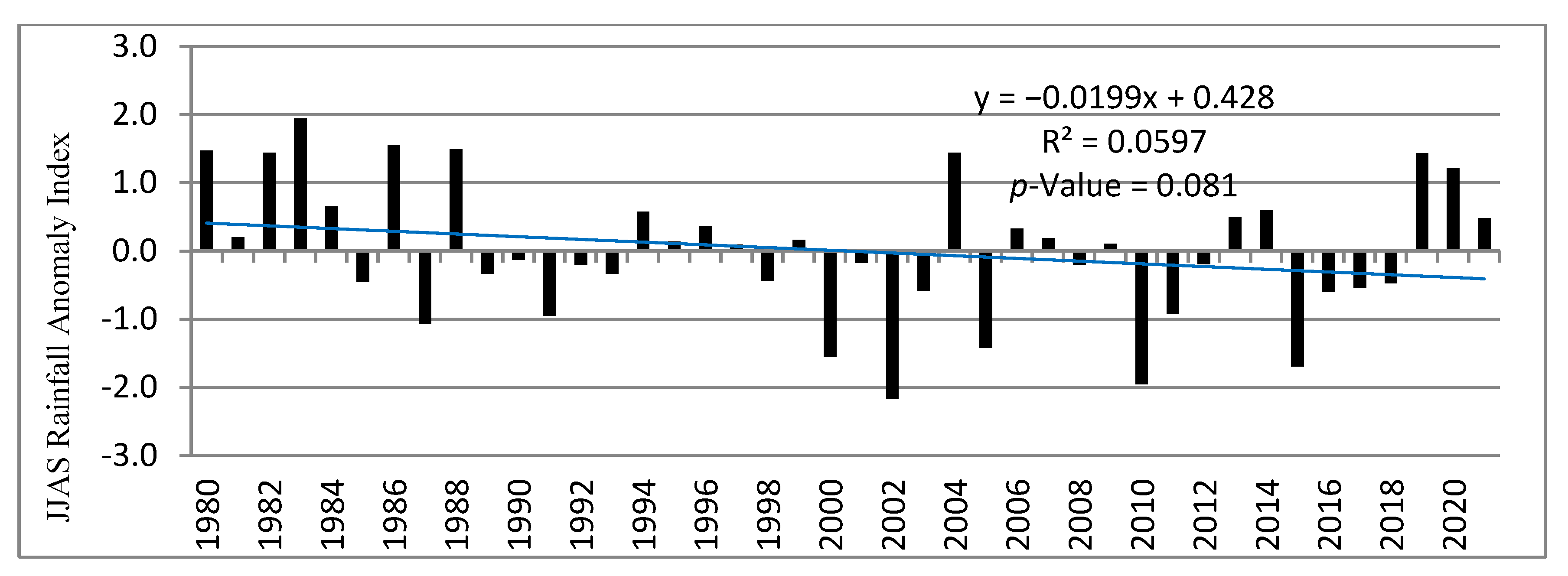
2.4.2. Inter-Seasonal to Seasonal Rainfall Anomaly Analysis
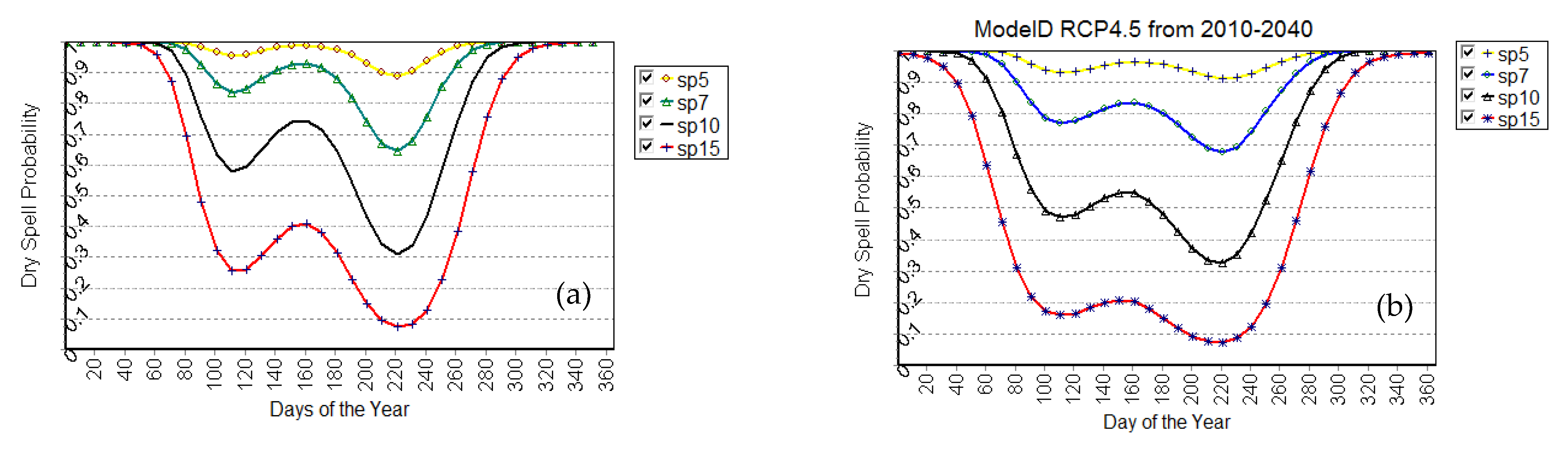
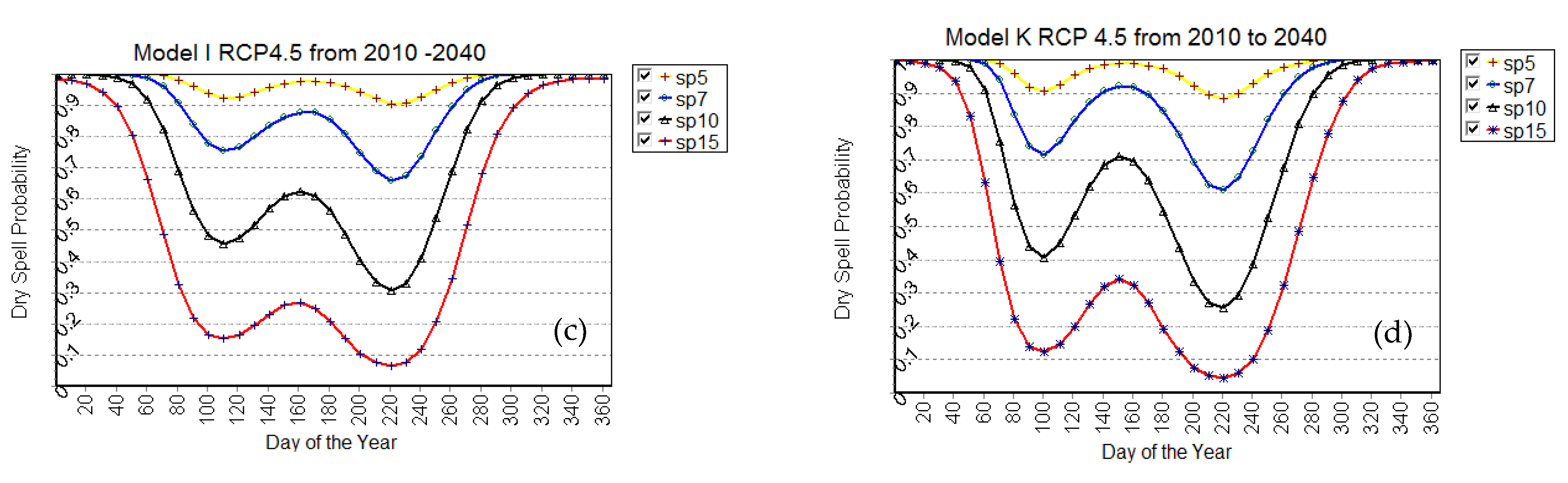
2.4.3. Seasonal Dry Spell Probability Analysis
2.4.4. Calculation of Growing Degree Days of the Sorghum Crop
2.5. Sorghum Crop Yield and Climate Variability Relationship
2.6. Sorghum Crop Grain Yield Responses to Climate Variability
2.7. Trend and Variability of Sorghum Crop Yield Analysis
3. Results and Discussion
3.1. Analysis of Observed Climate Variability
3.1.1. Extreme Temperature Variability Analysis
3.1.2. Variations in Rainfall Amounts and Number of Rainy Days
3.1.3. Variability and Anomalies in Seasonal Rainfall
3.2. Dry Spell Probability Analysis
3.3. Rainfall Trend and Variability Analysis over Babile District
3.4. Temperature Trend and Variability Analysis over Babile District
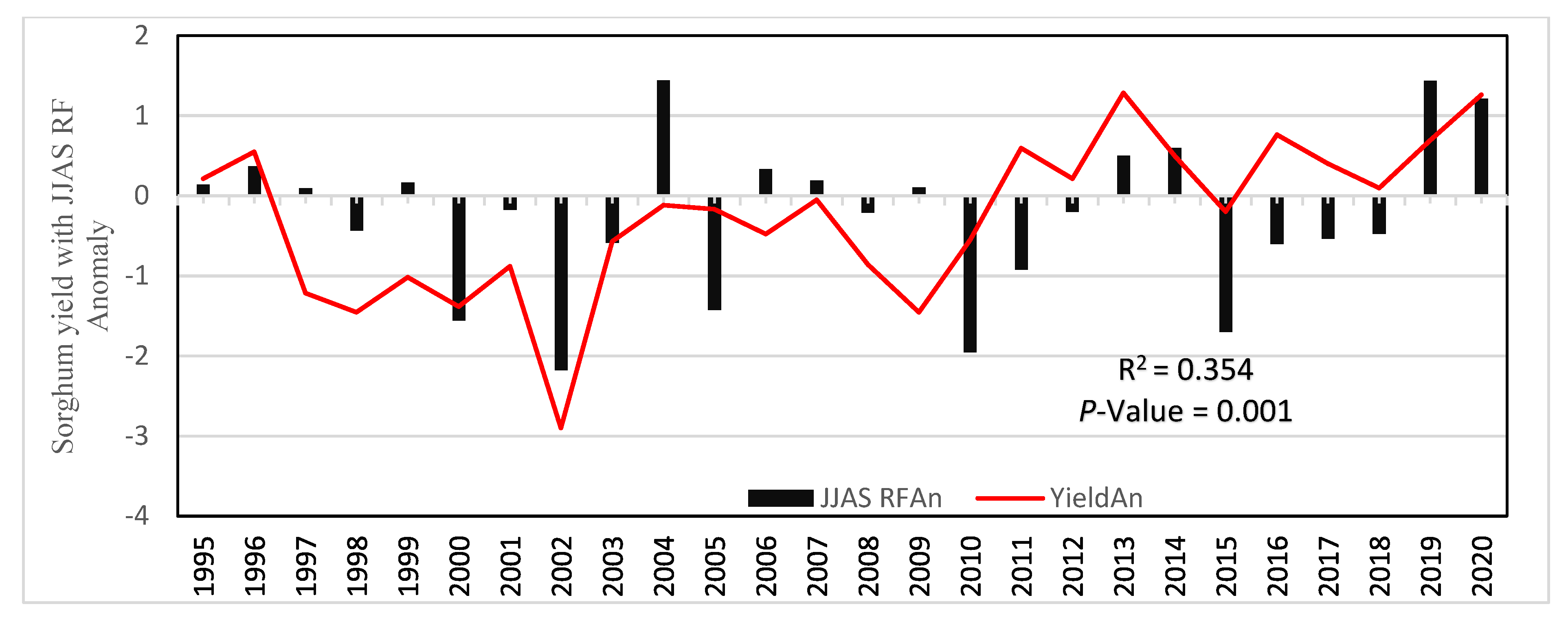
3.5. Sorghum Crop Production
3.6. Correlation and Regression of Sorghum versus its Growing Period Climate Variables
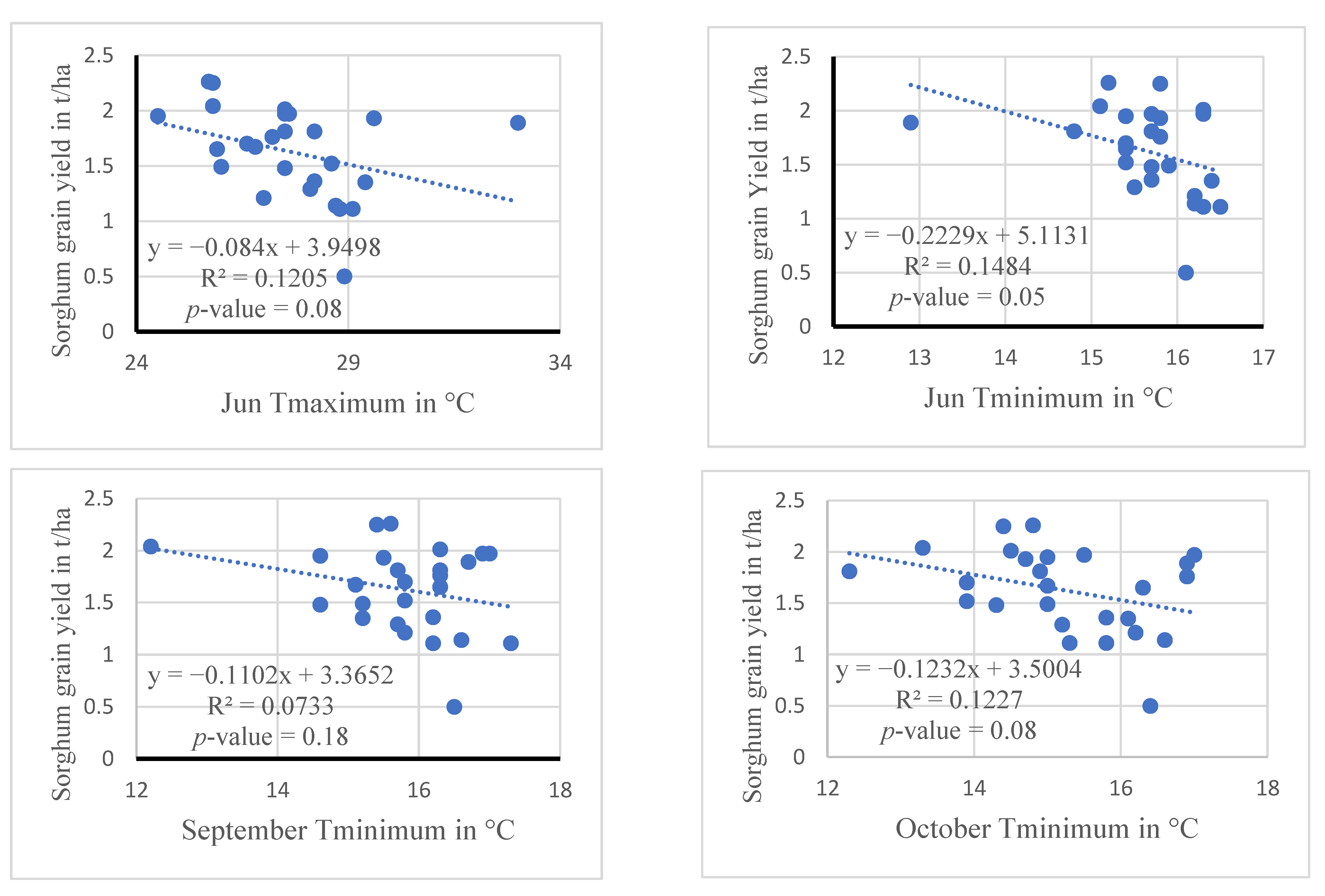
3.6.1. Analysis of Sorghum Grain Yield Response to Climate Variability
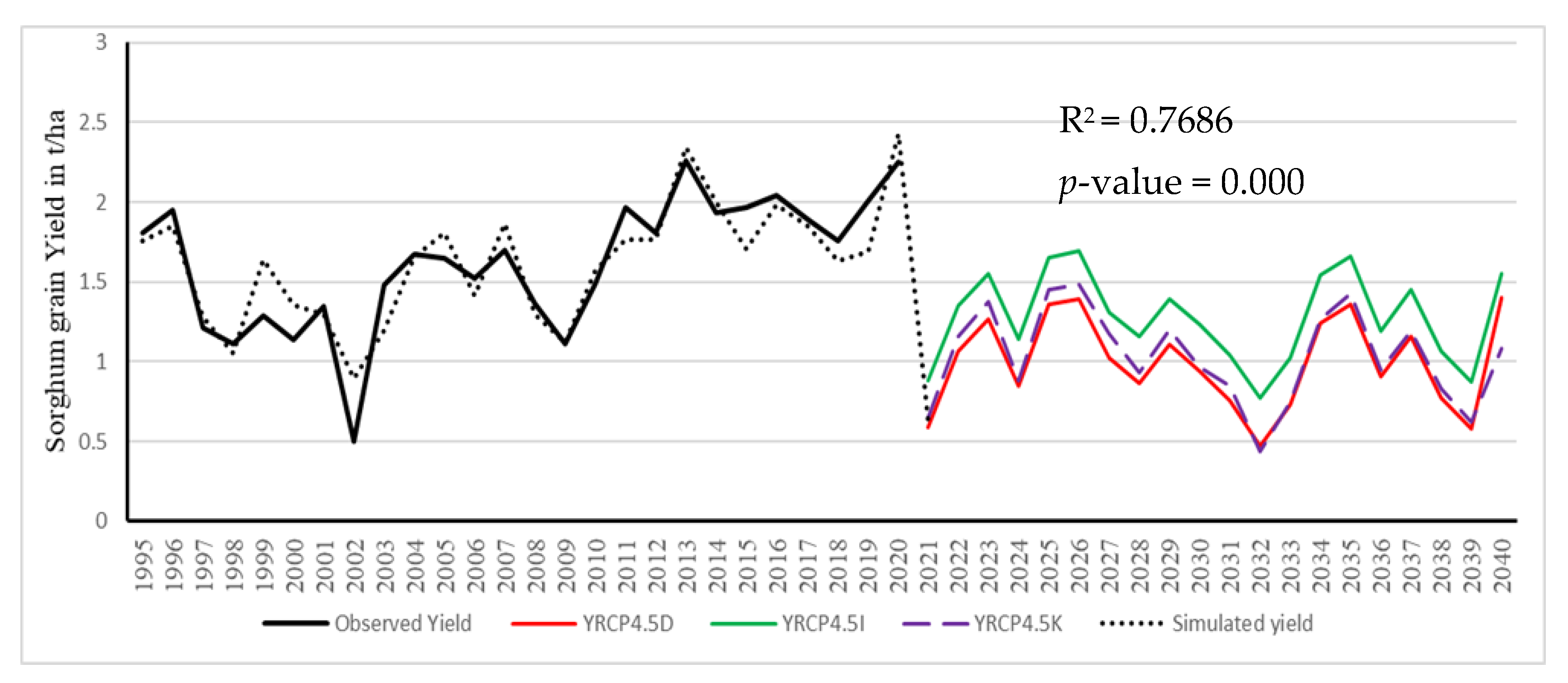
3.6.2. Sorghum Yield Prediction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Olayide, O.E.; Tetteh, I.K.; Popoola, L. Differential impacts of rainfall and irrigation on agricultural production in Nigeria: Any lessons for climate-smart agriculture? Agric. Water Manag. 2016, 178, 30–36. [Google Scholar] [CrossRef]
- Siebert, S.; Ewert, F. Future crop production threatened by extreme heat. Environ. Res. Lett. 2014, 9, 041001. [Google Scholar] [CrossRef]
- Yu, Q.; Li, L.; Luo, Q.; Eamus, D.; Xu, S.; Chen, C.; Wang, E.; Liu, J.; Nielsen, D.C. Year patterns of climate impact on wheat yields. Int. J. Clim. 2014, 34, 518–528. [Google Scholar] [CrossRef]
- IPCC. Climate Change. The Physical Science Basis. Working Group I Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- IPCC. Climate Change Fifth Assessment Synthesis Report of Inter-Governmental Panel of Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Vizy, E.K.; Cook, K.H. Seasonality of the observed amplified Sahara warming trend and implications for Sahel rainfall. J. Clim. 2017, 30, 3073–3094. [Google Scholar] [CrossRef]
- Endris, S.; Philip, O.; Suman, J.; Christopher, L.; Bruce, H.; Ladislaus, C.; Alessandro, D. Assessment of the Performance of CORDEX Regional Climate Models in Simulating East African Rainfall. Am. Meteorol. Soc. 2013, 26, 8453–8475. [Google Scholar]
- NMSA. Initial National Communication of Ethiopia to the UNFCCC; NMSA, National Meteorological Services Agency: Addis Ababa, Ethiopia, 2001. [Google Scholar]
- Aklilu, A.; Alebachew, A. Assessment of Climate Change-Induced Hazards, Impacts and Responses in the Southern Lowlands of Ethiopia; Forum for Social Studies: Addis Ababa, Ethiopia, 2009. [Google Scholar]
- Osman, M.A.A.; Onono, J.O.; Olaka, L.A.; Elhag, M.M.; Abdel-Rahman, E.M. Climate Variability and Change Affect Crops Yield under Rainfed Conditions: A Case Study in Gedaref State, Sudan. Agronomy 2021, 11, 1680. [Google Scholar] [CrossRef]
- Tesfaye, K. Field Comparison of Resource Utilization and Productivity of Three-Grain Legumes under Water Stress. Ph.D. Thesis, Agrometeorology, Department of Soil, Crop and Climate Sciences, University of the Free State, Bloemfontein, South Africa, 2004; pp. 12–37. [Google Scholar]
- Shumetie, A.; Alemayehu, M. Effect of Climate Variability on Crop Income and Indigenous Adaptation Strategies of Households. Int. J. Clim. Change Strateg. Manag. 2018, 10, 580–595. [Google Scholar] [CrossRef]
- WFP (World Food Program). Ethiopia Food Security Outlook; WFP: Rome, Italy, 2019. [Google Scholar]
- NMSA. Climate and Agro-Climatic Resources of Ethiopia, Meteorological Research Report Series; National Meteorological Services Agency: Addis Ababa, Ethiopia, 1996; Volume 1, p. 137. [Google Scholar]
- FEWS NET. Illustrating the Extent and Severity of Drought of Special Report in East Africa; FEWSNET Home Office: Washington, DC, USA, 2015; Available online: https://fews.net/east-africa/ethiopia/special-report/december-17-2015 (accessed on 1 January 2023).
- Srivastava, A.; Naresh Kumar, S.; Aggarwal, P.K. Assessment on the vulnerability of Sorghum to climate change in India. Agric. Ecosyst. Environ. 2010, 138, 160–169. [Google Scholar]
- CSA. The Federal Democratic Republic of Ethiopia Central Statistical Agency (CSA) Agricultural Sample Survey; Report on Area and Production of Major Crops; Statistical Bulletin; Central Statistical Agency of Ethiopia, CSA: Addis Ababa, Ethiopia, 2018; Volume I, 586p. [Google Scholar]
- FAOSTAT. Food and Agriculture Organization of the United Nations Database of Agricultural Production. FAO Statistical Databases. 2017. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 5 August 2022).
- Deb, U.K.; Bantilan, M.C.S.; Hash, C.T.; Ndjeunga, J. Adoption of Improved Sorghum Cultivars. In Sorghum Genetic Enhancement: Research Process, Dissemination, and Impacts; International Crops Research Institute for the Semi-Arid Tropics: Patancheru, India, 2004. [Google Scholar]
- Tolk, J.A.; Howell, T.A.; Miller, F.R. Yield component analysis of grain Sorghum grown under water stress. Field Crops Res. 2013, 145, 44–51. [Google Scholar]
- Borrell, A.K.; Mullet, J.E.; George-Jaeggli, B.; Osterom, V.E. Drought adaptation of stay-green cereals is associated with canopy development, leaf anatomy, root growth, and water uptake. J. Exp. Bot. 2014, 65, 6251–6263. [Google Scholar]
- Mar, S.; Nomura, H.; Takahashi, Y.; Ogata, K.; Yabe, M. Impact of erratic rainfall from climate change on pulse production efficiency in Lower Myanmar. Sustainability 2018, 10, 402. [Google Scholar] [CrossRef]
- Varshneya, M.C.; Sabale, R.N.; Bote, N.L.; Salunke, S.S.; More, D.B.; Thanedar, P.V. Response of CERES Sorghum model for different agroclimatic conditions. J. Agrometeorol. 2004, 6, 119–124. [Google Scholar] [CrossRef]
- FAO. Agricultural-Based Livelihood Systems in Dry Lands in the Context of Climate Change; FAO: Rome, Italy, 2010. [Google Scholar]
- FAO. Analysis of Climate Change and Variability Risks in the Smallholder Sector: Case Studies of the Laikipia and Narok Districts Representing Major Agro-Ecological Zones in Kenya. In Environmental and Natural Resources Working Paper; Gordon, O.O., Jaspat, A., Charles, S., Eds.; Department of Resource Surveys and Remote Sensing (DRSRS) in Collaboration with the Food and Agriculture Organization of the United Nations: Rome, Italy, 2010; Volume 41. [Google Scholar]
- MOA. Agro-Ecological Zones of Ethiopia. Natural Resources Management and Regulatory Department; With the Support of German Agency for Technical Cooperation (GTZ); MoA: Addis Ababa, Ethiopia, 1998. [Google Scholar]
- Rosenzweig, C.; Allen, L.H.; Jones, J.W.; Tsuji, G.Y.; Hildebrand, P. (Eds.) Climate Change and Agriculture: Analysis of Potential International Impacts (ASA Special Publication No. 59); American Society of Agronomy: Madison, WI, USA, 1995; p. 382. [Google Scholar]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E.; et al. Coauthors. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Change 2014, 109, 77–94. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Yang, J.; A Zaitlen, N.; E Goddard, M.; Visscher, P.M.; Price, A.L. Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet. 2014, 46, 100–106. [Google Scholar] [CrossRef]
- Martin, G.M.; Bellouin, N. HadGEM2 family of Met Office unified model climate configurations. Geosci. Model Dev. 2011, 4, 723–757. [Google Scholar]
- Chylek, P.; Dubey, J.; Wang, M.; Lesins, G. Observed and model simulated 20th century Arctic temperature variability: Canadian Earth system model CanESM2. Atmos. Chem. Phys. Discuss. 2011, 11, 22893–22907. [Google Scholar]
- Dunne, J.P.; John, J.G.; Shevliakova, E.N.; Stouffer, R.J.; Krasting, J.P.; Malyshev, S.L.; Milly, P.C.; Sentman, L.T.; Adcroft, A.J.; Cooke, W.; et al. GFDL’s ESM2 global coupled climate-carbon Earth System Models Part II: Carbon system formulation and baseline simulation characteristics. J. Clim. 2013, 26, 2247–2267. [Google Scholar] [CrossRef]
- Marie, E.; Michael, R.; Penny, H. An appraisal of downscaling methods used in climate change research. WIREs Clim. Change 2015, 6, 301–319. [Google Scholar]
- Hennemuth, B.; Bender, S.; Bülow, K.; Dreier, N.; Keup-Thiel, E.; Krüger, O.; Mudersbach, C.; Radermacher, C.; Schoetter, R. Statistical Methods for the Analysis of Simulated and Observed Climate Data, Applied in Projects and Institutions Dealing with Climate Change Impact and Adaptation; CSC Report 13; Climate Service Center: Hamburg, Germany, 2013. [Google Scholar]
- Patle, G.T.; Singh, D.K.; Sarangi, A.; Rai, A.; Khanna, M.; Saoo, R.N. Temporal variability of climatic parameters and potential evapotranspiration. Indian J. Agric. Sci. 2013, 83, 518–524. [Google Scholar]
- Zhao, C.; Jianguo, C.; Peng, D.; Hongyong, Y. Characteristics of Climate Change and Extreme Weather from 1951 to 2011 in China. Int. J. Environ. Res. Public Health 2018, 15, 2540. [Google Scholar] [CrossRef]
- Hare, W. Assessment of Knowledge on Impacts of Climate Change, Contribution to the Specification of Art, 2 of the UNFCCC; WBGU: Berlin, Germany, 2003. [Google Scholar]
- Van Rooy, M.P. A Rainfall anomaly index (RAI) independent of time and space. Notos 1965, 575, 43–48. [Google Scholar]
- Rahim, A. Analysis of Annual Precipitation and Water Table Changes in Shahrekord Aquifer. Int. J. Curr. Microbiol. App. Sci. 2018, 7, 560–568. [Google Scholar]
- Stern, R.; Knock, J.; Rijks, D.; Dale, I. INSTAT Climatic Guide. 2003, p. 398. Available online: http://www.reading.ac.uk/ssc/software/instat/climatic.pdf (accessed on 10 July 2022).
- Tadross, M.; Suarez, P.; Lotsch, A.; Hachigonta, S.; Mdoka, M.; Unganai, L.; Lucio, F.; Kamdonyo, F.; Muchinda, M. Growing-season rainfall and scenarios of future change in southeast Africa: Implications for cultivating maize. Climate Res. 2009, 40, 147–161. [Google Scholar] [CrossRef]
- Baskerville, G.L.; Emin, P. Rapid Estimation of Heat Accumulation from Maximum and Minimum Temperatures. Ecology 1969, 50, 514–517. [Google Scholar] [CrossRef]
- Plessis, D.U.J. Sorghum Production. Republic of South Africa Department of Agriculture. 2008. Available online: www.nda.agric.za/publications (accessed on 15 October 2022).
- Owusu, K.; Waylen, P.R. Identification of historic shifts in daily rainfall regime, Wenchi, Ghana. Clim. Change 2013, 117, 133–147. [Google Scholar] [CrossRef]
- Baffour-Ata, F.; Antwi-Agyei, P.; Nkiaka, E.; Dougill, A.J.; Anning, A.K.; Kwakye, S.O. Effect of climate variability on yields of selected staple food crops in northern Ghana. J. Agric. Food Res. 2021, 6, 100205. [Google Scholar] [CrossRef]
- Hsiang, S.M. Climate econometrics. Annu. Rev. Resour. Econ. 2016, 8, 43–75. [Google Scholar] [CrossRef]
- Miao, R.; Khanna, M.; Huang, H. Responsiveness of crop yield and acreage to prices and climate. Am. J. Agric. Econ. 2016, 98, 191–211. [Google Scholar] [CrossRef]
- Najafi, E.; Devineni, N.; Khanbilvardi, R.M.; Kogan, F. Understanding the changes in global crop yields through changes in climate and technology. Earth’s Future 2018, 6, 410–427. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Theil, H.A. Rank-Invariant Method of Linear and Polynomial Analysis; Part 3. Nederlandse Akademie van Wettenschappen. Proceedings; Springer: Dordrecht, The Netherlands, 1950; Volume 53, pp. 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Silva, R.M.; Santos, C.A.G.; Macedo, M.L.A.; Silva, L.; Freire, P.K.M.M. Space–time variability of rainfall and hydrological trends in the Alto São Francisco River basin. In Proceedings of the H01, IAHS-IAPSO-IASPEI Assembly, Gothenburg, Sweden, 22–26 July 2013; Volume 359, pp. 48–54. [Google Scholar]
- Fazzini, M.; Bisci, C.; Billi, P. The Climate of Ethiopia. In Landscapes and Landforms of Ethiopia; Billi, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Yilma, S.; Zanke, U. Recent changes in rainfall and rainy days in Ethiopia. Int. J. Clim. 2004, 24, 973–983. [Google Scholar] [CrossRef]
- Viste, E.; Korecha, D.; Sorteberg, A. Recent drought precipitation trends in Ethiopia. Theor. Appl. Clim. 2012, 112, 535–551. [Google Scholar] [CrossRef]
- Arragaw, A.; Woldeamlak, B. Local spatiotemporal variability and trends in rainfall and temperature in the central highlands of Ethiopia. Geogr. Ann. Phys. Geogr. 2017, 99, 85–101. [Google Scholar] [CrossRef]
- Anyah, R.O.; Qiu, W. Characteristic 20th and 21st Century Precipitation and Temperature Patterns and Changes over the Greater Horn of Africa. Int. J. Clim. 2012, 32, 347–363. [Google Scholar] [CrossRef]
- Endris, H.S.; Lennard, C.; Hewitson, B.; Dosio, A.; Nikulin, G.; Panitz, H.-J. Teleconnection responses in multi-GCM driven CORDEX RCMs over Eastern Africa. Clim. Dyn. 2015, 46, 2821–2846. [Google Scholar] [CrossRef]
- Mpelasoka, F.; Awange, J.L.; Zerihun, A. Influence of coupled ocean-atmosphere phenomena on the Greater Horn of Africa droughts and their implications. Sci. Total Environ. 2018, 610–611, 691–702. [Google Scholar] [CrossRef]
- Teshome, H.; Tesfaye, K.; Dechassa, N.; Tana, T.; Huber, M. Analysis of Past and Projected Trends of Rainfall and Temperature Parameters in Eastern and Western Hararghe Zones, Ethiopia. Atmosphere 2022, 13, 67. [Google Scholar] [CrossRef]
- Weldegebriel, Z.; Prowse, M.P. Climate change adaptation in Ethiopia: To what extent does social protection influence livelihood diversification? Dev. Policy Rev. 2013, 31 (Suppl. S2), 35–56. [Google Scholar] [CrossRef]
- Hochman, Z.; Gobbett, D.; Holzworth, D.; McClelland, T.; Rees, H.V.; Marinoni, O.; Garcia, J.N.; Horan, H. Reprint of “Quantifying Yield Gaps in Rainfed Cropping Systems: A Case Study of Wheat in Australia”. Field Crops Res. 2013, 143, 65–75. [Google Scholar] [CrossRef]
- Tsheko, R.; Tapela, M.; Mashungwa, G.; Kayombo, B. Sorghum yield and associated satellite-derived meteorological parameters in semi-arid Botswana. Afr. Crop Sci. J. 2015, 23, 151–164. [Google Scholar]
- Teka, B.A.; Girma, M.D.; Alemayehu, R.T. Impact of climate variability on rain-fed maize and Sorghum yield among smallholder farmers. Cogent Food Agric. 2022, 8, 2057656. [Google Scholar]
- Workneh, B. Analysis of production, yield and cultivation area trends in major cereal crops in Ethiopia. Agric. For. Fish. 2021, 10, 123. [Google Scholar] [CrossRef]
- Hargreaves, G.L.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Knox, J.; Daccache, A.; Wheeler, T. Climate change impacts on crop productivity in Africa and South Asia. Environ. Res. Lett. 2012, 7, 8. [Google Scholar] [CrossRef]
- Berg, A.; Noblet-Ducoudr’e, N.; Sultan, B.; Lengaigne, N.; Guimberteau, M. Projections of climate change impacts on potential C4 crop productivity over tropical regions. Agric. For. Meteorol. 2013, 170, 89–102. [Google Scholar] [CrossRef]
- Waha, K.; Müller, C.; Rolinski, C. Separate and combined effects of temperature and rainfall change on maize yields in sub-Saharan Africa for a mid-to late-21st century. Glob. Planet. Change 2013, 106, 1–12. [Google Scholar] [CrossRef]



| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Annual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tx | 36.6 | 36.6 | 37.5 | 38.8 | 36.0 | 36.4 | 36.6 | 36.5 | 35.6 | 38.6 | 37.6 | 36.6 | 38.8 |
| Tn | 4.5 | 6.0 | 6.0 | 9.6 | 11.5 | 9.0 | 10.0 | 11.0 | 9.0 | 6.5 | 4.0 | 6.0 | 4.0 |
| Txmean | 30.2 | 31.4 | 31.2 | 29.2 | 28.5 | 27.5 | 26.2 | 26.6 | 27.4 | 28.8 | 29.3 | 29.6 | 28.8 |
| Tnmean | 14.2 | 15.2 | 16.5 | 16.9 | 16.8 | 15.7 | 15.5 | 15.5 | 15.6 | 15.3 | 13.9 | 13.4 | 15.4 |
| Tmean | 22.2 | 23.3 | 23.8 | 23 | 22.6 | 21.6 | 20.9 | 21.1 | 21.5 | 22.1 | 21.6 | 21.5 | 22.1 |
| Temporal Rainfall Distribution (mm) | Number of Rainy Days (NRD) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | Min | Max | Avg | SD | CV% | Cbn% | Min | Max | Avg | SD | CV% |
| Jan | 0.0 | 27.3 | 4.2 | 7.8 | 185.7 | 0.6 | 0 | 7 | 0.9 | 1.8 | 200.0 |
| Feb | 0.0 | 87.6 | 8.9 | 17.5 | 196.6 | 1.2 | 0 | 7 | 1.5 | 1.9 | 126.7 |
| Mar | 0.0 | 251.7 | 55.8 | 63.0 | 113.0 | 7.6 | 0 | 19 | 5.4 | 4.8 | 88.9 |
| Apr | 12.2 | 431.3 | 133.1 | 95.5 | 71.8 | 18.2 | 1 | 23 | 10.6 | 5.6 | 52.8 |
| May | 0.0 | 252.1 | 112.0 | 75.8 | 67.7 | 15.3 | 0 | 30 | 12.4 | 8.5 | 68.5 |
| Jun | 0.0 | 276.4 | 76.6 | 59.0 | 77.0 | 10.5 | 0 | 26 | 9.8 | 7.4 | 75.5 |
| Jul | 0.0 | 191.0 | 64.5 | 49.6 | 76.9 | 8.8 | 0 | 23 | 8.8 | 6.4 | 72.7 |
| Aug | 5.3 | 241.9 | 92.9 | 45.0 | 48.4 | 12.7 | 2 | 29 | 12.1 | 6.2 | 51.2 |
| Sep | 0.7 | 286.9 | 100.6 | 65.0 | 64.6 | 13.8 | 0.0 | 27.0 | 12.2 | 5.6 | 45.9 |
| Oct | 0.0 | 334.1 | 61.0 | 68.6 | 112.5 | 8.3 | 0.0 | 25.0 | 6.5 | 6.4 | 98.5 |
| Nov | 0.0 | 68.2 | 12.9 | 18.1 | 140.3 | 1.8 | 0.0 | 10.0 | 2.1 | 2.5 | 119.0 |
| Dec | 0.0 | 104.8 | 8.6 | 21.0 | 244.2 | 1.2 | 0.0 | 5.0 | 0.9 | 1.5 | 166.7 |
| MAM | 57.1 | 656.6 | 301.0 | 142.5 | 47.3 | 41.2 | 9.0 | 56.0 | 28.4 | 14.0 | 49.3 |
| JJAS | 43.3 | 569.5 | 334.6 | 125.7 | 37.6 | 45.8 | 9.0 | 89.0 | 43.0 | 21.6 | 50.2 |
| Annual | 112.5 | 1240 | 731.2 | 232 | 31.7 | 100.0 | 25.0 | 176 | 83.2 | 41.3 | 49.0 |
| RAI Range | Category of the Occurrence of Drought | The Intensity of Drought in % during MAM | The Intensity of Drought in % during JJAS | ||
|---|---|---|---|---|---|
| −0.99 ≤ RAI < 0.0 | Mild dryness | 17 years | 41.5% | 15 years | 36.6% |
| −1.0 ≤ RAI ≤ −1.99 | Moderate dryness | 4 years | 9.8% | 4 years | 9.8% |
| −2.0 ≤ SPI ≤ −2.99 | Severe dryness | 1 year | 2.4% | 2 years | 4.9% |
| ≤−3.0 | Extreme dryness | 0 | 0 | 0 | 0 |
| CanESM2 (1980–2040) | HadGEM2 (1980–2040) | GFDLESM2M (1980–2040) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time Series | MKZ | Sen’s Slope | p-Value | CV% | MKZ | Sen’s Slope | p-Value | CV% | MKZ | Sen’s Slope | p-Value | CV% |
| Jan | 1.03 | 0.0 | 0.30 | 201 | 0.41 | 0.0 | 0.68 | 238 | 1.06 | 0.0 | 0.29 | 202 |
| Feb | −0.45 | 0.0 | 0.65 | 186 | −0.44 | 0.0 | 0.66 | 185 | 0.39 | 0.0 | 0.69 | 177 |
| Mar | 1.11 | 0.26 | 0.27 | 112 | 1.34 | 0.39 | 0.18 | 112 | 0.62 | 0.09 | 0.53 | 114 |
| Apr | −1.02 | −0.56 | 0.31 | 72 | 0.63 | 0.35 | 0.53 | 69 | −1.45 | −0.65 | 0.15 | 72 |
| May | −1.31 | −0.59 | 0.19 | 71 | −1.17 | −0.54 | 0.24 | 70 | −0.39 | −0.2 | 0.69 | 69 |
| Jun | −1.47 | −0.41 | 0.14 | 80 | −3.35 | −0.8 * | 0.01 | 91 | −0.37 | −0.13 | 0.71 | 76 |
| Jul | 1.07 | 0.28 | 0.28 | 73 | −0.16 | −0.05 | 0.87 | 74 | 0.40 | 0.15 | 0.68 | 73 |
| Aug | −4.43 | −1.16 * | 0.00 | 54 | −3.48 | −0.88 * | 0.00 | 50 | −4.54 | −1.19 * | 0.00 | 55 |
| Sep | −1.64 | −0.57 | 0.10 | 63 | −3.52 | −1.02 * | 0.00 | 70 | −1.64 | −0.57 | 0.10 | 62 |
| Oct | 0.72 | 0.24 | 0.47 | 121 | 0.06 | 0.01 | 0.95 | 112 | 0.11 | 0.01 | 0.91 | 113 |
| Nov | 2.33 | 0.16 * | 0.02 | 158 | 0.88 | 0.0 | 0.38 | 156 | 1.21 | 0.0 | 0.23 | 153 |
| Dec | −0.01 | 0.0 | 0.99 | 244 | 0.18 | 0.0 | 0.86 | 234 | 0.35 | 0.0 | 0.73 | 225 |
| MAM | −0.87 | −0.94 | 0.39 | 50 | 0.43 | 0.51 | 0.67 | 49 | −0.81 | −0.66 | 0.42 | 49 |
| JJAS | −2.53 | −1.98 * | 0.01 | 40 | −4.17 | −3.29* | 0.00 | 44 | −2.49 | −1.96 * | 0.01 | 39 |
| Annual | −0.79 | −1.47 | 0.43 | 33 | −1.44 | −2.39 | 0.15 | 33 | −1.34 | −2.20 | 0.18 | 32 |
| CanESM2 (1980–2040) | HadGEM2 (1980–2040) | GFDLESM2M (1980–2040) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time Series | MKZ | Sen’s Slope | p-Value | CV% | MKZ | Sen’s Slope | p-Value | CV% | MKZ | Sen’s Slope | p-Value | CV% |
| Jan | 4.48 | 0.04 * | 0.00 | 4.2 | 5.25 | 0.05 * | 0.00 | 4.6 | 4.79 | 0.043 * | 0.00 | 4.3 |
| Feb | 5.09 | 0.07 * | 0.00 | 6.3 | 4.91 | 0.06 * | 0.00 | 6.1 | 3.92 | 0.045 * | 0.00 | 5.6 |
| Mar | 4.51 | 0.06 * | 0.00 | 6.8 | 4.26 | 0.056 * | 0.00 | 6.6 | 4.12 | 0.053 * | 0.00 | 6.5 |
| Apr | 3.39 | 0.05 * | 0.00 | 6.9 | 3.28 | 0.045 * | 0.00 | 6.9 | 3.13 | 0.043 * | 0.00 | 6.9 |
| May | 3.73 | 0.05 * | 0.00 | 6.8 | 3.96 | 0.056 * | 0.00 | 6.9 | 3.51 | 0.047 * | 0.00 | 6.7 |
| Jun | 2.57 | 0.03 * | 0.01 | 6.2 | 2.42 | 0.031 * | 0.02 | 6.1 | 1.99 | 0.025 * | 0.05 | 6.0 |
| Jul | 2.18 | 0.02 * | 0.03 | 4.9 | 2.18 | 0.021 * | 0.03 | 4.9 | 3.20 | 0.033 * | 0.00 | 5.2 |
| Aug | 2.47 | 0.02 * | 0.01 | 4.5 | 2.47 | 0.022 * | 0.01 | 4.5 | 4.88 | 0.054 * | 0.00 | 5.4 |
| Sep | 3.06 | 0.03 * | 0.00 | 5.0 | 4.60 | 0.052 * | 0.00 | 5.7 | 2.37 | 0.022 * | 0.02 | 4.9 |
| Oct | 3.64 | 0.04 * | 0.00 | 6.3 | 3.73 | 0.041 * | 0.00 | 6.3 | 3.19 | 0.033 * | 0.00 | 6.2 |
| Nov | 2.76 | 0.03 * | 0.01 | 5.5 | 4.02 | 0.042 * | 0.00 | 5.8 | 2.21 | 0.019 * | 0.03 | 5.4 |
| Dec | 4.14 | 0.04 * | 0.00 | 5.3 | 3.93 | 0.035 * | 0.00 | 5.3 | 3.93 | 0.035 * | 0.00 | 5.3 |
| MAM | 4.77 | 0.06 * | 0.00 | 5.6 | 4.73 | 0.056 * | 0.00 | 5.6 | 4.51 | 0.051 * | 0.00 | 5.4 |
| JJAS | 3.33 | 0.03 * | 0.00 | 3.9 | 3.70 | 0.031 * | 0.00 | 4.0 | 3.89 | 0.033 * | 0.00 | 4.1 |
| Annual | 6.19 | 0.04 * | 0.00 | 3.4 | 6.50 | 0.043 * | 0.00 | 3.5 | 5.93 | 0.039 * | 0.00 | 3.3 |
| CanESM2 (1980–2040) | HadGEM2 (1980–2040) | GFDLESM2M (1980–2040) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time Series | MKZ | Sen’s Slope | p-Value | CV% | MKZ | Sen’s Slope | p-Value | CV% | MKZ | Sen’s Slope | p-Value | CV% |
| Jan | 1.14 | 0.02 | 0.25 | 18 | 0.73 | 0.01 | 0.46 | 19 | 0.73 | 0.01 | 0.46 | 19 |
| Feb | 1.71 | 0.03 | 0.08 | 15 | 1.05 | 0.02 | 0.28 | 16 | 0.00 | 0.0 | 0.99 | 16 |
| Mar | 3.97 | 0.07 * | 0.00 | 14 | 1.34 | 0.02 | 0.18 | 14 | 0.89 | 0.01 | 0.37 | 15 |
| Apr | 4.89 | 0.05 * | 0.00 | 9 | 3.26 | 0.03 * | 0.00 | 8 | 3.77 | 0.03 * | 0.00 | 9 |
| May | 4.91 | 0.04 * | 0.00 | 7 | 4.51 | 0.03 * | 0.00 | 7 | 4.31 | 0.03 * | 0.00 | 7 |
| Jun | 3.86 | 0.03 * | 0.00 | 8 | 2.76 | 0.02 * | 0.01 | 7 | 1.69 | 0.01 * | 0.09 | 7 |
| Jul | 3.26 | 0.02 * | 0.00 | 8 | 2.49 | 0.02 * | 0.01 | 8 | 2.73 | 0.02 * | 0.01 | 8 |
| Aug | 4.15 | 0.03 * | 0.00 | 5 | 3.84 | 0.02 * | 0.00 | 5 | 5.02 | 0.03 * | 0.00 | 6 |
| Sep | 5.45 | 0.04 * | 0.00 | 7 | 5.20 | 0.04 * | 0.00 | 6 | 2.34 | 0.02 * | 0.02 | 6 |
| Oct | 3.85 | 0.06 * | 0.00 | 13 | 2.69 | 0.03 * | 0.01 | 12 | 1.86 | 0.02 | 0.06 | 12 |
| Nov | 3.12 | 0.04 * | 0.00 | 14 | 1.90 | 0.02 * | 0.05 | 14 | 1.07 | 0.01 | 0.28 | 15 |
| Dec | 2.37 | 0.04 * | 0.02 | 15 | 1.95 | 0.03 * | 0.05 | 15 | 1.37 | 0.02 | 0.17 | 15 |
| MAM | 4.81 | 0.05 * | 0.00 | 9 | 2.74 | 0.02 * | 0.01 | 8 | 2.55 | 0.02 * | 0.01 | 8 |
| JJAS | 4.82 | 0.03 * | 0.00 | 6 | 4.1 | 0.03 * | 0.00 | 6 | 3.60 | 0.02 * | 0.00 | 5 |
| Annual | 3.39 | 0.03 * | 0.00 | 8 | 2.30 | 0.02 * | 0.02 | 8 | 1.64 | 0.01 | 0.10 | 8 |
| Variables | Mean | Std. dev | CV | Min | Max | Corre | t-Value | p-Value | R2 |
|---|---|---|---|---|---|---|---|---|---|
| Grain yields (t/ha) | 1.62 | 4.1 | 25.3 | 0.5 | 2.26 | ||||
| (GDDs) May–November | 2594.4 | 181.0 | 7.0 | 2170.2 | 3039.1 | 0.2 | 0.473 | 0.064 | 0.092 |
| May RF (mm) | 106.7 | 76.9 | 72.1 | 0 | 255.6 | 0.23 | 1.154 | 0.260 | 0.052 |
| June RF (mm) | 56 | 42.7 | 76.3 | 0 | 173.4 | 0.12 | 0.567 | 0.575 | 0.015 |
| July RF (mm) | 75.2 | 42.8 | 56.9 | 5.8 | 190.8 | 0.27 | 1.365 | 0.185 | 0.072 |
| August RF (mm) | 82.6 | 45.1 | 54.6 | 5.3 | 201.8 | 0.34 | 1.761 | 0.051 * | 0.115 |
| September RF(mm) | 79.4 | 54.2 | 68.3 | 0.7 | 233.5 | 0.39 | 2.102 | 0.046 * | 0.156 |
| JJAS RF (mm) | 292.1 | 106.3 | 36.4 | 43.3 | 505.6 | 0.26 | 1.322 | 0.199 | 0.068 |
| NRD in Sept (days) | 11 | 7.0 | 63.6 | 0 | 26 | 0.31 | 1.595 | 0.063 | 0.096 |
| MayTmax (°C) | 28 | 2.0 | 7.0 | 25.7 | 32.5 | −0.37 | −1.923 | 0.066 | 0.134 |
| JunTmax (°C) | 27.7 | 1.7 | 6.1 | 24.5 | 33.0 | −0.35 | −1.813 | 0.082 | 0.121 |
| SeptTmax (°C) | 27.8 | 1.6 | 5.8 | 25.3 | 32.2 | −0.24 | −1.217 | 0.235 | 0.058 |
| JunTmin (°C) | 15.7 | 0.7 | 4.5 | 12.9 | 16.5 | −0.39 | −2.045 | 0.05 * | 0.148 |
| AugTmin (°C) | 15.6 | 0.6 | 3.9 | 14.4 | 16.4 | −0.24 | −1.221 | 0.233 | 0.059 |
| SeptTmin (°C) | 15.8 | 1.0 | 6.4 | 12.2 | 17.3 | −0.27 | −1.377 | 0.181 | 0.073 |
| OctTmin(°C) | 15.2 | 1.2 | 7.7 | 12.3 | 17.0 | −0.35 | −1.832 | 0.079 | 0.123 |
| Parameter | Estimate | Std. Error | t-Value | Pr (>|t|) |
|---|---|---|---|---|
| (Intercept) | 7.6585998 | 1.3591759 | 5.635 | 1.63 × 10−5 * |
| JunTmin | −0.3606583 | 0.0608823 | −5.924 | 8.56 × 10−6 * |
| GDDMN | 0.0014246 | 0.0002712 | 5.253 | 3.85 × 10−5 * |
| JunTmax | −0.1712791 | 0.0261689 | −6.545 | 2.23 × 10−6 * |
| AugRF | 0.0037350 | 0.0008755 | 4.266 | 0.000377 * |
| Sept NRD | 0.0276674 | 0.0075862 | 3.647 | 0.001603 * |
| R-squared (R2) | 0.7686 | 1.015 × 10−6 * | ||
| F-statistics | 17.61 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tolosa, A.A.; Dadi, D.K.; Mirkena, L.W.; Erena, Z.B.; Liban, F.M. Impacts of Climate Variability and Change on Sorghum Crop Yield in the Babile District of Eastern Ethiopia. Climate 2023, 11, 99. https://doi.org/10.3390/cli11050099
Tolosa AA, Dadi DK, Mirkena LW, Erena ZB, Liban FM. Impacts of Climate Variability and Change on Sorghum Crop Yield in the Babile District of Eastern Ethiopia. Climate. 2023; 11(5):99. https://doi.org/10.3390/cli11050099
Chicago/Turabian StyleTolosa, Abdisa Alemu, Diriba Korecha Dadi, Lemma Wogi Mirkena, Zelalem Bekeko Erena, and Feyera Merga Liban. 2023. "Impacts of Climate Variability and Change on Sorghum Crop Yield in the Babile District of Eastern Ethiopia" Climate 11, no. 5: 99. https://doi.org/10.3390/cli11050099
APA StyleTolosa, A. A., Dadi, D. K., Mirkena, L. W., Erena, Z. B., & Liban, F. M. (2023). Impacts of Climate Variability and Change on Sorghum Crop Yield in the Babile District of Eastern Ethiopia. Climate, 11(5), 99. https://doi.org/10.3390/cli11050099






