Abstract
The aim of this work is to study the variability of winter (monthly mean of DJF) air temperatures in Saudi Arabia. The study of the coefficient of variation (CV) of winter air temperature time series shows that the CV is a function of latitude, decreasing generally gradually from north to south. The highest values of CV during the winter season are mainly because of the migrating extratropical cyclones (Mediterranean cyclones) from west to east, and active subtropical jet, as well as the polar jet. The trend analysis illustrates that all stations have positive trends for the wintertime series. The study of decadal fluctuations in the behavior of winter temperature shows that the period from 1982 to 2010 is characterized in general by negative trend values in most northern stations of Saudi Arabia. In the middle of Saudi Arabia, negative trend values also appear but for the period 1983 to 2003. The southern and middle stations are distinguished by a positive trend during the period from 2003 to 2018.
1. Introduction
One of the most significant elements of climate is the air temperature because of its importance in surface-atmospheric processes and interactions [1]. Surface air temperature changes are important in a number of environmental, ecological, hydrological, and sociological applications. Analysis of trends in climate variables has led to an improved knowledge of the climate and facilitated the development of effective adaptation strategies at both global and local levels in recent years [2]. Over the last few decades, air temperature variability and changes have received much attention, especially since the average global surface temperature increased by 0.7 °C in the second half of the twentieth century [3,4,5]. Numerous studies have examined the variability of temperature at various spatial and temporal scales during the previous few decades, indicating considerable warming in North Africa and the Middle East regions [6,7,8]. Many previous regionalized studies examined the trend of temperature and identified a positive trend, such as for Saudi Arabia (SA) [9,10,11,12,13,14,15], Egypt [16,17,18,19,20], Morocco [21], and Libya [22]. A major factor affecting the spatiotemporal distribution of temperature trend is climate change [23].
Saudi Arabia, located in the southwest of Asia between latitude 15.5° N and 32.5° N and longitude 35° E and 55° E, is the biggest country on the Arabian Peninsula (AP). SA is considered an arid and semi-arid region, one of the hottest regions in the world, largely consisting of sand desert. The defining characteristics of SA include clear and hazy skies with high daytime temperatures and low night-time temperatures. This results in significant demand on freshwater supplies [24,25,26,27,28]. SA is extremely vulnerable to climate change and more susceptible to climate variability [29,30,31,32]. To design adaptation plans and actions to lessen the consequences of climate change for SA, it is crucial to understand the various effects of temperatures. Recently, several studies have investigated temperature variation across SA and surrounding regions. For example, based on the annual mean of air temperature in SA, a warming rate of 0.60 °C per decade was calculated [9]. The annual average daily maximum temperature was also found to increase by 0.06 °C every year in SA [10]. Almazroui et al. [11] used a simple regression approach to examine the trend magnitudes for annual temperature extreme indicators from 1981 to 2010. They discovered a significant increase (decrease) in the annual occurrence of warm (cool) days/nights. Moreover, the temperature extremes (hot and cold) in SA were discovered to have grown dramatically with a larger magnitude in the recent past (1996–2010) compared to the prior time (1981–1995). Islam et al. [12] found that the annual mean daily maximum temperature increased by 0.086 °C/year when they investigated the trends of extreme temperatures using Sen’s slope to evaluate trend magnitudes and the Mann–Kendall (MK) test to determine trend significance. In addition, Raggad [13] and Alhathloul et al. [14] used Sen’s slope to evaluate trend magnitudes and the MK test to determine trend significance in annual mean daily maximum temperature over SA during the period 1985–2014 and 1985–2018, respectively. The estimated trends are 0.053 °C/year and 0.047 °C/year during the examined period, respectively. Hasanean and Almazroui [15] discovered an abrupt change in surface air temperature in the 1980s over SA. Alhathloul et al. [14] discovered an abrupt change in 1987 (1988) in the stations located in the western (eastern) area of SA.
Additionally, the winter air temperatures (WAT) (average of air temperature at 2 m above the surface during the months of December, January, and February) have risen more quickly than other seasons of the year during the past two decades, according to a several studies [32,33,34,35]. Global temperatures are rising, particularly during the winter season [36]. These changes are more pronounced in the northern hemisphere and during seasons with lower levels of solar energy [37]. The climate of the semi-arid and arid regions in the middle latitudes of Asia has a warming trend in the cold seasons (November–March), with an increase of 2.4 °C more than the rest of the year [38]. Other studies confirm this winter warming in Korea [39], Venezuela and Colombia [40], and Iran [41].
The temperature fluctuation in SA has significant ramifications for human health, water resources, and agricultural productivity [42,43,44,45]. Despite the region’s major environmental, agricultural, and water resource challenges, our understanding of SA temperature changes remains restricted in comparison to other locations [46]. Therefore, this work aimed to study the variability of WAT at 2 m above the surface over Saudi Arabia. The data and methodology are described in Section 2. Section 3 contains the results and a discussion of winter temperature analysis and variability in SA, the Mann–Whitney test for the abrupt change of the time series for 25 SA stations, and the spatial analysis of winter temperature. Finally, the conclusions are presented in Section 4.
2. Data and Methodology
2.1. Data
Two types of data were used in this study. First, observed daily temperature records were compiled from 25 stations (Figure 1) from the Presidency of Meteorology and Environment (PME) in SA, where the stations under study cover most parts of SA. These stations were chosen for the quality and consistency of their recordings. After checking the accuracy of temperature time series data, the monthly time series is calculated by averaging the values of the daily data for each month. The monthly time series were used to create the wintertime series by averaging the temperature readings over three months (December to February). Table 1 illustrates the names, location (latitude and longitude), elevation, and the available period for each station. The observed dataset was used for studying the variability and the trend of WAT at SA stations.
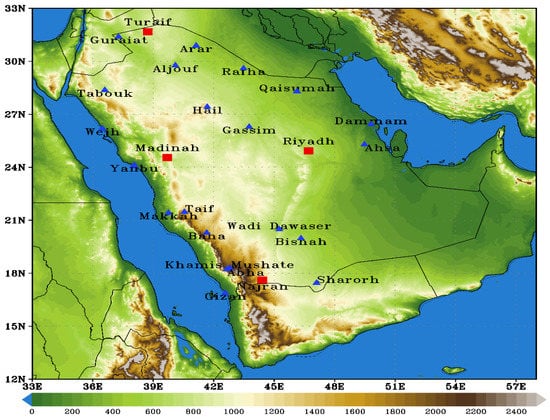
Figure 1.
The name and location of Saudi Arabia stations are marked by blue triangles with shaded elevations (m). The red mark represents the stations that were used to evaluate the ERA-5 data.

Table 1.
Name, location, elevation, and the available data period for each of Saudi Arabia stations.
The second type of data is the monthly temperature from the European Centre for Medium-Range Weather Forecasts (ECMWF) fifth-generation reanalysis ERA-5 dataset [47], with 0.5° × 0.5° grid spacing for the period from 1959 to 2022. The reanalysis dataset was used for investigating the spatial distribution of the mean, variability, and trend of WAT over SA during the period from 1959 to 2022.
2.2. Methodology
2.2.1. Homogeneity of the Data
To examine the homogeneity of the observed data, Bartlett test [48] was used to consider a Gaussian distribution of values. The procedure is simply carried out by splitting the time series into L subperiods and these subperiods have an equal number of data values (L ≥ 2). The variance of each subperiod () is calculated using the following relation [49]:
where (m) is the number of samples in each subperiods (L), is the observed value, and is the average of observations. We can estimate the value of the ratio between the highest and smallest variances of samples. This ratio is known as the F-ratio and is computed from the following formula:
where: and .
The estimated F-ratio value is compared to the values given in Table 31 by Pearson and Hartley [50] with n − 1 degrees of freedom and at a 0.95 confidence level. The value of the F-ratio can be used to determine whether the WAT values in the L samples have equal variances (homogeneous) or not (heterogeneous).
2.2.2. Variability of the Data
In this study, the coefficient of variation (CV) technique was used to examine the variability of WAT time series of 25 stations in SA and calculated as follows:
where is the average for N years and σ is the standard deviation.
2.2.3. Trend Analysis
Different methods have been applied to estimate the magnitude of the WAT trend in studied area. These methods are (a) simple linear regression (SLR) [51], and (b) Sen’s slope method (SS). One of the methods with the highest usage rate for identifying linear trends is simple linear regression. However, this approach necessitates the presumption of residual normality [52]. The least-squares method (the most popular technique) is used to calculate the coefficients of the linear regression equation.
The trend magnitudes are also estimated as °C/year using Sen’s slope approach [53] and is computed from the following formula:
where and are the data at times i and j. Sen’s slope is superior to regression’s slope in that it is less affected by outliers.
The Mann–Kendall (MK) test [54,55] was used to find any probable trend in the WAT series and determine whether or not it was statistically significant. The MK statistics do not make any assumptions about the data’s probability distribution. The standard normal distribution is used to assess the trend significance. According to [56], the MK test statistics S is computed from Equation (5) for a time series :
The time series tends to have later observations that are greater than those that arrive earlier if S > 0, and the reverse is true if S < 0. This means there is a decreasing trend if S is negative and an increasing trend if S is positive. To examine the monotonic trend with a 95% confidence level, standardized value (Z) should be computed. When the absolute value of Z is more than the value of (taken from Z-table) the null hypothesis (no trend) is rejected and the alternative hypothesis (a significant trend is existed) is accepted. Before calculating the standardized value, the variance should be calculated. The variance of S is computed by Equation (6) when n ≥ 8.
where is the ties number for the value and is the total tied groups number. The standardized test statistics Z is given by Equation (7).
Kendall’s Tau () is used to evaluate monotonicity’s strength [55] and is computed from the following formula:
The value fluctuates between −1 and 1, and it is negative when the trend decreases and positive when it increases.
The MK test’s variance rises as a result of autocorrelation in time series data [56] Trend analysis may be greatly questionable when there is a positive autocorrelation [57]. If autocorrelation exists in the time series, the modified MK tests such as [57,58,59] can be used to eliminate the autocorrelation effect. The Hamed and Rao modified MK test [58] was used in this study, as in [14].
2.2.4. The Cumulative Seasonal Means
The cumulative seasonal means (CSM) technique [60,61,62] was used to examine the persistence or the fluctuations (decadal and inter-decadal) in the behavior of the WAT over SA. This technique (CSM) has the advantage of identifying time-varying structures in time series. The time series of CSM can be defined as follows:
where is the WAT and is the number of years of data used.
2.2.5. Abrupt Change
The Mann–Whitney (M-W) test for step trend (rank-based) is used to determine the abrupt change points and significant fluctuations in WAT mean throughout the given climatic period [63,64,65]. The WAT data vector’s can split into two series:
and where every series has its distribution function F(x). The M-W test statistics is given by
where are the rank of the t observations. The H0 (null hypothesis) is accepted when where α is the significance level of the test.
2.2.6. Evaluation Metrics of ERA5 Dataset
The accuracy of ERA-5 data was tested by comparing it with the data of the measured stations by calculating the different types of differences (errors) at four separate stations. The used statistical approaches are correlation coefficient (R), coefficient of determination (R2), Willmott index of agreement (d), root mean square error (RMSE), mean bias error (MBE), and mean percentage error (MPE%) [66]. The higher values (approximately one) of R, R2, and d indicate a perfect match between ERA-5 and observed data, while the lower values of RMSE, MBE, and MPE% reveal higher accuracy and less residual variance [66].
3. Results and Discussion
3.1. Homogeneity Test of the Data
In climatology, studies on the homogeneity of data are essential. Therefore, it is necessary for conducting a statistical climatic study on climate element data. In this study, the Bartlett test was used to analyses the homogeneity of the WAT time series for the SA stations. Table 2 illustrates the results from the Bartlett test for WAT at 25 stations. All stations data are sufficiently homogenous according to the results of this test at a 5% significance level.

Table 2.
Bartlet test (short-cut) result of the Winter Air Temperatures for Saudi Arabia stations (m is the number of terms in each subperiod, and k is the number of the subperiod).
3.2. WAT Tnalysis
Figure 2 illustrates the average of mean, maximum and minimum air temperature during the winter for each station. It reveals that the higher values of maximum Temperature (Tmax) appear in the middle of SA at Makkah, Gizan, Sharorh, Yanbo, Najran, Bishah, and Wadi Dawaser, respectively, while the lower values of Tmax appear at the northern stations, especially at Turaif. The southern stations also have higher values of Tmax except the mountain stations. Figure 2 also shows that the behavior of temperature mean (Tmean) and minimum temperature (Tmin) are similar that of Tmax, where the higher values of Tmean and Tmin appear in the middle and southern stations except the mountain stations. The lower values of Tmean and Tmin appear in the northern stations. Figure 2 shows that the maximum range (difference between the Tmax and Tmin) occurs at Bishah, Najran, Sharorh, and Wadi Dawaser, while the lower range occurs at Gizan and Wejh.
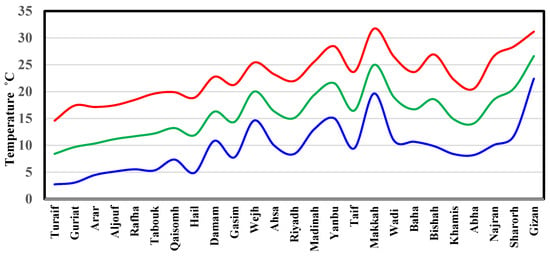
Figure 2.
The average of mean (green line), maximum (red line) and minimum (blue line) values of air temperature of Saudi Arabia stations during the winter. The stations are arranged from north to south.
3.3. Coefficient of Variation
The CV values of WAT time series are presented in Figure 3. It is obvious that the values of CV of WAT decrease gradually from the north to the south of SA. The greater values of the CV of winter happen at the northern region of SA, especially at the stations Arar, Turaif, Aljouf, Guriat, and Rafha with the largest one at Turaif. In the middle SA the highest values occur at Gassim and Riyadh. In the southwestern area the highest values of CV for winter occur in Bishah, Khamis Mushate, and Wadi Dawaser. The highest CV values during winter can be attributed to the presence of several synoptic patterns that cause weather activity in SA. The most important of these patterns is that of the Mediterranean cyclones traveling from west to east, in association with upper air troughs and active subtropical jet, as well as the polar jet, causing rainfall during their traveling over the SA. The ability of Mediterranean cyclones to produce the activity of weather decreases generally from north to south, except at the mountainous regions where altitude acts as an intrinsic factor. The second important pattern is the interaction between the westerly frontal troughs transporting cold air from the northwest of Europe and the southerly moist warm air coming from Somalia and Sudan, producing a huge amount of cloud over the area of convergence. Finally, weather activity is strong over the eastern Mediterranean near the end of the winter season (February), where the secondary traveling depressions (secondary from the Mediterranean cyclones) are frequently linked with sandstorms might arrive and affect our region. Occasionally, these secondary depressions cause heavy rainfall in February and March, when the associated cold air meets the hot, moist southerly air.
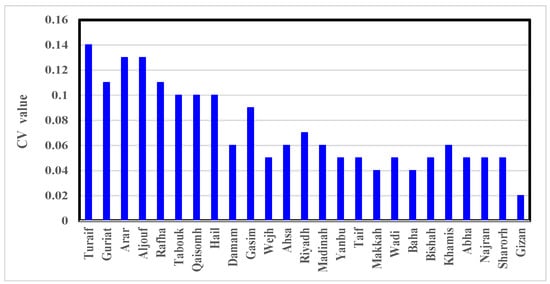
Figure 3.
The coefficient of variation of Winter Air Temperatures for Saudi Arabia stations. The stations are arranged from north to south.
3.4. Trend Analysis
The WAT time series for the 25 SA stations under investigation were examined in order to determine long-term trend behavior. The two procedures that are used to estimate the magnitude (°C/year) of the WAT trend in this study are SLR and SS. Table 3 illustrates the results of trend analysis for WAT at 25 stations. In general, the results of the SLR method are consistent with those obtained using SS method. The results of the SLR and SS illustrates that the positive trend is dominant at 23 stations while two stations only (Wadi Dawaser and Sharorh) have negative trends. The average increase trend for WAT is 0.038 using SLR and 0.037 using SS. The average decrease trend is 0.030 using SLR and 0.025 using SS. Moreover, it is obvious that the higher positive trend (0.046 SLR and 0.044 SS) appears in the center of SA (Gassim Wejh, Riyadh Madinah, Taif, Makkah, and Yanbu) with the maximum positive trend in Khamis Mushate (0.061 SLR and 0.063 SS) and Abha (0.044 for SLR and SS). The minimum positive trend appears in Turaif (0.017 SLR and 0.012 SS) and Ahsa (0.021 SLR and 0.02 SS). Generally, the central region contains the highest positive trend, followed by the southern region (Baha, Bishah, Khamis Mushate, Abha, Najran, Sharorh, and Gizan), while the northern region (Turaif, Guriat, Aljouf, Rafha, and Tabouk) contains the smallest positive trend during the study period. The average increase trend for WAT in the southern region is 0.037 using SLR and 0.037 using SS. The average trend in the northern region is 0.034 using SLR and 0.031 using SS. All stations have a significant trend, except for three (Rafha, Damam, and Sharorh) having a non-significant trend.

Table 3.
Results of trend analysis of Winter Air Temperatures for the 25 stations. The positive sign (+) denotes an increasing trend and the Negative sign (−) denotes a decreasing trend. S denotes a significant trend and NS denotes an non-significant trend.
3.5. Cumulative Seasonal Means
The CSM technique has a smoothing effect and is used here to show the persistence or the fluctuations (decadal and inter-decadal) in the behavior of the WAT time series of SA stations. Figure 4a,b show the behavior of temperature values of each station. The results of CSM for Turaif station illustrate that there are two periods of lower temperatures than its CSM average. The first one is from 1983 to 1987 while the second period is from 1992 to 2002. The last period (2002–2015) shows a fluctuation of WAT values around the CSM average. Guriat has lower temperatures than its CSM average for the period 1992–2010. Two periods of higher WAT values occur throughout the behavior of the CSM of Guriat. The first one is from 1985 to 1992, while the second period is from 2010 to 2018. The CSMs for Arar and Aljouf show similar behavior during the period of study. They indicate lower WAT values than its CSM average from 1983 to 2011, followed by a higher value in WAT up to 2018. The average CSMs of these stations (Arar and Aljouf) are approximately 9.9 and 10.9 °C, respectively. Lower WAT values than its CSM average are found in Tabouk for the period 1982–1986 and from 1991 to 2007, followed by continuous higher values until 2018. The CSMs for Rafha and Qaisumah show similar behavior during the period of study. They indicate higher values in WAT from 1978 to 1983, followed by permanent lower values in WAT till 2013.
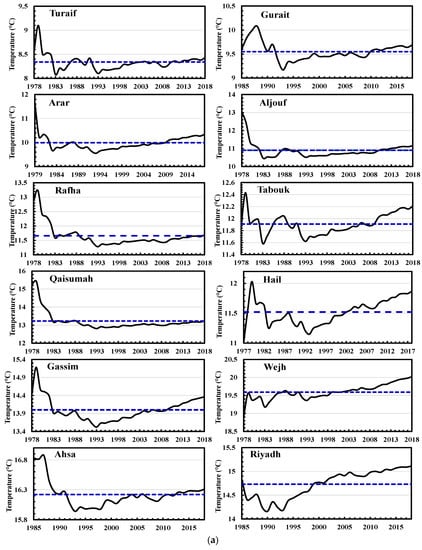
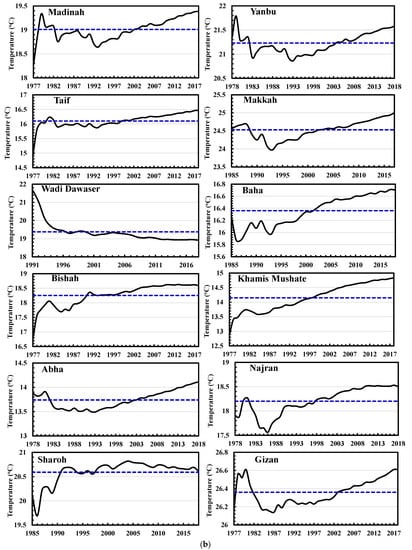
Figure 4.
(a) The Cumulative Seasonal Means time series and the averaged Cumulative Seasonal Means in Turaif, Guriat, Arar, Aljouf, Rafha, Tabouk, Qaisumah, Hail, Gassim, Wejh, Ahsa and Riyadh.  The means of CSM and
The means of CSM and  the CSM time series. The stations are arranged from north to south. (b) As in (a) but for the stations Madinha, Yanbu, Taif, Makkah, Wadi Dawaser, Baha, Bishah, Khamis Mushate, Abha, Najran, Sharoh and Gizan.
the CSM time series. The stations are arranged from north to south. (b) As in (a) but for the stations Madinha, Yanbu, Taif, Makkah, Wadi Dawaser, Baha, Bishah, Khamis Mushate, Abha, Najran, Sharoh and Gizan.
 The means of CSM and
The means of CSM and  the CSM time series. The stations are arranged from north to south. (b) As in (a) but for the stations Madinha, Yanbu, Taif, Makkah, Wadi Dawaser, Baha, Bishah, Khamis Mushate, Abha, Najran, Sharoh and Gizan.
the CSM time series. The stations are arranged from north to south. (b) As in (a) but for the stations Madinha, Yanbu, Taif, Makkah, Wadi Dawaser, Baha, Bishah, Khamis Mushate, Abha, Najran, Sharoh and Gizan.
Results obtained from Hail and Gassim show that higher values in WAT than CAMs average are detected for the period from 1978 to 1982 and lower values in WAT from 1983 until 2002, followed by permanent higher values in WAT up to 2018.
Results obtained from Riyadh, Madinah, and Yanbu stations confirm that the CSM time series can be split into two periods. The first period illustrates lower WAT values, while the second one shows higher values in WAT than the average of CSMs. For Riyadh, the first extends from 1985 to 1999, and for Madinah and Yanbu, it is from 1983 to 2003 and 2005, respectively. Throughout the period 1985–1991, higher WAT values than the CSM average were the constant features at Ahsa. This period was followed by lower values until 2012. Results from Wejh station show that the CSM time series can be split into two periods. The first one (1978–1999) illustrates lower WAT values than the CSM average, while the second one shows higher WAT values (1999–2018). The lower values in WAT than the CSM average are the permanent features throughout the period from 1977 to 2001 in Taif, while the higher values are the permanent features from 2002 to the end of the record. This period was followed by higher WAT values until the end of the record. Results for Baha station confirm that there was a lower temperature from 1985 to 2001 than the CSM average and higher values from 2002 to the end of the record. Bishah and Khamis Mushate stations have the same behavior where the first period is characterized by lower values up to 1997, while the last period is characterized by higher WAT values than the CSM average. Except for 1985–1989, lower WAT values than the average have been detected in Makkah for the period 1985–2003, followed by higher values afterward. Except for 1978 to 1982, lower values of WAT than the average have been detected at Abha for the period from 1978 to 2003, and higher values from 2004 to 2018. During the period 1978–1998, Najran station had significantly lower WAT values than the CSM average, with higher values from 1999 to 2018. The Sharorh station experienced lower values in temperature during the first period from 1985 to 1991, followed by higher WAT values afterward. This station’s CSM average temperature is 20.59 °C.
3.6. Abrupt Change Analysis
The changes in the climate are non-linear because the climate system is a non-linear, chaotic system. As a result, it is essential to evaluate and comprehend the climate system’s change process utilizing nonlinear theories and methodologies, such as the theory of abrupt changes and the detection technique [67]. The definition and approaches of detection that can assist to comprehend and recognize abrupt changes were explored by [68]. Table 4 illustrates the years of abrupt cooling or warming of the WAT of SA stations by the M-W test for abrupt change. The results of the Mann–Whitney test for the abrupt change of the time series of 10 stations (Arar, Tabouk, Madinah, Riyadh, Taif, Makkah, Khamis Mushate, Abha, Gizan, and Najran) are illustrated in Figure 5 as an example of all stations.

Table 4.
The detected years of abrupt warming (cooling) of the Winter Air Temperatures of Saudi Arabia stations by the Mann–Whitney test for abrupt change.
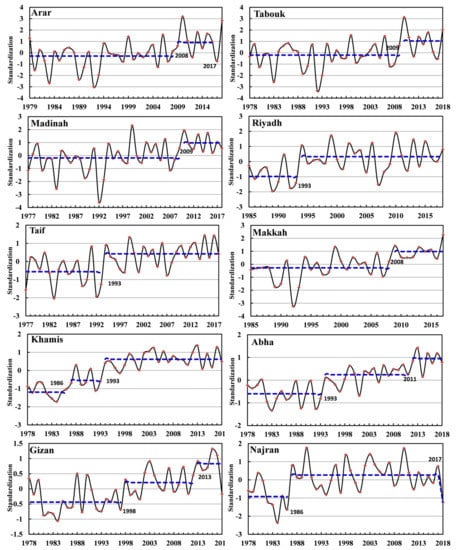
Figure 5.
Shifts in the mean for standardization of the Winter Air Temperatures of Arar, Tabouk, Madinah, Riyadh, Taif, Makkah, Khamis, Abha, Gizan and Najran.  Weighted arithmetic means and
Weighted arithmetic means and  the standardization time series.
the standardization time series.
 Weighted arithmetic means and
Weighted arithmetic means and  the standardization time series.
the standardization time series.
Figure 5 shows the M-W test findings for sudden changes in the standardized WAT time series for the 10 selected stations across SA at a 95% confidence level. The test identified two increasing abrupt changes in the WAT time series of Arar station, the first occurring in 2008 and the second appearing around 2017. The years of abnormal decrease between 2009 and 2018 are 1983, 1989, 1992, and 1993, while the highest temperature appeared in 2010 and was higher than the average of the whole period by 3.2 °C. The WAT of Madinah (Tabouk) in 2009 shows an increasing abrupt change, according to the results of the M-W test (Figure 5). There are two periods in Madinah (Tabouk). The first is from 1977 to 2008, in which the average WAT is 0.27 (0.3) °C lower than the average of the whole period. The second one is from 2010 to 2018, in which the average WAT is 0.98 °C and 1.08 °C higher than the average of the whole period. The Mann–Whitney test of Riyadh (Taif) detected an increasing abrupt change in WAT about 1993 (Figure 5); it also shows two obvious periods in the past 34 (42) years. The first period is from 1985 to 1992, in which the average WAT is 0.93 (0.6) °C lower than the average of the whole period. The second is the higher period from 1994 to 2018, in which the WAT is 0.33 (0.41) °C higher than the average of the whole period. Figure 5 also shows that the M-W test identified an increasing abrupt change in the WAT time series of Makkah in 2008. Moreover, there are two periods. The first is the lower period from 1985 to 2007, in which the average WAT is 0.3 °C lower than the average of the whole period and the abnormal decrease years are 1989, 1990, 1992 and 1993 respectively. The second period is from 2009 to 2018, in which the mean WAT is 1.02 °C higher than the average of the whole period, and the highest temperature recorded was 1.9 °C above the average in 2010. The M-W test identified two increasing abrupt changes in the WAT of Khamis Mushate; the first one was found in 1986, while the second one was found in 1993 (Figure 5). The first lower period of WAT is 1977–1986, in which the mean WAT is 1.2 °C lower than the average of the whole period. The second lower period of WAT is 1987–1993, in which the mean WAT is 0.49 °C lower than the average of the whole period. The higher period of WAT is from 1994 to 2018, in which the mean WAT is 0.62 °C higher than the average of the whole period. The M-W test identified two increasing abrupt changes in the WAT of Abha; the first one is around 1993, while the second one is around 2011 (Figure 5). The lower period of WAT is 1978–1993, in which the mean WAT is 0.61°C lower than the average of the whole period. The first higher period of WAT is 1994–2011, in which the mean WAT is 0.2 °C higher than the average of the whole period. The second higher period of WAT is 2012–2018, in which the mean WAT is 0.9 °C above the average of the whole period. The W-M test determined two increasing abrupt changes in the WAT time series of Gizan; the first one is around 1998, while the second one is around 2013. Figure 5 illustrates that there are three obvious periods, the lower period of WAT is 1977–1997, in which the mean WAT is 0.37 °C lower than the average of the whole period. The first higher period of WAT is 1998–2012, in which the mean WAT is 0.22 °C higher than the average of the whole period. The second higher period of WAT is 2013–2018, in which the mean WAT is 0.75 °C higher than the average of the whole period.
3.7. Spatial Analysis of WAT
To clarify the spatial distribution of air temperature above the surface over all SA during the winter season, we used the gridded temperature at 2 m dataset from the European Centre for Medium-Range Weather Forecasts (ECMWF) fifth-generation reanalysis ERA-5 dataset. The ERA-5 data accuracy was assessed and investigated against the measurements from SA stations using the available period of each station (Table 1). In order to compare the reanalysis data with the observed data, four stations were selected from the grid dataset covering SA, the temperature time series for these stations were extracted. After that we compared these time series with the corresponding observed data at each station by calculating the correlation coefficient (R), coefficient of determination (R2), Willmott index of agreement (d), root mean square error (RMSE), mean bias error (MBE), and mean percentage error (MPE%). Table 5 illustrates the R, R2, d, RMSE, MBE and MPE% for the WAT between ERA-5 reanalysis data and observed data at Turaif, Madinah, Riyadh, and Najran stations in SA. According to Table 5, there is excellent agreement between observed data and ERA-5 reanalysis data for the four stations. Based on the results in Table 5, the Madinah station has the best agreement between the observed data and ERA-5 reanalysis data, where the values of R, d, R2, RMSE, MBE and MPE are 0.99%, 0.98%, 0.97%, 0.197%, 0.10%, and 0.76%, respectively. The Najran station had the lowest accuracy, although is still considered to represent a reasonably good agreement. Figure 6 displays an example of observed (solid black line) and ERA-5 (dotted blue line) seasonal mean of WAT data for Turaif, Madinah, Riyadh, and Najran stations, demonstrating their convenience and consistency. As a result, ERA-5 analysis data have been used to fill in the gaps on location where there are no observing stations.

Table 5.
R, R2, d, RMSE, MBE and MPE% for the Winter Air Temperatures between ERA-5 reanalysis data and observed data at the selected four stations in Saudi Arabia.
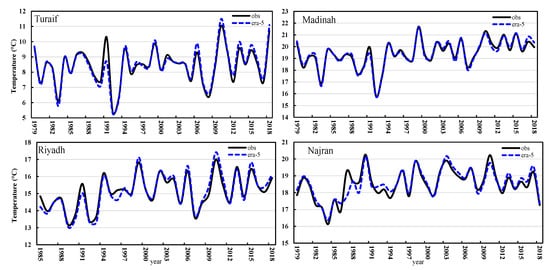
Figure 6.
The comparison between ERA-5 Winter Air Temperatures data and its corresponding observed data for the stations Turaif, Madinah, Riyadh, and Najran.
Figure 7 illustrates the horizontal distribution of the mean, CV, trend magnitude (SS), Kendall’s Taum, and P-value of WAT during the period (1959–2022) using ERA-5 reanalysis data. Generally, the WAT in SA increases with latitude from north to south. The lowest WAT values are found north of 25° N, while the highest values of WAT occur in the south, particularly in the south-east regions of SA (Figure 7a). The WAT difference between the north and south of SA is approximately 12 °C. The latitudinal gradient of temperature is strong, especially north of 20° N. The region south of 20° N exhibits the lowest temperature gradient in winter. The strong latitudinal temperature gradient over northern SA is caused by the passage of Mediterranean cyclones (midlatitude traveling cyclones) from west to east, which impact the weather at this period. The distribution of the temperature gradient over the Red Sea region may be used to determine the influence of the Red Sea trough and the Red Sea water. Figure 7b shows the horizontal distribution of CV of WAT over SA. It is clear that the CV of WAT increases gradually from south to north of SA. The northern part of SA is characterized by higher variability in winter compared with other regions which may be because of the effects of the traveling Mediterranean cyclones and their interface with the Red Sea trough (inverted-V shape trough) as the extension of the Sudan monsoon low. Figure 7c shows the horizontal distribution of the trend magnitude (°C/year) of WAT over SA (computed by SS method) for the period 1959–2022. In general, the pattern of trend indicates positive trend (warming) over the most regions of SA (Figure 7c,d). The maximum values of the trend with highly statistically significant confidence level (95–100 %) are found in the southern and central regions of the SA, particularly over the southwestern region (Figure 7c,d). By comparing the results mentioned in Section 3.4 with the results here, note that there is an agreement between the results of the observed data and the reanalysis data in the CV, trend direction, and the strength of monotonicity. The length of the time series in the measured data differs from one station to another according to the origin of the station, and to benefit from the length of the ERA5 data period, the trend was calculated from it to know its direction and compare to the previously calculated data for other stations. Therefore, the comparison here is for the general direction of the trend and not for the accuracy of the magnitude.
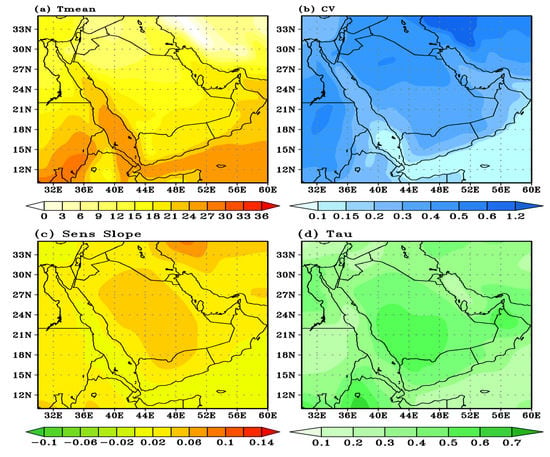
Figure 7.
The horizontal distribution of (a) Tmean, (b) coefficient of variation, (c) trend magnitude (Sen’s slope °C/year), and (d) Kendall’s Tau of Winter Air Temperatures during (1959–2022) over Saudi Arabia.
Many researchers [9,10,11,12,13,14] indicate that surface temperature has increased in the last three decades. They noted that the current worldwide warming from 1976 to 2000 was basically synchronous, but it was more prominent in the Northern Hemisphere continents during winter and spring. Moreover, numerous studies have revealed that, during the past years, winter temperatures have risen more quickly than at other times of the year [32,33,34,35].
4. Conclusions
This research aimed to study the variability of WAT over SA. Results from the study of the CV of WAT of SA stations show that the CV of the WAT is a function of latitude. CV values are greater in the northern sections of SA and gradually decline in the southern areas. The greatest values of CV over the north of SA arise from the weather activity over this area, where the Mediterranean cyclones travel from west to east in association with upper air troughs at 500 hPa. These cyclones are usually associated with the activity of subtropical and polar jets and cause weather activity over the north of SA. The ability of Mediterranean cyclones to produce such weather activity generally decreases from north to south, except for mountainous regions where altitude acts as an intrinsic factor. The trend analysis by the SLR, SS, and MK methods for the WAT time series of 25 locations distributed over SA were made. The most significant finding is that all stations have warming trends for the WAT time series. A higher warming rate is observed in the stations located in the northeast region of SA. In general, the stations, located in the central, northeastern, and southeastern parts of SA, show the strongest warming trend in the WAT time series. Overall, it was found the highland stations in the western region have higher trend magnitudes in winter, while the northern stations have lower trend magnitudes.
The CSM technique is used to detect the persistence or the fluctuations (decadal and inter-decadal) in the behavior of the WAT over SA. It is found that the period from 1982 to 2010 is characterized in general by lower WAT values than its CSM average (cooling trend) in most northern stations of SA. The southern and middle stations are characterized by higher WAT values than their CSM average (warming trend) during the period from 2003 to 2018. The study of the Mann–Whitney test for the abrupt change of the time series of WAT for SA stations confirms that a change towards increasing WAT appears at many stations in the years 1986, 1993, 1998, 2008, and 2009, while a change towards decreasing WAT appears only at Wadi Dawaser in the year 2006. The abrupt change in the stations of the northeast region occurred later than the west region stations. However, the trend strength of the northeast region is higher. The climate change signal was detected in the western region at the highland stations earlier than other stations. The occurrence of abrupt changes may be related to El Niño and La Niña [69]. Overall, the results from the MK tests suggest the existence of a warming trend in temperatures in the regions.
Author Contributions
Conceptualization, M.A.-M., H.A.B. and A.A.; data curation, M.A.-M., A.A. and A.L.; formal analysis, M.A.-M. and H.A.B.; funding acquisition, A.L.; methodology, M.A.-M., H.A.B. and A.L.; project administration, M.A.-M.; resources, M.A.-M.; software, A.A. and A.L.; supervision, M.A.-M. and H.A.B.; validation, A.A. and A.L.; visualization, A.A. and A.L.; writing—original draft, H.A.B.; writing—review & editing, H.A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R241), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The observed monthly temperature data are provided by the Presidency of Meteorology and Environment (PME) in KSA. The EAR5 dataset can downloaded from the Copernicus Climate Change Service (https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels-monthly-means?tab=form, accessed on 16 January 2023).
Acknowledgments
The researchers express their great thanks and appreciation to the Princess Nourah bint Abdulrahman University for their support and funding of this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vinnikov, K.Y.; Groisman, P.Y.; Lugina, K.M. Empirical Data on Contemporary Global Climate Changes (Temperature and Precipitation). J. Clim. 1990, 3, 662–677. [Google Scholar] [CrossRef]
- Ponce, C. Intra-seasonal climate variability and crop diversification strategies in the Peruvian Andes: A word of caution on the sustainability of adaptation to climate change. World Dev. 2020, 127, 104740. [Google Scholar] [CrossRef]
- Folland, C.K.; Karl, T.P.; Christy, J.R.; Clarke, R.A.; Gruza, G.V.; Jouzel, J.; Mann, M.E.; Oerlemans, J.; Salinger, M.J.; Wang, S.W. Observed climate variability and change. In Chapter 2 of Climate Change 2001; The Scientific Basis, Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change (IPCC); Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Xiaoxu, D., Eds.; Cambridge University Press: Cambridge, UK, 2001; pp. 99–181. [Google Scholar]
- Trenberth, K.E.; Fasullo, J.T. An apparent hiatus in global warming? Earth’s Future 2013, 1, 19–32. [Google Scholar] [CrossRef]
- IPCC. Climate change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Paeth, H.; Born, K.; Girmes, R.; Podzun, R.; Jacob, D. Regional Climate Change in Tropical and Northern Africa due to Greenhouse Forcing and Land Use Changes. J. Clim. 2009, 22, 114–132. [Google Scholar] [CrossRef]
- Fontaine, B.; Janicot, S.; Monerie, P.A. Recent changes in air temperature, heat waves occurrences, and atmospheric circulation in Northern Africa. J. Geophys. Res.-Atmos. 2013, 118, 8536–8552. [Google Scholar] [CrossRef]
- El Kenawy, A.; López-Moreno, J.I.; McCabe, M.F.; Brunsell, N.A.; Vicente-Serrano, S.M. Daily Temperature Changes and Variability in ENSEMBLES Regional Models Predictions: Evaluation and Intercomparison for the Ebro Valley (NE Iberia). Atmos. Res. 2015, 155, 141–157. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Jones, P.D.; Athar, H.; Rahman, M.A. Recent climate change in the Arabian Peninsula: Seasonal rainfall and temperature climatology of Saudi Arabia for 1979–2009. Atmos. Res. 2012, 111, 29–45. [Google Scholar] [CrossRef]
- Athar, H. Trends in observed extreme climate indices in Saudi Arabia during 1979–2008. Int. J. Climatol. 2014, 34, 1561–1574. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Dambul, R.; Jones, P.D. Trends of temperature extremes in Saudi Arabia. Int. J. Climatol. 2014, 34, 808–826. [Google Scholar] [CrossRef]
- Islam, M.N.; Almazroui, M.; Dambul, R.; Jones, P.D.; Alamoudi, A.O. Long-term changes in seasonal temperature extremes over Saudi Arabia during 1981–2010. Int. J. Climatol. 2015, 15, 1579–1592. [Google Scholar] [CrossRef]
- Raggad, B. Statistical assessment of changes in extreme maximum temperatures over Saudi Arabia, 1985–2014. Theor. Appl. Climatol. 2018, 132, 1217–1235. [Google Scholar] [CrossRef]
- Alhathloul, S.H.; Khan, A.A.; Mishra, A.K. Trend and change point detection in mean annual and seasonal maximum temperatures over Saudi Arabia. Arab. J. Geosci. 2021, 14, 1–6. [Google Scholar] [CrossRef]
- Hasanean, H.M.; Almazroui, M. Teleconnections of the tropical sea surface temperatures to the surface air temperature over Saudi Arabia in summer season. Int. J. Climatol. 2016, 37, 1040–1049. [Google Scholar] [CrossRef]
- Hasanean, H.M. Wintertime surface temperature in Egypt in relation to the associated atmospheric circulation. Int. J. Climatol. 2004, 24, 985–999. [Google Scholar] [CrossRef]
- Domroes, M.; El-Tantawi, A. Recent temporal and spatial temperature changes in Egypt. Int. J. Climatol. 2005, 25, 51–63. [Google Scholar] [CrossRef]
- Hasanean, H.M.; Abdel-Basset, H. Variability of summer temperature over Egypt. Int. J. Climatol. 2006, 26, 1619–1634. [Google Scholar] [CrossRef]
- El Kenawy, A.; López-Moreno, J.I.; Vicente-Serrano, S.M.; Abd-Elaal, M. Temperature variability along the Mediterranean Coast and its links to Large Scale Atmospheric Circulations (1957–2006). Bull. De La Soc. De Geogr. D’Egypte 2010, 83, 12–26. [Google Scholar]
- El Kenawy, A.; López-Moreno, J.I.; Vicente-Serrano, S.M.; Mekld, M.S. Temperature trends in Libya over the second half of the 20th century. Theor. Appl. Climatol. 2009, 98, 1–8. [Google Scholar] [CrossRef]
- Khomsi, K.; Mahe, G.; Tramblay, Y.; Sinan, M.; Snoussi, M. Regional impacts of global change: Seasonal trends in extreme rainfall, run-off and temperature in two contrasting regions of Morocco. Nat. Hazards Earth Syst. Sci. 2016, 16, 1079–1090. [Google Scholar] [CrossRef]
- Zhang, X.; Aguilar, E.; Sensoy, S.; Melkonyan, H.; Tagiyeva, U.; Ahmed, N.; Kutaladze, N.; Rahimzadeh, F.; Taghipour, A.; Hantosh, T.; et al. Trends in Middle East climate extreme indices from 1950 to 2003. J. Geophys. Res. 2005, 110, D22104. [Google Scholar] [CrossRef]
- Wang, X.J.; Zhang, J.Y.; Shahid, S.; Guan, E.H.; Wu, Y.X.; Gao, J.; He, R.M. Adaptation to climate change impacts on water demand. Mitig. Adapt. Strateg. Glob. Chang. 2016, 21, 81–99. [Google Scholar] [CrossRef]
- World Bank. Making the Most of Scarcity: Accountability for Better Water Management Results in the Middle East and North Africa Report; World Bank: Washington, DC, USA, 2010. [Google Scholar]
- Al-Zahrani, K.H.; Baig, M.B. Water in the Kingdom of Saudi Arabia: Sustainable management options. J. Anim. Plant Sci. 2011, 21, 601–604. [Google Scholar]
- Kaniewski, D.; Van Campo, E.; Weiss, H. Drought is a recurring challenge in the Middle East. Proc. Natl. Acad. Sci. USA 2012, 109, 3862–3867. [Google Scholar] [CrossRef] [PubMed]
- Odhiambo, G.O. Water scarcity in the Arabian Peninsula and socio-economic implications. Appl. Water Sci. 2017, 7, 2479–2492. [Google Scholar] [CrossRef]
- Attada, R.; Dasari, H.P.; Parekh, A.; Chowdary, J.S.; Langodan, S.; Knio, O.; Ibrahim, H. The role of the Indian summer monsoon variability on Arabian Peninsula summer climate. Clim. Dyn. 2018, 52, 3389–3404. [Google Scholar] [CrossRef]
- Bannayan, M.; Sanjani, S.; Alizadeh, A.; Lotfabadi, S.S.; Mohamadian, A. Association between climate indices, aridity index, and rainfed crop yield in northeast of Iran. Field Crops Res. 2010, 118, 105–114. [Google Scholar] [CrossRef]
- Almazroui, M.; Hasanean, H.M.; Al-Khalaf, A.K.; Abdel Basset, H. Detecting climate change signals in Saudi Arabia using mean annual surface air temperatures. Theor. Appl. Climatol. 2013, 113, 585–598. [Google Scholar] [CrossRef]
- Kunchala, R.; Attada, R.; Dasari, H.P.; Vellore, R.K.; Langodan, S.; Abualnaja, Y.O.; Ibrahim, H. Aerosol optical depth variability over the Arabian Peninsula as inferred from satellite measurements. Atmos. Environ. 2018, 187, 346–357. [Google Scholar]
- Otterman, J.; Angell, J.K.; Ardizzone, J.; Atlas, R.; Schubert, S.; Starr, D.; Wu, M.L. North-Atlantic surface winds examined as the source of winter warming in Europe. Geophys. Res. Lett. 2002, 29, 18. [Google Scholar] [CrossRef]
- Croitoru, A.E.; Drignei, D.; Dragotă, C.S.; Imecs, Z.; Burada, D.C. Sharper detection of winter temperature changes in the Romanian higher-elevations. Glob. Planet. Chang. 2014, 122, 122–129. [Google Scholar] [CrossRef]
- Hillebrand, E.; Proietti, T. Phase changes and seasonal warming in early instrumental temperature records. J. Clim. 2017, 30, 6795–6821. [Google Scholar] [CrossRef]
- Zhao, C.; Gong, J.; Wang, H.; Wei, S.; Song, Q.; Zhou, Y. Changes of temperature and precipitation extremes in a typical arid and semiarid zone: Observations and multi-model ensemble projections. Int. J. Climatol. 2020, 40, 5128–5153. [Google Scholar] [CrossRef]
- Karl, T.R.; Jones, P.D.; Knight, R.W.; Kukla, G.; Plummer, N.; Razuvayev, V.; Gallo, K.P.; Lindseay, J.; Charlson, R.J.; Peterson, T.C. 1993 A new perspective on recent global warming: Asymmetric trends of daily maximum and minimum temperature. Bull. Am. Meteorol. Soc. 1993, 74, 1007–1024. [Google Scholar] [CrossRef]
- Houghton, J.T.; Meria, F.L.G.; Callander, B.A.; Harris, N.; Kattenberg, A.; Maskell, K. 1996 Climate Change. In The IPCC Second Assessment Report; Cambridge University Press: New York, NY, USA, 1996; p. 572. [Google Scholar]
- IPCC. Climate Change 2014: Mitigation of Climate Change. In Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Chung, Y.S.; Yoon, M.B. Interpretation of recent temperature and precipitation trends observed in Korea. Theor. Appl. Climatol. 2000, 67, 171–180. [Google Scholar] [CrossRef]
- Quintana-Gomez, R.A. Trends of maximum and minimum temperatures in Northern South America. J. Clim. 1999, 12, 2104–2112. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Askari, A. Attitudinal differences between minimum and maximum rate of temperature and the decrease in diurnal temperature range in the country. J. Geogr. Res. 2004, 73, 155–171. [Google Scholar]
- Easterling, D.R.; Meehl, G.A.; Parmesanm, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Alkolibi, F.M. Possible effects of global warming on agriculture and water resources in Saudi Arabia: Impacts and responses. Clim. Chang. 2002, 54, 225–245. [Google Scholar] [CrossRef]
- Walther, G.R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Alghamdi, A.S.; Moore, T.W. Analysis and comparison of trends in extreme temperature indices in Riyadh City, Kingdom of Saudi Arabia, 1985–2010. J. Climatol. 2014, 1, 1–10. [Google Scholar] [CrossRef]
- Almazroui, M. RegCM4 in climate simulation over CORDEX-MENA/Arab domain: Selection of suitable domain, convection and land surface schemes. Int. J. Climatol. 2016, 36, 236–351. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 1999, 146, 2049. [Google Scholar] [CrossRef]
- Bartlett, M.S. Properties of sufficiency and statistical tests. Proceedings of the Royal Society of London. Ser. A Math. Phys. Sci. 1937, 160, 268–282. [Google Scholar]
- Mitchell, J.M.; Dzerdzeevskii, B.; Flohn, H.; Hofmery, W.L. Climatic change. In WMO Tech. Note 79. WMO No. 195. TP-100; World Meteorological Organization: Geneva, Switzerland, 1966; p. 79. [Google Scholar]
- Pearson, E.S.; Hartley, H.O. Biometrika Tables for Statisticians; Cambridge University Press: Cambridge, UK, 1958; 240p. [Google Scholar]
- Panofsky, H.A.; Brier, G.W. Some Applications of Statistics to Meteorology; Pennsylvania State University Press: University Park, PA, USA, 1963; p. 224. [Google Scholar]
- McBean, E.; Motiee, H. Assessment of impact of climate change on water resources. Hydrol. Earth Syst. Sci. 2008, 12, 239–255. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: Salisbury South, SA, Australia, 1948. [Google Scholar]
- Sonali, P.; Kumar, D.N. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of statistical analysis in climate. In Analysis of Climate Variability: Applications of Statistical Techniques; Von Storch, H., Navarra, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 11–26. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Al-Kallas, S.; Al-Mutairi, M.; Abdel Basset, H.; Abdeldym, A.; Morsy, M.; Badawy, A. Climatological Study of Ozone over Saudi Arabia. Atmosphere 2021, 12, 1275. [Google Scholar] [CrossRef]
- Kamel, A.M.; Abdel Basset, H.; Sayad, T. Rainfall analysis and variability over Egypt. Al-Azhar Bull. Sci. 2017, 28, 41–62. [Google Scholar]
- Pavia, E.G.; Graef, F. The recent rainfall climatology of the Mediterranean Californias. J. Clim. 2002, 15, 2697–2701. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Conover, W.J. Practical Nonparametric Statistics, 1st ed.; John Wiley & Sons: New York, NY, USA, 1971; pp. 97–104. [Google Scholar]
- Mendenhall, W.; Wackerly, D.D.; Sheaffer, R.L. Mathematical Statistics with Applications, 4th ed.; PWS-Kent: Boston, MA, USA, 1990. [Google Scholar]
- Sayad, T.A.; Ali, A.M.; Kamel, A.M. Study the impact of climate change on maximum and minimum temperature over Alexandria, Egypt using statistical downscaling model (SDSM). Glob. J. Adv. Res. 2016, 3, 694–712. [Google Scholar]
- Yan, M.H.; Deng, W.; Chen, P.Q. Analysis of climate jumps in the Sanjiang Plain. Sci. Geogr. Sin. 2003, 23, 661–667. [Google Scholar]
- Fu, C.; Wang, Q. The defnition and detection of the abrupt climatic change. Sci. Atmos. A Sin. 1992, 16, 482–493. [Google Scholar]
- Vorhees, D.C. The Impact of Global Scale Climate Variation on Southwest Asia. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).