Amplification of Extreme Hot Temperatures over Recent Decades
Abstract
1. Introduction
2. Methods
2.1. Extreme Heat and Amplification Measure
2.2. Reanalysis Data
2.3. Station-Based Data
2.4. Ancillary Data
2.5. Significance Testing
3. Results
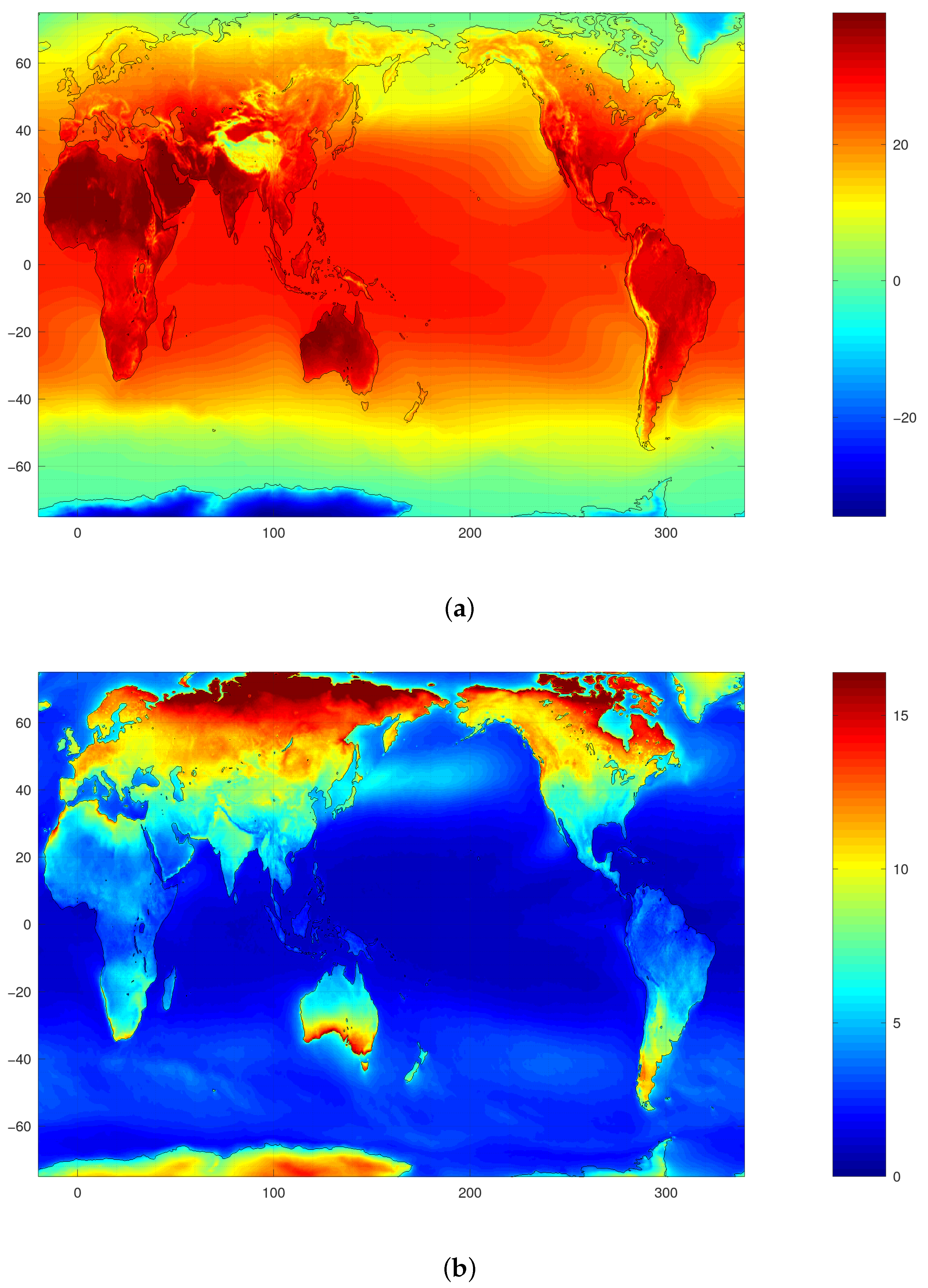
3.1. Mean Spatial Patterns
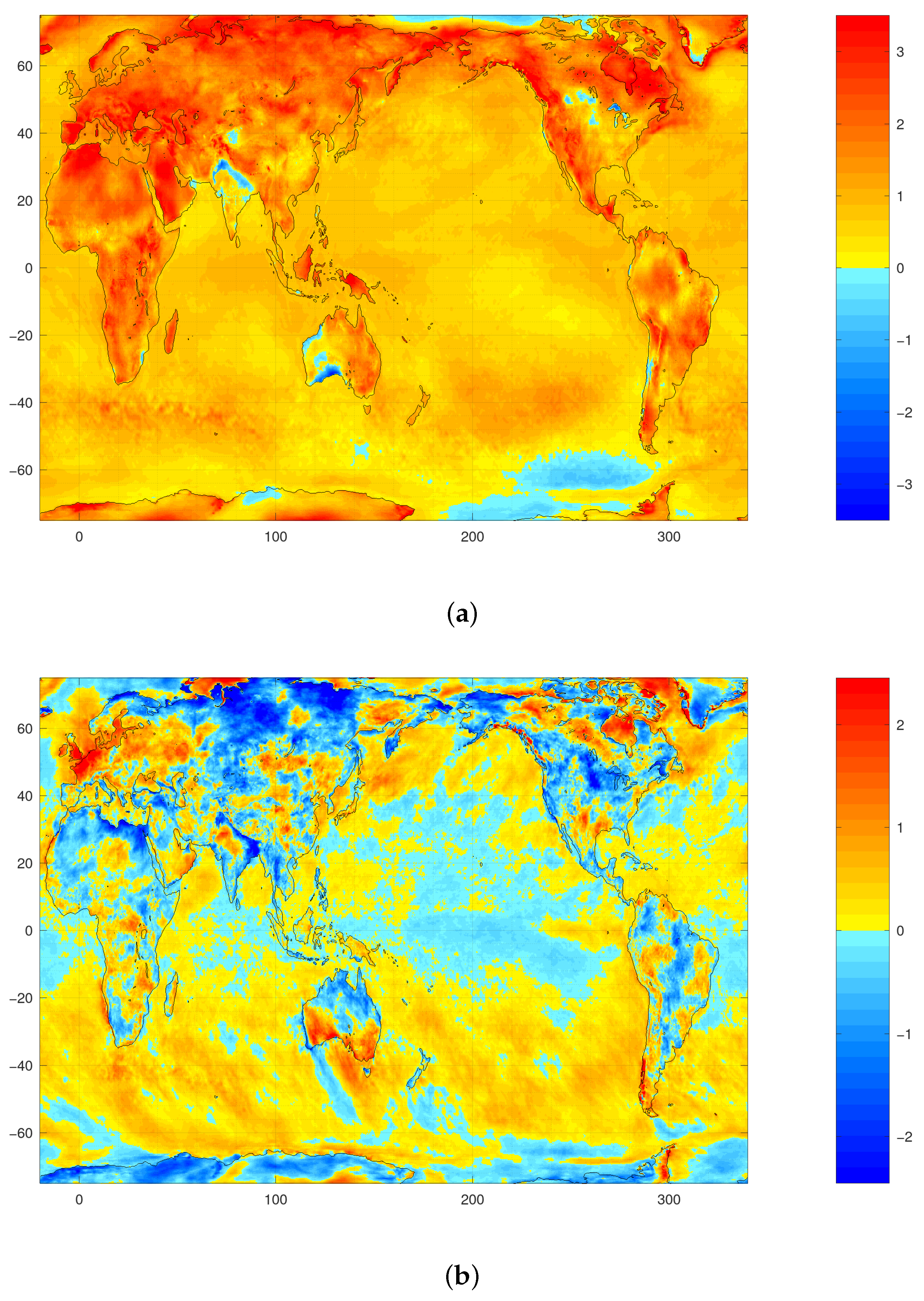
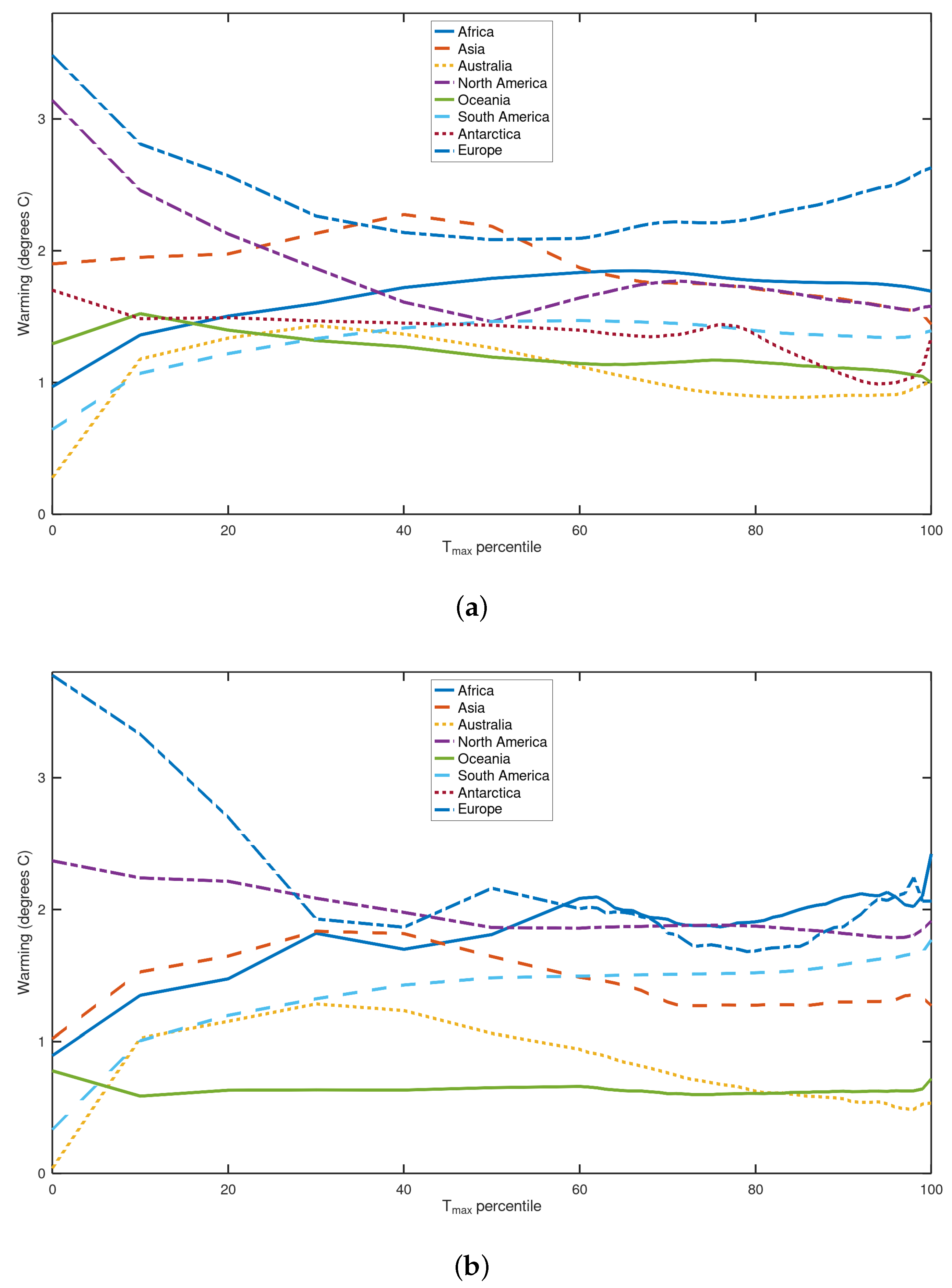
3.2. Warming and Amplification
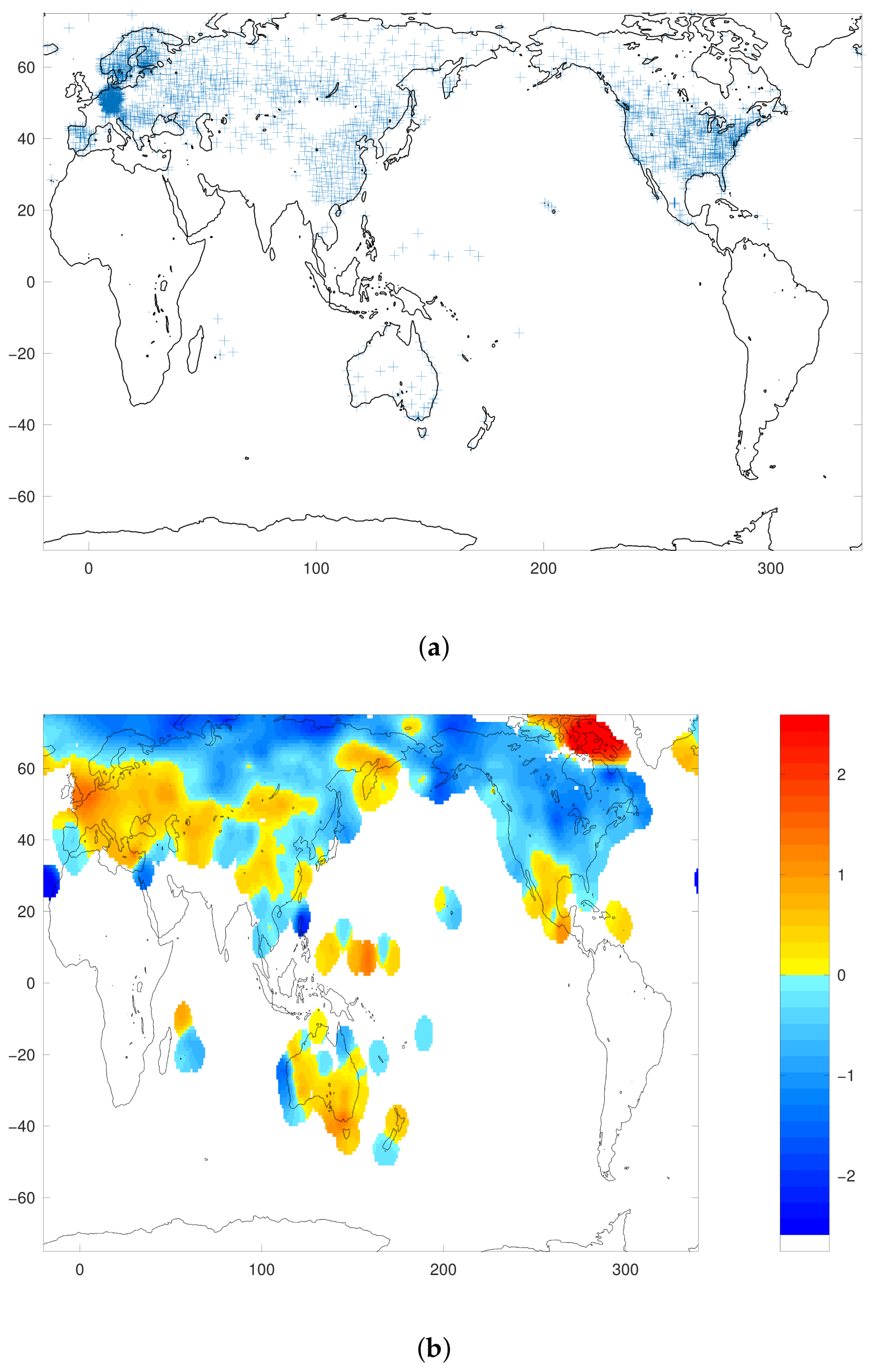
3.3. Comparison with GHCN-D Station Data
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the extremes. Clim. Chang. 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111, D05109. [Google Scholar] [CrossRef]
- McKinnon, K.A.; Rhines, A.; Tingley, M.P.; Huybers, P. The changing shape of Northern Hemisphere summer temperature distributions. J. Geophys. Res. Atmos. 2016, 121, 8849–8868. [Google Scholar] [CrossRef]
- Tamarin-Brodsky, T.; Hodges, K.; Hoskins, B.J.; Shepherd, T.G. Changes in Northern Hemisphere temperature variability shaped by regional warming patterns. Nat. Geosci. 2020, 13, 414–421. [Google Scholar] [CrossRef]
- Klein Tank, A.M.; Zwiers, F.W.; Zhang, X. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; Technical Report; World Meteorological Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Zwiers, F.W. Attribution and prediction of extreme events: Editorial on the special issue. Weather Clim. Extrem. 2015, 9, 2–5. [Google Scholar] [CrossRef]
- Easterling, D.R. Global Data Sets for Analysis of Climate Extremes. In Extremes in a Changing Climate; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 65, pp. 347–361. [Google Scholar] [CrossRef]
- Coumou, D.; Robinson, A. Historic and future increase in the global land area affected by monthly heat extremes. Environ. Res. Lett. 2013, 8, 034018. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Milagros de los Skansi, M.; Brunet, M.; Sigro, J.; Aguilar, E.; Groening, J.A.A.; Bentancur, O.J.; Geier, Y.R.C.; Amaya, R.L.C.; Jácome, H.; Ramos, A.M.; et al. Warming and wetting signals emerging from analysis of changes in climate extreme indices over South America. Glob. Planet. Chang. 2013, 100, 295–307. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multi-model ensemble. Part 1: Model evaluation in the present climate. J. Geophys. Res. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Mistry, M. A High-Resolution Global Gridded Historical Dataset of Climate Extreme Indices. Data 2019, 4, 41. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Tuholske, C. Earth observations of extreme heat events: Leveraging current capabilities to enhance heat research and action. Environ. Res. Lett. 2021, 16, 111002. [Google Scholar] [CrossRef]
- Mishra, V.; Ganguly, A.R.; Nijssen, B.; Lettenmaier, D.P. Changes in observed climate extremes in global urban areas. Environ. Res. Lett. 2015, 10, 024005. [Google Scholar] [CrossRef]
- Habeeb, D.; Vargo, J.; Stone, B. Rising heat wave trends in large US cities. Nat. Hazards 2015, 76, 1651–1665. [Google Scholar] [CrossRef]
- Stillman, J.H. Heat Waves, the New Normal: Summertime Temperature Extremes Will Impact Animals, Ecosystems, and Human Communities. Physiology 2019, 34, 86–100. [Google Scholar] [CrossRef]
- Kennedy-Asser, A.T.; Andrews, O.; Mitchell, D.M.; Warren, R.F. Evaluating heat extremes in the UK Climate Projections (UKCP18). Environ. Res. Lett. 2020, 16, 014039. [Google Scholar] [CrossRef]
- Mueller, N.D.; Butler, E.E.; McKinnon, K.A.; Rhines, A.; Tingley, M.; Holbrook, N.M.; Huybers, P. Cooling of US Midwest summer temperature extremes from cropland intensification. Nat. Clim. Chang. 2015, 6, 317–322. [Google Scholar] [CrossRef]
- Thiery, W.; Visser, A.J.; Fischer, E.M.; Hauser, M.; Hirsch, A.L.; Lawrence, D.M.; Lejeune, Q.; Davin, E.L.; Seneviratne, S.I. Warming of hot extremes alleviated by expanding irrigation. Nat. Commun. 2020, 11, 290. [Google Scholar] [CrossRef]
- Wu, X.; Wang, L.; Yao, R.; Luo, M.; Li, X. Identifying the dominant driving factors of heat waves in the North China Plain. Atmos. Res. 2021, 252, 105458. [Google Scholar] [CrossRef]
- Oldenborgh, G.J.V.; Wehner, M.F.; Vautard, R.; Otto, F.E.L.; Seneviratne, S.I.; Stott, P.A.; Hegerl, G.C.; Philip, S.Y.; Kew, S.F. Attributing and Projecting Heatwaves Is Hard: We Can Do Better. Earth’s Future 2022, 10, e2021EF002271. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Weather and climate extreme events in a changing climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Di Luca, A.; de Elía, R.; Bador, M.; Argüeso, D. Contribution of mean climate to hot temperature extremes for present and future climates. Weather Clim. Extrem. 2020, 28, 100255. [Google Scholar] [CrossRef]
- Di Luca, A.; Pitman, A.J.; de Elía, R. Decomposing Temperature Extremes Errors in CMIP5 and CMIP6 Models. Geophys. Res. Lett. 2020, 47, e2020GL088031. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Shifting hardiness zones: Trends in annual minimum temperature. Climate 2018, 6, 15. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Willett, K.M.; Thorne, P.W.; Woolley, E.V.; Durre, I.; Dai, A.; Parker, D.E.; Vose, R.S. HadISD: A quality-controlled global synoptic report database for selected variables at long-term stations from 1973–2011. Clim. Past 2012, 8, 1649–1679. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Willett, K.M.; Parker, D.E.; Mitchell, L. Expanding HadISD: Quality-controlled, sub-daily station data from 1931. Geosci. Instrum. Methods Data Syst. 2016, 5, 473–491. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Simonoff, J.S.; Tsai, C.L. Smoothing parameter selection in nonparametric regression using an improved Akaike information criterion. J. R. Stat. Soc. 1998, 60B, 271–293. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Estimating climate trends: Application to United States plant hardiness zones. Adv. Meteorol. 2012, 2012, 404876. [Google Scholar] [CrossRef]
- ERA5 Reanalysis (0.25 Degree Latitude-Longitude Grid). 2019. Available online: https://rda.ucar.edu/datasets/ds633.0/ (accessed on 3 January 2023). [CrossRef]
- Hersbach, H.; de Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational Global Reanalysis: Progress, Future Directions and Synergies with NWP; Technical Report 27; ECMWF: London, UK, 2018. [Google Scholar] [CrossRef]
- Domínguez-Castro, F.; Reig, F.; Vicente-Serrano, S.M.; Aguilar, E.; Peña-Angulo, D.; Noguera, I.; Revuelto, J.; van der Schrier, G.; El Kenawy, A.M. A multidecadal assessment of climate indices over Europe. Sci. Data 2020, 7, 125, Uses European Climate Assessment & Dataset (ECA&D) E-OBS gridded dataset and ERA5. [Google Scholar] [CrossRef] [PubMed]
- Mishra, V.; Ambika, A.K.; Asoka, A.; Aadhar, S.; Buzan, J.; Kumar, R.; Huber, M. Moist heat stress extremes in India enhanced by irrigation. Nat. Geosci. 2020, 13, 722–728. [Google Scholar] [CrossRef]
- Freychet, N.; Hegerl, G.; Mitchell, D.; Collins, M. Future changes in the frequency of temperature extremes may be underestimated in tropical and subtropical regions. Commun. Earth Environ. 2021, 2, 28. [Google Scholar] [CrossRef]
- Li, X.X. Heat wave trends in Southeast Asia during 1979–2018: The impact of humidity. Sci. Total Environ. 2020, 721, 137664. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Cook, B.I.; Puma, M.J. Effect of irrigation on humid heat extremes. Environ. Res. Lett. 2020, 15, 094010. [Google Scholar] [CrossRef]
- Menne, M.; Durre, I.; Vose, R.; Gleason, B.; Houston, T. An overview of the Global Historical Climatology Network-Daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Jaffrés, J.B. GHCN-Daily: A treasure trove of climate data awaiting discovery. Comput. Geosci. 2019, 122, 35–44. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive automated quality assurance of daily surface observations. J. Appl. Meteorol. Climatol. 2010, 49, 1615–1633. [Google Scholar] [CrossRef]
- Doxsey-Whitfield, E.; MacManus, K.; Adamo, S.B.; Pistolesi, L.; Squires, J.; Borkovska, O.; Baptista, S.R. Taking Advantage of the Improved Availability of Census Data: A First Look at the Gridded Population of the World, Version 4. Pap. Appl. Geogr. 2015, 1, 226–234. [Google Scholar] [CrossRef]
- Center For International Earth Science Information Network-CIESIN-Columbia University. Gridded Population of the World, Version 4 (GPWv4): Population Count, Revision 11; Columbia University: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Siebert, S.; Döll, P.; Hoogeveen, J.; Faures, J.M.; Frenken, K.; Feick, S. Development and validation of the global map of irrigation areas. Hydrol. Earth Syst. Sci. 2005, 9, 535–547. [Google Scholar] [CrossRef]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation—A global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef]
- Wilcox, R. A Note on the Theil-Sen Regression Estimator When the Regressor Is Random and the Error Term Is Heteroscedastic. Biom. J. 1998, 40, 261–268. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Chen, L.; Dirmeyer, P.A. Global observed and modelled impacts of irrigation on surface temperature. Int. J. Climatol. 2019, 39, 2587–2600. [Google Scholar] [CrossRef]
- Albaladejo-García, J.A.; Alcon, F.; Martínez-Paz, J.M. The Irrigation Cooling Effect as a Climate Regulation Service of Agroecosystems. Water 2020, 12, 1553. [Google Scholar] [CrossRef]
- Lebassi-Habtezion, B.; González, J.; Bornstein, R. Modeled large-scale warming impacts on summer California coastal-cooling trends. J. Geophys. Res. 2011, 116, D20114. [Google Scholar] [CrossRef]
- Potter, C. Understanding climate change on the California coast: Accounting for extreme daily events among long-term trends. Climate 2014, 2, 18–27. [Google Scholar] [CrossRef]
- Mason, L.A.; Riseng, C.M.; Gronewold, A.D.; Rutherford, E.S.; Wang, J.; Clites, A.; Smith, S.D.P.; McIntyre, P.B. Fine-scale spatial variation in ice cover and surface temperature trends across the surface of the Laurentian Great Lakes. Clim. Chang. 2016, 138, 71–83. [Google Scholar] [CrossRef]
- Zhong, Y.; Notaro, M.; Vavrus, S.J. Spatially variable warming of the Laurentian Great Lakes: An interaction of bathymetry and climate. Clim. Dyn. 2018, 52, 5833–5848. [Google Scholar] [CrossRef]
- White, C.; Heidinger, A.; Ackerman, S.; McIntyre, P. A Long-Term Fine-Resolution Record of AVHRR Surface Temperatures for the Laurentian Great Lakes. Remote Sens. 2018, 10, 1210. [Google Scholar] [CrossRef]
- Alexander, L.; Perkins, S. Debate heating up over changes in climate variability. Environ. Res. Lett. 2013, 8, 041001. [Google Scholar] [CrossRef]
- Byrne, M.P.; O’Gorman, P.A. Trends in continental temperature and humidity directly linked to ocean warming. Proc. Natl. Acad. Sci. USA 2018, 115, 4863–4868. [Google Scholar] [CrossRef]
- Byrne, M.P. Amplified warming of extreme temperatures over tropical land. Nature Geosci. 2021, 14, 837–841. [Google Scholar] [CrossRef]
- Fischer, E.M.; Seneviratne, S.I.; Vidale, P.L.; Luthi, D.; Schar, C. Soil moisture—Atmosphere interactions during the 2003 European summer heat wave. J. Clim. 2007, 20, 5081–5099. [Google Scholar] [CrossRef]
- Zampieri, M.; D’Andrea, F.; Vautard, R.; Ciais, P.; de Noblet-Ducoudré, N.; Yiou, P. Hot European summers and the role of soil moisture in the propagation of Mediterranean drought. J. Clim. 2009, 22, 4747–4758. [Google Scholar] [CrossRef]
- Stéfanon, M.; Drobinski, P.; D’Andrea, F.; Lebeaupin-Brossier, C.; Bastin, S. Soil moisture-temperature feedbacks at meso-scale during summer heat waves over Western Europe. Clim. Dyn. 2014, 42, 1309–1324. [Google Scholar] [CrossRef]
- Lemordant, L.; Gentine, P. Vegetation Response to Rising CO2 Impacts Extreme Temperatures. Geophys. Res. Lett. 2018, 46, 1383–1392. Available online: https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/2018GL080238 (accessed on 3 January 2023). [CrossRef]
- Lobell, D.B.; Bonfils, C.J.; Kueppers, L.M.; Snyder, M.A. Irrigation cooling effect on temperature and heat index extremes. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Thiery, W.; Davin, E.L.; Lawrence, D.M.; Hirsch, A.L.; Hauser, M.; Seneviratne, S.I. Present-day irrigation mitigates heat extremes. J. Geophys. Res. Atmos. 2017, 122, 1403–1422. [Google Scholar] [CrossRef]
- Xu, Y.; Lamarque, J.F.; Sanderson, B.M. The importance of aerosol scenarios in projections of future heat extremes. Clim. Chang. 2018, 146, 393–406. [Google Scholar] [CrossRef]
- Hirschi, M.; Seneviratne, S.I.; Alexandrov, V.; Boberg, F.; Boroneant, C.; Christensen, O.B.; Formayer, H.; Orlowsky, B.; Stepanek, P. Observational evidence for soil-moisture impact on hot extremes in southeastern Europe. Nat. Geosci. 2011, 4, 17–21. [Google Scholar] [CrossRef]
- Fan, Y.; Miguez-Macho, G. Potential groundwater contribution to Amazon evapotranspiration. Hydrol. Earth Syst. Sci. 2010, 14, 2039–2056. [Google Scholar] [CrossRef]
- Markewitz, D.; Devine, S.; Davidson, E.A.; Brando, P.; Nepstad, D.C. Soil moisture depletion under simulated drought in the Amazon: Impacts on deep root uptake. New Phytol. 2010, 187, 592–607. [Google Scholar] [CrossRef]
- Swann, A.L.S.; Koven, C.D. A Direct Estimate of the Seasonal Cycle of Evapotranspiration over the Amazon Basin. J. Hydrometeorol. 2017, 18, 2173–2185. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Cui, D.; Liang, S.; Wang, D. Observed and projected changes in global climate zones based on Köppen climate classification. WIREs Clim. Chang. 2021, 12, e701. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
| TXx | A | ||
|---|---|---|---|
| Water | 0.72 | 0.85 | 0.13 * |
| Land | 1.60 (0.82) | 1.56 (0.92) | −0.04 * (0.10) |
| Africa | 1.71 (1.90) | 1.69 (2.40) | −0.02 (0.49 *) |
| Asia | 1.68 (1.15) | 1.46 (1.27) | −0.22 * (0.12) |
| Australia | 0.01 (0.39) | 1.00 (0.52) | 0.99 (0.13) |
| North America | 1.70 (1.43) | 1.57 (1.92) | −0.13 (0.59) |
| Oceania | 1.32 (0.61) | 1.13 (0.72) | −0.19 (0.11 *) |
| South America | 1.10 (1.20) | 1.04 (1.44) | −0.06 (0.25 *) |
| Antarctica | 1.34 | 1.30 | −0.05 |
| Europe | 2.19 (1.70) | 2.48 (2.14) | 0.29 * (0.44) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krakauer, N.Y. Amplification of Extreme Hot Temperatures over Recent Decades. Climate 2023, 11, 42. https://doi.org/10.3390/cli11020042
Krakauer NY. Amplification of Extreme Hot Temperatures over Recent Decades. Climate. 2023; 11(2):42. https://doi.org/10.3390/cli11020042
Chicago/Turabian StyleKrakauer, Nir Y. 2023. "Amplification of Extreme Hot Temperatures over Recent Decades" Climate 11, no. 2: 42. https://doi.org/10.3390/cli11020042
APA StyleKrakauer, N. Y. (2023). Amplification of Extreme Hot Temperatures over Recent Decades. Climate, 11(2), 42. https://doi.org/10.3390/cli11020042






