Abstract
High quality and long-term precipitation data are required to study the variability and trends of rainfall and the impact of climate change. In developing countries like Morocco, the quality of climate data collected from various weather stations faces numerous obstacles. This paper presents methods for collecting, correcting, reconstructing, and homogenizing precipitation series of Morocco’s Fez-Meknes region from 1961 to 2019. Data collected from national specialized agencies based on 83 rain gauge stations was processed through an algorithm specially designed for the homogenization of climatic data (Climatol). We applied the Mann-Kendall test and Sen’s slope estimator to raw and homogenized data to calculate rainfall trend magnitudes and significance. The homogenization process allows for the detection of a larger number of stations with statistically significant negative trends with 95% and 90% confidence levels, particularly in the mountain ranges, that threatens the main sources of water in the largest watershed in the country. The regionalization of our rain gauge stations is highlighted and compared to previous studies. The monthly and annual means of raw and homogenized data show minor differences over the three main climate zones of the region.
1. Introduction
Morocco is located at a hot spot of climate change [1,2,3]. Multiple studies suggest a reduction in rainfall and an increase in extreme temperatures [4,5,6], with harmful consequences to agriculture and other economic activities [7,8,9,10].
Among the major problems that hinder any study of climate variability are the availability and quality of the data collected by the various measurement stations [11]. The quality of these data in developing countries is often uncertain [12], and their spatial and temporal coverage is limited. The homogenization of climate data is imperative in order to gain a clear vision of climate variability and change, versus changes that are specific to the observation methods [13] (changes in measuring instruments, changes in land use around the stations, changes in the station location, etc.) [14,15]. Climate series are considered to be homogeneous when their variations are related to climate variability alone, and not to these human factors [16]. Changes or alterations in the observation conditions, known as inhomogeneities, can conceal real changes in climate and can mislead the conclusions drawn from their study [17,18].
The detection of these artificial anomalies in climate data is widely studied by scientists. Data on station history (metadata) is one of the methods used to detect the origin of these anomalies [13]. These metadata are not always available, especially in developing countries such as Morocco. Without them, it is difficult to know the origin of certain abrupt changes in the climate variable series. Scientists are forced to opt for the use of approaches based on statistical methods and intercomparing of different observation series.
Scientists have developed homogenization methods that eliminate or minimize these unwanted alterations [19]. One such method is to compare one problematic series with another supposedly homogeneous one [20]. If such a series cannot be demonstrated, a reference series would be constructed from the average of others selected for their proximity or their strong correlation, thus diluting possible inhomogeneities at any one station [17,21]. As this does not guarantee that the reference series is homogeneous, other methods compare all available series in pairs, so repeated detection of inhomogeneity can identify erroneous series [16,22].
The study of climate variability and global trends in the regional climate requires data that reflect climate reality, while the climatic data in Morocco suffers from several difficulties linked to spatial and temporal gaps and discontinuities that harm climate variability monitoring on a regional scale. Given this, we have collected the maximum amount of data available on our territory (83 stations), especially in the more remote areas poorly served by the observation network. Manual homogenization of the data is not possible, given the scale of the calculations and the process. To overcome these issues, the Climatol tool (version 3.1.1) (https://www.climatol.eu/ accessed on 27 March 2022) [23], developed by Guijarro, was used. Climatol is implemented as an open-source R package and employs an adaptation of the Paulhus & Kohler [24] method to estimate all data as an (optionally weighted) average of the closest normalized data at any time step. The normalization consists simply in scaling by the respective means of the series. These estimations are then used to calculate the anomalies of the series to check the presence of outliers and the homogeneity of the series, and also to fill in any missing data. This method was chosen because it is simple and allows the usage of data from nearby stations even without a common period of observation with the problem series, which would otherwise prevent the adjustment of the regression models [25].
This package has been used in several studies to homogenize climate data. One application was to analyze trends and variability in wind speed in Saudi Arabia between 1978–2013 [26]. An in-depth analysis of homogenization methods for the Irish rainfall series was carried out by [27], using several packages including HOMER, ACMANT, Climatol, and AHOPS, and comparing the breaks detected between the homogenization methods. [28] adopted Climatol to homogenize Australian wind speed data by adding data from NCEP/NCAR reanalysis, producing the first homogenized series of wind speeds in Australia. The performance of the Climatol algorithm was evaluated by [29] by applying it to daily temperature series, for which quality metrics confirmed the good capacity of the Climatol package to suppress systematic errors related to jumps in the averages. [30] built a reference database (temperature and precipitation) for the Abruzzo region (central Italy), based on Climatol. Close to our study area, [31] used Climatol to homogenize the rainfall series in the Sous-Massa region, southern Morocco.
The purpose of this paper is to present the process of quality control, correction, reconstruction, and homogenization of the monthly rainfall series in the region of Fez-Meknes, and based on the obtained homogenization, study their general trend during the period 1961–2019. We also present the regionalization of our stations based on the process of homogenization achieved by the Climatol tool.
2. Study Area
The Fez-Meknes region is one of the 12 regions that make up the Kingdom of Morocco, located in the north of the country between the upper Moulouya to the southeast and the Rif mountains to the north, passing through the Middle Atlas range, the Sais plateau, and the Prerifan hills (Figure 1).
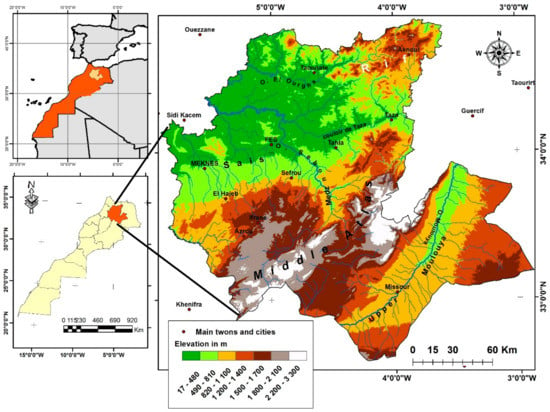
Figure 1.
Geographical location of the Fez-Meknes region.
Largely determined by the relief and exposure, the region of Fez-Meknes has a very varied climate. Different subtypes of Mediterranean climate prevail in the western part, with mean annual rainfall ranging from 423 mm in Fez, 508 mm in Meknes, up to 741 mm in Bab Ounder. The wettest conditions are on the mountain peaks of the Atlas and the Rif (988 mm in Ifrane, 1555 mm in Jbel Oudka). The southeast is arid to semi-arid, especially in the upper Moulouya, with 137 mm at Outat El Haj and 161 mm at Missour. The rainy season starts around October and ends around April, while the dry season lasts between May and September.
The region covers 5.6% of the national territory and is home to 4.2 million inhabitants, roughly 12.5% of the Moroccan population [32]. It provides about 15% of the usable agricultural land in Morocco. The region’s contribution to national cereal production remains significant, at around 21% during 2011–2012 [33]. The region’s water resources consist mainly of surface water (including the Sebou hydrological basin, which is the richest in water nationally), enhanced by 18 dams, including two large dams (El Wahda dam and Idriss 1st dam). This made it possible to guarantee the irrigation of large agricultural areas, in addition to supplying drinking water to cities not only within the region of Fez-Meknes, but also in the Gharb, which is part of the region of Rabat-Salé-Kénitra through a large project of water transfer [34]. Fossil water is heavily exploited as well. As a result, there are social and environmental imbalances [35,36,37,38]. The increase in water exploitation, combined with the country’s recent drought, as well as extreme events such as floods and torrential rains [39], raises the potential for serious problems for the region in the context of climate change [4].
3. Methods and Data
3.1. Methods
The homogenization of the precipitation series is based on the work of Guijarro [23] as implemented in the Climatol software tool. The method is based on orthogonal regression, widely known as the reduced major axis (RMA), which is specifically formulated to handle errors in both the x and y variables. It is a popular and alternative strategy to ordinary least squares (OLS) for fitting bivariate relations [40].
The model fitting procedure supposes a linear regression model y = α + βx + ε, where y and x are dependent and independent variables, respectively, α and β are OLS regression coefficients, and ε is a random error term. The RMA slope coefficient is βRMA = β/|ryx|, where ryx is the Pearson correlation coefficient between y and x. The standard error S.E. of βRMA is equal to the S.E. of β. The RMA intercept coefficient is αRMA = y − βRMA, and the S.E. of αRMA is equal to the S.E. of α. [41,42].
This algorithm was utilized through the homogenization process to calculate and estimate the missing data in our series iteratively based on fitting linear relationships between stations in the region until stabilization of the averages is achieved. The algorithm arranges stations in a tree structure, where clusters that show high correlations are grouped in the same branch. The correction of outliers is carried out automatically, and predefined criteria are used to monitor the operation’s quality, through the detection of relative inhomogeneities using the Standard Normal Homogeneity Test (SNHT) [19].
As part of Climatol, based on the rainfall behavior of each station, a tree of clusters of stations with similar subregional precipitation behavior was constructed, both before and after the homogenization of data. A generalization map was drawn to present the final regionalization of our stations.
Once the precipitation series have been homogenized and their missing data filled in, precipitation trends were calculated with the Mann-Kendall non-parametric test [43,44], at three levels of significance and the Sen’s slope estimator [45]. The goal of this study was to look at the rainfall trend in the region from 1961 to 2019. These results are expected to help in the planning of the water resources management in this area, improving the quality of life of its inhabitants and increasing the resilience in front of the precipitation variability induced by climate change.
3.2. Data
The data used in this study was collected from the appropriate administrative authorities in this field, namely the Sebou hydraulic basin agency (ABHS), the Oum Er Rabia hydraulic basin agency (ABHOER), and the hydraulic basin agency of the Moulouya (ABHM), as well as the National Meteorological Directorate (DMN) for some reference stations. Among other things, these agencies look after the water resources in each watershed and gather rainfall statistics. The spatial distribution of the measurement stations is shown in Figure 2, while the other geographic information such as each station’s elevation, length of the observation period, and percentage of missing data are shown in Table 1.
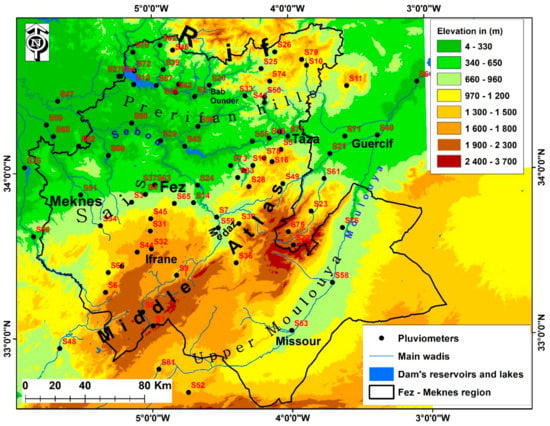
Figure 2.
Spatial distribution of rain gauge stations in the Fez-Meknes region and its surrounding areas.

Table 1.
Geographical location of stations, observation period and percentage of missing data.
The bulk of these stations are within the Fez-Meknes region. There are also some stations just outside this region, to make up for data gaps in places where the rain gauge network is poor within the region. Figure 2 shows the location and code of each station to facilitate the switching between the data table (Table 1) and the map.
4. Results
4.1. Quality Control and Homogenization
Before proceeding with the final homogenization of the series, we used the Climatol package to correct and reconstruct the missing data, where the ratio to the mean is the type of normalization that has been defined with the Climatol tool to allow the comparison of data from stations with very different mean rainfall [23]. After examining the diagnostic graphs of the data generated by Climatol, we increased the threshold to accept outliers up to 14 standard deviations. This was in order to tolerate certain extreme values that represent the region’s climatic reality, notably in mountainous areas and during certain seasons when this type of phenomenon occurs (for example, mountain storms during the period of transition between wet spring and summer or between summer and fall).
Referring to the quality flags file generated by the tool (Table 2), the final database consists of 58,764 monthly values for 83 measurement stations between 1961 and 2019, where 61.5% of the data is observed as original and unmodified. Another 4.2% was data that have been corrected after comparison with nearby stations: these are in particular outliers that do not necessarily reflect climate reality. The remaining 34.3% consists of data reconstituted by the Climatol package through adopting the method of [24], a process in which the contribution of nearby stations is critical.

Table 2.
Data characteristics after homogenization.
The original data in our database is illustrated in Figure 3. The year 1961 has been picked as the start date, to have a beginning relatively well covered with data on the whole of the regional territory, while the end of the data base is dictated by the need to use the latest data available.
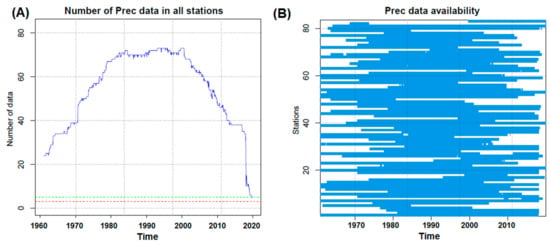
Figure 3.
Data availability per year. The green and red lines mark respectively the desired and critical number of data availability threshold.
The amount of information available is more than enough to develop homogenized series and estimate regional and subregional precipitation trends. In Figure 3, the green and red lines respectively mark the desired number (critical threshold) of data availability required for this package. Overall, during the 1960s the amount of data gathered was increasing. After 1970 the network became relatively dense until the 2000s. We then notice the beginning of the observation network’s degeneration, which had a negative impact on the quality and quantity of the data collected.
Correlograms illustrate the correlation vs distance (calculated with first differences) in the station series between the raw and the homogenized data. Figure 4 shows a change in favor of homogenized data, where the physically unlikely large negative correlations between a few stations were corrected by the homogenization process. We note that stations less than 150 km apart are better correlated with each other. With increasing distance, a decrease in the correlation coefficient is noticeable in both the original and homogenized data. This prompted us to use the homogenized data to study the final rainfall trends in the region.
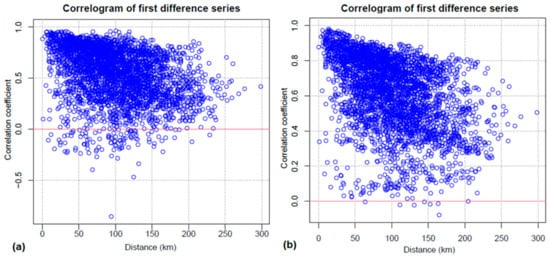
Figure 4.
Correlograms of the first differences of the series stations (a) raw data and (b) adjusted data.
The detection of breaks in the time series allowed the identification of 13 stations affected by anomalous changes in the mean, including two stations (Tahla and Pont Sebou) with a maximum of two breaks each. These discontinuities are concentrated between the years 1970 and 1980, when Morocco experienced the driest years during the 20th century, so some discontinuities may be due to real changes in climate and not just station-specific factors. This is in agreement with the conclusions of [2,46,47].
The quality of the homogenization applied to the database is also evaluated by the root mean square error (RMSE), between observed and estimated data (Figure 5). This indicator varies between a minimum of 1.2 mm and a maximum of 58.3 mm, the median is 15.2 mm while the average is 18.3 mm. The standard normal homogeneity test SNHT (on anomaly series) for the adjusted data ranges between a minimum of 0.9 and a maximum of 43.8, the median is 7.4 while the average is 9.0. The comparison between the station’s RMSE reveals that the mountain stations register the highest values of the root mean square error. In a mountainous and rugged environment, the challenge of anticipating or interpolating precipitation has previously been noted [48,49].
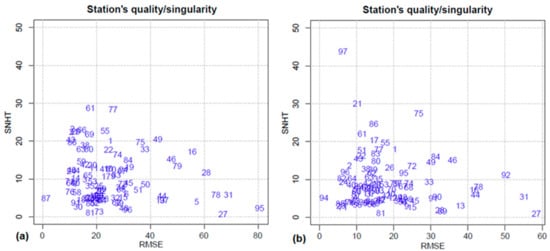
Figure 5.
Plot of quality/singularity of the stations of (a) raw and (b) adjusted data.
The comparison of the observed means and those generated after homogenization shows general similarities, and the overall distribution of rainfall remains unchanged (Figure 6).
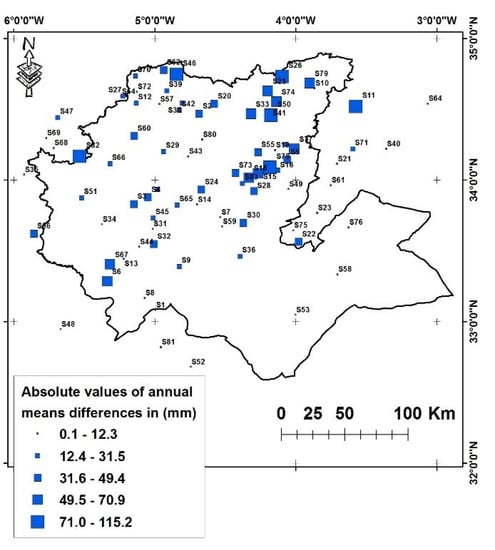
Figure 6.
At the top, the comparison between the annual averages of the two types of data, at the bottom the absolute difference with the observed average.
Nevertheless, mapping the absolute differences between the means of the two types of data (Figure 6-bottom) shows a clear change in some mountainous stations, especially the stations with short observation periods, which generate a fairly strong correction through the homogenization process, since the averages observed over a short period do not necessarily represent the local climatic reality (stations Zeggouta S82, Marticha S50, Sidi El Mokhfi S67, Anguid MZ S11, etc.). This correction is also made in special cases of stations located at the top of mountains, such as Tazzeka S78 (1971 m.a.s.l), Jbel Oudka S46 (1589 m.a.s.l), which reflect a very small-scale microclimate.
The comparison of monthly means between the raw series and the homogenized series reflects the strength and validity of the homogenization process. The temporal distribution of the average annual rainfall has also been largely preserved despite the homogenization process.
The absolute difference between the monthly mean values of the two types of data does not exceed the maximum of 4 mm during the month of March, followed by 2.6 mm and 2.3 mm for the months of December and November, respectively (Figure 7). The other values vary between minimums of 0.1 for the months of September and August and 0.4 mm for the months of May and February. The absolute difference between the seasonal averages of the raw data and the homogenized ones remains very small, at 5 mm as a maximum in spring and 1.5 mm in winter. The relationship between the annual averages of the raw data and the homogenized data is shown in (Figure 8).
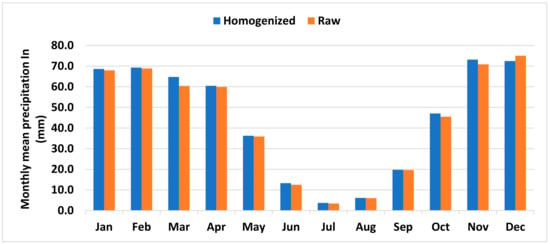
Figure 7.
Monthly means of raw and homogenized data for all data available for the region.
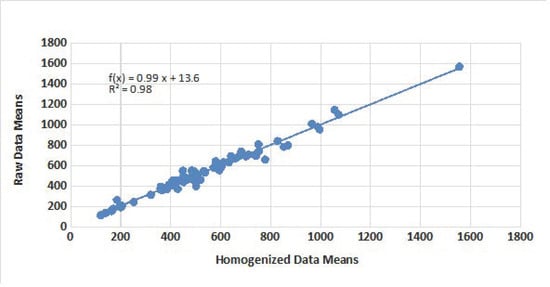
Figure 8.
Correlation between annual means of raw and homogenized data.
Across all stations in the region, the maximum annual precipitation occurs in the winter season, with 212 mm during the months (December, January, and February), followed by the spring precipitation with an average height of 156 mm (March, April, and May). The fall season comes in third place with 136 mm. The monthly maximum occurs in the month of December, followed by the month of November, then January, and February. We also notice the increase in precipitation in mountain areas, which is consistent with the findings of Abahous et al. [31].
4.2. Regionalization of Stations
Given the station clusters or groups proposed by the Climatol tool (Figure 9), we distinguish three broad zones that are each relatively climatically homogeneous. Their boundaries are largely dictated by the orography, the prevailing wind, and distance to the ocean.
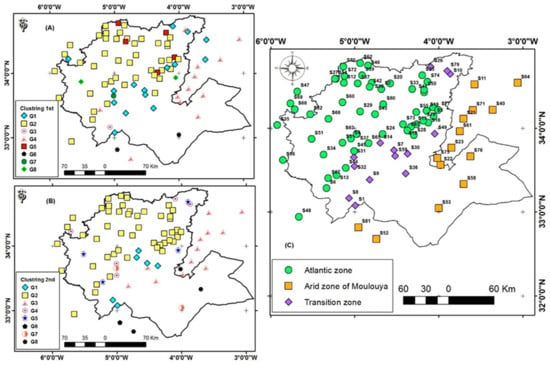
Figure 9.
Clusters of stations (A) before and (B) after homogenization (C) generalization map.
The three zones are (1) a humid Atlantic zone with a Mediterranean climate located at the west of the Middle Atlas mountain range; (2) a more arid zone to the south-east and east of the region (Upper Moulouya and Guercif basin); and (3) a transition zone between the two, located on the Atlas peaks, the Medaz basin, and the region’s northeastern tip (Figure 9).
This transition zone marks the passage between a mild climate shaped by the oceanic influences of the Atlantic through the west of the mountain range of the Middle Atlas and that of the Rif, and an arid climate zone shaped by the combined effects of continentality, the mountain barrier (which induces dry foehn winds), and the great Sahara, which impacts eastern Morocco all the way to the Mediterranean Sea.
A. Humid or “Atlantic” zone
This zone is mainly found in the north-western part of the region. Its rainfall regime is presented in Figure 10, with the peak of precipitation occurring in November and December. The absolute difference between the monthly averages of the two types of data does not exceed the maximum of 6 mm in March and 4.3 mm in December. The minimum values are around 0.3 mm, 0.4 mm, and 0.6 mm for the months of September, April, and May, respectively.
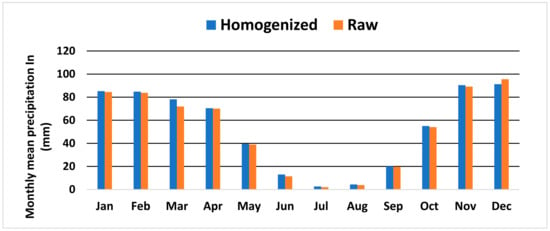
Figure 10.
Monthly averages of raw and homogenized data for the Atlantic zone.
B. The Arid zone of Moulouya
This zone is made up of the lands of the upper Moulouya region of Missour, the Guercif basin, and its neighboring areas (Figure 2). The precipitation regime has a very marked spring component with a maximum of rain in April and March, while the second peak happens in autumn, centered on the two months of October and November (Figure 11). We can distinguish two parts within this zone: The Guercif zone, with more Mediterranean contributions to the north, and the upper Moulouya around Missour, with a double effect on the mountain and the Sahara, which infiltrates via the high plateaus.
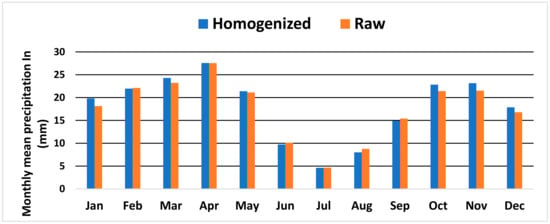
Figure 11.
Monthly averages of raw and homogenized data for the arid zone beyond the mountainous barrier.
The absolute difference between the monthly averages of the raw and homogenized data varies between a maximum of 1.7 mm and 1.6 mm during the months of January and November. The minimum is around 0 mm in April and July, and 0.1 to 0.3 mm for the months of February and May, respectively.
C. Transition zone or «Mountains»
These are the drier mountain peaks of the Middle Atlas and the Rif, which mark the passage between the two previous areas. The variability of precipitation reaches its maximum, and the representativeness of the stations does not necessarily reflect the subregional climatic reality, which is largely shaped by the exposure of the slopes, the opening, and the orientation of the valleys.
The absolute difference between the monthly averages of the raw and homogenized data oscillates between an autumn maximum of 6 mm and 3.6 mm for the months of November and October. The minimum is around 0.3 mm, 0.4, and 1 mm for the months of May, January, and February, respectively, as shown in Figure 12.
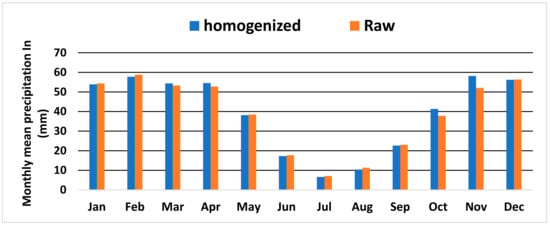
Figure 12.
Monthly means of raw and homogenized data for the transition zone.
4.3. Trend Analysis
To examine the trend of precipitation in the region, we have used the Mann-Kendall non-parametric test [43,44] at the alpha thresholds α = 0.01; 0.05; and 0.10, and the Sen slope [45] was applied to the raw and homogenized data.
The results of the trend test are presented in the maps in Figure 13. In both types of data, the trend is negative with significance level α = (0.01; 0.05; 0.10). More of the trends in the raw data are significant at the alpha level α = 0.01 (10 stations). The homogenization process reduces this number to a single station. But this same process made it possible to increase the number of series with negative trends at the SL α = 0.05 from (9 in the raw data to 23 in the homogenized series). For the threshold α = 0.10 the homogenization process increased the number of stations with a negative trend from four in the raw data to 17 stations in the homogenized data.
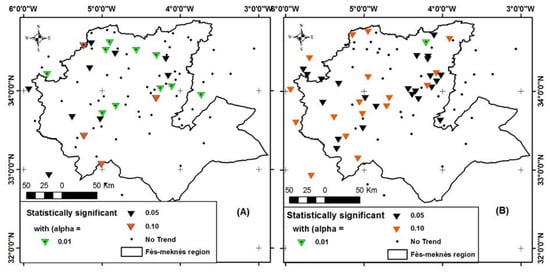
Figure 13.
Spatial distribution of significant precipitation trends before (A) and after homogenization (B).
As for the spatial distribution of the negative trends detected, there is a concentration of these negative trends in the mountainous areas of the Middle Atlas and the Rif north of Taza. The arid to semi-arid areas of Moulouya do not show any significant trends, and the same for the western Rif foothills except for two stations (Tabouda and Ratba) which show a downward trend at the 0.10 significance level.
The Sen slope, for the homogenized series which recorded a significant downward trend at the threshold α = 0.05, varies between a maximum of −6.52 and −6, for the Bab Boudir and Echoyeb stations, respectively. Significant minimum values of −2.70, −3.42, −2.38, and −4.05 were seen for the stations of Fez DRH, Meknes, Sidi Kacem, and Taza, respectively. After homogenization, more of the station series thus reflect the global climate trend, which threatens the water resources in the mountains above all, knowing that mountains are the water reservoir for Morocco.
5. Discussion
In this study, we presented the process of quality control, reconstruction, and homogenization of monthly precipitation data in the Fez-Meknes region, northern Morocco. We also studied the trend of precipitation in the raw and homogenized series between 1961 to 2019.
The comparison between raw and homogenized data through correlograms of the first differences reports a small change related to the correction and reconstruction of the data. The mean monthly rainfall distribution was not greatly affected by homogenization, with differences between the annual and monthly averages of the two data types not exceeding 6 mm.
The quality control flags of the final gap-filled and homogenized dataset showed that our database consists of approximately 62% of the original observed and unmodified data, while 4% is represented by corrected data, and finally, reconstructed data represents nearly 34% of the total.
The validity of the homogenization process is examined through the root mean square error between raw and homogenized data for each station. The RMSE values vary between a minimum of 1.2 mm and a maximum of 80.4 mm, the median is 21.2 mm while the average is 25.3 mm; all these values are far less than those of [31], which may reflect greater station density or more complete data in our study compared to [31]. We have underlined the relevance of the RMSE at stations with shorter observation periods, particularly in mountainous areas where the measuring network is deteriorating. The homogenization operation, therefore, made it possible to correct data from certain stations which represent particular microclimates on the mountain tops but still share temporal variability with nearby stations.
The algorithm’s strength is shown in the regionalization of our stations using clusters, which group stations with similar rainfall behavior and divide the Fez-Meknes region into three main climatic zones. These are a humid Atlantic zone to the west, an arid to semi-arid zone to the southeast and east, and finally a transition zone that marks the passage between them. It is worth noting that our results on precipitation regionalization in this Fez-Meknes region are quite similar to those of [50,51,52]; and [47], on the regionalization of precipitation across all of Morocco. There appear to be some differences due to the limited number of stations used by Knippertz [52]. Although the national scale used is much larger than our small region, the three large groups proposed by Ward et al. [50]: the Atlantic zone (I) and the Atlas zone (III), and the Mediterranean zone (V), integrated into the arid zone in our case, are largely recognizable in the regionalization produced in this work.
According to the clustering map (Figure 9) based on the dendrogram of station clusters, the Middle Atlas stations do not join into a single group, as has been proposed by [47] with its so-called meso grouping. Instead, they are placed in two different groups, one in the Atlantic group for the wettest fringes in the north and west, while the stations located inside the mountain with little rainfall are placed into another group that we have named "Transition zone", towards the arid zones of Moulouya. This corresponds with the so-called micro regions proposed by the same author [47], at least for the Middle Atlas. The northeastern tip of the region also marks the transition between a more humid climate in the west and a drier climate towards the eastern Rif and the Guercif basin in the east.
The power of the Climatol algorithm lies in its ability to detect transition stations between the relative wetness in the west of the region, and the arid zone in the south-east and east. The stations of the Medaz basin, in the eastern and southern parts of Middle Atlas are logically placed in this group that we have called the “transition zone”.
The breaks detected by the SNHT test reveal a concentration of ruptures in the 1970s and 1980s, which coincides with a wave of drought which negatively impacted Morocco, in harmony with the results of [2,47,53]. As for the general trends in precipitation series in the Fez-Meknes region, the application of the Mann-Kendall test and the Sen slope to the homogenized series allowed us to observe a general trend towards a decrease in precipitation in mountain areas. This trend is significant at the alpha levels = 0.05 and 0.10. Homogenization made it possible to increase the number of stations with a significant downward trend at the alpha threshold = 0.05, this is in agreement with the results of [7,31,54].
6. Conclusions
Climate data are important to study climate variability and climate change around the globe, but the quality of this data remains concerning in developing countries. Spatial and temporal discontinuities are the most frequent problems that hinder climate change monitoring. In this study, we presented the first effort at mass collection, reconstruction, and homogenization of rainfall series in the Fez-Meknes region, northern Morocco. Our paper is the second nationally, after that of Abahous et al. [31], to present such an operation in one of the most important regions in the country.
While there are many techniques for homogenization of climatic data, our results suggest that Climatol algorithms perform well in Morocco, consistent with diverse studies around the globe [31,55]. The quality of the result is judged through two elements: the low levels of RMSE between raw and homogenized data, and the regionalization generated for our stations, where data homogenization was accompanied by generating a tree of clusters of homogeneous subregions based on the rainfall behavior of each station. Further, trend analysis in raw and homogenized data shows a clear negative trend in the majority of rain gauge stations located in mountain areas and on the western side of the regional territory. The negative trend of precipitation in mountain areas should prompt decision-makers to rethink adaptation and mitigation strategies in mountain ranges first and foremost. Mountain areas are the main sources of water because of their high levels of rainfall, and many dams and reservoirs are built in those regions. The results of this research will also help in hydrological modeling in the most important watershed of Morocco.
Author Contributions
Conceptualization, R.K.; methodology, R.K. and M.H.; software, R.K., A.S. and J.A.G.; formal analysis, R.K.; validation: R.K., M.H., J.A.G. and N.Y.K.; investigation, R.K., M.B., R.A.; data curation, R.K. and A.S.; writing—original draft preparation, R.K., M.H., M.B. and N.Y.K.; writing—review and editing, R.K., N.Y.K., M.H. and J.A.G.; visualization, R.K.; supervision, M.H., J.A.G. and N.Y.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We would like to thank the ABHS, ABHOER, ABHM, staffs for providing data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xoplaki, E.; González-Rouco, J.F.; Luterbacher, J.; Wanner, H. Wet season Mediterranean precipitation variability: Influence of large-scale dynamics and trends. Clim. Dyn. 2004, 23, 63–78. [Google Scholar] [CrossRef] [Green Version]
- Driouech, F. Distribution des Précipitations Hivernales sur le Maroc Dans le Cadre d’un Changement Climatique: Descente d’Echelle et Incertitudes; L’université de Toulouse: Toulouse, France, 2010; pp. 1–164. [Google Scholar]
- Tramblay, Y.; Badi, W.; Driouech, F.; el Adlouni, S.; Neppel, L.; Servat, E. Climate change impacts on extreme precipitation in Morocco. Glob. Planet. Change 2012, 82–83, 104–114. [Google Scholar] [CrossRef]
- Tomaszkiewicz, M.A. Future Seasonal Drought Conditions over the CORDEX-MENA/Arab Domain. Atmosphere 2021, 12, 856. [Google Scholar] [CrossRef]
- Lelieveld, J.; Proestos, Y.; Hadjinicolaou, P.; Tanarhte, M.; Tyrlis, E.; Zittis, G. Strongly increasing heat extremes in the Middle East and North Africa (MENA) in the 21st century. Clim. Change 2016, 137, 245–260. [Google Scholar] [CrossRef] [Green Version]
- Zittis, G. Observed rainfall trends and precipitation uncertainty in the vicinity of the Mediterranean, Middle East and North Africa. Theor. Appl. Climatol. 2018, 134, 1207–1230. [Google Scholar] [CrossRef]
- Driouech, F.; Mahé, G.; Deque, M.; Dieulin, C.; El Heirech, T.; Milano, M. Evaluation d’impacts potentiels de changements climatiques sur l’hydrologie du bassin versant de la Moulouya au Maroc. In Proceedings of the Sixth World FRIEND Conference, Fez, Morocco, 25–29 October 2010; AISH Publications: Wallingford, UK, 2010; Volume 340, pp. 561–567. [Google Scholar]
- Filahi, S.; Tramblay, Y.; Mouhir, L.; Diaconescu, E.P. Projected changes in temperature and precipitation indices in Morocco from high-resolution regional climate models. Int. J. Climatol. 2017, 37, 4846–4863. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A.B. Why Is the Mediterranean a Climate Change Hot Spot? J. Clim. 2020, 33, 5829–5843. [Google Scholar] [CrossRef]
- Schilling, J.; Freier, K.P.; Hertig, E.; Scheffran, J. Climate change, vulnerability and adaptation in North Africa with focus on Morocco. Agric. Ecosyst. Environ. 2012, 156, 12–26. [Google Scholar] [CrossRef]
- Gubler, S.; Hunziker, S.; Begert, M.; Croci-Maspoli, M.; Konzelmann, T.; Brönnimann, S.; Schwierz, C.; Oria, C.; Rosas, G. The influence of station density on climate data homogenization. Int. J. Climatol. 2017, 37, 4670–4683. [Google Scholar] [CrossRef] [Green Version]
- Easterling, D.R.; Alexander, L.V.; Mokssit, A.; Detemmerman, V. CCI/CLIVAR workshop to develop priority climate indices. Bull. Am. Meteorol. Soc. 2003, 84, 1403–1407. [Google Scholar]
- Ribeiro, S.; Caineta, J.; Costa, A.C. Review and discussion of homogenisation methods for climate data. Phys. Chem. Earth Parts A/B/C 2016, 94, 167–179. [Google Scholar] [CrossRef]
- Karl, T.R.; Williams, C.N. An Approach to Adjusting Climatological Time Series for Discontinuous Inhomogeneities. J. Appl. Meteorol. Climatol. 1987, 26, 1744–1763. [Google Scholar] [CrossRef] [Green Version]
- Hunziker, S.; Brönnimann, S.; Calle, J.; Moreno, I.; Andrade, M.; Ticona, L.; Huerta, A.; Lavado-Casimiro, W. Effects of undetected data quality issues on climatological analyses. Clim. Past 2018, 14, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.C.; Wieringa, J. Guidelines on Climate Metadata and Homogenization; World Meteorological Organization: Geneva, Switzerland, 2003; Volume 53. [Google Scholar]
- Guijarro, J.A. Daily series homogenization and gridding with Climatol v.3. In Proceedings of the Ninth Seminar for Homogenization and Quality Control in Climatological Databases and Fourth Conference on Spatial Interpolation Techniques in Climatology and Meteorology, Budapest, Hungary, 3–7 April 2017; WMO: Geneva, Switzerland, 2017; Volume 85, pp. 175–180. [Google Scholar]
- Shi, P.; Zhang, G.; Kong, F.; Chen, D.; Azorin-Molina, C.; Guijarro, J.A. Variability of winter haze over the Beijing-Tianjin-Hebei region tied to wind speed in the lower troposphere and particulate sources. Atmos. Res. 2019, 215, 1–11. [Google Scholar] [CrossRef]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Beaulieu, C.; Ouarda, T.; Seidou, O. A review of homogenization techniques for climate data and their applicability to precipitation series. Hydrol. Sci. J. 2007, 52, 18–37. [Google Scholar] [CrossRef] [Green Version]
- Azorin-Molina, C.; Guijarro, J.A.; McVicar, T.R.; Vicente-Serrano, S.M.; Chen, D.; Jerez, S.; Espírito-Santo, F. Trends of daily peak wind gusts in Spain and Portugal, 1961–2014. J. Geophys. Res. Atmos. 2016, 121, 1059–1078. [Google Scholar] [CrossRef] [Green Version]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Guijarro, J.A. Homogenization of Climatological Series with Climatol Version 3.1.1; State Meteorological Agency (AEMET): Balearic Islands, Spain, 2018; Volume 1, p. 20. [Google Scholar]
- Paulhus, J.L.H.; Kohler, M.A. Interpolation of Missing Precipitation Records. Mon. Weather Rev. 1952, 80, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Guijarro, J.A.; López Díaz, J.A.; Aguilar, E.; Domonkos, P.; Venema, V.K.; Sigró, J.; Brunet, M. Comparison of homogenization packages applied to monthly series of temperature and precipitation: The MULTITEST Project. In Proceedings of the 9th Seminar for Homogenization and Quality Control in Climatological Databases, Budapest, Hungary, 3–7 April 2017; pp. 46–62. [Google Scholar]
- Azorin-Molina, C. Recent trends in wind speed across Saudi Arabia, 1978–2013: A break in the stilling. Int. J. Climatol. 2018, 38, e966–e984. [Google Scholar] [CrossRef]
- Coll, J. Application of homogenization methods for Ireland’s monthly precipitation records: Comparison of break detection results. Int. J. Climatol. 2020, 40, 6169–6188. [Google Scholar] [CrossRef] [PubMed]
- Azorin-Molina, C.; Guijarro, J.A.; McVicar, T.R.; Trewin, B.C.; Frost, A.J.; Chen, D. An approach to homogenize daily peak wind gusts: An application to the Australian series. Int. J. Climatol. 2019, 39, 2260–2277. [Google Scholar] [CrossRef] [Green Version]
- Skrynyk, O.; Aguilar, E.; Guijarro, J.; Randriamarolaza, L.Y.A.; Bubin, S. Uncertainty evaluation of Climatol’s adjustment algorithm applied to daily air temperature time series. Int. J. Climatol. 2021, 41, E2395–E2419. [Google Scholar] [CrossRef]
- Curci, G.; Guijarro, J.A.; di Antonio, L.; di Bacco, M.; di Lena, B.; Scorzini, A.R. Building a local climate reference dataset: Application to the Abruzzo region (Central Italy), 1930–2019. Int. J. Climatol. 2021, 41, 4414–4436. [Google Scholar] [CrossRef]
- Abahous, H.; Guijarro, J.A.; Sifeddine, A.; Chehbouni, A.; Ouazar, D.; Bouchaou, L. Monthly precipitations over semi-arid basins in Northern Africa: Homogenization and trends. Int. J. Climatol. 2020, 40, 6095–6105. [Google Scholar] [CrossRef]
- HCP. Recensement Général de la Populatiion et de l’Habitat. Monograpie de la Région Marrakech-Safi; Direction Régionale de Marrakech-Safi; Ministère de l’Intérieur: Rabat, Morocco, 2014; p. 171. Available online: https://www.regions-maroc.ma/wp-content/uploads/2020/10/MONOGRAPPHIE-DE-LA-REGION-DE-MARRAKECH-SAFI.pdf (accessed on 27 March 2022).
- DGCL. In Monographie Générale, Région de Fès-Meknès; Ministère de l’Intérieur: Rabat, Morocco, 2015; p. 62. Available online: https://hazbane.asso-web.com/uploaded/monographie-de-la-region-de-fes-meknes-fr.pdf (accessed on 27 March 2022).
- El Moçayd, N.; Kang, S.; Eltahir, E.A.B. Climate change impacts on the Water Highway project in Morocco. Hydrol. Earth Syst. Sci. 2020, 24, 1467–1483. [Google Scholar] [CrossRef] [Green Version]
- Ameur, F.; Kuper, M.; Lejars, C.; Dugué, P. Prosper, survive or exit: Contrasted fortunes of farmers in the groundwater economy in the Saiss plain (Morocco). Agric. Water Manag. 2017, 191, 207–217. [Google Scholar] [CrossRef]
- Hssaisoune, M.; Bouchaou, L.; Sifeddine, A.; Bouimetarhan, I.; Chehbouni, A. Moroccan Groundwater Resources and Evolution with Global Climate Changes. Geosciences 2020, 10, 81. [Google Scholar] [CrossRef] [Green Version]
- Quarouch, H.; Kuper, M.; Abdellaoui, E.H.; Bouarfa, S. Eaux souterraines, sources de dignité et ressources sociales: Cas d’agriculteurs dans la plaine du Saïss au Maroc. Cah. Agric. 2014, 23, 158–165. [Google Scholar]
- Fofack, R. The social and political impact of the privatization of groundwater: Conflict and cooperation around the aquifer of Sais, Morocco. Water Soc. 2015, 200, 11143. [Google Scholar]
- Hanchane, M. Variabilité des pluies exceptionnelles dans le bassin versant de Sebou (Maroc): Intensité et période de retour selon l’hypothèse de non stationnarité temporelle. In Proceedings of the XXIX Colloque de l’Association Internationale de Climatologie, Lausanne Besançon, Switzerland, 6–9 July 2016; pp. 279–283. [Google Scholar]
- Leduc, D.J. A comparative analysis of the reduced major axis technique of fitting lines to bivariate data. Can. J. For. Res. 1987, 17, 654–659. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Gove, J.H.; Heath, L.S. A comparison of alternative methods for estimating the self-thinning boundary line. Can. J. For. Res. 2005, 35, 1507–1514. [Google Scholar] [CrossRef]
- Solomon, D.S.; Zhang, L.Z. Maximum size-density relationships for mixed-hardwood forest stands in New England. In Integrated Tools for Natural Resources Inventories in the 21st Century; General Technical Reports; Department of Agriculture, Forest Service, North Central Forest Experiment Station: St. Paul, MN, USA, 2000. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics; Macmillan: New York, NY, USA, 1977; Volume 1, p. 168. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Driouech, F.; Déqué, M.; Mokssit, A. Numerical simulation of the probability distribution function of precipitation over Morocco. Clim. Dyn. 2009, 32, 1055–1063. [Google Scholar] [CrossRef]
- Singla, S.; Mahé, G.; Dieulin, C.; Driouech, F.; Milano, M.; El Guelai, F.Z.; Ardoin-Bardin, S. Evolution des relations pluie-débit sur des bassins versants du Maroc. In Proceedings of the Sixth World FRIEND Conference, Fez, Morocco, 25–29 October 2010; AISH Publications: Wallingford, UK, 2010; Volume 340, pp. 679–687. [Google Scholar]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Pellicone, G.; Caloiero, T.; Modica, G.; Guagliardi, I. Application of several spatial interpolation techniques to monthly rainfall data in the Calabria region (southern Italy). Int. J. Climatol. 2018, 38, 3651–3666. [Google Scholar] [CrossRef]
- Ward, M.N.; Lamb, P.J.; Portis, D.H.; el Hamly, M.; Sebbari, R. Climate Variability in Northern Africa: Understanding Droughts in the Sahel and the Maghreb. In Beyond El Niño: Decadal and Interdecadal Climate Variability; Navarra, A., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 119–140. [Google Scholar]
- Knippertz, P.; Christoph, M.; Speth, P. Long-term precipitation variability in Morocco and the link to the large-scale circulation in recent and future climates. Meteorol. Atmos. Phys. 2003, 83, 67–88. [Google Scholar] [CrossRef]
- Knippertz, P. A Simple Identification Scheme for Upper-Level Troughs and Its Application to Winter Precipitation Variability in Northwest Africa. J. Clim. 2004, 17, 1411–1418. [Google Scholar]
- Zamrane, Z.; Mahé, G.; Laftouhi, N.E. Wavelet analysis of rainfall and runoff multidecadal time series on large river basins in western north Africa. Water 2021, 13, 3243. [Google Scholar] [CrossRef]
- Driouech, F.; Stafi, H.; Khouakhi, A.; Moutia, S.; Badi, W.; El Rhaz, K.; Chehbouni, A. Recent observed country-wide climate trends in Morocco. Int. J. Climatol. 2021, 41, E855–E874. [Google Scholar] [CrossRef]
- Joelsson, L.M.T.; Sturm, C.; Södling, J.; Engström, E.; Kjellström, E. Automation and evaluation of the interactive homogenization tool HOMER. Int. J. Climatol. 2021, 42, 2861–2880. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).