Forecasting of SPI and SRI Using Multiplicative ARIMA under Climate Variability in a Mediterranean Region: Wadi Ouahrane Basin, Algeria
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Area and Data
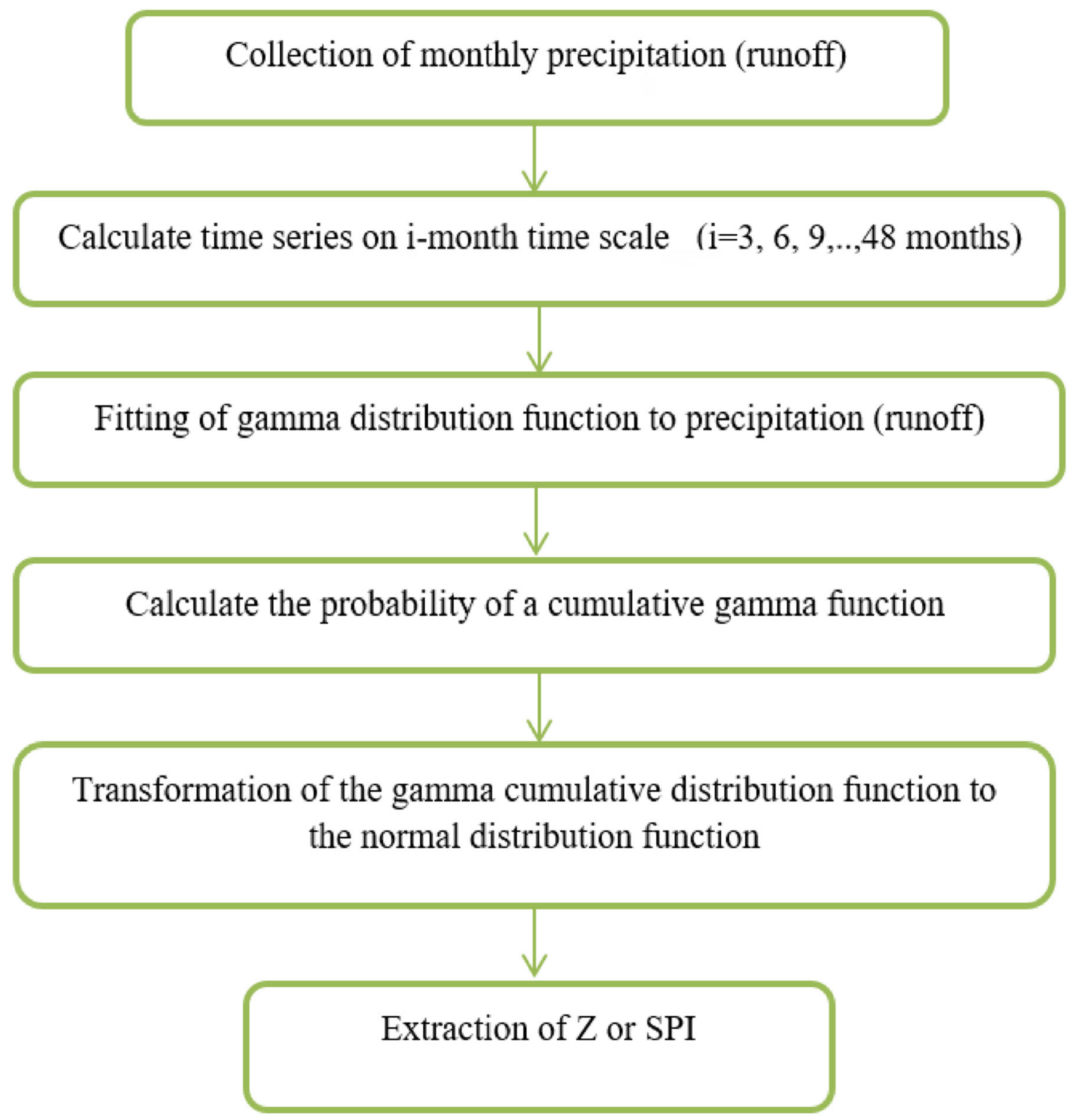
2.2. Standardized Precipitation (Runoff) Index
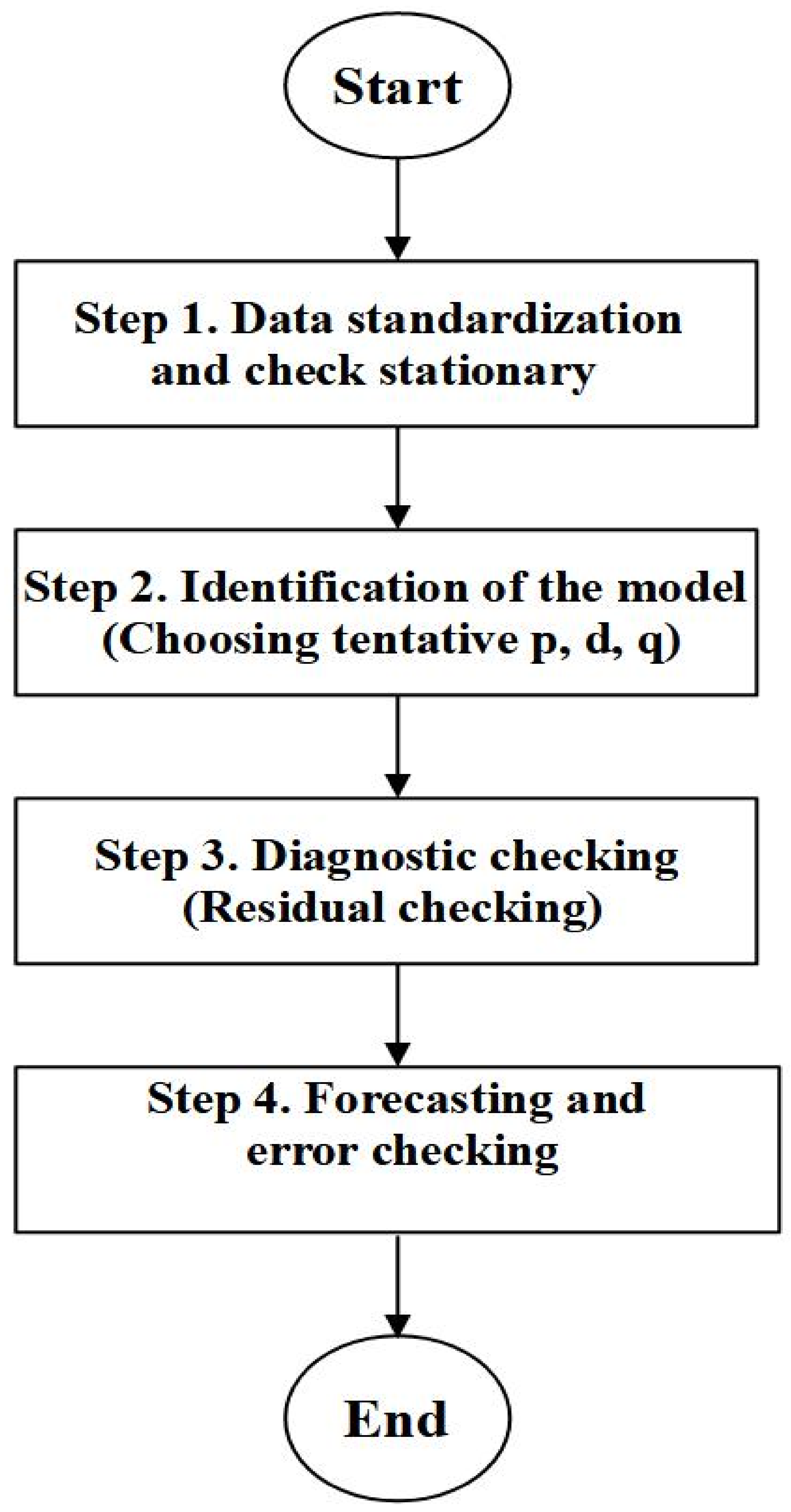
2.3. Model Development
2.4. Kappa (κ)
2.5. Model Validation
3. Results
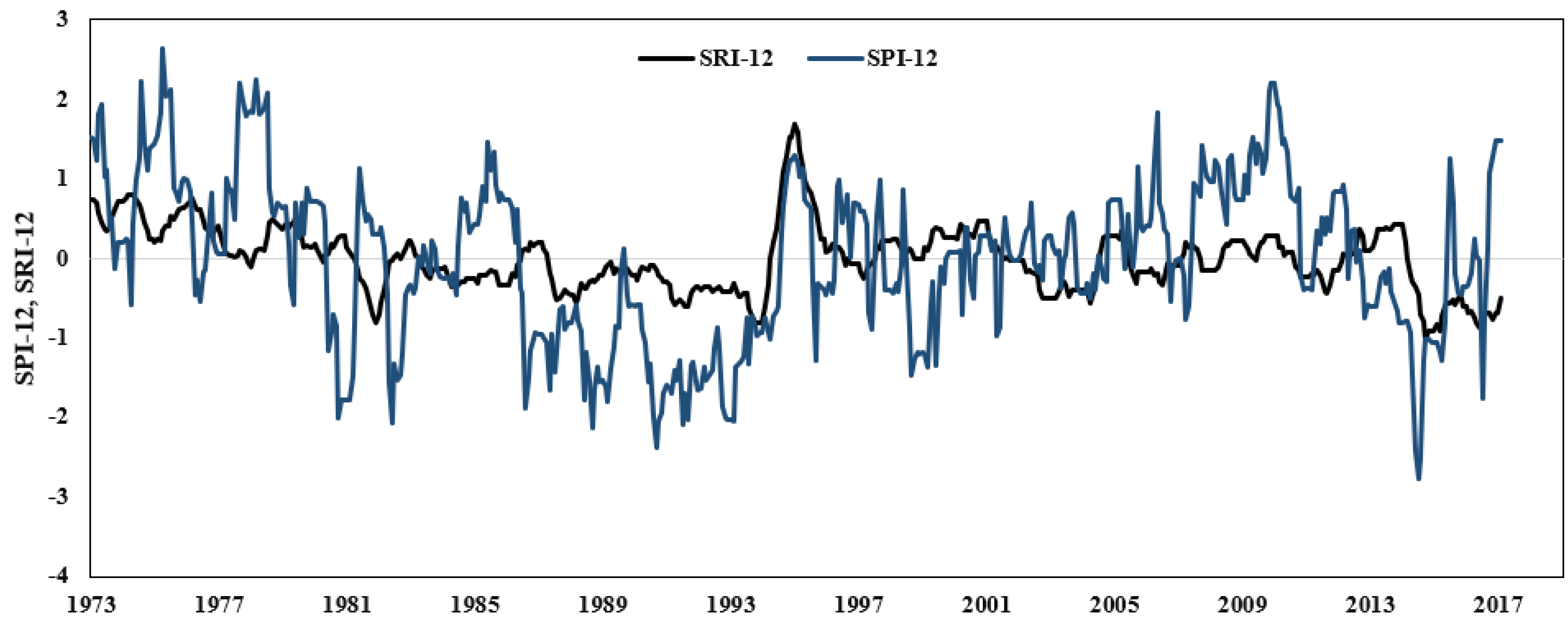
3.1. Assessment of Drought Based on SPI and SRI
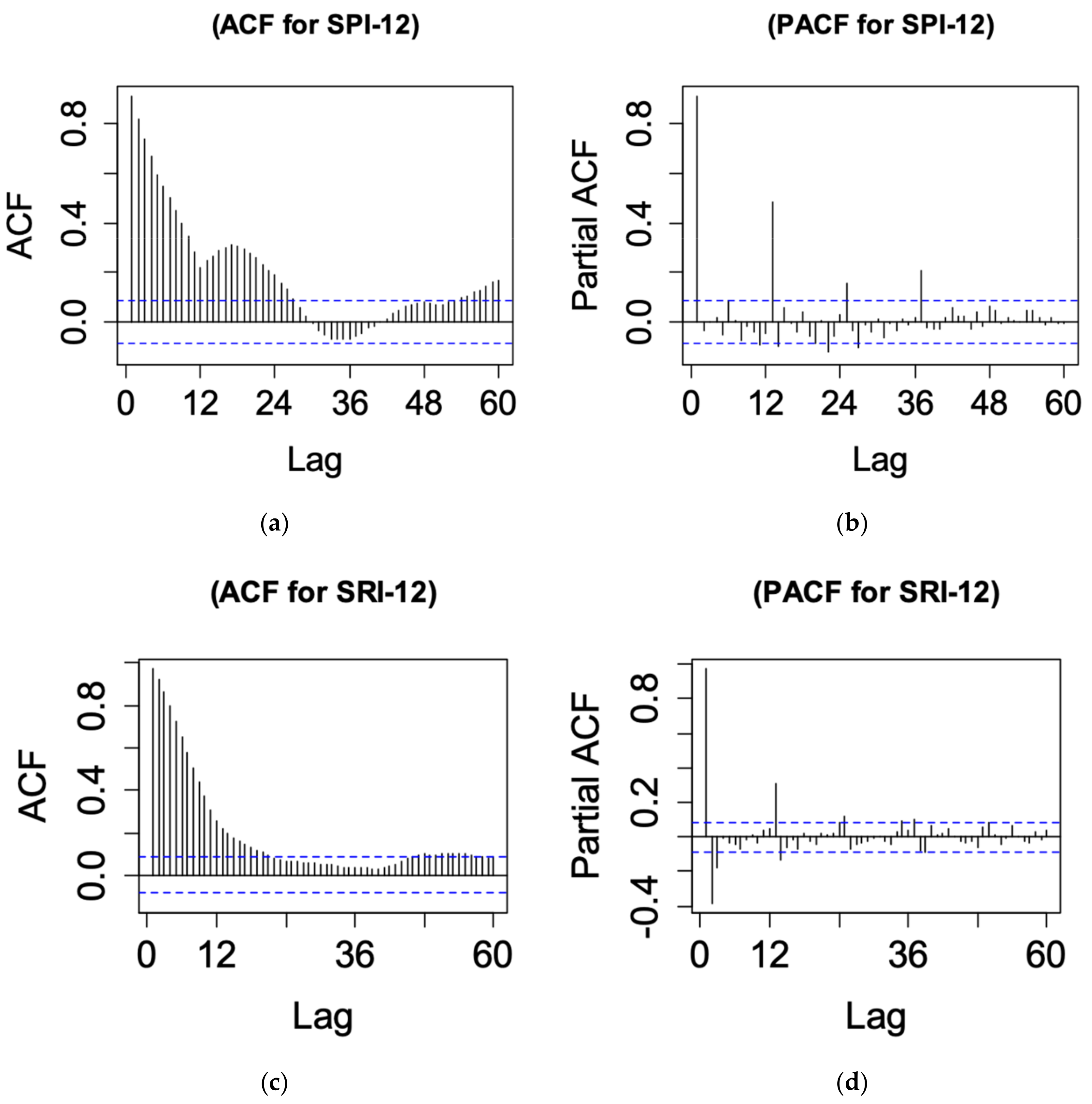
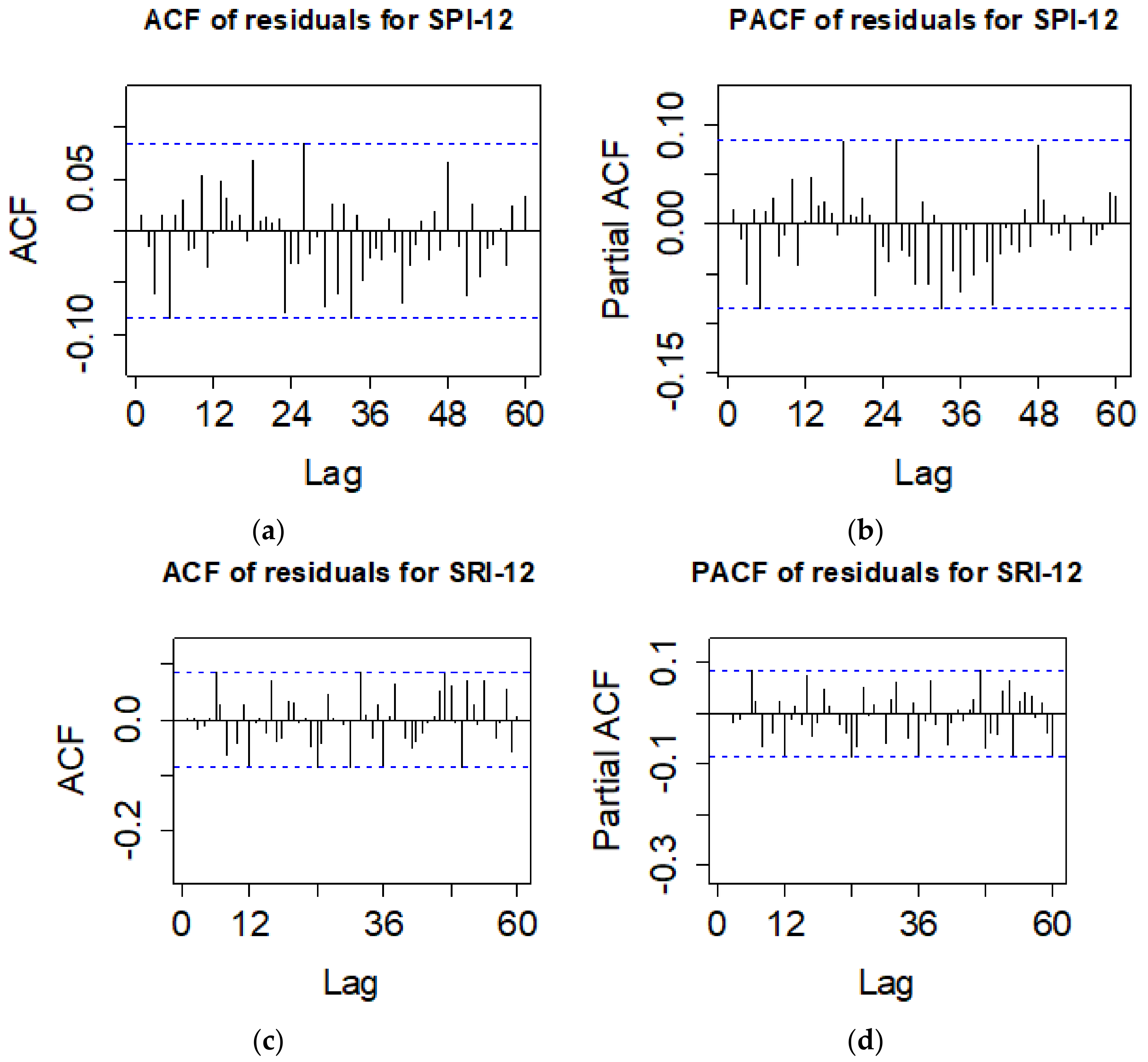
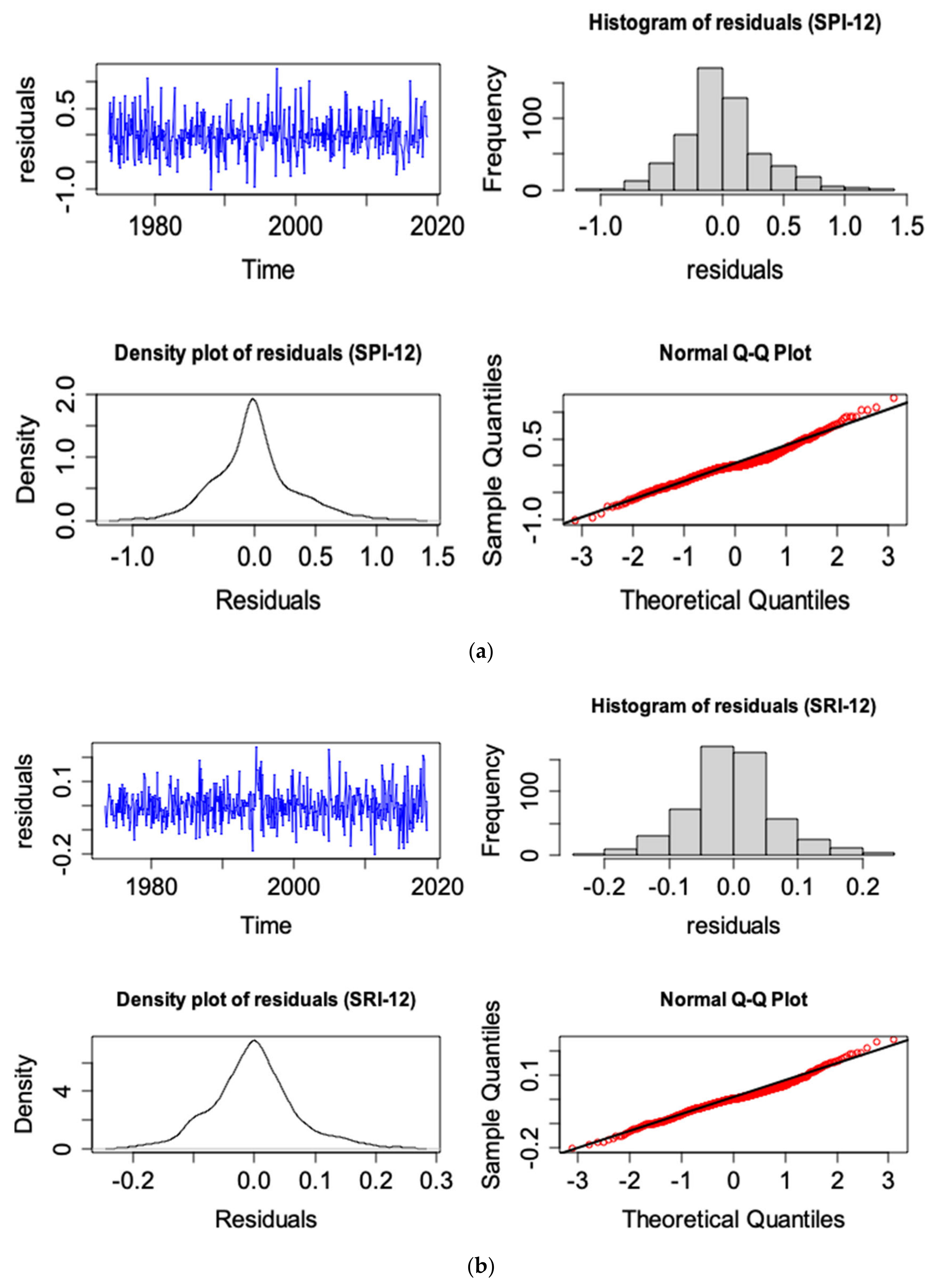
3.2. Stochastic Model Development
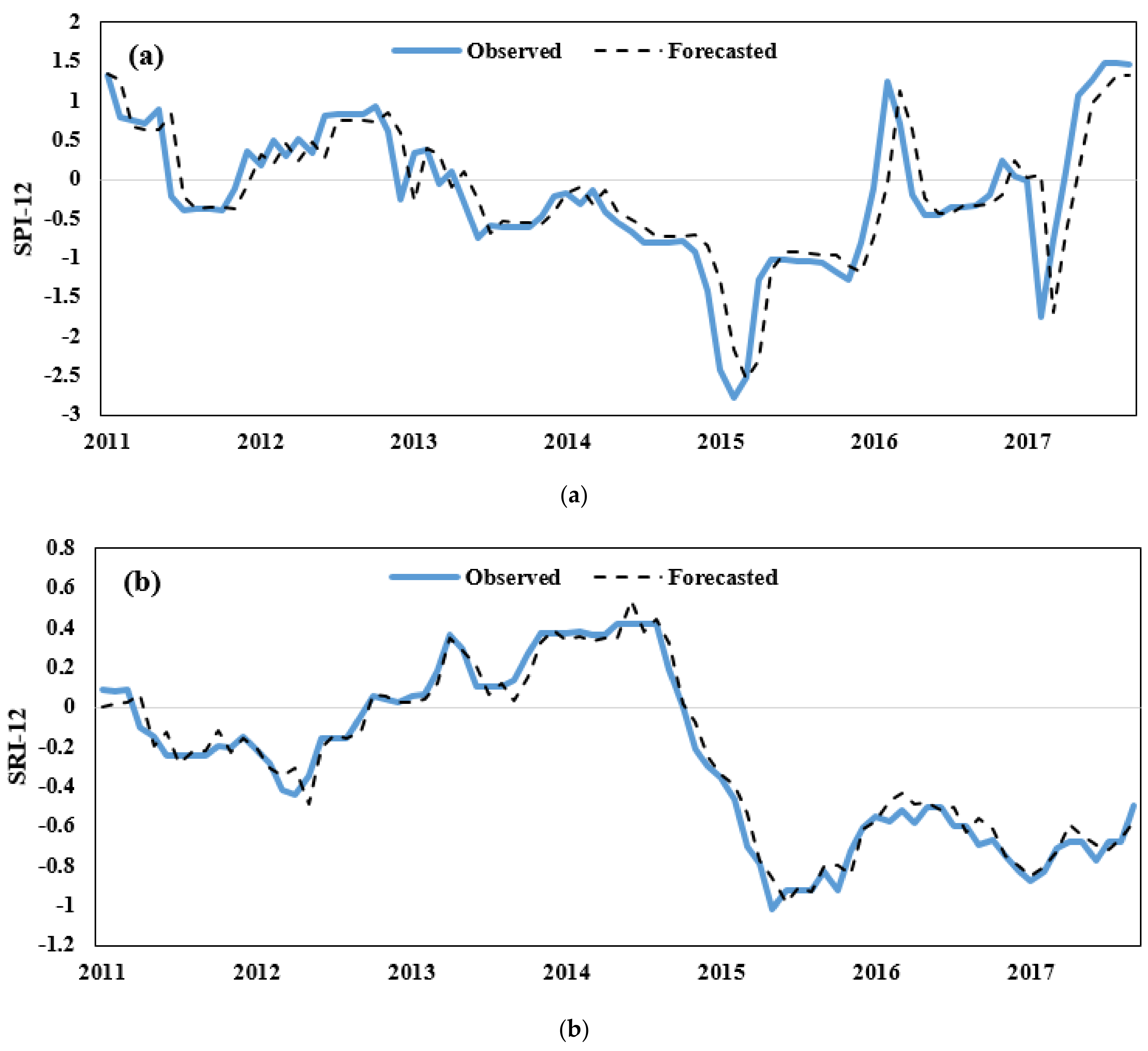
3.3. Drought Forecasting Using Selected Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Res. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Eur. Water 2005, 9–10, 3–11. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Boken, V.K.; Cracknell, A.P.; Heathcote, R.L. Monitoring and Predicting Agricultural Drought: A Global Study; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Wilhite, D.A.; Svoboda, M.D.; Hayes, M.J. Understanding the complex impacts of drought: A key to enhancing drought mitigation and preparedness. Water Resour. Manag. 2007, 21, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D. A methodology for drought preparedness. Nat. Hazards 1996, 13, 229–252. [Google Scholar] [CrossRef] [Green Version]
- Palmer, W.C. Meteorlogical Drought; Research Paper No. 45; US Department of Commerce Weather Bureau: Washington, DC, USA, 1965; pp. 1–58.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Bera, B.; Shit, P.K.; Sengupta, N.; Saha, S.; Bhattacharjee, S. Trends and variability of drought in the extended part of Chhota Nagpur plateau (Singbhum Protocontinent), India applying SPI and SPEI indices. Environ. Chall. 2021, 5, 100310. [Google Scholar] [CrossRef]
- Stagge, J.H.; Kingston, D.G.; Tallaksen, L.M.; Hannah, D.M. Observed drought indices show increasing divergence across Europe. Sci. Rep. 2017, 7, 14045. [Google Scholar] [CrossRef]
- Dukat, P.; Bednorz, E.; Ziembińska, K.; Urbaniak, M. Trends in drought occurrence and severity at mid-latitude European stations (1951–2015) estimated using standardized precipitation (SPI) and precipitation and evapotranspiration (SPEI) indices. Meteorol. Atmos. Phys. 2022, 134, 20. [Google Scholar] [CrossRef]
- Guttman, N.B. Comparing the Palmer drought severity index and the standardized precipitation Index. J. Am. Water Res. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- Caloiero, T. Drought analysis in New Zealand using the standardized precipitation index. Environ. Earth Sci. 2017, 76, 569. [Google Scholar] [CrossRef]
- Hayes, M.J.; Svoboda, M.; Wilhite, D.A.; Vanyarkho, O. Monitoring the 1996 drought using the SPI. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef] [Green Version]
- Paulo, A.A.; Pereira, L.S. Drought concepts and characterization: Comparing drought indices applied at local and regional scales. Water Int. 2006, 31, 37–49. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, 226–236. [Google Scholar] [CrossRef] [Green Version]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control, 1st ed.; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Hu, W.; Tong, S.; Mengersen, K.; Connell, D. Weather variability and the incidence of cryptosporidiosis: Comparison of time series Poisson regression and SARIMA models. Ann. Epidemiol. 2007, 17, 679–688. [Google Scholar] [CrossRef]
- Modarres, R. Streamflow drought time series forecasting. Stoch. Environ. Res. Risk Assess. 2007, 21, 223–233. [Google Scholar] [CrossRef]
- Mishra, A.; Desai, V. Drought Forecasting Using Stochastic Models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Fernandez, C.; Vega, J.A.; Fonturbel, T.; Jimenez, E. Streamflow drought time series forecasting: A case study in a small watershed in North West Spain. Stoch. Environ. Res. Risk Assess. 2009, 23, 1063–1070. [Google Scholar] [CrossRef]
- Durdu, O.F. Application of Linear Stochastic Models for Drought Forecasting in the Buyuk Menderes River Basin, Western Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 1145–1162. [Google Scholar] [CrossRef]
- Bazrafshan, O.; Salajegheh, A.; Bazrafshan, J.; Mahdavi, M.; Maraj, A.F. Hydrological drought forecasting using ARIMA models (case study: Karkheh Basin). Ecopersia 2015, 3, 1099–1117. [Google Scholar]
- Al Sayah, M.J.; Abdallah, C.A.; Khouri, M.; Darwich, T. A framework for climate change assessment in Mediterranean data-sparse watersheds using remote sensing and ARIMA modeling. Theor. Appl. Climatol. 2021, 143, 639–658. [Google Scholar] [CrossRef]
- Shatanawi, K.; Bahbeh, M.; Shatanawi, M. Characterizing, Monitoring and Forecasting of Drought in Jordan River Basin. J. Water Resour. Prot. 2013, 5, 12. [Google Scholar] [CrossRef] [Green Version]
- Buttafuoco, G.; Caloiero, T. Drought events at different timescales in southern Italy (Calabria). J. Maps 2014, 10, 529–537. [Google Scholar] [CrossRef]
- Caloiero, T.; Veltri, S. Drought assessment in the Sardinia region (Italy) during 1922–2011 using the standardized precipitation index. Pure Appl. Geophys. 2019, 176, 925–935. [Google Scholar] [CrossRef]
- Zhu, B.; Chevallier, J. Carbon Price Forecasting with a Hybrid ARIMA and Least Squares Support Vector Machines Methodology. In Pricing and Forecasting Carbon Markets; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Benkhaled, A.; Remini, B. Variabilité temporelle de la concentration en sédiments et phénomène d’hystérésis dans le bassin de l’Oued Wahrane (Algérie). Hydrol. Sci. J. 2003, 48, 243–255. [Google Scholar] [CrossRef] [Green Version]
- Köppen, W. Das Geographische System der Klimate. Handbuch der Klimatologie; Köppen, W., Geiger, R., Eds.; Verlag von Gebrüder Borntraeger: Berlin, Germany, 1936; Volume 1, pp. 1–44. [Google Scholar]
- Mikosch, T.; Gadrich, T.; Klüppelberg, C.; Adler, R.J. Parameter Estimation for ARMA Models with Infinite Variance Innovations. Ann. Stat. 1995, 23, 305–326. [Google Scholar] [CrossRef]
- Yevjevich, V. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts; Colorado State University: Fort Collins, CO, USA, 1967. [Google Scholar]
- Akaike, H. On the likelihood of a time series model. J. R. Stat. Soc. Ser. D 1978, 27, 217–235. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Cohen, J. Weighted kappa: Nominal scale agreement provision for scaled disagreement or partial credit. Psychol. Bull. 1968, 70, 213. [Google Scholar] [CrossRef]
- Kumar, M.N.; Murthy, C.S.; Sai, M.V.R.S.; Roy, P.S. On the use of Standardized Precipitation Index (SPI) for drought intensity assessment. Meteorol. Appl. 2009, 16, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Landis, J.R.; Koch, G.G. An Application of Hierarchical Kappa-type Statistics in the Assessment of Majority Agreement among Multiple Observers. Biometrics 1977, 33, 363. [Google Scholar] [CrossRef] [PubMed]
- Roughani, M.; Ghafouri, M.; Tabatabaei, M. An innovative methodology for the prioritization of sub-catchments for flood control. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 79–87. [Google Scholar] [CrossRef]
- Pińskwar, I.; Choryński, A.; Kundzewicz, Z.W. Severe Drought in the Spring of 2020 in Poland—More of the Same? Agronomy 2020, 10, 1646. [Google Scholar] [CrossRef]
- Młyński, D.; Wałega, A.; Kuriqi, A. Influence of meteorological drought on environmental flows in mountain catchments. Ecol. Indic. 2021, 133, 108460. [Google Scholar] [CrossRef]
- Tokarczyk, T.; Szalińska, W. Drought hazard assessment in the process of drought risk management. Acta Sci. Pol. Form. Circumiectus 2018, 18, 217–229. [Google Scholar] [CrossRef]
- Kubiak-Wójcicka, K.; Pilarska, A.; Kamiński, D. The Analysis of Long-Term Trends in the Meteorological and Hydrological Drought Occurrences Using Non-Parametric Methods—Case Study of the Catchment of the Upper Noteć River (Central Poland). Atmosphere 2021, 12, 1098. [Google Scholar] [CrossRef]
- Li, Y.; Gong, Y.; Huang, C. Construction of combined drought index based on bivariate joint distribution. Alex. Eng. J. 2021, 60, 2825–2833. [Google Scholar] [CrossRef]
- Niu, J.; Chen, J.; Sun, L.Q. Exploration of drought evolution using numerical simulations over the Xijiang (West River) basin in South China. J. Hydrol. 2015, 526, 68–77. [Google Scholar] [CrossRef]
- Sattar, M.N.; Kim, T.W. Probabilistic characteristics of lag time between meteorological and hydrological droughts using a Bayesian model. Terr. Atmos. Ocean. Sci. 2018, 29, 709–720. [Google Scholar] [CrossRef] [Green Version]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought forecasting based on the remote sensing data using ARIMA models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Lloyd-Huhes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Conte, M.; Giuffrida, A.; Tedesco, S. The Mediterranean Oscillation. Impact on Precipitation and Hydrology in Italy Climate Water; Publications of the Academy of Finland: Helsinki, Finland, 1989. [Google Scholar]
- Muthoni, F.K.; Odongo, V.O.; Ochieng, J.; Mugalavai, E.M.; Mourice, S.K.; Hoesche-Zeledon, I.; Mwila, M.; Bekunda, M. Long-term spatial-temporal trends and variability of precipitation over Eastern and Southern Africa. Theor. Appl. Climatol. 2019, 137, 1869–1882. [Google Scholar] [CrossRef] [Green Version]
- Martín-Vide, J.; López-Bustins, J.A. The Western Mediterranean Oscillation and Precipitation in the Iberian Peninsula. Int. J. Climatol. 2006, 26, 1455–1475. [Google Scholar] [CrossRef]
- Kelley, C.; Ting, M.; Seager, R.; Kushnir, Y. Mediterranean precipitation climatology, seasonal cycle, and trend as simulated by CMIP5. Geophys. Res. Lett. 2012, 39, L21703. [Google Scholar] [CrossRef] [Green Version]
- Papastefanopoulos, V.; Linardatos, P.; Kotsiantis, S. COVID-19: A Comparison of Time Series Methods to Forecast Percentage of Active Cases per Population. Appl. Sci. 2020, 10, 3880. [Google Scholar] [CrossRef]
- Karimi, M.; Meleese, A.M.; Khosravi, M.; Mamuye, M.; Zhang, J. Chapter 26—Analysis and prediction of meteorological drought using SPI index and ARIMA model in the Karkheh River Basin Iran. In Extreme Hydrology and Climate Variability; Melesse, A.M., Abtew, W., Senay, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 343–353. [Google Scholar] [CrossRef]
- Beyaztas, U.; Yaseen, Z.M. Drought interval simulation using functional data analysis. J. Hydrol. 2019, 579, 124141. [Google Scholar] [CrossRef]
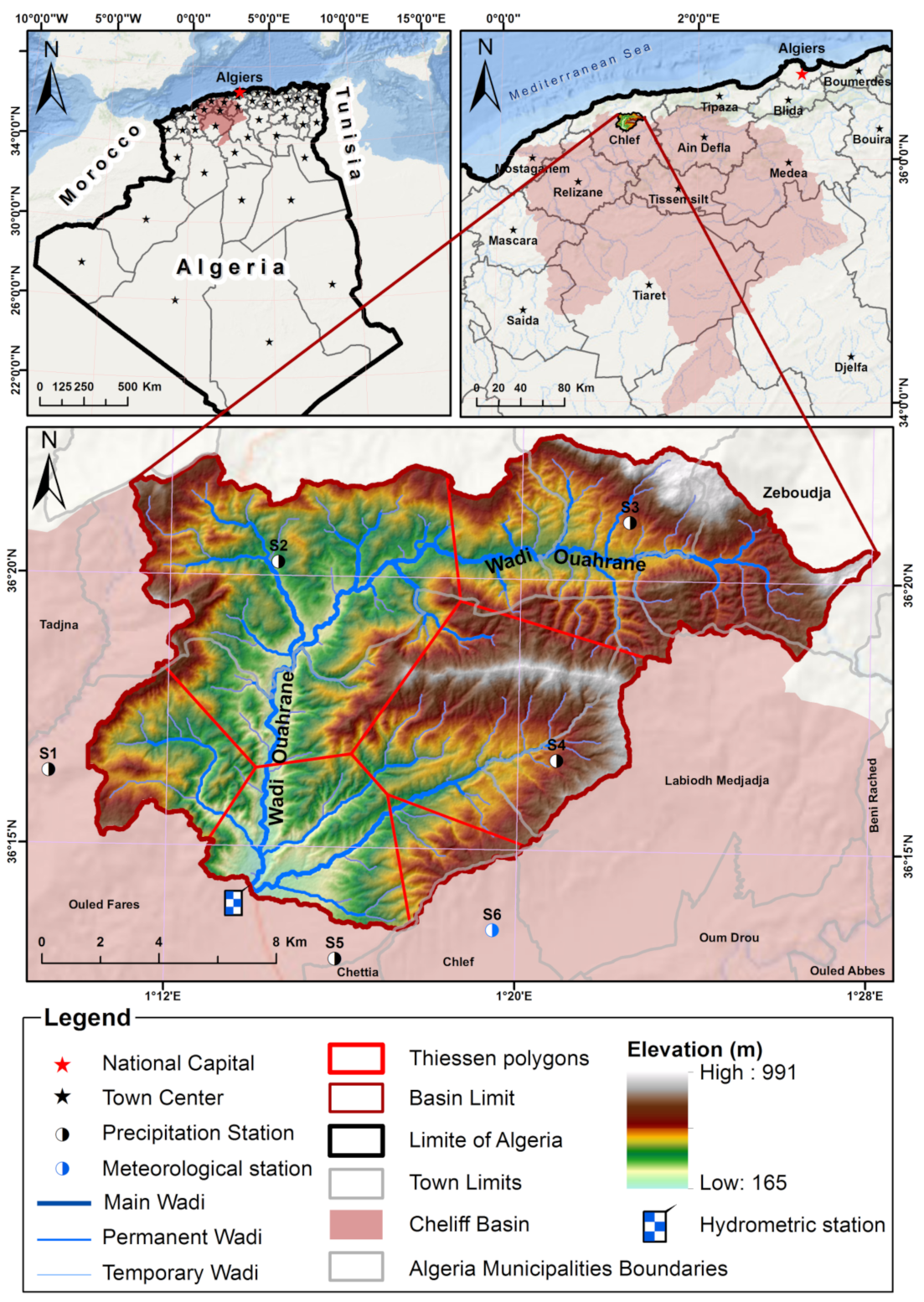
| Stations | ID | Name | Geographical Coordinates | Elevation | |
|---|---|---|---|---|---|
| Longitude | Latitude | ||||
| (° ′ ″) | (° ′ ″) | (m) | |||
| Precipitation Stations | |||||
| S1 | 012201 | LARBAT OULED FARES | 01°09′18″ | 36°16′20″ | 116 |
| S2 | 012224 | BOUZGHAIA | 01°14′27″ | 36°20′15″ | 217 |
| S3 | 012205 | BENAIRIA | 01°22′28″ | 36°21′04″ | 320 |
| S4 | 012221 | MEDJAJA | 01°20′53″ | 36°16′39″ | 487 |
| S5 | 012209 | CHETIA | 01°15′53″ | 36°12′56″ | 108 |
| S6 | NMO | Airport, Chlef | 01°19′28″ | 36°13′31″ | 158 |
| Hydrometric Station | |||||
| HS1 | 012201 | LARBAT OULED FARES | 01°13′56″ | 36°14′14″ | 173 |
| Index | Model | AIC | BIC |
|---|---|---|---|
| SPI-12 | ARIMA(0,1,0)(0,1,1)12 | 605.25 | 613.74 |
| ARIMA(0,1,1)(0,0,1)12 | 321.57 | 334.38 | |
| ARIMA(1,0,1)(1,1,0)12 | 754.55 | 771.54 | |
| ARIMA(1,0,1)(0,1,1)12 | 587.61 | 604.61 | |
| ARIMA(1,0,0)(2,0,1)12 | 320.11 | 345.74 | |
| SRI-12 | ARIMA(1,0,1)(1,0,0)12 | −1277.37 | −1255.90 |
| ARIMA(2,0,0)(2,0,0)12 | −1355.60 | −1329.84 | |
| ARIMA(2,0,1)(1,0,0)12 | −1305.33 | −1279.57 | |
| ARIMA(2,1,0)(2,0,0)12 | −1360.34 | −1338.88 | |
| ARIMA(2,1,2)(1,0,1)12 | −1481.87 | −1451.83 |
| Index | Variables in the Model | |||||
|---|---|---|---|---|---|---|
| Model | Parameter | Value of Parameters | Standard Error | t-Ratio | p | |
| SPI | ARIMA (0,1,0)(0,1,1)12 | Θ1 | −1.00 | 0.02 | −57.66 | 0 |
| ARIMA(0,1,1)(0,0,1)12 | θ1 | −0.01 | 0.04 | −0.29 | 0.77 | |
| Θ1 | −0.71 | 0.03 | −24.54 | 0 | ||
| ARIMA(1,0,1)(1,1,0)12 | ϕ1 | 0.87 | 0.02 | 34.87 | 0 | |
| θ1 | 0.11 | 0.05 | 2.09 | 0.04 | ||
| Φ1 | −0.71 | 0.03 | −22.22 | 0 | ||
| ARIMA(1,0,1)(0,1,1)12 | ϕ1 | 0.91 | 0.02 | 45.49 | 0 | |
| θ1 | 0.01 | 0.05 | 0.25 | 0.81 | ||
| Θ1 | −1.00 | 0.02 | −53.63 | 0 | ||
| ARIMA(1,0,0)(2,0,1)12 | ϕ1 | 0.98 | 0.01 | 121.44 | 0 | |
| Φ1 | −0.15 | 0.08 | −1.93 | 0.05 | ||
| Φ2 | −0.01 | 0.06 | −0.23 | 0.82 | ||
| Θ1 | −0.62 | 0.07 | −9.21 | 0 | ||
| SRI | ARIMA(1,0,1)(1,0,1)12 | ϕ1 | 0.98 | 0.01 | 118.45 | 0 |
| θ1 | 0.35 | 0.03 | 10.22 | 0 | ||
| Φ1 | −0.46 | 0.04 | −11.66 | 0 | ||
| ARIMA(2,0,0)(2,0,0)12 | ϕ1 | 1.42 | 0.04 | 36.79 | 0 | |
| ϕ2 | −0.44 | 0.04 | −11.22 | 0 | ||
| Φ1 | −0.59 | 0.04 | −13.88 | 0 | ||
| Φ2 | −0.29 | 0.04 | −6.82 | 0 | ||
| ARIMA(1,0,1)(1,0,0)12 | ϕ1 | 1.37 | 0.11 | 12.91 | 0 | |
| θ1 | 0.08 | 0.1 | 0.77 | 0.44 | ||
| Φ1 | −0.47 | 0.04 | −12.03 | 0 | ||
| ARIMA(2,1,0)(2,0,0)12 | ϕ1 | 0.38 | 0.04 | 8.83 | 0 | |
| ϕ2 | 0.12 | 0.04 | 2.69 | 0.01 | ||
| Φ1 | −0.59 | 0.04 | −13.98 | 0 | ||
| Φ2 | −0.30 | 0.04 | −7.13 | 0 | ||
| ARIMA(2,1,2)(1,0,1)12 | ϕ1 | −0.06 | 0.36 | −0.18 | 0.86 | |
| ϕ2 | 0.45 | 0.26 | 1.74 | 0.08 | ||
| θ1 | 0.45 | 0.36 | 1.25 | 0.21 | ||
| θ2 | −0.14 | 0.15 | −0.93 | 0.35 | ||
| Φ1 | 0.05 | 0.05 | 0.99 | 0.32 | ||
| Θ1 | −0.95 | 0.03 | −36.98 | 0 | ||
| Index | SPI | SRI |
|---|---|---|
| Model | ARIMA (1,0,1)(0,1,1)12 | ARIMA (1,0,1)(1,0,1)12 |
| Kw | 0.79 | 0.88 |
| Variance (Observed) | 0.97 | 0.17 |
| Variance (Forecasted) | 0.81 | 0.16 |
| F test | 1.12 | 1.06 |
| Mean (Observed) | −0.187 | −0.263 |
| Mean (Forecasted) | −0.174 | −0.26 |
| Z | −0.013 | −0.012 |
| RMSE | 0.46 | 0.067 |
| MAE | 0.02 | −0.002 |
| R | 0.89 | 0.98 |
| Lead Time | SPI-12 | SRI-12 | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| 1 | 0.96 | 0.43 | −0.026 | 0.97 | 0.061 | −0.001 |
| 2 | 0.9 | 0.45 | −0.028 | 0.966 | 0.06 | −0.016 |
| 3 | 0.87 | 0.55 | −0.049 | 0.961 | 0.058 | −0.018 |
| 4 | 0.86 | 0.58 | −0.054 | 0.96 | 0.11 | 0.03 |
| 5 | 0.85 | 0.64 | −0.089 | 0.95 | 0.14 | 0.07 |
| 6 | 0.8 | 0.67 | −0.001 | 0.92 | 0.17 | 0.09 |
| 7 | 0.78 | 0.78 | −0.012 | 0.91 | 0.19 | 0.1 |
| 8 | 0.71 | 0.84 | −0.022 | 0.88 | 0.23 | 0.12 |
| 9 | 0.68 | 0.89 | −0.033 | 0.86 | 0.28 | 0.15 |
| 10 | 0.65 | 0.91 | −0.052 | 0.84 | 0.29 | 0.16 |
| 11 | 0.58 | 0.93 | −0.080 | 0.74 | 0.37 | 0.19 |
| 12 | 0.51 | 0.98 | −0.091 | 0.7 | 0.39 | 0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achite, M.; Bazrafshan, O.; Azhdari, Z.; Wałęga, A.; Krakauer, N.; Caloiero, T. Forecasting of SPI and SRI Using Multiplicative ARIMA under Climate Variability in a Mediterranean Region: Wadi Ouahrane Basin, Algeria. Climate 2022, 10, 36. https://doi.org/10.3390/cli10030036
Achite M, Bazrafshan O, Azhdari Z, Wałęga A, Krakauer N, Caloiero T. Forecasting of SPI and SRI Using Multiplicative ARIMA under Climate Variability in a Mediterranean Region: Wadi Ouahrane Basin, Algeria. Climate. 2022; 10(3):36. https://doi.org/10.3390/cli10030036
Chicago/Turabian StyleAchite, Mohammed, Ommolbanin Bazrafshan, Zahra Azhdari, Andrzej Wałęga, Nir Krakauer, and Tommaso Caloiero. 2022. "Forecasting of SPI and SRI Using Multiplicative ARIMA under Climate Variability in a Mediterranean Region: Wadi Ouahrane Basin, Algeria" Climate 10, no. 3: 36. https://doi.org/10.3390/cli10030036
APA StyleAchite, M., Bazrafshan, O., Azhdari, Z., Wałęga, A., Krakauer, N., & Caloiero, T. (2022). Forecasting of SPI and SRI Using Multiplicative ARIMA under Climate Variability in a Mediterranean Region: Wadi Ouahrane Basin, Algeria. Climate, 10(3), 36. https://doi.org/10.3390/cli10030036









