Expectations of Future Natural Hazards in Human Adaptation to Concurrent Extreme Events in the Colorado River Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources and Scales
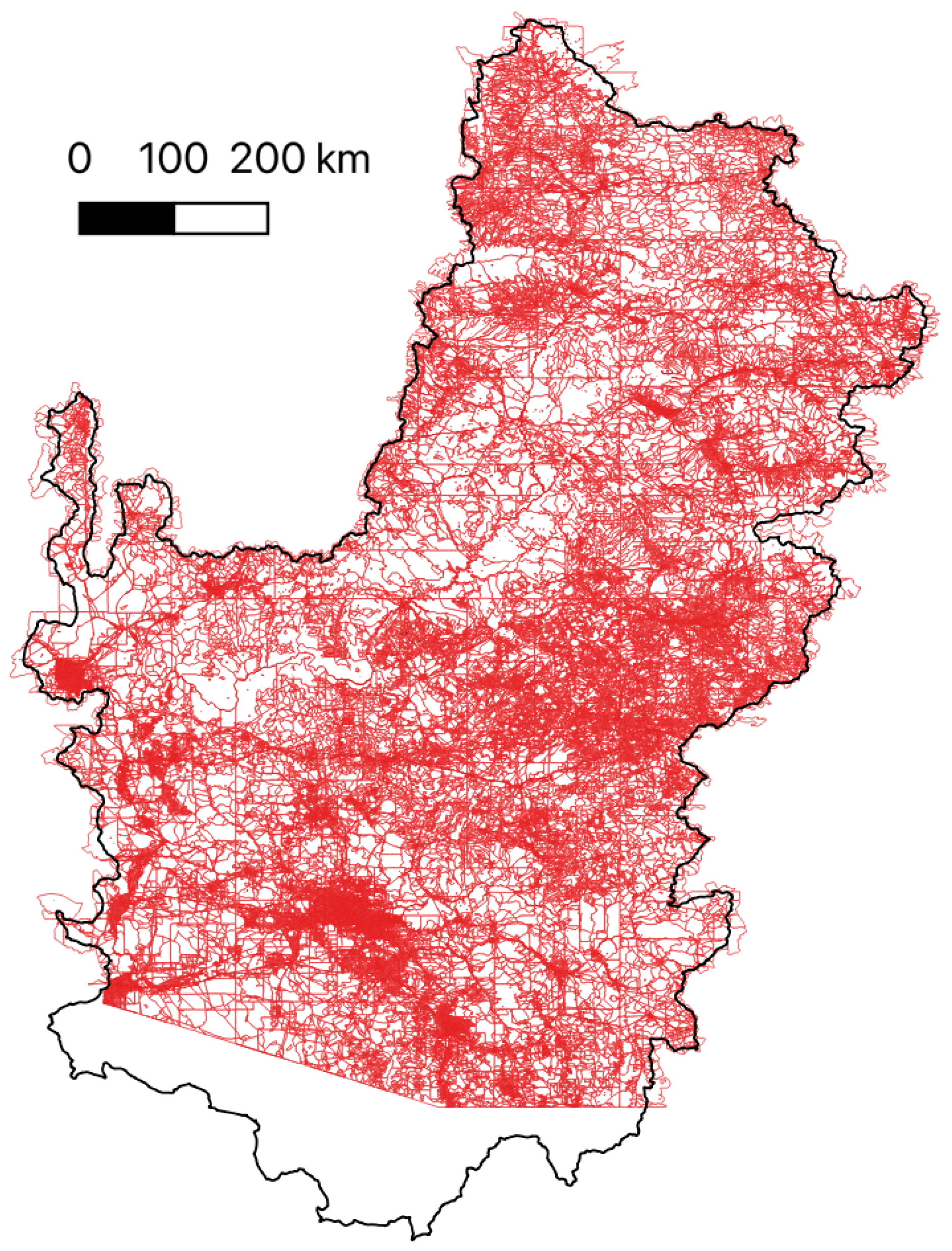
2.1.1. Hazard
2.1.2. Exposure
2.1.3. Damage
2.2. Model calibration
3. Results and Discussion
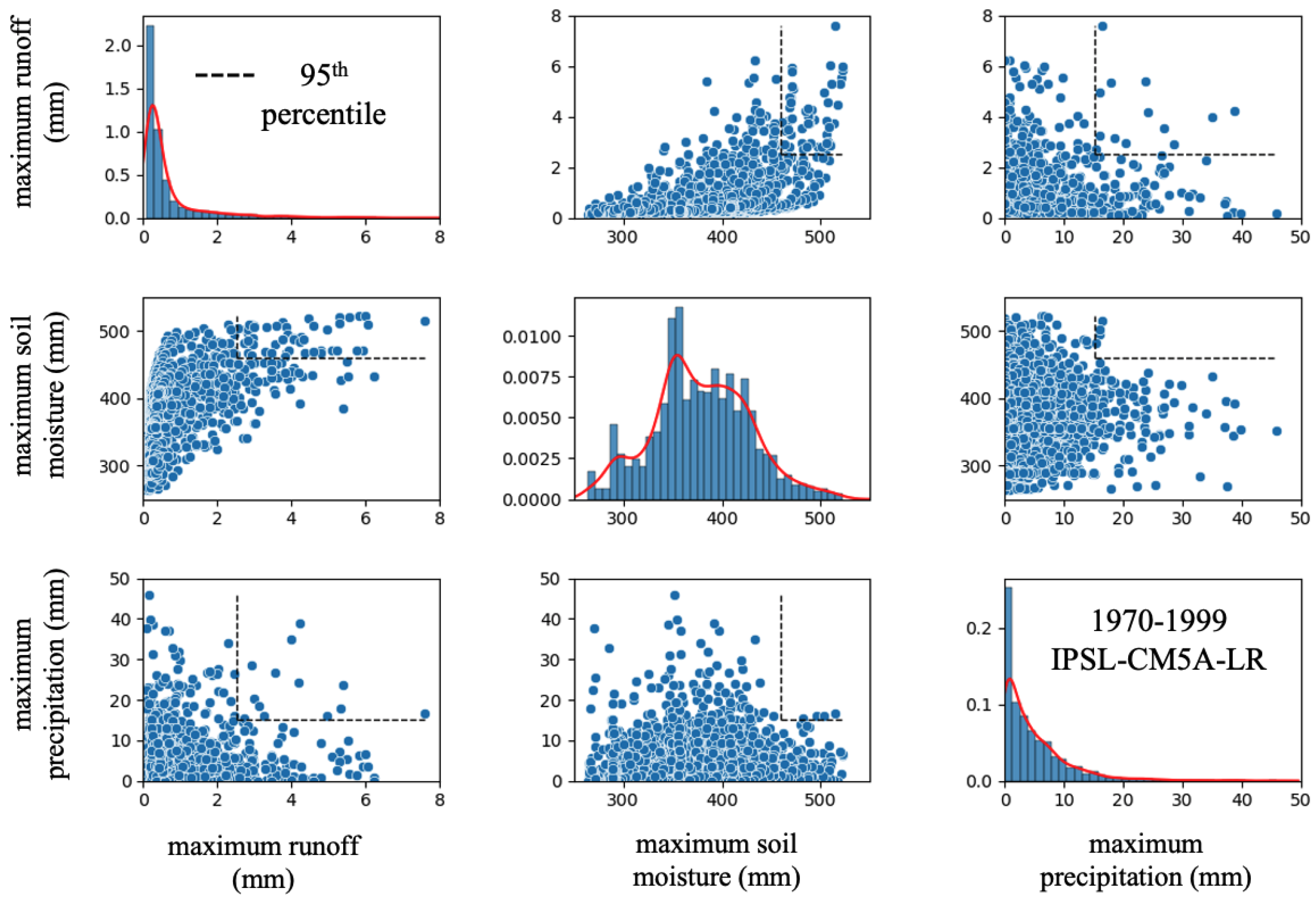
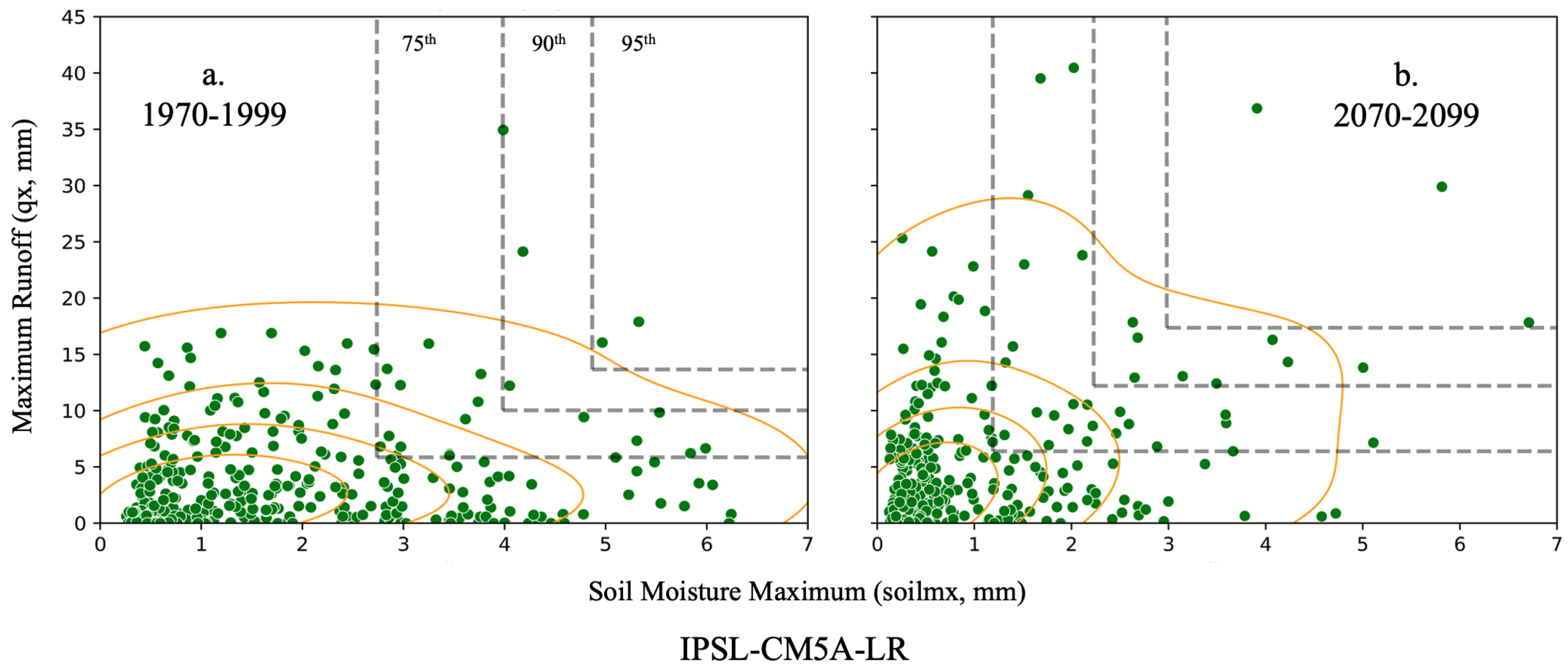
3.1. Floodings as Concurrent Extremes
3.2. Adaptation Model
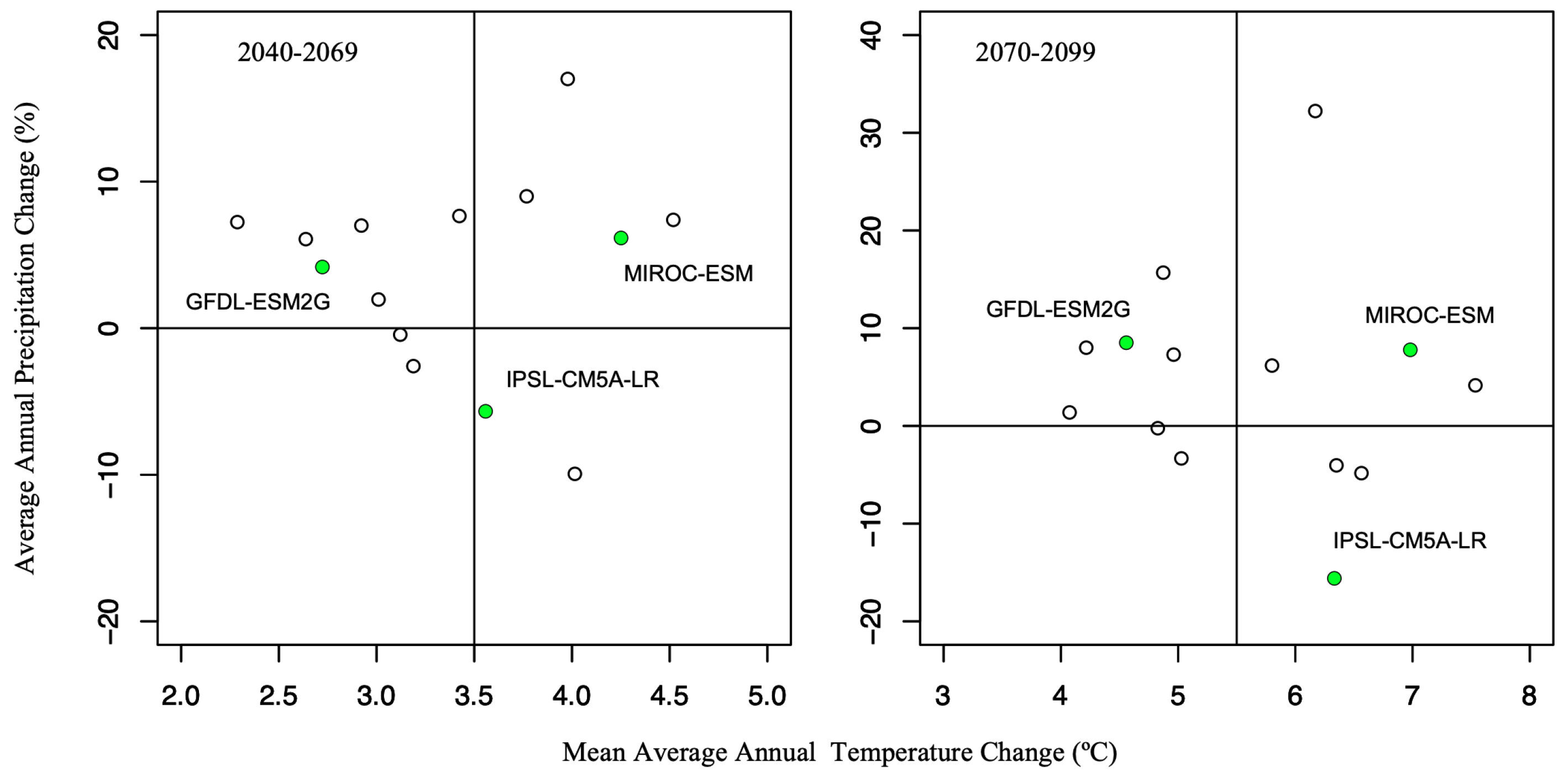
3.3. Scenarios until the End of the Century
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCarthy, J.J.; Canziani, O.F.; Leary, N.A.; Dokken, D.J.; White, K.S. (Eds.) Climate Change 2001: Impacts, Adaptation, and Vulnerability: Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001; Volume 2. [Google Scholar]
- Adger, W.N. Scales of governance and environmental justice for adaptation and mitigation of climate change. J. Int. Dev. 2001, 13, 921–931. [Google Scholar] [CrossRef]
- Adger, W.N.; Arnell, N.W.; Tompkins, E.L. Successful adaptation to climate change across scales. Glob. Environ. Chang. 2005, 15, 77–86. [Google Scholar] [CrossRef]
- Agrawal, A. The Role of Local Institutions in Adaptation to Climate Change; World Bank: Bretton Woods, NH, USA, 2008. [Google Scholar]
- Agrawal, A. Local institutions and adaptation to climate change. Soc. Dimens. Clim. Chang. Equity Vulnerability A Warm. World 2010, 2, 173–178. [Google Scholar]
- Carpenter, S.R.; Arrow, K.J.; Barrett, S.; Biggs, R.; Brock, W.A.; Crépin, A.S.; Engström, G.; Folke, C.; Hughes, T.P.; Kautsky, N.; et al. General resilience to cope with extreme events. Sustainability 2012, 4, 3248–3259. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; Van Den Hurk, B.J.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Raymond, C.; Horton, R.M.; Zscheischler, J.; Martius, O.; AghaKouchak, A.; Balch, J.; Bowen, S.G.; Camargo, S.J.; Hess, J.; Kornhuber, K.; et al. Understanding and managing connected extreme events. Nat. Clim. Chang. 2020, 10, 611–621. [Google Scholar] [CrossRef]
- Stott, P. How climate change affects extreme weather events. Science 2016, 352, 1517–1518. [Google Scholar] [CrossRef]
- Chen, Y.; Moufouma-Okia, W.; Masson-Delmotte, V.; Zhai, P.; Pirani, A. Recent progress and emerging topics on weather and climate extremes since the fifth assessment report of the intergovernmental panel on climate change. Annu. Rev. Environ. Resour. 2018, 43, 35–59. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Shepherd, T.G. Attribution of climate extreme events. Nat. Clim. Chang. 2015, 5, 725–730. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Attribution of Extreme Weather Events in the Context of Climate Change; National Academies Press: Washington, DC, USA, 2016. [Google Scholar]
- Swain, D.L.; Singh, D.; Touma, D.; Diffenbaugh, N.S. Attributing extreme events to climate change: A new frontier in a warming world. One Earth 2020, 2, 522–527. [Google Scholar] [CrossRef]
- Leonard, M.; Westra, S.; Phatak, A.; Lambert, M.; van den Hurk, B.; McInnes, K.; Risbey, J.; Schuster, S.; Jakob, D.; Stafford-Smith, M. A compound event framework for understanding extreme impacts. WIREs Clim. Chang. 2014, 5, 113–128. [Google Scholar] [CrossRef]
- McPhillips, L.E.; Chang, H.; Chester, M.V.; Depietri, Y.; Friedman, E.; Grimm, N.B.; Kominoski, J.S.; McPhearson, T.; Méndez-Lázaro, P.; Rosi, E.J.; et al. Defining Extreme Events: A Cross-Disciplinary Review. Earth’s Future 2018, 6, 441–455. [Google Scholar] [CrossRef]
- Markandya, A.; Galarraga, I.; de Murieta, E.S. Routledge Handbook of the Economics of Climate Change Adaptation; Routledge: London, UK; New York, NY, USA, 2014. [Google Scholar]
- Huggel, C.; Stone, D.; Auffhammer, M.; Hansen, G. Loss and damage attribution. Nat. Clim. Chang. 2013, 3, 694–696. [Google Scholar] [CrossRef]
- Cardona, O.D.; Van Aalst, M.K.; Birkmann, J.; Fordham, M.; Mc Gregor, G.; Rosa, P.; Pulwarty, R.S.; Schipper, E.L.F.; Sinh, B.T.; Décamps, H.; et al. Determinants of risk: Exposure and vulnerability. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012; pp. 65–108. [Google Scholar]
- Schumacher, I.; Strobl, E. Economic Development and Losses Due to Natural Disasters: The Role of Risk; Working Paper Hal—00356286; HAL: Paris, France, 2008. [Google Scholar]
- Schumacher, I.; Strobl, E. Economic development and losses due to natural disasters: The role of hazard exposure. Ecol. Econ. 2011, 72, 97–105. [Google Scholar] [CrossRef]
- Boero, R.; Bianchini, L.; Pasqualini, D. Vulnerability and adaptation to severe weather events in the American southwest. Weather Clim. Extrem. 2015, 8, 12–25. [Google Scholar] [CrossRef][Green Version]
- Shrader, J. Expectations and Adaptation to Environmental Risks; University of California: Los Angeles, CA, USA, 2020; pp. 1–68, SSRN 3212073. [Google Scholar]
- Osberghaus, D. The determinants of private flood mitigation measures in Germany—Evidence from a nationwide survey. Ecol. Econ. 2015, 110, 36–50. [Google Scholar] [CrossRef]
- Wilby, R.L.; Keenan, R. Adapting to flood risk under climate change. Prog. Phys. Geogr. 2012, 36, 348–378. [Google Scholar] [CrossRef]
- Birkmann, J.; Garschagen, M.; Tuan, V.V.; Binh, N.T. Vulnerability, coping and adaptation to water related hazards in the Vietnamese Mekong Delta. In The Mekong Delta System; Springer: Berlin/Heidelberg, Germany, 2012; pp. 245–289. [Google Scholar]
- Bennett, K.E.; Tidwell, V.C.; Llewellyn, D.; Behery, S.; Barrett, L.; Stansbury, M.; Middleton, R.S. Threats to a Colorado river provisioning basin under coupled future climate and societal scenarios. Environ. Res. Commun. 2019, 1, 095001. [Google Scholar] [CrossRef]
- James, T.; Evans, A.; Madly, E.; Kelly, C. The Economic Importance of the Colorado River to the Basin Region; Final Rep.; L. William Seidman Research Institute: Tempe, AZ, USA, 2014; Volume 54, pp. 1–42. [Google Scholar]
- NOAA National Centers for Environmental Information (NCEI). U.S. Billion-Dollar Weather and Climate Disasters. 2021. Available online: https://www.ncdc.noaa.gov/billions/ (accessed on 15 August 2021).
- Bennett, K.E.; Talsma, C.; Boero, R. Concurrent Changes in Extreme Hydroclimate Events in the Colorado River Basin. Water 2021, 13, 978. [Google Scholar] [CrossRef]
- Bennett, K.E.; Bohn, T.J.; Solander, K.; McDowell, N.G.; Xu, C.; Vivoni, E.; Middleton, R.S. Climate-driven disturbances in the San Juan River sub-basin of the Colorado River. Hydrol. Earth Syst. Sci. 2018, 22, 709–725. [Google Scholar] [CrossRef]
- Vano, J.A.; Udall, B.; Cayan, D.R.; Overpeck, J.T.; Brekke, L.D.; Das, T.; Hartmann, H.C.; Hidalgo, H.G.; Hoerling, M.; McCabe, G.J.; et al. Understanding Uncertainties in Future Colorado River Streamflow. Bull. Am. Meteorol. Soc. 2014, 95, 59–78. [Google Scholar] [CrossRef]
- Kousky, C. Informing climate adaptation: A review of the economic costs of natural disasters. Energy Econ. 2014, 46, 576–592. [Google Scholar] [CrossRef]
- Thomalla, F.; Downing, T.; Spanger-Siegfried, E.; Han, G.; Rockström, J. Reducing hazard vulnerability: Towards a common approach between disaster risk reduction and climate adaptation. Disasters 2006, 30, 39–48. [Google Scholar] [CrossRef] [PubMed]
- van Valkengoed, A.M.; Steg, L. Meta-analyses of factors motivating climate change adaptation behaviour. Nat. Clim. Chang. 2019, 9, 158–163. [Google Scholar] [CrossRef]
- Wilson, R.S.; Herziger, A.; Hamilton, M.; Brooks, J.S. From incremental to transformative adaptation in individual responses to climate-exacerbated hazards. Nat. Clim. Chang. 2020, 10, 200–208. [Google Scholar] [CrossRef]
- Dessai, S.; Hulme, M. Does climate adaptation policy need probabilities? Clim. Policy 2004, 4, 107–128. [Google Scholar] [CrossRef]
- Huggel, C.; Scheel, M.; Albrecht, F.; Andres, N.; Calanca, P.; Jurt, C.; Khabarov, N.; Mira-Salama, D.; Rohrer, M.; Salzmann, N.; et al. A framework for the science contribution in climate adaptation: Experiences from science-policy processes in the Andes. Environ. Sci. Policy 2015, 47, 80–94. [Google Scholar] [CrossRef]
- US Census Bureau. 2010 TIGER/Line® Shapefiles. Available online: https://www.census.gov/cgi-bin/geo/shapefiles/index.php (accessed on 15 August 2021).
- Liang, X.; Wood, E.F.; Lettenmaier, D.P. Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification. Glob. Planet. Chang. 1996, 13, 195–206. [Google Scholar] [CrossRef]
- Livneh, B.; Bohn, T.J.; Pierce, D.W.; Munoz-Arriola, F.; Nijssen, B.; Vose, R.; Cayan, D.R.; Brekke, L. A spatially comprehensive, hydrometeorological data set for Mexico, the U.S., and Southern Canada 1950–2013. Sci. Data 2015, 2, 150042. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Brown, T.J. A comparison of statistical downscaling methods suited for wildfire applications. Int. J. Climatol. 2012, 32, 772–780. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Multi-objective global optimization for hydrologic models. J. Hydrol. 1998, 204, 83–97. [Google Scholar] [CrossRef]
- Rana, A.; Moradkhani, H.; Qin, Y. Understanding the joint behavior of temperature and precipitation for climate change impact studies. Theor. Appl. Climatol. 2017, 129, 321–339. [Google Scholar] [CrossRef]
- Battiti, R.; Masulli, F. BFGS optimization for faster and automated supervised learning. In Proceedings of the International Neural Network Conference; Springer: Berlin/Heidelberg, Germany, 1990; pp. 757–760. [Google Scholar]
- Clark, M.P.; Wilby, R.L.; Gutmann, E.D.; Vano, J.A.; Gangopadhyay, S.; Wood, A.W.; Fowler, H.J.; Prudhomme, C.; Arnold, J.R.; Brekke, L.D. Characterizing uncertainty of the hydrologic impacts of climate change. Curr. Clim. Chang. Rep. 2016, 2, 55–64. [Google Scholar] [CrossRef]
- Toya, H.; Skidmore, M. Economic development and the impacts of natural disasters. Econ. Lett. 2007, 94, 20–25. [Google Scholar] [CrossRef]
- Boero, R.; Edwards, B.K.; Rivera, M.K. Regional input–output tables and trade flows: An integrated and interregional non-survey approach. Reg. Stud. 2017, 52, 225–238. [Google Scholar] [CrossRef]
- Kniesner, T.J.; Viscusi, W.K.; Ziliak, J.P. Policy relevant heterogeneity in the value of statistical life: New evidence from panel data quantile regressions. J. Risk Uncertain. 2010, 40, 15–31. [Google Scholar] [CrossRef]
- Kellenberg, D.K.; Mobarak, A.M. Does rising income increase or decrease damage risk from natural disasters? J. Urban Econ. 2008, 63, 788–802. [Google Scholar] [CrossRef]
- Milly, P.C.; Dunne, K.A. Colorado River flow dwindles as warming-driven loss of reflective snow energizes evaporation. Science 2020, 367, 1252–1255. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Chen, Y.D.; Singh, V.P. Future joint probability behaviors of precipitation extremes across China: Spatiotemporal patterns and implications for flood and drought hazards. Glob. Planet. Chang. 2015, 124, 107–122. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; He, S.; Guo, J.; Hong, X.; Liu, Z. A copula-based analysis of projected climate changes to bivariate flood quantiles. J. Hydrol. 2018, 566, 23–42. [Google Scholar] [CrossRef]
- Hall, J.W.; Brown, S.; Nicholls, R.J.; Pidgeon, N.F.; Watson, R.T. Proportionate adaptation. Nat. Clim. Chang. 2012, 2, 833–834. [Google Scholar] [CrossRef]
- Wobus, C.; Lawson, M.; Jones, R.; Smith, J.; Martinich, J. Estimating monetary damages from flooding in the U nited S tates under a changing climate. J. Flood Risk Manag. 2014, 7, 217–229. [Google Scholar] [CrossRef]
- Musselman, K.N.; Lehner, F.; Ikeda, K.; Clark, M.P.; Prein, A.F.; Liu, C.; Barlage, M.; Rasmussen, R. Projected increases and shifts in rain-on-snow flood risk over western North America. Nat. Clim. Chang. 2018, 8, 808–812. [Google Scholar] [CrossRef]
- Mahoney, K.; Alexander, M.; Scott, J.D.; Barsugli, J. High-resolution downscaled simulations of warm-season extreme precipitation events in the Colorado Front Range under past and future climates. J. Clim. 2013, 26, 8671–8689. [Google Scholar] [CrossRef]
- Albright, E.A.; Crow, D. Beliefs about climate change in the aftermath of extreme flooding. Clim. Chang. 2019, 155, 1–17. [Google Scholar] [CrossRef]
- Mulder, K.J. Predicting Responses to Flash Flooding: A Case Study of Boulder, Colorado; East Carolina University: Greenville, NC, USA, 2012. [Google Scholar]
- Brink, E.; Wamsler, C. Citizen engagement in climate adaptation surveyed: The role of values, worldviews, gender and place. J. Clean. Prod. 2019, 209, 1342–1353. [Google Scholar] [CrossRef]
- Schwaller, N.L.; Kelmenson, S.; BenDor, T.K.; Spurlock, D. From abstract futures to concrete experiences: How does political ideology interact with threat perception to affect climate adaptation decisions? Environ. Sci. Policy 2020, 112, 440–452. [Google Scholar] [CrossRef]
- Fischer, H.W. Decentralization and the governance of climate adaptation: Situating community-based planning within broader trajectories of political transformation. World Dev. 2021, 140, 105335. [Google Scholar] [CrossRef]
- Kuklicke, C.; Demeritt, D. Adaptive and risk-based approaches to climate change and the management of uncertainty and institutional risk: The case of future flooding in England. Glob. Environ. Chang. 2016, 37, 56–68. [Google Scholar] [CrossRef]
- Anderegg, W.R.; Prall, J.W.; Harold, J.; Schneider, S.H. Expert credibility in climate change. Proc. Natl. Acad. Sci. USA 2010, 107, 12107–12109. [Google Scholar] [CrossRef]
- Lacey, J.; Howden, M.; Cvitanovic, C.; Colvin, R. Understanding and managing trust at the climate science–policy interface. Nat. Clim. Chang. 2018, 8, 22–28. [Google Scholar] [CrossRef]
- Fischhoff, B. Nonpersuasive Communication about Matters of Greatest Urgency: Climate Change. Environ. Sci. Technol. 2007, 41, 7204–7208. [Google Scholar] [CrossRef] [PubMed]

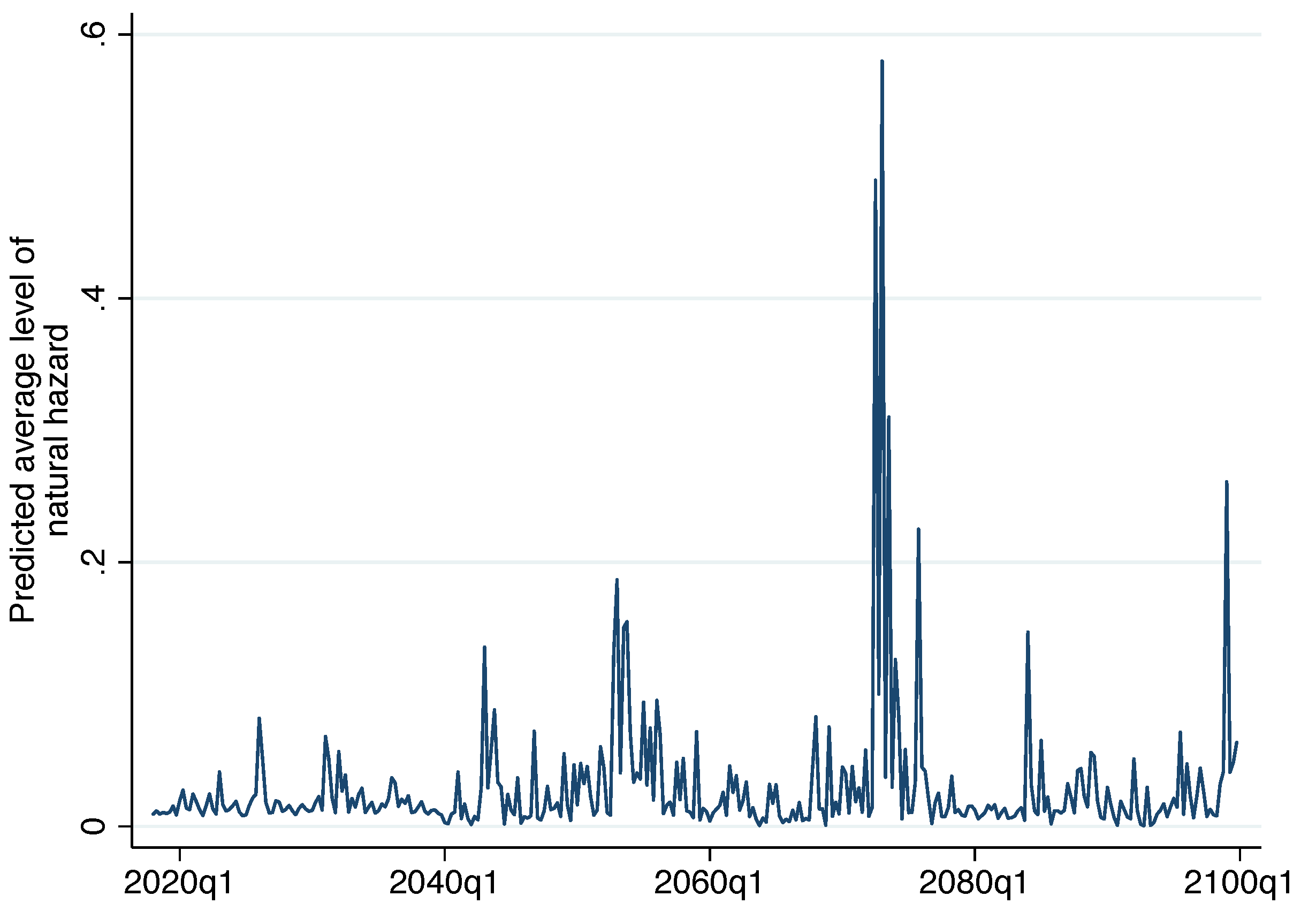
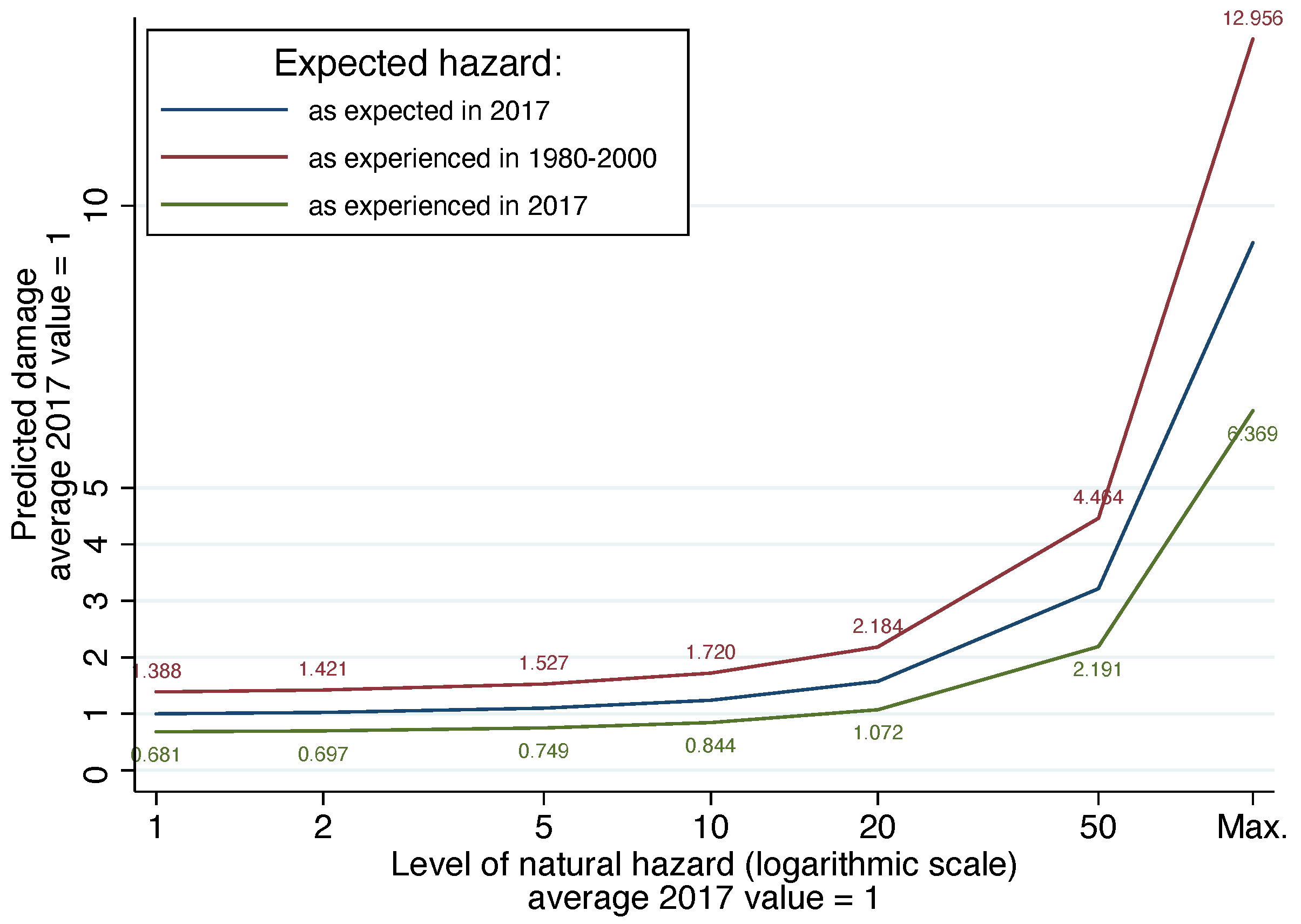
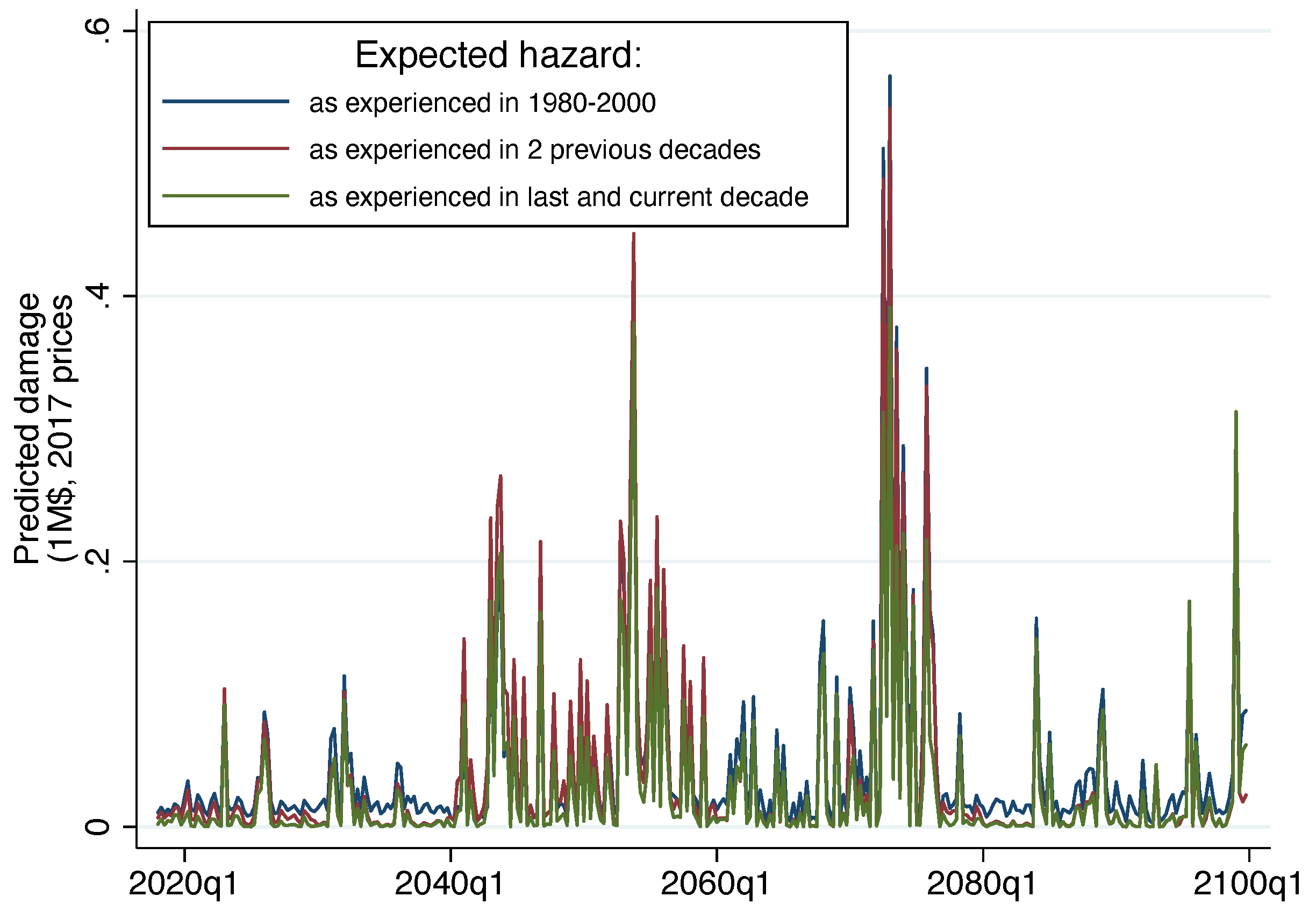
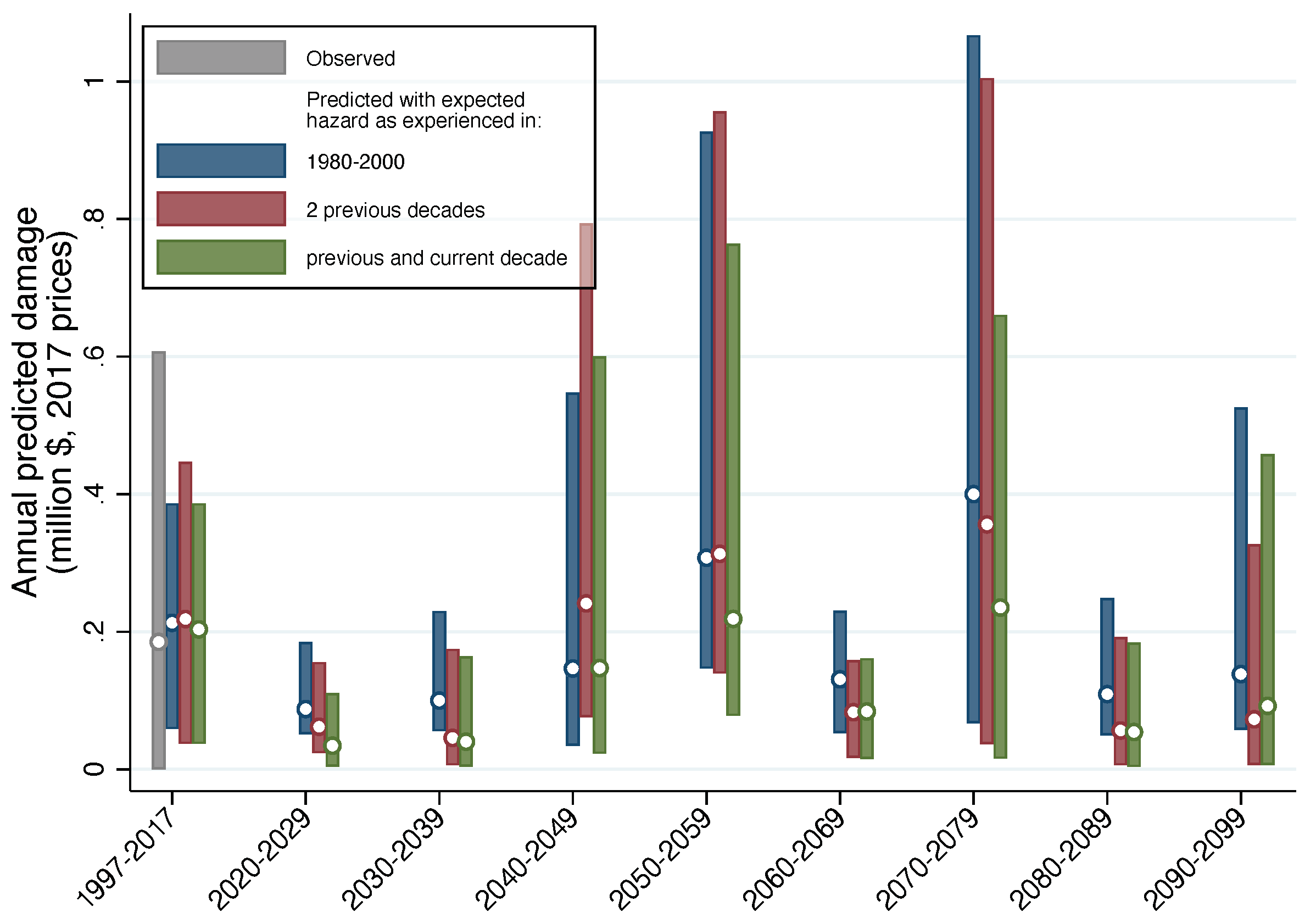
| Type of Unit | Number | Average Area | Area S. D. | Median Area |
|---|---|---|---|---|
| States | 7 | 289,840.90 | 59,742.19 | 284,331.90 |
| Counties | 89 | 11,213.40 | 10,399.06 | 8394.01 |
| Blocks | 395,526 | 2.18 | 19.57 | 0.04 |
| Variable | Obs. | Mean | S.D. | Minimum | Maximum |
|---|---|---|---|---|---|
| Hazard A (GFDL-ESM2G) | 331,560 | 2.24 | 5.81 | 0 | 54 |
| Hazard B (IPSL-CM5A-LR) | 331,560 | 1.30 | 3.66 | 0 | 57 |
| Hazard C (MIROC-ESM) | 331,560 | 0.47 | 2.17 | 0 | 54 |
| Exposure (MUSD – 2017 prices) | 331,560 | 6.43 | 34.60 | 0 | 2690 |
| Damage (USD – 2017 prices) | 331,560 | 27.89 | 7619.99 | 0 | 3,491,619 |
| Negative Binomial | IRR (Std. Err.) |
|---|---|
| Hazard (H) | 0.977 (0.056) |
| Exposure (X) | 1.000 *** (0.000) |
| Hazard Expectation () | 0.325 (0.258) |
| Constant | 170,153.8 *** (56,058.52) |
| Inflation Model (Logit) | Odds Ratio (Std. Err.) |
| Hazard (H) | 0.939 *** (1.019) |
| Exposure (X) | 1.000 ** (1.000) |
| Hazard Expectation () | 1.657 * (1.355) |
| Constant | 4081.558 (1.168) *** |
| Observations | 331,560 |
| Log likelihood |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boero, R.; Talsma, C.J.; Oliveto, J.A.; Bennett, K.E. Expectations of Future Natural Hazards in Human Adaptation to Concurrent Extreme Events in the Colorado River Basin. Climate 2022, 10, 27. https://doi.org/10.3390/cli10020027
Boero R, Talsma CJ, Oliveto JA, Bennett KE. Expectations of Future Natural Hazards in Human Adaptation to Concurrent Extreme Events in the Colorado River Basin. Climate. 2022; 10(2):27. https://doi.org/10.3390/cli10020027
Chicago/Turabian StyleBoero, Riccardo, Carl James Talsma, Julia Andre Oliveto, and Katrina Eleanor Bennett. 2022. "Expectations of Future Natural Hazards in Human Adaptation to Concurrent Extreme Events in the Colorado River Basin" Climate 10, no. 2: 27. https://doi.org/10.3390/cli10020027
APA StyleBoero, R., Talsma, C. J., Oliveto, J. A., & Bennett, K. E. (2022). Expectations of Future Natural Hazards in Human Adaptation to Concurrent Extreme Events in the Colorado River Basin. Climate, 10(2), 27. https://doi.org/10.3390/cli10020027







