Numerical Simulation of Winter Precipitation over the Western Himalayas Using a Weather Research and Forecasting Model during 2001–2016
Abstract
1. Introduction
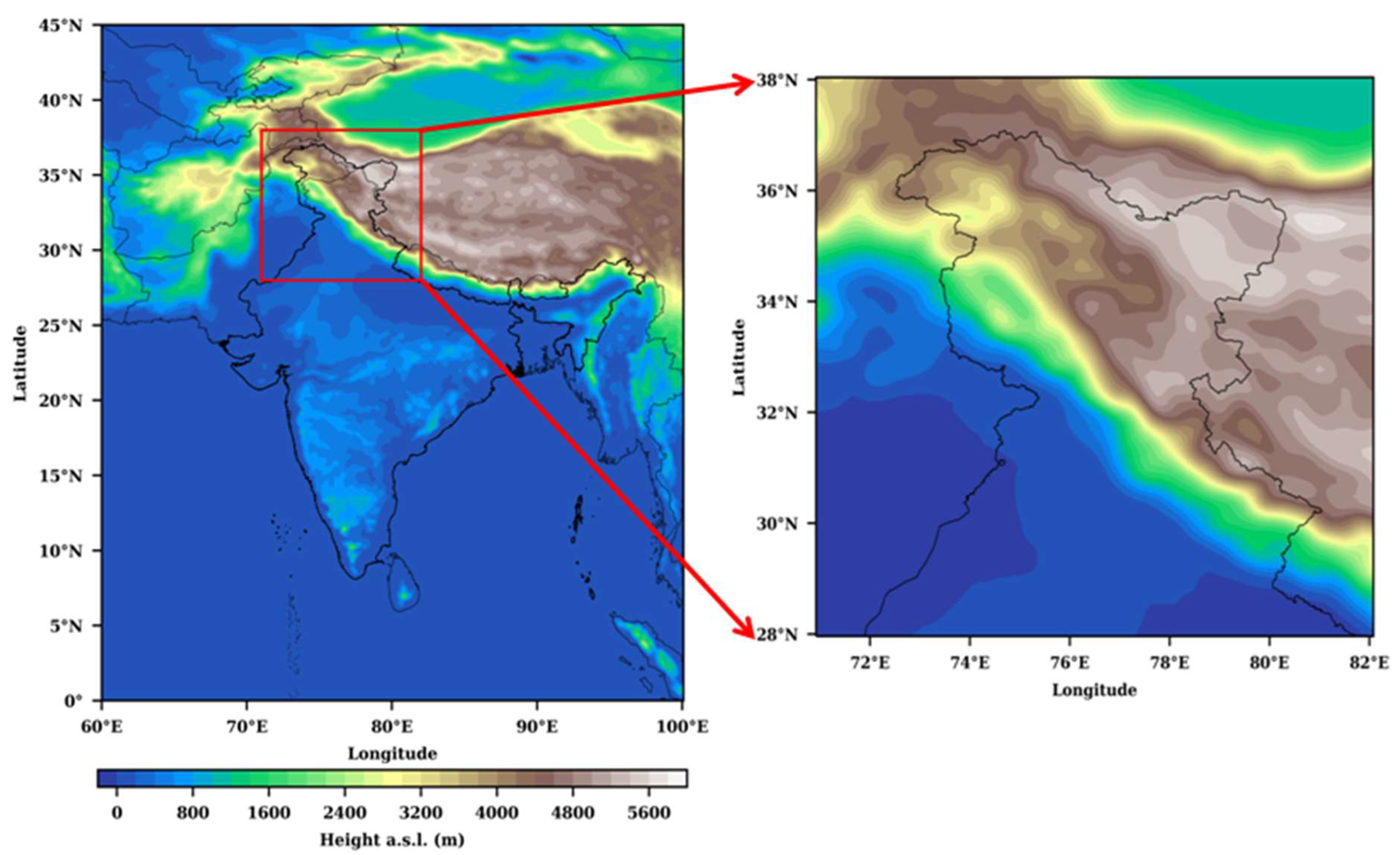
2. Study Area
3. Materials and Methods
3.1. Model Configuration
3.2. Data
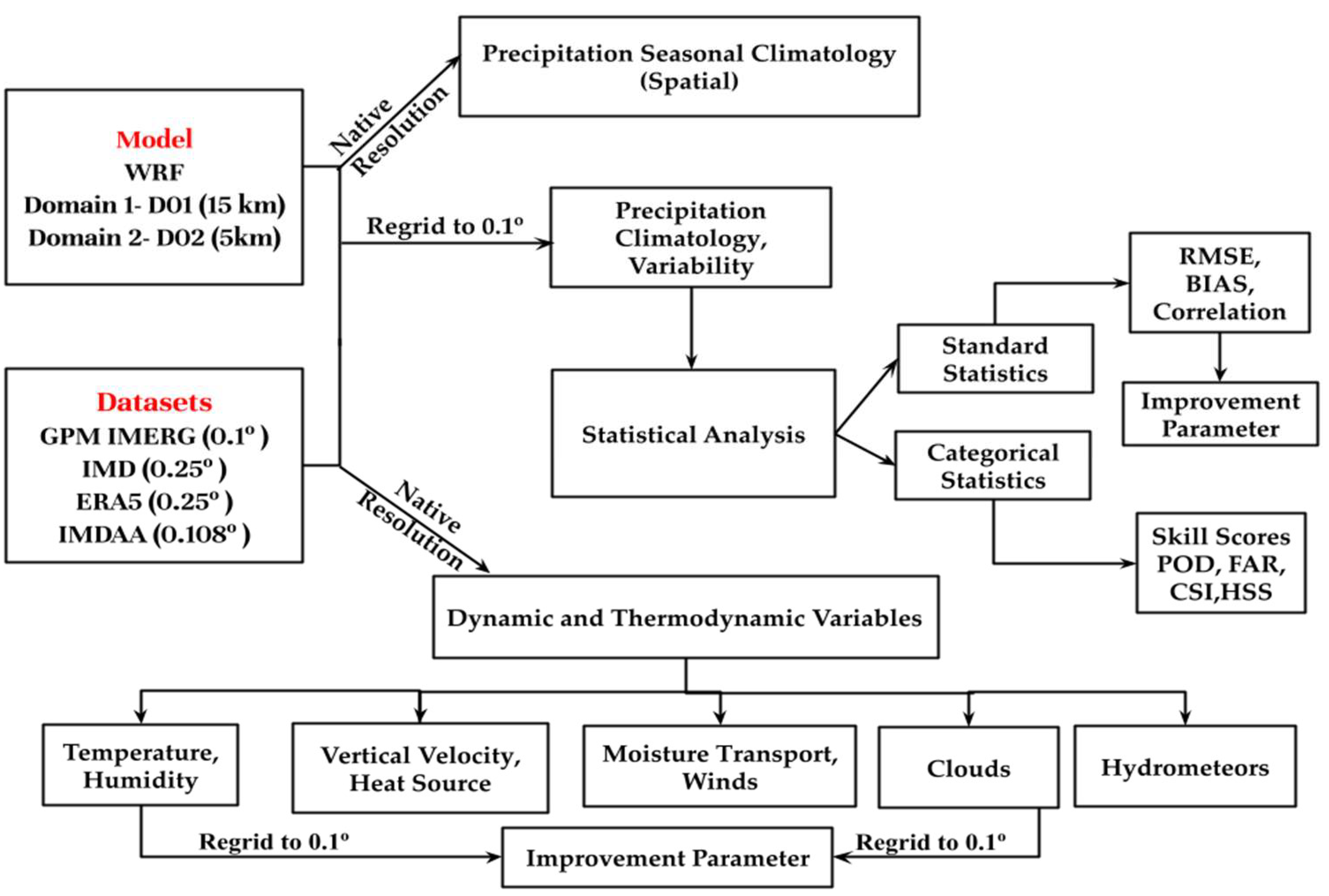
3.3. Methodology
4. Results
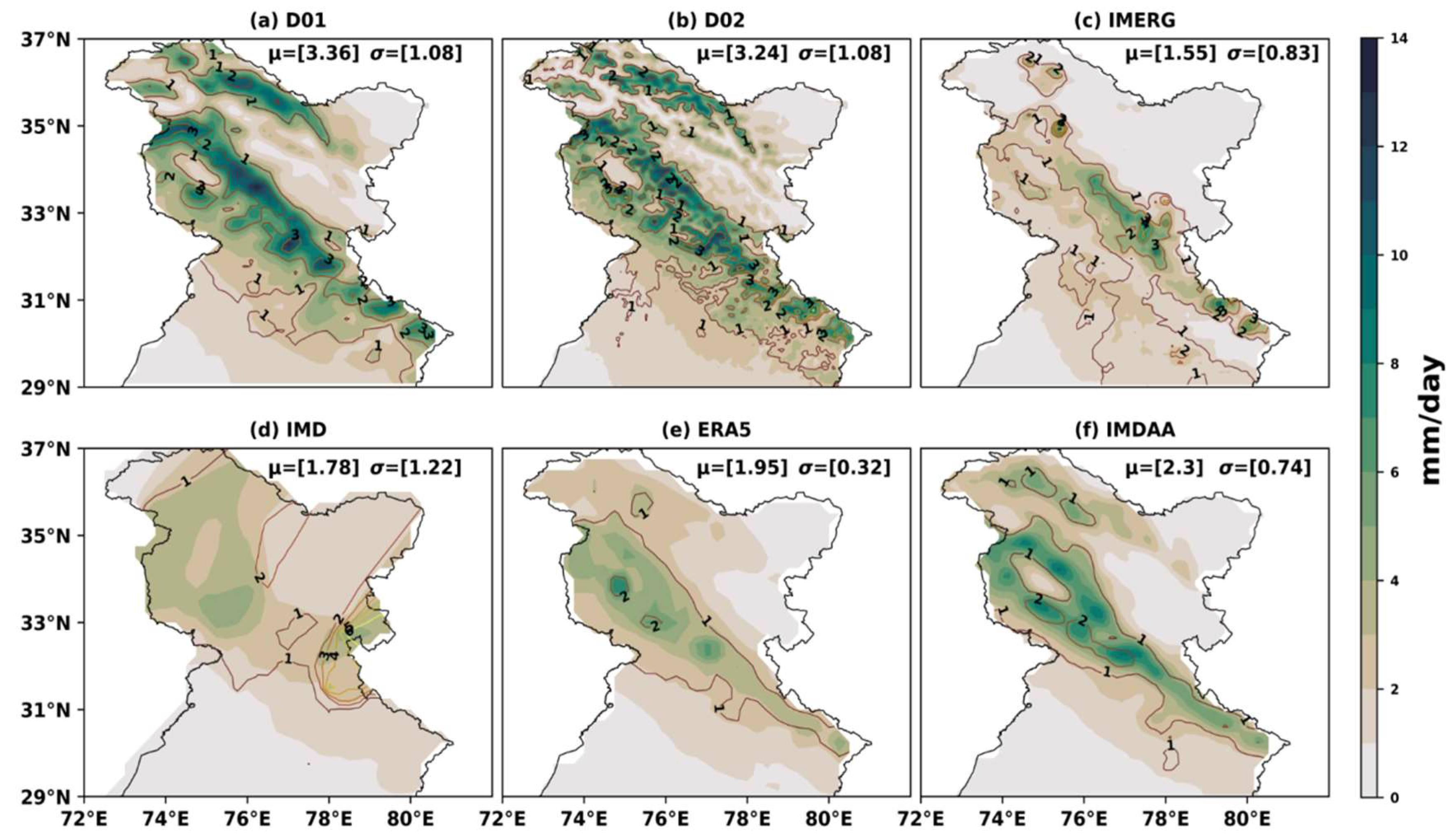
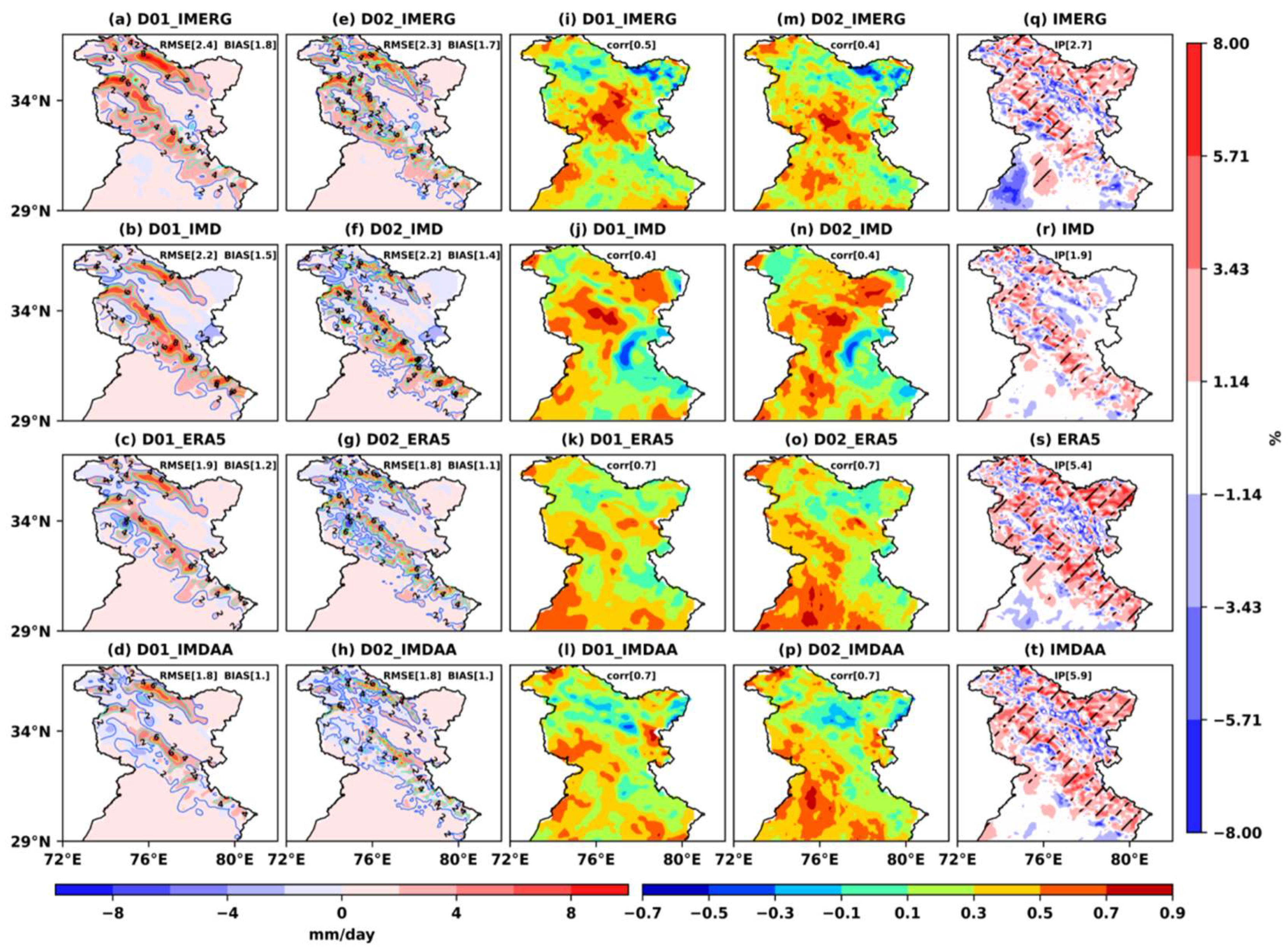
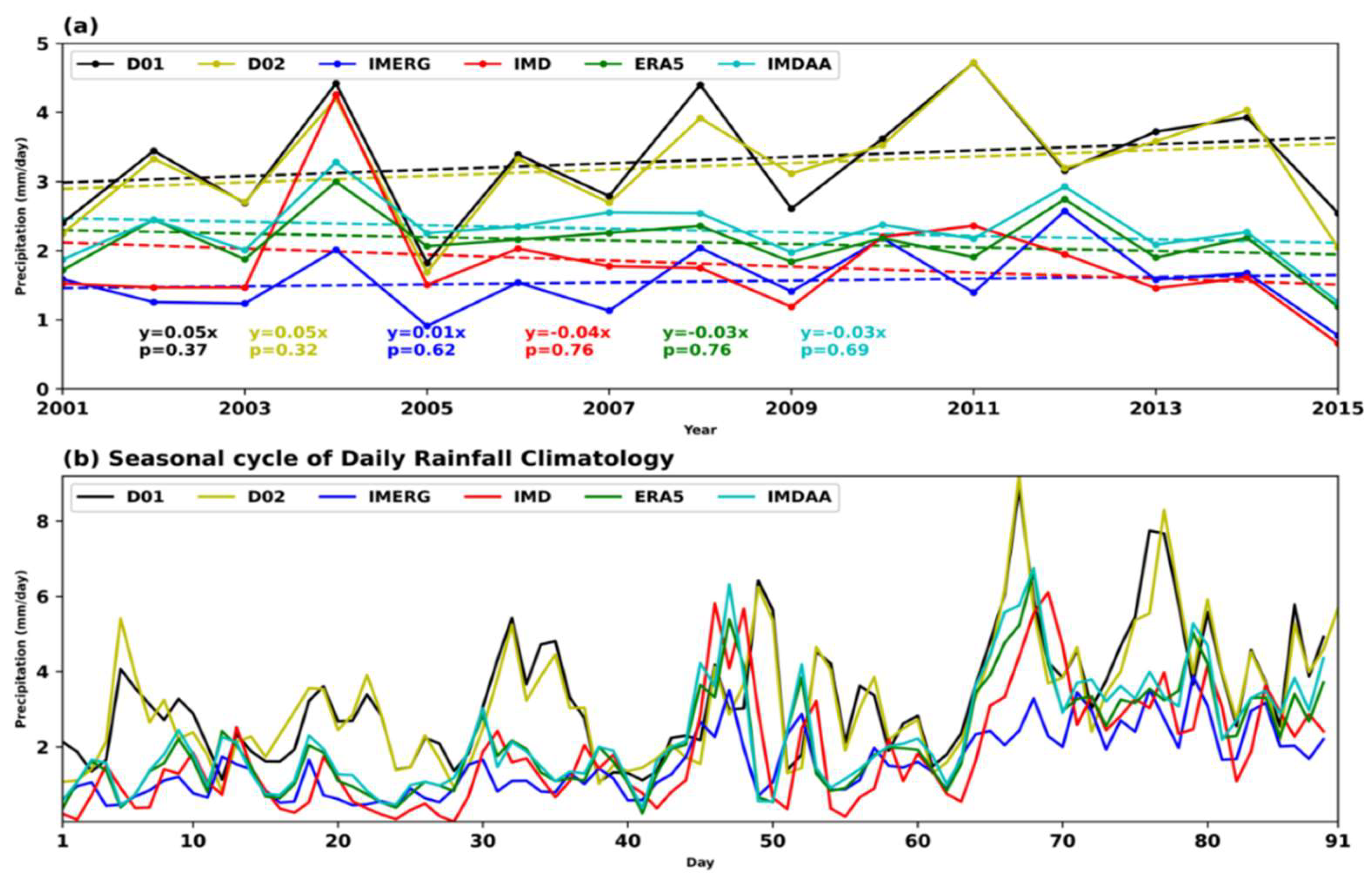
4.1. Winter Precipitation Climatology, Variability and Trends over WH
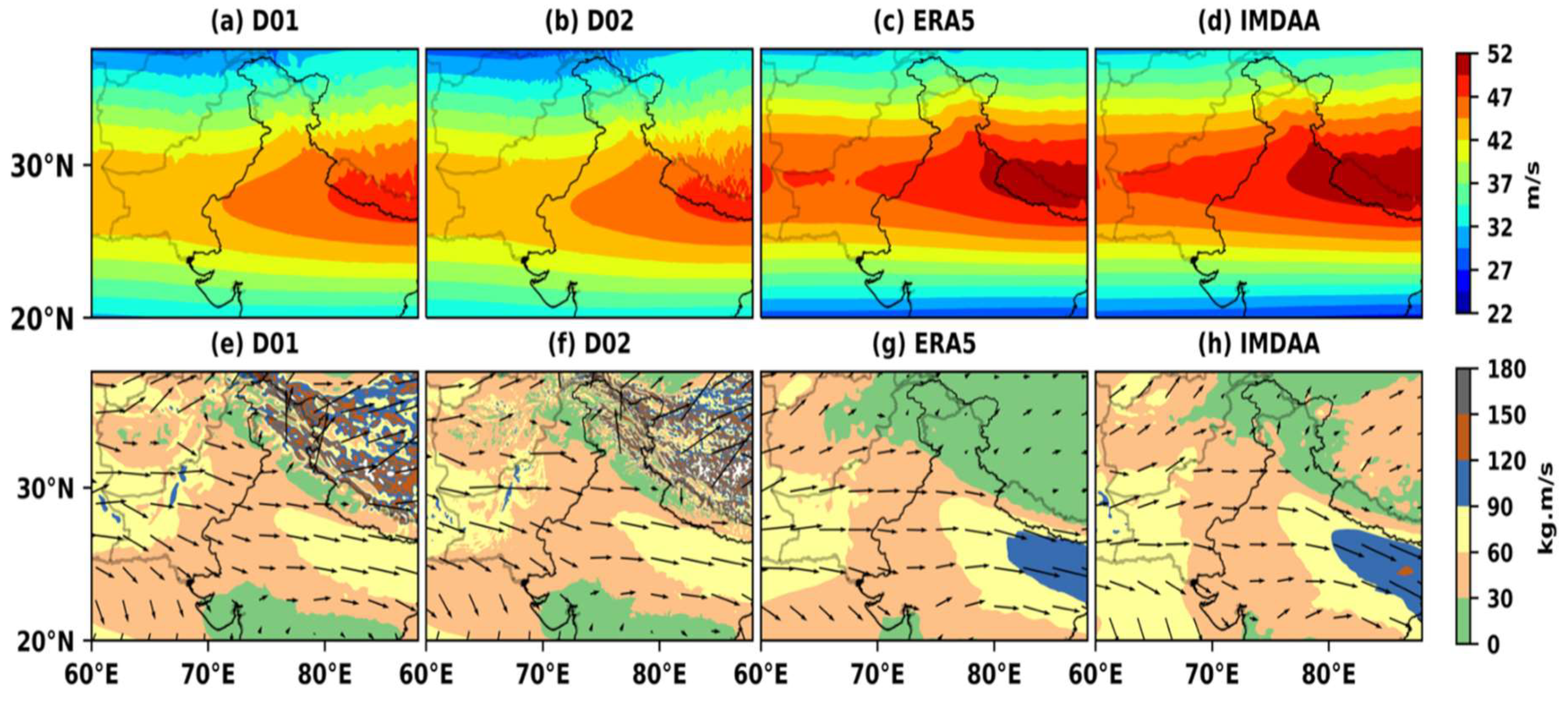
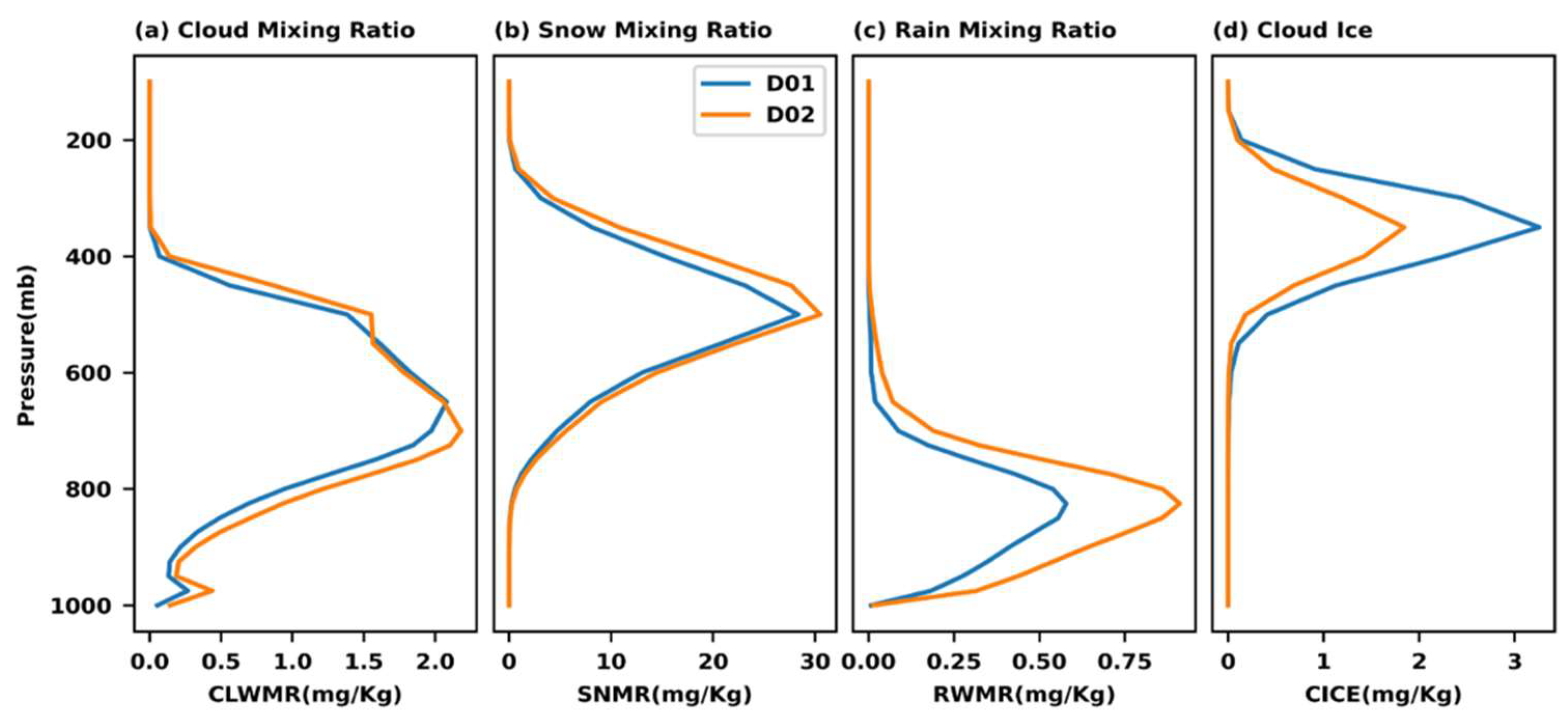
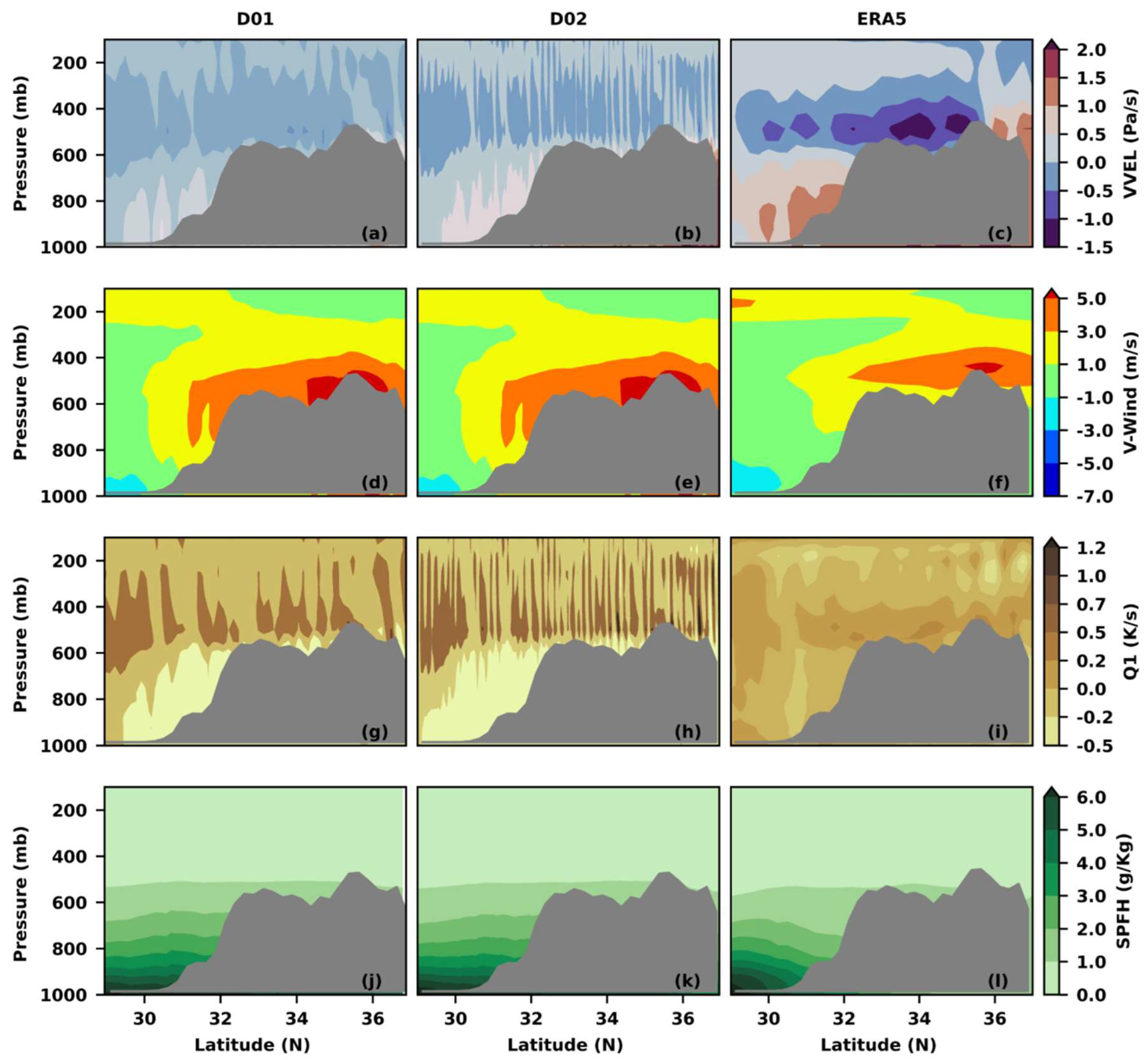
4.2. Atmospheric Dynamics and Thermodynamics during the Winter Season
4.3. Skill Scores for Different Rainfall Amounts
5. Discussion and Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yadav, R.K.; Kumar, K.R.; Rajeevan, M. Characteristic features of winter precipitation and its variability over northwest India. J. Earth Syst. Sci. 2012, 121, 611–623. [Google Scholar] [CrossRef]
- Dimri, A.P.; Yasunari, T.; Kotlia, B.S.; Mohanty, U.C.; Sikka, D.R. Indian winter monsoon: Present and past. Earth Sci. Rev. 2016, 163, 297–322. [Google Scholar] [CrossRef]
- Hunt, K.M.R.; Curio, J.; Turner, A.G.; Schiemann, R. Subtropical Westerly jet influence on occurrence of Western disturbances and Tibetan Plateau vortices. Geophys. Res. Lett. 2018, 45, 8629–8636. [Google Scholar] [CrossRef]
- Tiwari, P.R.; Kar, S.C.; Mohanty, U.C.; Kumari, S.; Sinha, P.; Nair, A.; Dey, S. Skill of precipitation prediction with GCMs over north India during winter season. Int. J. Climatol. 2014, 34, 3440–3455. [Google Scholar] [CrossRef]
- Midhuna, T.M.; Kumar, P.; Dimri, A.P. A new Western Disturbance Index for the Indian winter monsoon. J. Earth Syst. Sci. 2020, 129, 59. [Google Scholar] [CrossRef]
- Midhuna, T.M.; Dimri, A.P. Future projection of winter precipitation over northwest India and associated regions using CORDEX-SA experiments. Theor. Appl. Climatol. 2020, 139, 1317–1331. [Google Scholar] [CrossRef]
- Pisharoty, P.R.; Desai, B.N. Western disturbances and Indian weather. Indian J. Meteor. Geophys. 1956, 8, 333–338. [Google Scholar] [CrossRef]
- Mooley, D.A. The role of western disturbances in the production of weather over India during different seasons. Indian J. Meteor. Geophys. 1957, 8, 253–260. [Google Scholar] [CrossRef]
- Agnihotri, C.L.; Singh, M.S. Satellite study of western disturbances. Mausam 1982, 33, 249–254. [Google Scholar] [CrossRef]
- Dimri, A.P.; Niyogi, D.; Barros, A.P.; Ridley, J.; Mohanty, U.C.; Yasunari, T.; Sikka, D.R. Western Disturbances: A review. Rev. Geophys. 2015, 53, 225–246. [Google Scholar] [CrossRef]
- Dimri, A.P.; Niyogi, D. Regional climate model application at subgrid scale on Indian winter monsoon over the western Himalayas. Int. J. Climatol. 2013, 33, 2185–2205. [Google Scholar] [CrossRef]
- Ridley, J.; Wiltshire, A.; Mathison, C. More frequent occurrence of westerly disturbances in Karakoram up to 2100. Sci. Total Environ. 2013, 468–469, S31–S35. [Google Scholar] [CrossRef] [PubMed]
- Dimri, A.P.; Chevuturi, A.; Niyogi, D.; Thayyen, R.J.; Ray, K.; Tripathi, S.N.; Pandey, A.K.; Mohanty, U.C. Cloudbursts in Indian Himalayas: A review. Earth Sci. Rev. 2017, 168, 1–23. [Google Scholar] [CrossRef]
- Chug, D.; Pathak, A.; Indu, J.; Jain, S.K.; Jain, S.K.; Dimri, A.P.; Niyogi, D.; Ghosh, S. Observed evidence for steep rise in the extreme flow of western Himalayan rivers. Geophys. Res. Lett. 2020, 47, e2020GL087815. [Google Scholar] [CrossRef]
- Das, J.; Meher, K. Drivers of climate over the Western Himalayan region of India: A review. Earth Sci. Rev. 2019, 198, 102935. [Google Scholar] [CrossRef]
- Archer, D.R.; Fowler, H.J. Spatial and temporal variations in precipitation in the Upper Indus Basin, global teleconnections and hydrological implications. Hydrol. Earth Syst. Sci. 2004, 8, 47–61. [Google Scholar] [CrossRef]
- Rasmussen, R.; Baker, B.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Smith, C. How well are we measuring snow: The NOAA/FAA/NCAR winter precipitation test bed. Bull. Am. Meteorol. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef]
- Dimri, A.P.; Yasunari, T.; Wiltshire, A.; Kumar, P.; Mathison, C.; Ridley, J.; Jacob, D. Application of regional climate models to the Indian winter monsoon over the western Himalayas. Sci. Total Environ. 2013, 468–469, S36–S47. [Google Scholar] [CrossRef]
- Hussain, S.; Song, X.; Ren, G.; Hussain, I.; Han, D.; Zaman, M.H. Evaluation of gridded precipitation data in the Hindu Kush—Karakoram—Himalaya mountainous area. Hydrol. Sci. J. 2017, 62, 2393–2405. [Google Scholar] [CrossRef]
- Baudouin, J.P.; Herzog, M.; Petrie, C.A. Cross-validating precipitation datasets in the Indus River basin. Hydrol. Earth Syst. Sci. 2020, 24, 427–450. [Google Scholar] [CrossRef]
- Nischal; Attada, R.; Hunt, K.M. Evaluating winter precipitation over the western Himalayas in a high-resolution Indian regional reanalysis using multi-source climate datasets. J. Appl. Meteorol. Climatol. 2022, 61, 1607–1627. [Google Scholar]
- Vergara-Temprado, J.; Ban, N.; Panosetti, D.; Schlemmer, L.; Schär, C. Climate models permit convection at much coarser resolutions than previously considered. J. Clim. 2020, 33, 1915–1933. [Google Scholar] [CrossRef]
- White, B.A.; Buchanan, A.M.; Birch, C.E.; Stier, P.; Pearson, K.J. Quantifying the effects of horizontal grid length and parameterized convection on the degree of convective organization using a metric of the potential for convective interaction. J. Atmos. Sci. 2018, 75, 425–450. [Google Scholar] [CrossRef]
- Giorgi, F. Thirty years of regional climate modeling: Where are we and where are we going next? J. Geophys. Res. Atmos. 2019, 124, 5696–5723. [Google Scholar] [CrossRef]
- Berg, P.; Wagner, S.; Kunstmann, H.; Schädler, G. High resolution regional climate model simulations for Germany: Part I—Validation. Clim. Dyn. 2013, 40, 401–414. [Google Scholar] [CrossRef]
- Singh, J.; Singh, N.; Ojha, N.; Sharma, A.; Pozzer, A.; Nadimpally, K.K.; Rajeev, K.; Gunthe, S.S.; Rao, K.V. Effects of spatial resolution on WRF v3.8.1 simulated meteorology over the central Himalaya. Geosci. Model Dev. 2021, 14, 1427–1443. [Google Scholar] [CrossRef]
- Rummukainen, M. State-of-the-art with regional climate models. Wiley Interdiscip. Rev. Clim. Change 2010, 1, 82–96. [Google Scholar] [CrossRef]
- Srinivas, C.V.; Dasari, H.P.; Rao, D.V.B.; Anjaneyulu, Y.; Baskaran, R.; Venkatraman, B. Simulation of the Indian summer monsoon regional climate using advanced research WRF model. Int. J. Climatol. 2013, 33, 1195–1210. [Google Scholar] [CrossRef]
- Attada, R.; Dasari, H.P.; Ghostine, R.; Kondapalli, N.K.; Kunchala, R.K.; Luong, T.M.; Hoteit, I. Diagnostic evaluation of extreme winter rainfall events over the Arabian Peninsula using high-resolution weather research and forecasting simulations. Meteorol. Appl. 2022, 29, e2095. [Google Scholar] [CrossRef]
- Jiménez-Esteve, B.; Udina, M.; Soler, M.R.; Pepin, N.; Miró, J.R. Land use and topography influence in a complex terrain area: A high resolution mesoscale modelling study over the Eastern Pyrenees using the WRF model. Atmos. Res. 2018, 202, 49–62. [Google Scholar] [CrossRef]
- Kar, S.C.; Tiwari, S.; Tiwari, P.R. High-Resolution Dynamic Downscaling of Winter Climate over the Himalaya. In Climate Change and the White World; Goel, P., Ravindra, R., Chattopadhyay, S., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Xue, Y.; Vasic, R.; Janjic, Z.; Mesinger, F.; Mitchell, K.E. Assessment of dynamic downscaling of the continental U.S. regional climate using the Eta/SSiB regional climate model. J. Clim. 2007, 20, 4172–4193. [Google Scholar] [CrossRef]
- Lee, D.K.; Cha, D.H.; Kang, H.S. Regional climate simulation of the 1998 summer flood over East Asia. J. Meteorol. Soc. Jpn. 2004, 82, 1735–1753. [Google Scholar] [CrossRef]
- Im, E.S.; Park, E.H.; Kwon, W.T.; Giorgi, F. Present climate simulation over Korea with a regional climate model using a one-way double-nested system. Theor. Appl. Climatol. 2006, 86, 187–200. [Google Scholar] [CrossRef]
- Gao, X.; Xu, Y.; Zhao, Z.; Pal, J.S.; Giorgi, F. Impacts of horizontal resolution and topography on the numerical simulation of East Asian precipitation. Chin. J. Atmos. Sci. 2006, 30, 185–192. [Google Scholar]
- Tang, J.; Zhao, M.; Su, B. Effects of model resolution on the simulation of regionally climatic extreme events. Acta Meteorol. Sin. 2006, 64, 432–442. [Google Scholar]
- Dimri, A.P. Impact of horizontal model resolution and orography on the simulation of a western disturbance and its associated precipitation. Meteorol. Appl. 2004, 11, 115–127. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.L.; Wang, B. Impact of horizontal resolution on the regional climate simulations of the summer 1998 extreme rainfall along the Yangtze River Basin. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Mishra, A.K.; Kumar, P.; Dubey, A.K.; Javed, A.; Saharwardi, M.S.; Sein, D.V.; Martyanov, S.D.; Jacob, D. Impact of horizontal resolution on monsoon precipitation for CORDEX-South Asia: A regional earth system model assessment. Atmos. Res. 2021, 259, 105681. [Google Scholar] [CrossRef]
- Dimri, A.P.; Dash, S.K. Wintertime climatic trends in the western Himalayas. Clim. Change 2012, 111, 775–800. [Google Scholar] [CrossRef]
- Vedwan, N.; Rhoades, R.E. Climate change in the Western Himalayas of India: A study of local perception and response. Clim. Res. 2001, 19, 109–117. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Technical Notes, NCAR/TN-4751STR; NCAR: Boulder, CO, USA, 2018.
- Attada, R.; Dasari, H.P.; Kunchala, R.K.; Langodan, S.; Kumar, K.N.; Knio, O.; Hoteit, I. Evaluating cumulus parameterization schemes for the simulation of Arabian Peninsula winter rainfall. J. Hydrometeorol. 2020, 21, 1089–1114. [Google Scholar] [CrossRef]
- Raju, A.; Parekh, A.; Kumar, P.; Gnanaseelan, C. Evaluation of the impact of AIRS profiles on prediction of Indian summer monsoon using WRF variational data assimilation system. J. Geophys. Res. Atmos. 2015, 120, 8112–8131. [Google Scholar] [CrossRef]
- Mishra, P.; Kannan, S.R.; Radhakrishnan, C. The Effect of Anthropogenic Heat and Moisture on Local Weather at Industrial Heat Islands: A Numerical Experiment. Atmosphere 2022, 13, 357. [Google Scholar] [CrossRef]
- Chandrasekar, R.; Balaji, C. Sensitivity of Tropical Cyclone Jal Simulations to Physics Parameterisations. J. Earth Syst. Sci. 2012, 121, 923–946. [Google Scholar] [CrossRef]
- Subramani, D.; Chandrasekar, R.; Ramanujam, K.S.; Balaji, C. A New Ensemble-Based Data Assimilation Algorithm to Improve Track Prediction of Tropical Cyclones. Nat. Hazard. 2014, 71, 659–682. [Google Scholar] [CrossRef]
- Chandrasekar, R.; Balaji, C. Impact of Physics Parameterisation and 3DVAR Data Assimilation on Prediction of Tropical Cyclones in the Bay of Bengal Region. Nat. Hazard. 2016, 80, 223–247. [Google Scholar] [CrossRef]
- Chandrasekar, R.; Sahu, R.K.; Balaji, C. Assimilation of multi-channel radiances in mesoscale models with an ensemble technique to improve track forecasts of Tropical cyclones. J. Earth Syst. Sci. 2022, 131, 83. [Google Scholar] [CrossRef]
- Mittal, R.; Tewari, M.; Radhakrishnan, C.; Ray, P.; Singh, T.; Nickerson, A. Response of Tropical Cyclone Phailin (2013) in the Bay of Bengal to Climate Perturbations. Clim. Dyn. 2019, 53, 2013–2030. [Google Scholar] [CrossRef]
- Ansari, T.U.; Ojha, N.; Chandrasekar, R.; Balaji, C.; Singh, N.; Gunthe, S.S. Competing Impact of Anthropogenic Emissions and Meteorology on the Distribution of Trace Gases Over Indian Region. J. Atmos. Chem. 2016, 73, 363–380. [Google Scholar] [CrossRef]
- Radhakrishnan, C.; Chandrasekar, V. CASA Prediction System over Dallas—Fort Worth Urban Network: Blending of Nowcasting and High-Resolution Numerical Weather Prediction Model. J. Atmospheric Ocean. Technol. 2020, 37, 211–228. [Google Scholar] [CrossRef]
- Ramanujam, S.; Chandrasekar, R.; Chakravarthy, B. A New PCA-ANN Algorithm for Retrieval of Rainfall Structure in a Precipitating Atmosphere. Int. J. Numer. Method. Heat Fluid Flow 2011, 21, 1002–1025. [Google Scholar] [CrossRef]
- Ramanujam, S.; Radhakrishnan, C.; Subramani, D.; Chakravarthy, B. On the Effect of Non-Raining Parameters in Retrieval of Surface Rain Rate Using TRMM PR and TMI Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 735–743. [Google Scholar] [CrossRef]
- Balaji, C.; Krishnamoorthy, C.; Chandrasekar, R. On the Possibility of Retrieving Near-Surface Rain Rate from the Microwave Sounder SAPHIR of the Megha-Tropiques Mission. Curr. Sci. 2014, 106, 587–593. [Google Scholar]
- Kain, J.S. The Kain—Fritsch convective parameterization: An update. J. Appl. Meteor. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. Convective parameterization for mesoscale models: The Kain—Fritsch scheme. The Representation of Cumulus Convection in Numerical Models. In Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 1993; pp. 165–170. [Google Scholar]
- Thompson, G.; Tewari, M.; Ikeda, K.; Tessendorf, S.; Weeks, C.; Otkin, J.A.; Kong, F. Explicitly-coupled cloud physics and radiation parameterizations and subsequent evaluation in WRF high-resolution convective forecasts. Atmos. Res. 2016, 168, 92–104. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor—Yamada level-3 model with condensation physics: Its design and verification. Bound. Layer Meteorol. 2004, 112, 1–31. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface hydrology model with the Penn State—NCAR MM5 modelling system. Part I: Model implementation and sensitivity. Mon. Weather. Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Ashrit, R.; Rani, S.I.; Kumar, S.; Karunasagar, S.; Arulalan, T.; Francis, T.; Routray, A.; Laskar, S.I.; Mahmood, S.; Jermey, P.; et al. IMDAA regional reanalysis: Performance evaluation during Indian summer monsoon season. J. Geophys. Res. Atmos. 2020, 125, e2019JD030973. [Google Scholar] [CrossRef]
- Rani, S.I.; Arulalan, T.; George, J.P.; Rajagopal, E.N.; Renshaw, R.; Maycock, A.; Barker, D.M.; Rajeevan, M. IMDAA: High resolution satellite-era reanalysis for the Indian monsoon region. J. Clim. 2021, 34, 5109–5133. [Google Scholar] [CrossRef]
- Pai, D.S.; Latha, S.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Xie, P. NASA Global Precipitation Measurement Integrated MultisatellitE Retrievals for GPM (IMERG). In Algorithm Theoretical Basis Document, Version 4.5; NASA: Washington, DC, USA, 2015. [Google Scholar]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R. NASA global precipitation measurement (GPM) integrated multi-satellitE Retrievals for GPM (IMERG). In Algorithm Theoretical Basis Document (ATBD); NASA: Washington, DC, USA, 2019. [Google Scholar]
- Zandler, H.; Haag, I.; Samimi, C. Evaluation needs and temporal performance differences of gridded precipitation products in peripheral mountain regions. Sci. Rep. 2019, 9, 15118. [Google Scholar] [CrossRef] [PubMed]
- Thornes, J.; Stephenson, E.; David, B. How to judge the quality and value of weather forecast products. Meteorol. Appl. 2001, 8, 307–314. [Google Scholar] [CrossRef]
- Mcbride, J.L.; Ebert, E.E. Verification of quantitative precipitation forecasts from operational numerical weather prediction models over Australia. Weather Forecast. 2000, 15, 103–121. [Google Scholar] [CrossRef]
- Aggarwal, D.; Attada, R.; Shukla, K.K.; Chakraborty, R.R.; Kunchala, K. Monsoon precipitation characteristics and extreme precipitation events over Northwest India using Indian high-resolution regional reanalysis. Atmos. Res. 2022, 267, 105993. [Google Scholar] [CrossRef]
- Liu, C.; Moncrieff, M.W. Sensitivity of cloud-resolving simulations of warm season convection to cloud microphysics parameterizations. Mon. Weather Rev. 2007, 135, 2854–2868. [Google Scholar] [CrossRef]
- Wilks, D. Statistical Methods in the Atmospheric Sciences: An Introduction, 3rd ed.; Academic Press: London, UK, 2011. [Google Scholar]
- Dimri, A.P.; Mohanty, U.C. Simulation of mesoscale features associated with intense western disturbances over western Himalayas. Meteorol. Appl. 2009, 16, 289–308. [Google Scholar] [CrossRef]
- Kanda, N.; Negi, H.S.; Rishi, M.S.; Kumar, A. Performance of Various Gridded Temperature and Precipitation Datasets over Northwest Himalayan Region. Environ. Res. Commun. 2020, 2, 85002. [Google Scholar] [CrossRef]
- Ménégoz, M.; Gallée, H.; Jacobi, H.W. Precipitation and snow cover in the Himalaya: From reanalysis to regional climate simulations. Hydrol. Earth Syst. Sci. 2013, 17, 3921–3936. [Google Scholar] [CrossRef]
- Kishore, P.; Jyothi, S.; Basha, G.; Rao, S.V.B.; Rajeevan, M.; Velicogna, I.; Sutterley, T.C. Precipitation climatology over India: Validation with observations and reanalysis datasets and spatial trends. Clim. Dyn. 2016, 46, 541–556. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Mann, H.B. Non-parametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Tiwari, S.; Kar, S.C.; Bhatla, R. Dynamic downscaling over western Himalayas: Impact of cloud microphysics schemes. Atmos. Res. 2018, 201, 1–16. [Google Scholar] [CrossRef]
- Hunt, K.M.; Turner, A.G.; Shaffrey, L.C. The evolution, seasonality and impacts of western disturbances. Q. J. R. Meteorol. Soc. 2018, 144, 278–290. [Google Scholar] [CrossRef]
- Hunt, K.M.R.; Turner, A.G.; Shaffrey, L.C. The impacts of climate change on the winter water cycle of the western Himalaya. Clim. Dyn. 2020, 55, 2287–2307. [Google Scholar] [CrossRef]
- Norris, J.; Carvalho, L.M.V.; Jones, C.; Cannon, F.; Bookhagen, F.; Palazzi, E.; Tahir, A.A. The spatiotemporal variability of precipitation over the Himalaya: Evaluation of one-year WRF model simulation. Clim. Dyn. 2017, 49, 2179–2204. [Google Scholar] [CrossRef]
- Shekhar, M.S.; Rao, N.N.; Paul, S.; Bhan, S.C.; Singh, G.P.; Singh, A. Winter precipitation climatology over Western Himalaya: Altitude and Range wise study. J. Indian Geophys. Union 2017, 21, 148–152. [Google Scholar]
- Nageswararao, M.M.; Mohanty, U.C.; Osuri, K.K.; Ramakrishna, S.S.V.S. Prediction of winter precipitation over northwest India using ocean heat fluxes. Clim. Dyn. 2016, 47, 2253–2271. [Google Scholar] [CrossRef]
| WRF Model Setup | |
|---|---|
| Initial, lateral boundary condition | European Centre for Medium-Range Weather Forecasts Interim Reanalysis (ERAI) (0.758°) |
| Domain extends | 30 °W–130 °E, 30 °S–45 °N |
| Convective Parameterization Scheme | KF scheme [42,51] |
| Microphysical scheme | Thompson scheme [53] |
| Radiation schemes (Shortwave, Longwave) | Rapid Radiative Transfer Model for global circulation models (RRTMG) [55] |
| Planetary boundary layer scheme | Mellor–Yamada–Nakanishi–Niino turbulent kinetic energy scheme [54] |
| Land surface scheme | Noah land surface model scheme [56] |
| Dataset | Spatial Coverage | Temporal Coverage | Spatial Resolution | Temporal Resolution | Reference |
|---|---|---|---|---|---|
| GPM-IMERG | Global | 2001–2016 | 0.1° × 0.1° | Half hourly | Huffman et al., 2015 [61] |
| IMD | India | 2001–2016 | 0.25° × 0.25° | Daily | Pai et al., 2014 [60] |
| ERA5 | Global | 2001–2016 | 0.25° × 0.25° | 1 hourly | Hersbach et al., 2020 [57] |
| IMDAA | South Asia and adjoining regions | 2001–2016 | 0.108° × 0.108° | 1 hourly, 3-hourly | Rani et al., 2021 [59] |
| IMERG | IMD | |||||||
|---|---|---|---|---|---|---|---|---|
| D01 (D02) | <25 P | 25–90 P | 90–95 P | >95 P | <25 P | 25–90 P | 90–95 P | >95 P |
| POD | 0.42 (0.38) | 0.65 (0.65) | 0.52 (0.52) | 0.31 (0.28) | 0.04 (0.02) | 0.86 (0.86) | 0.52 (0.52) | 0.41 (0.36) |
| FAR | 0.65 (0.70) | 0.26 (0.26) | 0.49 (0.49) | 0.91 (0.91) | 0.00 (0.00) | 0.01 (0.01) | 0.49 (0.49) | 0.78 (0.81) |
| CSI | 0.24 (0.20) | 0.53 (0.53) | 0.35 (0.35) | 0.08 (0.07) | 0.04 (0.02) | 0.79 (0.79) | 0.35 (0.35) | 0.17 (0.14) |
| HSS | 0.15 (0.07) | 0.01 (0.01) | 0.00 (0.00) | 0.08 (0.06) | 0.06 (0.03) | 0.15 (0.16) | 0.00 (0.00) | 0.24 (0.20) |
| ERA5 | IMDAA | |||||||
| D01 (D02) | <25 P | 25–90 P | 90–95 P | >95 P | <25 P | 25–90 P | 90–95 P | >95 P |
| POD | 0.36 (0.40) | 0.73 (0.72) | 0.52 (0.52) | 0.28 (0.27) | 0.36 (0.38) | 0.74 (0.73) | 0.52 (0.52) | 0.34 (0.30) |
| FAR | 0.55 (0.56) | 0.26 (0.26) | 0.49 (0.49) | 0.84 (0.85) | 0.54 (0.57) | 0.26 (0.26) | 0.49 (0.49) | 0.79 (0.82) |
| CSI | 0.25 (0.26) | 0.53 (0.53) | 0.35 (0.35) | 0.11 (0.11) | 0.26 (0.26) | 0.59 (0.59) | 0.35 (0.35) | 0.15 (0.13) |
| HSS | 0.23 (0.23) | 0.03 (0.03) | 0.00 (0.00) | 0.15 (0.13) | 0.24 (0.23) | 0.03 (0.03) | 0.00 (0.00) | 0.21 (0.18) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Punde, P.; Nischal; Attada, R.; Aggarwal, D.; Radhakrishnan, C. Numerical Simulation of Winter Precipitation over the Western Himalayas Using a Weather Research and Forecasting Model during 2001–2016. Climate 2022, 10, 160. https://doi.org/10.3390/cli10110160
Punde P, Nischal, Attada R, Aggarwal D, Radhakrishnan C. Numerical Simulation of Winter Precipitation over the Western Himalayas Using a Weather Research and Forecasting Model during 2001–2016. Climate. 2022; 10(11):160. https://doi.org/10.3390/cli10110160
Chicago/Turabian StylePunde, Pravin, Nischal, Raju Attada, Deepanshu Aggarwal, and Chandrasekar Radhakrishnan. 2022. "Numerical Simulation of Winter Precipitation over the Western Himalayas Using a Weather Research and Forecasting Model during 2001–2016" Climate 10, no. 11: 160. https://doi.org/10.3390/cli10110160
APA StylePunde, P., Nischal, Attada, R., Aggarwal, D., & Radhakrishnan, C. (2022). Numerical Simulation of Winter Precipitation over the Western Himalayas Using a Weather Research and Forecasting Model during 2001–2016. Climate, 10(11), 160. https://doi.org/10.3390/cli10110160







