Debiased/Double Machine Learning for Instrumental Variable Quantile Regressions
Abstract
1. Introduction
2. The Model and Algorithm
2.1. The Double Machine Learning
- I.
- [Sample splitting] Split the data into K random and roughly equally sized folds. For , a machine learner is used to fit the high-dimensional nuisance functions, and , using all data except for the kth fold.
- II.
- [Cross-fitting and residualizing] Calculate out-of-sample residuals for these fitted nuisance functions on the kth fold; that is, and .
- III.
- [Treatment effect estimation and inference] Collect all of the out-of-sample residuals from the cross-fitting stage, and use the ordinary least squares to regress on to obtain , the estimator of . The resulting estimate can be paired with heteroskedastic consistent standard errors to obtain a confidence interval for the treatment effect.
2.2. The Instrumental Variable Quantile Regression
2.3. Estimation with High-Dimensional Controls
2.4. Weak-Identification Robust Inference
3. Monte Carlo Experiments
3.1. Residualizing Z on X
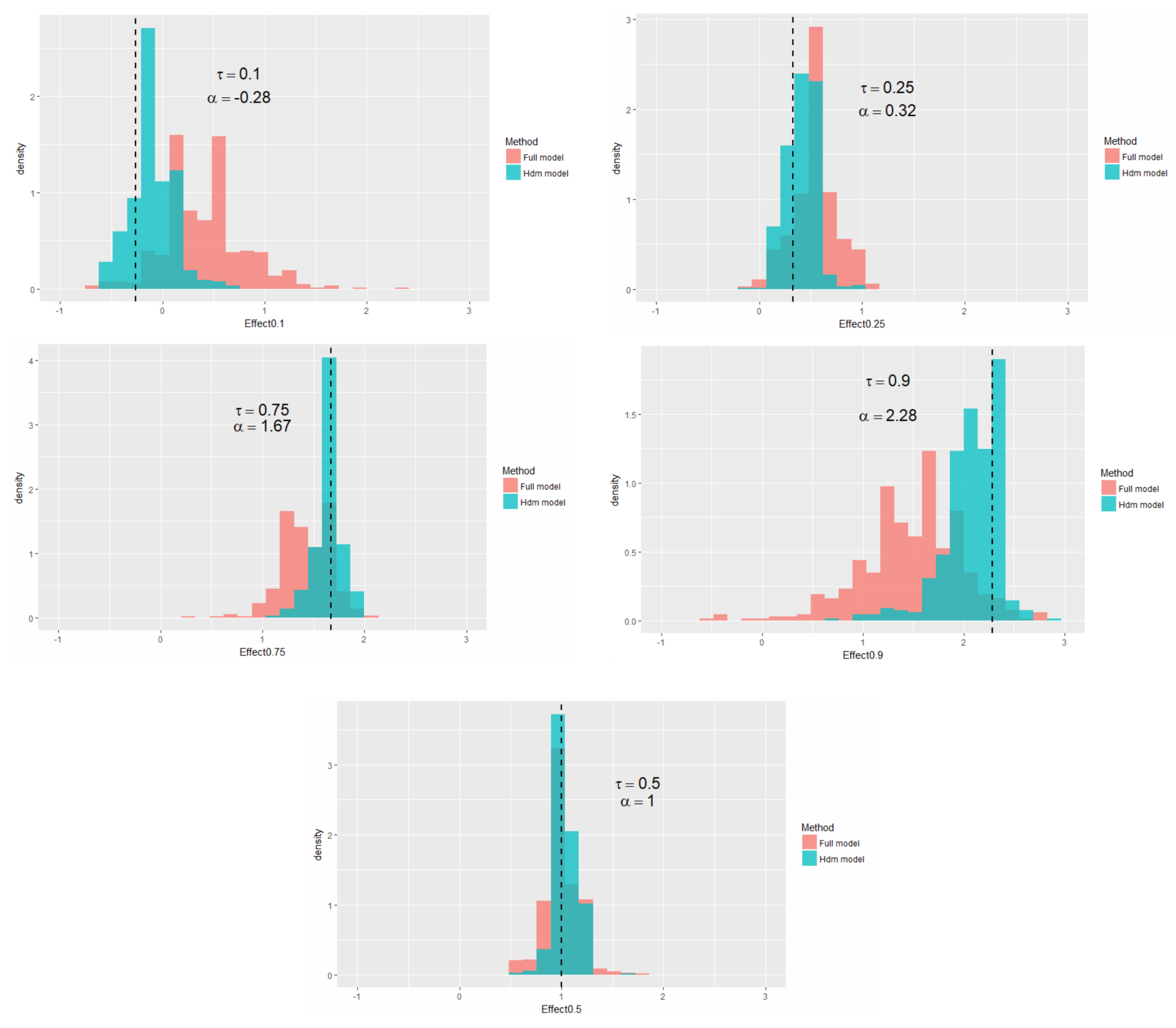
3.2. IVQR with High-Dimensional Controls
4. An Empirical Study: Quantile Treatment Effects of 401(k) Participation on Accumulated Wealth
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DML | Double machine learning |
| GMM | Generalized method of moments |
| GRF | Generalized random forests |
| IVQR | Instrumental variable quantile regression |
| Lasso | Least absolute shrinkage and selection operator |
References
- Athey, Susan. 2017. Beyond prediction: Using big data for policy problem. Science 355: 483–85. [Google Scholar] [CrossRef] [PubMed]
- Athey, Susan, and Guido W. Imbens. 2019. Machine learning method that economists should know about. Annual Review of Economics 11: 685–725. [Google Scholar] [CrossRef]
- Athey, Susan, Julie Tibshirani, and Stefan Wager. 2019. Generalized random forests. Annals of Statistics 47: 1148–78. [Google Scholar] [CrossRef]
- Belloni, Alexandre, and Victor Chernozhukov. 2011. l1-penalized quantile regression in high-dimensional sparse models. Annals of Statistics 39: 82–130. [Google Scholar] [CrossRef]
- Belloni, Alexandre, Victor Chernozhukov, Iván Fernández-Val, and Christian Hansen. 2017. Program evaluation and causal inference with high-dimensional data. Econometrica 85: 233–98. [Google Scholar] [CrossRef]
- Chen, Jau-er, and Chen-Wei Hsiang. 2019. Causal random forests model using instrumental variable quantile regression. Econometrics 7: 49. [Google Scholar] [CrossRef]
- Chen, Le-Yu, and Sokbae Lee. 2018. Exact computation of GMM estimators for instrumental variable quantile regression models. Journal of Applied Econometrics 33: 553–67. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, and Christian Hansen. 2004. The effects of 401(k) participation on the wealth distribution: An instrumental quantile regression analysis. Review of Economics and Statistics 86: 735–51. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, and Christian Hansen. 2005. An IV model of quantile treatment effects. Econometrica 73: 245–61. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, and Christian Hansen. 2008. Instrumental variable quantile regression: A robust inference approach. Journal of Econometrics 142: 379–98. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, and Christian Hansen. 2013. NBER 2013 Summer Institute: Econometric Methods for High-Dimensional Data. Available online: https://www.nber.org/lecture/summer-institute-2013-methods-lectures-econometric-methods-high-dimensional-data (accessed on 15 July 2013).
- Chernozhukov, Victor, Christian Hansen, and Martin Spindler. 2015. Valid post-selection and post-regularization inference: An elementary, general approach. Annual Review of Economics 7: 649–88. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, Christian Hansen, and Kaspar Wüthrich. 2018. Instrumental variable quantile regression. In Handbook of Quantile Regression. Boca Raton: Chapman & Hall/CRC. [Google Scholar]
- Chernozhukov, Victor, Denis Chetverikov, Mert Demirer, Esther Duflo, Christian Hansen, Whitney Newey, and James Robins. 2018. Double/debiased machine learning for treatment and structural parameters. The Econometrics Journal 21: C1–C68. [Google Scholar] [CrossRef]
- Chetverikov, Denis, Zhipeng Liao, and Victor Chernozhukov. 2021. On cross-validated lasso in high dimensions. Annals of Statistics. forthcoming. [Google Scholar]
- Chiou, Yan-Yu, Mei-Yuan Chen, and Jau-er Chen. 2018. Nonparametric regression with multiple thresholds: Estimation and inference. Journal of Econometrics 206: 472–514. [Google Scholar] [CrossRef]
- Davis, Jonathan, and Sara B. Heller. 2017. Using causal forests to predict treatment heterogeneity: An application to summer jobs. American Economic Review 107: 546–50. [Google Scholar] [CrossRef]
- Gilchrist, Duncan Sheppard, and Emily Glassberg Sands. 2016. Something to talk about: Social spillovers in movie consumption. Journal of Political Economy 124: 1339–82. [Google Scholar] [CrossRef]
- Yi, Congrui, and Jian Huang. 2017. Semismooth Newton coordinate descent algorithm for elastic-net penalized Huber loss regression and quantile regression. Journal of Computational and Graphical Statistics 26: 547–57. [Google Scholar] [CrossRef]
| 1 | The R scripts conducting the estimation and inference of the Double Machine Learning for Instrumental Variable Quantile Regressions can be downloaded at https://github.com/FieldTien/DML-IVQR/tree/master/example (accessed on 20 March 2021). |
| 2 | We have conducted Monte Carlo experiments indicating that the choice of based on (13) or 5-fold cross-validation leads to similar finite sample performances of our proposed procedure in terms of root-mean-square error, mean absolute error, and bias. Simulation findings are tabulated in Section 3. When there are many binary control variables, the -norm penalized quantile regression may suffer singularity issues in estimation. If this is the case, researchers can utilize the algorithm developed by Yi and Huang (2017) using the Huber loss function to approximate the quantile loss function. |





| n = 500 | n = 1000 | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | BIAS | RMSE | MAE | BIAS | |
| (res-GMM) | 0.1888 | 0.1510 | −0.0893 | 0.1219 | 0.0950 | −0.0551 |
| (GMM) | 0.4963 | 0.2559 | −0.1775 | 0.1631 | 0.1138 | −0.0627 |
| (res-GMM) | 0.1210 | 0.0966 | −0.0334 | 0.0812 | 0.0654 | −0.0256 |
| (GMM) | 0.1782 | 0.1179 | −0.0254 | 0.0963 | 0.0754 | −0.0234 |
| (res-GMM) | 0.0989 | 0.0716 | 0.0091 | 0.0689 | 0.0436 | −0.0020 |
| (GMM) | 0.1436 | 0.1016 | 0.0340 | 0.0801 | 0.0542 | 0.0078 |
| (res-GMM) | 0.1374 | 0.1066 | 0.0552 | 0.0828 | 0.0676 | 0.0212 |
| (GMM) | 0.2403 | 0.1710 | 0.1294 | 0.1146 | 0.0848 | 0.0442 |
| (res-GMM) | 0.2437 | 0.1839 | 0.1225 | 0.1391 | 0.1067 | 0.0667 |
| (GMM) | 0.8483 | 0.5340 | 0.4959 | 0.3481 | 0.1967 | 0.1613 |
| n = 500 | |||
|---|---|---|---|
| RMSE (Ratio) | MAE (Ratio) | BIAS | |
| (full-GMM) | 0.7648 (4.05) | 0.6645 (4.40) | −0.6533 |
| (oracle-GMM) | 0.1888 (1.00) | 0.1510 (1.00) | −0.0893 |
| (DML-IVQR) | 0.3112 (1.64) | 0.2389 (1.58) | −0.2039 |
| (full-GMM) | 0.2712 (2.24) | 0.2212 (2.28) | −0.1876 |
| (oracle-GMM) | 0.1210 (1.00) | 0.0966 (1.00) | −0.0334 |
| (DML-IVQR) | 0.1562 (1.29) | 0.1254 (1.29) | −0.0796 |
| (full-GMM) | 0.1627 (1.64) | 0.1234 (1.72) | 0.0190 |
| (oracle-GMM) | 0.0989 (1.00) | 0.0716 (1.00) | 0.0091 |
| (DML-IVQR) | 0.1168 (1.18) | 0.0846 (1.18) | −0.0186 |
| (full-GMM) | 0.3421 (2.48) | 0.2806 (2.63) | 0.2502 |
| (oracle-GMM) | 0.1374 (1.00) | 0.1066 (1.00) | 0.0552 |
| (DML-IVQR) | 0.1495 (1.08) | 0.1167 (1.09) | 0.0516 |
| (full-GMM) | 0.9449 (3.87) | 0.8032 (4.36) | 0.7891 |
| (oracle-GMM) | 0.2437 (1.00) | 0.1839 (1.00) | 0.1225 |
| (DML-IVQR) | 0.3567 (1.46) | 0.2608 (1.41) | 0.2011 |
| n= 1000 | |||
| RMSE (Ratio) | MAE (Ratio) | BIAS | |
| (full-GMM) | 0.3917 (3.21) | 0.3442 (3.62) | −0.3303 |
| (oracle-GMM) | 0.1219 (1.00) | 0.0950 (1.00) | −0.0551 |
| (DML-IVQR) | 0.1376 (1.12) | 0.1085 (1.14) | −0.0759 |
| (full-GMM) | 0.1646 (2.02) | 0.1361 (2.08) | −0.1134 |
| (oracle-GMM) | 0.0812 (1.00) | 0.0654 (1.00) | −0.0256 |
| (DML-IVQR) | 0.0991 (1.22) | 0.0804 (1.22) | −0.0436 |
| (full-GMM) | 0.1038 (1.50) | 0.0754 (1.72) | −0.0002 |
| (oracle-GMM) | 0.0689 (1.00) | 0.0436 (1.00) | −0.0020 |
| (DML-IVQR) | 0.0775 (1.12) | 0.0510 (1.16) | −0.0142 |
| (full-GMM) | 0.1747 (2.10) | 0.1452 (2.14) | 0.1174 |
| (oracle-GMM) | 0.0828 (1.00) | 0.0676 (1.00) | 0.0212 |
| (DML-IVQR) | 0.0930 (1.12) | 0.0741 (1.09) | 0.0226 |
| (full-GMM) | 0.4320 (3.10) | 0.3681 (3.45) | 0.3495 |
| (oracle-GMM) | 0.1391 (1.00) | 0.1067 (1.00) | 0.0667 |
| (DML-IVQR) | 0.1649 (1.18) | 0.1231 (1.15) | 0.0731 |
| n = 500 | n = 1000 | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | BIAS | RMSE | MAE | BIAS | |
| ( Belloni and Chernozhukov) | 0.1716 | 0.1325 | −0.0716 | 0.0849 | 0.0683 | 0.0056 |
| ( 5-fold Cross-Validation) | 0.1720 | 0.1368 | −0.0986 | 0.0995 | 0.0811 | −0.0589 |
| ( Belloni and Chernozhukov) | 0.1273 | 0.0962 | 0.0270 | 0.0800 | 0.0556 | 0.0384 |
| ( 5-fold Cross-Validation) | 0.1374 | 0.1032 | −0.0384 | 0.0779 | 0.0536 | −0.0236 |
| ( Belloni and Chernozhukov) | 0.1572 | 0.1272 | 0.0876 | 0.1142 | 0.0961 | 0.0839 |
| ( 5-fold Cross-Validation) | 0.1526 | 0.1179 | 0.0286 | 0.0838 | 0.0677 | 0.0205 |
| n = 500 | n = 1000 | |||||
|---|---|---|---|---|---|---|
| RMSE | MAE | BIAS | RMSE | MAE | BIAS | |
| DML-IVQR | 0.1571 | 0.1238 | 0.0181 | 0.0954 | 0.0754 | 0.0415 |
| cross-fitted DML-IVQR | 0.2165 | 0.1745 | −0.1184 | 0.1130 | 0.0896 | −0.0202 |
| DML-IVQR | 0.1316 | 0.1024 | 0.0704 | 0.0965 | 0.0724 | 0.0632 |
| cross-fitted DML-IVQR | 0.1436 | 0.1155 | 0.0484 | 0.1038 | 0.0855 | 0.0629 |
| DML-IVQR | 0.1735 | 0.1457 | 0.1280 | 0.1280 | 0.1105 | 0.1016 |
| cross-fitted DML-IVQR | 0.2098 | 0.1802 | 0.1726 | 0.1707 | 0.1517 | 0.1502 |
| Quantiles | 0.1 | 0.15 | 0.25 | 0.5 | 0.75 | 0.85 | 0.9 |
|---|---|---|---|---|---|---|---|
| TW(IVQR) | 4400 | 5300 | 4900 | 6700 | 8000 | 8300 | 10,800 |
| TW(res-GMM) | 4400 | 5100 | 4900 | 6300 | 8200 | 7500 | 9100 |
| TW(GMM) | 4400 | 5200 | 4800 | 6300 | 8400 | 8000 | 8700 |
| NFTA(IVQR) | 3600 | 3600 | 3700 | 5700 | 13,200 | 15,800 | 17,700 |
| NFTA(res-GMM) | 3500 | 3600 | 3700 | 5600 | 13,900 | 15,800 | 17,700 |
| NFTA(GMM) | 3500 | 3600 | 3700 | 5700 | 13,900 | 16,100 | 18,200 |
| Quantiles | 0.1 | 0.15 | 0.25 | 0.5 | 0.75 | 0.85 | 0.9 |
|---|---|---|---|---|---|---|---|
| NFTA(std-DML-IVQR ×63522) | 3176 | 3049 | 3303 | 5844 | 18,802 | 26,298 | 28,076 |
| TW(std-DML-IVQR ×111529) | 2453 | 3011 | 3457 | 7695 | 15,056 | 18,736 | 16,394 |
| NFTA(std-DML-IVQR) | 0.05 | 0.048 | 0.052 | 0.092 | 0.296 | 0.414 | 0.442 |
| TW(std-DML-IVQR) | 0.022 | 0.027 | 0.031 | 0.069 | 0.135 | 0.168 | 0.147 |
| Quantile | Selected Variables |
|---|---|
| 0.15 | |
| 0.25 | |
| 0.5 | |
| 0.75 | |
| 0.85 | |
| Quantile | Selected Variables |
|---|---|
| 0.15 | |
| 0.25 | |
| 0.5 | |
| 0.75 | |
| 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-e.; Huang, C.-H.; Tien, J.-J. Debiased/Double Machine Learning for Instrumental Variable Quantile Regressions. Econometrics 2021, 9, 15. https://doi.org/10.3390/econometrics9020015
Chen J-e, Huang C-H, Tien J-J. Debiased/Double Machine Learning for Instrumental Variable Quantile Regressions. Econometrics. 2021; 9(2):15. https://doi.org/10.3390/econometrics9020015
Chicago/Turabian StyleChen, Jau-er, Chien-Hsun Huang, and Jia-Jyun Tien. 2021. "Debiased/Double Machine Learning for Instrumental Variable Quantile Regressions" Econometrics 9, no. 2: 15. https://doi.org/10.3390/econometrics9020015
APA StyleChen, J.-e., Huang, C.-H., & Tien, J.-J. (2021). Debiased/Double Machine Learning for Instrumental Variable Quantile Regressions. Econometrics, 9(2), 15. https://doi.org/10.3390/econometrics9020015





