Teaching Graduate (and Undergraduate) Econometrics: Some Sensible Shifts to Improve Efficiency, Effectiveness, and Usefulness
Abstract
1. Introduction
- (1)
- The abstract equations and high-level math should be replaced with real examples;
- (2)
- There should be greater emphasis on choosing the best set of control variables for causal interpretation of some treatment variable;
- (3)
- There should be a shift towards randomized control trials and quasi-experimental methods (e.g., regression-discontinuities and difference-in-difference methods), as these are the methods most often used by economists these days.
- A.
- Increase emphasis on some regression basics (“holding other factors constant” and regression objectives)
- B.
- Reduce emphasis on getting the standard errors correct
- C.
- Adopt new approaches for teaching how to recognize biases
- D.
- Shift focus to the more practical quasi-experimental methods
- E.
- Add emphasis on interpretations on statistical significance and p-values
- F.
- Advocate less complexity
- G.
- Add a simple ethical component.
2. Why a Redesign Is Needed
- There are concerns on the validity of much economic research;
- Biases in coefficient estimates threaten a model’s validity much more than biases in standard errors;
- The conventional methods for teaching econometrics do not adequately prepare students to recognize biases to coefficient estimates;
- The high-level math and proofs are unnecessary and take valuable time away from more important concepts; and
- There are ethical problems in research, namely on the search for significance and not fully disclosing potential sources of bias.
2.1. There Are Concerns on the Validity of Much Economic Research
2.2. Biases in Coefficient Estimates Threaten a Model’s Validity More Than Biases in Standard Errors
2.3. Current Methods Do Not Teach How to Recognize Biases
2.4. The High-Level Math and Proofs Are Unnecessary and Take Valuable Time Away from More Important Concepts
2.5. There Is an Ethical Problem in Economic Research
2.6. What the Textbooks Teach
3. Research Topics with Decades of Research Errors
- (A)
- The hot hand in basketball, continuing the discussion from the Introduction;
- (B)
- The public-finance/macroeconomic topic of how state tax rates affect Gross State Product;
- (C)
- How occupation-specific bonuses affect the probability of reenlistment in the military.
3.1. The Hot Hand in Basketball
3.2. How State Income Tax Rates Affect Gross State Product
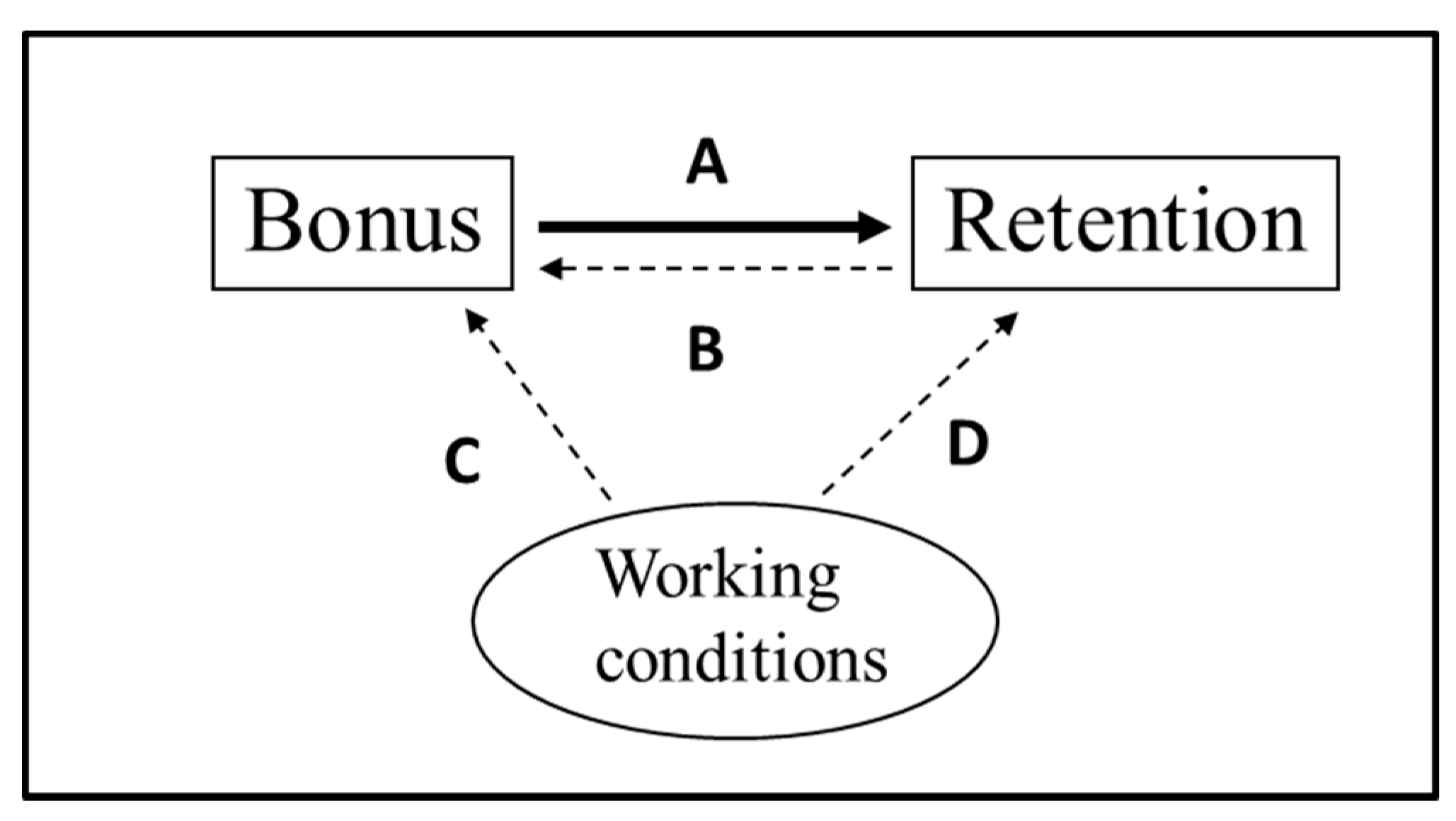
3.3. How Occupation-Specific Bonuses Affect the Probability of Reenlistment
- There is the obvious bias of reverse causality in that lower reenlistment rates lead to higher bonuses.
- Enlisted personnel often have latitude on when they reenlist, so if they were planning to reenlist, they may time it to when the bonus appears to be higher than normal; so, the bonus is endogenous in that it is chosen to some extent by those reenlisting. This is an indirect reverse causality, in that the choice of reenlisting or not (R) would affect the timing of the reenlistment; and those choosing to reenlist would tend to do so when the bonus is relatively high within their reenlistment window.
- There is likely bias from measurement error, as servicepersons often have a few different bonuses during their reenlistment window, and the one most often recorded is the one at the official reenlistment date, not the one when they sign the new contract (which is not among the available data and can be up to two months earlier).
- There is unobserved heterogeneity because excess supply for reenlistments can mean that we only observe whether a person reenlists rather than whether he/she is willing to reenlist (or actual reenlistment supply). Excess supply of reenlistments could result from reduced demand from the military (e.g., occupations being eliminated) or worsening civilian prospects for the skill. Excess supply when an occupation is eliminated (and the reenlistment rate and bonus equals zero) could lead to a large exaggeration of the bonus effect.
3.4. Summary
4. Recommended Changes and New Topics for Graduate Econometrics
- Replace the math with intuition and examples
- Focus on choosing the best set of control variables.
- A.
- Increase emphasis on some regression basics (“holding other factors constant” and regression objectives)
- B.
- Reduce emphasis on getting the standard errors correct
- C.
- Adopt new approaches for teaching how to recognize biases
- D.
- Shift focus to the more practical quasi-experimental methods
- E.
- Add emphasis on interpretations on statistical significance and p-values
- F.
- Advocate less complexity
- G.
- Add a simple ethical component
“If applied economists narrow the focus of their research and critical reading to various forms of pseudo-experimental, the profession loses a good part of its ability to provide advice about the effects and uncertainties surrounding policy issues”.
- (1)
- As described above in some things I had missed in my own research, bias from measurement error can be exacerbated by fixed effects;
- (2)
- The estimated treatment effect with fixed effects is a weighted average of the estimated treatment effects within each fixed-effects group;
- (3)
- The natural regression weights of the fixed-effects groups with a higher variance of the treatment are disproportionately higher—this concept and the correction is described in Gibbons et al. (2018) and Arkes (2019, Section 8.3); and so shifting the natural weight of a group could partly explain why fixed-effects estimates are different from the corresponding estimates without fixed effects; also besides fixed effects, this concept applies to cases in which one simply controls for categories (e.g., race). Reweighting observations can help address this problem.
5. Implications for Undergraduate Econometrics
- replace the math with examples, which is a basic tenet of fostering student motivation (Ambrose et al. 2010)
- increase the emphasis on choosing the correct set of control variables.
6. Conclusions and Topics for Further Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Abadie, Alberto. 2020. Statistical Nonsignificance in Empirical Economics. American Economic Review: Insights 2: 193–208. [Google Scholar] [CrossRef]
- Aczel, Balazs, Bence Palfi, Aba Szollosi, Marton Kovacs, Barnabas Szaszi, Peter Szecsi, Mark Zrubka, Quentin F. Gronau, Don van den Bergh, and Eric-Jan Wagenmakers. 2018. Quantifying support for the null hypothesis in psychology: An empirical investigation. Advances in Methods and Practices in Psychological Science 1: 357–66. [Google Scholar] [CrossRef]
- Ambrose, Susan A., Michael W. Bridges, Michele DiPietro, Marsha C. Lovett, and Marie K. Norman. 2010. How Learning Works: Seven Research-Based Principles for Smart Teaching. Hoboken: John Wiley & Sons. [Google Scholar]
- Amrhein, Valentin, Sander Greenland, and Blake McShane. 2019. Scientists rise up against statistical significance. Nature 567: 305–7. [Google Scholar] [CrossRef] [PubMed]
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2009. Mostly Harmless Econometrics: An Empiricist’s Companion. Princeton: Princeton University Press. [Google Scholar]
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2010. The credibility revolution in empirical economics: How better research design is taking the con out of econometrics. Journal of Economic Perspectives 24: 3–30. [Google Scholar] [CrossRef]
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2015. Mastering Metrics: The Path from Cause to Effect. Princeton: Princeton University Press. [Google Scholar]
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2017. Undergraduate econometrics instruction: Through our classes, darkly. Journal of Economic Perspectives 31: 125–44. [Google Scholar] [CrossRef]
- Arkes, Jeremy. 2010. Revisiting the hot hand theory with free throw data in a multivariate framework. Journal of Quantitative Analysis in Sports 6. [Google Scholar] [CrossRef]
- Arkes, Jeremy. 2018. Empirical biases and some remedies in estimating the effects of selective reenlistment bonuses on reenlistment rates. Defence and Peace Economics 29: 475–502. [Google Scholar] [CrossRef]
- Arkes, Jeremy. 2019. Regression Analysis: A Practical Introduction. Oxford: Routledge. [Google Scholar]
- Arkes, Jeremy, Thomas Ahn, Amilcar Menichini, and William Gates. 2019. Retention Analysis Model (RAM) for Navy Manpower Analysis. Report NPS-GSBPP-19-003. Monterey: Naval Postgraduate School. [Google Scholar]
- Baicker, Katherine, Sarah L. Taubman, Heidi L. Allen, Mira Bernstein, Jonathan H. Gruber, Joseph P. Newhouse, Eric C. Schneider, Bill J. Wright, Alan M. Zaslavsky, and Amy N. Finkelstein. 2013. The Oregon experiment—effects of Medicaid on clinical outcomes. New England Journal of Medicine 368: 1713–22. [Google Scholar] [CrossRef]
- Baltagi, Badi H. 2011. Econometrics, 3rd ed. Heildelberg: Springer. [Google Scholar]
- Bania, Neil, Jo Anna Gray, and Joe A. Stone. 2007. Growth, Taxes, and Government Expenditures: Growth Hills for U.S. States. National Tax Journal 60: 193–204. [Google Scholar] [CrossRef]
- Bar-Eli, Michael, Simcha Avugos, and Markus Raab. 2006. Twenty years of “hot hand” research: Review and critique. Psychology of Sport and Exercise 7: 525–53. [Google Scholar] [CrossRef]
- Bartik, Timothy J. 1991. Who Benefits from State and Local Economic Development Policies? Kalamazoo: W.E. Upjohn Institute for Employment Research. [Google Scholar]
- Bocskocsky, Andrew, John Ezekowitz, and Carolyn Stein. 2014. The hot hand: A new approach to an old ‘fallacy’. Paper presented at 8th Annual MIT Sloan Sports Analytics Conference, Boston, MA, USA, 28 February 2014–1 March 2014; pp. 1–10. [Google Scholar]
- Bound, John, David A. Jaeger, and Regina M. Baker. 1995. Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. Journal of the American Statistical Association 90: 443–50. [Google Scholar] [CrossRef]
- Brooks, David. 2013. The Philosophy of Data. New York Times. February 4. Available online: http://www.nytimes.com/2013/02/05/opinion/brooks-the-philosophy-of-data.html (accessed on 6 November 2015).
- Christensen, Garret, and Edward Miguel. 2018. Transparency, Reproducibility, and the Credibility of Economics Research. Journal of Economic Literature 56: 920–80. [Google Scholar] [CrossRef]
- Cready, William M., Bo Liu, and Di Wang. 2019. A Content Based Assessment of the Relative Quality of Leading Accounting Journals. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3438405 (accessed on 4 September 2020).
- Cunningham, Scott. 2018. Causal Inference: The MIX Tape (v. 1.7). Available online: tufte-latex.googlecode.com (accessed on 4 September 2020).
- Dougherty, Christopher. 2016. Introduction to Econometrics. New York: Oxford University Press. [Google Scholar]
- Ehrlich, Isaac. 1975. The deterrent effect of capital punishment: A question of life and death. American Economic Review 65: 397–417. [Google Scholar]
- Ettinger, Bruce, Gary D. Friedman, Trudy Bush, and Charles P. Quesenberry, Jr. 1996. Reduced mortality associated with long-term postmenopausal estrogen therapy. Obstetrics & Gynecology 87: 6–12. [Google Scholar]
- Funderburg, Richard, Timothy J. Bartik, Alan H. Peters, and Peter S. Fisher. 2013. The impact of marginal business taxes on state manufacturing. Journal of Regional Science 53: 557–82. [Google Scholar] [CrossRef]
- Gertler, Paul. 2004. Do conditional cash transfers improve child health? Evidence from PROGRESA’s control randomized experiment. American Economic Review 94: 336–41. [Google Scholar] [CrossRef]
- Gibbons, Charles E., Juan Carlos Suárez Serrato, and Michael B. Urbancic. 2018. Broken or fixed effects? Journal of Econometric Methods 8. [Google Scholar] [CrossRef]
- Gigerenzer, Gerd. 2004. Mindless statistics. The Journal of Socio-Economics 33: 587–606. [Google Scholar] [CrossRef]
- Gill, D. 2018. Why It’s so Hard to Study the Impact of Minimum Wage Increases. Available online: https://qz.com/work/1415401/why-minimum-wage-research-is-full-of-conflicting-studies/ (accessed on 11 June 2020).
- Gilovich, Thomas, Robert Vallone, and Amos Tversky. 1985. The hot hand in basketball: On the misperception of random sequences. Cognitive Psychology 17: 295–314. [Google Scholar] [CrossRef]
- Goldberg, Matthew S. 2001. A Survey of Enlisted Retention: Models and Findings. Report # CRM D0004085.A2. Alexandria: Center for Naval Analyses. [Google Scholar]
- Goldberger, Arthur Stanley. 1991. A Course in Econometrics. Harvard: Harvard University Press. [Google Scholar]
- Gould, Stephen Jay. 1989. The streak of streaks. Chance 2: 10–16. [Google Scholar] [CrossRef]
- Greene, W. 2012. Econometric Analysis, 7th ed. Upper Saddle River: Prentice Hall. [Google Scholar]
- Gujarati, Damodar N., and D. Porter. 2009. Basic Econometrics. New York: McGraw-Hill. [Google Scholar]
- Hansen, Michael L., and Jennie W. Wenger. 2005. Is the pay responsiveness of enlisted personnel decreasing? Defence and Peace Economics 16: 29–43. [Google Scholar] [CrossRef]
- Harford, Tim. 2014. Big data: A big mistake? Significance 11: 14–19. [Google Scholar] [CrossRef]
- Hayashi, Fumio. 2000. Econometrics. Princeton: Princeton University Press. [Google Scholar]
- Head, Megan L., Luke Holman, Rob Lanfear, Andrew T. Kahn, and Michael D. Jennions. 2015. The extent and consequences of p-hacking in science. PLoS Biology 13: e1002106. [Google Scholar] [CrossRef] [PubMed]
- Ioannidis, John P. A. 2005. Why Most Published Research Findings Are False. PLoS Medicine 2: e124. [Google Scholar] [CrossRef]
- Kahneman, Daniel. 2011. Thinking Fast and Slow. New York: Farrar, Straus and Giroux. [Google Scholar]
- Kass, Robert E., and Adrian E. Raftery. 1995. Bayes factors. Journal of the American Statistical Association 90: 773–95. [Google Scholar] [CrossRef]
- Kennedy, Peter. 2008. A Guide to Econometrics, 6th ed. Hoboken: Wiley-Blackwell. [Google Scholar]
- Kim, Jae H. 2020. Decision-theoretic hypothesis testing: A primer with R package OptSig. The American Statistician. in press. [Google Scholar] [CrossRef]
- Kim, Jae H., and Philip Inyeob Ji. 2015. Significance testing in empirical finance: A critical review and assessment. Journal of Empirical Finance 3: 1–14. [Google Scholar] [CrossRef]
- Kling, Jeffrey R., Jeffrey B. Liebman, and Lawrence F. Katz. 2007. Experimental analysis of neighborhood effects. Econometrica 75: 83–119. [Google Scholar] [CrossRef]
- Leamer, Edward E. 1983. Let’s take the con out of econometrics. Modelling Economic Series 73: 31–43. [Google Scholar]
- Leamer, Edward E. 1988. 3 Things that bother me. Economic Record 64: 331–35. [Google Scholar] [CrossRef]
- Manson, JoAnn E., Aaron K. Aragaki, Jacques E. Rossouw, Garnet L. Anderson, Ross L. Prentice, Andrea Z. LaCroix, Rowan T. Chlebowski, Barbara V. Howard, Cynthia A. Thomson, Karen L. Margolis, and et al. 2017. Menopausal Hormone Therapy and Long-term All-Cause and Cause-Specific Mortality: The Women’s Health Initiative Randomized Trials. Journal of the American Medical Association 318: 927–38. [Google Scholar] [CrossRef]
- Miller, Joshua B., and Adam Sanjurjo. 2018. Surprised by the hot hand fallacy? A truth in the law of small numbers. Econometrica 86: 2019–47. [Google Scholar] [CrossRef]
- Mofidi, Alaeddin, and Joe A. Stone. 1990. Do state and local taxes affect economic growth? The Review of Economics and Statistics 72: 686–91. [Google Scholar] [CrossRef]
- Nuzzo, Regina. 2014. Statistical errors. Nature 506: 150–52. [Google Scholar] [CrossRef] [PubMed]
- Paolella, Marc S. 2018. Fundamental Statistical Inference: A Computational Approach. Hoboken: John Wiley & Sons, vol. 216. [Google Scholar]
- Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. New York: Basic Books. [Google Scholar]
- Petersen, Mitchell A. 2009. Estimating standard errors in finance panel data sets: Comparing approaches. The Review of Financial Studies 22: 435–80. [Google Scholar] [CrossRef]
- Poulson, Barry W., and Jules Gordon Kaplan. 2008. State Income Taxes and Economic Growth. Cato Journal 28: 53–71. [Google Scholar]
- Reed, W. Robert. 2008. The robust relationship between taxes and US state income growth. National Tax Journal 61: 57–80. [Google Scholar] [CrossRef]
- Rossouw, Jacques E., Garnet L. Anderson, Ross L. Prentice, Andrea Z. LaCroix, Charles Kooperberg, Marcia L. Stefanick, Rebecca D. Jackson, Shirley A. A. Beresford, Barbara V. Howard, Karen C. Johnson, and et al. 2002. Risks and benefits of estrogen plus progestin in healthy postmenopausal women: Principal results from the Women’s Health Initiative randomized controlled trial. JAMA 288: 321–33. [Google Scholar]
- Russell, Davidson, and James G. MacKinnon. 2004. Econometric Theory and Methods. New York: Oxford University Press. [Google Scholar]
- Sims, Christopher A. 2010. But economics is not an experimental science. Journal of Economic Perspectives 24: 59–68. [Google Scholar] [CrossRef]
- Startz, Richard. 2014. Choosing the More Likely Hypothesis. Foundations and Trends in Econometrics 7: 119–89. [Google Scholar] [CrossRef]
- Stock, Wendy A. 2017. Trends in economics and other undergraduate majors. American Economic Review 107: 644–49. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2018. Introduction to Econometrics, 4th ed. London: Pearson. [Google Scholar]
- Stone, Daniel F. 2012. Measurement error and the hot hand. The American Statistician 66: 61–66. [Google Scholar] [CrossRef][Green Version]
- Studenmund, A. H. 2010. Using Econometrics: A Practical Guide. London: Pearson Education. [Google Scholar]
- Thaler, Richard H., and Cass R. Sunstein. 2009. Nudge: Improving Decisions about Health, Wealth, and Happiness. New York: Penguin. [Google Scholar]
- Wasserstein, Ronald L., and Nicole A. Lazar. 2016. The ASA statement on p-values: Context, process, and purpose. The American Statistician 70: 129–33. [Google Scholar] [CrossRef]
- Wasserstein, Ronald L., Allen L. Schirm, and Nicole A. Lazar. 2019. Moving to a world beyond “p <0.05”. The American Statistician 73: 1–19. [Google Scholar]
- Wasylenko, Michael, and Therese McGuire. 1985. Jobs and taxes: The effect of business climate on states’ employment growth rates. National Tax Journal 38: 497–511. [Google Scholar]
- Wooldridge, Jeffrey M. 2012. Econometric Analysis of Cross Section and Panel Data. Cambridge: MIT Press. [Google Scholar]
- Wooldridge, Jeffrey M. 2015. Introductory Econometrics: A Modern Approach. Toronto: Nelson Education. [Google Scholar]
- Yeoh, Melissa, and Dean Stansel. 2013. Is Public Expenditure Productive: Evidence from the Manufacturing Sector in US Cities, 1880–1920. Cato Journal 33: 1. [Google Scholar]
| 1 | See https://www.youtube.com/watch?v=BNHjX_08FE0. One extra 3-pointer he made came after a referee whistle, so he was actually (but not officially) 10 of 10. This performance harkens back to a game in which Boston Celtic Larry Bird hit every low-probability shot he put up, as he racked up 60 points against the Atlanta Hawks in 1985—https://www.youtube.com/watch?v=yX61Aurz3VM. (The best part of the video is the reaction by the Hawks’ bench to some of Bird’s last shots—those opponents knew Bird had the “hot hand”). |
| 2 | The new source of bias on improper reference groups is available under the “eResources” tab at https://www.routledge.com/Regression-Analysis-A-Practical-Introduction-1st-Edition/Arkes/p/book/9781138541405 or at https://tinyurl.com/yytmnq65. |
| 3 | |
| 4 |

| Goldberger and Goldberger (1991) | Hayashi (2000) | Russell and MacKinnon (2004) | Angrist and Pischke (2009) | Greene (2012) | Wooldridge (2012) | |
|---|---|---|---|---|---|---|
| Causes of bias in the standard errors | ||||||
| Heteroskedasticity | 0 | 10 | 11 | 2 | 2 | 8 |
| Multicollinearity | 7 | 0 | 1 | 0 | 2 | 0 |
| Causes of bias in the coefficient estimates | ||||||
| Simultaneity | 6 | 3 | 13 | 0 | 22 | 32 |
| Omitted-variables bias | 1 | 1 | 0 | 4 | 1 | 1 |
| Measurement error | 0 | 3 | 2 | 1 | 2 | 6 |
| Mediating factors | 0 | 0 | 0 | 4 | 0 | 0 |
| Other important topics | ||||||
| Holding other factors constant | 0 | 1 | 0 | 0 | 0 | 0 |
| Fixed effects | 0 | 23 | 5 | 12 | 12 | 9 |
| Bayesian critique of p-values | 0 | 0 | 0 | 0 | 0 | 0 |
| Correctly indicates an insignificant coef. estimate does not mean accept the null | No | No | Yes | N/A | No | N/A |
| Kennedy (2008) | Gujarati and Porter (2009) | Studenmund (2010) | Baltagi (2011) | Wooldridge (2015) | Angrist and Pischke (2015) | Dougherty (2016) | Stock and Watson (2018) | |
|---|---|---|---|---|---|---|---|---|
| Causes of bias in the standard errors | ||||||||
| Heteroskedasticity | 5 | 47 | 1 | 12 | 28 | 1 | 17 | 5 |
| Multicollinearity | 10 | 31 | 28 | 3 | 5 | 0 | 9 | 3 |
| Causes of bias in the coefficient estimates | ||||||||
| Simultaneity | 18 | 32 | 27 | 24 | 20 | 0 | 4 | 4 |
| Omitted-variables bias | 2 | 6 | 8 | 0 | 5 | 13 | 9 | 9 |
| Measurement error | 7 | 5 | 4 | 1 | 7 | 9 | 7 | 3 |
| Mediating factors | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 |
| Other important topics | ||||||||
| Holding other factors constant | 2 | 5 | 5 | 2 | 9 | 11 | 2 | 1 |
| Fixed effects | 6 | 15 | 0 | 3 | 8 | 0 | 6 | 12 |
| Bayesian critique of p-values | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Correctly indicates an insignificant coef. estimate does not mean accept the null | N/A | Yes | Yes (in a footnote) | N/A | Yes | N/A | Yes | N/A |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arkes, J. Teaching Graduate (and Undergraduate) Econometrics: Some Sensible Shifts to Improve Efficiency, Effectiveness, and Usefulness. Econometrics 2020, 8, 36. https://doi.org/10.3390/econometrics8030036
Arkes J. Teaching Graduate (and Undergraduate) Econometrics: Some Sensible Shifts to Improve Efficiency, Effectiveness, and Usefulness. Econometrics. 2020; 8(3):36. https://doi.org/10.3390/econometrics8030036
Chicago/Turabian StyleArkes, Jeremy. 2020. "Teaching Graduate (and Undergraduate) Econometrics: Some Sensible Shifts to Improve Efficiency, Effectiveness, and Usefulness" Econometrics 8, no. 3: 36. https://doi.org/10.3390/econometrics8030036
APA StyleArkes, J. (2020). Teaching Graduate (and Undergraduate) Econometrics: Some Sensible Shifts to Improve Efficiency, Effectiveness, and Usefulness. Econometrics, 8(3), 36. https://doi.org/10.3390/econometrics8030036




