1. Introduction
We investigate econometrically whether collective agreements in the manufacturing sector have defined norms for wage adjustments in the other sectors of the Norwegian economy over the period 1980(1)–2014(4). By linking the evolution of the wage cost level to economic fundamentals (e.g., business sector profitability and productivity), wage norms can give a sustainable national wage path. Wage pattern bargaining can also stabilize wage relativities at the industry level. The econometric model include both the short-run and long-term relationships of the national wage system. We therefore use the integrated and cointegrated VAR (CVAR) framework to which Johansen and Juselius have contributed significantly, see
Johansen and Juselius (
1990);
Johansen (
1995b);
Juselius (
2007).
There are several milestones in the history of economic research that give econometric treatment to wage formation, see
Forder (
2014, chp. 1–4) and
Bårdsen et al. (
2005, chp. 3–4). A new epoch in the econometric modelling of wages commenced with the development of the theory of cointegration,
Engle and Granger (
1987);
Johansen (
1988). “Error-correction” mechanisms in dynamic models of wage and price setting, which had been used by Denis Sargan in several important applied papers that accompanied his seminal methodological contribution (e.g.,
Sargan (
1964);
Sargan (
1980)), could now be recognized as having a clear foundation in cointegration methodology. Economic models could also be formulated that incorporated both deterministic drift and stochastic trends in wage formation,
Nymoen (
1989a). The new econometrics of wage modelling also clarified how restrictive the Phillips curve models had been by imposing untested unit root restrictions that forced a particular natural rate of unemployment dynamics on the system of wage and price setting, see
Bårdsen and Nymoen (
2003);
Kolsrud and Nymoen (
2014) and
Kolsrud and Nymoen (
2015).
One advantage of the VAR (CVAR) approach is that we can test hypotheses of absence of cointegration between wages in different industries without assuming anything about the bargaining pattern from the outset. Conditional on cointegration, we can develop empirical models of wage adjustments relevant for testing specific bargaining patterns. For example, we can investigate whether a stochastic trend in the manufacturing wage level is transmitted to the private service sector, which we would expect if the two sectors act as wage leader and wage follower.
CVARs have previously been used to estimate wage leadership models (
Lindquist and Vilhelmsson (
2006) (Sweden);
Lamo et al. (
2012);
Camarero et al. (
2014) (multiple countries)). Unlike these studies, we include the foreign sector, which is important for representing an imported nominal stochastic trend in the econometric model, and to test whether the importance of this trend may have changed. We also show that the simultaneous equations model (SEM) can be useful for modelling the structure of wage pattern bargaining.
Nymoen (
1991) specified a SEM for Norwegian wages and prices with two sectors, which was estimated by full information maximum likelihood (FIML), but without any formal analysis of cointegration rank.
Historically, the wage leader model was one of several initiatives to curb inflation in the post-war period, in a situation with full employment and with a commitment to free collective bargaining,
Aukrust (
1977);
Meade (
1982);
Forder (
2014) among others. Similar systems were developed in Sweden
Edgren et al. (
1969); France
Courbis (
1974) and the Netherlands
Driehuis and de Wolff (
1976). A key point was that in the export and import competing sectors of the economy, considerations about the required return to capital served as an automatic stabilizer of nominal wage cost growth. Over time, it was one of the corrective mechanisms that would make the wage cost level fluctuate around a growth path determined by product price and average labour productivity, which defined the scope for sustainable compensation to wage earners. The sheltered sectors, without foreign competition, could compensate for increased wages (increased production costs) by adjusting prices. In Norway, the manufacturing sector was given the role of wage leader, and if the followers were loyal to the system, they would, on average, get the value of a much higher productivity growth than if they broke out of the system. The manufacturing sector also signs the leading collective agreements in several other European countries, see
Knell and Stiglbauer (
2009).
However, in a recent theoretical contribution,
Calmfors and Seim (
2013) challenge the conventional wisdom that such pattern bargaining produces wage restraint. They show theoretically that wage restraint depends on the monetary policy regime and the size of the leading sector. This serves as a reminder that wage bargaining has a clear institutional dimension, and that institutions change over time, cf.
Soskice (
1990);
Camarero et al. (
2016). The possibility of a connection between monetary policy regimes and the system of wage and price setting has also been analysed by
Cukierman and Lippi (
1999);
Iversen (
1999);
Soskice and Iversen (
2000) and
Holden (
2005), among others.
The system of pattern wage bargaining represents an advanced product of civilization. Disruption of such institutions can occur due to changes elsewhere in the economy, or in the wider society. Hence we look for signs of structural breaks. Two important events stand out in the period covered by our data set: a change in monetary policy, and a historic increase in labour immigration. One-third of the sample used represents the era after inflation targeting was introduced in 2001, and about one quarter of the sample is from the period of high labour immigration due to EU enlargement. Hence, if the monetary policy regime change or the new immigration flow, or both, have affected wage formation with any force, the structural break should be detectable empirically.
The paper is organized as follows: In
Section 2, the main theoretical model equations are specified, together with the hypotheses that we aim to test empirically. In
Section 3, the data set is presented and the VAR that we use for the econometric analysis is formulated. The common ground of the pattern wage bargaining tests is provided by the cointegration analysis, and is presented in
Section 4. Our estimation results for the pattern wage bargaining parameters are presented in
Section 5. Our results indicate that the Norwegian wage model has preserved its main leader-follower relationships also in the period of inflation targeting, while the rise in immigration appears to have reduced the wage target that the wage setters tends to compromise. Our conclusions are also summarized in
Section 6, together with a short discussion.
2. Wage Pattern Relationship
In practice, national wage setting takes place in mixed system, made up of collective agreements, individual contracts and where legislative measures (e.g., minimum wages) have a role to play. The Norwegian system is no exception, but is it also custom to regard it as relatively more regulated by voluntary collective agreements than is seen in most other industrial economies,
Evju (
2014) and
Nymoen (
2017).
The results of collective bargaining typically represent compromises about annual wage adjustments that balance the concerns about required profitability with fairness in the workers’ share of the industry’s added value. A wage path that has a common trend with the value of average labour productivity, often referred to as wage scope (or ability to pay), is then implied. Another term for this kind of relationship is rent-sharing in wage formation.
In the following, we focus on three sectors: manufacturing (labelled sector 1), the private service industry (sector 2), and the public sector (i.e., government administration, labelled sector 3).
2.1. Manufacturing Sector
We model wage, price and productivity in natural logarithms. We let denote the wage (per man hour), denotes the producer price index (in domestic currency) and denotes labour productivity in fixed prices.
We also measure the national unemployment rate in log scale, and denote it by . However, to represent the potential impact of EU labour market integration on manufacturing sector wages we also include the variable representing the immigration as a percent of the working population. This variable has not been log-transformed.
In terms of these variables, a long-run wage equation for manufacturing can be written as:
see e.g.,
Nickell and Andrews (
1983),
Hoel and Nymoen (
1988),
Forslund et al. (
2008) among others.
is an unobservable error-term. A typical feature of the data set is that there are dominating positive trends in
and
.
For clarity we assume that
and
are random walks with drifts:
where
and
are taken to be two Gaussian processes, for the sake of simplicity. (
2) and (
3) imply that
and
are integrated of order 1, denoted
. Below, we assume that also
and
are
.
Given these assumptions,
can logically be either
or
. Earlier empirical models of manufacturing wage formation, some of them using data going back to the 1960s, have provided supportive evidence of cointegration, i.e.,
, see e.g.,
Nymoen (
1989a),
Johansen (
1995a),
Nymoen and Rødseth (
2003). However, none of these studies included the labour immigration variable,
, since the data sets used in these papers ended before EU labour marked enlargement took place.
Equation (
1) has interesting implications for wage coordination and pattern wage bargaining. First, since the relationship only involves trending variables from inside the manufacturing sector (i.e.,
and
), it gives a sustainable wage evolution for manufacturing. For wage coordination in particular, the exclusion of wages in the other sectors of the economy is important, as otherwise relative wage effects could damage the profitability and investments in the manufacturing sector, and lack of coordination could lead to wage–wage spirals in the economy.
Second, in the case of cointegration (
1) implies that
is an equilibrium correction variable which should logically predict
. Third, for manufacturing to act as a wage-leader, the equilibrium correction variable
should also predict
and
. The predictive power of
can be tested in for example a cointegrated VAR (CVAR), or in a simultaneous equation model (SEM). In the CVAR, with
as left hand side variables, it implies that the loading coefficients of
should be non-zero in each of the three rows. In the identified SEM framework we use below, the implication is that
should have a non-non zero coefficient in the
equation, and that
should have non zero coefficients in the equations of
and
.
2.2. Private Service Sector and Public Sector
Potential long-run relationships for the private service sector wage,
, and the government sector wage,
are:
Conversely, if we find empirically that , are , this particular wage pattern does not hold in the data.
In a clear cut pattern wage bargaining model, with manufacturing in the role as the wage leader, the equilibrium correction variable should predict and , but not . Likewise, should predict , but not and . In a SEM framework, the implication is that the matrix of contemporaneous coefficients is (lower) diagonal. Subject to (exact) identification assumptions, stated below, these restrictions are testable.
Patterns that are less “clean” than this can also be interpreted as consistent with broad sense wage leader–followership coordination. For example, instead of (5), may cointegrate directly with . Additionally, in the SEM formulation we can allow a not completely diagonal matrix, for example the coefficient of in the equation may be non-zero (allowing wage-wage effects between the two sectors), without compromising the wage-leadership of the manufacturing sector.
2.3. Wage–Price Inflation
Although the focus of our investigation is the pattern of wage adjustments, it cannot be seen as completely separate from development of consumer prices. In real world wage settlements, demands for wage growth to compensate cost-of-living increases are always on the negotiating table. Since CPI inflation, in turn, depends on growth in wage costs, it is probably unrealistic to have a model of , , and which is recursive. In the short run, nominal wage adjustment also in the wage-leading manufacturing sector is very likely to depend on changes in CPI. For this reason, we attempt to include a model of the logarithm of CPI, and its change (i.e., inflation) in our multiple equation system.
Norway is a small open economy and this also affects CPI inflation. Therefore, an import price index,
in log form, is included in the data set. Since import prices are in domestic currency, the inclusion of
represents a second channel through which the market for foreign exchange can influence wage-price inflation in our framework, the first being through the wage scope variable. The empirical relevance of this kind of “imported inflation”, together with domestic wage adjustments, has been demonstrated in earlier studies, see e.g.,
Bårdsen et al. (
2005, chp. 8)).
More recently,
Choo and Kurita (
2015) using multivariate cointegration analysis, found that disequilibrium in the money marked have contributed to inflation impetus in Norway. Hence, while it is beyond the scope of this paper, a more consolidated empirical assessment of the different dimensions of inflation dynamics is an interesting topic for further research.
3. Data Set and VAR Formulation
We use time series for three wage rates, as well as price and productivity indices. As mentioned, it is conceivable that targets for wage shares and relative wages shift when the labour market fundamentals change. We include the labour immigration rate and the official unemployment rate as indicators of such structural determinants. The definitions of the variables included in the investigation are
1:
: index for hourly wage in sector i = 1, 2, 3.
: consumer price index.
: price deflator of gross value added, manufacturing industry.
: labour productivity, output per hour in manufacturing.
: price deflator of imports of goods and services.
: unemployment rate, in per cent, civilian unemployment.
: immigration from EU/EFTA countries, North America, Australia and New Zealand and non-EU Eastern Europe, in per cent of the population aged 15–74.
As mentioned above, lower case letters refer to the logarithm of the original variables. For example, denotes the log of the unemployment rate. Variables in first differences are denoted by . Subscripts denote time period. For example, refers to the log of the price level four periods back.
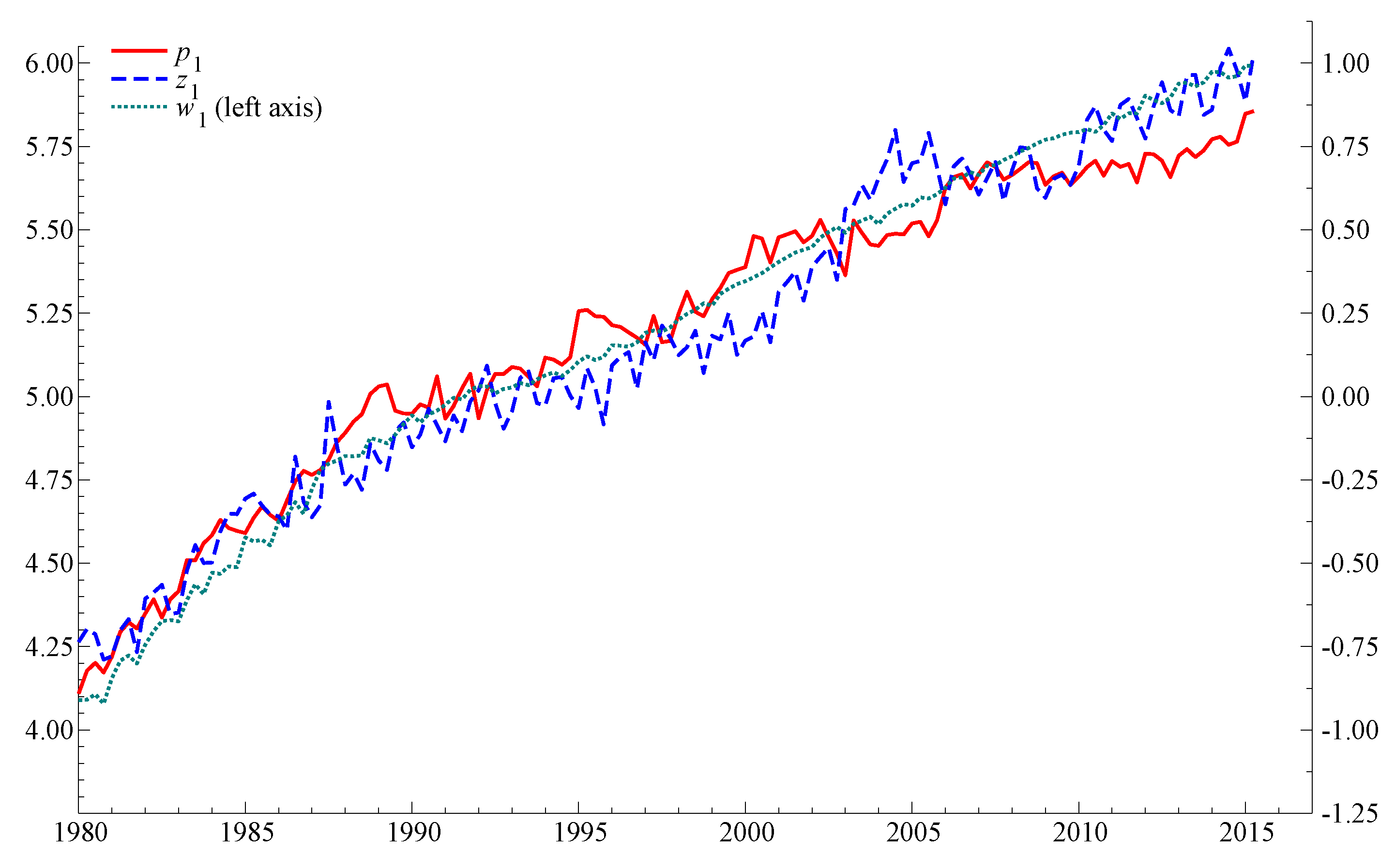
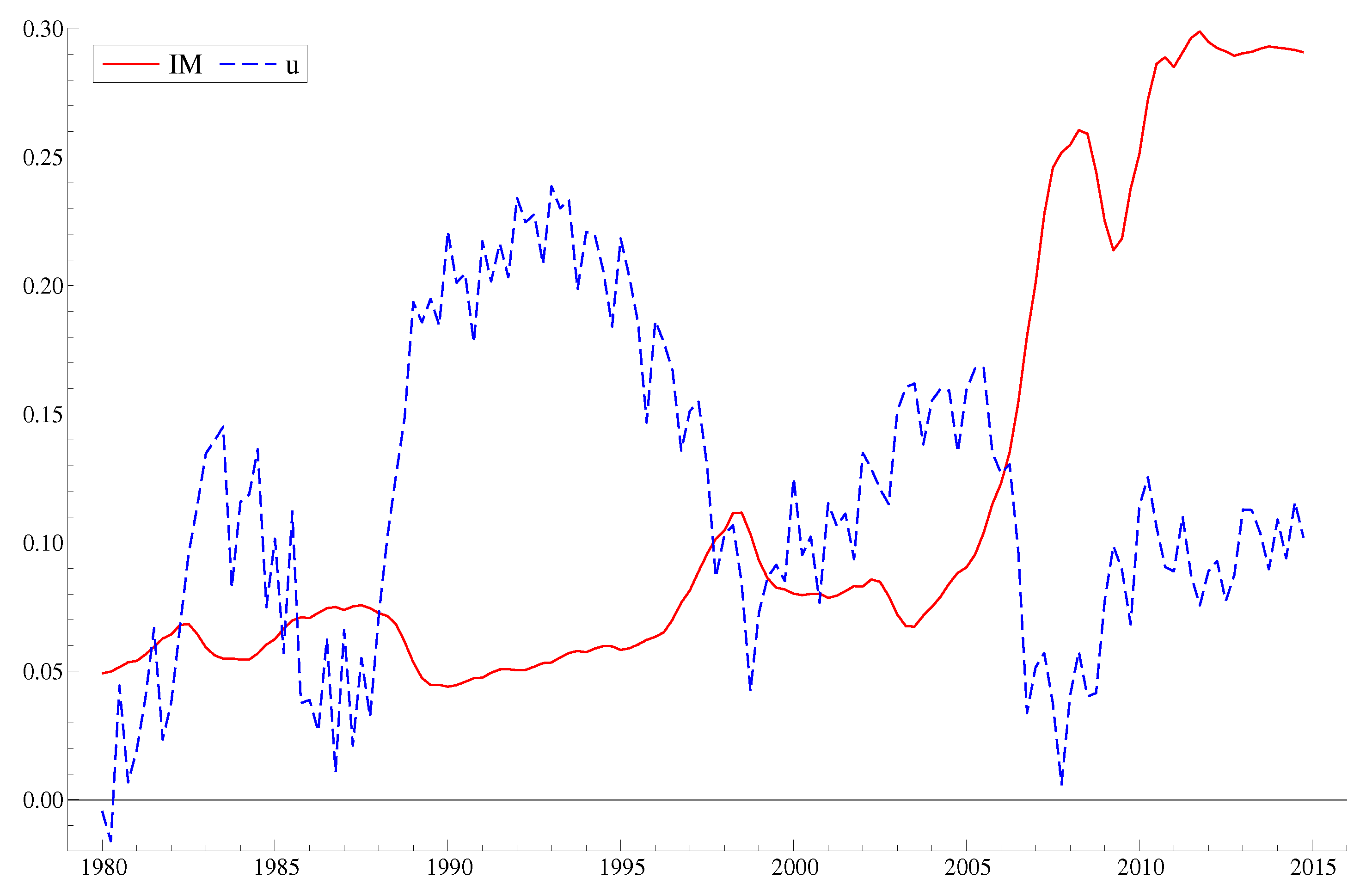
Figure 1 shows the time series for manufacturing wage, value added price index and productivity. It is clearly possible to imagine that these series can contain both unit-root trends and deterministic trends, possibly with breaks. As noted above, in this paper we attempt to model them as
trends with unrestricted drift terms. When testing for cointegration we allow for deterministic trends and for regime shifts in the form of step-dummies. The time plots of the other two key variable,
and
are shown in
Figure 2.
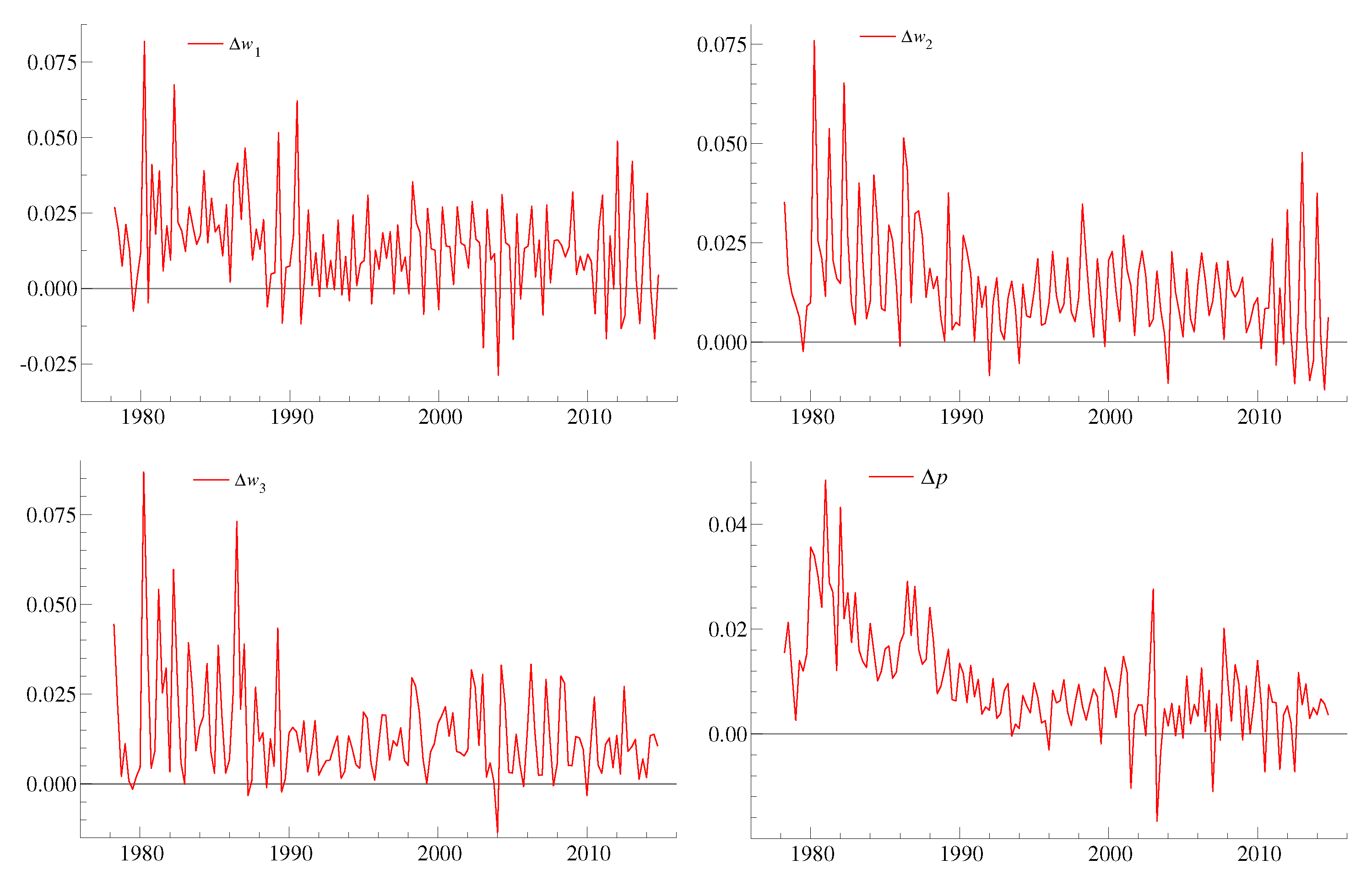
We aim to model wage per man hour in three sectors and the domestic price level. The first differences of the four variables are shown in
Figure 3. The empirical mean of CPI inflation was higher during the 1990s and later. The same evolution is seen in the wage change data, although less markedly, and more clearly for
and
than for
. All four series are characterized by short-run oscillations (negative autocorrelation), mainly due to seasonality. However, the short-run variation is not constant. The CPI-inflation graph indicates heteroscedasticity: compared to the 1980s, the variance of inflation went down became reduced during the 1990s before increasing again early in the new millennium. Heteroscedasticity is also detectable for wage changes. The wage growth variances were lower during the 1990s than either before or since. Indeed, a four-quarter moving average of the four variables would remove seasonality and would probably indicate that they are not
, suggesting an
model for further research.
2The vector of modelled log-level variables is denoted by
. We write the VAR as:
where all variables in the cointegration space are included in the extended data vector
.
In , we have introduced as notation for the wage scope variable, i.e., . The appearance of the import price index () is a consequence of the decision to model the CPI level as well as wages. As already noted, and are also treated as I(1).
in
denotes a vector of components that affect the level of
. In the unrestricted case it includes a constant, a trend and two dummies for regimes:
is an incomes policy dummy which is one from 1988q1 to 2002q4, and zero elsewhere, see
Bowitz and Cappelen (
2001) and
Nymoen (
2017).
represents the international financial crisis, and is one in the sub-sample 2009q1-2014q1, and zero elsewhere. We added the two variables into the cointegration relations (i.e., added them to the set of so called restricted variables). We considered using a third dummy, for the monetary policy regime shift in 2001q2, but we found little in support for its inclusion in the model. This decision seems to be validated by the results of the robustness tests mentioned in
Section 5.
represents differences of the variables in , as well as centered seasonal dummies and impulse indicators for outliers, notably for 1986q3 (industrial conflict and devaluation) and the first quarters of 2011–2014 (breaks in National accounts).
4. Cointegration Analysis
The focus in the cointegration analysis is the matrix with dimension . Let r denote the rank of . Since , u, , and are non-modelled variables, r can be 0, 1, 2, 3 or 4. corresponds to no cointegration, which would imply rejection of the theory we formulated above. If, on the other hand, , the variables , , , , and represent five common trends in the three nominal wage rates and the price index. The theory of wage leadership points to the wage scope variable as one dominant trend in the system, and (“imported inflation”) as another.
can be written as , where is and () is the matrix with cointegration parameters. The wage system outlined above, with a long-run wage setting equation in manufacturing, and two normal wage relativities, is consistent with . A decision about may be interpreted as a potential long-run relationship between the consumer prices index and, for example, an import price index and domestic unit labour costs.
Regarding structural breaks, we adopt a broken trend interpretation with three regimes. This seems to be a reasonable model interpretation and representation of the two dummies
and
that were introduced above. This approach also allows ut to make use of the recent advance made by
Kurita and Nielsen (
2019) in the testing of cointegration rank in partial systems with deterministic terms.
The result of the trace tests for cointegration rank is given in
Table 2, together with
critical values that are due to the work of
Kurita and Nielsen (
2019, Table A1), who have provided code for simulation of the asymptotic distributions of the trace statistics for specifications such as ours.
3 The values of the trace test statistic are well above the corresponding critical values for test of zero and one cointegration relationships, which supports that the number of stationary long-run relationships may be assumed to be at least two. The third row shows that the hypothesis
fails to be rejected.
Multiple cointegration relationships are unidentified even after normalization on one endogenous variable in each equation. Identification is therefore relative to theory, which in our case is the system of long-run relationships in
Section 2. In
Table 3, an (over) identified long-run system is shown. For completeness, we have chosen to continue with
to investigate whether also the full set potential long-run relationships in our model can be estimated with economically meaningful results, even though the third and fourth relationship do not have the same formal test support as the first two.
4The second and third relationships exclude the wage scope variable
. In order to separate the second from the third relationship, we exclude
and
from the third, and
from the second relationship. The three identified wage relationships show a close correspondence with the theory of national wage regulation that we presented above. Finally, the fourth equation in
Table 3 represents a long-run price equation. As the last line in
Table 3 shows, the over-identifying restrictions cannot be rejected at the 11% level.
The coefficients of the wage relationships are also economically interpretable. In the manufacturing sector, the coefficient (
) with respect to unemployment is somewhat higher in absolute value than the estimates in
Nymoen (
1989b) and
Johansen (
1995a), for example, who used data from the 1980s. In private service the numerical significance of the estimated coefficient of
u is much smaller. In the public sector the estimated coefficient was so small that it was practical to set it to zero. However, in both sectors, the implied wage responsiveness to unemployment will be inherited from wage setting in manufacturing, through the equations of the system.
The two coefficients of the immigration rate () imply that increased labour supply has affected the nominal wage path negatively. Clearly, since the wave of European labour immigrants only arrived late in our sample, after 2005, these estimates must be interpreted with care, perhaps as a mere “first generation” of estimates of euro-area labour immigration effects on aggregate wages. Nevertheless they represent evidence that the system of wage formation has not been immune to EU labour market enlargement. According to the results, the rather large shift upward in has reduced the level of manufacturing sector wage level in particular.
The estimated CPI equation, the fourth line of the table, is interpretable as well. The coefficients of the wage and productivity variables are correctly signed, and the elasticities of wage and import price are realistic, see
Bårdsen et al. (
2003). The additional restriction of long-run price homogeneity of degree one changed the estimated coefficients of the wage relationships very little. However, that homogeneity restriction was rejected statistically, and therefore we did not impose it on the models we report below.
Conditional on the identified long-run relationships, we can test for the minimum restrictions that imply no feed-back from and to . The increase in the test of the over-identifying restrictions is small. Therefore it is not surprising that the three restrictions, , are statistically acceptable and the test for the over-identifying restrictions is (the incremental test yields ).
We now turn to the results of the SEM parameterization of the cointegrated VAR to investigate the short run properties of the wage-leader/follower model. The SEM represents a relevant framework for analysis of pattern bargaining. In particular, we can test the system of pattern wage bargaining without assuming a particular ordering from the outset.
5. Testing the Wage-Leading Hypothesis within a SEM
We can interpret the cointegrated VAR as the reduced form of the SEM:
hence the elements in the diagonal of the contemporaneous coefficient matrix
are equal to one.
is the vector which has as elements the equilibrium correction variables defined in accordance with (3):
The economic theory of wage pattern bargaining has nothing to say about the covariance matrix of SEM disturbances, call it . Hence, in order to be of empirical relevance, that theory must be shown to be identified (or not) for the case of unrestricted . In our study, exact identification of the SEM is therefore based on the specification that is diagonal. From that starting point, several specific hypotheses about wage leader/followeship are testable as overidentifying restrictions on . In the following we focus mainly on restriction on .
In
Table 4 we report the FIML estimates of
, and
, after imposing over-identifying restrictions on the
and
matrices. These restrictions aid the estimation of the focus parameters, and are statistically valid, as the test statistic of the over-identifying restrictions, denoted
at the bottom of the table, shows, cf.
Doornik and Hendry (
2018).
Table 4 shows that all the elements of the
matrix (in the last four columns) with estimated coefficients for the equilibrium correction terms are statistically significant. These estimates are consistent with the conclusions of the cointegration analysis in the previous section.
The estimates of the contemporaneous parameters in show a clear pattern: In the row for , the estimated coefficients of and are negative (“wrong sign”), but they are statistically insignificant. Conversely, has sizeable and significant coefficients in the rows for and , which supports the hypothesis that the manufacturing sector is wage-leading, with private service production and the public sector as wage-followers.
The column with estimated coefficients of
gives an indication of the contemporaneous compensation of cost-of-living increases in all three sectors. The estimates are statistically significant. In addition, all though not shown in the table, the wage equations contain significant lags of CPI inflation, in addition to
(see
Gjelsvik et al. (
2015) for details). In sum, the model confirms the role of cost of living consideration in wage formation.
The last row of
Table 4, with the results for the inflation equation
, shows that only
enters significantly and that increased wages increase prices. This implies that there are within-quarter effects of increased wage cost in private service production to consumer price inflation. In addition, since
includes the domestic wage level with a sizeable weight, the model is consistent with monopolistic price setting. Hence, through private service production and equilibrium correction, the consumer price index is influenced by both domestic wages and the price on imports in domestic currency.
Table 5 contains test statistics for the different pattern bargaining hypotheses that can be formulated as restrictions on the
matrix. The first two rows in
Table 5 test in various aspects whether sector 1 is wage leading the other two sectors. The first row shows three versions of the null hypothesis that manufacturing is not wage leading one or both of the two following sectors. Each test is statistically significant at the 1% level. In the second line of tests, the second entry supports the assumption that neither wages in the private service nor those in the public sector enter significantly into the identified SEM equation for the manufacturing wage (sector 1). Therefore, the first two rows of
Table 5 support the wage leadership of sector 1 in the pattern wage bargaining. The third row illustrates the relationship between sectors 2 and 3. The results show that there is a less clear-cut short-run relationship between wages in the private service sector and the public sector.
Table 6 shows the results of a restricted estimation where we have imposed wage-leadership on the contemporaneous matrix
discussed above. Compared to
Table 4, the remaining estimated coefficients therefore change only little.
As already noted there are several dummies in the model. However, none of them are closely related to change in monetary policy regime that took place in 2001(2), or to the impact that the EU labour market enlargement might have had on wage regulation.
When a step-dummy for the a monetary policy is added to the price equation, the t-value is
and therefore insignificant. However, inflation targeters anticipated that also wage formation would undergo a change after the new monetary policy regime was introduced, cf.
Norges Bank (
2002). We find no evidence of this kind of structural break in our investigation: the test of joint significance of the monetary policy change in the three wage equations became
with
p-value 0.58. None of the individual t-values were significant.
5 6. Conclusions
We formulated a theoretical model of nominal wage regulation in an open economy. The interpretation of the model as a mechanism of national wage coordination is simple enough: If the wage growth in the manufacturing sector leads the wage setting in the other sectors, the functional income distribution will be relatively stable both in the wage-leading and in the wage-following sectors. The wage relativities between sectors will also be stable.
The empirical testing of the theoretical wage regulation model involves several important steps: Decision of cointegration rank in a partial system, identification of multiple long-run relationships and specification of a dynamic econometric model that allows the testing of alternative hypotheses about the interactions between wage changes in the different sectors of the model. The empirical model must allow for the typical broad sense non-stationarity of the data.
The formal tests of cointegration rank allowed us to reject the hypothesis that there was no cointegration in the system, and gave formal support to two long-run relationships. Tests of over-identifying restriction on the long-run equations supported the interpretation of one of the relationships as a wage curve equation of the manufacturing sector, and of the other as a long-run relativity between the manufacturing wage level, and the wage level in rest of the business sector. In order to complete the model, we chose to include also two other potential long-run relationships. One between wages in the government sector wages and the private sector and another relationship that we identify as a long-run price level equation.
The main conclusion of the testing of alternative hypotheses about pattern wage bargaining within the empirical model, was that the manufacturing sector has operated as a wage leader, and with corresponding clear roles of construction, private service production and retail, and the government sector as wage followers. The relationships are however moderated by labour market indicators. First, we obtain coefficients of the rate of unemployment with expected signs. Second, the econometric results support the hypothesis that the long term wage level may have been reduced as a consequence of immigration made possible by EU labour market enlargement in 2004. However, care must be taken since our results may be affected by an composition effect, i.e., if immigrants have replaced natives in the lowest paid jobs, the average hourly wage may become lowered. Hence, our results are not conclusive evidence of reduced capacity of collective action as a result of increased labour immigration during the first 15 years of the 2000s. Hopefully, ongoing research where natives’ wages are modelled, will contribute towards clarification of this issue, cf.
Dapi et al. (
2019).
We find no indication that the new Norwegian monetary policy established in 2001 has changed the system of wage formation as we have modelled it. In the light of the evidence, the position taken by Norwegian inflation targeters, that an implied “over-determination” of the new regime would force a structural break in wage pattern bargaining, overstated how invasive the monetary policy change would become, cf.
Norges Bank (
2002). After all, the target of the new monetary policy was the inflation forecast, not inflation itself.