Frequency-Domain Evidence for Climate Change
Abstract
1. Introduction
Literature Review
2. Methods
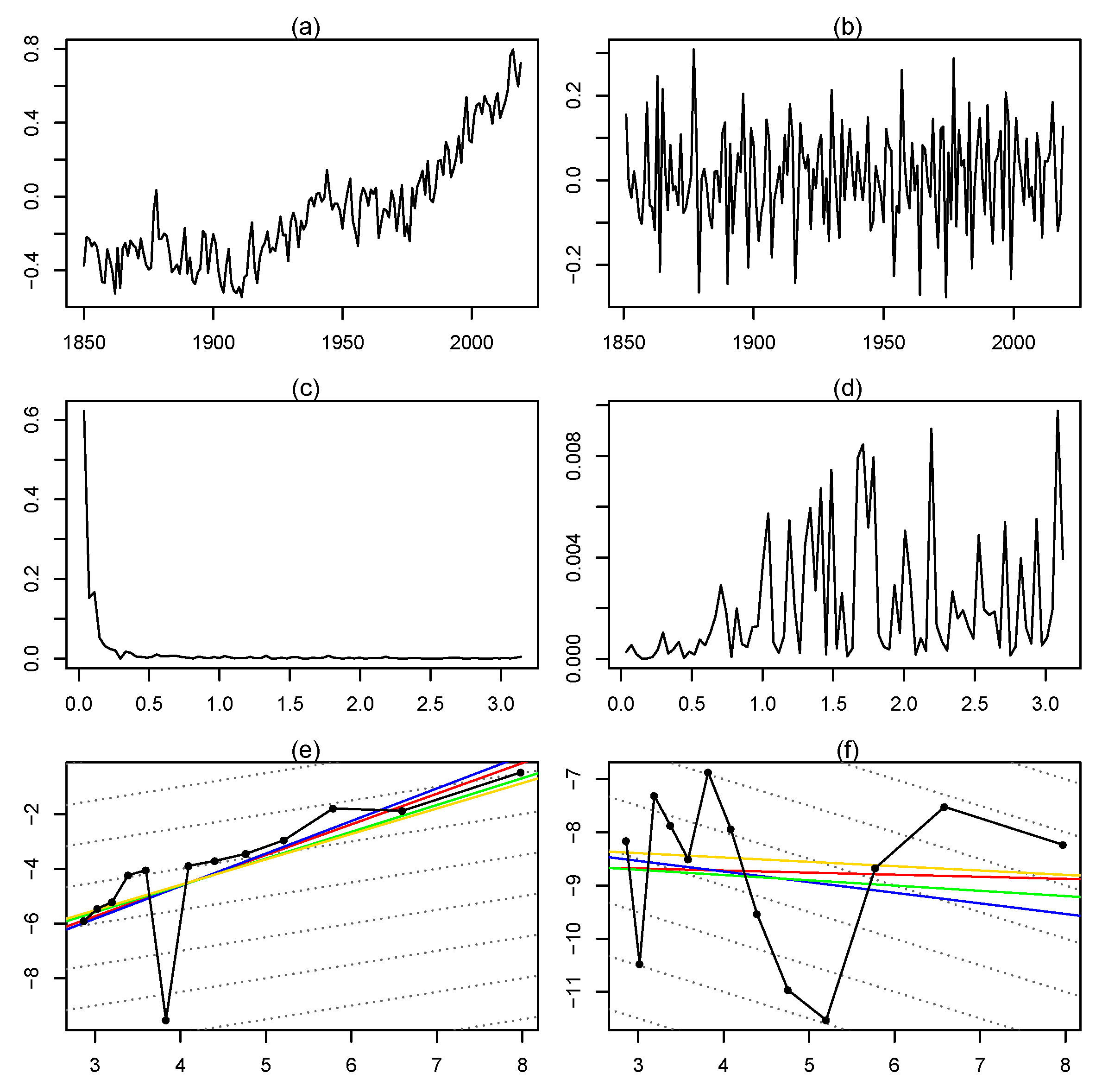
2.1. Estimation of the Memory Parameter
2.2. Testing
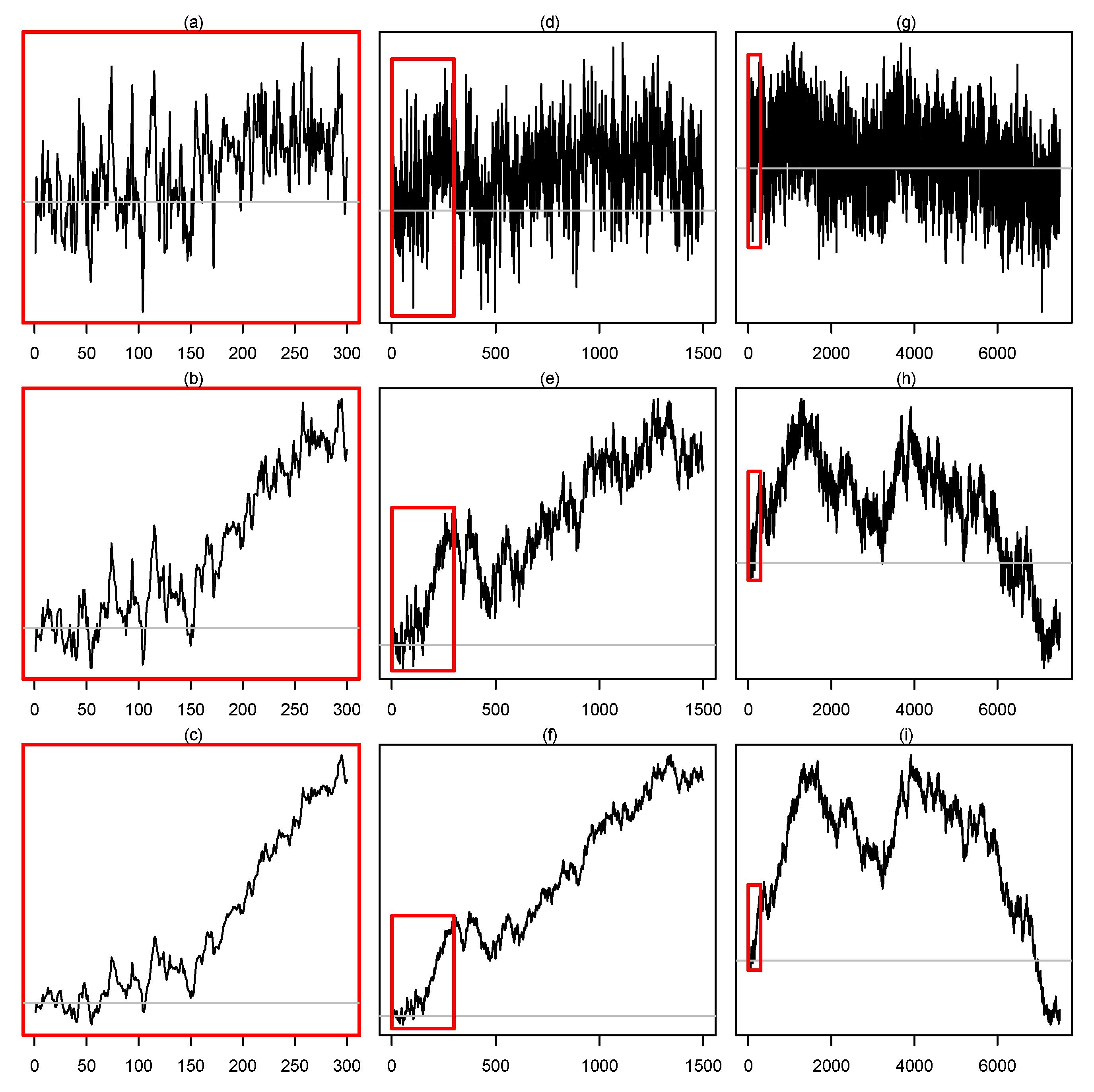
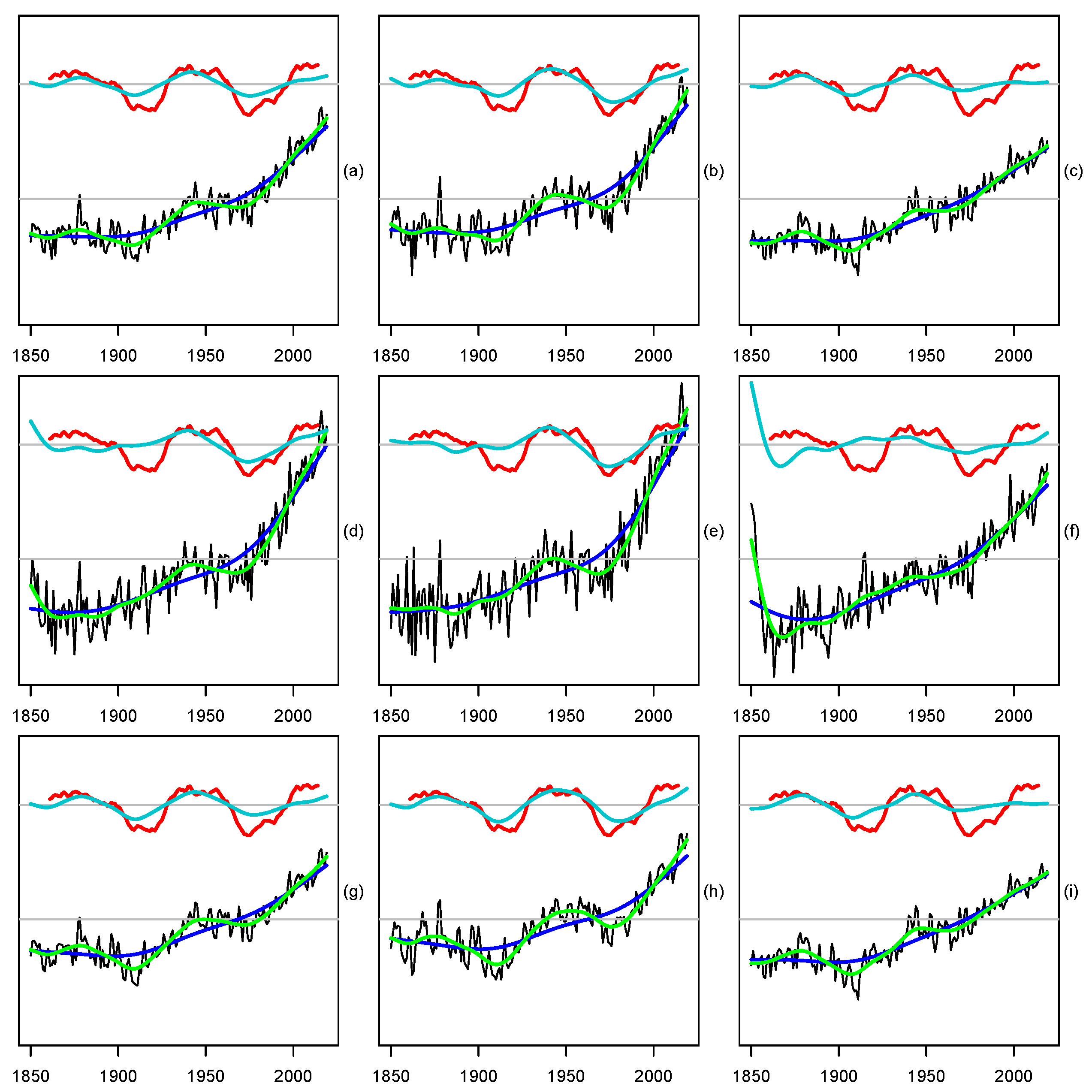
3. Empirical Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baiardi, Donatella, and Claudio Morana. 2020. Climate Change Awareness: Empirical Evidence for the European Union. University of Milan Bicocca Department of Economics, Management and Statistics Working Paper No. 426. January. Available online: https://ssrn.com/abstract=3513061 (accessed on 5 July 2020).
- Chang, Yoosoon, Robert K. Kaufmann, Chang Sik Kim, J. Isaac Miller, Joon Y. Park, and Sungkeun Park. 2020. Evaluating trends in time series of distributions: A spatial fingerprint of human effects on climate. Journal of Econometrics 214: 274–94. [Google Scholar] [CrossRef]
- Davidson, James E.H., David B. Stephenson, and Alemtsehai A. Turasie. 2016. Time series modeling of paleoclimate data. Environmetrics 27: 55–65. [Google Scholar] [CrossRef]
- Delworth, Thomas L., and Michael E. Mann. 2000. Observed and simulated multidecadal variability in the northern hemisphere. Climate Dynamics 16: 661–76. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica: Journal of the Econometric Society 49: 1057–72. [Google Scholar] [CrossRef]
- Estrada, Francisco, Luis Filipe Martins, and Pierre Perron. 2017. Characterizing and attributing the warming trend in sea and land surface temperatures. Atmósfera 30: 163–87. [Google Scholar] [CrossRef]
- Estrada, Francisco, and Pierre Perron. 2019. Breaks, trends and the attribution of climate change: A time-series analysis. Economía 42: 1–31. [Google Scholar] [CrossRef]
- Estrada, Francisco, Pierre Perron, and Benjamín Martínez-López. 2013. Statistically derived contributions of diverse human influences to twentieth-century temperature changes. Nature Geoscience 6: 1050–55. [Google Scholar] [CrossRef]
- Fomby, Thomas B., and Timothy J. Vogelsang. 2002. The application of size-robust trend statistics to global-warming temperature series. Journal of Climate 15: 117–23. [Google Scholar] [CrossRef]
- Gay-Garcia, Carlos, Francisco Estrada, and Armando Sánchez. 2009. Global and hemispheric temperatures revisited. Climatic Change 94: 333–49. [Google Scholar] [CrossRef]
- Geweke, John, and Susan Porter-Hudak. 1983. The estimation and application of long memory time series models. Journal of Time Series Analysis 4: 221–38. [Google Scholar] [CrossRef]
- Granger, Clive W.J., and Roselyne Joyeux. 1980. An introduction to long-memory time series models and fractional differencing. Journal of Time Series Analysis 1: 15–29. [Google Scholar] [CrossRef]
- Grenander, Ulf, and Murray Rosenblatt. 1957. Statistical Analysis of Stationary Time Series. New York: John Wiley and Sons. [Google Scholar]
- Harvey, David I., Stephen J. Leybourne, and A.M. Robert Taylor. 2013. Testing for unit roots in the possible presence of multiple trend breaks using minimum dickey–fuller statistics. Journal of Econometrics 177: 265–84. [Google Scholar] [CrossRef]
- Hassler, Uwe. 1993. Regression of spectral estimators with fractionally integrated time series. Journal of Time Series Analysis 14: 369–80. [Google Scholar] [CrossRef]
- Hosking, Jonathan R. M. 1981. Fractional differencing. Biometrika 68: 165–76. [Google Scholar] [CrossRef]
- Hurvich, Clifford M., Rohit Deo, and Julia Brodsky. 1998. The mean squared error of geweke and porter-hudak’s estimator of the memory parameter of a long-memory time series. Journal of Time Series Analysis 19: 19–46. [Google Scholar] [CrossRef]
- Jones, Philip. D., Dave H. Lister, Timothy J. Osborn, Colin Harpham, Melissa Salmon, and Colin P. Morice. 2012. Hemispheric and large-scale land-surface air temperature variations: An extensive revision and an update to 2010. Journal of Geophysical Research: Atmospheres 117. [Google Scholar] [CrossRef]
- Kaufmann, Robert K., Heikki Kauppi, and James H. Stock. 2006. Emissions, concentrations, & temperature: A time series analysis. Climatic Change 77: 249–78. [Google Scholar]
- Kaufmann, Robert K., Heikki Kauppi, and James H. Stock. 2010. Does temperature contain a stochastic trend? evaluating conflicting statistical results. Climatic Change 101: 395–405. [Google Scholar] [CrossRef]
- Kaufmann, Robert K., and David I. Stern. 2002. Cointegration analysis of hemispheric temperature relations. Journal of Geophysical Research: Atmospheres 107: ACL-8. [Google Scholar] [CrossRef]
- Kennedy, John J., Nick A. Rayner, Robert O. Smith, David E. Parker, and Michael Saunby. 2011. Reassessing biases and other uncertainties in sea surface temperature observations measured in situ since 1850: 2. Biases and homogenization. Journal of Geophysical Research: Atmospheres 116. [Google Scholar] [CrossRef]
- Künsch, Hans Rudolph. 1986. Discrimination between monotonic trends and long-range dependence. Journal of applied Probability 23: 1025–30. [Google Scholar] [CrossRef]
- Künsch, Hans Rudolph. 1987. Statistical aspects of self-similar processes. In Proceedings of the First World Congress of the Bernoulli Society. Tashkent: VNU Science Press, pp. 67–74. [Google Scholar]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Lai, Kon S., and Mann Yoon. 2018. Nonlinear trend stationarity in global and hemispheric temperatures. Applied Economics Letters 25: 15–18. [Google Scholar] [CrossRef]
- Lee, Tien Ming, Ezra M. Markowitz, Peter D. Howe, Chia-Ying Ko, and Anthony A. Leiserowitz. 2015. Predictors of public climate change awareness and risk perception around the world. Nature Climate Change 5: 1014–20. [Google Scholar] [CrossRef]
- Lenssen, Nathan J. L., Gavin A. Schmidt, James E. Hansen, Matthew J. Menne, Avraham Persin, Reto Ruedy, and Daniel Zyss. 2019. Improvements in the gistemp uncertainty model. Journal of Geophysical Research: Atmospheres 124: 6307–26. [Google Scholar] [CrossRef]
- Mangat, Manveer Kaur, and Erhard Reschenhofer. 2019. Testing for long-range dependence in financial time series. Central European Journal of Economic Modelling and Econometrics (CEJEME) 11: 93–106. [Google Scholar]
- Mills, Terence C. 2012. Semi-parametric modelling of temperature records. Journal of Applied Statistics 39: 361–83. [Google Scholar] [CrossRef]
- Morana, Claudio, and Giacomo Sbrana. 2019. Climate change implications for the catastrophe bonds market: An empirical analysis. Economic Modelling 81: 274–94. [Google Scholar] [CrossRef]
- Morice, Colin P., John J. Kennedy, Nick A. Rayner, and Phil D. Jones. 2012. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The hadcrut4 data set. Journal of Geophysical Research: Atmospheres 117. [Google Scholar] [CrossRef]
- Ng, Serena, and Pierre Perron. 2001. Lag length selection and the construction of unit root tests with good size and power. Econometrica 69: 1519–54. [Google Scholar] [CrossRef]
- Peiris, M. Shelton, and J. R. Court. 1993. A note on the estimation of degree of differencing in long memory time series analysis. Probability and Mathematical Statistics 14: 223–229. [Google Scholar]
- Perron, Pierre, and Zhongjun Qu. 2007. A simple modification to improve the finite sample properties of ng and perron’s unit root tests. Economics Letters 94: 12–19. [Google Scholar] [CrossRef]
- Perron, Pierre, and Gabriel Rodríguez. 2003. Gls detrending, efficient unit root tests and structural change. Journal of Econometrics 115: 1–27. [Google Scholar] [CrossRef]
- Perron, Pierre, and Tomoyoshi Yabu. 2009. Testing for shifts in trend with an integrated or stationary noise component. Journal of Business & Economic Statistics 27: 369–96. [Google Scholar]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Poortinga, Wouter, Stephen Fisher, Gisela Bohm, Linda Steg, Lorraine Whitmarsh, and Charles Ogunbode. 2018. European Attitudes to Climate Change and Energy: Topline Results from Round 8 of the European Social Survey. ESS Topline Results Series; London: University of London. [Google Scholar]
- Pötscher, Benedikt M. 2002. Lower risk bounds and properties of confidence sets for ill-posed estimation problems with applications to spectral density and persistence estimation, unit roots, and estimation of long memory parameters. Econometrica 70: 1035–65. [Google Scholar] [CrossRef]
- Pretis, Felix. 2020. Econometric modelling of climate systems: The equivalence of energy balance models and cointegrated vector autoregressions. Journal of Econometrics 214: 256–73. [Google Scholar] [CrossRef]
- Reisen, Valderio A. 1994. Estimation of the fractional difference parameter in the arima (p, d, q) model using the smoothed periodogram. Journal of Time Series Analysis 15: 335–50. [Google Scholar] [CrossRef]
- Reschenhofer, Erhard. 2013. Robust testing for stationarity of global surface temperature. Journal of Applied Statistics 40: 1349–61. [Google Scholar] [CrossRef]
- Reschenhofer, Erhard, and Manveer Kaur Mangat. 2020. Detecting long-range dependence with truncated ratios of periodogram ordinates. Communications in Statistics—Theory and Methods, 1–16. [Google Scholar] [CrossRef]
- Reschenhofer, Erhard, Manveer Kaur Mangat, and Thomas Stark. 2020. Improved estimation of the memory parameter. Theoretical Economics Letters 10: 47–68. [Google Scholar] [CrossRef]
- Robinson, Peter M. 1995. Gaussian semiparametric estimation of long range dependence. The Annals of Statistics 23: 1630–61. [Google Scholar] [CrossRef]
- Schmidt, Peter, and Peter C. B. Phillips. 1992. Lm tests for a unit root in the presence of deterministic trends. Oxford Bulletin of Economics and Statistics 54: 257–87. [Google Scholar] [CrossRef]
- Stern, David I., and Robert K. Kaufmann. 1999. Econometric analysis of global climate change. Environmental Modelling & Software 14: 597–605. [Google Scholar]
- Vogelsang, Timothy J. 1998. Trend function hypothesis testing in the presence of serial correlation. Econometrica 66: 123–48. [Google Scholar] [CrossRef]

| K | ||||||
|---|---|---|---|---|---|---|
| 6 | 0.90 | 0.95 | 1.14 | 0.94 | 0.90 | 0.93 |
| 7 | 0.90 | 0.94 | 1.15 | 0.97 | 0.90 | 0.92 |
| 8 | 1.48 | 1.98 | 1.11 | 0.97 | 1.06 | 1.16 |
| 9 | 1.30 | 1.57 | 1.10 | 0.97 | 0.96 | 0.90 |
| 10 | 1.17 | 1.32 | 1.04 | 0.95 | 0.91 | 0.87 |
| 11 | 1.14 | 1.25 | 1.01 | 0.94 | 0.94 | 0.92 |
| 12 | 1.12 | 1.20 | 0.98 | 0.93 | 0.97 | 0.96 |
| 13 | 1.12 | 1.19 | 0.98 | 0.93 | 1.00 | 1.00 |
| 14 | 1.10 | 1.16 | 0.96 | 0.91 | 1.02 | 1.03 |
| 15 | 1.02 | 1.04 | 0.93 | 0.90 | 0.93 | 0.86 |
| K | Global | Excl. 3rd | NH | SH | NH (GISS) | AMO-detr. (HP) | |
|---|---|---|---|---|---|---|---|
| 0.4 | 8 | 0.446 ** | 0.486 ** | 0.444 ** | 0.444 ** | 0.46 ** | 0.444 ** |
| 10 | 0.437 ** | 0.447 ** | 0.447 ** | 0.42 ** | 0.46 ** | 0.447 ** | |
| 12 | 0.456 *** | 0.448 ** | 0.473 *** | 0.427 ** | 0.418 ** | 0.473 *** | |
| 14 | 0.468 *** | 0.459 *** | 0.475 *** | 0.444 *** | 0.412 *** | 0.475 *** | |
| 0.49 | 8 | 0.404 * | 0.425 * | 0.405 * | 0.398 * | 0.407 * | 0.405 * |
| 10 | 0.382 * | 0.375 * | 0.397 ** | 0.358 * | 0.403 ** | 0.397 ** | |
| 12 | 0.396 ** | 0.376 ** | 0.42 ** | 0.36 ** | 0.353 ** | 0.42 ** | |
| 14 | 0.41 *** | 0.387 ** | 0.418 *** | 0.375 ** | 0.345 ** | 0.418 *** | |
| 0.5 | 8 | 0.399 * | 0.418 * | 0.4 * | 0.393 * | 0.401 * | 0.4 * |
| 10 | 0.376 * | 0.367 * | 0.391 ** | 0.351 * | 0.397 ** | 0.391 ** | |
| 12 | 0.39 ** | 0.369 * | 0.414 ** | 0.352 * | 0.346 * | 0.414 ** | |
| 14 | 0.403 ** | 0.379 ** | 0.412 *** | 0.367 ** | 0.338 ** | 0.412 *** | |
| −0.4 | 8 | 0.468 ** | 0.494 ** | 0.525 ** | 0.292 | 0.528 ** | 0.525 ** |
| 10 | 0.444 ** | 0.47 ** | 0.504 *** | 0.268 | 0.5 *** | 0.504 *** | |
| 12 | 0.414 ** | 0.439 ** | 0.469 *** | 0.25 | 0.442 *** | 0.469 *** | |
| 14 | 0.404 *** | 0.428 *** | 0.455 *** | 0.23 | 0.419 *** | 0.455 *** |
| 1% | 5% | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.4 | −0.1 | 0.011 | 0.011 | 0.012 | 0.010 | 0.052 | 0.054 | 0.058 | 0.052 |
| 0 | 0.010 | 0.012 | 0.010 | 0.010 | 0.059 | 0.049 | 0.055 | 0.062 | |
| 0.1 | 0.011 | 0.012 | 0.011 | 0.012 | 0.056 | 0.060 | 0.059 | 0.050 | |
| 0.49 | −0.1 | 0.014 | 0.012 | 0.011 | 0.012 | 0.059 | 0.059 | 0.056 | 0.064 |
| 0 | 0.012 | 0.012 | 0.012 | 0.013 | 0.053 | 0.061 | 0.058 | 0.059 | |
| 0.1 | 0.012 | 0.014 | 0.015 | 0.014 | 0.062 | 0.059 | 0.060 | 0.064 | |
| 0.5 | −0.1 | 0.010 | 0.013 | 0.013 | 0.012 | 0.054 | 0.057 | 0.058 | 0.056 |
| 0 | 0.013 | 0.016 | 0.011 | 0.012 | 0.062 | 0.059 | 0.059 | 0.060 | |
| 0.1 | 0.009 | 0.013 | 0.010 | 0.013 | 0.059 | 0.063 | 0.065 | 0.058 | |
| −0.4 | −0.1 | 0.017 | 0.014 | 0.015 | 0.015 | 0.069 | 0.066 | 0.072 | 0.071 |
| 0 | 0.016 | 0.017 | 0.014 | 0.019 | 0.070 | 0.070 | 0.065 | 0.067 | |
| 0.1 | 0.014 | 0.017 | 0.017 | 0.015 | 0.073 | 0.069 | 0.065 | 0.068 | |
| 0.4 | −0.1 | 0.363 | 0.45 | 0.545 | 0.619 | 0.649 | 0.777 | 0.854 | 0.914 | 0.797 | 0.903 | 0.963 | 0.983 |
| 0 | 0.381 | 0.459 | 0.555 | 0.623 | 0.663 | 0.781 | 0.877 | 0.915 | 0.797 | 0.897 | 0.960 | 0.985 | |
| 0.1 | 0.372 | 0.476 | 0.551 | 0.63 | 0.653 | 0.785 | 0.864 | 0.915 | 0.792 | 0.906 | 0.956 | 0.985 | |
| 0.49 | −0.1 | 0.259 | 0.321 | 0.393 | 0.439 | 0.527 | 0.659 | 0.762 | 0.837 | 0.658 | 0.812 | 0.901 | 0.949 |
| 0 | 0.259 | 0.331 | 0.384 | 0.445 | 0.526 | 0.668 | 0.754 | 0.84 | 0.663 | 0.805 | 0.903 | 0.947 | |
| 0.1 | 0.271 | 0.321 | 0.389 | 0.446 | 0.547 | 0.67 | 0.774 | 0.839 | 0.663 | 0.818 | 0.900 | 0.946 | |
| 0.5 | −0.1 | 0.257 | 0.314 | 0.372 | 0.428 | 0.517 | 0.643 | 0.748 | 0.817 | 0.657 | 0.795 | 0.895 | 0.942 |
| 0 | 0.248 | 0.299 | 0.374 | 0.413 | 0.517 | 0.659 | 0.745 | 0.817 | 0.656 | 0.792 | 0.891 | 0.948 | |
| 0.1 | 0.252 | 0.326 | 0.379 | 0.431 | 0.518 | 0.64 | 0.755 | 0.828 | 0.651 | 0.808 | 0.883 | 0.943 | |
| −0.4 | −0.1 | 0.142 | 0.171 | 0.194 | 0.211 | 0.394 | 0.498 | 0.578 | 0.655 | 0.697 | 0.809 | 0.891 | 0.937 |
| 0 | 0.140 | 0.181 | 0.195 | 0.221 | 0.392 | 0.493 | 0.591 | 0.665 | 0.704 | 0.810 | 0.892 | 0.939 | |
| 0.1 | 0.152 | 0.170 | 0.202 | 0.224 | 0.406 | 0.506 | 0.588 | 0.669 | 0.692 | 0.813 | 0.894 | 0.943 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangat, M.K.; Reschenhofer, E. Frequency-Domain Evidence for Climate Change. Econometrics 2020, 8, 28. https://doi.org/10.3390/econometrics8030028
Mangat MK, Reschenhofer E. Frequency-Domain Evidence for Climate Change. Econometrics. 2020; 8(3):28. https://doi.org/10.3390/econometrics8030028
Chicago/Turabian StyleMangat, Manveer Kaur, and Erhard Reschenhofer. 2020. "Frequency-Domain Evidence for Climate Change" Econometrics 8, no. 3: 28. https://doi.org/10.3390/econometrics8030028
APA StyleMangat, M. K., & Reschenhofer, E. (2020). Frequency-Domain Evidence for Climate Change. Econometrics, 8(3), 28. https://doi.org/10.3390/econometrics8030028




