Triple the Gamma—A Unifying Shrinkage Prior for Variance and Variable Selection in Sparse State Space and TVP Models
Abstract
1. Introduction
2. The Triple Gamma as a Prior for Variance Parameters
2.1. Motivation and Definition
2.2. Properties of the Triple Gamma Prior
- (a)
- It has following representation as a local-global shrinkage prior:
- (b)
- The marginal prior takes the following form with ,where is the confluent hyper-geometric function of the second kind:
- (a)
- For and small values of ,
- (b)
- For and small values of ,where is the digamma function.
- (c)
- For ,
- (d)
- As ,
2.3. Relation of the Triple Gamma to Other Shrinkage Priors
2.4. Using the Triple Gamma for Variance Selection in TVP Models
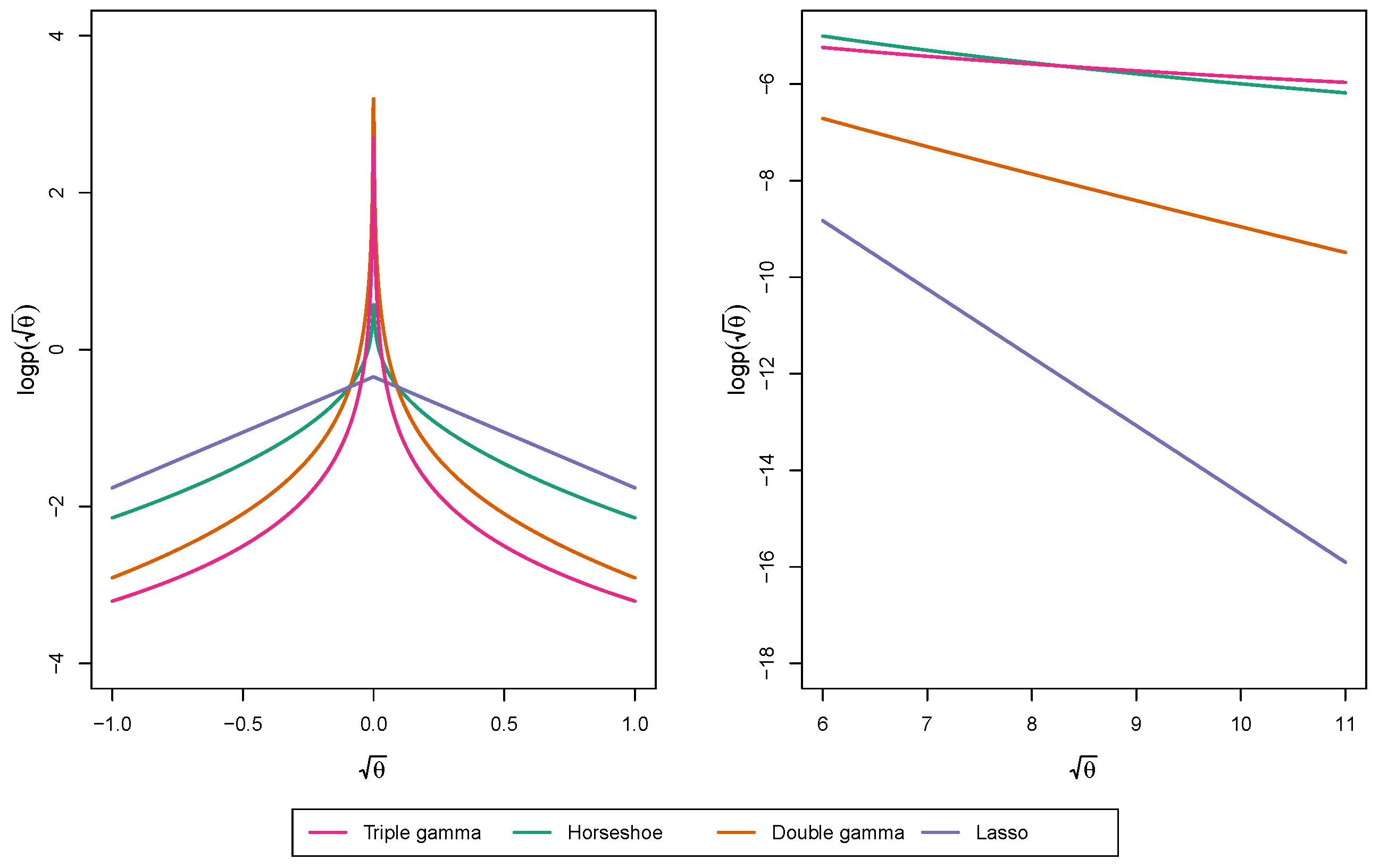
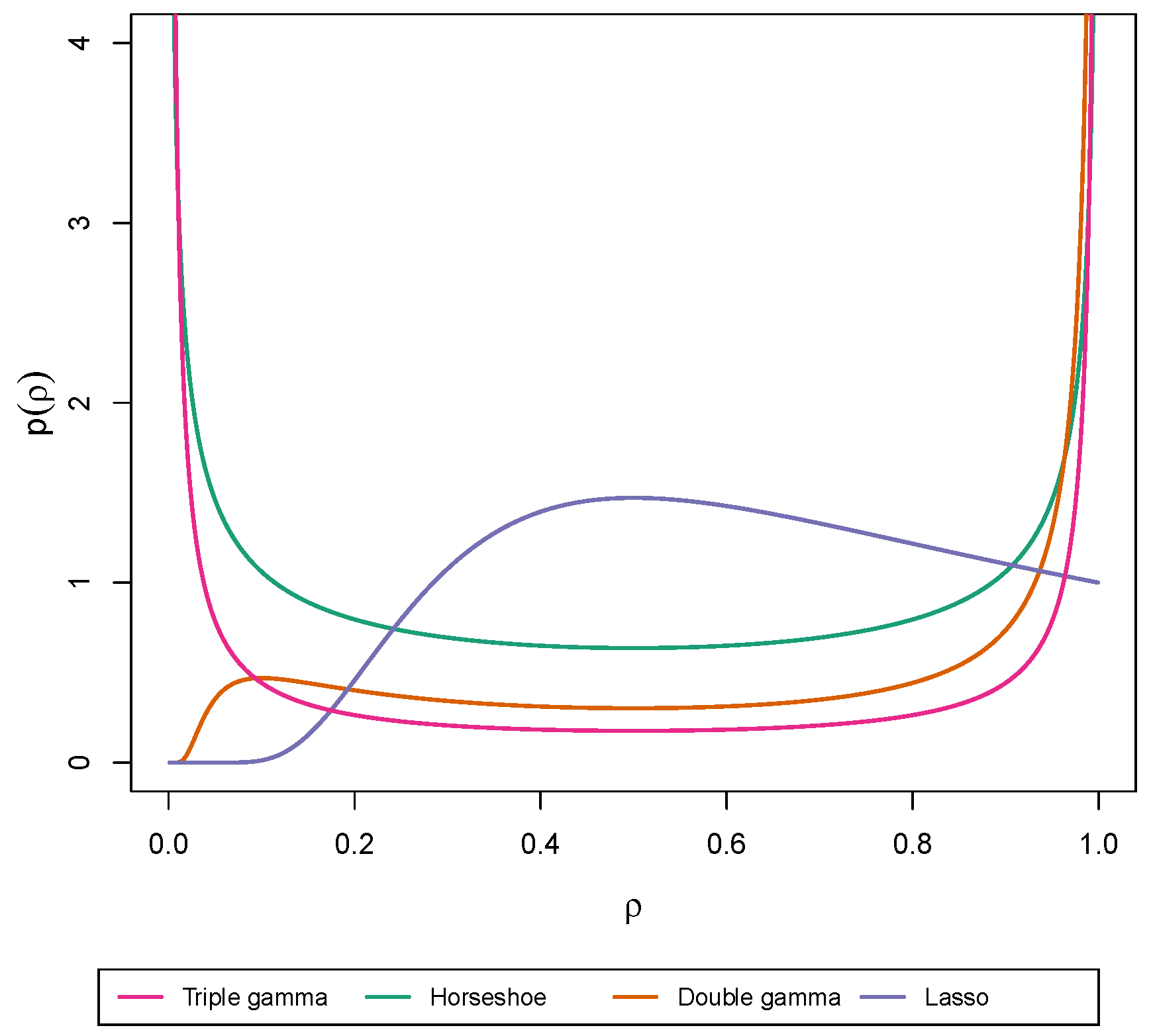
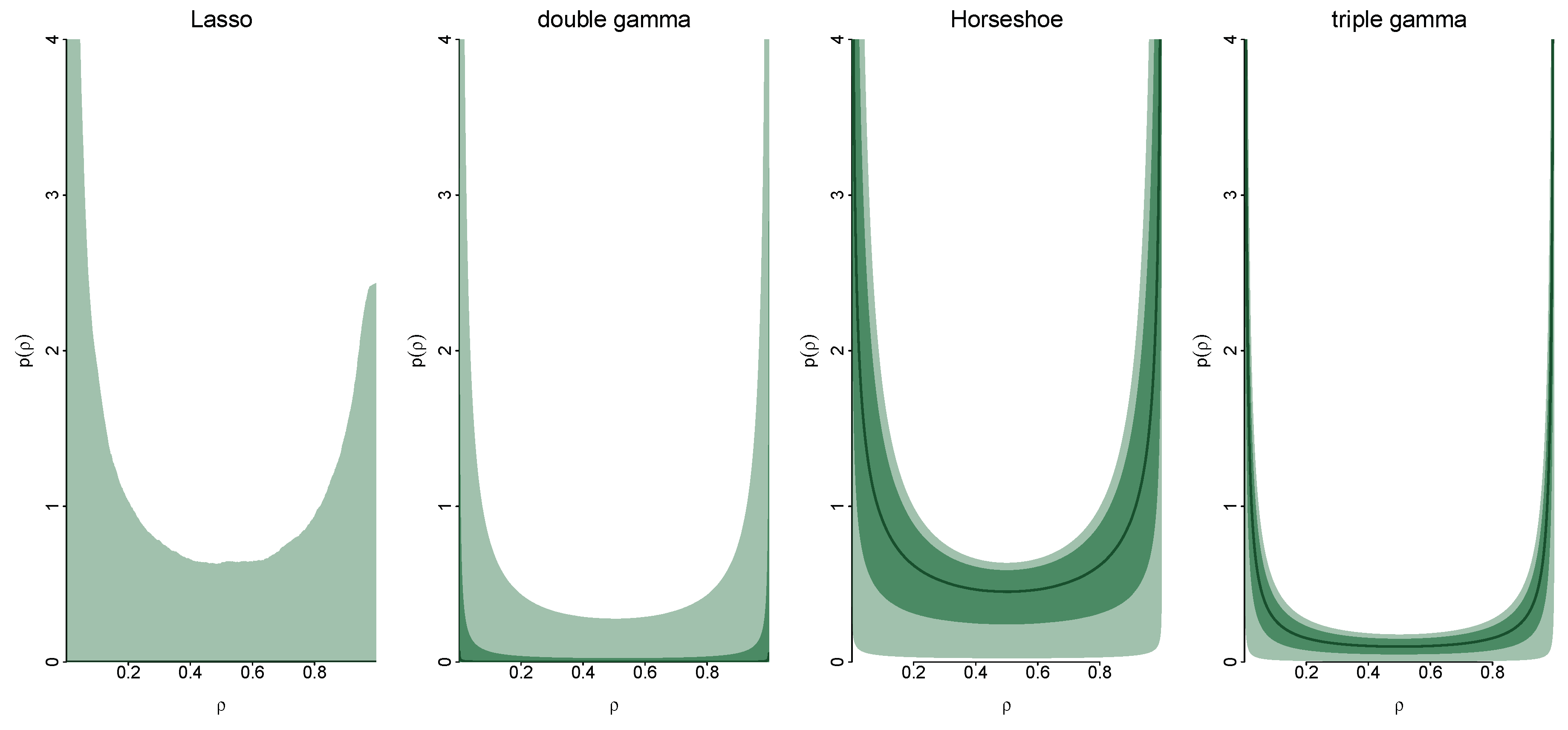
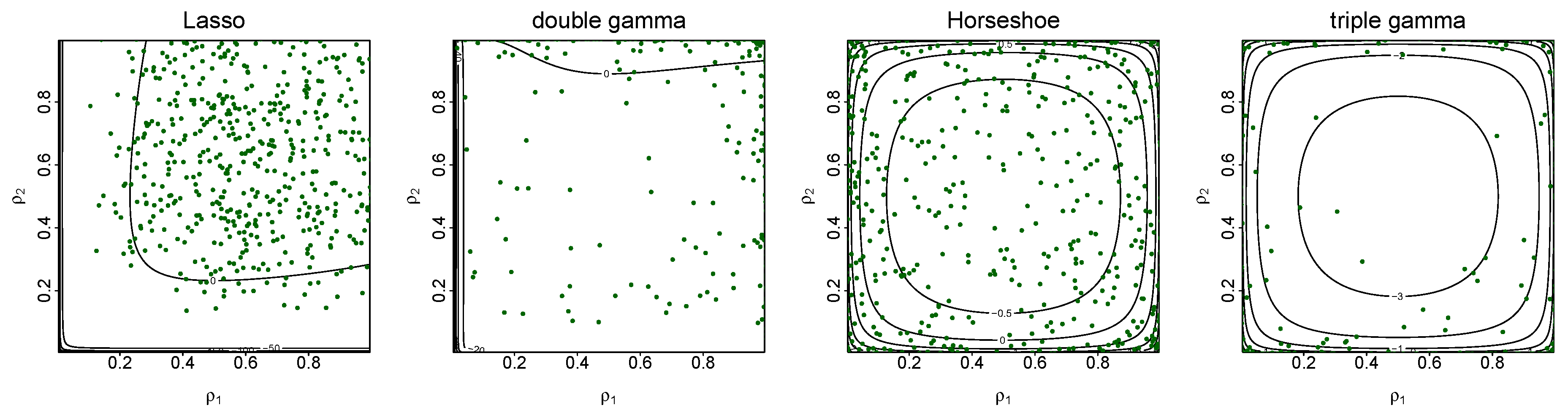
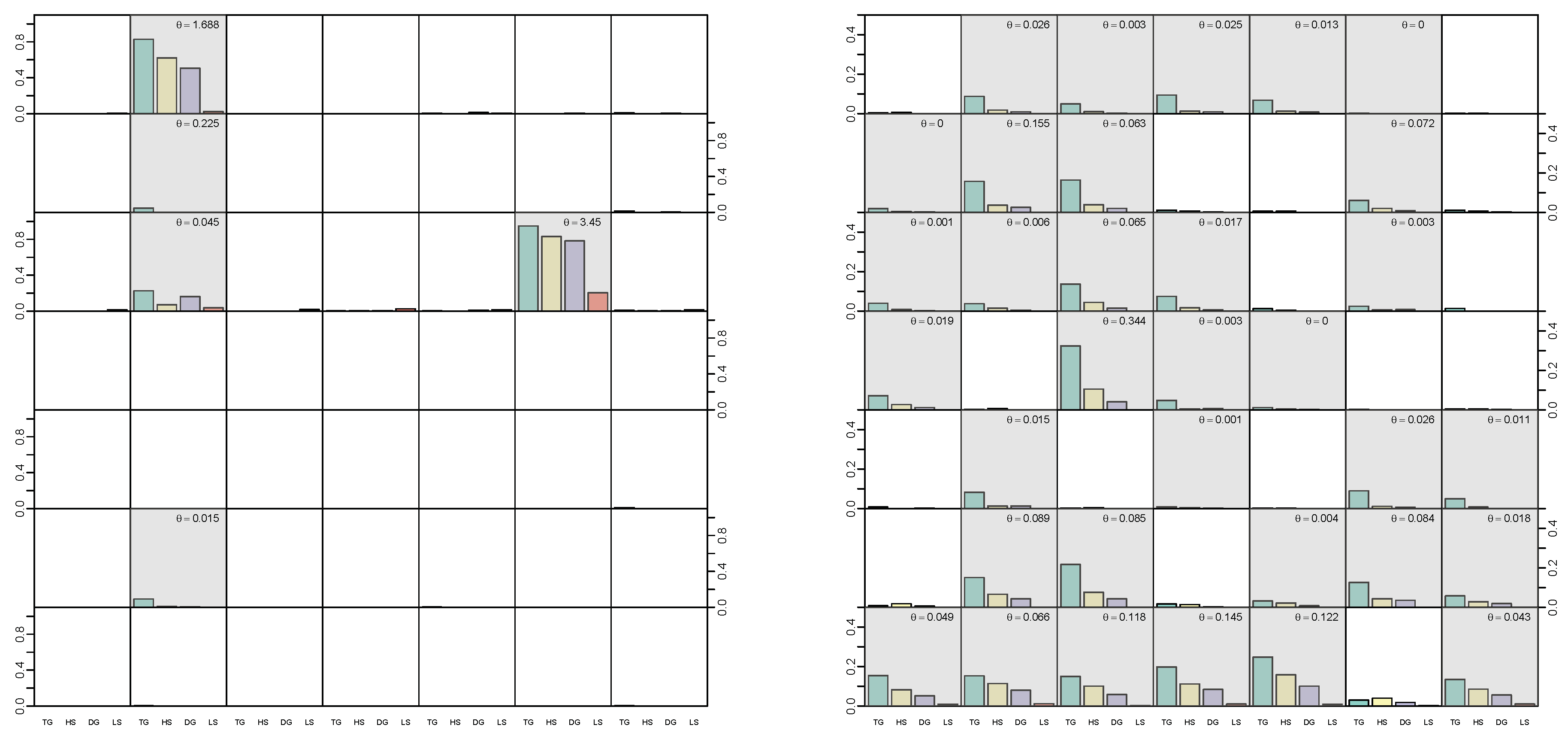
3. Shrinkage Profiles and BMA-Like Behavior
3.1. Shrinkage Profiles
3.2. BMA-Type Behaviour
4. MCMC Algorithm
| Algorithm 1. MCMC inference for TVP models under the triple gamma prior. |
Choose starting values for all global shrinkage parameters and local shrinkage parameters , and repeat the following steps:
|
5. Applications to TVP-VAR-SV Models
5.1. Model
5.2. A Brief Sketch of the TVP-VAR-SV MCMC Algorithm
| Algorithm 2. MCMC inference for TVP-VAR-SV models under the triple gamma prior. |
| Choose starting values for all global and local shrinkage parameters in prior (31) for each equation and repeat the following steps: |
For , update all the unknowns in the ith equation:
|
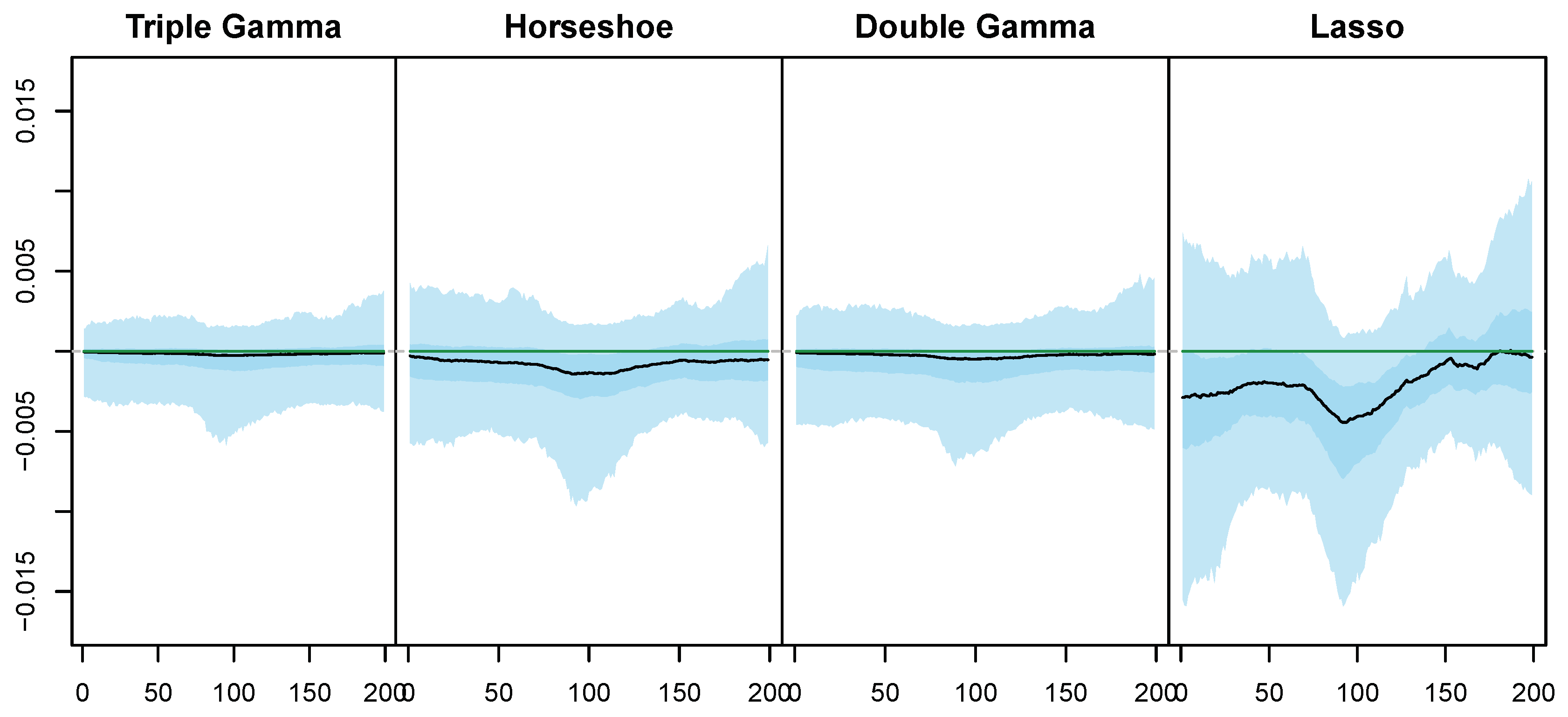
5.3. Illustrative Example with Simulated Data
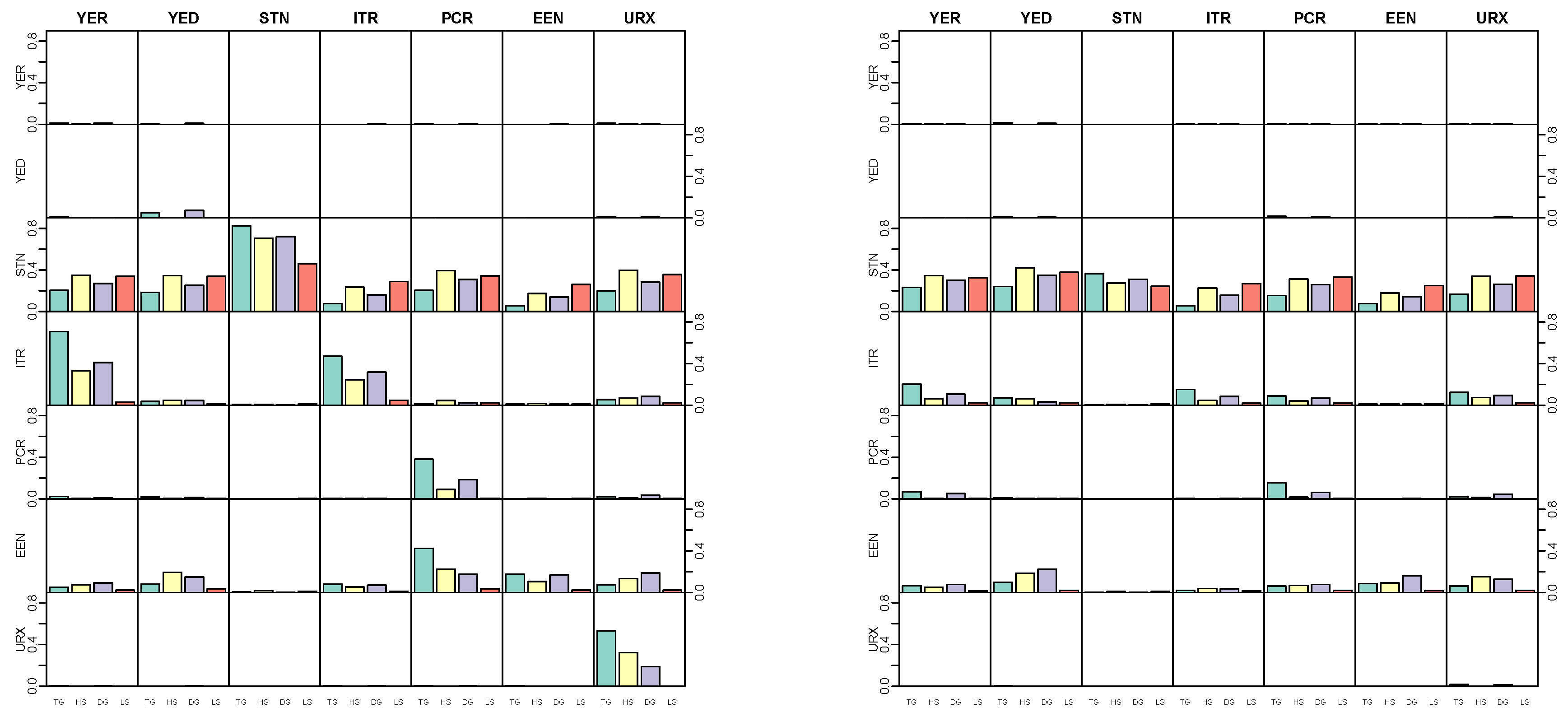
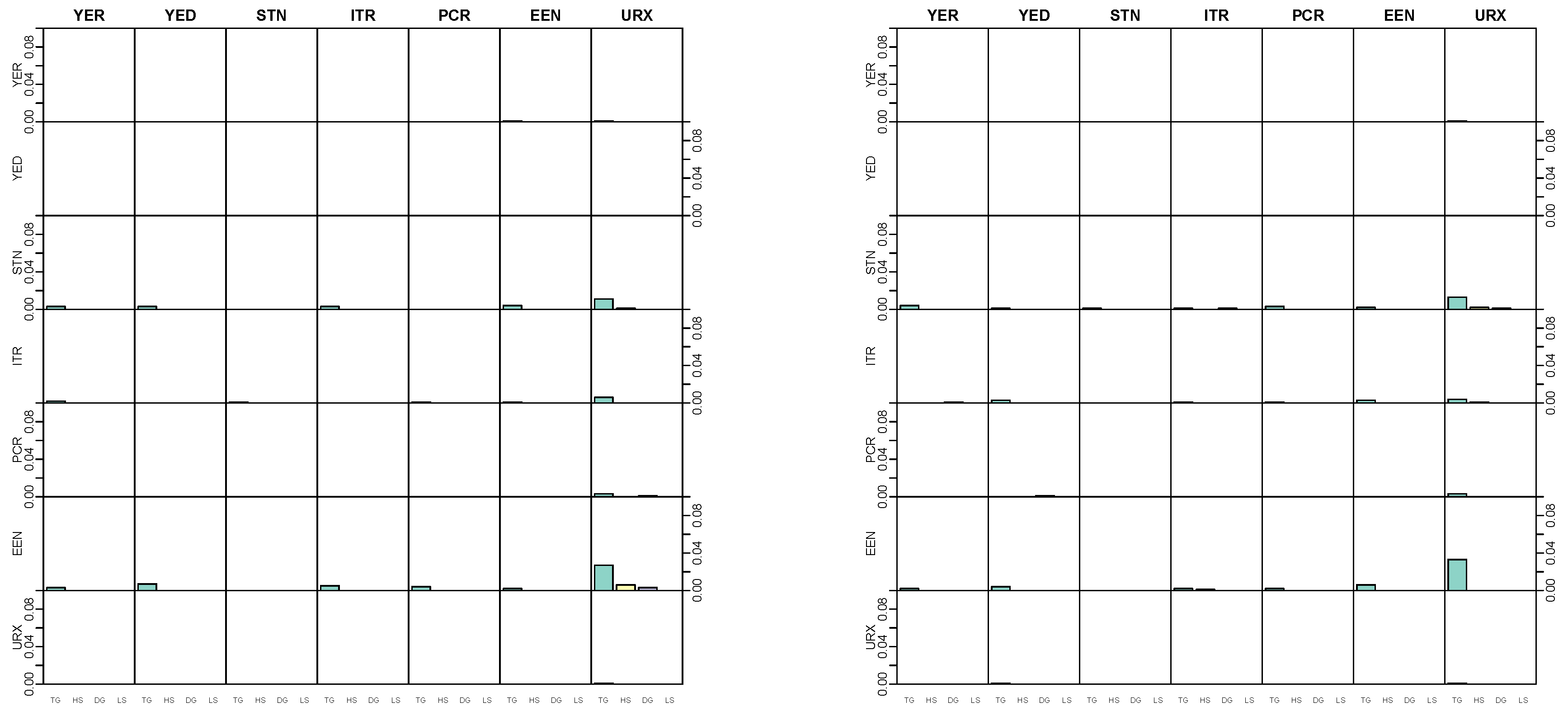
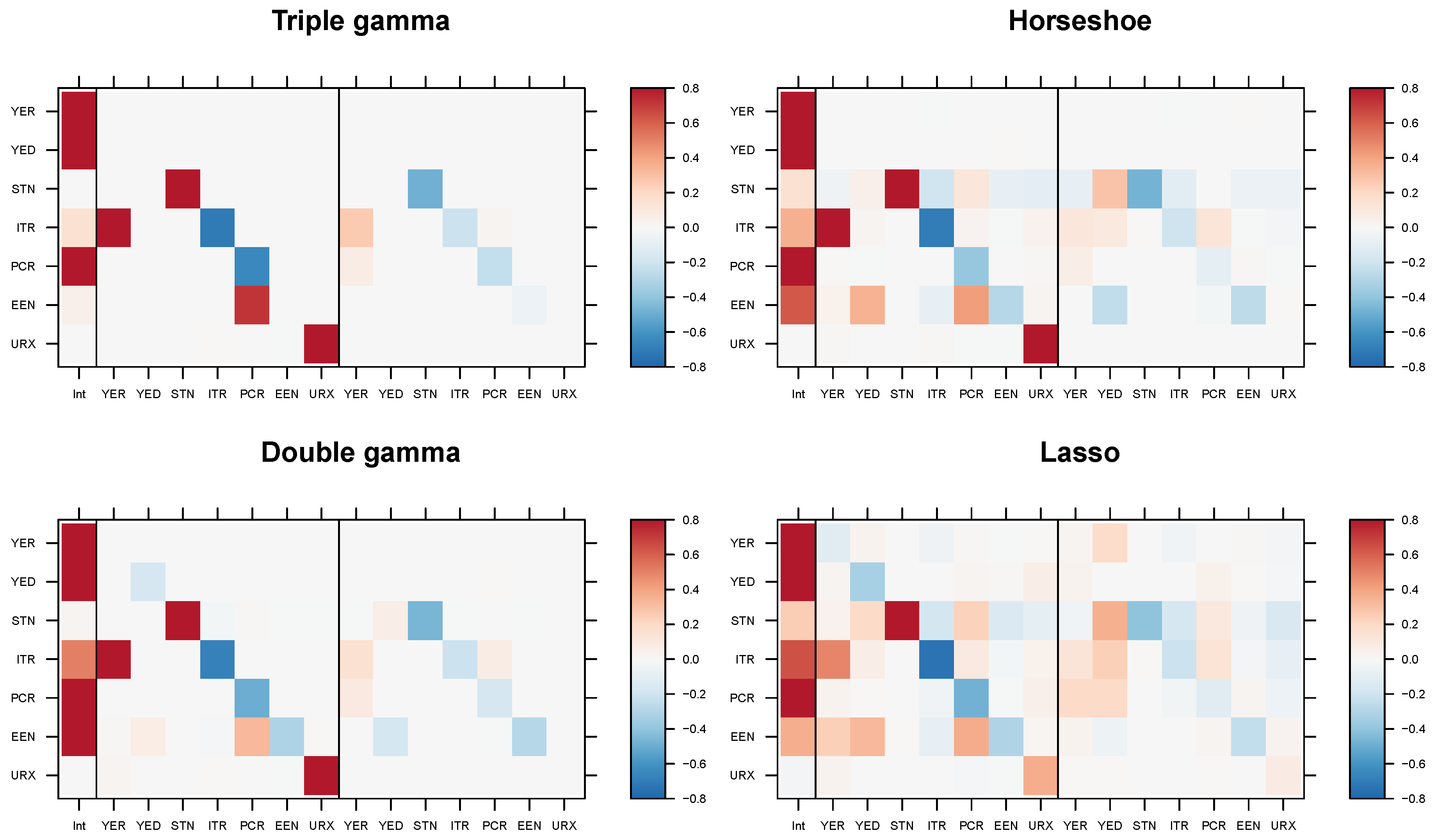
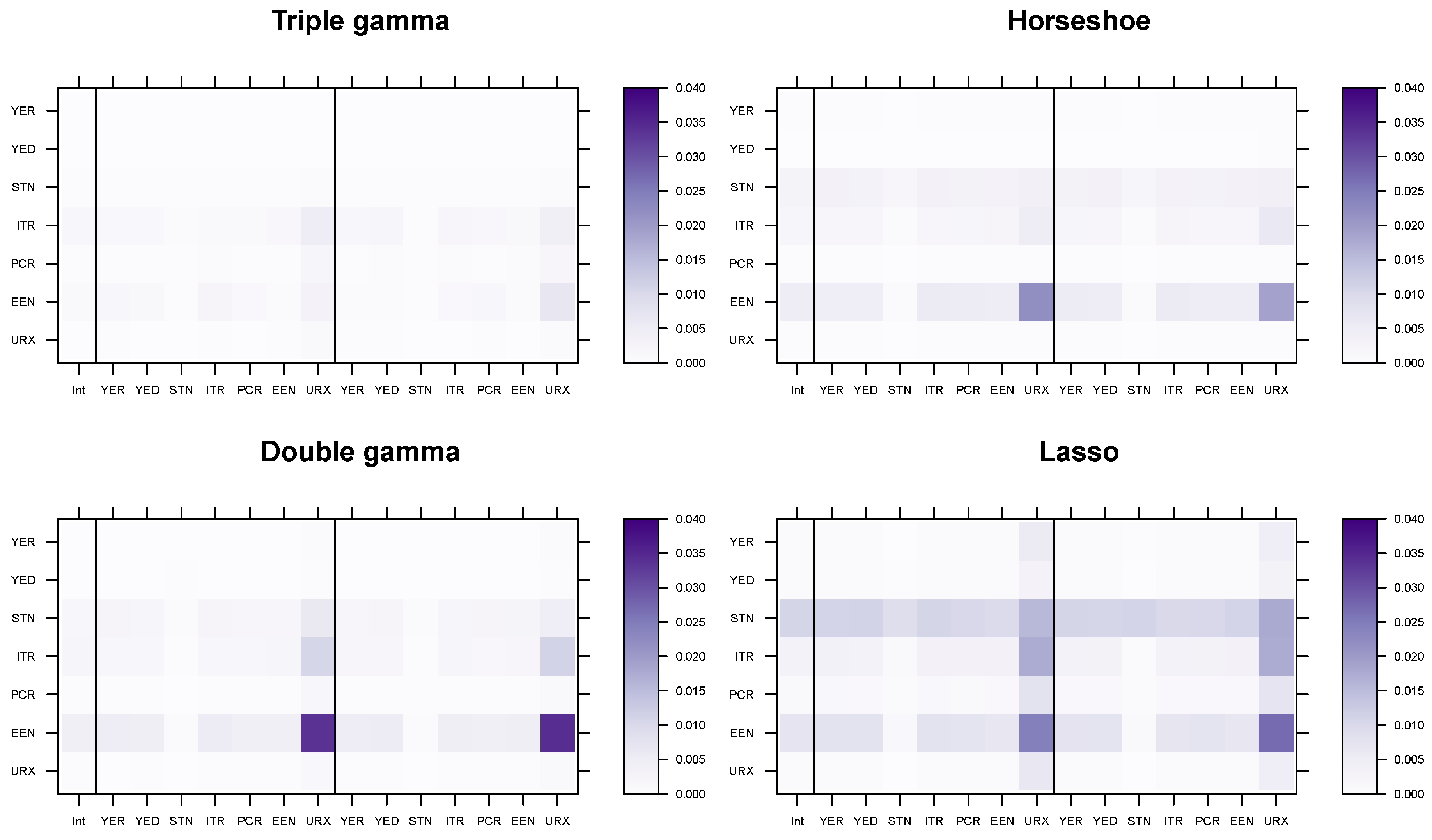
5.4. Modeling Area Macroeconomic and Financial Variables in the Euro Area
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Proofs
Appendix B. Details on the MCMC Scheme
Appendix C. Posterior Paths for the Simulated Data
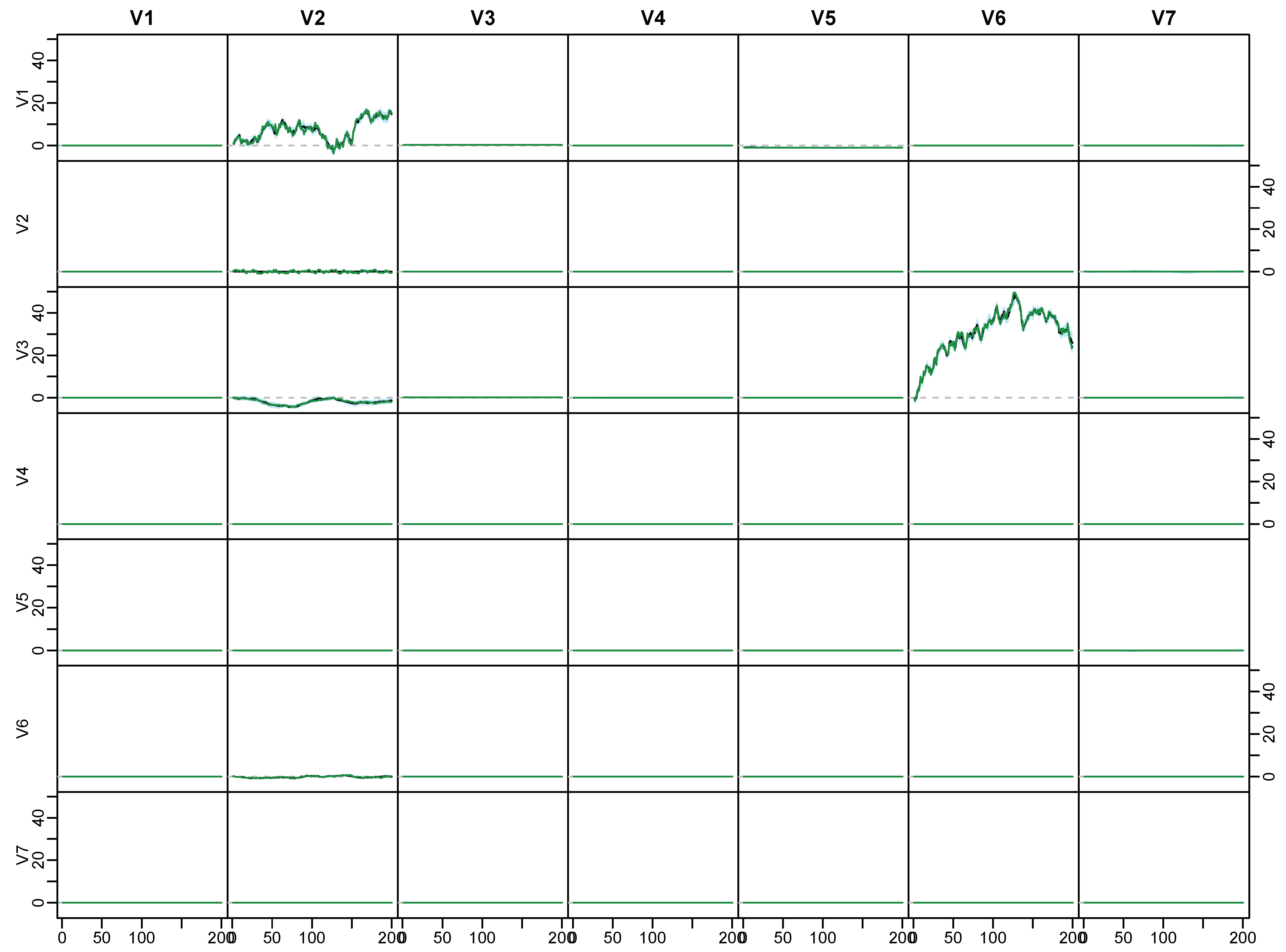
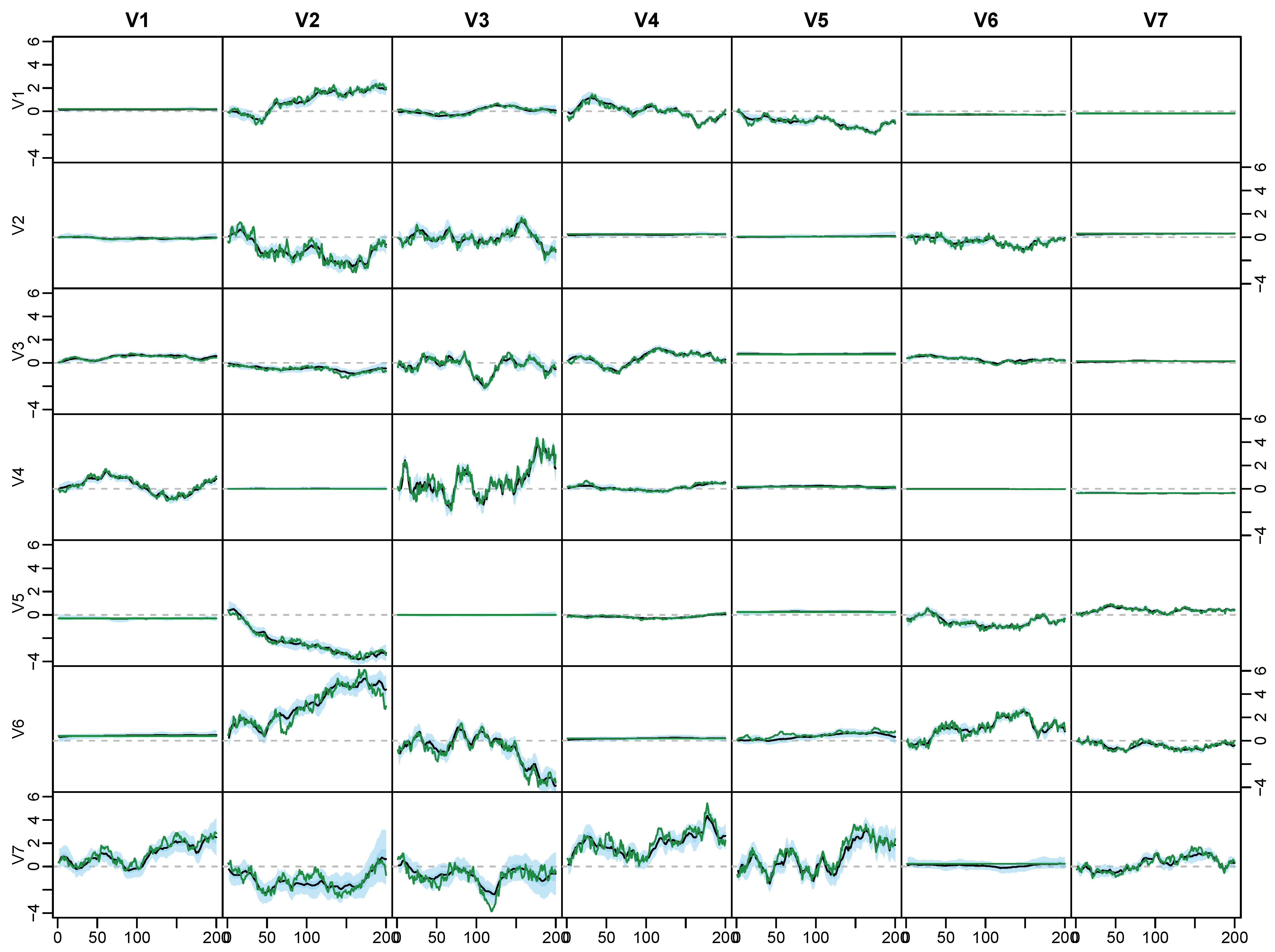
Appendix D. Application
Appendix D.1. Data Overview
| Variable | Abbreviation | Description | Tcode |
|---|---|---|---|
| Real output | YER | Gross domestic product (GDP) at market prices in millions of Euros, chain linked volume, calendar and seasonally adjusted data, reference year 1995. | 1 |
| Prices | YED | GDP deflator, index base year 1995. Defined as the ratio of nominal and real GDP. | 1 |
| Short-term interest rate | STN | Nominal short-term interest rate, Euribor 3-month, percent per annum | 2 |
| Investment | ITR | Gross fixed capital formation in millions of Euros, chain linked volume, calendar and seasonally adjusted data, reference year 1995. | 1 |
| Consumption | PCR | Individual consumption expenditure in millions of Euros, chain linked volume, calendar and seasonally adjusted data, reference year 1995. | 1 |
| Exchange rate | EEN | Nominal effective exchange rate, Euro area-19 countries vis-à-vis the NEER-38 group of main trading partners, index base Q1 1999. | 1 |
| Unemployment | URX | Unemployment rate, percentage of civilian work force, total across age and sex, seasonally adjusted, but not working day adjusted. | 2 |
Appendix D.2. Posterior Paths
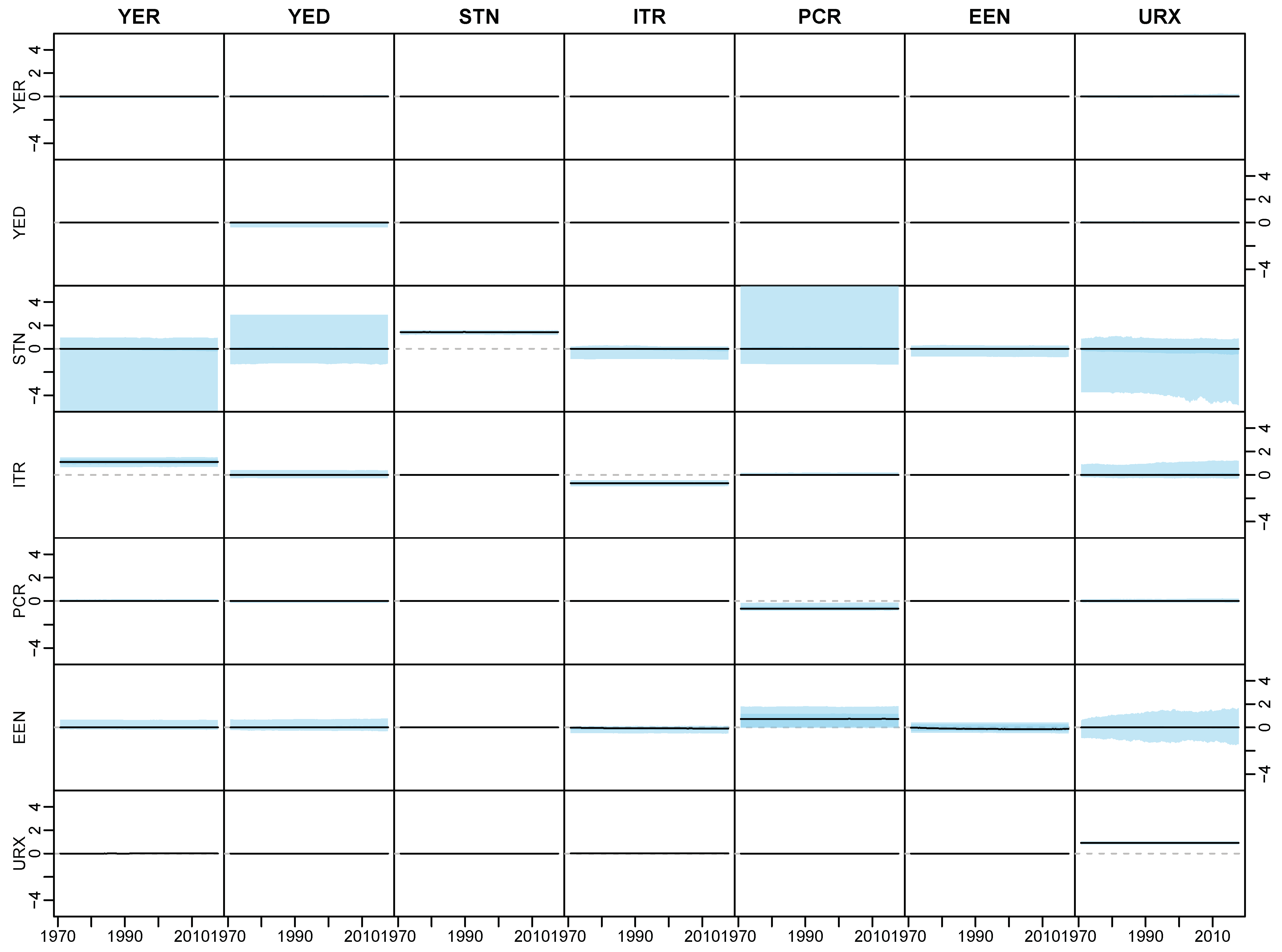
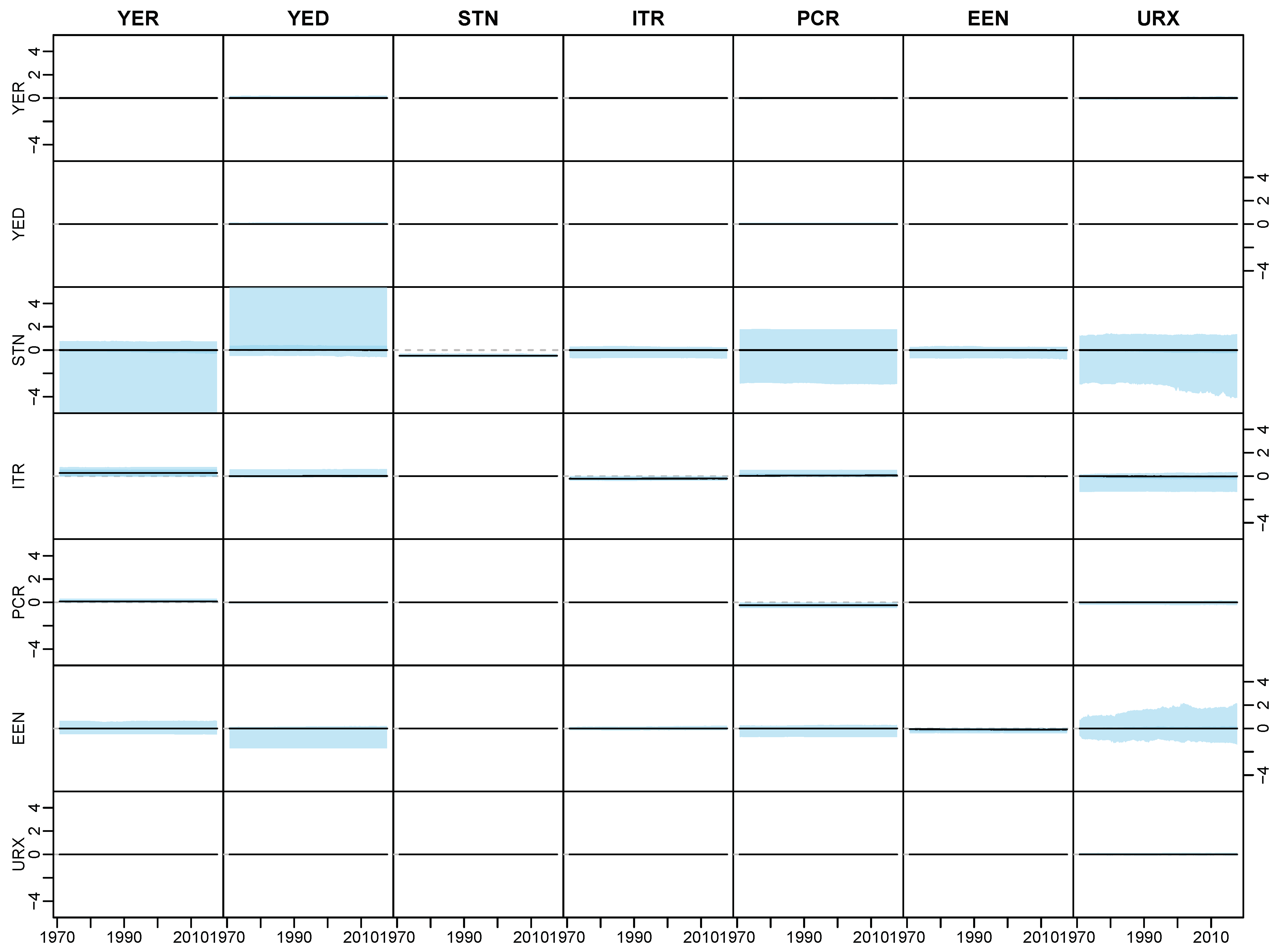
References
- Abramowitz, Milton, and Irene A. Stegun, eds. 1973. Handbook of Mathematical Functions. New York: Dover Publications. [Google Scholar]
- Armagan, Artin, David B. Dunson, and Merlise Clyde. 2011. Generalized beta mixtures of Gaussians. In Advances in Neural Information Processing Systems. Vancouver: NIPS, pp. 523–31. [Google Scholar]
- Belmonte, Miguel, Gary Koop, and Dimitris Korobolis. 2014. Hierarchical shrinkage in time-varying parameter models. Journal of Forecasting 33: 80–94. [Google Scholar] [CrossRef]
- Berger, James O. 1980. A robust generalized Bayes estimator and confidence region for a multivariate normal mean. The Annals of Statistics 8: 716–61. [Google Scholar] [CrossRef]
- Bhadra, Anindya, Jyotishka Datta, Nicholas G. Polson, and Brandon Willard. 2017a. The horseshoe+ estimator of ultra-sparse signals. Bayesian Analysis 12: 1105–31. [Google Scholar] [CrossRef]
- Bhadra, Anindya, Jyotishka Datta, Nicholas G. Polson, and Brandon Willard. 2017b. Horseshoe regularization for feature subset selection. arXiv arXiv:1702.07400. [Google Scholar] [CrossRef]
- Bhadra, Anindya, Jyotishka Datta, Nicholas G. Polson, and Brandon Willard. 2019. Lasso meets horseshoe: A survey. Statistical Science 34: 405–27. [Google Scholar] [CrossRef]
- Bitto, Angela, and Sylvia Frühwirth-Schnatter. 2019. Achieving shrinkage in a time-varying parameter model framework. Journal of Econometrics 210: 75–97. [Google Scholar] [CrossRef]
- Brown, Philip J., Marina Vannucci, and Tom Fearn. 2002. Bayes model averaging with selection of regressors. Journal of the Royal Statistical Society, Ser. B 64: 519–36. [Google Scholar] [CrossRef]
- Carriero, Andrea, Todd E. Clark, and Massimiliano Marcellino. 2019. Large Bayesian vector autoregressions with stochastic volatility and non-conjugate priors. Journal of Econometrics 212: 137–54. [Google Scholar] [CrossRef]
- Carvalho, Carlos M., Nicholas G. Polson, and James G. Scott. 2009. Handling sparsity via the horseshoe. Journal of Machine Learing Research W&CP 5: 73–80. [Google Scholar]
- Carvalho, Carlos M., Nicholas G. Polson, and James G. Scott. 2010. The horseshoe estimator for sparse signals. Biometrika 97: 465–80. [Google Scholar] [CrossRef]
- Chan, Joshua C. C., and Eric Eisenstat. 2016. Bayesian model comparison for time-varying parameter VARs with stochastic volatilty. Journal of Applied Econometrics 218: 1–24. [Google Scholar]
- Cottet, Remy, Robert J. Kohn, and David J. Nott. 2008. Variable selection and model averaging in semiparametric overdispersed generalized linear models. Journal of the American Statistical Association 103: 661–71. [Google Scholar] [CrossRef]
- Del Negro, Marco, and Giorgio E. Primiceri. 2015. Time Varying Structural Vector Autoregressions and Monetary Policy: A Corrigendum. The Review of Economic Studies 82: 1342–45. [Google Scholar] [CrossRef]
- Eisenstat, Eric, Joshua C.C. Chan, and Rodney W. Strachan. 2014. Stochastic model specification search for time-varying parameter VARs. SSRN Electronic Journal 01/2014. [Google Scholar] [CrossRef]
- Fagan, Gabriel, Jerome Henry, and Ricardo Mestre. 2005. An area-wide model for the euro area. Economic Modelling 22: 39–59. [Google Scholar] [CrossRef]
- Fahrmeir, Ludwig, Thomas Kneib, and Susanne Konrath. 2010. Bayesian regularisation in structured additive regression: A unifying perspective on shrinkage, smoothing and predictor selection. Statistics and Computing 20: 203–19. [Google Scholar] [CrossRef]
- Feldkircher, Martin, Florian Huber, and Gregor Kastner. 2017. Sophisticated and small versus simple and sizeable: When does it pay off to introduce drifting coefficients in Bayesian VARs. arXiv arXiv:1711.00564. [Google Scholar]
- Fernández, Carmen, Eduardo Ley, and Mark F. J. Steel. 2001. Benchmark priors for Bayesian model averaging. Journal of Econometrics 100: 381–427. [Google Scholar] [CrossRef]
- Figueiredo, Mario A. T. 2003. Adaptive sparseness for supervised learning. IEEE Transaction on Pattern Analysis and Machine Intelligence 25: 1150–59. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, Sylvia. 2004. Efficient Bayesian parameter estimation. In State Space and Unobserved Component Models: Theory and Applications. Edited by Andrew Harvey, Siem Jan Koopman and Neil Shephard. Cambridge: Cambridge University Press, pp. 123–51. [Google Scholar]
- Frühwirth-Schnatter, Sylvia, and Regina Tüchler. 2008. Bayesian parsimonious covariance estimation for hierarchical linear mixed models. Statistics and Computing 18: 1–13. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, Sylvia, and Helga Wagner. 2010. Stochastic model specification search for Gaussian and partially non-Gaussian state space models. Journal of Econometrics 154: 85–100. [Google Scholar] [CrossRef]
- Gelman, Andrew. 2006. Prior distributions for variance parameters in hierarchical models (Comment on Article by Browne and Draper). Bayesian Analysis 1: 515–34. [Google Scholar] [CrossRef]
- Griffin, Jim E., and Phil J. Brown. 2011. Bayesian hyper-lassos with non-convex penalization. Australian & New Zealand Journal of Statistics 53: 423–42. [Google Scholar]
- Griffin, Jim E., and Phil J. Brown. 2017. Hierarchical shrinkage priors for regression models. Bayesian Analysis 12: 135–59. [Google Scholar] [CrossRef]
- Jacquier, Eric, Nicholas G. Polson, and Peter E. Rossi. 1994. Bayesian analysis of stochastic volatility models. Journal of Business & Economic Statistics 12: 371–417. [Google Scholar]
- Johnstone, Iain M., and Bernard W. Silverman. 2004. Needles and straw in haystacks: Empirical Bayes estimates of possibly sparse sequences. The Annals of Statistics 32: 1594–649. [Google Scholar] [CrossRef]
- Kalli, Maria, and Jim E. Griffin. 2014. Time-varying sparsity in dynamic regression models. Journal of Econometrics 178: 779–93. [Google Scholar] [CrossRef]
- Kastner, Gregor. 2016. Dealing with stochastic volatility in time series using the R package stochvol. Journal of Statistical Software 69: 1–30. [Google Scholar] [CrossRef]
- Kastner, Gregor, and Sylvia Frühwirth-Schnatter. 2014. Ancillarity-sufficiency interweaving strategy (ASIS) for boosting MCMC estimation of stochastic volatility models. Computational Statistics and Data Analysis 76: 408–23. [Google Scholar] [CrossRef]
- Kleijn, Richard, and Herman K. van Dijk. 2006. Bayes model averaging of cyclical decompositions in economic time series. Journal of Applied Econometrics 21: 191–212. [Google Scholar] [CrossRef]
- Koop, Gary, and Dimitris Korobilis. 2013. Large time-varying parameter VARs. Journal of Econometrics 177: 185–98. [Google Scholar] [CrossRef]
- Koop, Gary, and Simon M. Potter. 2004. Forecasting in dynamic factor models using Bayesian model averaging. Econometrics Journal 7: 550–65. [Google Scholar] [CrossRef]
- Kowal, Daniel R., David S. Matteson, and David Ruppert. 2019. Dynamic shrinkage processes. Journal of the Royal Statistical Society, Ser. B 81: 673–806. [Google Scholar] [CrossRef]
- Ley, Eduardo, and Mark F. J. Steel. 2009. On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. Journal of Applied Econometrics 24: 651–74. [Google Scholar] [CrossRef]
- Makalic, Enes, and Daniel F. Schmidt. 2016. A simple sampler for the horseshoe estimator. IEEE Signal Processing Letters 23: 179–82. [Google Scholar] [CrossRef]
- Nakajima, Jouchi. 2011. Time-varying parameter VAR model with stochastic volatility: An overview of methodology and empirical applications. Monetary and Economic Studies 29: 107–42. [Google Scholar]
- Park, Trevor, and George Casella. 2008. The Bayesian Lasso. Journal of the American Statistical Association 103: 681–86. [Google Scholar] [CrossRef]
- Pérez, Maria-Eglée, Luis Raúl Pericchi, and Isabel Cristina Ramírez. 2017. The scaled beta2 distribution as a robust prior for scales. Bayesian Analysis 12: 615–37. [Google Scholar] [CrossRef]
- Polson, Nicholas G., and James G. Scott. 2011. Shrink globally, act locally: Sparse Bayesian regularization and prediction. In Bayesian Statistics 9. Edited by José M. Bernardo, M. J. Bayarri, James O. Berger, Phil Dawid, David Heckerman, Adrian F. M. Smith and Mike West. Oxford: Oxford University Press, pp. 501–38. [Google Scholar]
- Polson, Nicholas G., and James G. Scott. 2012a. Local shrinkage rules, Lévy processes, and regularized regression. Journal of the Royal Statistical Society, Ser. B 74: 287–311. [Google Scholar] [CrossRef]
- Polson, Nicholas G., and James G. Scott. 2012b. On the half-Cauchy prior for a global scale parameter. Bayesian Analysis 7: 887–902. [Google Scholar] [CrossRef]
- Primiceri, Giorgio E. 2005. Time varying structural vector autoregressions and monetary policy. Review of Economic Studies 72: 821–52. [Google Scholar] [CrossRef]
- Raftery, Adrian E., David Madigan, and Jennifer A. Hoeting. 1997. Bayesian model averaging for linear regression models. Journal of the American Statistical Association 92: 179–91. [Google Scholar] [CrossRef]
- Ročková, Veronika, and Kenichiro McAlinn. 2020. Dynamic variable selection with spike-and-slab process priors. Bayesian Analysis. [Google Scholar]
- Sala-i-Martin, Xavier, Gernot Doppelhofer, and Ronald I. Miller. 2004. Determinants of long-term growth: A Bayesian averaging of classical estimates (BACE) approach. The American Economic Review 94: 813–35. [Google Scholar] [CrossRef]
- Scheipl, Fabian, and Thomas Kneib. 2009. Locally adaptive Bayesian p-splines with a normal-exponential-gamma prior. Computational Statistics and Data Analysis 53: 3533–52. [Google Scholar] [CrossRef]
- Strawderman, William E. 1971. Proper Bayes minimax estimators of the multivariate normal mean. The Annals of Statistics 42: 385–88. [Google Scholar] [CrossRef]
- Tibshirani, Ryan. 1996. Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society, Ser. B 58: 267–88. [Google Scholar] [CrossRef]
- van der Pas, Stéphanie, Bas Kleijn, and Aad van der Vaart. 2014. The horseshoe estimator: Posterior concentration around nearly black vectors. Electronic Journal of Statistics 8: 2585–618. [Google Scholar] [CrossRef]
- Zhang, Yan, Brian J. Reich, and Howard D. Bondell. 2017. High dimensional linear regression via the R2-D2 shrinkage prior. Technical report. arXiv arXiv:1609.00046v2. [Google Scholar]
| 1 | Let and be, respectively, the pdf and cdf of the random variable . The cdf of the random variable is given by
|
| 2 | Note that the -distribution has pdf
Furthermore, follows the -distribution. |
| 3 | The pdf of a -distribution reads:
|
| 4 | Using (3), we obtain the following prior for by the law of transformation of densities:
|
| 5 | The pdf of the -distribution is given by
|
| Prior for | |||||
|---|---|---|---|---|---|
| normal-gamma-gamma | |||||
| generalized beta mixture | |||||
| hierarchical scaled beta2 | |||||
| normal-exponential-gamma | 1 | ||||
| Horseshoe | |||||
| Strawderman-Berger | 1 | 4 | 1 | ||
| double gamma | ∞ | - | |||
| Lasso | 1 | ∞ | - | ||
| half-t | ∞ | - | |||
| half-Cauchy | ∞ | - | |||
| normal | ∞ | ∞ | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadonna, A.; Frühwirth-Schnatter, S.; Knaus, P. Triple the Gamma—A Unifying Shrinkage Prior for Variance and Variable Selection in Sparse State Space and TVP Models. Econometrics 2020, 8, 20. https://doi.org/10.3390/econometrics8020020
Cadonna A, Frühwirth-Schnatter S, Knaus P. Triple the Gamma—A Unifying Shrinkage Prior for Variance and Variable Selection in Sparse State Space and TVP Models. Econometrics. 2020; 8(2):20. https://doi.org/10.3390/econometrics8020020
Chicago/Turabian StyleCadonna, Annalisa, Sylvia Frühwirth-Schnatter, and Peter Knaus. 2020. "Triple the Gamma—A Unifying Shrinkage Prior for Variance and Variable Selection in Sparse State Space and TVP Models" Econometrics 8, no. 2: 20. https://doi.org/10.3390/econometrics8020020
APA StyleCadonna, A., Frühwirth-Schnatter, S., & Knaus, P. (2020). Triple the Gamma—A Unifying Shrinkage Prior for Variance and Variable Selection in Sparse State Space and TVP Models. Econometrics, 8(2), 20. https://doi.org/10.3390/econometrics8020020





