New Evidence of the Marginal Predictive Content of Small and Large Jumps in the Cross-Section
Abstract
1. Introduction
2. Model Setup and Estimation Methodology
3. Data
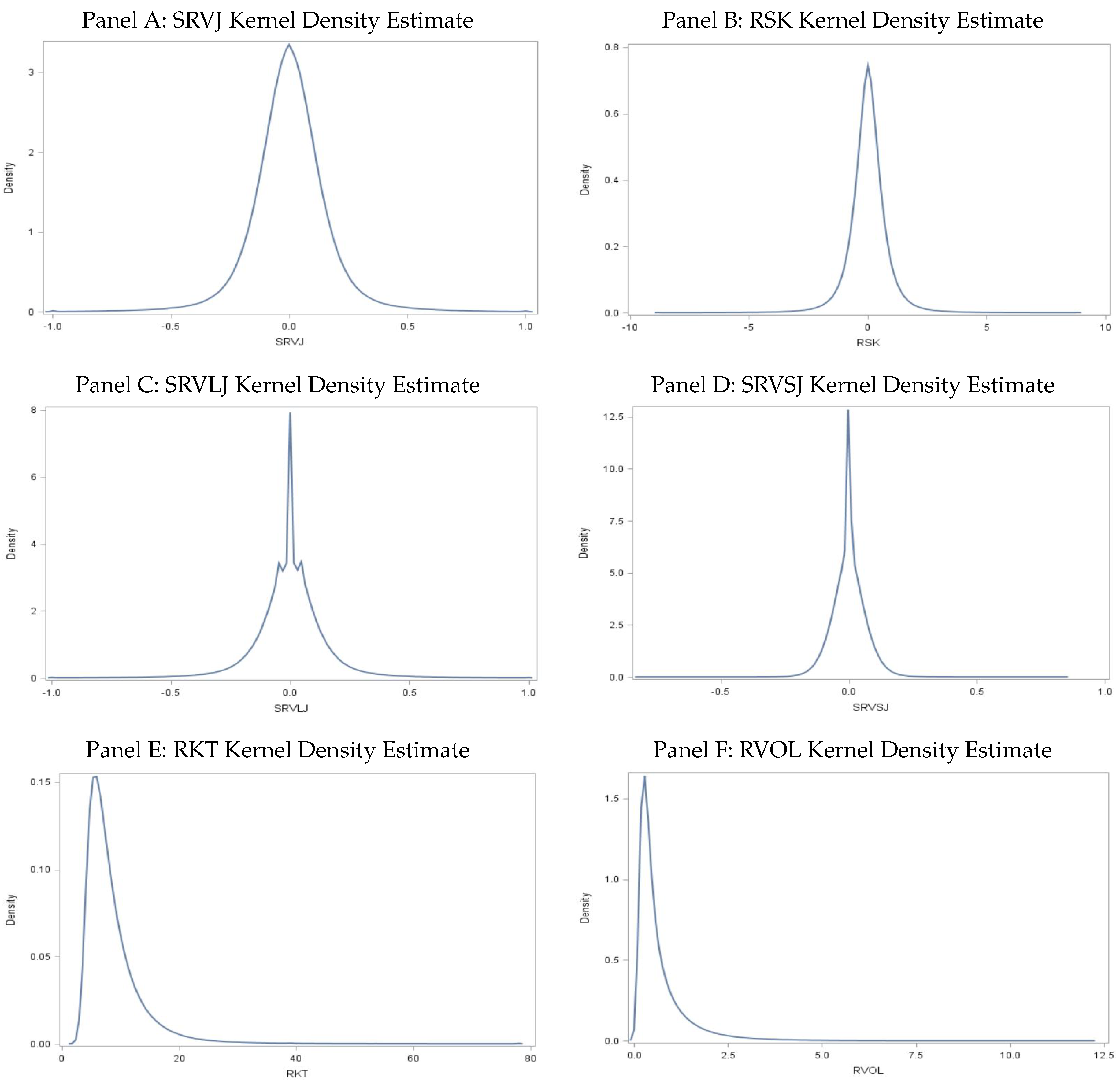
3.1. Unconditional Distributions of Realized Measures
3.2. Summary Statistics and Portfolio Characteristics
4. Empirical Results
4.1. Single (Univariate) Portfolio Sorts Based on Realized Measures
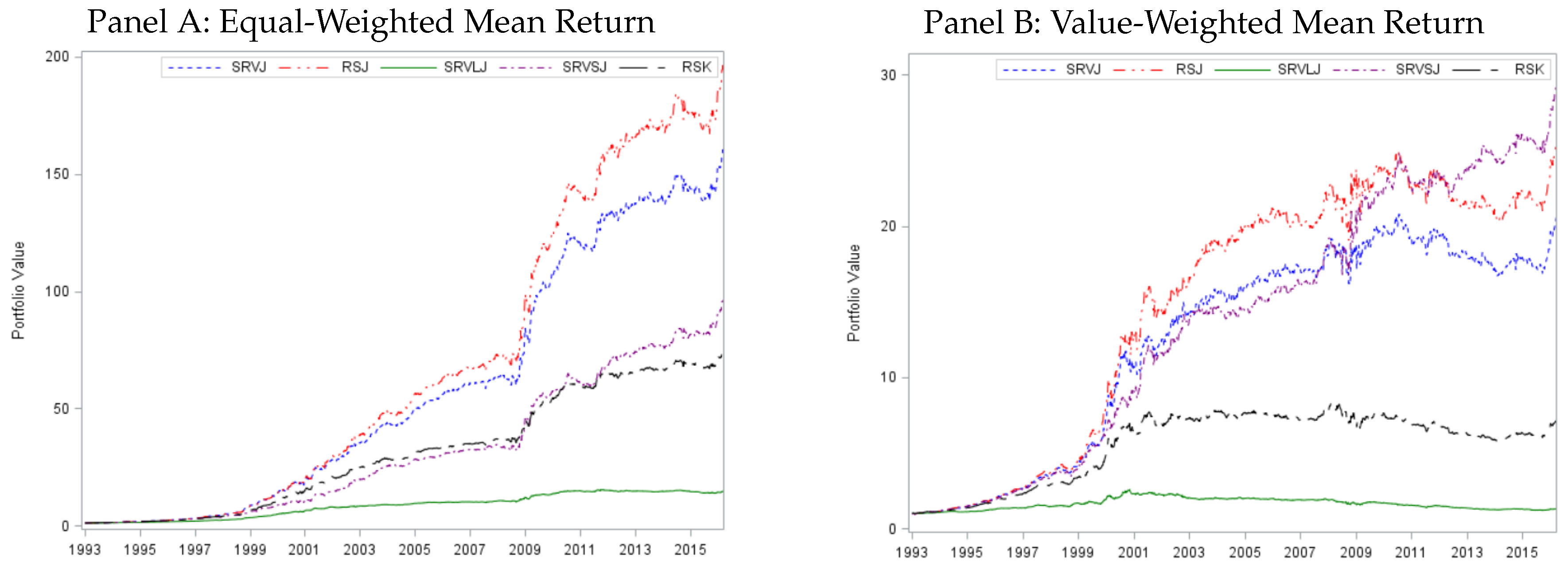
4.2. Cumulative Returns and Sharpe Ratios
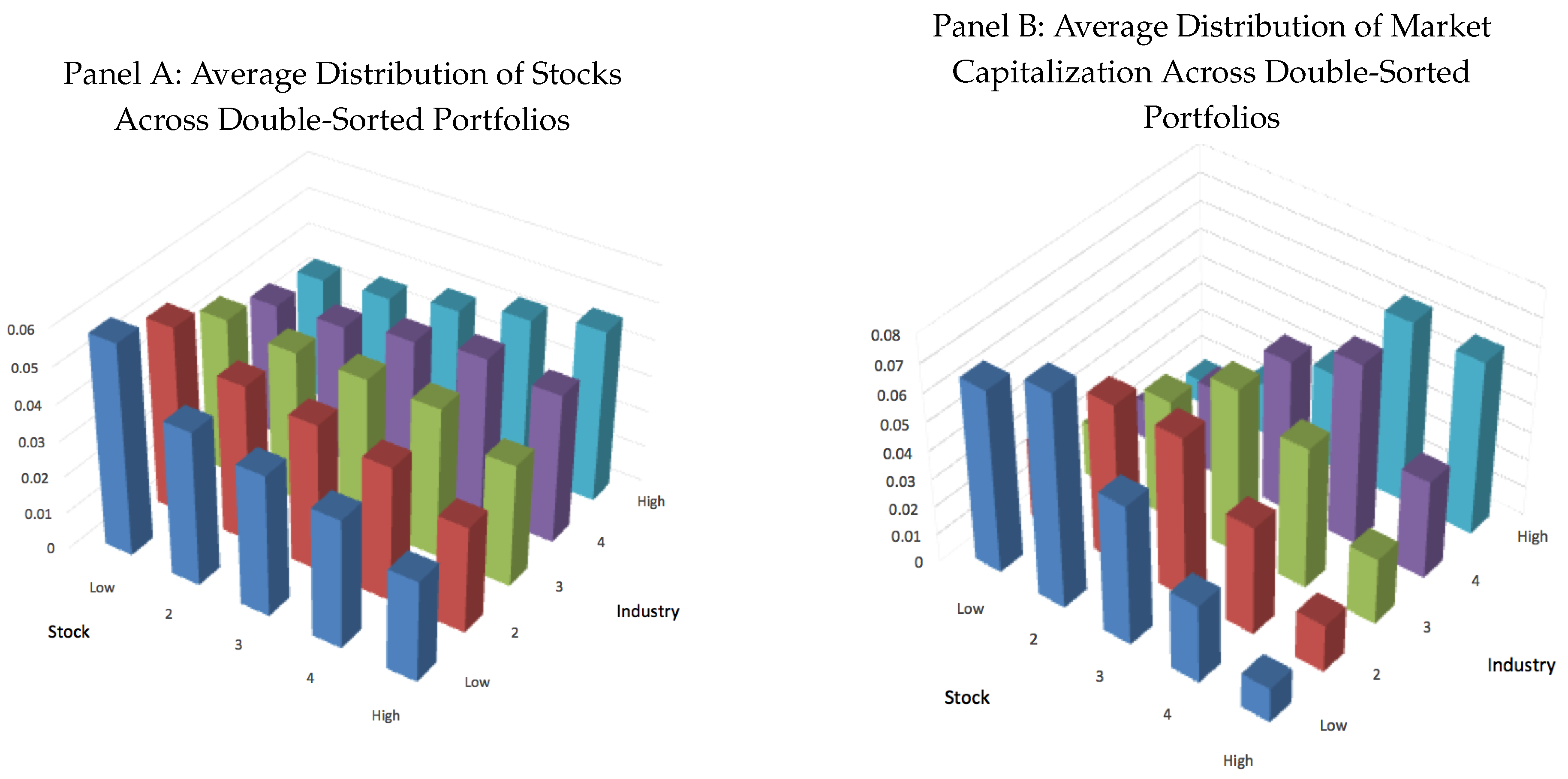
4.3. Double Portfolio Sorts Based on Realized Measures
4.4. Using Double Portfolio Sorts to Examine Stock-Level versus Industry-Level Predictability
4.5. Firm-Level Fama–MacBeth Regressions
4.6. Pricing Distinctions between Small and Large Jumps
4.6.1. Jumps and News Announcement
4.6.2. Systematic versus Idiosyncratic Risks
5. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aït-Sahalia, Yacine, and Jean Jacod. 2012. Analyzing the spectrum of asset returns: Jump and volatility components in high frequency data. Journal of Economic Literature 50: 1007–50. [Google Scholar] [CrossRef]
- Amaya, Diego, Peter Christoffersen, Kris Jacobs, and Aurelio Vasquez. 2015. Does realized skewness predict the cross-section of equity returns? Journal of Financial Economics 118: 135–67. [Google Scholar] [CrossRef]
- Amihud, Yakov. 2002. Illiquidity and stock returns: Cross-section and time-series effects. Journal of Financial Markets 5: 31–56. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, and Francis X. Diebold. 2007. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility. The Review of Economics and Statistics 89: 701–20. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2003. Modeling and forecasting realized volatility. Econometrica 71: 579–625. [Google Scholar] [CrossRef]
- Ang, Andrew, Robert J. Hodrick, Yuhang Xing, and Xiaoyan Zhang. 2006. The cross-section of volatility and expected returns. The Journal of Finance 61: 259–99. [Google Scholar] [CrossRef]
- Ang, Andrew, Robert J. Hodrick, Yuhang Xing, and Xiaoyan Zhang. 2009. High idiosyncratic volatility and low returns: International and further u.s. evidence. Journal of Financial Economics 91: 1–23. [Google Scholar] [CrossRef]
- Bajgrowicz, Pierre, and Olivier Scaillet. 2012. Technical trading revisited: False discoveries, persistence tests, and transaction costs. Journal of Financial Economics 106: 473–91. [Google Scholar] [CrossRef]
- Bajgrowicz, Pierre, Olivier Scaillet, and Adrien Treccani. 2016. Jumps in high-frequency data: Spurious detections, dynamics, and news. Management Science 62: 2198–217. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Svend Erik Graversen, Jean Jacod, and Neil Shephard. 2006. Limit theorems for bipower variation in financial econometrics. Econometric Theory 22: 677–719. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Silvia Kinnebrouk, and Neil Shephard. 2010. Measuring downside risk: Realised semivariance. In Volatility and Time Series Econometrics: Essays in Honor of Robert F. Engle. Edited by Tim Bollerslev, Jeffrey Russell and Mark Watson. Oxford: Oxford University Press, pp. 117–36. [Google Scholar]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2004. Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2: 1–37. [Google Scholar] [CrossRef]
- Barras, Laurent, Olivier Scaillet, and Russ Wermers. 2010. False discoveries in mutual fund performance: Measuring luck in estimated alphas. The Journal of Finance 65: 179–216. [Google Scholar] [CrossRef]
- Bernard, Victor L., and Jacob K. Thomas. 1989. Post-earnings-announcement drift: Delayed price response or risk premium? Journal of Accounting Research 27: 1–36. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Tzuo Hann Law, and George Tauchen. 2008. Risk, jumps, and diversification. Journal of Econometrics 144: 234–56. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Sophia Zhengzi Li, and Bingzhi Zhao. 2020. Good volatility, bad volatility, and the cross-section of stock returns. Journal of Financial and Quantitative Analysis 55: 751–81. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Viktor Todorov. 2011. Estimation of jump tails. Econometrica 79: 1727–83. [Google Scholar]
- Bollerslev, Tim, Viktor Todorov, and Lai Xu. 2015. Tail risk premia and return predictability. Journal of Financial Economics 118: 113–34. [Google Scholar] [CrossRef]
- Campbell, John Y., and Tuomo Vuolteenaho. 2004. Bad beta, good beta. American Economic Review 94: 1249–75. [Google Scholar] [CrossRef]
- Christensen, Kim, Roel C. A. Oomen, and Mark Podolskij. 2014. Fact or friction: Jumps at ultra high frequency. Journal of Financial Economics 114: 576–99. [Google Scholar] [CrossRef]
- Duong, Diep, and Norman R. Swanson. 2011. Volatility in discrete and continuous-time models: A survey with new evidence on large and small jumps. In Missing Data Methods: Time-Series Methods and Applications. Edited by David M. Drukker. Advances in Econometrics, vol. 27B. Bingley: Emerald Press, pp. 179–233. [Google Scholar]
- Duong, Diep, and Norman R. Swanson. 2015. Empirical evidence on the importance of aggregation, asymmetry, and jumps for volatility prediction. Journal of Econometrics 187: 606–21. [Google Scholar] [CrossRef]
- Fang, Nengsheng, Wen Jiang, and Ronghua Luo. 2017. Realized semivariances and the variation of signed jumps in china’s stock market. Emerging Markets Finance and Trade 53: 563–86. [Google Scholar] [CrossRef]
- Feunou, Bruno, Mohammad R. Jahan-Parvar, and Romeo Tedongap. 2013. Modeling market downside volatility. Review of Finance 17: 443–81. [Google Scholar] [CrossRef]
- Feunou, Bruno, Mohammad R. Jahan-Pravar, and Cédric Okou. 2018. Downside variance risk premium. Journal of Financial Econometrics 16: 341–83. [Google Scholar] [CrossRef]
- Gu, Shihao, Bryan Kelly, and Dacheng Xiu. 2019. Empirical Asset Pricing via Machine Learning. Working Paper. Chicago: University of Chicago. [Google Scholar]
- Guo, Hui, Kent Wang, and Hao Zhou. 2015. Good Jumps, Bad Jumps, and Conditional Equity Premium. Working Paper. Cincinnati: University of Cincinnati. [Google Scholar]
- Jacod, Jean. 2008. Asymptotic properties of realized power variations and related functionals of semimartingales. Stochastic Processes and their Applications 118: 517–59. [Google Scholar] [CrossRef]
- Jiang, George J., and Tong Yao. 2013. Stock price jumps and cross-sectional return predictability. Journal of Financial and Quantitative Analysis 48: 1519–44. [Google Scholar] [CrossRef]
- Lee, Suzanne S., and Per A. Mykland. 2008. Jumps in financial markets: A new nonparametric test and jump dynamics. Review of Financial Studies 21: 2535–63. [Google Scholar] [CrossRef]
- Lee, Suzanne S., and Per A. Mykland. 2012. Jumps in equilibrium prices and market microstructure noise. Journal of Econometrics 168: 396–406. [Google Scholar] [CrossRef]
- Li, Jia, Viktor Todorov, George Tauchen, and Rui Chen. 2017. Mixed-scale jump regressions with bootstrap inference. Journal of Econometrics 201: 417–32. [Google Scholar] [CrossRef]
- Livnat, Joshua, and Richard R. Mendenhall. 2006. Comparing the post-earnings announcement drift for surprises calculated from analyst and time series forecasts. Journal of Accounting Research 44: 177–205. [Google Scholar] [CrossRef]
- Maheu, John M., and Thomas H. McCurdy. 2004. News arrival, jump dynamics, and volatility components for individual stock returns. Journal of Finance 59: 755–93. [Google Scholar] [CrossRef]
- Mancini, Cecilia. 2009. Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps. Scandinavian Journal of Statistics 36: 270–96. [Google Scholar] [CrossRef]
- Patton, Andrew J., and Kevin Sheppard. 2015. Good volatility, bad volatility: Signed jumps and the persistence of volatility. Review of Economics and Statistics 97: 683–97. [Google Scholar] [CrossRef]
- Petersen, Mitchell A. 2009. Estimating standard errors in finance panel data sets: Comparing approaches. Review of Financial Studies 22: 435–80. [Google Scholar] [CrossRef]
- Rossi, Alberto G., and Allan Timmermann. 2015. Modeling covariance risk in merton’s icapm. Review of Financial Studies 28: 1428–61. [Google Scholar] [CrossRef]
- Scaillet, Olivier, Adrien Treccani, and Christopher Trevisan. 2018. High-frequency jump analysis of the bitcoin market. Journal of Financial Econometrics. [Google Scholar] [CrossRef]
- Todorov, Viktor, and George Tauchen. 2010. Activity signature functions for high-frequency data analysis. Journal of Econometrics 154: 125–38. [Google Scholar] [CrossRef]
- Woodward, George, and Heather M. Anderson. 2009. Does beta react to market conditions? Estimates of ‘bull’ and ‘bear’ betas using a nonlinear market model with an endogenous threshold parameter. Quantitative Finance 9: 913–24. [Google Scholar] [CrossRef]
- Xiong, James X., Thomas M. Idzorek, and Roger G. Ibbotson. 2016. The economic value of forecasting left-tail risk. Journal of Portfolio Management 42: 114–23. [Google Scholar] [CrossRef]
- Yan, Shu. 2011. Jump risk, stock returns, and slope of implied volatility smile. Journal of Financial Economics 99: 216–33. [Google Scholar] [CrossRef]
- Yang, Hanxue, and Juho Kanniainen. 2016. Jump and volatility dynamics for the s&p 500: Evidence for infinite-activity jumps with non-affine volatility dynamics from stock and option markets. Review of Finance 21: 811–44. [Google Scholar]
| 1. | In 2017, Morningstar reported that this approach to investing has attracted over one trillion dollars in assets (see e.g., Jennifer Thompson, Financial Times, 27 December 2017). |
| 2. | In a related paper, Duong and Swanson (2015) construct both small and large jump measures based on some fixed truncation levels. They exploit the risk predictability of different jump measures using both index data and Dow 30 stocks and find that small jump variation has more volatility predictability than large jump variation. |
| 3. | The methods that we implement to separate jump variation use recent advances in financial econometrics due to Andersen et al. (2007, 2003), Jacod (2008), Mancini (2009), Barndorff-Nielsen et al. (2010), Todorov and Tauchen (2010), Aït-Sahalia and Jacod (2012), and Patton and Sheppard (2015). Most importantly, the reader is referred to Aït-Sahalia and Jacod (2012), who survey the methods used in this paper. |
| 4. | As noted by the editor, an important issue in the context of the estimation of jump variation components is the assessment of the importance of the cutoff methods used in this paper when disentangling small and large jump variations. Our approach to this issue in the sequel is to assess the robustness of our empirical findings to the use of various different cutoffs. However, Monte Carlo simulation may shed further light on the issue. In undertaking Monte Carlo simulations, one must carefully simulate both infinite-activity and finite-activity jump processes, consider various portfolios of simulated assets, and calibrate DGPs using models fitted to panels of high-frequency asset prices and returns. Although this topic is important, it is beyond the scope of the current paper, and is left to future research. |
| 5. | When equal-weighted portfolios are instead examined, sorting on total jump variation yields higher average returns and alphas than when sorting on small or large jump variation. However, deeper inspection of our tabulated results in this case reveals that average returns associated with large jump variation sorts are much smaller—around 1/2 of the magnitude of those associated with small and total jump variation sorts. Also, the magnitude of average returns associated with small jump variation sorts is much closer (within 10%) to the average returns associated with total jump variation sorts, when our truncation parameter uses a 5 standard-deviation cutoff instead of a 4 standard-deviation cutoff. This suggests that the jump-threshold differs depending upon portfolio type, and indicates that our findings based on equal-weighted portfolios are largely in accord with the findings elucidated above. |
| 6. | This result is not in contradiction with the extant literature on the importance of large jumps. This is because all our conclusions are for the cross-section (our paper is the first one that investigates the return predictability of large/small jump variation measured in the cross-section). It is true that large jumps have been shown to have return/variance predictability for individual stocks/portfolios. But in the cross-section, we do not observe such return predictability. In this cross-section, this is simply because large jumps are rare, so that they provide little (or at least infrequent) information for future weekly returns, in the cross-section. |
| 7. | This result is consistent with the finding of Amaya et al. (2015) that preference for positive asymmetry (skewness) may partially explain the idiosyncratic volatility puzzle, especially for small firms. |
| 8. | A jump process has finite activity when it makes a finite number of jumps, almost surely, in each finite time interval, otherwise it is said to have infinite activity. |
| 9. | As an example of how our cutoff level compares with others used in the literature, consider Li et al. (2017). These authors use bipower variation as the fixed value for . We instead use bipower variation as the initial value for the integrated volatility , say, and is estimated using truncated bipower variation with threshold , say, where is fixed only when is smaller than . |
| 10. | Here, the threshold, , is estimated using the same procedure as in footnote 9. |
| 11. | In some cases, multiple TAQ symbols are matched with a unique Center for Research in Security Prices (CRSP) PERMNO. Over each quarter, the TAQ symbol which has the most observations is kept and the other overlapping observations are dropped. |
| 12. | The kurtosis of signed jump variation is 4.36. For realized skewness, the analogous statistic is 12.04. |
| 13. | The unconditional kurtosis is 6.43 and 3.51, for signed small and large jump variation, based on truncation level ; and 8.87 and 3.09 based on truncation level , respectively. |
| 14. | The kurtosis is 15.85 and 27.24, for the unconditional distribution of realized volatility and realized kurtosis, respectively. |
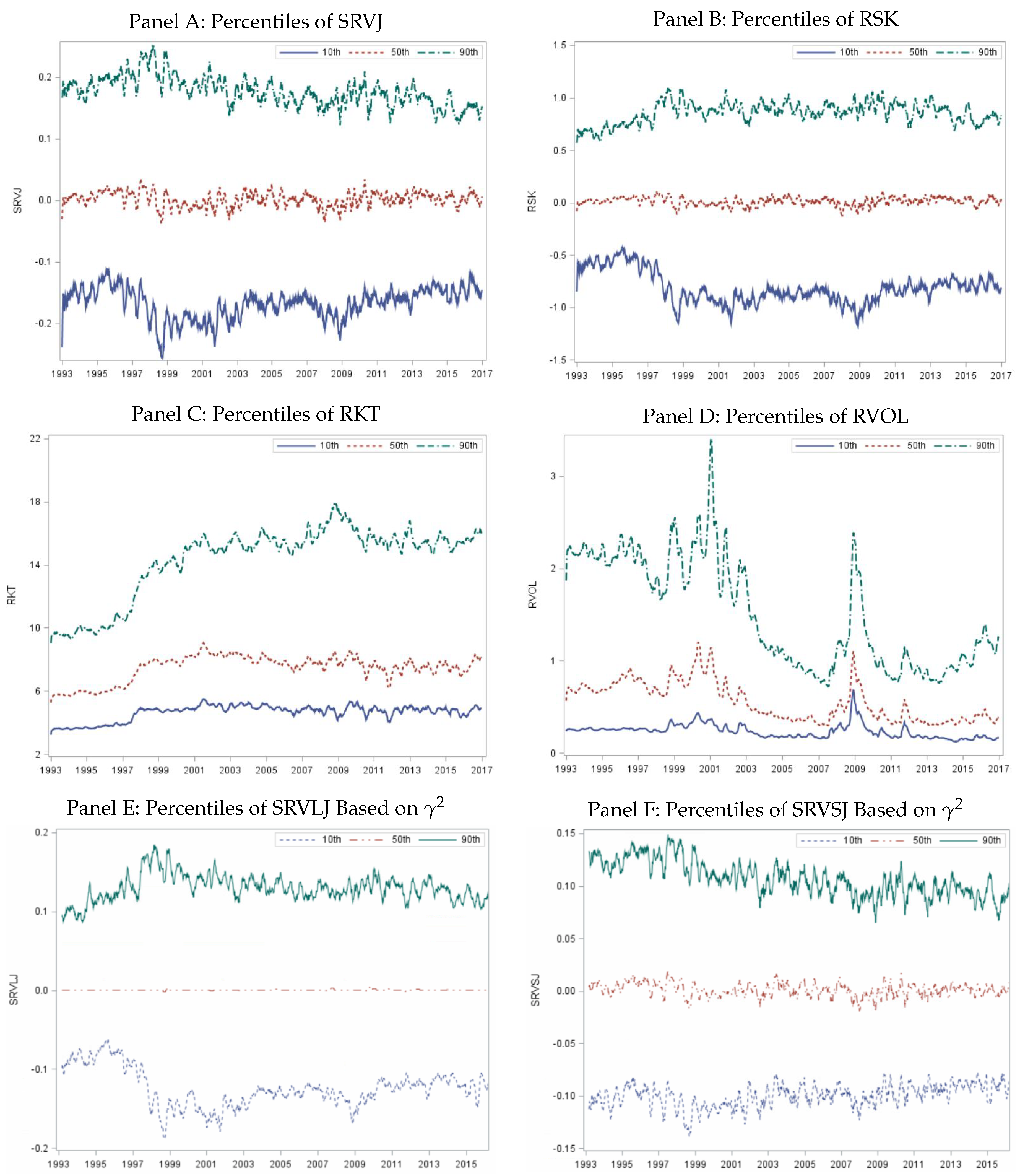
| 15. | See the Supplementary Appendix for results based on the examination of additional quintile portfolios that are constructed based on ex-ante risk measures and displayed with ex-post risk measures. It is clear that sorting stocks based on jump risk measures results in portfolios with the desired risk exposures. |
| 16. | Empirical findings based on are similar to those discussed above, and hence are not reported. This robustness of our findings to the choice of also characterizes the other empirical findings discussed in the sequel. |
| 17. | Cumulative returns calculations do not include the risk-free rate. For a definition of cumulative returns both with and without the weekly risk-free rate, see Bollerslev et al. (2020). |
| 18. | Please note that RSJ, which measures the same signed jump variation as SRVJ, although using different estimation methodology, generates the highest cumulative return for equal-weighted portfolios, but is dominated by SRVSJ for value-weighted portfolios. |
| 19. | Results are virtually identical if we only include days in which at least 12 or 24 firms report earnings surprises. |
| 20. | See the Supplementary Appendix for plots of jump variation measures for the other quintile portfolios. |
| 21. | Specifically, our objective in this section is to discuss regressions of the form given in Equation (15), with the dependent variable replaced by various realized variables. |
| 22. | See the Supplementary Appendix for results from double-sorted portfolios that condition on various control variables. In these tables, it is noteworthy that when stocks are first sorted by a control variable (e.g., illiquidity, volatility, firm size and reversal), the SRVJ (SRVLJ and SRVSJ) effect is much higher within quintile portfolios with high illiquidity, high volatility, small firm size, and low reversal. This result suggests that all these control variables significantly contribute to the predictability of jump variation measures. This result provides additional confirmation to earlier findings reported in Bollerslev et al. (2020). |
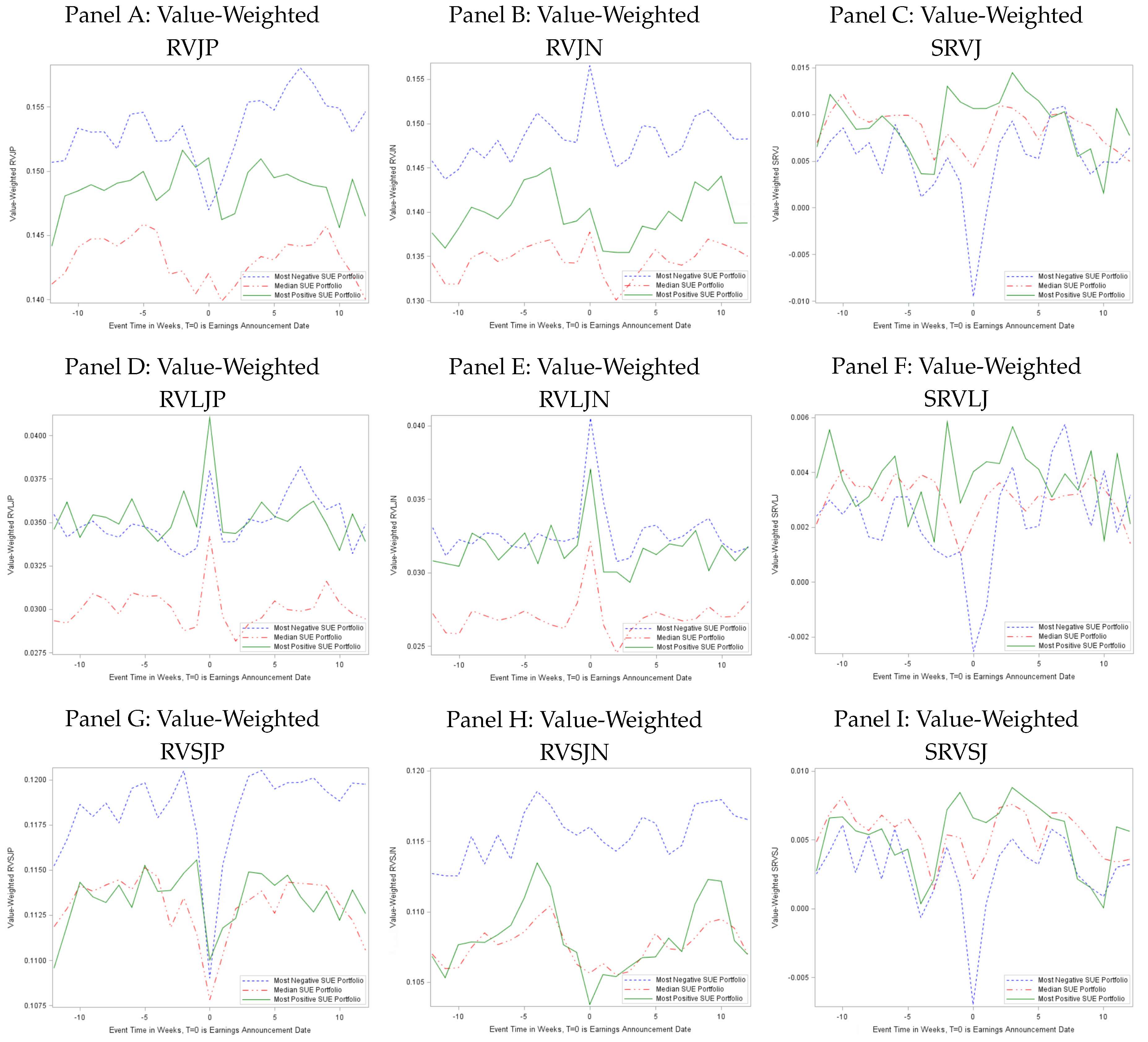
| Panel A: Realized Measures Used in Portfolio Sorts and Fama–MacBeth Regressions | |||||||
|---|---|---|---|---|---|---|---|
| RVJP | Positive (upside) jump variation, see (1). | ||||||
| RVJN | Negative (downside) jump variation, see (2). | ||||||
| SRVJ | Signed jump variation, , see (3). | ||||||
| RVLJP | Positive (upside) large jump variation, see (4). | ||||||
| RVLJN | Negative (downside) large jump variation, see (5). | ||||||
| SRVLJ | Signed large jump variation, , see (6). | ||||||
| RVSJP | Positive (upside) small jump variation, see (7). | ||||||
| RVSJN | Negative (downside) small jump variation, see (8). | ||||||
| SRVSJ | Signed small jump variation, , see (9). | ||||||
| RVOL | Realized volatility | ||||||
| RSK | Realized skewness, see (12). | ||||||
| RKT | Realized kurtosis, see (13). | ||||||
| Panel B: Explanatory Variables and Firm Characteristics Used in Fama–MacBeth Regressions | |||||||
| BETA | Market beta | ||||||
| log(Size) | Natural logarithm of firm size | ||||||
| BEME | Book-to-market ratio | ||||||
| MOM | Momentum | ||||||
| REV | Short-term reversal | ||||||
| IVOL | Idiosyncratic volatility | ||||||
| CSK | Co-skewness | ||||||
| CKT | Co-kurtosis | ||||||
| MAX | Maximum daily return | ||||||
| MIN | Minimum daily return | ||||||
| ILLIQ | Illiquidity | ||||||
| Panel A: Cross-Sectional Summary Statistics | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRVJ | RVJP | RVJN | SRVLJ | RVLJP | RVLJN | SRVSJ | RVSJP | RVSJN | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ | |
| Part I: Jump Truncation Level = | |||||||||||||||||||||||
| Mean | 0.0061 | 0.2698 | 0.2637 | 0.0045 | 0.1518 | 0.1472 | 0.0015 | 0.1180 | 0.1165 | 0.9489 | 0.0288 | 8.2569 | 1.0794 | 6.5280 | 0.5969 | 2023.8456 | 70.6077 | 0.0293 | −0.0263 | 1.1438 | 412.1094 | −346.7608 | −5.2826 |
| Std | 0.1537 | 0.1350 | 0.1347 | 0.1424 | 0.1555 | 0.1523 | 0.0635 | 0.0783 | 0.0783 | 2.1211 | 0.8159 | 4.5706 | 0.5566 | 1.8359 | 0.7224 | 7464.5273 | 927.3551 | 0.0250 | 0.3283 | 0.8474 | 572.1454 | 359.6789 | 2.4047 |
| Part II: Jump Truncation Level = | |||||||||||||||||||||||
| Mean | 0.0061 | 0.2698 | 0.2637 | 0.0029 | 0.0983 | 0.0954 | 0.0031 | 0.1715 | 0.1684 | 0.9489 | 0.0288 | 8.2569 | 1.0794 | 6.5280 | 0.5969 | 2023.8456 | 70.6077 | 0.0293 | −0.0263 | 1.1438 | 412.1094 | −346.7608 | −5.2826 |
| Std | 0.1537 | 0.1350 | 0.1347 | 0.1303 | 0.1401 | 0.1368 | 0.0859 | 0.0911 | 0.0909 | 2.1211 | 0.8159 | 4.5706 | 0.5566 | 1.8359 | 0.7224 | 7464.5273 | 927.3551 | 0.0250 | 0.3283 | 0.8474 | 572.1454 | 359.6789 | 2.4047 |
| Panel B: Cross-Sectional Correlations | |||||||||||||||||||||||
| SRVJ | RVJP | RVJN | SRVLJ | RVLJP | RVLJN | SRVSJ | RVSJP | RVSJN | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ | |
| Part I: Jump Truncation Level = | |||||||||||||||||||||||
| SRVJ | 1.00 | 0.57 | −0.57 | 0.91 | 0.43 | −0.40 | 0.37 | 0.13 | −0.18 | −0.02 | 0.94 | 0.03 | −0.03 | 0.01 | 0.01 | 0.01 | 0.30 | −0.03 | 0.09 | 0.00 | 0.17 | 0.22 | 0.00 |
| RVJP | 1.00 | 0.33 | 0.52 | 0.85 | 0.37 | 0.21 | 0.04 | −0.13 | 0.22 | 0.54 | 0.45 | −0.26 | −0.49 | 0.14 | −0.10 | 0.15 | 0.12 | 0.04 | −0.24 | 0.15 | 0.06 | 0.56 | |
| RVJN | 1.00 | −0.52 | 0.35 | 0.84 | −0.22 | −0.10 | 0.08 | 0.24 | −0.54 | 0.41 | −0.23 | −0.49 | 0.13 | −0.11 | −0.19 | 0.15 | −0.06 | −0.24 | −0.05 | −0.20 | 0.55 | ||
| SRVLJ | 1.00 | 0.48 | −0.44 | −0.04 | −0.05 | −0.01 | −0.01 | 0.92 | 0.03 | −0.02 | 0.00 | 0.01 | 0.00 | 0.20 | −0.02 | 0.05 | 0.00 | 0.12 | 0.16 | 0.00 | |||
| RVLJP | 1.00 | 0.57 | −0.02 | −0.46 | −0.45 | 0.23 | 0.44 | 0.61 | −0.25 | −0.47 | 0.12 | −0.06 | 0.09 | 0.13 | 0.02 | −0.24 | 0.12 | −0.02 | 0.54 | ||||
| RVLJN | 1.00 | 0.01 | −0.44 | −0.45 | 0.24 | −0.41 | 0.59 | −0.23 | −0.48 | 0.11 | −0.06 | −0.10 | 0.15 | −0.03 | −0.24 | 0.01 | −0.17 | 0.54 | |||||
| SRVSJ | 1.00 | 0.42 | −0.42 | −0.02 | 0.19 | 0.00 | −0.03 | 0.01 | 0.01 | 0.01 | 0.26 | −0.03 | 0.08 | 0.00 | 0.14 | 0.18 | 0.00 | ||||||
| RVSJP | 1.00 | 0.64 | −0.04 | 0.06 | −0.40 | 0.06 | 0.03 | 0.01 | −0.05 | 0.10 | −0.03 | 0.04 | 0.04 | 0.02 | 0.11 | −0.06 | |||||||
| RVSJN | 1.00 | −0.03 | −0.10 | −0.40 | 0.08 | 0.02 | 0.01 | −0.06 | −0.12 | −0.01 | −0.03 | 0.03 | −0.09 | −0.04 | −0.06 | ||||||||
| RVOL | 1.00 | −0.01 | 0.22 | −0.05 | −0.55 | 0.08 | −0.12 | 0.06 | 0.56 | −0.01 | −0.27 | 0.44 | −0.47 | 0.56 | |||||||||
| RSK | 1.00 | 0.04 | −0.02 | 0.00 | 0.01 | 0.00 | 0.22 | −0.02 | 0.06 | 0.00 | 0.13 | 0.17 | 0.00 | ||||||||||
| RKT | 1.00 | −0.20 | −0.34 | 0.09 | −0.02 | 0.00 | 0.10 | −0.01 | −0.19 | 0.08 | −0.10 | 0.40 | |||||||||||
| BETA | 1.00 | 0.10 | −0.09 | 0.00 | −0.04 | 0.06 | 0.01 | 0.30 | 0.03 | −0.09 | −0.16 | ||||||||||||
| ME | 1.00 | −0.19 | 0.11 | −0.05 | −0.52 | 0.01 | 0.40 | −0.32 | 0.35 | −0.93 | |||||||||||||
| BEME | 1.00 | 0.03 | 0.02 | 0.05 | 0.00 | −0.06 | 0.05 | −0.03 | 0.18 | ||||||||||||||
| MOM | 1.00 | 0.00 | −0.08 | −0.07 | 0.06 | −0.05 | 0.05 | −0.15 | |||||||||||||||
| REV | 1.00 | 0.12 | 0.16 | −0.04 | 0.49 | 0.29 | 0.05 | ||||||||||||||||
| IVOL | 1.00 | 0.02 | −0.35 | 0.50 | −0.47 | 0.47 | |||||||||||||||||
| CSK | 1.00 | 0.01 | 0.07 | 0.07 | 0.00 | ||||||||||||||||||
| CKT | 1.00 | −0.16 | 0.15 | −0.37 | |||||||||||||||||||
| MAX | 1.00 | −0.28 | 0.34 | ||||||||||||||||||||
| MIN | 1.00 | −0.35 | |||||||||||||||||||||
| ILLIQ | 1.00 | ||||||||||||||||||||||
| SRVJ | RVJP | RVJN | SRVLJ | RVLJP | RVLJN | SRVSJ | RVSJP | RVSJN | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ | |
| Part II: Jump Truncation Level = | |||||||||||||||||||||||
| SRVJ | 1.00 | 0.57 | −0.57 | 0.83 | 0.40 | −0.37 | 0.52 | 0.23 | −0.27 | −0.02 | 0.94 | 0.03 | −0.03 | 0.01 | 0.01 | 0.01 | 0.30 | −0.03 | 0.09 | 0.00 | 0.17 | 0.22 | 0.00 |
| RVJP | 1.00 | 0.33 | 0.48 | 0.77 | 0.33 | 0.30 | 0.30 | 0.01 | 0.22 | 0.54 | 0.45 | −0.26 | −0.49 | 0.14 | −0.10 | 0.15 | 0.12 | 0.04 | −0.24 | 0.15 | 0.06 | 0.56 | |
| RVJN | 1.00 | −0.47 | 0.31 | 0.75 | −0.31 | 0.03 | 0.33 | 0.24 | −0.54 | 0.41 | −0.23 | −0.49 | 0.13 | −0.11 | −0.19 | 0.15 | −0.06 | −0.24 | −0.05 | −0.20 | 0.55 | ||
| SRVLJ | 1.00 | 0.49 | −0.44 | −0.04 | −0.05 | −0.01 | −0.01 | 0.89 | 0.04 | −0.01 | 0.00 | 0.01 | 0.00 | 0.16 | −0.02 | 0.04 | 0.00 | 0.09 | 0.13 | 0.00 | |||
| RVLJP | 1.00 | 0.56 | −0.02 | −0.36 | −0.34 | 0.20 | 0.43 | 0.64 | −0.24 | −0.40 | 0.11 | −0.05 | 0.06 | 0.11 | 0.01 | −0.22 | 0.10 | −0.02 | 0.47 | ||||
| RVLJN | 1.00 | 0.01 | −0.34 | −0.35 | 0.21 | −0.40 | 0.62 | −0.23 | −0.41 | 0.10 | −0.06 | −0.09 | 0.13 | −0.03 | −0.22 | 0.01 | −0.14 | 0.47 | |||||
| SRVSJ | 1.00 | 0.47 | −0.47 | −0.02 | 0.32 | 0.00 | −0.03 | 0.01 | 0.01 | 0.01 | 0.30 | −0.03 | 0.09 | 0.00 | 0.16 | 0.21 | 0.00 | ||||||
| RVSJP | 1.00 | 0.55 | 0.03 | 0.13 | −0.30 | −0.02 | −0.14 | 0.04 | −0.07 | 0.13 | 0.02 | 0.04 | −0.04 | 0.07 | 0.10 | 0.13 | |||||||
| RVSJN | 1.00 | 0.05 | −0.17 | −0.30 | 0.01 | −0.15 | 0.04 | −0.07 | −0.15 | 0.05 | −0.04 | −0.04 | −0.08 | −0.09 | 0.13 | ||||||||
| RVOL | 1.00 | −0.01 | 0.22 | −0.05 | −0.55 | 0.08 | −0.12 | 0.06 | 0.56 | −0.01 | −0.27 | 0.44 | −0.47 | 0.56 | |||||||||
| RSK | 1.00 | 0.04 | −0.02 | 0.00 | 0.01 | 0.00 | 0.22 | −0.02 | 0.06 | 0.00 | 0.13 | 0.17 | 0.00 | ||||||||||
| RKT | 1.00 | −0.20 | −0.34 | 0.09 | −0.02 | 0.00 | 0.10 | −0.01 | −0.19 | 0.08 | −0.10 | 0.40 | |||||||||||
| BETA | 1.00 | 0.10 | −0.09 | 0.00 | −0.04 | 0.06 | 0.01 | 0.30 | 0.03 | −0.09 | −0.16 | ||||||||||||
| ME | 1.00 | −0.19 | 0.11 | −0.05 | −0.52 | 0.01 | 0.40 | −0.32 | 0.35 | −0.93 | |||||||||||||
| BEME | 1.00 | 0.03 | 0.02 | 0.05 | 0.00 | −0.06 | 0.05 | −0.03 | 0.18 | ||||||||||||||
| MOM | 1.00 | 0.00 | −0.08 | −0.07 | 0.06 | −0.05 | 0.05 | −0.15 | |||||||||||||||
| REV | 1.00 | 0.12 | 0.16 | −0.04 | 0.49 | 0.29 | 0.05 | ||||||||||||||||
| IVOL | 1.00 | 0.02 | −0.35 | 0.50 | −0.47 | 0.47 | |||||||||||||||||
| CSK | 1.00 | 0.01 | 0.07 | 0.07 | 0.00 | ||||||||||||||||||
| CKT | 1.00 | −0.16 | 0.15 | −0.37 | |||||||||||||||||||
| MAX | 1.00 | −0.28 | 0.34 | ||||||||||||||||||||
| MIN | 1.00 | −0.35 | |||||||||||||||||||||
| ILLIQ | 1.00 | ||||||||||||||||||||||
| Panel A: Stocks Sorted by SRVJ | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Quintile | RVJP | RVJN | RVLJP | RVLJN | RVSJP | RVSJN | SRVLJ | SRVSJ | SRVJ | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ |
| 1 | 0.2021 | 0.3959 | 0.1161 | 0.2723 | 0.0860 | 0.1235 | −0.1563 | −0.0375 | −0.1938 | 0.9394 | −0.9324 | 9.8720 | 1.0369 | 6.1326 | 0.6235 | 0.2006 | −0.0363 | 0.0317 | −0.0708 | 1.0482 | 0.0295 | −0.0494 | −4.6903 |
| 2 | 0.2200 | 0.2777 | 0.1015 | 0.1391 | 0.1185 | 0.1385 | −0.0376 | −0.0200 | −0.0576 | 0.9513 | −0.2504 | 7.1729 | 1.1351 | 6.7041 | 0.5711 | 0.2051 | −0.0111 | 0.0293 | −0.0443 | 1.1987 | 0.0346 | −0.0383 | −5.5835 |
| 3 | 0.2435 | 0.2399 | 0.1127 | 0.1103 | 0.1308 | 0.1296 | 0.0023 | 0.0012 | 0.0036 | 1.0360 | 0.0194 | 6.9162 | 1.1301 | 6.8171 | 0.5695 | 0.2030 | 0.0077 | 0.0283 | −0.0242 | 1.2222 | 0.0397 | −0.0328 | −5.7301 |
| 4 | 0.2801 | 0.2138 | 0.1441 | 0.1005 | 0.1360 | 0.1132 | 0.0436 | 0.0227 | 0.0663 | 0.9162 | 0.2954 | 7.2497 | 1.1096 | 6.7855 | 0.5778 | 0.2097 | 0.0266 | 0.0278 | −0.0066 | 1.2055 | 0.0454 | −0.0282 | −5.6668 |
| 5 | 0.4035 | 0.1914 | 0.2846 | 0.1138 | 0.1189 | 0.0775 | 0.1708 | 0.0413 | 0.2121 | 0.9018 | 1.0138 | 10.0739 | 0.9851 | 6.2007 | 0.6427 | 0.1936 | 0.0485 | 0.0293 | 0.0145 | 1.0443 | 0.0569 | −0.0247 | −4.7419 |
| Panel B: Stocks Sorted by SRVLJ | |||||||||||||||||||||||
| Quintile | RVJP | RVJN | RVLJP | RVLJN | RVSJP | RVSJN | SRVLJ | SRVSJ | SRVJ | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ |
| Part I: Jump Truncation Level = | |||||||||||||||||||||||
| 1 | 0.2255 | 0.3959 | 0.1250 | 0.3016 | 0.1005 | 0.0943 | −0.1766 | 0.0062 | −0.1703 | 0.9429 | −0.9075 | 10.2967 | 1.0163 | 6.0403 | 0.6329 | 0.1966 | −0.0221 | 0.0316 | −0.0548 | 1.0357 | 0.0347 | −0.0461 | −4.5515 |
| 2 | 0.2222 | 0.2603 | 0.0874 | 0.1297 | 0.1347 | 0.1307 | −0.0422 | 0.0041 | −0.0382 | 0.9128 | −0.2003 | 6.9378 | 1.1314 | 6.7639 | 0.5678 | 0.2104 | −0.0011 | 0.0288 | −0.0329 | 1.2050 | 0.0374 | −0.0357 | −5.6652 |
| 3 | 0.2296 | 0.2252 | 0.0968 | 0.0936 | 0.1329 | 0.1316 | 0.0032 | 0.0013 | 0.0044 | 1.1510 | 0.0218 | 6.5571 | 1.1308 | 6.9059 | 0.5648 | 0.1997 | 0.0069 | 0.0282 | −0.0245 | 1.2380 | 0.0390 | −0.0326 | −5.8581 |
| 4 | 0.2726 | 0.2229 | 0.1493 | 0.0981 | 0.1233 | 0.1248 | 0.0512 | −0.0016 | 0.0497 | 0.8314 | 0.2602 | 7.2170 | 1.1237 | 6.7993 | 0.5764 | 0.2118 | 0.0169 | 0.0280 | −0.0166 | 1.2086 | 0.0421 | −0.0304 | −5.6962 |
| 5 | 0.4041 | 0.2153 | 0.3149 | 0.1234 | 0.0891 | 0.0920 | 0.1915 | −0.0028 | 0.1887 | 0.9158 | 0.9900 | 10.5179 | 0.9873 | 6.0946 | 0.6471 | 0.1887 | 0.0354 | 0.0299 | −0.0021 | 1.0376 | 0.0533 | −0.0284 | −4.6003 |
| Part II: Jump Truncation Level = | |||||||||||||||||||||||
| 1 | 0.2412 | 0.3897 | 0.0841 | 0.2403 | 0.1571 | 0.1494 | −0.1561 | 0.0076 | −0.1485 | 0.9355 | −0.8465 | 10.5599 | 1.0128 | 6.0603 | 0.6360 | 0.1928 | −0.0152 | 0.0313 | −0.0478 | 1.0403 | 0.0366 | −0.0438 | −4.5663 |
| 2 | 0.2189 | 0.2314 | 0.0341 | 0.0519 | 0.1848 | 0.1794 | −0.0178 | 0.0054 | −0.0124 | 0.9321 | −0.0762 | 6.4172 | 1.1366 | 6.8798 | 0.5622 | 0.2132 | 0.0045 | 0.0283 | −0.0278 | 1.2310 | 0.0388 | −0.0340 | −5.8322 |
| 3 | 0.2438 | 0.2405 | 0.0805 | 0.0770 | 0.1633 | 0.1635 | 0.0035 | −0.0001 | 0.0033 | 1.6847 | 0.0202 | 7.7437 | 1.0936 | 6.5831 | 0.6248 | 0.1664 | 0.0063 | 0.0322 | −0.0021 | 1.2281 | 0.0426 | −0.0360 | −5.3661 |
| 4 | 0.2985 | 0.2611 | 0.1233 | 0.0854 | 0.1752 | 0.1756 | 0.0379 | −0.0004 | 0.0375 | 1.0724 | 0.2140 | 8.0742 | 1.0912 | 6.4686 | 0.5995 | 0.1944 | 0.0125 | 0.0294 | −0.0213 | 1.1478 | 0.0418 | −0.0324 | −5.2346 |
| 5 | 0.3985 | 0.2321 | 0.2526 | 0.0837 | 0.1459 | 0.1484 | 0.1690 | −0.0025 | 0.1664 | 0.9201 | 0.9332 | 10.8242 | 0.9935 | 6.1033 | 0.6466 | 0.1896 | 0.0285 | 0.0300 | −0.0084 | 1.0418 | 0.0506 | −0.0301 | −4.6103 |
| Panel C: Stocks Sorted by SRVSJ | |||||||||||||||||||||||
| Quintile | RVJP | RVJN | RVLJP | RVLJN | RVSJP | RVSJN | SRVLJ | SRVSJ | SRVJ | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ |
| Part I: Jump Truncation Level = | |||||||||||||||||||||||
| 1 | 0.2060 | 0.2784 | 0.1085 | 0.0968 | 0.0975 | 0.1815 | 0.0116 | −0.0840 | −0.0724 | 0.7622 | −0.1832 | 7.1817 | 1.1514 | 6.7378 | 0.5654 | 0.2183 | −0.0270 | 0.0292 | −0.0637 | 1.2017 | 0.0302 | −0.0438 | −5.6348 |
| 2 | 0.2711 | 0.2845 | 0.1758 | 0.1649 | 0.0952 | 0.1197 | 0.0110 | −0.0244 | −0.0135 | 1.0260 | −0.0157 | 8.6959 | 1.0715 | 6.4139 | 0.6062 | 0.1933 | −0.0046 | 0.0302 | −0.0417 | 1.1242 | 0.0380 | −0.0375 | −5.1168 |
| 3 | 0.3077 | 0.3003 | 0.2186 | 0.2126 | 0.0891 | 0.0877 | 0.0060 | 0.0014 | 0.0074 | 1.2309 | 0.0345 | 9.7978 | 1.0053 | 6.1262 | 0.6382 | 0.1754 | 0.0066 | 0.0309 | −0.0275 | 1.0469 | 0.0423 | −0.0356 | −4.6619 |
| 4 | 0.2743 | 0.2492 | 0.1413 | 0.1438 | 0.1330 | 0.1053 | −0.0026 | 0.0277 | 0.0251 | 0.9562 | 0.0709 | 8.0830 | 1.0906 | 6.6614 | 0.5854 | 0.2098 | 0.0190 | 0.0283 | −0.0099 | 1.1752 | 0.0436 | −0.0305 | −5.4837 |
| 5 | 0.2830 | 0.1981 | 0.1004 | 0.1051 | 0.1826 | 0.0930 | −0.0047 | 0.0896 | 0.0849 | 0.7380 | 0.2395 | 7.1974 | 1.0947 | 6.8064 | 0.5783 | 0.2217 | 0.0428 | 0.0272 | 0.0136 | 1.1959 | 0.0517 | −0.0251 | −5.6801 |
| Part II: Jump Truncation Level = | |||||||||||||||||||||||
| 1 | 0.2058 | 0.3081 | 0.0749 | 0.0650 | 0.1309 | 0.2431 | 0.0099 | −0.1121 | −0.1023 | 0.8104 | −0.3171 | 7.6436 | 1.1207 | 6.5435 | 0.5792 | 0.2179 | −0.0318 | 0.0301 | −0.0682 | 1.1558 | 0.0296 | −0.0461 | −5.3493 |
| 2 | 0.2561 | 0.2841 | 0.1103 | 0.1027 | 0.1458 | 0.1814 | 0.0077 | −0.0356 | −0.0280 | 1.0119 | −0.0747 | 8.4222 | 1.0918 | 6.5103 | 0.5957 | 0.1964 | −0.0079 | 0.0298 | −0.0427 | 1.1482 | 0.0363 | −0.0379 | −5.2661 |
| 3 | 0.2906 | 0.2847 | 0.1423 | 0.1381 | 0.1484 | 0.1465 | 0.0041 | 0.0019 | 0.0060 | 1.1729 | 0.0308 | 9.3041 | 1.0385 | 6.3412 | 0.6204 | 0.1788 | 0.0065 | 0.0301 | −0.0273 | 1.0955 | 0.0413 | −0.0346 | −4.9812 |
| 4 | 0.2821 | 0.2444 | 0.0950 | 0.0979 | 0.1871 | 0.1465 | −0.0029 | 0.0405 | 0.0377 | 0.9731 | 0.1235 | 8.1884 | 1.0851 | 6.6358 | 0.5919 | 0.2046 | 0.0220 | 0.0284 | −0.0086 | 1.1700 | 0.0447 | −0.0299 | −5.4350 |
| 5 | 0.3137 | 0.1959 | 0.0671 | 0.0713 | 0.2466 | 0.1246 | −0.0043 | 0.1220 | 0.1178 | 0.7734 | 0.3845 | 7.6692 | 1.0627 | 6.6238 | 0.5954 | 0.2153 | 0.0469 | 0.0278 | 0.0158 | 1.1527 | 0.0543 | −0.0245 | −5.4040 |
| Panel D: Stocks Sorted by RVOL | |||||||||||||||||||||||
| Quintile | RVJP | RVJN | RVLJP | RVLJN | RVSJP | RVSJN | SRVLJ | SRVSJ | SRVJ | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ |
| 1 | 0.2255 | 0.2140 | 0.1013 | 0.0943 | 0.1241 | 0.1197 | 0.0070 | 0.0044 | 0.0114 | 0.2290 | 0.0485 | 6.8794 | 0.8390 | 8.3393 | 0.5407 | 0.1686 | 0.0040 | 0.0137 | −0.0213 | 1.4325 | 0.0177 | −0.0154 | −7.4961 |
| 2 | 0.2375 | 0.2282 | 0.1136 | 0.1071 | 0.1240 | 0.1211 | 0.0065 | 0.0028 | 0.0094 | 0.3596 | 0.0403 | 7.2835 | 1.0471 | 7.4505 | 0.5506 | 0.1853 | 0.0044 | 0.0187 | −0.0213 | 1.3708 | 0.0257 | −0.0227 | −6.4401 |
| 3 | 0.2567 | 0.2493 | 0.1387 | 0.1327 | 0.1180 | 0.1166 | 0.0060 | 0.0014 | 0.0074 | 0.5331 | 0.0341 | 7.9018 | 1.2246 | 6.6274 | 0.5581 | 0.2598 | 0.0051 | 0.0253 | −0.0249 | 1.2373 | 0.0346 | −0.0304 | −5.5465 |
| 4 | 0.2864 | 0.2823 | 0.1717 | 0.1675 | 0.1147 | 0.1148 | 0.0042 | −0.0001 | 0.0041 | 0.8136 | 0.0216 | 8.7067 | 1.2761 | 5.7649 | 0.5997 | 0.3071 | 0.0058 | 0.0338 | −0.0308 | 1.0491 | 0.0464 | −0.0405 | −4.4310 |
| 5 | 0.3429 | 0.3449 | 0.2336 | 0.2347 | 0.1093 | 0.1102 | −0.0011 | −0.0010 | −0.0021 | 2.8115 | −0.0003 | 10.5156 | 1.0101 | 4.4547 | 0.7443 | 0.0910 | 0.0160 | 0.0548 | −0.0331 | 0.6286 | 0.0817 | −0.0645 | −2.4951 |
| Panel E: Stocks Sorted by RSK | |||||||||||||||||||||||
| Quintile | RVJP | RVJN | RVLJP | RVLJN | RVSJP | RVSJN | SRVLJ | SRVSJ | SRVJ | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ |
| 1 | 0.2077 | 0.3914 | 0.1200 | 0.2822 | 0.0877 | 0.1091 | −0.1622 | −0.0215 | −0.1837 | 0.9182 | −0.9829 | 10.3573 | 1.0293 | 6.1615 | 0.6212 | 0.2118 | −0.0274 | 0.0312 | −0.0611 | 1.0555 | 0.0324 | −0.0472 | −4.7275 |
| 2 | 0.2203 | 0.2758 | 0.0967 | 0.1366 | 0.1235 | 0.1393 | −0.0398 | −0.0157 | −0.0556 | 0.9332 | −0.2596 | 6.8740 | 1.1303 | 6.7033 | 0.5719 | 0.2052 | −0.0077 | 0.0291 | −0.0412 | 1.1981 | 0.0353 | −0.0374 | −5.5757 |
| 3 | 0.2430 | 0.2394 | 0.1057 | 0.1035 | 0.1373 | 0.1359 | 0.0023 | 0.0014 | 0.0037 | 1.1222 | 0.0189 | 6.5111 | 1.1288 | 6.8070 | 0.5748 | 0.1932 | 0.0073 | 0.0283 | −0.0238 | 1.2155 | 0.0391 | −0.0325 | −5.7121 |
| 4 | 0.2786 | 0.2142 | 0.1418 | 0.0960 | 0.1368 | 0.1182 | 0.0459 | 0.0186 | 0.0644 | 0.8769 | 0.3040 | 6.9460 | 1.1139 | 6.7671 | 0.5790 | 0.2056 | 0.0231 | 0.0280 | −0.0098 | 1.2017 | 0.0444 | −0.0290 | −5.6422 |
| 5 | 0.3996 | 0.1978 | 0.2947 | 0.1179 | 0.1049 | 0.0800 | 0.1769 | 0.0249 | 0.2018 | 0.8942 | 1.0656 | 10.5964 | 0.9944 | 6.2012 | 0.6374 | 0.1963 | 0.0400 | 0.0297 | 0.0045 | 1.0482 | 0.0549 | −0.0272 | −4.7552 |
| Panel F: Stocks Sorted by RKT | |||||||||||||||||||||||
| Quintile | RVJP | RVJN | RVLJP | RVLJN | RVSJP | RVSJN | SRVLJ | SRVSJ | SRVJ | RVOL | RSK | RKT | BETA | log(Size) | BEME | MOM | REV | IVOL | CSK | CKT | MAX | MIN | ILLIQ |
| 1 | 0.1804 | 0.1785 | 0.0257 | 0.0248 | 0.1548 | 0.1536 | 0.0008 | 0.0011 | 0.0019 | 0.6884 | 0.0110 | 4.4470 | 1.1920 | 7.6130 | 0.5303 | 0.1864 | 0.0054 | 0.0248 | −0.0222 | 1.3529 | 0.0339 | −0.0290 | −6.7592 |
| 2 | 0.2242 | 0.2206 | 0.0757 | 0.0738 | 0.1484 | 0.1468 | 0.0020 | 0.0017 | 0.0036 | 0.7285 | 0.0167 | 5.7679 | 1.1586 | 6.9411 | 0.5522 | 0.2203 | 0.0077 | 0.0276 | −0.0252 | 1.2505 | 0.0387 | −0.0324 | −5.9541 |
| 3 | 0.2630 | 0.2582 | 0.1340 | 0.1310 | 0.1291 | 0.1272 | 0.0030 | 0.0019 | 0.0048 | 0.8130 | 0.0215 | 7.0711 | 1.1103 | 6.5028 | 0.5817 | 0.2175 | 0.0083 | 0.0296 | −0.0265 | 1.1627 | 0.0417 | −0.0347 | −5.3464 |
| 4 | 0.3070 | 0.3004 | 0.2067 | 0.2017 | 0.1004 | 0.0987 | 0.0049 | 0.0017 | 0.0066 | 0.9433 | 0.0292 | 8.9744 | 1.0438 | 6.0841 | 0.6186 | 0.2085 | 0.0076 | 0.0313 | −0.0281 | 1.0644 | 0.0440 | −0.0370 | −4.6922 |
| 5 | 0.3745 | 0.3612 | 0.3171 | 0.3051 | 0.0574 | 0.0561 | 0.0119 | 0.0013 | 0.0133 | 1.5722 | 0.0660 | 15.0322 | 0.8918 | 5.4974 | 0.7022 | 0.1793 | 0.0064 | 0.0332 | −0.0295 | 0.8881 | 0.0478 | −0.0403 | −3.6585 |
| Panel A: Stocks Sorted by RVJP | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 33.65 | 30.50 | 33.04 | 28.08 | 20.64 | −13.01 *** | 23.52 | 19.48 | 17.93 | 20.91 | 18.27 | −5.25 | |
| (3.54) | (3.28) | (3.49) | (2.87) | (2.19) | (−2.75) | (3.54) | (3.27) | (2.93) | (3.35) | (2.83) | (−1.35) | ||
| Alpha | 10.59 | 7.47 | 11.24 | 7.52 | 2.88 | −7.71 | 2.88 | −0.63 | −2.30 | 0.67 | −2.75 | −5.63 * | |
| (4.16) | (3.64) | (4.34) | (2.33) | (0.72) | (−1.64) | (2.31) | (−0.44) | (−1.22) | (0.32) | (−1.19) | (−1.87) | ||
| Panel B: Stocks Sorted by RVJN | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 13.17 | 23.01 | 26.77 | 33.79 | 49.23 | 36.06 *** | 16.23 | 25.44 | 26.41 | 26.62 | 31.36 | 15.13 *** | |
| (1.52) | (2.59) | (2.84) | (3.36) | (4.62) | (6.47) | (2.55) | (4.11) | (4.08) | (3.93) | (4.29) | (3.75) | ||
| Alpha | −9.36 | −0.03 | 4.18 | 13.24 | 31.71 | 41.07 *** | −3.55 | 4.94 | 5.27 | 5.49 | 10.05 | 13.60 *** | |
| (−4.46) | (−0.02) | (1.86) | (3.93) | (6.34) | (7.51) | (−3.08) | (3.02) | (2.64) | (2.37) | (4.13) | (4.52) | ||
| Panel C: Stocks Sorted by SRVJ | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 51.85 | 39.02 | 26.15 | 17.86 | 11.02 | −40.82 *** | 34.67 | 27.43 | 19.93 | 13.64 | 9.65 | −25.02 *** | |
| (5.14) | (3.85) | (2.70) | (1.98) | (1.33) | (−9.85) | (4.85) | (4.12) | (3.10) | (2.16) | (1.59) | (−5.78) | ||
| Alpha | 30.54 | 17.81 | 4.56 | −3.58 | −9.64 | −40.18 *** | 13.44 | 6.94 | −0.52 | −6.53 | −10.25 | −23.69 *** | |
| (8.40) | (5.78) | (1.74) | (−1.56) | (−4.05) | (−10.10) | (5.01) | (3.95) | (−0.40) | (−4.48) | (−4.47) | (−5.56) | ||
| Panel A: Stocks Sorted by RVLJP | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Part I: Jump Truncation Level = | |||||||||||||
| Mean Return | 31.40 | 30.00 | 29.17 | 31.04 | 23.78 | −7.61 ** | 21.78 | 20.61 | 20.72 | 18.56 | 17.75 | −4.03 | |
| (3.31) | (3.19) | (3.10) | (3.28) | (2.48) | (−2.05) | (3.41) | (3.21) | (3.33) | (2.95) | (2.66) | (−1.09) | ||
| Alpha | 10.07 | 7.64 | 6.65 | 9.04 | 6.08 | −3.98 | 1.97 | 0.68 | −0.42 | −2.32 | −2.83 | −4.80 * | |
| (4.20) | (3.44) | (2.81) | (3.35) | (1.53) | (−1.08) | (1.95) | (0.52) | (−0.26) | (−1.27) | (−1.21) | (−1.71) | ||
| Part II: Jump Truncation Level = | |||||||||||||
| Mean Return | 29.42 | 43.86 | 30.00 | 29.12 | 25.77 | −3.65 | 20.42 | 27.59 | 20.12 | 22.50 | 20.39 | −0.03 | |
| (3.15) | (2.16) | (3.04) | (3.07) | (2.74) | (−1.11) | (3.25) | (1.77) | (2.98) | (3.63) | (3.14) | (−0.01) | ||
| Alpha | 7.74 | 32.93 | 7.28 | 7.02 | 7.70 | −0.04 | 0.45 | 13.80 | −0.27 | 1.60 | −0.52 | −0.97 | |
| (3.70) | (3.23) | (2.92) | (2.62) | (2.02) | (−0.01) | (0.72) | (1.35) | (−0.13) | (0.83) | (−0.22) | (−0.37) | ||
| Panel B: Stocks Sorted by RVLJN | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Part I: Jump Truncation Level = | |||||||||||||
| Mean Return | 23.80 | 23.68 | 27.64 | 28.85 | 41.56 | 17.76 *** | 19.65 | 19.58 | 25.63 | 22.38 | 25.24 | 5.59 | |
| (2.65) | (2.59) | (2.98) | (2.95) | (4.10) | (4.47) | (3.10) | (3.10) | (4.00) | (3.27) | (3.44) | (1.41) | ||
| Alpha | 2.31 | 1.11 | 5.00 | 7.10 | 23.74 | 21.43 *** | −0.20 | −1.32 | 4.52 | 0.89 | 4.34 | 4.54 | |
| (1.11) | (0.55) | (2.32) | (2.47) | (5.39) | (5.53) | (−0.18) | (−0.92) | (2.47) | (0.40) | (1.82) | (1.61) | ||
| Part II: Jump Truncation Level = | |||||||||||||
| Mean Return | 24.76 | 6.46 | 27.89 | 29.12 | 38.62 | 13.86 *** | 19.69 | 13.21 | 21.46 | 23.20 | 22.34 | 2.66 | |
| (2.71) | (0.33) | (2.75) | (3.03) | (3.88) | (4.01) | (3.13) | (0.93) | (3.05) | (3.61) | (3.15) | (0.75) | ||
| Alpha | 3.02 | 6.75 | 6.58 | 7.06 | 20.62 | 17.60 *** | −0.30 | 6.52 | 1.26 | 2.28 | 1.58 | 1.88 | |
| (1.63) | (1.08) | (2.50) | (2.67) | (4.81) | (5.06) | (−0.45) | (0.91) | (0.57) | (1.06) | (0.66) | (0.70) | ||
| Panel C: Stocks Sorted by SRVLJ | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Part I: Jump Truncation Level = | |||||||||||||
| Mean Return | 44.35 | 32.94 | 31.08 | 22.72 | 16.04 | −28.31 *** | 26.27 | 22.99 | 22.36 | 17.77 | 16.27 | −10.01 *** | |
| (4.52) | (3.36) | (3.13) | (2.44) | (1.88) | (−9.00) | (3.92) | (3.58) | (3.29) | (2.79) | (2.71) | (−3.09) | ||
| Alpha | 23.47 | 11.38 | 8.91 | 0.96 | −4.90 | −28.36 *** | 5.00 | 2.42 | 1.83 | −2.64 | −4.26 | −9.25 *** | |
| (7.13) | (4.20) | (3.04) | (0.40) | (−2.17) | (−9.39) | (2.24) | (1.64) | (1.01) | (−1.82) | (−2.24) | (−2.87) | ||
| Part II: Jump Truncation Level = | |||||||||||||
| Mean Return | 40.55 | 28.37 | 33.05 | 24.16 | 19.03 | −21.52 *** | 22.59 | 20.48 | 16.45 | 18.86 | 20.14 | −2.45 | |
| (4.19) | (2.91) | (1.48) | (2.55) | (2.19) | (−8.22) | (3.40) | (3.18) | (1.14) | (3.02) | (3.27) | (−0.80) | ||
| Alpha | 19.59 | 8.18 | 24.26 | 2.23 | −1.97 | −21.55 *** | 1.82 | 0.76 | 6.85 | −2.41 | −0.26 | −2.08 | |
| (6.15) | (3.29) | (2.16) | (0.82) | (−0.84) | (−8.33) | (0.86) | (0.68) | (1.04) | (−1.23) | (−0.13) | (−0.69) | ||
| Panel A: Stocks Sorted by RVSJP | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Part I: Jump Truncation Level = | |||||||||||||
| Mean Return | 32.01 | 32.51 | 29.03 | 26.59 | 25.72 | −6.29 ** | 27.93 | 26.10 | 18.44 | 16.52 | 15.37 | −12.55 ** | |
| (3.44) | (3.43) | (3.09) | (2.85) | (2.65) | (−2.14) | (3.65) | (3.84) | (2.91) | (2.75) | (2.45) | (−2.54) | ||
| Alpha | 13.11 | 9.39 | 6.37 | 4.77 | 6.13 | −6.98 *** | 7.40 | 5.21 | −1.83 | −2.89 | −4.95 | −12.35 *** | |
| (3.74) | (4.21) | (3.02) | (2.08) | (1.82) | (−2.65) | (2.44) | (3.28) | (−1.39) | (−1.55) | (−2.32) | (−2.93) | ||
| Part II: Jump Truncation Level = | |||||||||||||
| Mean Return | 34.25 | 31.55 | 28.43 | 27.41 | 24.23 | −10.02 *** | 29.37 | 18.76 | 17.76 | 14.75 | 18.98 | −10.40 ** | |
| (3.72) | (3.37) | (3.04) | (2.90) | (2.48) | (−3.26) | (4.09) | (2.95) | (2.94) | (2.39) | (2.93) | (−2.25) | ||
| Alpha | 14.08 | 8.85 | 5.90 | 5.75 | 5.08 | −9.00 *** | 8.52 | −2.00 | −2.01 | −5.30 | −1.51 | −10.02 ** | |
| (4.93) | (4.12) | (2.73) | (2.32) | (1.42) | (−3.13) | (3.87) | (−1.52) | (−1.24) | (−2.67) | (−0.62) | (−2.54) | ||
| Panel B: Stocks Sorted by RVSJN | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Part I: Jump Truncation Level = | |||||||||||||
| Mean Return | 23.66 | 21.60 | 27.21 | 31.73 | 41.77 | 18.10 *** | 6.94 | 15.90 | 21.97 | 27.77 | 31.26 | 24.32 *** | |
| (2.64) | (2.38) | (2.97) | (3.35) | (3.93) | (5.07) | (1.00) | (2.42) | (3.46) | (4.34) | (4.68) | (5.00) | ||
| Alpha | 5.26 | −1.04 | 4.35 | 9.56 | 21.62 | 16.36 *** | −13.39 | −4.28 | 1.80 | 7.41 | 10.52 | 23.91 *** | |
| (1.59) | (−0.51) | (2.22) | (4.02) | (5.49) | (5.46) | (−4.54) | (−2.80) | (1.33) | (3.72) | (4.07) | (5.21) | ||
| Part II: Jump Truncation Level = | |||||||||||||
| Mean Return | 19.42 | 23.04 | 26.65 | 32.48 | 44.37 | 24.96 *** | 14.22 | 18.78 | 25.82 | 29.05 | 32.60 | 18.38 *** | |
| (2.23) | (2.60) | (2.93) | (3.35) | (4.09) | (6.07) | (2.13) | (3.00) | (4.13) | (4.42) | (4.43) | (3.80) | ||
| Alpha | −0.37 | 0.70 | 4.18 | 10.38 | 24.84 | 25.22 *** | −5.47 | −1.28 | 5.81 | 7.80 | 10.85 | 16.31 *** | |
| (−0.14) | (0.37) | (2.18) | (4.02) | (5.85) | (7.21) | (−2.72) | (−1.07) | (3.39) | (3.67) | (4.02) | (4.15) | ||
| Panel C: Stocks Sorted by SRVSJ | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Part I: Jump Truncation Level = | |||||||||||||
| Mean Return | 46.41 | 40.51 | 25.12 | 19.00 | 13.74 | −32.67 *** | 34.54 | 24.08 | 18.26 | 17.84 | 10.42 | −24.12 *** | |
| (4.57) | (4.04) | (2.67) | (2.06) | (1.62) | (−8.60) | (5.00) | (3.58) | (2.81) | (2.85) | (1.72) | (−6.60) | ||
| Alpha | 23.64 | 19.68 | 5.23 | −2.09 | −8.14 | −31.78 *** | 13.77 | 3.25 | −2.37 | −2.39 | −9.27 | −23.04 *** | |
| (7.62) | (6.10) | (1.53) | (−0.85) | (−4.17) | (−9.01) | (6.18) | (1.91) | (−1.07) | (−1.52) | (−5.00) | (−6.54) | ||
| Part II: Jump Truncation Level = | |||||||||||||
| Mean Return | 47.90 | 41.62 | 27.23 | 17.90 | 11.20 | −36.70 *** | 36.88 | 25.13 | 18.45 | 14.98 | 9.41 | −27.47 *** | |
| (4.70) | (4.13) | (2.87) | (1.98) | (1.34) | (−9.06) | (5.31) | (3.79) | (2.86) | (2.39) | (1.52) | (−6.94) | ||
| Alpha | 25.37 | 20.76 | 6.99 | −3.03 | −10.51 | −35.88 *** | 16.07 | 4.52 | −1.87 | −5.39 | −10.34 | −26.41 *** | |
| (7.79) | (6.65) | (2.23) | (−1.25) | (−5.21) | (−9.49) | (6.72) | (2.60) | (−1.23) | (−3.30) | (−5.00) | (−6.72) | ||
| Panel A: Stocks Sorted by RVOL | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 23.36 | 28.00 | 28.89 | 31.78 | 33.91 | 10.55 | 20.72 | 21.42 | 19.75 | 26.78 | 29.19 | 8.47 | |
| (4.47) | (3.92) | (2.96) | (2.59) | (2.24) | (0.81) | (4.09) | (2.83) | (1.84) | (1.98) | (1.92) | (0.64) | ||
| Alpha | 4.50 | 5.01 | 5.15 | 8.74 | 16.33 | 11.83 | 1.95 | −1.39 | −3.94 | 2.44 | 5.44 | 3.49 | |
| (2.07) | (2.94) | (2.57) | (2.54) | (2.11) | (1.37) | (1.35) | (−0.67) | (−1.01) | (0.43) | (0.67) | (0.40) | ||
| Panel B: Stocks Sorted by RSK | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 47.56 | 38.06 | 27.86 | 19.44 | 12.98 | −34.58 *** | 29.45 | 27.52 | 19.27 | 14.68 | 13.21 | −16.24 *** | |
| (4.85) | (3.82) | (2.86) | (2.12) | (1.54) | (−9.94) | (4.27) | (4.22) | (2.98) | (2.32) | (2.18) | (−4.29) | ||
| Alpha | 26.22 | 16.77 | 6.73 | −2.15 | −7.90 | −34.12 *** | 7.87 | 7.02 | −0.82 | −5.38 | −6.77 | −14.64 *** | |
| (7.93) | (5.66) | (2.41) | (−0.96) | (−3.51) | (−10.08) | (3.30) | (4.44) | (−0.60) | (−3.73) | (−3.23) | (−3.85) | ||
| Panel C: Stocks Sorted by RKT | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 28.95 | 28.59 | 29.91 | 29.42 | 29.07 | 0.12 | 19.87 | 21.57 | 21.12 | 22.17 | 19.55 | −0.32 | |
| (3.07) | (3.00) | (3.13) | (3.06) | (3.24) | (0.04) | (3.12) | (3.42) | (3.37) | (3.38) | (2.96) | (−0.10) | ||
| Alpha | 8.55 | 6.42 | 7.47 | 7.92 | 9.36 | 0.81 | 0.21 | 0.65 | −0.10 | 0.94 | −1.92 | −2.13 | |
| (3.21) | (2.87) | (3.05) | (2.87) | (3.07) | (0.28) | (0.20) | (0.46) | (−0.06) | (0.49) | (−0.91) | (−0.81) | ||
| Panel D: Stocks Sorted by RVC | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | |
| Mean Return | 36.18 | 31.82 | 28.23 | 27.47 | 22.21 | −13.97 ** | 24.36 | 24.80 | 22.94 | 23.40 | 20.41 | −3.95 | |
| (3.54) | (3.22) | (3.00) | (3.05) | (2.42) | (−2.58) | (3.53) | (3.65) | (3.59) | (3.87) | (3.20) | (−1.00) | ||
| Alpha | 19.82 | 10.62 | 5.54 | 4.66 | −0.94 | −20.76 *** | 4.27 | 3.29 | 2.42 | 3.27 | 0.06 | −4.22 | |
| (4.04) | (3.36) | (2.48) | (2.47) | (−0.41) | (−3.87) | (1.76) | (1.62) | (1.30) | (2.10) | (0.07) | (−1.46) | ||
| Panel A: Stocks Sorted by SRVLJ, Controlling for SRVJ Based on | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVJ Quintile | SRVJ Quintile | ||||||||||||
| SRVLJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 47.99 | 28.73 | 21.12 | 12.90 | 7.82 | 23.71 | 41.88 | 18.83 | 19.24 | 13.59 | 5.04 | 16.61 | |
| 2 | 50.55 | 37.24 | 22.38 | 26.91 | 12.99 | 33.21 | 29.61 | 25.26 | 18.26 | 17.39 | 14.08 | 22.70 | |
| 3 | 53.07 | 38.57 | 23.49 | 21.73 | 12.37 | 29.75 | 36.31 | 26.28 | 8.10 | 15.50 | 17.40 | 24.19 | |
| 4 | 56.29 | 21.42 | 35.09 | 14.59 | 17.86 | 27.51 | 36.38 | 7.94 | 18.53 | 13.64 | 16.59 | 20.33 | |
| 5 (High) | 47.70 | 45.92 | 32.70 | 26.10 | 7.59 | 32.00 | 32.64 | 39.20 | 23.00 | 20.20 | 19.84 | 27.00 | |
| High-Low | −0.24 | 17.19 | 11.58 | 13.20 | −0.23 | 8.30 | 6.38 | 20.37 | 3.76 | 6.61 | 14.81 | 10.38 | |
| Alpha | −6.48 | 16.64 | 10.80 | 13.88 | 2.60 | 7.49 | 3.69 | 19.41 | 2.46 | 6.06 | 13.84 | 9.09 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.15 | 2.90 | 2.26 | 1.48 | 0.92 | 2.68 | 3.45 | 2.66 | 2.89 | 2.08 | 0.75 | 2.67 | |
| 2 | 4.81 | 3.62 | 1.94 | 0.81 | 1.43 | 3.49 | 3.97 | 3.40 | 2.28 | 0.88 | 1.99 | 3.49 | |
| 3 | 4.87 | 3.03 | 0.75 | 1.89 | 1.39 | 3.03 | 4.65 | 3.06 | 0.37 | 1.92 | 2.65 | 3.73 | |
| 4 | 4.64 | 0.63 | 3.07 | 1.53 | 2.04 | 2.81 | 4.26 | 0.27 | 2.18 | 2.05 | 2.50 | 3.04 | |
| 5 (High) | 4.39 | 4.29 | 3.23 | 2.71 | 0.89 | 3.38 | 3.77 | 4.89 | 3.16 | 2.78 | 2.99 | 4.01 | |
| High-Low | −0.04 | 4.24 | 3.31 | 3.87 | −0.06 | 4.18 | 1.09 | 3.71 | 0.79 | 1.54 | 3.09 | 4.15 | |
| Alpha | −1.19 | 4.11 | 3.06 | 4.09 | 0.67 | 3.80 | 0.62 | 3.40 | 0.49 | 1.44 | 2.96 | 3.53 | |
| Panel B: Stocks Sorted by SRVSJ, Controlling for SRVJ Based on | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVJ Quintile | SRVJ Quintile | ||||||||||||
| SRVSJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 56.90 | 44.50 | 34.78 | 26.13 | 19.50 | 36.36 | 41.88 | 35.91 | 26.98 | 18.28 | 22.43 | 29.73 | |
| 2 | 55.66 | 47.02 | 30.91 | 18.59 | 10.34 | 32.50 | 40.76 | 34.11 | 20.84 | 13.23 | 16.52 | 25.09 | |
| 3 | 56.24 | 41.20 | 28.46 | 19.74 | 10.02 | 31.13 | 30.72 | 23.04 | 20.39 | 13.82 | 14.29 | 20.45 | |
| 4 | 53.58 | 37.21 | 16.75 | 12.62 | 10.19 | 26.07 | 28.23 | 23.82 | 12.02 | 14.94 | 6.93 | 17.19 | |
| 5 (High) | 34.30 | 25.12 | 19.72 | 12.12 | 5.79 | 19.41 | 17.03 | 16.65 | 18.03 | 12.69 | 3.77 | 13.63 | |
| High-Low | −22.60 | −19.38 | −15.06 | −14.01 | −13.71 | −16.95 | −28.00 | −19.26 | −8.95 | −5.59 | −18.66 | −16.09 | |
| Alpha | −19.26 | −18.83 | −14.19 | −14.86 | −16.20 | −16.67 | −25.86 | −20.41 | −6.87 | −4.79 | −18.22 | −15.23 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.44 | 4.22 | 3.40 | 2.67 | 2.16 | 3.76 | 5.47 | 4.75 | 3.58 | 2.54 | 3.33 | 4.44 | |
| 2 | 5.20 | 4.21 | 3.08 | 1.93 | 1.17 | 3.35 | 5.19 | 4.65 | 3.00 | 1.95 | 2.33 | 3.86 | |
| 3 | 5.15 | 3.99 | 2.77 | 2.14 | 1.17 | 3.26 | 4.04 | 3.21 | 2.89 | 2.02 | 2.20 | 3.20 | |
| 4 | 5.33 | 3.58 | 1.71 | 1.42 | 1.23 | 2.86 | 3.39 | 3.41 | 1.72 | 2.22 | 1.02 | 2.68 | |
| 5 (High) | 3.46 | 2.60 | 2.12 | 1.39 | 0.70 | 2.19 | 2.22 | 2.32 | 2.67 | 1.89 | 0.56 | 2.16 | |
| High-Low | −4.99 | −5.04 | −4.14 | −3.79 | −3.45 | −7.22 | −5.37 | −3.66 | −1.79 | −1.19 | −3.80 | −5.77 | |
| Alpha | −4.15 | −4.90 | −3.91 | −4.16 | −4.12 | −7.42 | −4.93 | −3.65 | −1.30 | −1.02 | −3.78 | −5.32 | |
| Panel C: Stocks Sorted by SRVSJ, Controlling for SRVLJ Based on | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVLJ Quintile | SRVLJ Quintile | ||||||||||||
| SRVSJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 60.34 | 51.38 | 40.69 | 44.93 | 31.91 | 47.28 | 41.88 | 35.33 | 35.90 | 34.10 | 30.94 | 36.43 | |
| 2 | 57.30 | 38.41 | 58.52 | 28.26 | 28.35 | 40.27 | 23.32 | 25.07 | 37.49 | 18.00 | 25.93 | 25.12 | |
| 3 | 35.25 | 26.42 | 4.21 | 28.76 | 14.62 | 25.17 | 16.19 | 21.74 | 9.63 | 20.36 | 21.71 | 19.86 | |
| 4 | 28.42 | 16.02 | 48.13 | 10.74 | 10.78 | 19.49 | 17.78 | 15.39 | 97.02 | 14.92 | 14.12 | 22.20 | |
| 5 (High) | 18.79 | 9.45 | −1.20 | 8.01 | 8.26 | 10.89 | 14.98 | 8.09 | 6.98 | 7.78 | 13.31 | 11.30 | |
| High-Low | −41.55 | −41.93 | −40.72 | −38.27 | −23.65 | −36.71 | −26.63 | −27.24 | −27.87 | −27.67 | −17.63 | −25.38 | |
| Alpha | −40.15 | −41.33 | −40.17 | −37.25 | −22.90 | −35.45 | −25.59 | −25.58 | −26.01 | −26.35 | −17.73 | −24.07 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.60 | 4.76 | 1.56 | 4.18 | 3.28 | 4.58 | 5.38 | 4.76 | 1.72 | 4.12 | 4.37 | 5.13 | |
| 2 | 5.40 | 3.61 | 2.17 | 2.64 | 3.02 | 3.97 | 3.03 | 3.41 | 1.61 | 2.34 | 3.60 | 3.62 | |
| 3 | 3.58 | 2.60 | 0.19 | 2.85 | 1.62 | 2.65 | 2.27 | 3.21 | 0.53 | 2.93 | 3.11 | 3.15 | |
| 4 | 2.83 | 1.70 | 1.20 | 1.10 | 1.23 | 2.01 | 2.49 | 2.30 | 1.11 | 2.03 | 2.07 | 2.35 | |
| 5 (High) | 2.12 | 1.06 | −0.06 | 0.93 | 1.01 | 1.31 | 2.12 | 1.22 | 0.46 | 1.08 | 2.02 | 1.82 | |
| High-Low | −8.29 | −8.49 | −2.04 | −6.08 | −5.33 | −8.59 | −5.15 | −5.54 | −1.50 | −4.14 | −3.64 | −6.61 | |
| Alpha | −8.24 | −8.75 | −2.03 | −6.22 | −5.50 | −8.80 | −4.90 | −5.18 | −1.39 | −3.87 | −3.66 | −6.13 | |
| Panel D: Stocks Sorted by SRVLJ, Controlling for SRVSJ Based on | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVSJ Quintile | SRVSJ Quintile | ||||||||||||
| SRVLJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 59.99 | 60.01 | 41.84 | 27.66 | 16.62 | 41.23 | 41.88 | 30.53 | 19.67 | 16.32 | 12.01 | 23.80 | |
| 2 | 49.75 | 41.95 | 27.20 | 17.65 | 11.51 | 29.31 | 35.69 | 25.91 | 18.85 | 17.68 | 8.92 | 20.89 | |
| 3 | 76.41 | 38.05 | 24.45 | 6.48 | 14.41 | 32.06 | 45.15 | 16.78 | 11.30 | 10.47 | 21.45 | 21.03 | |
| 4 | 43.99 | 30.88 | 23.29 | 13.82 | 11.84 | 24.86 | 38.54 | 18.80 | 17.59 | 15.79 | 10.15 | 20.55 | |
| 5 (High) | 32.38 | 28.64 | 10.59 | 8.97 | 6.78 | 17.47 | 31.35 | 25.93 | 18.89 | 13.97 | 10.03 | 20.03 | |
| High-Low | −27.61 | −31.38 | −31.25 | −18.69 | −9.84 | −23.75 | −9.14 | −4.60 | −0.78 | −2.35 | −1.98 | −3.77 | |
| Alpha | −26.51 | −31.63 | −31.28 | −19.37 | −9.80 | −23.72 | −8.62 | −3.72 | −0.59 | −2.79 | −1.66 | −3.47 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.51 | 5.59 | 4.22 | 2.85 | 1.85 | 4.25 | 5.37 | 4.03 | 2.69 | 2.23 | 1.71 | 3.59 | |
| 2 | 4.51 | 3.85 | 2.62 | 1.87 | 1.29 | 3.05 | 4.71 | 3.54 | 2.63 | 2.71 | 1.32 | 3.28 | |
| 3 | 2.31 | 1.95 | 1.61 | 0.41 | 0.80 | 2.49 | 1.53 | 1.16 | 1.08 | 0.78 | 1.49 | 2.25 | |
| 4 | 4.05 | 2.90 | 2.28 | 1.44 | 1.31 | 2.63 | 4.83 | 2.51 | 2.47 | 2.31 | 1.39 | 3.23 | |
| 5 (High) | 3.36 | 2.99 | 1.21 | 1.03 | 0.83 | 2.02 | 4.32 | 3.63 | 2.69 | 2.11 | 1.55 | 3.23 | |
| High-Low | −6.48 | −7.66 | −6.92 | −4.65 | −2.73 | −8.80 | −1.83 | −0.98 | −0.16 | −0.46 | −0.44 | −1.49 | |
| Alpha | −6.16 | −7.50 | −6.94 | −4.94 | −2.83 | −8.94 | −1.70 | −0.79 | −0.12 | −0.53 | −0.37 | −1.38 | |
| Panel A: Stocks Sorted by SRVJ, Controlling for RSK | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| RSK Quintile | RSK Quintile | ||||||||||||
| SRVJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 56.92 | 55.49 | 42.81 | 31.69 | 20.91 | 41.57 | 41.88 | 39.12 | 30.49 | 25.47 | 17.56 | 30.90 | |
| 2 | 56.77 | 46.17 | 33.30 | 22.89 | 15.27 | 34.88 | 41.63 | 35.10 | 21.38 | 17.20 | 13.71 | 25.81 | |
| 3 | 49.97 | 38.92 | 23.47 | 17.47 | 11.61 | 28.29 | 37.18 | 27.01 | 22.24 | 14.45 | 10.52 | 22.28 | |
| 4 | 42.67 | 29.57 | 21.68 | 13.20 | 12.18 | 23.86 | 28.53 | 20.24 | 15.10 | 11.99 | 11.47 | 17.47 | |
| 5 (High) | 31.39 | 20.03 | 17.94 | 11.86 | 4.85 | 17.21 | 18.32 | 21.67 | 12.23 | 7.31 | 12.60 | 14.42 | |
| High-Low | −25.54 | −35.46 | −24.87 | −19.83 | −16.06 | −24.35 | −23.56 | −17.46 | −18.27 | −18.16 | −4.95 | −16.48 | |
| Alpha | −28.79 | −36.20 | −24.40 | −18.40 | −12.75 | −24.11 | −24.22 | −18.52 | −18.40 | −16.82 | −4.88 | −16.57 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 6.13 | 5.04 | 3.97 | 3.04 | 2.22 | 4.21 | 5.72 | 4.87 | 3.97 | 3.35 | 2.51 | 4.58 | |
| 2 | 5.34 | 4.12 | 3.14 | 2.32 | 1.70 | 3.52 | 5.11 | 4.57 | 2.96 | 2.44 | 2.02 | 3.89 | |
| 3 | 4.67 | 3.80 | 2.30 | 1.90 | 1.35 | 2.99 | 4.90 | 3.78 | 3.07 | 2.14 | 1.63 | 3.51 | |
| 4 | 4.09 | 2.98 | 2.27 | 1.46 | 1.44 | 2.61 | 3.67 | 2.84 | 2.17 | 1.76 | 1.72 | 2.73 | |
| 5 (High) | 3.27 | 2.20 | 2.02 | 1.36 | 0.59 | 2.01 | 2.59 | 3.24 | 1.76 | 1.07 | 1.90 | 2.36 | |
| High-Low | −5.36 | −7.09 | −5.12 | −4.32 | −3.40 | −7.70 | −4.70 | −3.17 | −3.32 | −3.28 | −0.89 | −5.24 | |
| Alpha | −6.18 | −7.57 | −5.25 | −4.32 | −2.80 | −8.07 | −4.81 | −3.50 | −3.36 | −3.04 | −0.90 | −5.45 | |
| Panel B: Stocks Sorted by RSK, Controlling for SRVJ | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVJ Quintile | SRVJ Quintile | ||||||||||||
| RSK Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 51.14 | 29.34 | 21.71 | 17.58 | 12.40 | 26.43 | 41.88 | 18.33 | 20.91 | 12.07 | 4.09 | 18.48 | |
| 2 | 49.50 | 39.74 | 23.05 | 14.15 | 11.46 | 27.58 | 37.29 | 33.29 | 14.95 | 10.36 | 10.00 | 21.18 | |
| 3 | 49.96 | 37.41 | 27.26 | 18.14 | 12.93 | 29.14 | 28.38 | 23.82 | 22.52 | 14.80 | 15.23 | 20.95 | |
| 4 | 53.85 | 43.31 | 28.11 | 18.79 | 12.52 | 31.32 | 36.37 | 28.73 | 19.57 | 17.15 | 10.67 | 22.50 | |
| 5 (High) | 54.80 | 45.32 | 30.65 | 20.66 | 5.78 | 31.44 | 36.75 | 32.79 | 24.63 | 18.92 | 14.26 | 25.47 | |
| High-Low | 3.66 | 15.98 | 8.94 | 3.08 | −6.63 | 5.01 | −0.25 | 14.46 | 3.72 | 6.85 | 10.17 | 6.99 | |
| Alpha | 0.54 | 16.64 | 8.57 | 2.34 | −4.54 | 4.71 | −0.71 | 15.66 | 4.39 | 6.30 | 9.15 | 6.96 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.56 | 3.07 | 2.36 | 1.99 | 1.42 | 3.02 | 4.98 | 2.61 | 3.15 | 1.74 | 0.60 | 2.97 | |
| 2 | 4.76 | 3.75 | 2.33 | 1.57 | 1.30 | 2.94 | 4.89 | 4.50 | 2.06 | 1.53 | 1.52 | 3.29 | |
| 3 | 4.76 | 3.60 | 2.69 | 1.94 | 1.50 | 3.07 | 3.59 | 3.33 | 3.29 | 2.24 | 2.33 | 3.30 | |
| 4 | 4.99 | 3.98 | 2.77 | 1.97 | 1.49 | 3.27 | 4.70 | 3.89 | 2.69 | 2.39 | 1.63 | 3.45 | |
| 5 (High) | 5.00 | 4.19 | 2.99 | 2.17 | 0.68 | 3.27 | 4.50 | 4.20 | 3.29 | 2.83 | 2.09 | 3.87 | |
| High-Low | 0.85 | 3.98 | 2.31 | 0.84 | −1.61 | 2.35 | −0.05 | 2.85 | 0.74 | 1.48 | 2.19 | 2.87 | |
| Alpha | 0.14 | 4.40 | 2.24 | 0.66 | −1.09 | 2.42 | −0.14 | 3.05 | 0.89 | 1.38 | 2.01 | 2.92 | |
| Panel A: Stocks Sorted by SRVLJ, Controlling for RSK Based on | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| RSK Quintile | RSK Quintile | ||||||||||||
| SRVLJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 47.31 | 31.04 | 20.83 | 13.46 | 9.23 | 24.38 | 41.88 | 20.74 | 17.63 | 10.28 | 10.95 | 17.04 | |
| 2 | 48.24 | 35.53 | 18.15 | 41.82 | 10.40 | 30.72 | 27.52 | 25.93 | 13.06 | 22.40 | 13.21 | 21.88 | |
| 3 | 46.79 | 36.39 | −2.22 | 17.53 | 16.01 | 27.86 | 27.77 | 24.25 | 23.68 | 13.64 | 18.71 | 21.29 | |
| 4 | 47.56 | 9.61 | 27.36 | 19.04 | 20.92 | 27.46 | 27.71 | 8.29 | 20.27 | 17.45 | 16.06 | 20.34 | |
| 5 (High) | 43.55 | 43.48 | 34.14 | 26.41 | 7.84 | 31.13 | 35.80 | 32.07 | 20.61 | 23.70 | 18.89 | 26.28 | |
| High-Low | −3.57 | 12.44 | 13.30 | 12.95 | −1.39 | 6.75 | 10.42 | 11.33 | 2.98 | 13.42 | 7.94 | 9.22 | |
| Alpha | −8.76 | 11.52 | 13.22 | 13.09 | 1.59 | 6.13 | 8.26 | 11.20 | 1.91 | 12.69 | 7.30 | 8.27 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.10 | 3.13 | 2.17 | 1.51 | 1.08 | 2.73 | 3.34 | 2.85 | 2.51 | 1.59 | 1.63 | 2.68 | |
| 2 | 4.67 | 3.47 | 1.41 | 1.61 | 1.16 | 3.21 | 3.71 | 3.71 | 1.47 | 1.12 | 1.98 | 3.42 | |
| 3 | 4.48 | 2.95 | −0.07 | 1.54 | 1.79 | 2.91 | 3.81 | 2.87 | 0.85 | 1.56 | 2.89 | 3.30 | |
| 4 | 4.32 | 0.37 | 2.27 | 1.96 | 2.38 | 2.89 | 3.68 | 0.43 | 2.12 | 2.52 | 2.45 | 3.17 | |
| 5 (High) | 4.22 | 4.03 | 3.42 | 2.75 | 0.93 | 3.34 | 4.08 | 3.80 | 2.81 | 3.23 | 2.79 | 3.90 | |
| High-Low | −0.66 | 2.93 | 4.28 | 4.11 | −0.37 | 3.64 | 1.71 | 1.89 | 0.66 | 3.03 | 1.62 | 3.76 | |
| Alpha | −1.62 | 2.63 | 4.14 | 4.13 | 0.42 | 3.18 | 1.35 | 1.76 | 0.41 | 2.90 | 1.51 | 3.22 | |
| Panel B: Stocks Sorted by SRVSJ, Controlling for RSK Based on | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| RSK Quintile | RSK Quintile | ||||||||||||
| SRVSJ Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 56.15 | 51.19 | 42.56 | 31.93 | 24.16 | 41.20 | 41.88 | 40.69 | 31.16 | 31.49 | 21.39 | 33.55 | |
| 2 | 54.34 | 50.15 | 35.79 | 24.76 | 12.89 | 35.59 | 32.45 | 33.20 | 21.93 | 19.73 | 23.95 | 26.25 | |
| 3 | 55.24 | 38.53 | 26.29 | 18.62 | 11.09 | 29.95 | 27.91 | 22.64 | 18.61 | 12.36 | 16.37 | 19.58 | |
| 4 | 40.20 | 31.45 | 18.77 | 14.26 | 12.14 | 23.35 | 18.13 | 22.01 | 15.30 | 13.17 | 10.40 | 15.79 | |
| 5 (High) | 30.21 | 18.90 | 15.72 | 7.49 | 4.76 | 15.42 | 18.59 | 19.31 | 12.59 | 8.23 | 6.56 | 13.06 | |
| High-Low | −25.94 | −32.29 | −26.84 | −24.43 | −19.40 | −25.78 | −24.44 | −21.37 | −18.56 | −23.26 | −14.84 | −20.49 | |
| Alpha | −23.86 | −31.76 | −26.49 | −23.94 | −20.71 | −25.35 | −22.27 | −22.89 | −18.30 | −21.83 | −14.44 | −19.95 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.43 | 4.75 | 3.98 | 3.16 | 2.62 | 4.15 | 5.11 | 5.25 | 4.16 | 4.39 | 3.15 | 4.92 | |
| 2 | 5.17 | 4.48 | 3.42 | 2.47 | 1.43 | 3.61 | 4.30 | 4.53 | 2.96 | 2.68 | 3.39 | 3.95 | |
| 3 | 5.25 | 3.76 | 2.60 | 1.96 | 1.25 | 3.14 | 3.75 | 3.12 | 2.66 | 1.72 | 2.46 | 3.03 | |
| 4 | 4.11 | 3.13 | 1.96 | 1.58 | 1.45 | 2.59 | 2.50 | 3.20 | 2.27 | 1.98 | 1.57 | 2.55 | |
| 5 (High) | 3.18 | 2.06 | 1.71 | 0.87 | 0.58 | 1.79 | 2.56 | 2.86 | 1.79 | 1.23 | 0.97 | 2.09 | |
| High-Low | −5.78 | −7.15 | −6.04 | −5.58 | −4.72 | −8.41 | −4.21 | −4.04 | −3.67 | −4.56 | −2.93 | −6.31 | |
| Alpha | −5.36 | −7.20 | −6.12 | −5.75 | −5.27 | −8.89 | −3.83 | −4.29 | −3.51 | −4.09 | −2.83 | −6.01 | |
| Panel A: Stocks Sorted by RSK, Controlling for SRVLJ Based on | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVLJ Quintile | SRVLJ Quintile | ||||||||||||
| RSK Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 51.98 | 46.26 | 32.88 | 42.99 | 35.40 | 43.72 | 41.88 | 34.45 | 32.97 | 31.19 | 33.46 | 34.64 | |
| 2 | 48.38 | 38.05 | 55.49 | 31.86 | 20.58 | 37.03 | 30.03 | 23.16 | 48.38 | 17.47 | 16.06 | 24.56 | |
| 3 | 43.16 | 26.83 | 8.78 | 20.69 | 16.54 | 25.94 | 25.91 | 21.10 | 10.09 | 19.92 | 19.16 | 21.15 | |
| 4 | 37.70 | 22.51 | 55.61 | 11.20 | 14.84 | 24.67 | 18.23 | 18.69 | 8.48 | 13.82 | 14.50 | 16.23 | |
| 5 (High) | 21.43 | 8.10 | −0.87 | 14.29 | 7.74 | 12.81 | 13.59 | 7.52 | −8.20 | 15.74 | 15.50 | 12.31 | |
| High-Low | −30.55 | −38.16 | −30.25 | −30.06 | −27.66 | −31.07 | −23.12 | −26.93 | −37.56 | −16.82 | −17.96 | −22.43 | |
| Alpha | −32.89 | −37.85 | −28.79 | −30.01 | −24.81 | −30.46 | −23.34 | −24.74 | −36.67 | −14.80 | −18.66 | −21.39 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.63 | 4.46 | 1.33 | 4.16 | 3.61 | 4.48 | 4.94 | 4.65 | 1.67 | 4.00 | 4.80 | 5.06 | |
| 2 | 4.68 | 3.68 | 2.16 | 3.04 | 2.22 | 3.72 | 3.99 | 3.28 | 2.04 | 2.34 | 2.31 | 3.63 | |
| 3 | 4.14 | 2.66 | 0.40 | 2.04 | 1.84 | 2.69 | 3.32 | 3.22 | 0.59 | 2.66 | 2.87 | 3.29 | |
| 4 | 3.62 | 2.29 | 1.37 | 1.11 | 1.73 | 2.50 | 2.54 | 2.82 | 0.48 | 1.80 | 2.22 | 2.54 | |
| 5 (High) | 2.27 | 0.89 | −0.04 | 1.63 | 0.92 | 1.49 | 1.91 | 1.08 | −0.52 | 2.33 | 2.24 | 1.98 | |
| High-Low | −7.91 | −9.22 | −1.71 | −5.63 | −5.85 | −9.46 | −4.56 | −6.02 | −2.29 | −2.75 | −3.47 | −6.54 | |
| Alpha | −8.43 | −9.50 | −1.64 | −5.86 | −5.51 | −9.57 | −4.59 | −5.54 | −2.22 | −2.37 | −3.65 | −6.10 | |
| Panel B: Stocks Sorted by RSK, Controlling for SRVSJ Based on | |||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | ||||||||||||
| SRVSJ Quintile | SRVSJ Quintile | ||||||||||||
| RSK Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | 1 (Low) | 2 | 3 | 4 | 5 (High) | Average | |
| Part I: Mean Return and Alpha | |||||||||||||
| 1 (Low) | 57.49 | 56.03 | 40.07 | 26.79 | 17.75 | 39.62 | 41.88 | 24.28 | 18.84 | 16.57 | 12.21 | 23.20 | |
| 2 | 51.21 | 42.88 | 31.02 | 15.27 | 12.69 | 30.61 | 35.14 | 26.67 | 14.77 | 21.10 | 9.49 | 21.43 | |
| 3 | 54.96 | 41.34 | 25.81 | 20.97 | 10.12 | 30.64 | 37.20 | 24.66 | 20.50 | 10.79 | 7.58 | 20.15 | |
| 4 | 42.52 | 38.93 | 29.50 | 16.21 | 9.58 | 27.35 | 37.22 | 23.08 | 17.57 | 15.29 | 11.02 | 20.84 | |
| 5 (High) | 33.23 | 28.85 | 9.62 | 10.20 | 5.82 | 17.54 | 31.94 | 30.24 | 21.43 | 16.36 | 8.89 | 21.77 | |
| High-Low | −24.26 | −27.17 | −30.45 | −16.59 | −11.93 | −22.08 | −12.15 | 5.96 | 2.59 | −0.21 | −3.33 | −1.43 | |
| Alpha | −22.78 | −27.83 | −30.17 | −17.16 | −11.85 | −21.96 | −10.86 | 7.74 | 2.94 | −0.96 | −3.03 | −0.83 | |
| Part II: -Statistics | |||||||||||||
| 1 (Low) | 5.53 | 5.32 | 4.11 | 2.82 | 1.99 | 4.19 | 5.79 | 3.21 | 2.52 | 2.21 | 1.73 | 3.49 | |
| 2 | 4.84 | 4.00 | 3.06 | 1.62 | 1.44 | 3.20 | 4.45 | 3.56 | 2.02 | 3.25 | 1.42 | 3.30 | |
| 3 | 4.96 | 3.79 | 2.58 | 2.21 | 1.15 | 3.15 | 4.86 | 3.35 | 3.01 | 1.55 | 1.13 | 3.12 | |
| 4 | 4.01 | 3.79 | 2.86 | 1.73 | 1.12 | 2.87 | 5.03 | 3.26 | 2.44 | 2.17 | 1.62 | 3.22 | |
| 5 (High) | 3.41 | 3.05 | 1.09 | 1.17 | 0.72 | 2.03 | 4.19 | 4.35 | 2.91 | 2.49 | 1.38 | 3.48 | |
| High-Low | −5.79 | −6.79 | −6.74 | −4.40 | −3.12 | −8.56 | −2.27 | 1.17 | 0.48 | −0.04 | −0.69 | −0.49 | |
| Alpha | −5.33 | −6.78 | −6.68 | −4.61 | −3.19 | −8.57 | −2.06 | 1.50 | 0.53 | −0.17 | −0.61 | −0.29 | |
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Industry-Level Quintile | Industry-Level Quintile | |||||||||||||||
| Stock-Level Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | Alpha | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | Alpha | ||
| Part I: Mean Return and Alpha | ||||||||||||||||
| 1 (Low) | 39.23 | 47.42 | 53.00 | 61.43 | 72.18 | 32.94 | 34.74 | 36.50 | 33.40 | 32.78 | 36.58 | 25.03 | 10.19 | 9.28 | ||
| 2 | 30.55 | 33.28 | 38.69 | 48.44 | 55.77 | 25.22 | 25.86 | 28.37 | 27.31 | 20.24 | 37.10 | 14.64 | 7.20 | 6.68 | ||
| 3 | 14.07 | 21.47 | 24.27 | 30.98 | 43.15 | 29.07 | 29.60 | 18.16 | 24.85 | 17.56 | 20.35 | 8.69 | 10.64 | 11.98 | ||
| 4 | 6.90 | 12.45 | 15.65 | 19.51 | 34.51 | 27.61 | 28.30 | 12.97 | 11.96 | 10.38 | 14.58 | 2.67 | 9.54 | 9.99 | ||
| 5 (High) | −7.35 | 1.99 | 9.90 | 16.40 | 25.94 | 33.29 | 32.92 | −4.30 | 9.86 | 4.86 | 13.25 | −3.95 | 19.82 | 21.72 | ||
| High-Low | −46.58 | −45.43 | −43.09 | −45.03 | −46.24 | −40.80 | −23.54 | −27.92 | −23.33 | −31.16 | ||||||
| Alpha | −44.64 | −45.23 | −41.18 | −45.96 | −46.46 | −41.42 | −22.73 | −26.52 | −23.09 | −28.98 | ||||||
| Industry-Level Effect (average of High-Low column; Alpha column) | 29.63 | 30.29 | 11.48 | 11.93 | ||||||||||||
| Stock-Level Effect (average of High-Low row; Alpha row) | −45.28 | −44.70 | −29.35 | −28.55 | ||||||||||||
| Part II: t−Statistics | ||||||||||||||||
| 1 (Low) | 3.82 | 4.37 | 4.98 | 5.87 | 6.83 | 5.20 | 5.35 | 4.61 | 3.98 | 3.93 | 4.55 | 4.71 | 1.40 | 1.27 | ||
| 2 | 2.90 | 3.13 | 3.49 | 4.48 | 5.22 | 3.50 | 3.35 | 3.82 | 3.56 | 2.35 | 4.58 | 3.16 | 1.14 | 1.00 | ||
| 3 | 1.39 | 2.09 | 2.28 | 3.11 | 4.43 | 4.60 | 4.53 | 2.34 | 3.23 | 2.25 | 2.76 | 1.87 | 1.54 | 1.73 | ||
| 4 | 0.70 | 1.28 | 1.60 | 2.12 | 3.93 | 4.40 | 4.47 | 1.69 | 1.62 | 1.36 | 1.87 | 0.68 | 1.50 | 1.54 | ||
| 5 (High) | −0.79 | 0.22 | 1.07 | 1.88 | 3.16 | 5.88 | 5.93 | −0.51 | 1.27 | 0.62 | 1.93 | −1.00 | 2.82 | 3.06 | ||
| High-Low | −9.33 | −8.12 | −8.27 | −7.80 | −8.01 | −7.19 | −3.92 | −5.22 | −4.31 | −5.33 | ||||||
| Alpha, FFC4 | −9.00 | −8.16 | −7.97 | −7.93 | −8.34 | −7.37 | −3.73 | −5.06 | −4.31 | −5.47 | ||||||
| Industry-Level Effect (average of High-Low column; Alpha column) | 5.66 | 5.57 | 2.23 | 2.20 | ||||||||||||
| Stock-Level Effect (average of High-Low row; Alpha row) | −11.39 | −11.50 | −8.88 | −8.91 | ||||||||||||
| Panel A: Portfolios Sorted Based on SRVLJ | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | |||||||||||||||
| Industry-Level Quintile | Industry-Level Quintile | |||||||||||||||
| Stock-Level Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | Alpha | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | Alpha | ||
| Part I: Mean Return and Alpha | ||||||||||||||||
| 1 (Low) | 34.64 | 35.34 | 35.04 | 51.12 | 51.00 | 16.36 | 17.03 | 22.26 | 24.61 | 20.46 | 26.39 | 25.19 | 2.92 | 0.73 | ||
| 2 | 25.37 | 25.36 | 22.38 | 34.21 | 36.00 | 10.64 | 9.43 | 18.78 | 22.97 | 19.49 | 23.51 | 27.29 | 8.51 | 7.46 | ||
| 3 | 17.55 | 0.89 | 26.31 | 34.26 | 31.56 | 14.40 | 11.15 | 18.90 | 15.95 | 11.59 | 4.81 | 17.06 | −6.76 | −10.28 | ||
| 4 | 13.59 | 20.91 | 21.20 | 27.71 | 34.08 | 19.69 | 19.75 | 11.26 | 21.71 | 10.01 | 12.25 | 25.88 | 13.89 | 15.35 | ||
| 5 (High) | 12.22 | 11.90 | 14.43 | 25.57 | 25.57 | 13.36 | 12.93 | 14.16 | 21.60 | 16.13 | 20.63 | 22.85 | 8.69 | 11.30 | ||
| High-Low | −22.42 | −23.44 | −20.61 | −25.55 | −25.42 | −8.10 | −3.00 | −4.33 | −5.75 | −2.33 | ||||||
| Alpha | −22.02 | −23.37 | −20.45 | −25.74 | −26.12 | −9.58 | −3.52 | −4.34 | −5.40 | 1.00 | ||||||
| Industry-Level Effect (average of High-Low column; Alpha column) | 14.83 | 14.31 | 7.24 | 6.90 | ||||||||||||
| Stock-Level Effect (average of High-Low row; Alpha row) | −23.49 | −23.54 | −4.70 | −4.37 | ||||||||||||
| Part II: -Statistics | ||||||||||||||||
| 1 (Low) | 3.63 | 3.39 | 3.33 | 4.94 | 5.23 | 3.40 | 3.41 | 3.25 | 3.06 | 2.48 | 3.25 | 3.16 | 0.49 | 0.12 | ||
| 2 | 2.55 | 2.44 | 2.14 | 3.46 | 3.73 | 2.17 | 1.90 | 2.70 | 3.17 | 2.57 | 3.20 | 3.73 | 1.60 | 1.32 | ||
| 3 | 0.78 | 0.04 | 0.93 | 1.41 | 1.46 | 0.85 | 0.65 | 1.08 | 0.73 | 0.51 | 0.25 | 1.05 | −0.37 | −0.54 | ||
| 4 | 1.32 | 1.95 | 1.94 | 2.74 | 3.73 | 3.67 | 3.73 | 1.49 | 2.62 | 1.20 | 1.45 | 3.69 | 2.43 | 2.65 | ||
| 5 (High) | 1.31 | 1.24 | 1.50 | 2.84 | 2.99 | 2.97 | 2.91 | 1.83 | 2.83 | 2.12 | 2.83 | 3.56 | 1.50 | 2.09 | ||
| High-Low | −6.14 | −5.13 | −4.66 | −5.85 | −6.19 | −1.57 | −0.59 | −0.90 | −1.19 | −0.45 | ||||||
| Alpha, FFC4 | −6.09 | −5.03 | −4.58 | −5.91 | −6.38 | −1.93 | −0.68 | −0.87 | −1.09 | 0.21 | ||||||
| Industry-Level Effect (average of High-Low column; Alpha column) | 3.77 | 3.55 | 1.77 | 1.57 | ||||||||||||
| Stock-Level Effect (average of High-Low row; Alpha row) | −9.05 | −9.14 | −2.01 | −1.91 | ||||||||||||
| Panel B: Portfolios Sorted Based on SRVSJ | ||||||||||||||||
| Equal-Weighted Returns and Alphas | Value-Weighted Returns and Alphas | |||||||||||||||
| Industry-Level Quintile | Industry-Level Quintile | |||||||||||||||
| Stock-Level Quintile | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | Alpha | 1 (Low) | 2 | 3 | 4 | 5 (High) | High-Low | Alpha | ||
| Part I: Mean Return and Alpha | ||||||||||||||||
| 1 (Low) | 40.39 | 42.50 | 43.55 | 55.02 | 68.45 | 28.07 | 29.88 | 44.09 | 37.87 | 32.07 | 36.14 | 45.53 | 1.44 | 0.72 | ||
| 2 | 32.52 | 40.60 | 41.29 | 45.73 | 59.67 | 27.15 | 28.20 | 24.11 | 24.09 | 23.82 | 27.45 | 42.09 | 17.99 | 18.36 | ||
| 3 | 15.39 | 22.96 | 24.90 | 30.69 | 45.29 | 29.90 | 30.43 | 20.22 | 15.93 | 21.91 | 17.63 | 25.37 | 5.16 | 4.88 | ||
| 4 | 9.07 | 9.08 | 17.26 | 17.20 | 32.70 | 23.63 | 23.94 | 11.38 | 12.88 | 22.53 | 11.01 | 25.43 | 14.04 | 15.23 | ||
| 5 (High) | −2.44 | 3.16 | 7.13 | 12.21 | 22.30 | 24.73 | 26.19 | 8.91 | 7.91 | 11.60 | 9.76 | 11.23 | 2.32 | 5.33 | ||
| High-Low | −42.83 | −39.34 | −36.43 | −42.82 | −46.16 | −35.18 | −29.95 | −20.47 | −26.38 | −34.30 | ||||||
| Alpha | −42.27 | −39.03 | −34.75 | −42.27 | −45.96 | −36.51 | −30.26 | −18.68 | −25.89 | −31.90 | ||||||
| Industry-Level Effect (average of High-Low column; Alpha column) | 26.69 | 27.73 | 8.19 | 8.90 | ||||||||||||
| Stock-Level Effect (average of High-Low row; Alpha row) | −41.51 | −40.86 | −29.26 | −28.65 | ||||||||||||
| Part II: -Statistics | ||||||||||||||||
| 1 (Low) | 3.91 | 3.90 | 3.98 | 5.06 | 6.20 | 4.04 | 3.99 | 5.58 | 4.66 | 3.66 | 4.40 | 5.62 | 0.21 | 0.10 | ||
| 2 | 3.00 | 3.83 | 3.88 | 4.42 | 5.68 | 3.89 | 3.88 | 3.19 | 3.04 | 2.90 | 3.50 | 5.39 | 2.84 | 2.77 | ||
| 3 | 1.55 | 2.26 | 2.46 | 3.11 | 4.68 | 4.91 | 4.94 | 2.52 | 1.97 | 2.73 | 2.33 | 3.43 | 0.70 | 0.68 | ||
| 4 | 0.92 | 0.93 | 1.74 | 1.84 | 3.64 | 3.72 | 3.74 | 1.46 | 1.78 | 2.85 | 1.47 | 3.72 | 2.18 | 2.43 | ||
| 5 (High) | −0.25 | 0.33 | 0.77 | 1.41 | 2.70 | 3.94 | 4.15 | 1.06 | 0.96 | 1.49 | 1.36 | 1.74 | 0.34 | 0.76 | ||
| High-Low | −8.38 | −7.85 | −7.04 | −7.99 | −7.60 | −6.21 | −5.45 | −3.70 | −5.15 | −6.15 | ||||||
| Alpha, FFC4 | −8.38 | −7.95 | −6.85 | −8.19 | −8.02 | −6.55 | −5.68 | −3.41 | −5.15 | −5.69 | ||||||
| Industry-Level Effect (average of High-Low column; Alpha column) | 5.02 | 5.01 | 1.60 | 1.68 | ||||||||||||
| Stock-Level Effect (average of High-Low row; Alpha row) | −10.65 | −11.14 | −8.78 | −8.75 | ||||||||||||
| Panel A: Regressions Without Control Variables | ||||||||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | XIV | XV | XVI | |
| Intercept | 18.54 | 27.95 | 23.99 | 15.77 | 30.31 | 31.03 | 31.46 | 31.20 | 19.74 | 32.04 | 20.01 | 20.04 | 28.88 | 30.01 | 30.48 | 30.17 |
| (1.94) | (3.07) | (2.82) | (1.69) | (3.32) | (3.37) | (3.41) | (3.39) | (2.03) | (3.73) | (2.14) | (2.08) | (3.29) | (3.40) | (3.44) | (3.41) | |
| RVJP | −63.86 | −128.25 | ||||||||||||||
| (−6.00) | (−6.24) | |||||||||||||||
| RVJN | 107.11 | 196.57 | ||||||||||||||
| (8.29) | (8.98) | |||||||||||||||
| RVLJP | −53.42 | −44.85 | 76.84 | −79.63 | ||||||||||||
| (−6.46) | (−4.46) | (6.58) | (−3.94) | |||||||||||||
| RVLJN | 71.27 | 83.09 | −30.83 | 149.92 | ||||||||||||
| (8.12) | (7.45) | (−2.40) | (7.18) | |||||||||||||
| RVSJP | −130.77 | −99.16 | −88.56 | −129.39 | ||||||||||||
| (−8.97) | (−6.24) | (−6.64) | (−6.33) | |||||||||||||
| RVSJN | 165.05 | 161.39 | 129.24 | 195.31 | ||||||||||||
| (8.22) | (7.19) | (7.94) | (8.26) | |||||||||||||
| SRVLJ | −50.07 | −53.94 | 72.19 | −82.69 | ||||||||||||
| (−7.98) | (−8.37) | (6.60) | (−4.48) | |||||||||||||
| SRVSJ | −141.69 | −144.75 | −103.72 | −149.56 | ||||||||||||
| (−9.25) | (−9.32) | (−8.25) | (−7.66) | |||||||||||||
| SRVJ | −81.15 | −150.59 | ||||||||||||||
| (−10.15) | (−7.80) | |||||||||||||||
| RVOL | −8.94 | −7.46 | −6.74 | −9.08 | −5.90 | −6.31 | −6.40 | −6.38 | ||||||||
| (−1.60) | (−1.32) | (−1.21) | (−1.62) | (−1.05) | (−1.12) | (−1.14) | (−1.13) | |||||||||
| RSK | 16.12 | −22.16 | −9.87 | 9.12 | −24.75 | −10.15 | 4.08 | 14.02 | ||||||||
| (5.59) | (−9.55) | (−9.49) | (3.07) | (−10.41) | (−9.72) | (1.39) | (4.91) | |||||||||
| RKT | −0.68 | −0.68 | 0.46 | −0.68 | 0.12 | 0.09 | 0.08 | 0.09 | ||||||||
| (−2.25) | (−2.27) | (1.45) | (−2.24) | (0.42) | (0.30) | (0.28) | (0.32) | |||||||||
| Adjusted | 0.0063 | 0.0033 | 0.0035 | 0.0082 | 0.0005 | 0.0019 | 0.0024 | 0.0016 | 0.0204 | 0.0175 | 0.0185 | 0.0214 | 0.0160 | 0.0168 | 0.0172 | 0.0168 |
| Panel B: Regressions with Control Variables | ||||||||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | XIV | XV | XVI | |
| Intercept | 100.76 | 100.26 | 92.97 | 98.02 | 97.60 | 97.72 | 98.57 | 98.26 | 89.27 | 92.87 | 93.62 | 89.60 | 94.59 | 94.82 | 95.19 | 94.94 |
| (4.24) | (5.45) | (5.25) | (4.15) | (5.67) | (5.65) | (5.69) | (5.67) | (3.30) | (4.26) | (3.93) | (3.27) | (4.37) | (4.33) | (4.30) | (4.29) | |
| RVJP | −30.35 | −33.59 | ||||||||||||||
| (−3.04) | (−1.87) | |||||||||||||||
| RVJN | 28.77 | 50.58 | ||||||||||||||
| (3.26) | (3.48) | |||||||||||||||
| RVLJP | −27.56 | −27.07 | 11.55 | −28.36 | ||||||||||||
| (−4.46) | (−2.81) | (1.20) | (−1.53) | |||||||||||||
| RVLJN | 16.42 | 23.05 | −0.32 | 48.59 | ||||||||||||
| (2.67) | (2.61) | (−0.03) | (2.89) | |||||||||||||
| RVSJP | −26.94 | −34.15 | −24.07 | −38.20 | ||||||||||||
| (−2.78) | (−2.51) | (−2.20) | (−2.04) | |||||||||||||
| RVSJN | 44.62 | 45.83 | 26.48 | 52.34 | ||||||||||||
| (4.25) | (3.81) | (2.67) | (3.42) | |||||||||||||
| SRVLJ | −22.63 | −25.76 | 9.90 | −31.02 | ||||||||||||
| (−5.18) | (−5.67) | (1.10) | (−1.93) | |||||||||||||
| SRVSJ | −33.16 | −38.71 | −23.75 | −41.74 | ||||||||||||
| (−3.92) | (−4.45) | (−2.74) | (−2.83) | |||||||||||||
| SRVJ | −28.64 | −39.38 | ||||||||||||||
| (−6.26) | (−2.69) | |||||||||||||||
| RVOL | 4.79 | 5.07 | 4.59 | 4.68 | 4.94 | 4.87 | 4.86 | 4.84 | ||||||||
| (0.79) | (0.84) | (0.76) | (0.77) | (0.82) | (0.80) | (0.80) | (0.79) | |||||||||
| RSK | 3.02 | −4.90 | −3.58 | 2.67 | −5.53 | −3.67 | 1.42 | 2.46 | ||||||||
| (1.23) | (−3.01) | (−4.69) | (0.98) | (−3.45) | (−4.79) | (0.50) | (0.95) | |||||||||
| RKT | −0.53 | −0.61 | −0.38 | −0.56 | −0.49 | −0.46 | −0.44 | −0.44 | ||||||||
| (−2.00) | (−2.27) | (−1.08) | (−1.87) | (−1.78) | (−1.63) | (−1.49) | (−1.46) | |||||||||
| Beta | −8.28 | −8.11 | −8.09 | −8.27 | −8.07 | −8.26 | −8.29 | −8.16 | −7.71 | −7.75 | −8.18 | −7.72 | −8.10 | −8.18 | −8.22 | −8.14 |
| (−1.46) | (−1.40) | (−1.38) | (−1.46) | (−1.37) | (−1.41) | (−1.41) | (−1.39) | (−1.36) | (−1.35) | (−1.42) | (−1.37) | (−1.40) | (−1.42) | (−1.43) | (−1.41) | |
| log(Size) | −14.93 | −14.77 | −14.73 | −14.94 | −14.76 | −14.76 | −14.67 | −14.67 | −14.36 | −14.25 | −14.29 | −14.48 | −14.13 | −14.11 | −14.04 | −14.05 |
| (−5.24) | (−5.25) | (−5.21) | (−5.32) | (−5.15) | (−5.14) | (−5.13) | (−5.13) | (−5.19) | (−5.15) | (−5.16) | (−5.26) | (−5.08) | (−5.07) | (−5.06) | (−5.07) | |
| BE/ME | −0.76 | −0.75 | −0.65 | −0.76 | −0.67 | −0.61 | −0.59 | −0.62 | −0.72 | −0.57 | −0.57 | −0.69 | −0.56 | −0.54 | −0.56 | −0.58 |
| (−0.37) | (−0.36) | (−0.32) | (−0.37) | (−0.33) | (−0.30) | (−0.29) | (−0.30) | (−0.34) | (−0.27) | (−0.27) | (−0.33) | (−0.27) | (−0.26) | (−0.27) | (−0.28) | |
| MOM | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (0.96) | (0.97) | (0.94) | (0.98) | (0.93) | (0.93) | (0.93) | (0.93) | (1.26) | (1.19) | (1.18) | (1.22) | (1.19) | (1.21) | (1.20) | (1.21) | |
| REV | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 |
| (−5.63) | (−5.83) | (−5.63) | (−5.53) | (−5.84) | (−5.66) | (−5.55) | (−5.64) | (−5.74) | (−5.97) | (−5.82) | (−5.70) | (−5.99) | (−5.83) | (−5.77) | (−5.80) | |
| IVOL | −301.46 | −293.89 | −297.02 | −304.39 | −291.92 | −292.47 | −298.32 | −298.14 | −425.97 | −416.77 | −422.83 | −424.54 | −419.05 | −421.52 | −424.24 | −425.20 |
| (−2.18) | (−2.15) | (−2.17) | (−2.21) | (−2.13) | (−2.12) | (−2.16) | (−2.17) | (−4.69) | (−4.57) | (−4.63) | (−4.67) | (−4.59) | (−4.62) | (−4.65) | (−4.67) | |
| CSK | −7.52 | −8.67 | −8.13 | −7.29 | −8.69 | −8.23 | −7.62 | −7.87 | −7.00 | −7.84 | −7.44 | −6.89 | −7.91 | −7.45 | −7.35 | −7.52 |
| (−1.75) | (−2.01) | (−1.89) | (−1.70) | (−2.01) | (−1.91) | (−1.77) | (−1.82) | (−1.66) | (−1.86) | (−1.77) | (−1.64) | (−1.88) | (−1.77) | (−1.74) | (−1.78) | |
| CKT | 2.34 | 2.29 | 2.24 | 2.36 | 2.32 | 2.32 | 2.43 | 2.38 | 1.74 | 1.72 | 1.69 | 1.74 | 1.71 | 1.77 | 1.83 | 1.81 |
| (1.19) | (1.15) | (1.13) | (1.20) | (1.15) | (1.16) | (1.21) | (1.18) | (0.91) | (0.89) | (0.87) | (0.91) | (0.88) | (0.91) | (0.94) | (0.93) | |
| MAX | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 | −0.03 |
| (−5.33) | (−5.66) | (−5.57) | (−5.31) | (−5.64) | (−5.71) | (−5.55) | (−5.54) | (−7.37) | (−7.55) | (−7.45) | (−7.35) | (−7.59) | (−7.55) | (−7.57) | (−7.55) | |
| MIN | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.02 | −0.01 | −0.02 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 |
| (−2.79) | (−3.11) | (−3.14) | (−2.79) | (−3.11) | (−3.12) | (−2.83) | (−2.85) | (−2.81) | (−2.94) | (−2.80) | (−2.81) | (−2.88) | (−2.80) | (−2.73) | (−2.75) | |
| ILLIQ | −7.84 | −7.68 | −8.08 | −7.86 | −7.99 | −8.03 | −7.87 | −7.88 | −8.94 | −8.87 | −8.68 | −9.10 | −8.54 | −8.51 | −8.41 | −8.43 |
| (−5.24) | (−5.12) | (−5.22) | (−5.26) | (−5.15) | (−5.16) | (−5.08) | (−5.10) | (−4.79) | (−5.12) | (−4.96) | (−4.87) | (−4.97) | (−4.95) | (−4.86) | (−4.88) | |
| Adjusted | 0.0602 | 0.0597 | 0.0597 | 0.0609 | 0.0590 | 0.0592 | 0.0594 | 0.0592 | 0.0647 | 0.0641 | 0.0642 | 0.0652 | 0.0636 | 0.0637 | 0.0639 | 0.0638 |
| SRVJ | RSJ | SRVLJ | SRVSJ | RSK | ||
|---|---|---|---|---|---|---|
| Equal-Weighted | 2.1342 | 2.1363 | 1.8556 | 1.8161 | 2.2234 | |
| Value-Weighted | 1.1322 | 1.1310 | 0.1611 | 1.2755 | 0.8665 | |
| Panel A: Daily Average Percentage of Firms Exhibiting Various Types of Jumps, on Days Characterized by Earnings Surprises | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| A-SUE | RVJP | RVJN | SRVJ | RVLJP | RVLJN | SRVLJ | RVSJP | RVSJN | SRVSJ |
| Small | 0.8099 | 0.8180 | 0.9849 | 0.1951 | 0.2004 | 0.3042 | 0.7233 | 0.7258 | 0.8983 |
| Medium | 0.8310 | 0.8232 | 0.9841 | 0.2216 | 0.2173 | 0.3289 | 0.7319 | 0.7232 | 0.8928 |
| Large | 0.8605 | 0.8621 | 0.9909 | 0.2618 | 0.2572 | 0.3737 | 0.7455 | 0.7488 | 0.8829 |
| Panel B: Daily Average Percentage of Firms Exhibiting Various Types of Jumps, on Days Characterized by No Earnings Surprises | |||||||||
| RVJP | RVJN | SRVJ | RVLJP | RVLJN | SRVLJ | RVSJP | RVSJN | SRVSJ | |
| 0.8836 | 0.8786 | 0.9884 | 0.2252 | 0.2220 | 0.3107 | 0.7941 | 0.7900 | 0.9095 | |
| Panel C: -Statistics Associated with the Difference in Jump Size Percentages Between Portfolios | |||||||||
| Difference | SRVJ | SRVLJ | SRVSJ | ||||||
| Medium-Small | −0.55 | 4.98 | −1.68 | ||||||
| Large-Medium | 5.76 | 9.02 | −3.06 | ||||||
| Large-None | 3.54 | 16.85 | −10.85 | ||||||
| SRVLJ | SRVLJ | SRVSJ | SRVSJ | SRVJ | SRVJ | |
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
| Intercept | 0.0080 | 0.0176 | 0.0034 | 0.0159 | 0.0115 | 0.0335 |
| (5.81) | (10.78) | (2.59) | (11.64) | (4.63) | (12.31) | |
| RVOL | −0.0050 | 0.0025 | −0.0065 | 0.0006 | −0.0115 | 0.0032 |
| (−11.02) | (5.36) | (−15.37) | (1.88) | (−14.81) | (4.71) | |
| Beta | 0.0014 | −0.0011 | 0.0003 | |||
| (4.40) | (−3.76) | (0.79) | ||||
| log(Size) | 0.0013 | 0.0003 | 0.0030 | 0.0017 | 0.0043 | 0.0020 |
| (5.79) | (1.62) | (15.19) | (9.21) | (12.71) | (6.67) | |
| BE/ME | 0.0007 | 0.0003 | 0.0010 | |||
| (4.11) | (2.72) | (4.58) | ||||
| MOM | 0.0007 | 0.0011 | 0.0018 | |||
| (3.54) | (5.94) | (6.13) | ||||
| REV | 0.25166 | 0.1176 | 0.3172 | 0.1882 | 0.5688 | 0.3058 |
| (61.05) | (31.43) | (65.55) | (41.52) | (69.66) | (39.62) | |
| IVOL | −0.1424 | −0.1880 | −0.3303 | |||
| (−17.05) | (−23.23) | (−24.43) | ||||
| CSK | 0.0142 | 0.0206 | 0.0349 | |||
| (19.14) | (28.33) | (26.38) | ||||
| CKT | −0.0008 | −0.0008 | −0.0015 | |||
| (−2.28) | (−1.96) | (−2.31) | ||||
| MAX | 0.2456 | 0.2248 | 0.4704 | |||
| (43.77) | (25.28) | (35.84) | ||||
| MIN | 0.5115 | 0.4365 | 0.9480 | |||
| (54.63) | (48.47) | (58.64) | ||||
| ILLIQ | 0.0020 | 0.0016 | 0.0032 | 0.0023 | 0.0052 | 0.0039 |
| (6.33) | (5.32) | (18.60) | (16.36) | (12.20) | (10.28) | |
| Adjusted | 0.0322 | 0.0492 | 0.1070 | 0.1473 | 0.1049 | 0.1517 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Mizrach, B.; Swanson, N.R. New Evidence of the Marginal Predictive Content of Small and Large Jumps in the Cross-Section. Econometrics 2020, 8, 19. https://doi.org/10.3390/econometrics8020019
Yu B, Mizrach B, Swanson NR. New Evidence of the Marginal Predictive Content of Small and Large Jumps in the Cross-Section. Econometrics. 2020; 8(2):19. https://doi.org/10.3390/econometrics8020019
Chicago/Turabian StyleYu, Bo, Bruce Mizrach, and Norman R. Swanson. 2020. "New Evidence of the Marginal Predictive Content of Small and Large Jumps in the Cross-Section" Econometrics 8, no. 2: 19. https://doi.org/10.3390/econometrics8020019
APA StyleYu, B., Mizrach, B., & Swanson, N. R. (2020). New Evidence of the Marginal Predictive Content of Small and Large Jumps in the Cross-Section. Econometrics, 8(2), 19. https://doi.org/10.3390/econometrics8020019





