Forecast Accuracy Matters for Hurricane Damage
Abstract
1. Introduction
2. Modeling Framework
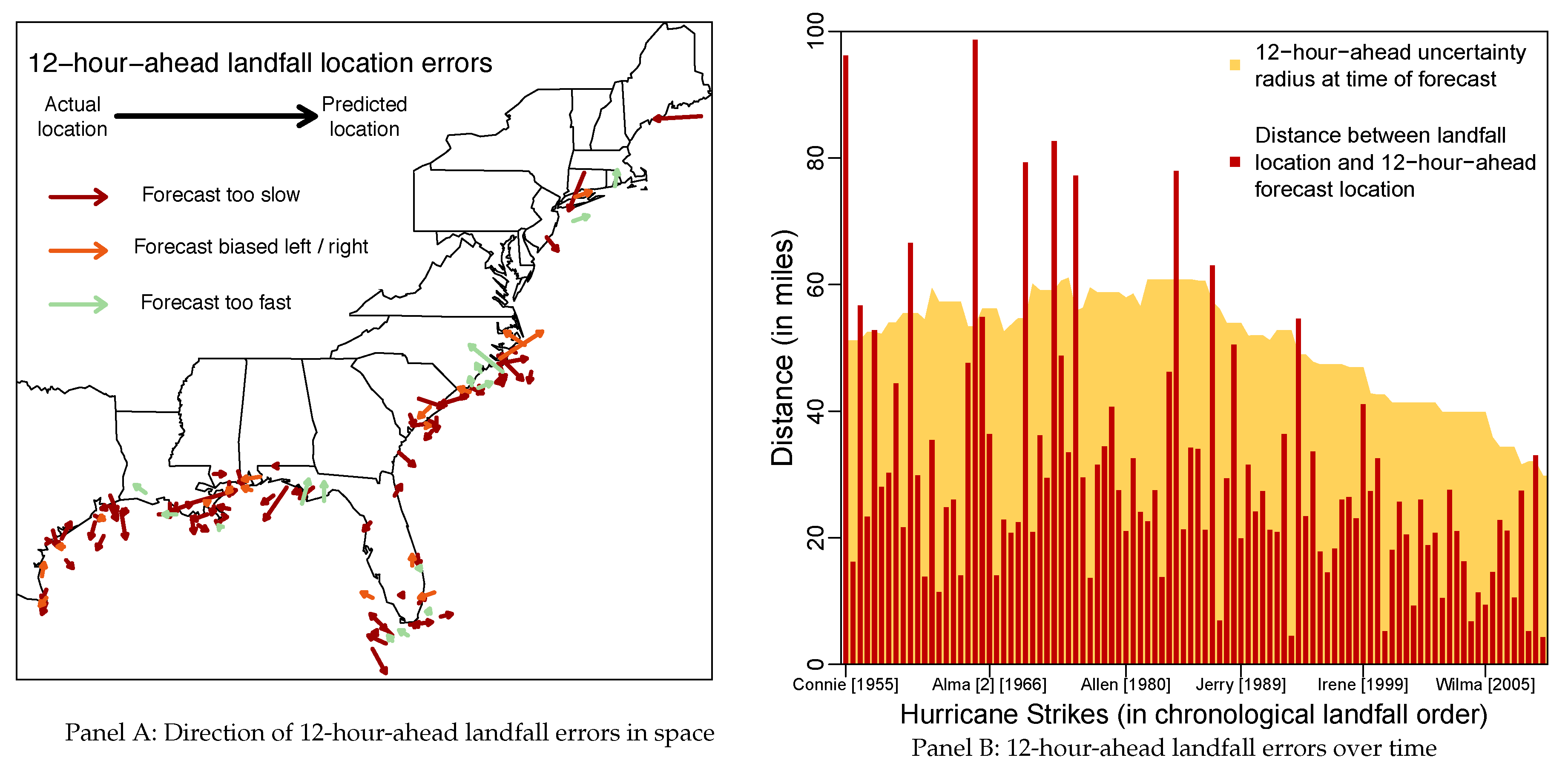
3. Hurricane Forecast Errors, Uncertainty and Damage
4. Model Selection Methods
5. Selecting a Model of Damage
6. Measuring the Impact of Forecast Accuracy
6.1. Post-Selection Inference
6.2. Exogenous Instruments
6.3. Model Invariance and Valuing Improved Forecast Accuracy
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Additional Tables and Figures
| Terminal Model: | Final GUM | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
|---|---|---|---|---|---|---|---|---|---|
| Housing density | 0.50 ** | 0.58 *** | 0.49 *** | 0.59 *** | 0.56 *** | 0.64 *** | 0.40 *** | 0.70 *** | 0.55 *** |
| (0.19) | (0.14) | (0.15) | (0.14) | (0.14) | (0.18) | (0.15) | (0.18) | (0.14) | |
| Income per household | 0.85 | 1.17 *** | 1.30 *** | 1.10 *** | |||||
| (0.62) | (0.20) | (0.20) | (0.21) | ||||||
| Historical fequency | −5.64 ** | −4.85 * | −5.18 ** | −6.47 *** | −5.49 ** | −5.05 ** | |||
| (2.55) | (2.47) | (2.26) | (2.28) | (2.44) | (2.23) | ||||
| Max rainfall | 0.62 * | 1.12 *** | 1.15 *** | 1.15 *** | |||||
| (0.37) | (0.32) | (0.32) | (0.31) | ||||||
| Max storm surge | 1.15 *** | 1.44 *** | 1.45 *** | 1.42 *** | 1.40 *** | 1.34 *** | 1.35 *** | 1.24 *** | |
| (0.41) | (0.38) | (0.39) | (0.38) | (0.38) | (0.38) | (0.38) | (0.40) | ||
| Min central pressure (-) | 60.2 *** | 53.9 *** | 80.4 *** | 53.2 *** | 67.2 *** | 50.8 *** | 52.2 *** | 65.5 *** | 54.2 *** |
| (14.0) | (8.66) | (13.3) | (8.90) | (13.5) | (8.59) | (8.58) | (14.1) | (8.79) | |
| Max wind speed | −1.02 | −0.92 | −1.50 | −1.32 | |||||
| (1.16) | (1.22) | (1.12) | (1.20) | ||||||
| Seasonal cyclone energy | 0.43 * | 0.60 ** | 0.58 ** | 0.64 ** | |||||
| (0.25) | (0.26) | (0.25) | (0.25) | ||||||
| Soil Moisture | 0.67 | 2.27 ** | |||||||
| (1.00) | (0.93) | ||||||||
| Year trend | 0.12 | −0.07 *** | −0.08 *** | −0.07 *** | |||||
| (0.10) | (0.01) | (0.01) | (0.01) | ||||||
| Strike trend | 0.09 | 0.05 *** | 0.05 *** | ||||||
| (0.06) | (0.01) | (0.01) | |||||||
| AUG | 0.48 | 0.47 | |||||||
| (0.36) | (0.39) | ||||||||
| SEP | 0.22 | 0.48 | |||||||
| (0.33) | (0.35) | ||||||||
| NY | -0.96 | −1.79 ** | −2.23 *** | ||||||
| (0.85) | (0.74) | (0.77) | |||||||
| VA | 1.66 ** | 2.09 ** | 2.14 ** | ||||||
| (0.81) | (0.86) | (0.82) | |||||||
| NC | −0.43 | −1.39 *** | −0.80 ** | ||||||
| (0.45) | (0.38) | (0.36) | |||||||
| FL | 0.48 | 0.55 * | |||||||
| (0.34) | (0.29) | ||||||||
| 12-h forecast error | 0.55 ** | 0.44 * | 0.25 | 0.33 | 0.47 * | 0.46 * | 0.47 * | 0.42 * | 0.39 |
| (0.24) | (0.24) | (0.25) | (0.24) | (0.24) | (0.24) | (0.24) | (0.25) | (0.24) | |
| 12-h radius | 2.34 | 2.35 * | 0.76 | 2.52 ** | 1.62 | 0.44 | 0.17 | −0.04 | 1.57 |
| (1.57) | (1.19) | (1.19) | (1.25) | (1.12) | (1.02) | (0.98) | (1.01) | (1.15) | |
| k | 17 | 5 | 10 | 6 | 7 | 7 | 5 | 8 | 8 |
| Log-likelihood (-) | 145.2 | 157.6 | 158.4 | 158.8 | 156.1 | 155.0 | 157.0 | 157.3 | 155.1 |
| AIC | 3.41 | 3.42 | 3.54 | 3.46 | 3.43 | 3.41 | 3.41 | 3.48 | 3.43 |
| HQ | 3.65 | 3.53 | 3.70 | 3.58 | 3.56 | 3.54 | 3.52 | 3.61 | 3.57 |
| BIC | 3.99 | 3.68 | 3.93 | 3.75 | 3.75 | 3.73 | 3.67 | 3.82 | 3.77 |
| 1.21 | 1.27 | 1.32 | 1.30 | 1.27 | 1.26 | 1.27 | 1.29 | 1.26 | |
| 0.86 | 0.82 | 0.82 | 0.81 | 0.82 | 0.83 | 0.82 | 0.82 | 0.83 |
| (1) Gets (3%) | (3) Extension (1%) | (4) Robust | |
|---|---|---|---|
| Housing density | 0.40 *** | 0.26 ** | 0.24 ** |
| (0.15) | (0.10) | (0.09) | |
| Income per housing unit | 1.30 *** | 1.71 *** | 1.76 *** |
| (0.20) | (0.21) | (0.19) | |
| Max rainfall | 1.15 *** | 0.54 ** | 0.56 *** |
| (0.31) | (0.21) | (0.20) | |
| Max storm surge | 1.34 *** | 0.95 *** | 0.98 *** |
| (0.38) | (0.25) | (0.24) | |
| Min central pressure (-) | 52.2 *** | 56.4 *** | 57.8 *** |
| (8.58) | (5.61) | (5.41) | |
| Forecast errors | 0.47 * | 0.26 | 0.27 * |
| (0.24) | (0.16) | (0.15) | |
| Ex-ante Uncertainty | 0.17 | 1.94 * | 2.10 ** |
| (0.98) | (1.06) | (0.96) | |
| Income per housing unit sq. | 0.65 *** | 0.44 *** | |
| (0.14) | (0.09) | ||
| Outlying storms: | -3.19 *** | ||
| (0.35) | |||
| Helene [1958] | −2.59 *** | ||
| (0.85) | |||
| Cindy [1959] | −4.09 *** | ||
| (0.85) | |||
| Gracie [1959] | −2.61 *** | ||
| (0.83) | |||
| Alma [1] [1966] | −4.28 *** | ||
| (0.83) | |||
| Bret [1999] | −2.45 *** | ||
| (0.85) | |||
| Alex [2004] | −3.20 *** | ||
| (0.84) | |||
| Arthur [2014] | −3.36 *** | ||
| (0.98) | |||
| 1.267 | 0.804 | 0.795 | |
| 0.821 | 0.934 | 0.930 | |
| 7.93 ** | 0.43 | 0.65 | |
| [0.019] | [0.806] | [0.722] | |
| 2.00 ** | 1.27 | 0.87 | |
| [0.028] | [0.237] | [0.617] | |
| 1.37 | 0.92 | 0.81 | |
| [0.139] | [0.615] | [0.769] | |
| 1.40 | 1.40 | 1.51 | |
| [0.253] | [0.253] | [0.226] |
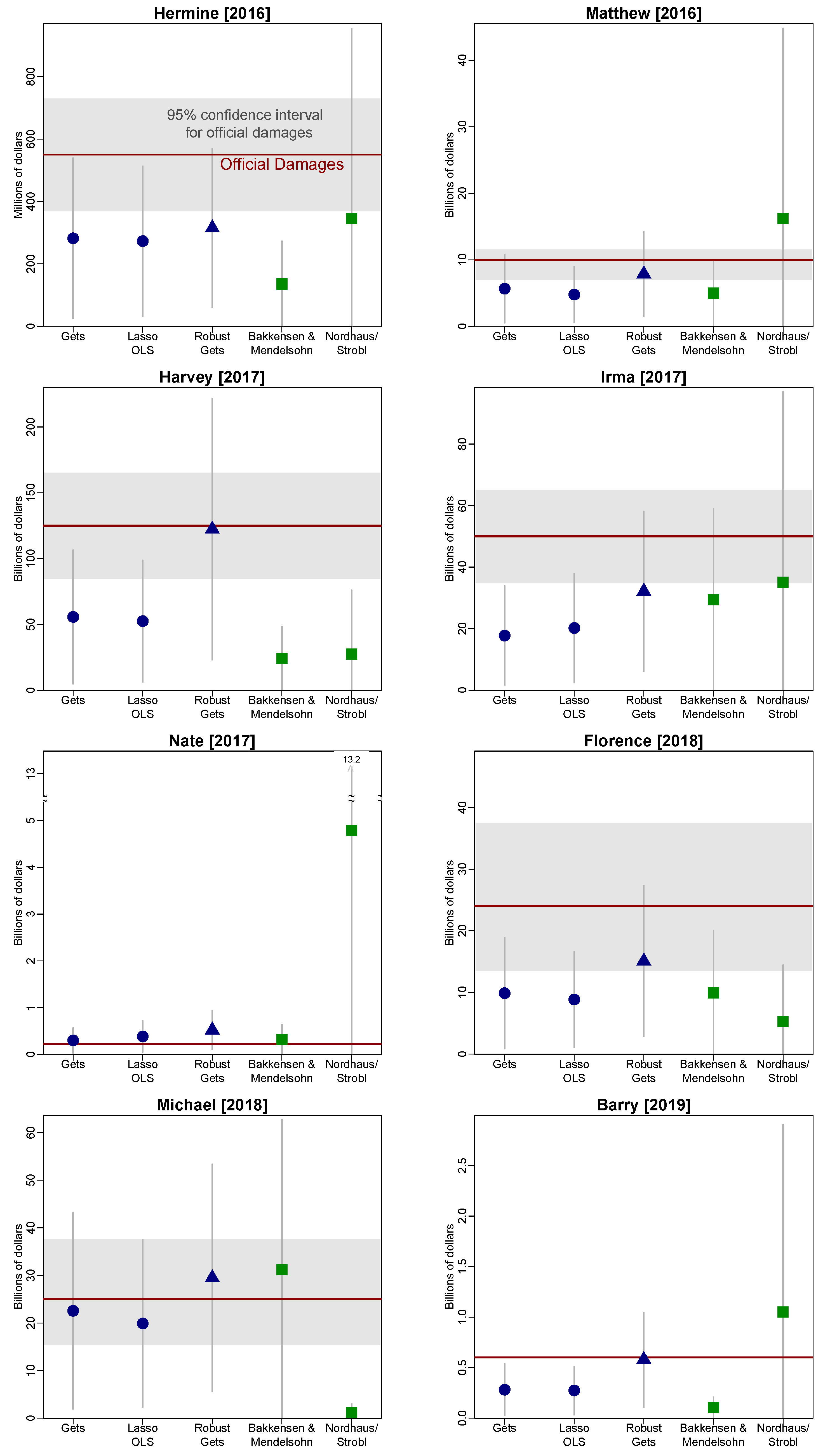
Appendix B. Descriptions of Other Variables
| Variable | Description | Years | Min | Average | Max | Source |
|---|---|---|---|---|---|---|
| Damage (D) | ||||||
| DAMAGE | Nominal Damage (U.S. $1000 ) | 1955–2015 | $28 | $3,990,506 | $105,900,000 | NOAA, NHC |
| Socio-Economic Vulnerabilities (V) | ||||||
| IP | Income Per Capita ($ per person) | 1955–2015 | $864 | $16,430 | $60,213 | BEA |
| HD | Housing Unit Density (houses per acre) | 1955–2015 | 5 | 104 | 1672 | Census |
| IH | Income Per Housing Unit ($1000 per unit) | 1955–2015 | $2 | $37 | $140 | BEA, Census |
| FREQ | Historical Hurricane Frequency (Average per year) | 1955–2015 | 0.01 | 0.09 | 0.32 | NOAA, HRD |
| LEVEE | Levee Length Density (miles per acre) | 1955-2015 | 0 | 0.03 | 0.22 | USACE, NLD |
| Natural Forces (F) | ||||||
| WIND | Max Sustained Wind Speed (kt) | 1955–2015 | 65 | 90.3 | 150 | NOAA, HRD |
| PRESS | Central Pressure at Landfall (mb) | 1955–2015 | 909 | 965 | 1003 | NOAA, HRD |
| RAIN | Max Rainfall (in) | 1955–2015 | 4.8 | 13.75 | 38.5 | NOAA, WPC |
| SURGE | Max Surge (ft) | 1955–2015 | 0 | 8.5 | 27.8 | NOAA, NHC |
| ACE | Accumulated Cyclone Energy (Seasonal) | 1955–2015 | 17 | 135 | 250 | NOAA, HRD |
| MOIST | Deviations from trend soil moisture (in) | 1955–2015 | −4.75 | 1 | 5.7 | NOAA, ESRL |
| GST | Land, Air and Sea-Surface Temp. index | 1955–2015 | 0.1 | 0.34 | 0.93 | NASA, GISS |
| Forecast Accuracy and Uncertainty (U) | ||||||
| FORC12 | 12-Hour Official Track Error (miles) | 1955–2015 | 5 | 34 | 114 | NOAA, NHC |
| RADII12 | Implied 12-Hour Radius of Uncertainty (miles) | 1955–2015 | 34 | 70 | 59 | NOAA, NHC |
| NAIVE12 | 12-Hour Naïve Track Error (miles) | 1970–2015 | 5 | 31 | 97 | NOAA, NHC |
| SKILL12 | Ratio of NAIVE12 to FORC12 | 1970–2015 | 0.19 | 1.44 | 10.35 | NOAA, NHC |
| WARN | Warning time over coast length (100 hours per mile) | 1955–2015 | 0.7 | 11.33 | 45.78 | NOAA, NHC |
Appendix C. Calculating the Uncertainty for Differences between Predictions
References
- Arjovsky, Martin, Léon Bottou, Ishaan Gulrajani, and David Lopez-Paz. 2019. Invariant risk minimization. arXiv arXiv:1907.02893. [Google Scholar]
- Bakkensen, Laura A., and Robert O. Mendelsohn. 2016. Risk and adaptation: Evidence from global hurricane damages and fatalities. Journal of the Association of Environmental and Resource Economists 3: 555–87. [Google Scholar] [CrossRef]
- Beatty, Timothy K. M., Jay P. Shimshack, and Richard J. Volpe. 2019. Disaster preparedness and disaster response: Evidence from sales of emergency supplies before and after hurricanes. Journal of the Association of Environmental and Resource Economists 6: 633–68. [Google Scholar] [CrossRef]
- Belloni, Alexandre, Victor Chernozhukov, and Christian Hansen. 2014. Inference on treatment effects after selection among high-dimensional controls. The Review of Economic Studies 81: 608–50. [Google Scholar] [CrossRef]
- Berk, Richard, Lawrence Brown, Andreas Buja, Kai Zhang, and Linda Zhao. 2013. Valid post-selection inference. The Annals of Statistics 41: 802–37. [Google Scholar] [CrossRef]
- Blake, Eric S., Edward N. Rappaport, and Christopher W. Landsea. 2011. The Deadliest, Costliest, and Most Intense United States Tropical Cyclones from 1851 to 2010 (and Other Frequently Requested Hurricane Facts). Silver Spring: NOAA, National Weather Service, National Centers for Environmental Prediction, National Hurricane Center. [Google Scholar]
- Broad, Kenneth, Anthony Leiserowitz, Jessica Weinkle, and Marissa Steketee. 2007. Misinterpretations of the “Cone of Uncertainty” in Florida during the 2004 hurricane season. Bulletin of the American Meteorological Society 88: 651–67. [Google Scholar] [CrossRef]
- Campos, Julia, David F. Hendry, and Hans-Martin Krolzig. 2003. Consistent model selection by an automatic gets approach. Oxford Bulletin of Economics and Statistics 65: 803–19. [Google Scholar] [CrossRef]
- Cangialosi, John P., and James L. Franklin. 2016. 2015 Hurricane Season. In NHC Forecast Verification Report. Silver Spring: NOAA (National Hurricane Center). [Google Scholar]
- Castle, Jennifer L. 2017. Sir Clive WJ Granger Model Selection. European Journal of Pure and Applied Mathematics 10: 133–56. [Google Scholar]
- Castle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2011. Evaluating automatic model selection. Journal of Time Series Econometrics 13: 1–31. [Google Scholar] [CrossRef]
- Castle, Jennifer L., Jurgen A. Doornik, and David F. Hendry. 2012. Model selection when there are multiple breaks. Journal of Econometrics 169: 239–46. [Google Scholar] [CrossRef]
- Castle, Jennifer L., Jurgen A. Doornik, David F. Hendry, and Felix Pretis. 2015. Detecting location shifts during model selection by step-indicator saturation. Econometrics 3: 240–64. [Google Scholar] [CrossRef]
- Castle, Jennifer L., David F. Hendry, and Andrew B. Martinez. 2017. Evaluating forecasts, narratives and policy using a test of invariance. Econometrics 5: 39. [Google Scholar] [CrossRef]
- Chavas, Daniel R., Kevin A. Reed, and John A. Knaff. 2017. Physical understanding of the tropical cyclone wind-pressure relationship. Nature Communications 8: 1–11. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, Denis Chetverikov, Mert Demirer, Esther Duflo, Christian Hansen, Whitney Newey, and James Robins. 2018. Double/debiased machine learning for treatment and structural parameters. The Econometrics Journal 21: C1–C68. [Google Scholar] [CrossRef]
- Clements, Michael P. 2014. Forecast uncertainty—Ex Ante and Ex Post: U.S. inflation and output growth. Journal of Business & Economic Statistics 32: 206–16. [Google Scholar]
- Davlasheridze, Meri, Karen Fisher-Vanden, and H. Allen Klaiber. 2017. The effects of adaptation measures on hurricane induced property losses: Which FEMA investments have the highest returns? Journal of Environmental Economics and Management 81: 93–114. [Google Scholar] [CrossRef]
- Dehring, Carolyn A., and Martin Halek. 2013. Coastal Building Codes and Hurricane Damage. Land Economics 89: 597–613. [Google Scholar] [CrossRef]
- DeMaria, Mark, John Knaff, Richard Knabb, Chris Lauer, Charles Sampson, and Robert DeMaria. 2009. A new method for estimating tropical cyclone wind speed probabilities. Weather and Forecasting 24: 1573–91. [Google Scholar] [CrossRef]
- Deryugina, Tatyana. 2017. The Fiscal Cost of Hurricanes: Disaster Aid Versus Social Insurance. American Economic Journal: Economic Policy 9: 168–98. [Google Scholar] [CrossRef]
- Deryugina, Tatyana, Laura Kawano, and Steven Levitt. 2018. The economic impact of hurricane katrina on its victims: Evidence from individual tax returns. American Economic Journal: Applied Economics 10: 202–33. [Google Scholar] [CrossRef]
- Doornik, Jurgen A. 2008. Encompassing and automatic model selection. Oxford Bulletin of Economics and Statistics 70: 915–25. [Google Scholar] [CrossRef]
- Doornik, Jurgen A. 2009. Autometrics. In The Methodology and Practice of Econometrics: A Festschrift in Honour of David F. Hendry. Edited by Neil Shephard and Jennifer L. Castle. Oxford: Oxford University Press, pp. 88–121. [Google Scholar]
- Doornik, Jurgen A., and Henrik Hansen. 2008. An omnibus test for univariate and multivariate normality. Oxford Bulletin of Economics and Statistics 70: 927–39. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., and David F. Hendry. 2013. Empirical Econometric Modelling. Volume I of PcGive 14. Richmond upon Thames: Timberlake Consultants Ltd. [Google Scholar]
- Emanuel, Kerry. 2005. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 436: 686–88. [Google Scholar] [CrossRef]
- Emanuel, Kerry. 2017a. Assessing the present and future probability of hurricane harvey’s rainfall. Proceedings of the National Academy of Sciences 114: 12681–84. [Google Scholar] [CrossRef]
- Emanuel, Kerry. 2017b. Will global warming make hurricane forecasting more difficult? Bulletin of the American Meteorological Society 98: 495–501. [Google Scholar] [CrossRef]
- Engle, Robert F., and David F. Hendry. 1993. Testing superexogeneity and invariance in regression models. Journal of Econometrics 56: 119–39. [Google Scholar] [CrossRef]
- Engle, Robert F., David F. Hendry, and Jean-Francois Richard. 1983. Exogeneity. Econometrica 51: 277–304. [Google Scholar] [CrossRef]
- Ericsson, Neil R. 2001. Forecast uncertainty in economic modeling. In Understanding Economic Forecasts. Edited by David F. Hendry and Neil R. Ericsson. Cambridge: MIT Press chp. 5, pp. 68–92. [Google Scholar]
- Estrada, Francisco, W. J. Wouter Botzen, and Richard S. J. Tol. 2015. Economic losses from US hurricanes consistent with an influence from climate change. Nature Geoscience 8: 880–84. [Google Scholar] [CrossRef]
- Friedman, Jerome, Trevor Hastie, and Rob Tibshirani. 2010. Regularization paths for generalized linear models via coordinate descent. Journal of Satistical Software 33: 1. [Google Scholar] [CrossRef]
- Gallagher, Justin, and Daniel Hartley. 2017. Household finance after a natural disaster: The case of hurricane katrina. American Economic Journal: Economic Policy 9: 199–228. [Google Scholar] [CrossRef]
- Geiger, Tobias, Katja Frieler, and Anders Levermann. 2016. High-income does not protect against hurricane losses. Environmental Research Letters 11: 084012. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Yongil Jeon. 2004. Thick modeling. Economic Modelling 21: 323–43. [Google Scholar] [CrossRef]
- Hendry, David F. 1995. Dynamic Econometrics. Oxford: Oxford University Press. [Google Scholar]
- Hendry, David F., and Jurgen A. Doornik. 2014. Empirical Model Discovery and Theory Evaluation: Automatic Selection Methods in Econometrics. Cambridge: MIT Press. [Google Scholar]
- Hendry, David F., and Søren Johansen. 2015. Model discovery and Trygve Haavelmo’s legacy. Econometric Theory 31: 93–114. [Google Scholar] [CrossRef]
- Hendry, David F., Søren Johansen, and Carlos Santos. 2008. Automatic selection of indicators in a fully saturated regression. Computational Statistics 23: 337–39. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 2014. Unpredictability in economic analysis, econometric modeling and forecasting. Journal of Econometrics 182: 186–95. [Google Scholar] [CrossRef]
- Hendry, David F., and Carlos Santos. 2010. An Automatic Test of Super Exogeneity. In Volatility and Time Series Econometrics. Edited by Mark W. Watson, Tim Bollerslev and Jeffrey R. Russell. Oxford: Oxford University Press, pp. 164–93. [Google Scholar]
- Hsiang, Solomon M., and Daiju Narita. 2012. Adaptation to cyclone risk: Evidence from the global cross-section. Climate Change Economics 3: 1250011. [Google Scholar] [CrossRef]
- Jarrell, Jerry D., Paul J. Hebert, and Max Mayfield. 1992. Hurricane Experience Levels of Coastal County Populations from Texas to Maine. Silver Spring: US Department of Commerce, National Oceanic and Atmospheric Administration, National Weather Service, National Hurricane Center, vol. 46. [Google Scholar]
- Johansen, Søren, and Bent Nielsen. 2016. Asymptotic theory of outlier detection algorithms for linear time series regression models. Scandinavian Journal of Statistics 43: 321–48. [Google Scholar] [CrossRef]
- Jurado, Kyle, Sydney C. Ludvigson, and Serena Ng. 2015. Measuring uncertainty. The American Economic Review 105: 1177–216. [Google Scholar] [CrossRef]
- Kaplan, John, Mark DeMaria, and John A. Knaff. 2010. A revised tropical cyclone rapid intensification index for the Atlantic and eastern North Pacific basins. Weather and Forecasting 25: 220–41. [Google Scholar] [CrossRef]
- Katz, Richard W., and Jeffrey K. Lazo. 2011. Economic value of weather and climate forecasts. In The Oxford Handbook on Economic Forecasting. Edited by Michael P Clements and David F Hendry. Oxford: Oxford University Press. [Google Scholar]
- Kellenberg, Derek K., and Ahmed Mushfiq Mobarak. 2008. Does rising income increase or decrease damage risk from natural disasters? Journal of Urban Economics 63: 788–802. [Google Scholar] [CrossRef]
- Kidder, Stanley Q., John A. Knaff, Sheldon J. Kusselson, Michael Turk, Ralph R. Ferraro, and Robert J. Kuligowski. 2005. The tropical rainfall potential (TRaP) technique. Part i: Description and examples. Weather and Forecasting 20: 456–64. [Google Scholar] [CrossRef]
- Knutson, Thomas R., John L. McBride, Johnny Chan, Kerry Emanuel, Greg Holland, Chris Landsea, Isaac Held, James P. Kossin, A. K. Srivastava, and Masato Sugi. 2010. Tropical cyclones and climate change. Nature Geoscience 3: 157–63. [Google Scholar] [CrossRef]
- Kruttli, Mathias, Brigitte Roth Tran, and Sumudu W. Watugala. 2019. Pricing Poseidon: Extreme Weather Uncertainty and Firm Return Dynamics. Finance and Economics Discussion Series 2019-054. Washington, DC: Board of Governors of the Federal Reserve System. [Google Scholar]
- Letson, David, Daniel S. Sutter, and Jeffrey K. Lazo. 2007. Economic value of hurricane forecasts: An overview and research needs. Natural Hazards Review 8: 78–86. [Google Scholar] [CrossRef]
- Milch, Kerry, Kenneth Broad, Ben Orlove, and Robert Meyer. 2018. Decision science perspectives on hurricane vulnerability: Evidence from the 2010–2012 atlantic hurricane seasons. Atmosphere 9: 32. [Google Scholar] [CrossRef]
- Mitchell, James, and Kenneth F. Wallis. 2011. Evaluating density forecasts: Forecast combinations, model mixtures, calibration and sharpness. Journal of Applied Econometrics 26: 1023–40. [Google Scholar] [CrossRef]
- Morana, Claudio, and Giacomo Sbrana. 2019. Climate change implications for the catastrophe bonds market: An empirical analysis. Economic Modelling 81: 274–94. [Google Scholar] [CrossRef]
- Mullainathan, Sendhil, and Jann Spiess. 2017. Machine learning: An applied econometric approach. Journal of Economic Perspectives 31: 87–106. [Google Scholar] [CrossRef]
- Murnane, Richard J., and James B. Elsner. 2012. Maximum wind speeds and US hurricane losses. Geophysical Research Letters 39: 1–5. [Google Scholar] [CrossRef]
- National Science Board. 2007. Hurricane Warning: The Critical Need for a National Hurricane Research Initiative; Technical Report NSB-06-115. Alexandria: National Science Foundation.
- NOAA NCEI. 2018. U.S. Billion-Dollar Weather and Climate Disasters. Available online: https://www.ncdc.noaa.gov/billions/ (accessed on 7 September 2018).
- Nordhaus, William D. 2010. The economics of hurricanes and implications of global warming. Climate Change Economics 1: 1–20. [Google Scholar] [CrossRef]
- Peters, Jonas, Peter Bühlmann, and Nicolai Meinshausen. 2016. Causal inference by using invariant prediction: Identification and confidence intervals. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 78: 947–1012. [Google Scholar] [CrossRef]
- Pielke, Roger A., Jr., Joel Gratz, Christopher W. Landsea, Douglas Collins, Mark A. Saunders, and Rade Musulin. 2008. Normalized hurricane damage in the United States: 1900–2005. Natural Hazards Review 9: 29–42. [Google Scholar] [CrossRef]
- Pielke, Roger A., Jr., and Christopher W. Landsea. 1998. Normalized hurricane damages in the United States: 1925-95. Weather and Forecasting 13: 621–31. [Google Scholar] [CrossRef]
- Pretis, Felix, James Reade, and Genaro Sucarrat. 2018. Automated General-to-Specific (GETS) Regression Modeling and Indicator Saturation for Outliers and Structural Breaks. Journal of Statistical Software 86: 1–44. [Google Scholar] [CrossRef]
- Pretis, Felix, Lea Schneider, Jason E. Smerdon, and David F. Hendry. 2016. Detecting Volcanic Eruptions in Temperature Reconstructions by Designed Break-Indicator Saturation. Journal of Economic Surveys 30: 403–29. [Google Scholar] [CrossRef]
- Ramsey, James Bernard. 1969. Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society. Series B (Methodological) 31: 350–71. [Google Scholar] [CrossRef]
- Rappaport, Edward N., James L. Franklin, Lixion A. Avila, Stephen R. Baig, John L. Beven, Eric S Blake, Christopher A. Burr, Jiann-Gwo Jiing, Christopher A. Juckins, Richard D. Knabb, and et al. 2009. Advances and challenges at the National Hurricane Center. Weather and Forecasting 24: 395–419. [Google Scholar] [CrossRef]
- Ravn, Morten O., and Harald Uhlig. 2002. On adjusting the Hodrick-Prescott filter for the frequency of observations. The Review of Economics and Statistics 84: 371–76. [Google Scholar] [CrossRef]
- Regnier, Eva. 2008. Public evacuation decisions and hurricane track uncertainty. Management Science 54: 16–28. [Google Scholar] [CrossRef]
- Resio, Donald T., Nancy J. Powell, Mary A. Cialone, Himangshu S. Das, and Joannes J. Westerink. 2017. Quantifying impacts of forecast uncertainties on predicted storm surges. Natural Hazards 88: 1423–49. [Google Scholar] [CrossRef]
- Rossi, Barbara, and Tatevik Sekhposyan. 2015. Macroeconomic uncertainty indices based on nowcast and forecast error distributions. American Economic Review: Papers and Proceedings 105: 650–55. [Google Scholar] [CrossRef]
- Rossi, Barbara, Tatevik Sekhposyan, and Matthieu Soupre. 2017. Understanding the Sources of Macroeconomic Uncertainty. Barcelona GSE Working Paper Series No. 920. Barcelona: GSE. [Google Scholar]
- Sadowski, Nicole Cornell, and Daniel Sutter. 2005. Hurricane fatalities and hurricane damages: Are safer hurricanes more damaging? Southern Economic Journal 72: 422–32. [Google Scholar] [CrossRef]
- Shrader, Jeffrey. 2018. Expectations and Adaptation to Environmental Risks. SSRN Working Paper. Available online: https://ssrn.com/abstract=3212073 (accessed on 5 May 2020).
- Smith, Adam B., and Richard W. Katz. 2013. US billion-dollar weather and climate disasters: Data sources, trends, accuracy and biases. Natural Hazards 67: 387–410. [Google Scholar] [CrossRef]
- Strobl, Eric. 2011. The economic growth impact of hurricanes: Evidence from US coastal counties. Review of Economics and Statistics 93: 575–89. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. 2004. Hurricane Assessment Concerns and Recommendations. Available online: https://web.archive.org/web/20090726033748/http://chps.sam.usace.army.mil/USHESdata/Assessments/2004Storms/2004-Recommendations.htm (accessed on 22 December 2017).
- Van de Geer, Sara, Peter Bühlmann, Ya’acov Ritov, and Ruben Dezeure. 2014. On asymptotically optimal confidence regions and tests for high-dimensional models. The Annals of Statistics 42: 1166–202. [Google Scholar] [CrossRef]
- van den Dool, Huug, Jin Huang, and Yun Fan. 2003. Performance and analysis of the constructed analogue method applied to US soil moisture over 1981–2001. Journal of Geophysical Research: Atmospheres 108: 1–16. [Google Scholar] [CrossRef]
- Vincenty, Thaddeus. 1975. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Survey Review 23: 88–93. [Google Scholar] [CrossRef]
- Weinkle, Jessica, Chris Landsea, Douglas Collins, Rade Musulin, Ryan P. Crompton, Philip J. Klotzbach, and Roger Pielke. 2018. Normalized hurricane damage in the continental United States 1900–2017. Nature Sustainability 1: 808. [Google Scholar] [CrossRef]
- White, Halbert. 1980. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 48: 817–38. [Google Scholar] [CrossRef]
- Willoughby, Hugh E., E. N. Rappaport, and F. D. Marks. 2007. Hurricane forecasting: The state of the art. Natural Hazards Review 8: 45–49. [Google Scholar] [CrossRef]
| 1. | No forecasts are available for Debra [1959] and Ethel [1960], likely due to their short duration. Longer horizon forecasts are available for even fewer storms and intensity forecasts are only available since 1990. |
| 2. | Estimates prior to 1959 are based on samples less than five years since the database only goes back to 1954. |
| 3. | NHC used to measure the radius based on the previous ten years; see Broad et al. (2007). |
| 4. | Reports were published in the Monthly Weather Review through 2011 and are available from the Hurricane Research Division until 2011. The National Hurricane Center maintains the annual summaries since 2012. |
| 5. | The Storm Events database forms the basis for the SHELDUS database which is available since 1959. Despite its disaggregation of damage across counties, the SHELDUS database tends to underreport damage and often allocates them equally across counties. |
| 6. | Radiative forcing could also be included as in Morana and Sbrana (2019). |
| 7. | Based on estimates from CoreLogic and FEMA. |
| 8. | See Appendix C for details. |
| 9. | Obtained from the Office of the Federal Coordinator for Meteorology. |
| 10. | Pielke et al. (2008) use a similar approach. I aggregate counties using BEA’s modifications to Census codes: https://www.bea.gov/regional/pdf/FIPSModifications.pdf (last accessed November 2016). |
| 11. | The panel data model was estimated over for all U.S. counties from 1969 to 1999 using leads of income shares and population shares as explanatory variables. |
| 12. | I use the Hodrick-Prescott filter and set the smoothing parameter equal to 129,600 following Ravn and Uhlig (2002) for monthly data. |


| (1) Gets | (2) Lasso | (3) Robust Gets | |
|---|---|---|---|
| Selection Target: | 3% | BIC (9%) | 1% |
| Housing density | 0.40 *** | 0.40 *** | 0.24 ** |
| (0.15) | (0.15) | (0.09) | |
| Income per housing unit | 1.30 *** | 1.30 *** | 1.76 *** |
| (0.20) | (0.20) | (0.19) | |
| Historical frequency | −3.38 | ||
| (2.20) | |||
| Max rainfall | 1.15 *** | 0.96 *** | 0.56 *** |
| (0.31) | (0.32) | (0.20) | |
| Max storm surge | 1.34*** | 1.36*** | 0.98*** |
| (0.38) | (0.37) | (0.24) | |
| Min central pressure (-) | 52.2 *** | 50.2 *** | 57.8 *** |
| (8.58) | (8.45) | (5.41) | |
| Seasonal cyclone energy | 0.57 ** | ||
| (0.24) | |||
| Forecast errors | 0.47 * | 0.48 ** | 0.27 * |
| (0.24) | (0.24) | (0.15) | |
| Ex-ante uncertainty | 0.17 | 0.78 | 2.10 ** |
| (0.98) | (1.00) | (0.96) | |
| Outliers: | No | No | Yes |
| Nonlinear terms: | No | No | Yes |
| 1.268 | 1.233 | 0.795 | |
| 0.821 | 0.834 | 0.930 | |
| BIC | 3.673 | 3.688 | 2.774 |
| (1) Errors | (2) Errors/Radius | (3) R&S (2015) | (4) RMSE | |
|---|---|---|---|---|
| Housing density | 0.27 *** | 0.28 *** | 0.28 *** | 0.26 *** |
| (0.10) | (0.10) | (0.10) | (0.10) | |
| Income per housing unit | 1.43 *** | 1.36 *** | 1.36 *** | 1.44 *** |
| (0.12) | (0.12) | (0.12) | (0.13) | |
| Min central pressure (-) | 56.6 *** | 56.8 *** | 56.9 *** | 57.3 *** |
| (5.49) | (5.55) | (5.58) | (5.51) | |
| Max rainfall | 0.57 *** | 0.55 *** | 0.54 ** | 0.56 *** |
| (0.21) | (0.21) | (0.21) | (0.21) | |
| Max storm surge | 0.99 *** | 0.97 *** | 0.97 *** | 0.95 *** |
| (0.24) | (0.25) | (0.25) | (0.24) | |
| Forecast errors | 0.34 ** | |||
| (0.15) | ||||
| Errors/ex-ante | 0.29 * | |||
| (0.16) | ||||
| Uncertainty | 0.23 * | |||
| (0.14) | ||||
| Weighted RMSE | 0.37 * | |||
| (0.19) | ||||
| Outliers: | Yes | Yes | Yes | Yes |
| Nonlinear terms: | Yes | Yes | Yes | Yes |
| 0.812 | 0.819 | 0.822 | 0.817 | |
| 0.927 | 0.925 | 0.925 | 0.926 | |
| BIC | 2.781 | 2.799 | 2.806 | 2.795 |
| (1) Bias | (2) RMSE | (3) MAPE | |
|---|---|---|---|
| Gets | 0.91 | 0.75 | 0.80 |
| Lasso OLS | 0.95 | 0.77 | 0.94 |
| Robust Gets | |||
| Nordhaus (2010) | 1.07 | 0.99 | 5.46 |
| (1) Orthogonal Gets | (2) Double Lasso | (3) IV | |
|---|---|---|---|
| Selection Target: | 3% | BIC (9%) | |
| Forecast errors | 0.39 * | 0.50 ** | 0.49 *** |
| (0.23) | (0.21) | (0.17) | |
| Ex-ante Uncertainty | −1.58 | 0.98 | 2.95 ** |
| (1.13) | (1.01) | (1.25) | |
| Obs. | 98 | 98 | 65 |
| (1) Marginal + IIS | (2) Augmented Conditional | |
|---|---|---|
| Retained Impulses: | Forecast Errors | Damage |
| Connie [1955] | 1.29 (0.57) ** | −0.96 (0.96) |
| Cleo [1964] | −1.21 (0.51) ** | 1.38 (0.87) |
| Opal [1995] | −1.48 (0.52) *** | 0.24 (0.89) |
| Isabel [2003] | −1.19 (0.50) ** | 0.98 (0.85) |
| Arthur [2014] | −1.73 (0.54) *** | −0.53 (0.94) |
| F-statistic | 1.05 | |
| p-value | [0.394] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez, A.B. Forecast Accuracy Matters for Hurricane Damage. Econometrics 2020, 8, 18. https://doi.org/10.3390/econometrics8020018
Martinez AB. Forecast Accuracy Matters for Hurricane Damage. Econometrics. 2020; 8(2):18. https://doi.org/10.3390/econometrics8020018
Chicago/Turabian StyleMartinez, Andrew B. 2020. "Forecast Accuracy Matters for Hurricane Damage" Econometrics 8, no. 2: 18. https://doi.org/10.3390/econometrics8020018
APA StyleMartinez, A. B. (2020). Forecast Accuracy Matters for Hurricane Damage. Econometrics, 8(2), 18. https://doi.org/10.3390/econometrics8020018





