Balanced Growth Approach to Tracking Recessions
Abstract
1. Introduction
2. Literature Review
3. US Postwar Recessions
4. Hybrid Tracking Models
4.1. Key Features
4.2. Implementation Details
4.2.1. Core Model
4.2.2. The State VAR Process
4.2.3. The ECM Measurement Process
4.2.4. Recursive Estimation, Calibration, and Model Validation
5. Pilot Application to the RBC Model
5.1. Model Specification
5.2. Recursive Estimation (Conditional on )
5.3. Recursive Tracking/Forecasting (Conditional on )
5.4. Calibration of
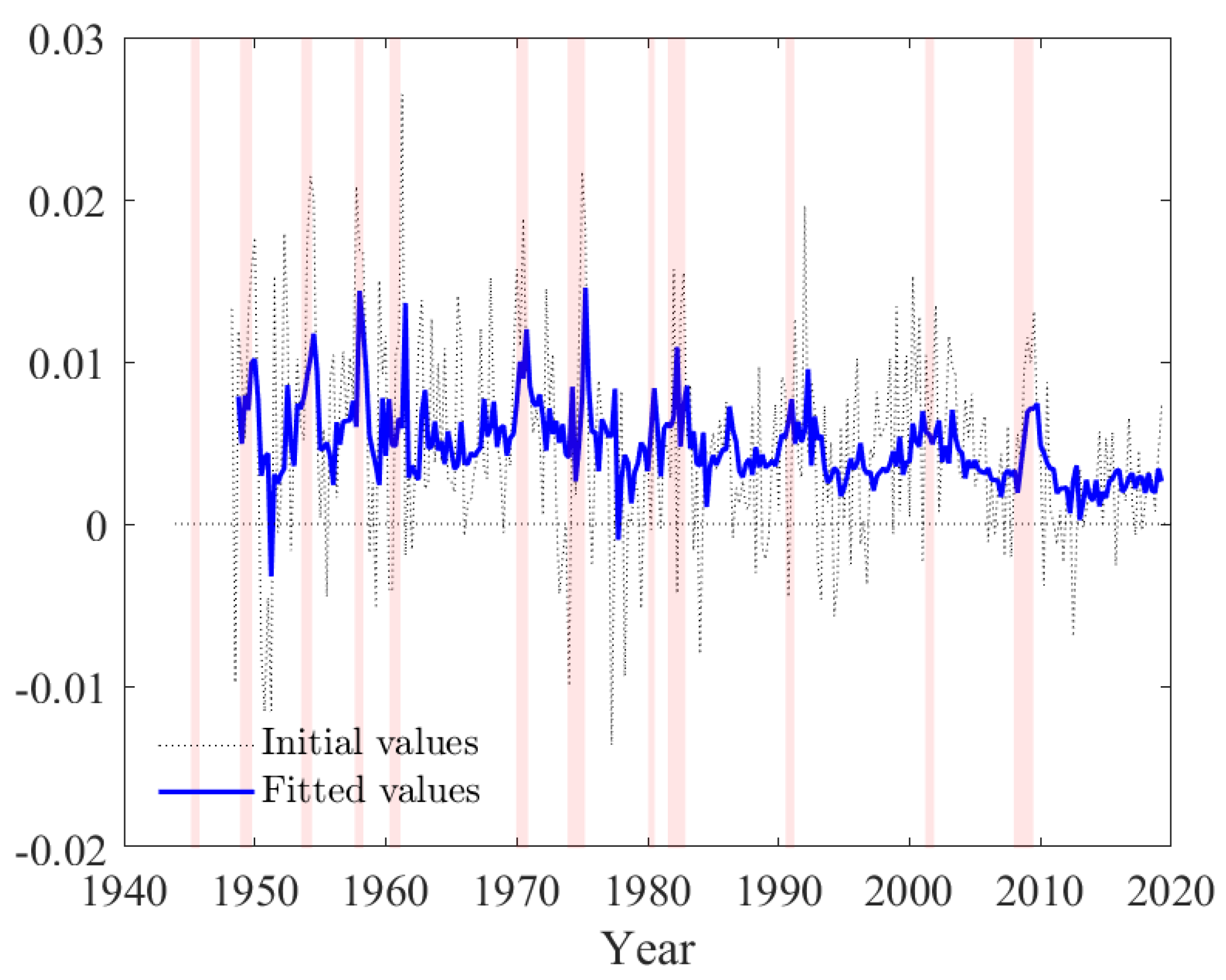
5.5. Results
5.6. Great Recession and FinancialSeries
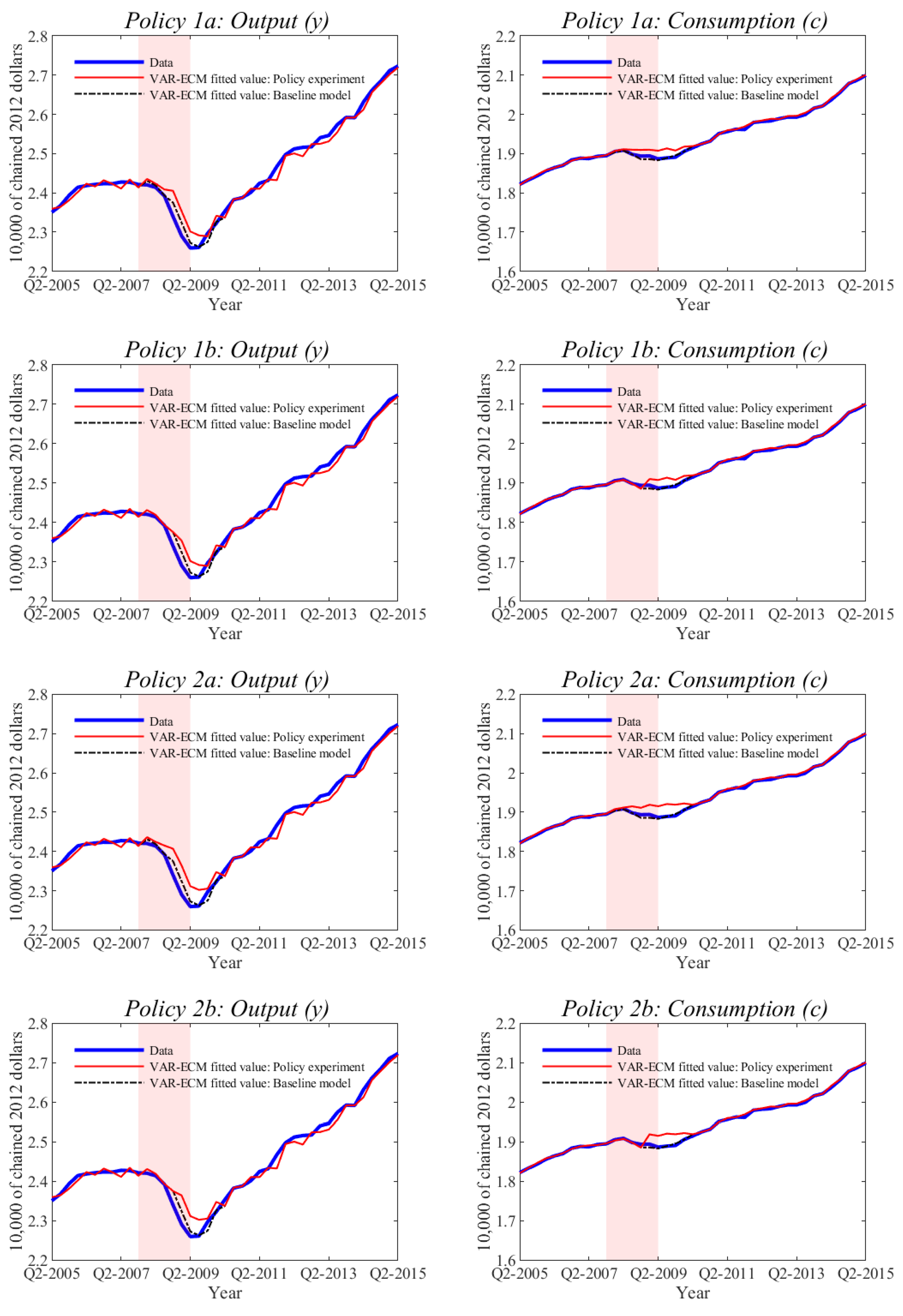
5.7. Policy Experiment
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Data
| Fred Series Name and Identification Code | Units and Seasonal Adjustment | Frequency | Range |
|---|---|---|---|
| Real Personal Consumption Expenditures: Services (DSERRA3Q086SBEA) | Index 2012=100, SA | Quarterly | 1948Q1–2019Q2 |
| Real Personal Consumption Expenditures: Services (PCESVC96) | Billions of chained 2012 dollars, SAAR | Quarterly | 2002Q1–2019Q2 |
| Real Personal Consumption Expenditures: Nondurable Goods (DNDGRA3Q086SBEA) | Index 2012=100, SA | Quarterly | 1948Q1–2019Q2 |
| Real Personal Consumption Expenditures: Nondurable Goods (PCNDGC96) | Billions of chained 2012 dollars, SAAR | Quarterly | 2002Q1–2019Q2 |
| Real Gross Private Domestic Investment | Billions of chained 2012 dollars, SAAR | Quarterly | 1948Q1–2019Q2 |
| (GPDIC1) | |||
| Civilian Noninstitutional Population: 25 to 54 Years (LNU00000060) | Thousands of persons, NSA | Quarterly | 1948Q1–2019Q2 |
Appendix A.1. Consumption
Appendix A.2. Output
Appendix A.3. Fraction of Time Spent Working
Appendix B. Pseudo Code for the RBC Application
- Set .
- Start calibration loop:
- 2.1.
- Select .
- Start recursive loop (given ):
- 3.1.
- Set .
- 3.2.
- Estimate state variables:Set to a principal component of and , .Given optimize in :where .
- 3.3.
- Estimate the VAR process for :where .Store and .
- 3.4.
- Estimate the ECM process for :where , andStore and .
- 3.5.
- Compute fitted values .
- 3.6.
- Conduct MC forecast simulation :
- 3.6.1.
- Forecast 1- to 3-step ahead from VAR: .
- 3.6.2.
- Forecast 1- to 3-step ahead from ECM: given .
- 3.6.3.
- Recover and store .
- If , then and go to 3.2. Else, end recursive loop.
- Evaluate recursive performance. For :
- 5.1.
- Graph and .
- 5.2.
- Compute mean 1- to 3-step ahead forecasts: , .
- 5.3.
- Graph fitted values and 1- to 3-step ahead mean forecasts .
- 5.4.
- Graph MC 95 percent confidence intervals for .
- 5.5.
- Compute the MAE and RMSE for , for , .
- As needed, return to 2.1 and select a different value of .
Appendix C. Additional Figures
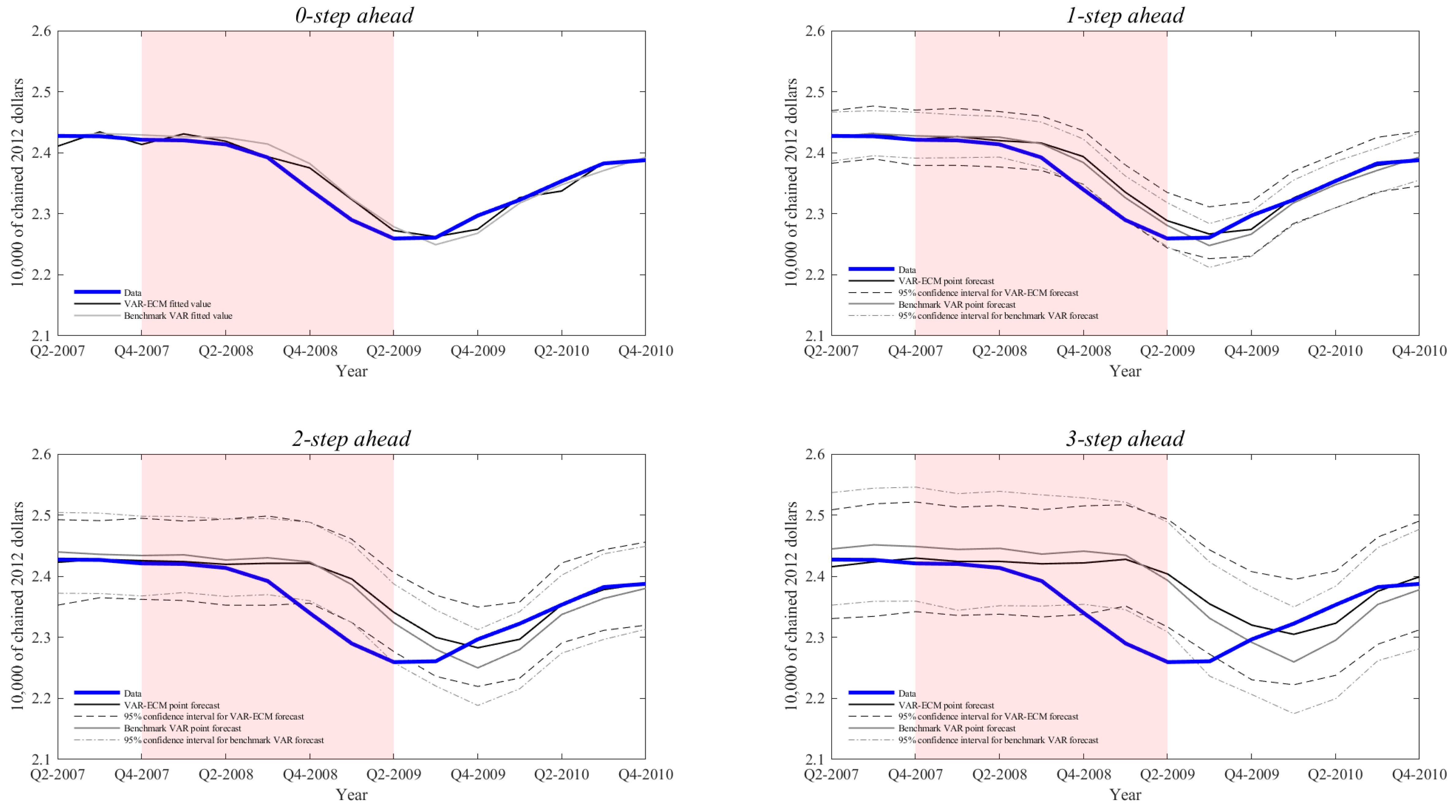
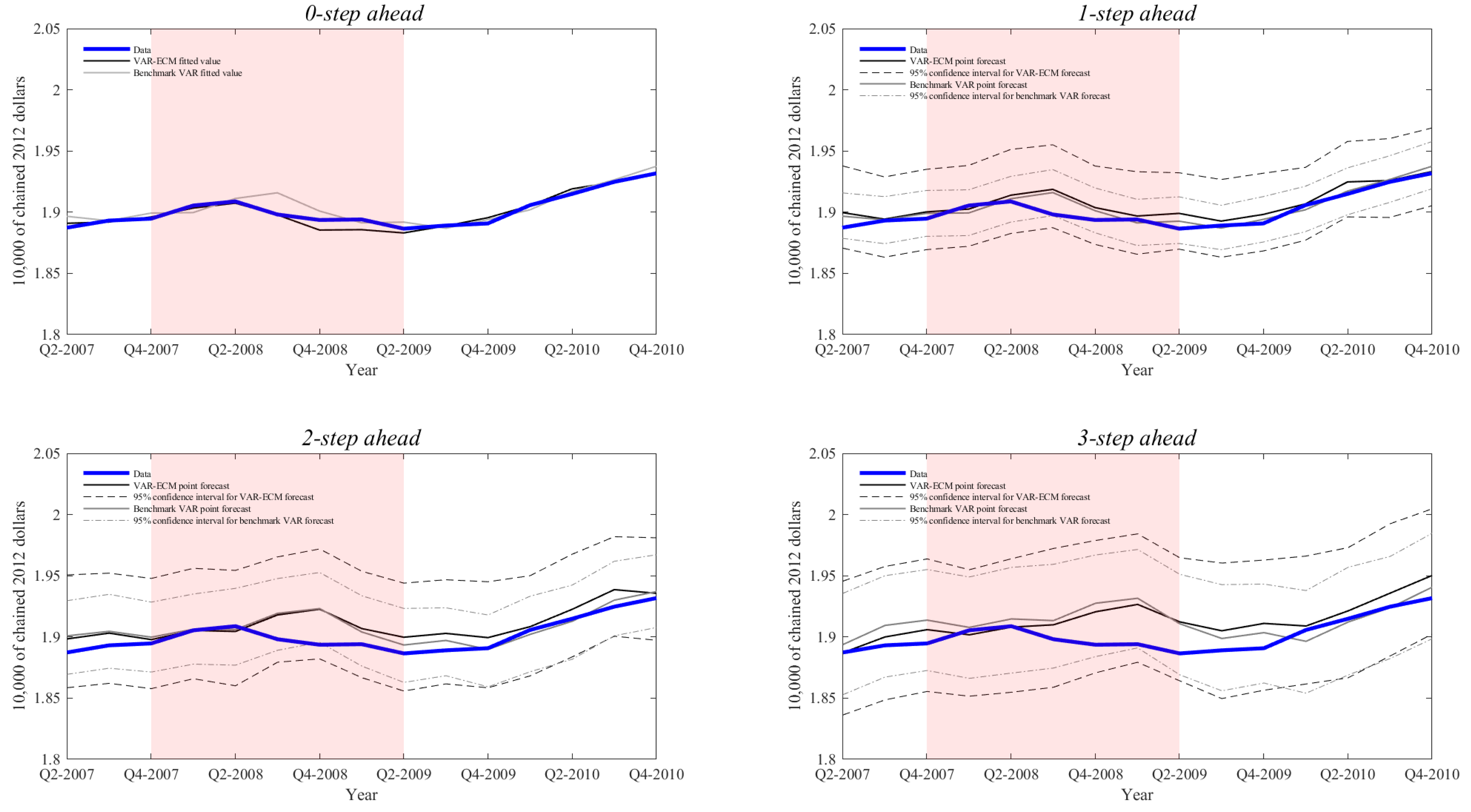
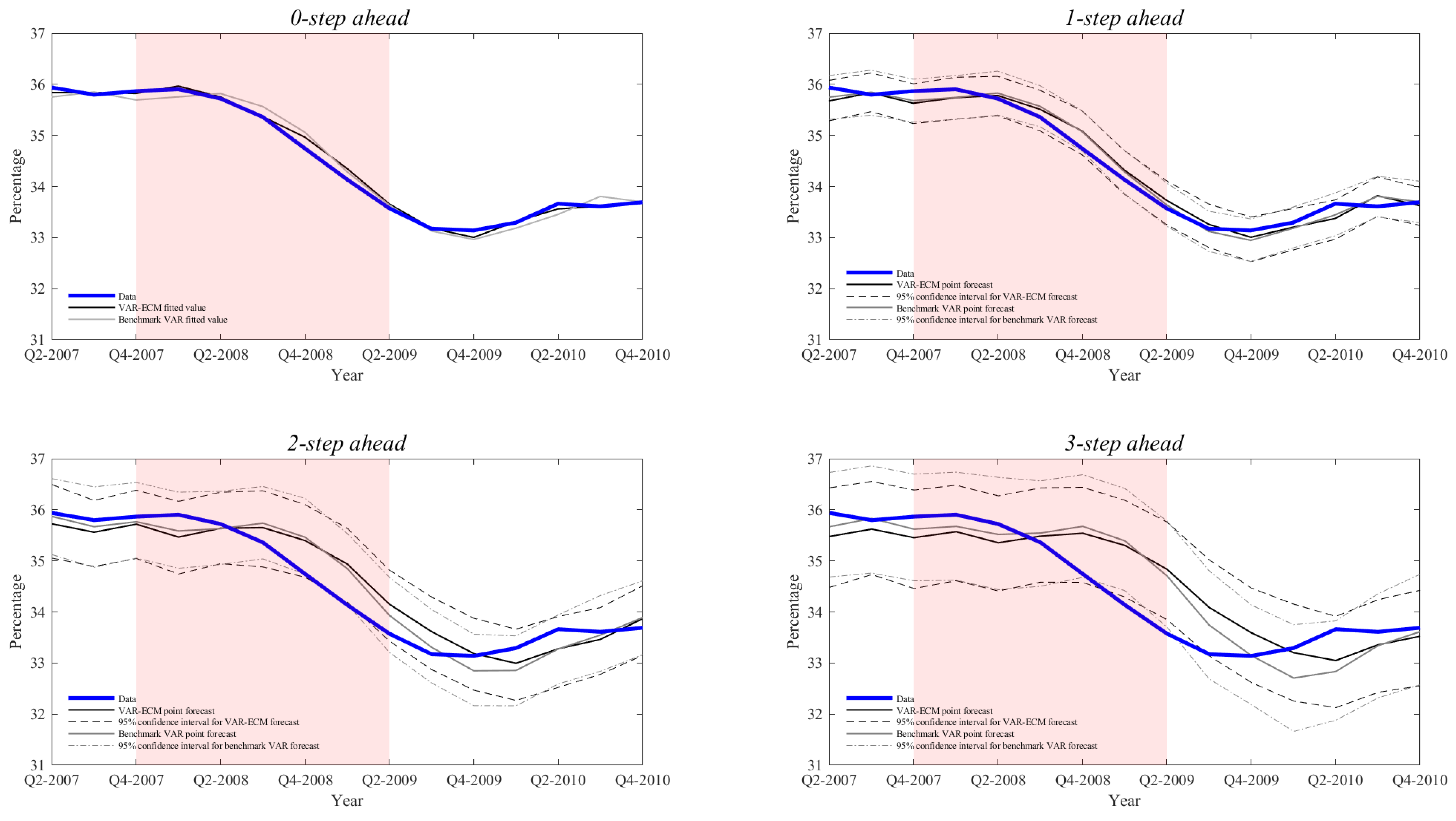


References
- An, Sungbae, and Frank Schorfheide. 2007. Bayesian analysis of DSGE models. Econometric Review 26: 113–72. [Google Scholar] [CrossRef]
- Bierens, Herman J., and Luis F. Martins. 2010. Time-varying cointegration. Econometric Theory 26: 1453–90. [Google Scholar] [CrossRef]
- Blanchard, Olivier. 2016. Do DSGE models have a future? In Policy Brief. Washington, DC: Peterson Institute for International Economics, pp. 16–11. [Google Scholar]
- Caballero, Ricardo J. 2010. Macroeconomics after the crisis: Time to deal with the pretense-of-knowledge syndrome. Journal of Economic Perspectives 24: 85–102. [Google Scholar] [CrossRef]
- Canova, Fabio, and Fernando J. Pérez Forero. 2015. Estimating overidentified, nonrecursive, time-varying coefficients structural vector autoregressions. Quantitative Economics 6: 359–84. [Google Scholar] [CrossRef]
- Cardinali, Alessandro, and Guy P. Nason. 2010. Costationarity of locally stationary time series. Journal of Time Series Econometrics 2: 1–33. [Google Scholar] [CrossRef]
- Carroll, Christopher D. 2000. Saving and growth with habit formation. American Economic Review 90: 341–55. [Google Scholar] [CrossRef]
- Castle, Jennifer L., Michael P. Clements, and David F. Hendry. 2016. An overview of forecasting facing breaks. Journal of Business Cycle Research 12: 3–23. [Google Scholar] [CrossRef][Green Version]
- Castle, Jennifer L., Nicholas W. P. Fawcett, and David F. Hendry. 2010. Forecasting with equilibrium-correction models during structural breaks. Journal of Econometrics 158: 25–36. [Google Scholar] [CrossRef]
- Chari, V. V., Patrick J. Kehoe, and Ellen R. McGrattan. 2007. Business cycle accounting. Econometrica 75: 781–836. [Google Scholar] [CrossRef]
- Chari, V. V., Patrick J. Kehoe, and Ellen R. McGrattan. 2009. New Keynesian models: Not yet useful for policy analysis. American Economic Journal: Macroeconomics 1: 242–66. [Google Scholar] [CrossRef]
- Christiano, Lawrence J., and Joshua M. Davis. 2006. Two Flaws in Business Cycle Accounting. NBER Working Papers 12647. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Christiano, Lawrence J., Martin S. Eichenbaum, and Mathias Trabandt. 2018. On DSGE models. Journal of Economic Perspectives 32: 113–40. [Google Scholar] [CrossRef]
- Clements, Michael P., and David F. Hendry. 1993. On the limitations of comparing mean square forecast errors. Journal of Forecasting 12: 617–37. [Google Scholar] [CrossRef]
- Deaton, Angus. 1991. Saving and liquidity constraints. Econometrica 59: 1221–48. [Google Scholar] [CrossRef]
- Del Negro, Marco, and Frank Schorfheide. 2008. Forming priors for DSGE models (and how it affects the assessment of nominal rigidities). Journal of Monetary Economics 55: 1191–208. [Google Scholar] [CrossRef]
- DeJong, David N., and Chetan Dave. 2011. Structural Macroeconomics, 2nd ed. Princeton: Princeton University Press. [Google Scholar]
- DeJong, David N., Roman Liesenfeld, Guilherme V. Moura, Jean-François Richard, and Hariharan Dharmarajan. 2013. Efficient likelihood evaluation of state-space representations. Review of Economic Studies 80: 538–67. [Google Scholar] [CrossRef]
- DeJong, David N., Roman Liesenfeld, and Jean-François Richard. 2005. A nonlinear forecasting model of GDP growth. The Review of Economics and Statistics 87: 697–708. [Google Scholar] [CrossRef]
- Elliott, Graham, and Allan Timmermann. 2016. Forecasting in economics and finance. Annual Review of Economics 8: 81–110. [Google Scholar] [CrossRef]
- Ericsson, Neil R., and Andrew B. Martinez. 2019. Evaluating government budget forecasts. In The Palgrave Handbook of Government Budget Forecasting. Edited by D. Williams and T. Calabrese. Cham: Palgrave Macmillan. [Google Scholar]
- Giandrea, Michael D., and Shawn Sprague. 2017. Estimating the U.S. Labor Share. Monthly Labor Review. U.S. Bureau of Labor Statistics: Available online: https://doi.org/10.21916/mlr.2017.7 (accessed on 12 August 2019).
- Grimit, Eric P., Tilmann Gneiting, Veronica J. Berrocal, and Nicholas A. Johnson. 2006. The continuous ranked probability score for circular variables and its application to mesoscale forecast ensemble verification. Quarterly Journal of the Royal Meteorological Society 132: 2925–42. [Google Scholar] [CrossRef]
- Hamilton, James D. 2018. Why you should never use the Hodrick-Prescott filter. Review of Economics and Statistics 100: 831–43. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 1993. Evaluating dynamic econometric models by encompassing the VAR. In Models, Methods and Applications of Econometrics. Edited by P. C. B. Phillips. Cambridge: Blackwell. [Google Scholar]
- Hendry, David F., and Grayham E. Mizon. 2014a. Unpredictability in economic analysis, econometric modeling and forecasting. Journal of Econometrics 182: 186–95. [Google Scholar] [CrossRef]
- Hendry, David F., and Grayham E. Mizon. 2014b. Why DSGEs crash during crises. VOX CEPR’s Policy Portal. Available online: https://voxeu.org/article/why-standard-macro-models-fail-crises (accessed on 12 August 2009).
- Hendry, David F., and John N. J. Muellbauer. 2018. The future of macroeconomics: Macro theory and models at the Bank of England. Oxford Review of Economic Policy 34: 287–328. [Google Scholar] [CrossRef]
- Hendry, David F., and Jean-François Richard. 1982. On the formulation of empirical models in dynamic econometrics. Journal of Econometrics 20: 3–33. [Google Scholar] [CrossRef]
- Hendry, David F., and Jean-François Richard. 1989. Recent developments in the theory of encompassing. In Contributions to Operation Research and Econometrics: The Twentieth Anniversary of CORE. Edited by B. Cornet and H. Tulkens. Cambridge: MIT press. [Google Scholar]
- Ingram, Beth F., and Charles H. Whiteman. 1994. Supplanting the ’Minnesota’ prior: Forecasting macroeconomic time series using real business cycle model priors. Journal of Monetary Economics 34: 497–510. [Google Scholar] [CrossRef]
- Jones, Janelle, and Valerie Wilson. 2018. Working Harder or Finding It Harder to Work: Demographic Trneds in Annual Work Hours Show an Increasingly Featured Workforce. Washington, DC: Economic Policy Institute. [Google Scholar]
- Jusélius, Katarina, and Massimo Franchi. 2007. Taking a DSGE model to the data meaningfully. Economics-ejournal 1: 1–38. [Google Scholar] [CrossRef]
- Juster, Thomas F., and Frank P. Stafford. 1991. The allocation of time: Empirical findings, behavioral models, and problems of measurement. Journal of Economic Literature 29: 471–522. [Google Scholar]
- Korinek, Anton. 2017. Thoughts on DSGE Macroeconomics: Matching the Moment, but Missing the Point? Paper presented at the 2015 Festschrift Conference ’A Just Society’ Honoring Joseph Stiglitz’s 50 Years of Teaching; Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3022009 (accessed on 29 August 2019).
- Matteson, David S., Nicholas A. James, William B. Nicholson, and Louis C. Segalini. 2013. Locally Stationary Vector Processes and Adaptive Multivariate Modeling. Paper presented at the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, May 26–31; pp. 8722–26. [Google Scholar]
- Mizon, Grayham E., and Jean-François Richard. 1986. The encompassing principle and its application to testing non-nested hypotheses. Econometrica 54: 657–78. [Google Scholar] [CrossRef]
- Mizon, Grayham E. 1984. The encompassing approach in econometrics. In Econometrics and Quantitative Economics. Edited by D. F. Hendry and K. F. Wallis. Oxford: Blackwell. [Google Scholar]
- Muellbauer, John N. J. 2016. Macroeconomics and consumption: Why central bank models failed and how to repair them. VOX CEPR’s Policy Portal. Available online: https://voxeu.org/article/why-central-bank-models-failed-and-how-repair-them (accessed on 15 February 2019).
- Pagan, Adrian. 2003. Report on Modelling and Forecasting at the Bank of England. Quarterly Bulletin. London: Bank of England. [Google Scholar]
- Pesaran, M. Hashem, and Allan Timmermann. 2007. Selection of estimation window in the presence of breaks. Journal of Econometrics 137: 134–61. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Davide Pettenuzzo, and Allan Timmermann. 2006. Forecasting time series subject to multiple structural breaks. Review of Economic Studies 73: 1057–84. [Google Scholar] [CrossRef]
- Romer, Paul. 2016. The trouble with macroeconomics. The American Economist. Forthcoming. [Google Scholar]
- Rubio-Ramírez, Juan F., and Jesús Fernández-Villaverde. 2005. Estimating dynamic equilibrium economies: Linear versus nonlinear likelihood. Journal of Applied Econometrics 20: 891–910. [Google Scholar]
- Schorfheide, Frank. 2011. Estimation and Evaluation of DSGE Models: Progress and Challenges. NBER Working Papers 16781. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Sims, Christopher A. 2007. Monetary Policy Models. CEPS Working Papers 155. Brussels: CEPS. [Google Scholar]
- Smets, Frank, and Raf Wouters. 2005. Comparing shocks and frictions in US and Euro area business cycles: A Bayesian DSGE approach. Journal of Applied Econometrics 20: 161–83. [Google Scholar] [CrossRef]
- Smets, Frank, and Raf Wouters. 2007. Shocks and frictions in US business cycles: A Bayesian DSGE approach. American Economic Review 97: 586–606. [Google Scholar] [CrossRef]
- Stiglitz, Joseph E. 2018. Where modern macroeconomics went wrong. Oxford Review of Economic Policy 34: 70–106. [Google Scholar] [CrossRef]
- Trichet, Jean-Claude. 2010. Reflections on the nature of monetary policy non-standard measures and finance theory. Opening address at the ECB Central Banking Conference, Frankfurt, Germany, November 18. [Google Scholar]
- Wallis, Kenneth F. 1974. Seasonal adjustment and relations between variables. Journal of the American Statistical Association 69: 18–31. [Google Scholar] [CrossRef]
- Wieland, Volker, and Maik Wolters. 2012. Macroeconomic model comparisons and forecast competitions. VOX CEPR’s Policy Portal. Available online: https://voxeu.org/article/failed-forecasts-and-financial-crisis-how-resurrect-economic-modelling (accessed on 15 January 2019).
| 1. | |
| 2. | It follows that the ECM parsimounsly encompasses the initial VAR model. See Hendry and Richard (1982, 1989); Mizon and Richard (1986); Mizon (1984) for a discussion of the concept of encompassing and its relevance for econometric models. |
| 3. | See also An and Schorfheide (2007) for a survey of Bayesian methods used to evaluate DSGE models and an extensive list of related references. |
| 4. | In the present paper, we follow Pagan (2003) by using an unrestricted VAR as a standard benchmark to assess the empirical relevance of our proposed model. Potential extensions to Bayesian VARs belong to future research (though imposing a DSGE-type prior density on VAR in order to improve its theoretical relevance could negatively impact its empirical performance). |
| 5. | A similar message was delivered by Jerome Powell in his swearing-in ceremony as the new Chair of the Federal Reserve: “The success of our institution is really the result of the way all of us carry out our responsibilities. We approach every issue through a rigorous evaluation of the facts, theory, empirical analysis and relevant research. We consider a range of external and internal views; our unique institutional structure, with a Board of Governors in Washington and 12 Reserve Banks around the country, ensures that we will have a diversity of perspectives at all times. We explain our actions to the public. We listen to feedback and give serious consideration to the possibility that we might be getting something wrong. There is great value in having thoughtful, well-informed critics”. (See https://www.federalreserve.gov/newsevents/speech/powell20180213a.htm for the complete speech given during the ceremonial swearing-in on February 13, 2018). |
| 6. | For more details see https://www.youtube.com/watch?v=lyzS7Vp5vaY (Stiglitz’s interview posted on May 6, 2019) and https://www.youtube.com/watch?v=rUYk2DA8PH8 (Schiller’s interview posted on April 1, 2019). |
| 7. | For the full article see https://www.theguardian.com/business/2019/feb/05/financial-crisis-us-uk-crash. February, 2019. |
| 8. | By doing so, we avoid producing “series with spurious dynamic relations that have no basis in the underlying data-generating process” (Hamilton 2018) as well as “mistaken influences about the strength and dynamic patterns of relationships” (Wallis 1974). |
| 9. | There is no evidence that seasonality plays a determinant role in recessions and recoveries. Therefore, without loss of generality we rely upon seasonally adjusted data, instead of substantially increasing the number of model parameters by inserting quarterly dummies, potentially in every equation of the state VAR and/or ECM processes. |
| 10. | NBER recession dating is based upon GDP growth, not per capita GDP growth. However, our objective is not that of dating recessions, for which there exists an extensive and expanding literature. Instead, our objective is that of tracking macroeconomic aggregates at times of rapid changes, and for that purpose per capita data can be used without loss of generality. Note that if needed per capita projections can be ex-post back-transformed into global projections. |
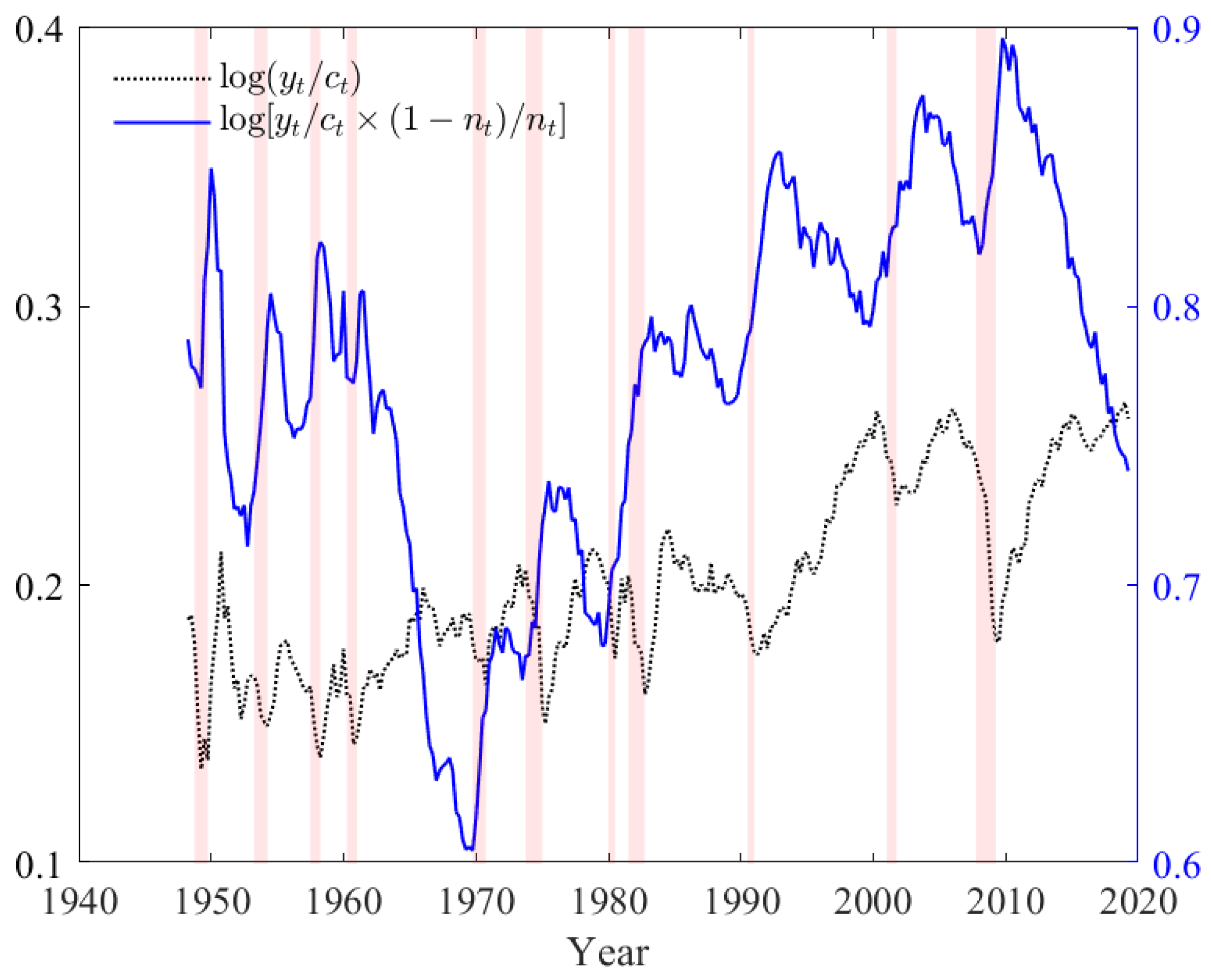
| 11. | Since we rely upon real data, it is apparent that the great ratios vary considerably over time. Most importantly, their long term dynamics appear to be largely synchronized with business cycles providing a solid basis for our main objective of tracking recessions. |
| 12. | It is sometimes argued that in order to be interpreted as structural and/or to be instrumental for policy analysis, a parameter needs to be time invariant. We find such a narrow definition to be unnecessarily restrictive and often counterproductive. The very fact that some key structural parameters are found to vary over time in ways that are linked to the business cycles and can be inferred from a state VAR process paves the way for policy interventions on these variables, which might not be available under the more restricted interpretation of structural parameters. An example is provided in Section 5.7. |
| 13. | Potential exogenous variables are omitted for the ease of notation. |
| 14. | It is also meant to be parsimonious in the sense that the number of state variables in has to be less that the number of equations. |
| 15. | The benchmark VAR process for is given by . |
| 16. | See Appendix A for the full description of the data. |
| 17. | See also DeJong and Dave (2011, sct. 5.1.2). |
| 18. | The risk aversion parameter could also be considered, except for the fact that it is loosely identified to the extent that letting vary over time serves no useful purpose, and worse, can negatively impact the subsequent recursive invariance of the model. |
| 19. | For the ease of interpretation, the second component of is redefined as the sum of the original great ratios in Equation (11). |
| 20. | It follows that standard cointegration rank tests are not applicable in this context. Bierens and Martins (2010) propose a vector ECM likelihood ratio test for time-invariant cointegration against time-varying cointegration. However, it is not applicable as such to our two stage model and, foremost, Figure 2 offers clear empirical evidence in favor of time-varying cointegration. |
| 21. | Individual elimination would be undermined by the fact that the estimated residual covariance matrix is ill-conditioned with condition numbers of the order of , which raises concerns about the validity of asymptotic critical values for system test statistics. One advantage of the sequential system elimination is that we can rely upon standard single equation t- and F-test statistics. |
| 22. | Both eliminations appear to be meaningful. First, equilibrium adjustments in are undoubtedly impeded by factors beyond agents control. Second, the elimination of is likely driven by the fact that the quarterly variations of are too small to have a significant impact on . |
| 23. | |
| 24. | We investigated a number of alternative time windows and arrived at similar qualitative results. |
| 25. | Depending upon an eventual decision context, alternative metrics could be used (see Elliott and Timmermann 2016). |
| 26. | It is important to note that the MAE and RMSE have inherent shortcomings because they measure a single variable’s forecast properties at a single horizon (see Clements and Hendry 1993). While measures do exist for assessing forecast accuracy for multiple series across multiple horizons, we believe that they would not impact our conclusions in view of the evidence provided further below (tables, figures, and hedgehog graphs). |
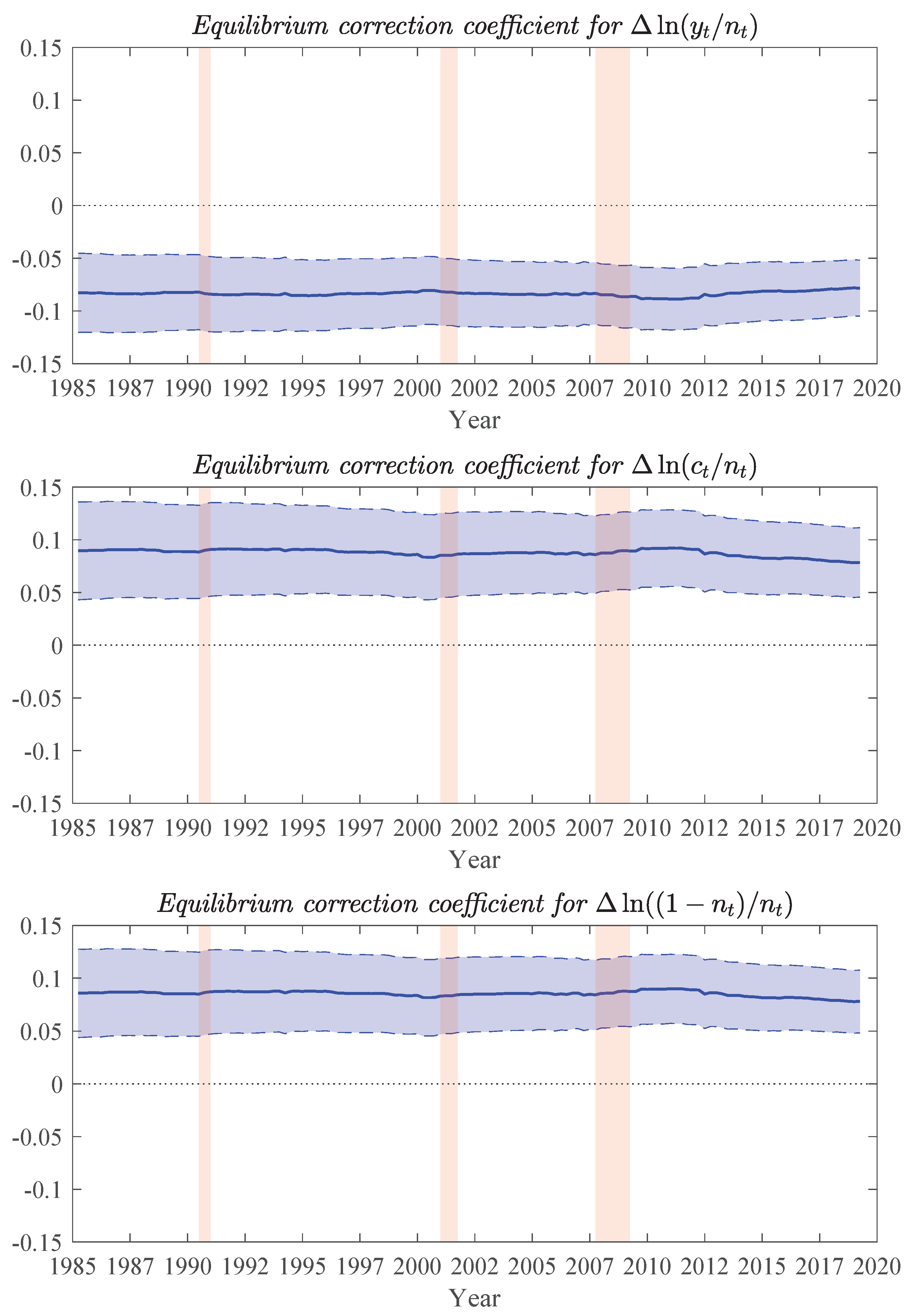
| 27. | Analogous figures for all other coefficients of the VAR-ECM model and of VAR benchmark are presented in Figures S2–S4 of the Online Supplementary Material and confirm the overall recursive invariance of our estimates and those of the VAR benchmark. |
| 28. | Analogous figures for the other two recessions are presented in Figures S17–S22 of the Online Supplementary Material. |
| 29. | Note that the 95 percent confidence intervals are those of the 1000 individual MC draws. The mean forecasts are much more accurate with standard deviations divided by the square root of 1000. |
| 30. | The average CRPS is given by , where stands for and denotes the predictive CDF. See Grimit et al. (2006, Formula (3)) for the discrete version of the CRPS. |
| 31. | The CRPS accounts for the full predictive CDF and as such was not used as one of the calibration criteria for since our objective is that of producing mean rather than point forecasts. |
| 32. | A four quarter lag allows us to produce 4-step ahead forecasts, without ex-ante forecasting any of the auxiliary series added into the VAR-ECM baseline model. 4-step ahead forecasts are available upon request and were not included in the paper as they only confirm further the ex-ante forecasting delays already illustrated in Figure A1, Figure A2 and Figure A3. |
| 33. | The history of earlier postwar recessions unambiguously suggest that even if such series were available for the entire postwar period, they would likely fail to explain earlier recessions and would, therefore, be irrelevant at those time. Hence, we believe that any potential bias resulting from the missing data would also be insignificant. This is confirmed further by the fact that the auxiliary series incorporated into the VAR component of the VAR-ECM model turn out to be largely insignificant for the Great Recession, even though they are directly related to its cause. |



| Regressor | Dependent Variable | |||||
|---|---|---|---|---|---|---|
| 0.014 | (2.66) | −0.002 | (−0.36) | 0.031 | (2.60) | |
| 2.422 | (3.94) | 2.715 | (3.87) | 3.768 | (2.79) | |
| 0.133 | (3.10) | 1.314 | (26.81) | 0.281 | (2.97) | |
| −1.019 | (−3.68) | −1.287 | (−4.07) | −1.565 | (−2.57) | |
| −2.162 | (−3.41) | −2.388 | (−3.30) | −5.470 | (−3.92) | |
| −0.139 | (−3.21) | −0.324 | (−6.56) | −0.294 | (−3.09) | |
| 0.994 | (3.58) | 1.300 | (4.10) | 2.517 | (4.11) | |
| Regressor | Dependent Variable | |||||
|---|---|---|---|---|---|---|
| 0.002 | (4.41) | −0.002 | (−3.98) | −0.002 | (−4.18) | |
| −0.078 | (−5.78) | 0.079 | (4.68) | 0.078 | (5.16) | |
| −0.258 | (−1.92) | 1.115 | (6.70) | 0.677 | (4.53) | |
| −0.224 | (−1.83) | 1.004 | (6.62) | 0.605 | (4.44) | |
| −0.053 | (−1.66) | 0.026 | (0.67) | 0.540 | (15.14) | |
| 0.169 | (0.40) | 3.865 | (7.39) | 1.941 | (4.13) | |
| −0.991 | (−5.15) | −0.461 | (−1.93) | 0.224 | (1.05) | |
| F-statistic | 1.64 | 2.30 | 1.92 | |||
| Mean Absolute Error | Root Mean Square Error | Continuous Rank Probability Score | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VAR-ECM | Benchmark VAR | VAR-ECM | Benchmark VAR | VAR-ECM | Benchmark VAR | ||||||||||||||||||
| n | y | ||||||||||||||||||||||
| Recession 1990–1991 | |||||||||||||||||||||||
| 50 | 11 | 0.44 | 104 | 73 | 0.99 | 59 | 13 | 0.51 | 137 | 88 | 1.20 | - | - | - | - | - | - | ||||||
| 98 | 67 | 1.10 | 108 | 74 | 1.04 | 135 | 86 | 1.38 | 140 | 89 | 1.24 | 334 | 436 | 6.32 | 210 | 345 | 6.33 | ||||||
| 141 | 97 | 1.87 | 193 | 111 | 2.01 | 222 | 116 | 2.36 | 271 | 141 | 2.45 | 1155 | 719 | 4.51 | 1377 | 846 | 4.50 | ||||||
| 207 | 89 | 3.17 | 275 | 124 | 3.45 | 277 | 117 | 3.77 | 359 | 167 | 4.04 | 5731 | 3803 | 5.13 | 5857 | 3828 | 5.31 | ||||||
| Recession 2001 | |||||||||||||||||||||||
| 62 | 16 | 0.43 | 138 | 38 | 1.52 | 79 | 22 | 0.56 | 167 | 49 | 1.96 | - | - | - | - | - | - | ||||||
| 106 | 45 | 1.44 | 144 | 39 | 1.60 | 134 | 57 | 1.74 | 173 | 51 | 2.05 | 4736 | 3140 | 3.79 | 4586 | 3063 | 3.72 | ||||||
| 164 | 60 | 2.45 | 268 | 75 | 3.05 | 237 | 90 | 2.71 | 319 | 98 | 3.53 | 1867 | 1400 | 5.33 | 1514 | 1306 | 6.75 | ||||||
| 211 | 68 | 3.07 | 376 | 107 | 4.46 | 292 | 112 | 3.33 | 455 | 138 | 5.36 | 2501 | 1768 | 3.35 | 2736 | 1849 | 3.30 | ||||||
| Recession 2007–2009 | |||||||||||||||||||||||
| 117 | 27 | 0.72 | 145 | 49 | 1.42 | 161 | 38 | 1.00 | 189 | 64 | 1.62 | - | - | - | - | - | - | ||||||
| 139 | 65 | 1.65 | 153 | 51 | 1.47 | 217 | 85 | 1.87 | 197 | 66 | 1.66 | 7103 | 5246 | 6.40 | 7074 | 5199 | 7.37 | ||||||
| 268 | 103 | 3.29 | 335 | 84 | 2.89 | 431 | 126 | 3.91 | 433 | 114 | 3.58 | 2442 | 2522 | 19.4 | 2116 | 2444 | 22.0 | ||||||
| 410 | 130 | 5.05 | 528 | 138 | 4.57 | 625 | 162 | 6.20 | 676 | 175 | 6.05 | 514 | 129 | 9.64 | 576 | 165 | 9.84 | ||||||
| Housing Variables | Financial Variables | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Absolute Error | Root Mean Square Error | Mean Absolute Error | Root Mean Square Error | |||||||||
| Housing Starts: Total: New Privately Owned Housing Units Started (1959Q1) | Chicago Fed National Financial Conditions Index (1971Q1) | |||||||||||
| h = 1 | −3.8 | −18.6 | −5.5 | −3.7 | −19.8 | 0.3 | −6.6 | −12.4 | −4.9 | −5.2 | −10.3 | −3.1 |
| h = 2 | −1.2 | −28.5 | 3.0 | −6.1 | −26.4 | −3.6 | −4.2 | −19.2 | −4.2 | −5.9 | −15.9 | −5.8 |
| h = 3 | −5.5 | −26.2 | 5.9 | −5.9 | −24.4 | −4.8 | −5.0 | −21.5 | −3.6 | −5.5 | −17.6 | −5.7 |
| Median Number of Months on Sales Market for Newly Completed Homes (1975Q1) | Delinquency Rate on Commercial and Industrial Loans at All Commercial Banks (1987Q1) | |||||||||||
| h = 1 | 2.6 | −17.2 | 0.2 | −2.0 | −10.5 | 0.6 | 3.3 | 1.3 | 0.3 | 2.3 | 2.8 | 0.1 |
| h = 2 | 11.4 | −14.8 | −0.1 | −1.7 | −10.2 | −0.2 | 8.2 | 7.6 | −0.4 | 2.5 | 8.2 | 1.5 |
| h = 3 | 7.6 | −5.0 | 2.7 | −1.1 | −8.7 | 0.4 | 7.5 | 14.8 | 1.2 | 4.0 | 13.0 | 2.6 |
| Median Sales Price of Houses Sold (1963Q1) | Delinquency Rate on Consumer Loans at All Commercial Banks (1987Q1) | |||||||||||
| h = 1 | 7.9 | 9.8 | −7.0 | −2.9 | 17.7 | −7.4 | −1.0 | −3.9 | −0.4 | −0.7 | −2.0 | 0.1 |
| h = 2 | 17.5 | 13.4 | −18.0 | −2.4 | 24.3 | −9.5 | −1.0 | −2.9 | 0.1 | −1.6 | −2.9 | 0.4 |
| h = 3 | 13.2 | 14.6 | −14.2 | −0.3 | 16.1 | −7.9 | −1.9 | 1.6 | 1.4 | −1.6 | −1.6 | 1.0 |
| Monthly Supply of Houses (1963Q1) | Delinquency Rate on Loans Secured by Real Estate at All Commercial Banks (1987Q1) | |||||||||||
| h = 1 | −4.9 | −9.2 | 0.9 | −3.9 | −5.4 | 1.3 | 4.2 | −11.9 | 0.3 | −1.5 | −9.7 | 0.4 |
| h = 2 | −1.9 | −10.5 | 2.2 | −3.7 | −8.0 | 2.0 | 9.4 | −15.8 | 0.3 | −1.6 | −10.8 | −0.4 |
| h = 3 | −4.0 | −11.5 | 2.9 | −4.0 | −10.4 | 2.7 | 4.5 | −12.8 | 3.1 | −1.0 | −10.5 | 0.2 |
| New One Family Homes for Sale (1963Q1) | Household Financial Obligations as a Percent of Disposable Personal Income (1980Q1) | |||||||||||
| h = 1 | 2.5 | 0.3 | −1.7 | 2.2 | −0.1 | −0.4 | 4.0 | 3.3 | 0.5 | 2.9 | 3.8 | 0.8 |
| h = 2 | 0.1 | 1.6 | −1.0 | 0.2 | −0.5 | −2.1 | 6.4 | 19.3 | −0.5 | 3.2 | 15.1 | 3.7 |
| h = 3 | 0.9 | 8.9 | 1.9 | 1.3 | 5.3 | −2.2 | 7.0 | 32.1 | −1.6 | 4.8 | 24.3 | 4.6 |
| New One Family Houses Sold (1963Q1) | Mortgage Debt Service Payments as a Percent of Disposable Personal Income (1980Q1) | |||||||||||
| h = 1 | 8.0 | −0.5 | 20.9 | −14.4 | −9.8 | 28.1 | 2.7 | 1.9 | −0.3 | 2.0 | 2.1 | 0.4 |
| h = 2 | 11.0 | −9.9 | 26.8 | −18.1 | −11.3 | 26.2 | 3.4 | 13.5 | 0.2 | 1.9 | 9.9 | 2.2 |
| h = 3 | −0.8 | −13.2 | 30.5 | −22.2 | −17.1 | 21.2 | 4.1 | 21.9 | −1.0 | 3.1 | 16.7 | 2.6 |
| New Private Housing Units Authorized by Building Permits (1960Q1) | Mortgage Real Estate Investment Trusts: Liability Level of Debt Securities (1969Q2) | |||||||||||
| h = 1 | −6.6 | −21.7 | −6.9 | −8.4 | −26.7 | 1.5 | 3.0 | 6.5 | −0.9 | 0.7 | 7.8 | −2.4 |
| h = 2 | 1.0 | −38.4 | 3.5 | −11.1 | −37.6 | −2.7 | 12.1 | 25.1 | −6.0 | 1.8 | 23.3 | 2.5 |
| h = 3 | −8.6 | −39.0 | 8.3 | −12.0 | −40.4 | −4.3 | 12.0 | 43.6 | −4.8 | 3.5 | 31.7 | 5.7 |
| New Privately-Owned Housing Units Completed (1968Q1) | Mortgage Real Estate Investment Trusts: Liability Level of Mortgage-Backed Bonds (1984Q1) | |||||||||||
| h = 1 | 23.5 | 30.0 | −0.5 | 15.2 | 23.9 | −0.7 | 1.3 | 5.1 | −1.8 | 0.3 | 6.0 | −3.3 |
| h = 2 | 18.9 | 54.0 | 0.8 | 13.3 | 44.0 | 1.8 | 8.7 | 17.7 | −8.7 | 0.7 | 16.7 | −0.2 |
| h = 3 | 21.0 | 80.2 | 3.2 | 17.7 | 65.7 | 2.8 | 7.6 | 31.9 | −6.4 | 1.8 | 22.0 | 2.5 |
| New Privately-Owned Housing Units Under Construction (1970Q1) | 10-Year Treasury Constant Maturity Minus 3-Month Treasury Constant Maturity (1982Q1) | |||||||||||
| h = 1 | 14.7 | 17.6 | −0.6 | 8.4 | 11.9 | −0.4 | −0.7 | −1.9 | 0.4 | 0.3 | −2.3 | 1.4 |
| h = 2 | 9.2 | 32.6 | 0.8 | 6.7 | 24.8 | 0.8 | −0.5 | 0.3 | 6.0 | −0.2 | −0.8 | 3.3 |
| h = 3 | 10.3 | 46.5 | 2.5 | 9.3 | 38.6 | 1.3 | −0.6 | 5.4 | 7.4 | 0.1 | 1.5 | 4.7 |
| S&P/Case-Shiller U.S. National Home Price Index (1987Q1) | 10-Year Treasury Constant Maturity Minus 2-Year Treasury Constant Maturity (1976Q3) | |||||||||||
| h = 1 | 8.0 | 4.8 | −0.3 | 3.2 | 5.5 | −1.2 | 5.8 | 17.8 | 0.9 | 3.6 | 9.6 | 2.5 |
| h = 2 | 15.6 | 19.3 | −3.3 | 3.8 | 17.5 | 0.1 | 5.4 | 21.0 | 8.5 | 3.3 | 16.0 | 5.8 |
| h = 3 | 16.7 | 37.6 | −2.0 | 6.4 | 26.5 | 1.2 | 5.1 | 28.8 | 8.0 | 4.2 | 21.6 | 7.8 |
| Year | Quarter | Policy 1a | Policy 1b | Policy 2a | Policy 2b |
|---|---|---|---|---|---|
| 2007 | Q4 | 0.0005 | - | −0.0030 | - |
| 2008 | Q1 | 0.0005 | - | −0.0030 | - |
| 2008 | Q2 | 0.0020 | - | −0.0100 | - |
| 2008 | Q3 | 0.0030 | - | −0.0200 | - |
| 2008 | Q4 | 0.0040 | 0.0060 | −0.0200 | −0.0200 |
| 2009 | Q1 | 0.0040 | 0.0060 | −0.0200 | −0.0200 |
| 2009 | Q2 | 0.0040 | 0.0060 | −0.0200 | −0.0200 |
| 2009 | Q3 | 0.0030 | 0.0030 | −0.0100 | −0.0100 |
| 2009 | Q4 | 0.0020 | 0.0030 | −0.0100 | −0.0100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boczoń, M.; Richard, J.-F. Balanced Growth Approach to Tracking Recessions. Econometrics 2020, 8, 14. https://doi.org/10.3390/econometrics8020014
Boczoń M, Richard J-F. Balanced Growth Approach to Tracking Recessions. Econometrics. 2020; 8(2):14. https://doi.org/10.3390/econometrics8020014
Chicago/Turabian StyleBoczoń, Marta, and Jean-François Richard. 2020. "Balanced Growth Approach to Tracking Recessions" Econometrics 8, no. 2: 14. https://doi.org/10.3390/econometrics8020014
APA StyleBoczoń, M., & Richard, J.-F. (2020). Balanced Growth Approach to Tracking Recessions. Econometrics, 8(2), 14. https://doi.org/10.3390/econometrics8020014





