Abstract
This paper discusses Bayesian model averaging (BMA) in Stochastic Frontier Analysis and investigates inference sensitivity to prior assumptions made about the scale parameter of (in)efficiency. We turn our attention to the “standard” prior specifications for the popular normal-half-normal and normal-exponential models. To facilitate formal model comparison, we propose a model that nests both sampling models and generalizes the symmetric term of the compound error. Within this setup it is possible to develop coherent priors for model parameters in an explicit way. We analyze sensitivity of different prior specifications on the aforementioned scale parameter with respect to posterior characteristics of technology, stochastic parameters, latent variables and—especially—the models’ posterior probabilities, which are crucial for adequate inference pooling. We find that using incoherent priors on the scale parameter of inefficiency has (i) virtually no impact on the technology parameters; (ii) some impact on inference about the stochastic parameters and latent variables and (iii) substantial impact on marginal data densities, which are crucial in BMA.
Keywords:
stochastic frontier analysis; Bayesian model averaging; Bayesian inference; model uncertainty; efficiency analysis; public policy JEL Classification:
C11; C44; C52; C54
1. Introduction
Economics is an odd discipline of science. It is common to have multiple, sometimes contradicting theories to explain observed phenomena. While this may not be too troubling for economic theorists, for empirical researchers it poses a considerable challenge to integrate diverse economic theories into one modelling framework. Moreover, not all aspects of econometric models can be derived from economic theories—many assumptions regarding, e.g., distribution of error terms or functional forms for conditional means are somewhat arbitrary. Since interpretable results are often sensitive to specifications of econometric models consequences of these assumptions should not be neglected.
Many approaches have been put forward to mitigate the problem—see, e.g., (Steel 2019) and references therein—but one approach has caught attention in recent years. Bayesian model averaging (BMA hereafter), also known as Bayesian inference pooling, is a statistical method of pooling inference from different models in order to explain the observed economic process. Although BMA has been around for several decades, the reason it has been recently gaining popularity is not entirely due to its sound foundations rooted in statistics and probability theory. Its increasing popularity is also likely due to other reasons, e.g., (i) increased computation power; (ii), development of specific computation algorithms and (iii) scarcity of alternatives in the frequentist approach.
The core concept of BMA is to deal with model uncertainty by averaging the results from different models using the concept of mixture, with weights interpreted as posterior model probabilities. In cases where one model clearly dominates over others (which is more likely with increasing sample size) it is practically equivalent to Bayesian model selection (BMS). This technique amounts to choosing the model which is clearly favored by the data. In that sense, BMA/S can be viewed as tools for empirical validation of economic theories. BMA is undoubtedly very helpful to address model uncertainty, although some care needs to be taken when using it as it is sensitive to prior assumptions. Fortunately, at least for standard regression models, this has been well addressed in the literature (Ley and Steel 2009, 2012).
We emphasize that although BMA is most often used for covariate selection problems, the approach is very general, and can be used to deal with uncertainty regarding all the aspects of model specification. Steel (2019) lists three types of uncertainty that need to be addressed, and our interest is in “specification uncertainty”. We focus on parametric models with known covariates, and the uncertainty here refers to the choice of the sampling model (in particular, its stochastic structure). Note, however, that in order for BMA to properly deal with this kind of uncertainty, certain conditions need to be met. The core idea of BMA is in pooling over a number of Bayesian models (and each Bayesian model consists of a likelihood and a prior). In order to be able to interpret the results of BMA as averaging over competing sampling models (likelihoods), we need to make sure that all the priors used reflect the same beliefs—this requirement is known as prior coherence. If prior coherence requirements are not met, BMA is feasible, but its results are driven not only by different performance of the sampling models under consideration, but also by differences in model-specific prior beliefs. In such cases, especially when prior incoherence is not explicitly discussed and justified, results are likely to be misinterpreted.
Two important aspects need to be mentioned. First, prior coherence is relatively easy to define for a class of nested sampling models. In such a framework, any sampling model under consideration is defined by a set of parametric restrictions imposed on the general model. Consequently, coherence requirement implies that it is necessary to set prior assumptions for the general sampling model only. Model-reducing restrictions need to be imposed on the prior in order to derive priors in all nested cases under consideration. Hence, in a nested family of sampling models prior elicitation is done only once, in the most general case. Second, even if prior coherence is met, the results of BMA still depend upon the chosen prior structure, and thus the prior needs to reflect reasonable (or justified) beliefs. Consequently, prior coherence is necessary but not sufficient when BMA is used to deal with model specification uncertainty. Note that prior incoherence is unlikely to be a problem in the usual application of BMA when the purpose is covariate selection.
Another requirement of BMA is that the priors for model-specific parameters have to be proper (hence ruling out many formal noninformative specifications), and even if prior coherence is met it is necessary to analyze sensitivity of BMA results with respect to the prior. However, without prior coherence, results of Bayesian model comparison or model averaging are difficult to interpret. Unfortunately, in many practical applications of BMA, prior coherence problems are implicit.
The practical use of BMA has often been concerned with rather simple models in terms of their stochastic structure. However, constant development in computational speed and algorithm design has made it possible for BMA to be applied in the areas which involve more complex stochastic model structures (e.g., complicated hierarchical priors). Still, two issues are of great importance here. First, increased model complexity with, e.g., many layers of latent variables or high-dimensional parameter spaces makes choice of priors more important (at least with fixed sample size). Obviously, such high-dimensional prior structures are difficult to investigate—hence the actual consequences of certain formally stated prior beliefs in terms of interpretable quantities are often unclear. Second, considerations regarding prior specification are still in practice motivated mostly by computational convenience. As priors are often restricted to certain parametric classes, the scope of sensitivity analysis is limited to disturbing the choice of hyperparameters (and even this is often neglected in empirical analyses), and then demonstrating some degree of robustness for selected characteristics of posterior distribution to changes in prior hyperparameters. However, it is well known that even if essential characteristics of a posterior distribution are robust to the choice of priors, the posterior model probabilities, crucial for BMA, are not; see, e.g., (Osiewalski and Steel 1993). Moreover, such robustness is more likely to hold for model parameters and not necessarily for latent variables (as the latter increase in dimensionality with the sample size). If latent variables are the quantities of interest, prior assumptions might still have considerable influence upon the results. To summarize, whenever BMA is used and the quantities of interest are latent variables, it is essential to use priors that are coherent and well-specified (i.e., represent beliefs that are actually reasonable, given the problem at hand).
One prominent example where latent variables are of great interest is Stochastic Frontier Analysis (SFA hereafter). It is a method used to benchmark (in)efficiencies of decision-making units (DMUs) and these (in)efficiencies are treated as latent variables. Depending on how we frame the objective function, referred to as the frontier, the efficiency can be technical (pure analysis of production) or economic. Economic efficiency in turn can be, e.g., cost, revenue or profit efficiency; depending on the type of process we consider—cost, revenue or profit functions. The core difference between a stochastic frontier (SF) model and a “standard” regression input(s)-output model is that the stochastic component, usually denoted by ε, is compound in SFA. Traditionally to maintain identification we assume additive structure of ε’s sub-components; e.g., . Subcomponent , which represents a random symmetric disturbance, is usually normally distributed, though new proposals emerge in this field (see, e.g., Tchumtchoua and Dey 2007; Griffin and Steel 2007; Wheat et al. 2019; Stead et al. 2018, 2019; Horrace and Parmeter 2018; Florens et al. 2019). Subcomponent represents inefficiency (latent variable), a nonnegative disturbance that results in asymmetry of the compound error ε and can only have a decreasing effect on the observed output. Given the traditional log-linear form of the frontier a simple transformation, , produces standardized measures of efficiency . Originally inefficiency has been assumed to follow either half-normal distribution in the normal-half-normal model (Aigner et al. 1977) or exponential distribution in the normal-exponential model (Meeusen and van den Broeck 1977). Many proposals about inefficiency distribution have been made since the introduction of SFA—see, e.g., (Griffin and Steel 2008)—and SF models can currently have a complex structure with as many as four stochastic components (Makieła 2017). However, the traditional normal-half-normal and normal-exponential SF models still dominate the applied research.
Efficiency estimates in SFA can vary depending on the distributional assumptions made about the compound error structure. The two most commonly used distributions of inefficiency—exponential and half-normal—have been reported to produce substantially different estimates; with gamma and truncated normal producing results somewhere “between” the two; see, e.g., (Greene 2008). Since we do not know what the prior should look like it makes even more sense to “average” our results from different specifications in respect to . BMA seems like a natural way to do so. Accurate inference about inefficiency is also important from the viewpoint of public policy (in the area of energy, education, health care, agriculture or finance, to mention some examples). Rankings of DMUs with respect to inefficiency are often used by public regulators. Moreover, extended stochastic frontier models might provide insights into sources of inefficiency. Proper application of BMA in SFA provides an important contribution into development of quantitative tools supporting policy-making.
Bayesian analysis of SF models was introduced in a seminal paper of (van den Broeck et al. 1994). Despite limitations of computational power at the time, the authors clearly stated all the related inferential problems and managed to conduct inference using Monte Carlo–Importance Sampling (MC–IS), including inference pooling for latent variables. Moreover, van den Broeck et al. (1994) provided careful discussion of their prior assumptions, extended in subsequent papers e.g., (Fernández et al. 1997). However, the actual popularity of Bayesian SFA followed the development of automated numerical methods, e.g., Gibbs sampling; see, e.g., (Osiewalski and Steel 1998). It is perhaps a paradox that a more widespread use of Bayesian techniques was not accompanied by equally careful usage of Bayesian reasoning developed by van den Broeck et al. (1994) (with a notable exception of Griffin and Steel 2008). Consequently, large part of the applied literature on Bayesian SFA is based on practical solutions that neglect the issue of model uncertainty or its linkage to prior elicitation. Thus, the purpose of this paper is to revisit the fundamental perspective outlined by van den Broeck et al. (1994) and to provide detailed discussion about the role of prior specification on model averaging in Bayesian SFA, using a somewhat more general model framework and advanced numerical methods.
Despite the contribution of van den Broeck et al. (1994), BMA/S usage in SFA has been infrequent at best. For example, (Makieła 2014) used posterior odds but only to choose a particular model rather than average inference across inefficiency scores. Bayes factors have also been used, e.g., by (Griffin and Steel 2008), or (Tsionas and Kumbhakar 2014) to test alternative specifications. Probably the first use of BMA in Bayesian SFA on a large scale can be found in (Makieła and Osiewalski 2018), who use this technique to find the optimal model in the sense of optimal set of explanatory variables. Although, Makieła and Osiewalski (2018) discuss the possibility of integrating different stochastic assumptions as regards inefficiency distribution for BMA, they stick to the normal-exponential model throughout the empirical study. One reason is that if we want to use different SFA specifications (in terms of inefficiency distribution) in BMA we need to be sure that we maintain prior coherence on inefficiency, and this may be a challenging task. In particular, Makieła (2014) reports substantial differences between the two popular normal-half-normal and normal-exponential models, some of which are likely due to incoherent priors. So this avenue is definitely worth exploring.
Our contribution to the literature is threefold. First, we propose a modelling framework that nests the two most commonly used SF models, that is, normal-half-normal and normal-exponential, so that formal comparative analysis is possible and effective. Second, we take the commonly used priors on inefficiency in the two models and review their impact on BMA in two scenarios: when prior coherence is neglected, and when it is accounted for. Third, we propose a prior which is intuitive and coherent, and thus allows us to effectively perform BMA across models with different distributional assumptions about inefficiency.
Griffin and Steel (2008) have considered a framework with a generalized inefficiency distribution and prior coherence, but without explicit consideration of sensitivity to full range of alternative priors suggested in the literature. Furthermore, we note that our usage of BMA is nonstandard because we apply it to average results across different distributions of inefficiency within the aforementioned model class. Traditionally BMA is used to decide which covariates should enter the model, and thus which variables should be selected. We do not comment on the variable selection aspect of BMA in this paper. We feel that for SF models this has been already well addressed in (Makieła and Osiewalski 2018).
2. Methodology
In order to reconsider issues of Bayesian model specification and inference pooling we make use of some of the results in (Makieła and Mazur 2020), who have recently proposed a generalized framework for parametric analysis of stochastic frontier (SF) models based on generalizations discussed by (Harvey and Lange 2017). van den Broeck et al. (1994) were the first to introduce Bayesian analysis of SF models along with an in-depth discussion of model uncertainty and inference pooling problems. However, some of their results reflect limitations of numerical methods available at the time. In the subsequent years, Bayesian applications of SF models had flourished following the successful use of the Gibbs sampling scheme (with full conditionals of the standard form, including the latent variables) as in (Koop et al. 1999, 2000). Numerical convenience of the Gibbs algorithm resulted in abundance of empirical studies using the method, with normal-exponential and normal-half-normal models serving as the workhorse for the applied work. However, the convenience of the Gibbs sampling approach comes at a cost. First, as conjugate-type results are used, the priors are restricted to specific classes. As a result, the popular normal-exponential and normal-half-normal models have been used with priors that reflect beliefs which are not necessarily compatible. Second, the perspective of model averaging or inference pooling, emphasized in the original paper of van den Broeck et al. (1994), has not been pursued further in the mainstream applied work; exceptions include, e.g., (Griffin and Steel 2007, 2008 and Makieła and Osiewalski 2018). The two problems are related, as it is well-known that the results of Bayesian model comparison are likely to be sensitive to prior specification. Therefore, careful prior elicitation together with prior sensitivity analysis is essential for adequate Bayesian inference pooling.
The results in (Makieła and Mazur 2020) imply that the two popular sampling models mentioned above are indeed nested within a broader model class, based on the Generalized Error Distribution (GED). Consequently, it is feasible to develop inference methods that do not require any particular form of priors, and thus to reconsider the original inference-pooling approach by van den Broeck et al. (1994). This can be now achieved based on various classes of priors that are coherent across sampling models and consequences for model comparison can be investigated.
Consider the counterpart of Equation (1) in van den Broeck et al. (1994), which defines the basic SF production model:
with representing the i.i.d. error term with symmetric and unimodal probability density function (pdf hereafter), being an i.i.d. latent variable, taking strictly positive values, representing the inefficiency term. Usually represents the log of output while denotes technology. The majority of practical applications assume that follows Gaussian distribution, while is half-normal or exponential. Our approach to statistical inference outlined below does not require the log transformation for , nor the linear form of with respect to . However, in the empirical part of the paper we make use of the restrictions in order to compare our results to those reported in previous studies.
Statistical inference relies on properties of the compound error term , with sampling distribution implied by properties of , defined in the general case by the convolution of densities for and (denoted by and respectively):
Since u’s are treated as latent variables, the likelihood function based on (2) is sometimes referred to as integrated likelihood (emphasizing the fact that the latent variables are “integrated out”). Although in the general case this integral has no exact analytical solution it can be evaluated (using numerical methods) with arbitrary precision, at any point in the parameter space. One evaluation of the integrated likelihood requires computation of T univariate integrals, which can be parallelized easily (as the observations are assumed to be i.i.d.). In our view nonstochastic methods of numerical integration are sufficient for this purpose, although some fine-tuning of the numerical procedure is indeed required.
We assume that follows the zero-mean GED distribution (see Subbotin 1923) of the form:
where denotes the Gamma function, denotes the scale parameter and controls shape, with special cases of = 2 (Gaussian) and = 1 (Laplace). For we assume that it follows the distribution of , i.e., half-GED: . The same special cases induce half-normal and exponential distributions, respectively. The GED distribution is continuous, but not differentiable at the mode for some values of (as it is “spiked” at the mode). However, the sum of a GED variable and a half-GED variable has smoother distribution, corresponding to a generalized four-parameter form of ‘skew GED’ (although it differs from some cases considered in the literature; see, e.g., (Theodossiou et al. 2020); for a recent application). Hence the integrated likelihood function implied by (2) and (3) is regular (given the parameter space considered here). Some theoretical problems might occur for boundary values of parameter, though in our view they are of little practical importance for the Bayesian inference strategy outlined below.
Crucially, we assume that the shape parameters in the distributions of and are not the same. This is reflected below by subscripts or : , , , denoting parameters of the distribution of and that of . We assume that , ≥ 1 if the parameters are not fixed. Compared to (Griffin and Steel 2008) we assume a more general distributional form of , although our assumption about is somewhat more restrictive. The authors assume that is distributed as generalized gamma following (Stacy 1962), which implies somewhat different parametrization of the scale parameter in their restricted case corresponding to the half-GED distribution of . The difference in parametrization leads to an observationally equivalent likelihood, but it might matter for prior specification, in particular the dependence between and . Our parametrization in (3) relies upon the fact that itself is a scale parameter (Makieła and Mazur 2020; demonstrate linkages with a more general formulation, which may also be of interest). This also means that our interpretation of the scale parameter of does not change with . Hence, the two approaches differ with respect to the assumptions regarding the prior dependence between and . We do not state that any of the two sets of assumptions is superior, though we indicate that the prior dependence should be somehow justified within the most general model used.
van den Broeck et al. (1994) assume to be Gaussian and to be truncated-normal or Erlang-type (i.e., Gamma with the shape parameter equal to 1, 2 or 3). We prefer to restrict ourselves to cases where the distribution of is characterized by a strictly decreasing pdf, therefore ruling out the Erlang-2 and Erlang-3 cases, as well as the truncated-normal one with truncation below 0. For the purpose of simplicity, we also rule out the truncated-normal case with positive truncation. It is important to note that it is possible to modify the above setup to encompass the fully general framework of van den Broeck et al. (1994). In this paper, however, we are motivated to remove the aforementioned cases for a number of reasons. First, we recognize that the SFA literature involving nonmonotonic distributions of is quite large; see, e.g., (Stevenson 1980; van den Broeck et al. 1994; Greene 2003; Griffin and Steel 2004, 2008; Tsionas 2006, 2007; Hajargasht 2015) among others. Many studies find support for nonmonotonic densities of inefficiency. Unfortunately, these studies also assume to be Gaussian. It may very well be that empirical evidence found in favor of nonmonotonic distributions is simply driven by, e.g., outliers and the restrictive assumption about ; see, e.g., (Wheat et al. 2019; Stead et al. 2018, 2019) for a series of discussions about outliers in SFA. Once the symmetric term is generalized to accommodate them the need for nonmonotonic distributions of inefficiency may no longer be supported by the data. Second, there is a more practical reason of statistical identification. Allowing for with distribution that does not satisfy the aforementioned monotonicity condition provides very limited gain in terms of overall model flexibility at the cost of potentially leading to a likelihood that is empirically very close to nonidentification (i.e., approximately flat in certain directions). In other words, from the viewpoint of potential statistical fit (within the parametric approach), it is sufficient to consider flexible distributional forms for and that satisfy the conditions outlined above. Third, we wish to concentrate on the two most widely used SF models, i.e., normal-half-normal and normal-exponential. Both of them have a strictly decreasing distribution of inefficiency.
To sum up, we rule out the Erlang-2, Erlang-3 and truncated normal cases of van den Broeck et al. (1994), while encompass the two essential special cases (half-normal, exponential) and introduce extra flexibility by allowing for and 1, 2. Furthermore, since it is possible for the model to encompass the fully general framework of van den Broeck et al. (1994) our main conclusions are likely to remain valid anyway.
Within the general structure we consider the following SF sampling models:
- (i)
- normal-exponential, labelled NEX, with = 2, = 1 and statistical parameters: , , ,
- (ii)
- normal-half-normal, NHN, with = 2, = 2 and statistical parameters: , , ,
- (iii)
- normal-half-GED, NHG, with = 2 and statistical parameters: , , , ,
- (iv)
- GED-half-GED, GHG, with statistical parameters , , , , .
The reader should note that the term “statistical parameters” is used throughout the paper to distinguish parameters from latent variables as well as strictly “statistical” parameters from “interpretable” parameters.
The GHG model (iv) nests the NHG case (iii), whereas the latter nests the NEX and NHN specifications. For the sequence of nested sampling models it is possible to develop a coherent Bayesian prior structure. The priors in the special cases (i)–(iii) are obtained from the prior in the general case (iv) by adequate conditioning, which reflects the model-reducing restrictions. Moreover, we also consider a model without inefficiency, i.e., a regression with i.i.d. GED errors, where the only statistical parameters are , and .
Crucially, our setup implies that is a common parameter in all SF models. This allows for a direct comparison of priors that have been proposed in the literature for the NHN and NEX models. For each of those models it is possible to analyze prior structures used in empirical applications by inducing the resulting prior on in our framework. Moreover, a prior that has been suggested for the NEX model can be used with NHN model and vice versa. This allows us to analyze consequences of applying “the usual” priors for model comparison.
For the purpose of Bayesian estimation of the model class we suggest an approach that relies on a generalization of the popular Gibbs sampling. Gibbs sampling is based on the data augmentation technique, which requires drawing all statistical parameters and the latent variables (). However, it is usually required that priors are restricted to certain classes (otherwise, it is less attractive from the computational viewpoint). As the focus here is on prior sensitivity, we suggest a direct approach using likelihood function with latent variables integrated out (we refer to it as “integrated likelihood” throughout the paper) based on the implied density of the compound error term. Such integrated likelihood can be used with any prior structure in order to analyze the posterior of the statistical parameters (marginal with respect to latent variables). Within this approach, any general Bayesian algorithm can be applied and we make use of the Metropolis-Hastings (MH hereafter) algorithm with Random-Walk proposal (MH-RW hereafter). Furthermore, given the results from the full Markov Chain Monte Carlo (MCMC) chain that approximates the posterior draws of the statistical parameters (marginal with respect to latent variables), it is possible to draw the latent variables (inefficiencies ). The full conditional is nonstandard (as a product of two shifted densities of truncated-GED and half-GED form), but it is possible to develop an efficient MH algorithm to sample them. Note that, compared to the Gibbs sampling, the approach advocated here requires more computational power due to numerical integration, though it imposes no restrictions upon the prior structure and is likely to display better mixing properties. The latter is due to the fact that the parameters are drawn from the posterior distribution marginalized with respect to the latent variables. The usual Gibbs sampler used in a typical SF model draws parameters and latent variables jointly and relies upon conditioning on draws for all the ’s. This results in a potentially stronger dependence in the resulting Markov chain (making it likely that the effective sample size from a given number of MCMC repetitions decreases).
We transform all the statistical parameters into an unrestricted space (taking the implied priors into account), which allows for a smooth operation of the MH-RW sampler. In particular, we use and . We have compared the output from this algorithm to results obtained with Gibbs sampling (for special cases where the latter is available) and found practically identical characteristics of posterior draws of statistical parameters as well as latent variables.
The Bayesian model averaging relies upon estimation of posterior model probabilities, which in turn require the estimates of p(y), often referred to as marginal data density. The latter quantity is particularly difficult to estimate in a reliable manner. As our method relies upon direct use of the integrated likelihood, we rely on the Laplace approximation of the posterior for the statistical parameters, within the unrestricted parametrization in order to make the underlying multivariate Gaussian approximation more adequate. Laplace approximation has the advantage that the prior structure is explicitly taken into account. Some alternative methods like the popular variant of the harmonic mean estimator of (Newton and Raftery 1994), depend upon priors only implicitly and therefore are likely to underestimate sensitivity of p(y) to changes in prior specification, which is of essential interest here. We are aware that a more advanced method could be used to estimate p(y); see, e.g., (Pajor 2017). However we believe that the Laplace approximation is sufficient to demonstrate the degree of prior sensitivity.
We assume that the priors for all the model parameters are proper, with prior independence across all the parameters. We focus on model-specific parameters, which have to follow proper priors in order to average models in the standard way, because improper priors would result in ill-defined Bayes factors. As for prior independence, the general structure advocated here (the GHG form) allows us to relax this assumption. If a reasonable dependent prior is developed, the model can allow for a coherent prior specification of the nested cases as well. Nevertheless, the idea of prior coherence applied here assumes prior independence. As mentioned, (Griffin and Steel 2008) have considered a model with inefficiency distribution of the generalized gamma class with prior dependence across its parameters. We do not adapt their prior structure here, although we note that it would be a feasible task as our approach allows for very general formulation of priors.
We assume that the priors in the general model (iv) are , where is multivariate Gaussian (with zero mean and covariance matrix 1002Ik), and are of the same form, implying that —consequently, we rule out < 1, although this assumption might be relaxed. For , we follow the suggestion of Koop et al. (2000), who elicit a Gamma-type prior that is assumed to mimic the traditional Jeffrey’s prior for precision in linear models (the latter is improper, so the interpretation is of course approximate). We take the prior (0.5Q, 0.5Q) with Q = 10−4 and make use of it in order to maintain comparability with the aforementioned papers. Though we leave the task to formulate adequate prior for for further research, we have checked sensitivity with respect to changes in and found our results to be quite robust.
3. Investigation Results
3.1. Prior Analysis
Although the focus of this paper is on NEX and NHN models—as these are the most likely to be used for BMA in practice—the other two models have two important features that we wish explore. First, NHG nests both NHN and NEX (GHG obviously does too). This allows us to meet the prior coherence task raised in Section 2 and see the implications different priors on may have. Second, GHG further generalizes NHG with respect to , which gives us a unique opportunity to analyze the interplay between shape and dispersion parameters of (more generalized) distributions of and . In particular, we are interested to learn, which of the two models—NEX, NHN—is more adequate given our data. We start the investigation by first exploring the general properties of the following priors on and the implications they carry for the marginal prior distribution of efficiency ():
- based on van den Broeck et al. (1994), which we refer to as prior 1;
- which is based on van den Broeck et al. (1994) for a = 0 (implying a half-normal distribution on ; see van den Broeck et al. 1994, p. 286); we refer to it as prior 2;
- following (Tsionas 2002; Tsionas and Kumbhakar 2014); we refer to it as prior 3.
Prior 1 (suggested originally for the NEX model) and prior 2 (formulated for the NHN model), are used widely in the applied SFA. However, within our framework is a common parameter and it is possible to apply prior 1 for any model (including NHN), and the same is true for prior 2. Clearly, one might make an attempt to pool results from NEX model with prior 1 and NHN model with prior 2. We label this strategy as ‘naïve BMA’ because under the assumption of prior independence of and , such prior specification is clearly incoherent. Moreover, it is not that easy to provide any justification for such a particular form of prior dependence between and (it would require a joint prior on and of such class that conditioning upon would result in prior 1 for , while conditioning on would lead to prior 2 for ).
Priors 1 and 2 require us to set r*, which is interpreted as the prior median of in NEX and NHN, respectively. van den Broeck et al. (1994) suggest that r* should reflect the researcher’s prior beliefs about efficiency. Makieła (2014, 2017) investigates the influence of different values of r*. Since r* is usually set around 0.5–0.875, we use r* = 0.75 in our applications throughout the paper, which is roughly in the middle of this interval; the impact of different r* values is also explored below. As for prior 3, following (Tsionas 2002; Tsionas and Kumbhakar 2014) we set N = 1 and Q = 10−4. Although, Q = 10−6 is also sometimes used, we find that the results are virtually the same for both values and that Q = 10−4 is somewhat less informative or restrictive. Thus, only results Q = 10−4 are presented, with a note that they remain virtually unchanged for Q = 10−6.
To complete the investigation we propose the following prior , which is a simple and intuitive prior to be used on a scale parameter for an additive inefficiency-related error term within an equation specified for logs of economic quantities (implying moderate scale of inefficiency-related percentage changes in outcome). We refer to it as prior 0.
Figure 1 presents densities of the four priors on while Figure 2 and Table 1 show the resulting marginal priors on given models (i–iv). One can easily notice that prior 3 is very restrictive. Its interquartile range (IQR) is extremely narrow relative to other priors while also having the highest median (0.99) and mean (0.96–0.97). This means that prior 3 assumes very high (almost full) efficiency with very little room for variation. Changing N or Q to any of the values known in the literature does not have much of an influence on this result. So, from the viewpoint of prior elicitation of , prior 3 makes little sense in SFA. Moreover, although this is a very informative prior on —with most of its prior mass near zero—the distribution is still separated from it. Such separation from zero poses a dilemma as it can be viewed as penalization (through prior) of models which assume no inefficiency. A similar concern can be raised for prior 1 and especially for prior 2. Although they are far less restrictive and lead to reasonable marginal priors on , both priors on are well separated from zero, which again may favor SF models over non-SF ones in BMA. On the one hand, under prior 2 is positioned much further away from zero than in prior 1. On the other hand, prior 1 leads to marginal prior on with a rather significant amount of probability mass near zero; see Figure 2. That is, the resulting distribution of is somewhat U-shaped, which is not necessarily a desirable feature for an efficiency distribution.
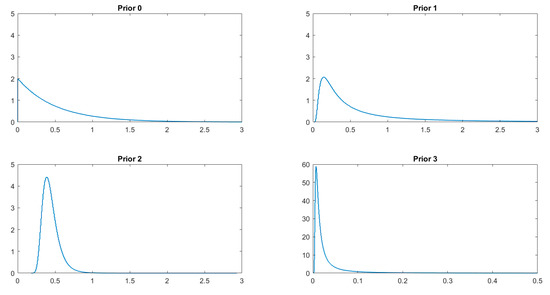
Figure 1.
Prior distribution of (r* = 0.75 for prior 1 and prior 2).
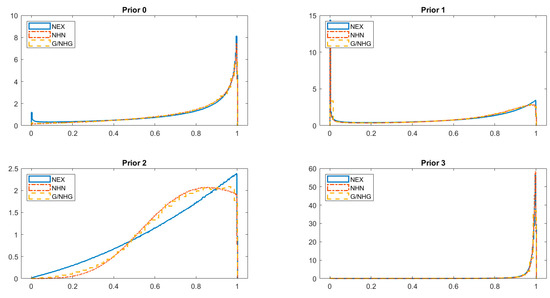
Figure 2.
Marginal prior distribution of efficiency (r).

Table 1.
Location and dispersion characteristics for marginal prior of r.
Both prior 1 and 2 have a hyperparameter (r*, interpreted as prior median; see van den Broeck et al. 1994), which allows the researcher to “tune” them based on particular needs. Figure 3 presents quantiles of marginal prior of based on prior 1 and prior 2 in NHN and NEX models. We can clearly see that prior 2 is much more restrictive for high r*. An equal shift in r* has significantly different consequences for other quantiles of under prior 1 and 2. Thus changes in r* can have a much different impact on p(y) and provide different BMA results than one would anticipate when looking just at r* (as prior median shifts the same). Indeed, this is also shown in Figure 4, which depicts Bayes factors for NHN and NEX under different r* values.
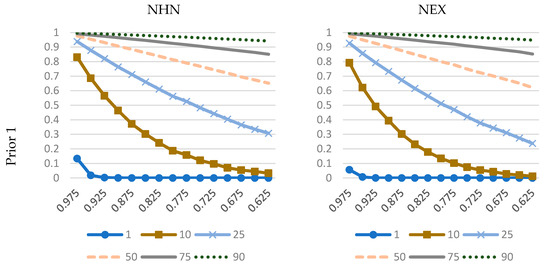
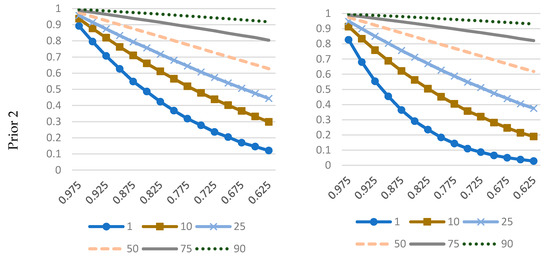
Figure 3.
Selected quantiles of marginal prior for r under different r*.
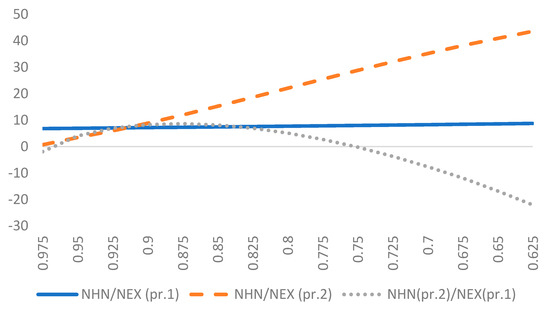
Figure 4.
Natural logs of Bayes factors for normal-half-normal (NHN) and normal-exponential (NEX) under different r*.
Given the above, the proposed prior 0 has several features which make it particularly appealing in BMA. First, the implied prior median is about 0.82 which is reasonable and around the middle of the usually assumed interval. Second, the prior on is not separated from zero. In fact it has zero mode and is strictly monotonic. Third, the tail of the distribution is not that fat, which leads to a well-behaved marginal prior on around zero (with only small prior mass around zero). For this reason, we use it as our baseline prior in further posterior results analysis of priors 1–3.
3.2. Posterior Analysis
We move on with our investigation to the posterior results. Naturally to acquire those one needs data to be fed into the models. We are interested in learning (A) how the models behave in BMA in the likely presence of (in)efficiency under priors 0–3 and (B) how they behave in BMA under full efficiency. For this reason we consider the following two datasets:
- A real-life dataset, labeled A, on aggregate production from (Makieła 2014). This is a well-researched dataset covering 27 EU Member States, USA, Japan and Switzerland in 1996–2010 (450 observations). It contains information on GDP, capital stock and labor. BMA is used here to average results over the four models mentioned in Section 2 (i–iv) based on different priors (0–3).
- An artificial dataset generated under the assumption of no inefficiency in the production process, labelled B (200 observations). This allows us to explore how popular SFA models (NHN, NEX) with different prior structures react to an “efficient” process. In this context BMA is used to confront non-SF models with NHN and NEX, again under different prior settings.
Prior model probability——is calculated throughout the paper based on a preposition in (Osiewalski and Steel 1993). That is, a priori we promote model simplicity (or, alternatively, penalize complexity) by making a decreasing function of the model size: , where is the number of model-specific parameters.
3.2.1. Results Based on Dataset A
We consider the following aggregate production process described by a translog function:
where y, k and l are natural logs of GDP, capital stock and labor input; i and t are country and time indices respectively. GDP and capital stock are given in Mrd PPS (millions of Purchasing Power Standard) in 2000 constant prices. Labor input is defined as “total number of hours worked annually” in a given country (in thousands). All variables have been mean-corrected, which means that parameters of the first order approximation () are interpreted as elasticities at the sample mean; see, e.g., (Makieła et al. 2017).
Although this is a panel dataset we do not introduce any country-specific effects, nor treat inefficiency as such (i.e., inefficiency as constant over time) due to a number of reasons. First and foremost, we wish to maintain a clear focus of this example, which is BMA and prior sensitivity in the popular NHN and NEX models. Further complication of the stochastic structure of these models (with panel data “add-ons”) would greatly diminish this goal. Second, though introducing random effects as in, e.g., true random-effects (TRE) model by (Greene 2005) would be relatively easy, it would also mean that our inference is in fact about the transient component of inefficiency; see, e.g., (Makieła 2017, for a discussion). Third, we note that treating inefficiency as an object-specific effect is quite common in panel data SFA; see, e.g., “Model I” in (Pitt and Lee 1981). However, we have a relatively long panel (15 years) and it would be difficult to justify a restriction to have inefficiency constant over time. Also, we would be making inference on “mean” inefficiency of each country in the analyzed period, which yields somewhat different results than, e.g., the TRE model mentioned earlier. All in all, the choice of panel data treatment in (in)efficiency analysis matters and we do not wish to get into this debate here.
Table 2 and Figure 5 summarize BMA results based on standard models computed using popular Gibbs sampling. Discrepancies between NHN and NEX specifications have been often reported, especially with respect to estimated inefficiencies. In the applied work it is often concluded that although individual inefficiency scores differ between NEX and NHN models, the point estimates are highly correlated and the ranking is similar. These differences are largely attributed to different sampling models. However, inefficiencies are latent variables, which are likely to be sensitive to prior specification. It is therefore not clear whether the differences are driven by priors (which in Gibbs sampling are unlikely to be coherent) or likelihoods (or both). A natural solution would be to address the issue using Bayesian inference pooling—BMA. Results of a naïve BMA, i.e., straightforward BMA under priors proposed in (van den Broeck et al. 1994 and Tsionas 2002), are reported in the last two columns of Table 2.

Table 2.
Bayesian model averaging (BMA) results based on models available via Gibbs sampling.

Figure 5.
Scatter plots between posterior estimates of r for normal-exponential (NEX) and normal-half-normal (NHN) models.
The reader should note that proper model averaging requires two things: (i) proper priors for model-specific parameters, which is not a serious practical limitation in our view; and (ii) prior coherence, which is somewhat more challenging. As for the latter, one can of course use incoherent priors, but this should be made explicit and the interpretation of BMA results under incoherent prior may be somewhat cumbersome (as we would introduce different prior beliefs). Since this paper is about model uncertainty we require the prior coherence assumption for proper comparison of competing sampling models. Also, the results might depend heavily upon posterior model probabilities, which are very sensitive to prior assumptions (even if coherence requirements are met). The naïve strategy of model pooling does not address these issues and such subtle aspects are often neglected by practitioners, which may have an adverse effect on the relevance of empirical conclusions. Thus, we go beyond the naïve strategy outlined above and demonstrate a more adequate way of dealing with model uncertainty and prior specification for BMA in SF models.
Table 3 presents results based on prior 0, which conforms to the prior coherence agenda. We see that though the estimated technology parameters are virtually unchanged, the results for ’s, the intercept and (in)efficiencies are noticeably different to each other (and different to what we report in Table 2). Most importantly, estimates of p(y) are substantially affected, and these quantities are crucial when calculating each model’s contribution (i.e., posterior probability) in BMA.

Table 3.
BMA results under prior coherence—prior 0.
Additionally, Table 4, Table 5 and Table 6 show results for models (i)–(iv) under coherent priors (1–3). Given Table 3, Table 4, Table 5 and Table 6, we can conclude that different priors (0–3):

Table 4.
BMA results under prior coherence—prior 1.

Table 5.
BMA results under prior coherence—prior 2.

Table 6.
BMA results under prior coherence—prior 3.
- have a negligible impact on technology parameters;
- have some impact on parameters of the stochastic structure (’s, ’s), the intercept (especially for prior 2 and NEX model) as well as latent variables (efficiencies); i.e., changes can be observed in terms of the “average” efficiency (“av. r” in the tables) and the relative location of object-specific efficiency-scores; however, correlations between the point estimates remain very high (often above 0.95);
- have a considerable impact on p(y); especially noticeable differences are for prior 2 and NEX model;
- differences in prior specifications have the least effect on NHG and GHG models, which give consistently stable results in terms of parameters, efficiencies and p(y).
To sum up, more substantial differences can be found between models (i)–(iv) under a given coherent prior structure than within a particular (sampling) model but under different priors (0–3), which reflects the influence of different sampling specifications. Moreover, differences in p(y) between sampling models are not the same under each prior (0–3), which can influence the results if models with incoherent priors are mixed in BMA, as in the naïve case. This is compelling evidence that shows that prior coherence should not be neglected in SFA, especially if model specification uncertainty is to be addressed. For example, if we were to take the NHN model under prior 2 and pool it with NEX model under prior 1 we would obtain approximately equal posterior probabilities and thus equal weights. As a result, the estimate of in BMA would be significantly downplayed because NEX model favors low values and would carry much higher weight in BMA than it should. This is clearly not the result we obtain under a coherent prior structure, which indicates that NEX specification is clearly not favored by the data.
Marginal data density values—p(y)—for NHN and NEX (obtained under coherent priors) already give us compelling evidence as to which sampling model is more accurate given the data. However, this can also be explored based on NHG model, as NHN and NEX are both its special cases; i.e., restriction = 2 leads to NHN and = 1 leads to NEX. Based on GHG model we can also explore the assumption of normality of ; i.e., restriction = 2 leads to being normally distributed. Figure 6 shows bivariate marginal posteriors (as heatmaps) for ’s and ’s. Based on that we can conclude the following:
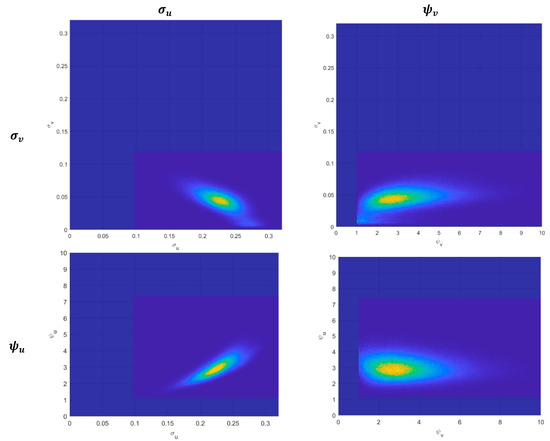
Figure 6.
Bivariate marginal posterior densities for the stochastic structure parameters.
- and are close to posterior independence;
- has a more concentrated distribution than ;
- restriction = 2 (half-normality of ) is in the tail of p(|data) and there is virtually no posterior probability around restriction = 1 ( being exponential); this reiterates our results based on p(y);
- restriction = 2 (normality of ) is within a region of high posterior density of p(|data); normality of is thus likely;
- and are positively correlated; this is not the case for and , which do not seem to show any particular dependence;
- and are negatively correlated (substitutability of variances) and positioned around quite different values.
To sum up, there is a clear evidence against the assumption that follows exponential distribution and even some that it is half-normal. To illustrate the observational consequences of differences induced by shape parameters, we compare the posterior-predictive type distribution in NEX ( = 1) and NHG ( varying freely) models. Histograms in Figure 7 represent the posterior-predictive density of in NEX and NHG (prior 0). It can be noticed that the two densities, though centered similarly, are indeed different. In particular, highly inefficient cases are more likely within NEX model. The assumption that is normal, however, is not without its merit. This result is in favor of a more traditional view in the SFA literature to generalize (in)efficiency term rather than the symmetric distribution, even though the latter has been gaining popularity in recent years (Stead et al. 2018, 2019). Moreover, the positive relationship between and is interesting. It seems that there is some sort of complementarity between scale and shape parameters of the inefficiency distribution, which is clearly not present in the symmetric term. This finding may provide some indirect justification to prior dependence of and see (Griffin and Steel 2008), which could be relevant to the discussion about prior coherence.
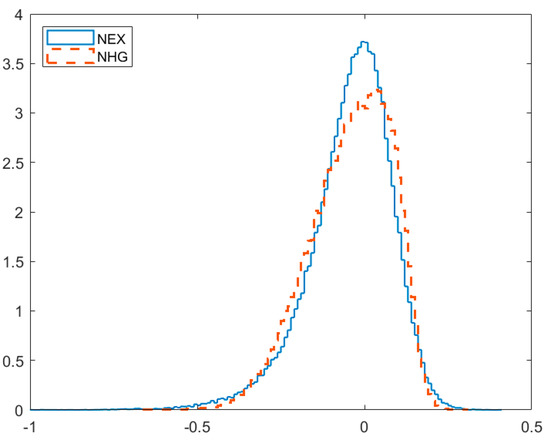
Figure 7.
Posterior predictive density of for normal-exponential (NEX) and normal-half-GED (NHG) under prior 0.
Following Makieła and Osiewalski (2018) we could also use BMA to consider simpler non-SF models, where and follows normal or GED distribution. However, the natural logs of marginal data density, p(y), for the two non-SF models are about 244.3 and 245.8 respectively. Thus, the data clearly suggest that there is inefficiency in this macro-scale production process and these models would be marginalized in BMA anyway.
3.2.2. Results Based on Dataset B
One of core issues in SFA is not only to quantify (in)efficiency but also to assess if the observed DMUs are indeed inefficient at all. In order to address this one can use the so-called Zero-Inefficiency Stochastic Frontier models (ZISF) proposed by (Kumbhakar et al. 2013); see also (Tran and Tsionas 2016). This is a proper course of action if a researcher is convinced that his sample is made up of a mix of inefficient and fully efficient DMUs. However, if there is uncertainty as regards the existence of inefficiency in the economic process as a whole, pooling SF and non-SF models seems like a more reasonable approach.
To investigate the impact of priors 0–3 on BMA under a “no-inefficiency” process we use an artificial dataset. This is a natural course of action, since we can never be sure if a real-life dataset contains some information on inefficiency. We generate two hundred observations based on a simple model:
where , , and Table 7 shows four sets of BMA results—one for each prior case (0–3)—using three models: non-SF, NEX and NHN. For almost all cases SFA models have turned out to be a posteriori significantly less likely, which is to be expected. Only models based on prior 3 “keep” their posterior odds in relation to the prior. Again, this is also to be expected because, as noted in Section 3.1, prior 3 produces a very restrictive marginal prior on , which is “squeezed” to one (full efficiency case). So, no wonder these SF models look competitive to the “true” non-SF specification. Furthermore, posterior distributions of efficiency in all SF models are much more distorted than in the example from previous section and their locations do not seem to change much in relation to the priors (especially for prior 3; compare Table 1). This result is quite common and may be used as a simple warning signal for practitioners: if your model is either (i) significantly less likely compared to a non-SF counterpart; or (ii) has good posterior odds but its posterior distribution of efficiency largely replicates the prior (in terms of location and dispersion) then it is likely that information in the data does not warrant the use of SFA specification.

Table 7.
BMA results for artificial data (no inefficiency).
4. Concluding Remarks
The paper discusses Bayesian model averaging, also known as Bayesian inference pooling, in Stochastic Frontier Analysis by making use of a generalized model structure introduced in (Makieła and Mazur 2020). It is important to note that the use of BMA in this paper differs from standard applications which focus on covariate selection. We apply BMA to average over competing sampling models that differ with respect to the stochastic structure (distribution of the compound error term). We consider the two most popular SFA specifications, namely the normal-half-normal and normal-exponential models, and demonstrate that it is possible to nest them within GED-half-GED specification. We show that Bayesian model comparison or averaging can be used to deal with specification uncertainty. However, there are two important reservations. First, in order to interpret the results of BMA as averaging over competing sampling models, it is necessary to maintain prior coherence. Otherwise, the comparison is affected by differences in prior beliefs across models. Second, even if prior coherence holds, posterior model probabilities are likely to be sensitive to prior specification. Consequently, it is necessary to verify robustness to alternative priors. We introduce a framework that allows to consider prior coherence for most popular SFA models and show how the popular priors used in Bayesian SFA can affect the results of BMA.
Our approach to statistical inference within the new GED-half-GED model class is based on the use of integrated likelihood with the latent variables integrated out (using non-stochastic numerical integration). It is computationally more demanding, especially compared to traditional specifications suitable for Gibbs sampling, but it offers considerable advantages:
- it allows for a formal model comparison within a broad, flexible parametric class;
- it allows for an in-depth analysis of prior sensitivity, as the numerical methods used do not impose any particular class of priors (contrary to the Gibbs sampling approach).
We indicate that the issue of prior elicitation is essential for two reasons. First, posterior model probabilities (crucial from the viewpoint of BMA) are likely to be sensitive to priors. Second, in SFA the quantities of interest are latent variables, which are generally less robust to changes in priors, e.g., compared to statistical parameters, for which dimensionality is independent of the sample size. In particular, we show that priors on , which are widely used in the applied Bayesian SFA, convey very specific (and potentially conflicting) information in certain cases, and this may affect the results of model comparison or inference pooling. We demonstrate that the two most popular models, NHN and NEX, when used with well-known and widely applied prior structures may produce distorted results. We suggest an alternative prior specification that is (informally) less informative. An in-depth analysis leads to the following conclusions about the prior on :
- it has virtually no impact on the technology parameters;
- it has some impact in terms of inference on the latent variables (i.e., the posterior efficiency estimates, especially in terms of “average” posterior mean and the relative spread of posterior means of efficiency);
- it has substantial impact on posterior model probabilities, which are crucial in BMA.
So for the technology parameters the prior on does not really matter much in BMA. However, adequate BMA for latent variables (inefficiencies) requires a prior, which is not only coherent but also well thought through.
We indicate that the problem of adequate prior specification in the general model—the GHG model in this paper, or a more general formulation as in (Makieła and Mazur 2020)—is still an open research problem. In our view it is reasonable to use proper priors (having the economic context in mind), though further research might lead to some form of relaxation of the prior independence assumption used here, e.g., along the direction proposed in (Griffin and Steel 2008).
Models considered in this study fall into the so-called Common Efficiency Distribution (CED) class. For further research, it would be interesting to take a step further and consider prior coherence within the so called Varying Efficiency Distribution (VED) class, which allows us to introduce inefficiency determinants (Koop et al. 1997, 2000). Although VED is traditionally used to extend the NEX it can be relatively easily adapted in NHN specification as well. Makieła and Mazur (2020) introduce a VED-type extension of a generalized CED model which nests the GHG specification. In principle it is possible to analyze prior coherence and prior sensitivity within this framework.
Panel data modelling is a large field in SFA. As noted in Section 3.2.1, the lack of panel data context in the empirical example was to maintain a clear focus of the paper. Of course, accounting for panel structure of the data can bring some new insights as to the nature of inefficiency distribution, especially with regard to its transient and persistent components; see, e.g., (Tsionas and Kumbhakar 2014; Makieła 2017). For example, fixing as constant over time and making it a “traditional” object-specific effect has some advantages over the pooled estimator used here (italic is used on purpose; the exact form of a pooled estimator in panel data literature does not account for inefficiency). Inefficiency is estimated based on t observations, which means there are more data points based on which the posterior is evaluated. This, in turn, may allow for a more accurate identification of the functional form of inefficiency distribution.
Although there is a considerable research that advocates non-monotonic (in)efficiency densities, (in)efficiency pdf’s considered in this study are monotonic. We feel this is reasonable in the presence of a generalized symmetric error (see discussion in Section 2). The modelling framework proposed by (Makieła and Mazur 2020), however, does not require monotonicity assumption of (in)efficiency. Hence, this avenue can be further researched based on the methodology presented here and in (Makieła and Mazur 2020).
Last but not least, simulation-based analyses within this framework are compelling. The SFA literature would benefit greatly from examples based on multiple artificial datasets generated based on data generating processes (DGPs) that assume different (in)efficiency distributions. This way one could compare how various sampling models and prior assumptions perform under different DGPs. Moreover, it would be also beneficial to present results based on several hundred or even thousand realizations of a given dataset. This way one would be certain that the results are not, at least partially, due to the idiosyncrasies of a single artificial dataset. However, given that the estimation procedure for the SFA framework proposed by (Makieła and Mazur 2020) is still at its infancy it would be extremely time-consuming to try such an endeavor now. Thus, we leave this for further research when the numerical procedures are fully developed (especially in terms of taking full advantage of parallelization) and packaged.
Author Contributions
K.M. and B.M. contributed equally to this work in all aspects. Conceptualization; methodology; software; validation; formal analysis; investigation; resources; data curation; writing—original draft preparation; writing—review and editing; visualization; supervision; project administration; funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financed by National Science Centre, Poland (NCN), grant number: UMO−2018/31/B/HS4/01565.
Acknowledgments
We would like to thank the editor and three anonymous referees for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aigner, Dennis J., C. A. Knox Lovell, and Peter Schmidt. 1977. Formulation and Estimation of Stochastic Frontier Production Function Models. Journal of Econometrics 6: 21–37. [Google Scholar] [CrossRef]
- Fernández, Carmen, Jacek Osiewalski, and Mark F. J. Steel. 1997. On the use of panel data in stochastic frontier models. Journal of Econometrics 79: 169–93. [Google Scholar] [CrossRef]
- Florens, Jean-Pierre, Léopold Simar, and Ingrid Van Keilegom. 2019. Estimation of the Boundary of a Variable Observed with Symmetric Error. Journal of the American Statistical Association 11. [Google Scholar] [CrossRef]
- Greene, William H. 2003. Simulated likelihood estimation of the normal-gamma stochastic frontier function. Journal of Productivity Analysis 19: 179–90. [Google Scholar] [CrossRef]
- Greene, William H. 2005. Fixed and random effects in stochastic frontier models. Journal of Productivity Analysis 23: 7–32. [Google Scholar] [CrossRef]
- Greene, William H. 2008. The Econometric Approach to Efficiency Analysis. In The Measurement of Productive Efficiency and Productivity Growth. Edited by Harold O. Fried, C. A. Knox Lovell and Shelton S. Schmidt. New York: Oxford University Press, pp. 92–250. [Google Scholar]
- Griffin, Jim E., and Mark F. J. Steel. 2004. Semiparametric Bayesian inference for stochastic frontier models. Journal of Econometrics 123: 121–52. [Google Scholar] [CrossRef]
- Griffin, Jim E., and Mark F. J. Steel. 2007. Bayesian stochastic frontier analysis using WinBUGS. Journal of Productivity Analysis 27: 163–76. [Google Scholar] [CrossRef]
- Griffin, Jim E., and Mark F. J. Steel. 2008. Flexible mixture modelling of stochastic frontiers. Journal of Productivity Analysis 29: 33–50. [Google Scholar] [CrossRef]
- Hajargasht, Gholamreza. 2015. Stochastic frontiers with a Rayleigh distribution. Journal of Productivity Analysis 44: 199–208. [Google Scholar] [CrossRef]
- Harvey, Andrew, and Rutger-Jan Lange. 2017. Volatility modeling with a generalized t distribution. Journal of Time Series Analysis 38: 175–90. [Google Scholar] [CrossRef]
- Horrace, William C., and Christopher F. Parmeter. 2018. A Laplace stochastic frontier model. Econometric Reviews 37: 260–80. [Google Scholar] [CrossRef]
- Koop, Gary, Jacek Osiewalski, and Mark F. J. Steel. 1997. Bayesian efficiency analysis through individual effects: Hospital cost frontiers. Journal of Econometrics 76: 77–105. [Google Scholar] [CrossRef]
- Koop, Gary, Jacek Osiewalski, and Mark F. J. Steel. 1999. The Components of Output Growth: A Stochastic Frontier Analysis. Oxford Bulletin of Economics and Statistics 61: 455–87. [Google Scholar] [CrossRef]
- Koop, Gary, Jacek Osiewalski, and Mark F. J. Steel. 2000. Modeling the Sources of Output Growth in a Panel of Countries. Journal of Business and Economic Statistics 18: 284–99. [Google Scholar]
- Kumbhakar, Subal C., Christopher F. Parmeter, and Efthymios G. Tsionas. 2013. A zero inefficiency stochastic frontier model. Journal of Econometrics 172: 66–76. [Google Scholar] [CrossRef]
- Ley, Eduardo, and Mark F. J. Steel. 2009. On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. Journal of Applied Econometrics 24: 651–74. [Google Scholar] [CrossRef]
- Ley, Eduardo, and Mark F. J. Steel. 2012. Mixtures of g-priors for Bayesian model averaging with economic applications. Journal of Econometrics 171: 251–66. [Google Scholar] [CrossRef]
- Makieła, Kamil. 2014. Bayesian Stochastic Frontier Analysis of Economic Growth and Productivity Change in the EU, USA, Japan and Switzerland. Central European Journal of Economic Modelling and Econometrics 6: 193–216. [Google Scholar]
- Makieła, Kamil. 2017. Bayesian Inference and Gibbs Sampling in Generalized True Random-Effects Models. Central European Journal of Economic Modelling and Econometrics 9: 69–95. [Google Scholar]
- Makieła, Kamil, and Błażej Mazur. 2020. Stochastic Frontier Analysis with Generalized Errors: Inference, Model Comparison and Averaging. Working Paper. Available online: http://arxiv.org/abs/2003.07150 (accessed on 16 March 2020).
- Makieła, Kamil, and Jacek Osiewalski. 2018. Cost Efficiency Analysis of Electricity Distribution Sector under Model Uncertainty. The Energy Journal 39: 31–56. [Google Scholar] [CrossRef]
- Makieła, Kamil, Jerzy Marzec, and Andrzej Pisulewski. 2017. Productivity change analysis in dairy farms following Polish accession to the EU—An output growth decomposition approach. Outlook on Agriculture 46: 295–301. [Google Scholar] [CrossRef]
- Meeusen, Wim, and Julien van den Broeck. 1977. Efficiency estimation from Cobb-Douglas Production Function with Composed Error. International Economic Review 18: 435–44. [Google Scholar] [CrossRef]
- Newton, Michael A., and Adrian E. Raftery. 1994. Approximate Bayesian Inference with the Weighted Likelihood Bootstrap. Journal of the Royal Statistical Society 56: 3–48. [Google Scholar] [CrossRef]
- Osiewalski, Jacek, and Mark F. J. Steel. 1993. Una perspectiva bayesiana en selección de modelos [A Bayesian Perspective on Model Selection]. Cuadernos Economicos 55: 327–51. [Google Scholar]
- Osiewalski, Jacek, and Mark F. J. Steel. 1998. Numerical Tools for the Bayesian Analysis of Stochastic Frontier Models. Journal of Productivity Analysis 10: 103–17. [Google Scholar] [CrossRef]
- Pajor, Anna. 2017. Estimating the marginal likelihood using the arithmetic mean identity. Bayesian Analysis 12: 261–87. [Google Scholar] [CrossRef]
- Pitt, Mark M., and Lung-Fei Lee. 1981. The Measurement and Sources of Technical Inefficiency in the Indonesian Weaving Industry. Journal of Development Economics 9: 43–64. [Google Scholar] [CrossRef]
- Stacy, E. Webb. 1962. A generalization of the gamma distribution. The Annals of Mathematical Statistics 33: 1187–92. [Google Scholar] [CrossRef]
- Stead, Alexander D., Phill Wheat, and William H. Greene. 2018. Estimating Efficiency in the Presence of Extreme Outliers: A Logistic-Half Normal Stochastic Frontier Model with Application to Highway Maintenance Costs in England. In Productivity and Inequality (Springer Proceedings in Business and Economics). Edited by William H. Greene, Lynda Khalaf, Paul Makdissi, Robin C. Sickles, Michael Veall and Marcel-Cristian Voia. Cham: Springer, pp. 1–20. [Google Scholar]
- Stead, Alexander D., Phill Wheat, and William H. Greene. 2019. Robust Stochastic Frontier Analysis: A Student’s t-Half Normal Model with Application to Highway Maintenance Costs in England. Journal of Productivity Analysis 51: 21–38. [Google Scholar]
- Steel, Mark F. J. 2019. Model averaging and its use in economics. Journal of Economic Literature. [Google Scholar] [CrossRef]
- Stevenson, Rodney E. 1980. Likelihood Functions for Generalized Stochastic Frontier Estimation. Journal of Econometrics 13: 58–66. [Google Scholar] [CrossRef]
- Subbotin, Mikhail. 1923. On the law of frequency of error. Математический сбoрник 31: 296–301. [Google Scholar]
- Tchumtchoua, Sylvie, and Dipak K. Dey. 2007. Bayesian Estimation of Stochastic Frontier Models with Multivariate Skew t Error Terms. Communications. Statistics: Theory and Methods 36: 907–16. [Google Scholar]
- Theodossiou, Panayiotis, Dimitris A. Tsouknidis, and Christos S. Savva. 2020. Freight Rates in Downside and Upside Markets: Pricing of Own and Spillover Risks from Other Shipping Segments. Journal of the Royal Statistical Society. in press. [Google Scholar] [CrossRef]
- Tran, Kien C., and Mike G. Tsionas. 2016. Zero-inefficiency stochastic frontier models with varying mixing proportion: A semiparametric approach. European Journal of Operational Research 249: 1113–23. [Google Scholar] [CrossRef]
- Tsionas, Efthymios G. 2002. Stochastic Frontier Models with Random Coefficients. Journal of Applied Econometrics 17: 127–47. [Google Scholar] [CrossRef]
- Tsionas, Efthymios G. 2006. Inference in dynamic stochastic frontier models. Journal of Applied Econometrics 21: 669–76. [Google Scholar] [CrossRef]
- Tsionas, Efthymios G. 2007. Efficiency Measurement with the Weibull Stochastic Frontier. Oxford Bulletin of Economics and Statistics 69: 693–706. [Google Scholar] [CrossRef]
- Tsionas, Efthymios G., and Subal C. Kumbhakar. 2014. Firm Heterogeneity, Persistent and Transient Technical Inefficiency: A Generalized True Random-Effects model. Journal of Applied Econometrics 29: 110–32. [Google Scholar] [CrossRef]
- van den Broeck, Julien, Gary Koop, Jacek Osiewalski, and Mark F. J. Steel. 1994. Stochastic Frontier Models: A Bayesian Perspective. Journal of Econometrics 61: 273–303. [Google Scholar] [CrossRef]
- Wheat, Phill, Alexander D. Stead, and William H. Greene. 2019. Controlling for Outliers in Efficiency Analysis: A Contaminated Normal-Half Normal Stochastic Frontier Model. Working Paper. Available online: http://www.its.leeds.ac.uk/fileadmin/documents/research/bear/Allowing_for_outliers_in_stochastic_frontier_models_200318.pdf (accessed on 10 December 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).