Simultaneous Indirect Inference, Impulse Responses and ARMA Models †
Abstract
1. Introduction
2. General Framework
2.1. Nuisance Parameters
3. Inference via Test Inversion
3.1. Exact p-Values
4. ARMA Special Case
4.1. Impulse-Response Confidence Bands
5. Simulation Study
5.1. Main Results
5.2. Robustness Checks
6. Empirical Application
6.1. Data
6.2. Impulse-Response Confidence Bands for Oil Series
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alquist, Ron, and Lutz Kilian. 2010. What do We Learn From the Price of Crude Oil Futures? Journal of Applied Econometrics 25: 539–73. [Google Scholar] [CrossRef]
- Alquist, Ron, Lutz Kilian, and Robert J. Vigfusson. 2013. Forecasting the Price of Oil. In Handbook of Economic Forecasting. Edited by Graham Elliott and Allan Timmermann. Amsterdam: Elsevier B.V., vol. 2, Part A. pp. 427–507. [Google Scholar]
- Andrews, Donald W. K., and Patrik Guggenberger. 2010. Asymptotic Size and a Problem with Subsampling and With the m out of n Bootstrap. Econometric Theory 26: 426–68. [Google Scholar] [CrossRef]
- Andrews, Donald W. K., and Xu Cheng. 2012. Estimation and Inference with Weak, Semi-Strong and Strong-Identification. Econometrica 80: 2153–11. [Google Scholar] [CrossRef]
- Andrews, Isaiah, and Anna Mikusheva. 2014. Weak Identification in Maximum Likelihood: A Question of Information. American Economics Review 104: 195–99. [Google Scholar] [CrossRef]
- Andrews, Isaiah, and Anna Mikusheva. 2015. Maximum Likelihood Inference in Weakly Identified Dynamic Stochastic General Equilibrium Models. Quantitative Economics 1: 123–52. [Google Scholar] [CrossRef]
- Ansley, Craig F., and Paul Newbold. 1980. Finite Sample Properties of Estimators for Auto-regressive Moving Average Processes. Journal of Econometrics 13: 159–84. [Google Scholar] [CrossRef]
- Ariel, Robert A. 1987. A Monthly Effect in Stock Returns. Journal of Financial Economics 18: 161–74. [Google Scholar] [CrossRef]
- Atkeson, Andrew, and Patrick J. Kehoe. 1999. Models of Energy Use: Putty-Putty versus Putty-Clay. American Economic Review 89: 1028–43. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2012. Real-Time Forecasts of the Real Price of Oil. Journal of Business & Economic Statistics 30: 326–36. [Google Scholar]
- Baumeister, Christiane, and Lutz Kilian. 2014a. Real-Time Analysis of Oil Price Risks Using Forecast Scenarios. IMF Economic Review 62: 120–45. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2014b. What Central Bankers Need to Know About Forecasting Oil Prices. International Economic Review 55: 869–89. [Google Scholar] [CrossRef]
- Baumeister, Christiane, Lutz Kilian, and Thomas K. Lee. 2014. Are There Gains from Pooling Real-Time Oil Price Forecasts? Energy Economics 46: 533–43. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2015. Forecasting the Real Price of Oil in a Changing World: A Forecast Combination Approach. Journal of Business and Economics Statistics 33: 338–51. [Google Scholar] [CrossRef]
- Baumeister, Christiane, Pierre Guérin, and Lutz Kilian. 2015. Do High-Frequency Financial Data Help Forecast Oil Prices? The MIDAS Touch at Work. International Journal of Forecasting 31: 238–52. [Google Scholar] [CrossRef]
- Beaulieu, Marie-Claude, Jean-Marie Dufour, and Lynda Khalaf. 2007. Multivariate Tests of Mean-Variance Efficiency with Possibly Non-Gaussian Errors: An Exact Simulation-Based Approach. Journal of Business and Economic Statistics 25: 398–410. [Google Scholar] [CrossRef]
- Beaulieu, Marie-Claude, Jean-Marie Dufour, and Lynda Khalaf. 2013. Identification-Robust Estimation and Testing of the Zero-Beta CAPM. Review of Economic Studies 80: 892–924. [Google Scholar] [CrossRef]
- Beaulieu, Marie-Claude, Jean-Marie Dufour, and Lynda Khalaf. 2014. Exact Confidence Set Estimation and Goodness of Fit Test Methods for Asymmetric Heavy Tailed Stable Distributions. Journal of Econometrics 181: 3–14. [Google Scholar] [CrossRef]
- Bernard, Jean-Thomas, Jean-Marie Dufour, Lynda Khalaf, and Maral Kichian. 2012. An Identification- Robust Test for Time-Varying Parameters in the Dynamics of Energy Prices. Journal of Applied Econometrics 27: 603–24. [Google Scholar] [CrossRef]
- Billio, Monica, and Alain Monfort. 2003. Kernel-Based Indirect Inference. Journal of Financial Econometrics 3: 297–326. [Google Scholar] [CrossRef]
- Calvet, Laurent E., and Veronika Czellar. 2015. Through the Looking Glass: Indirect Inference via Simple Equilibria. Journal of Econometrics 185: 343–58. [Google Scholar] [CrossRef]
- Calzolari, Giorgio, Gabriele Fiorentini, and Enrique Sentana. 2004. Constrained Indirect Estimation. The Review of Economic Studies Limited 71: 945–73. [Google Scholar] [CrossRef]
- Charles, Amelié, and Olivier Darné. 2014. Volatility Persistence in Crude Oil Markets. Energy Policy 65: 729–42. [Google Scholar] [CrossRef]
- Chaudhuri, Saraswata, David T. Frazier, and Eric Renault. 2018. Indirect Inference with Endogenously Missing Exogenous Variables. Journal of Econometrics 205: 55–75. [Google Scholar] [CrossRef]
- Choi, Kyongwook, and Shawkat Hammoudeh. 2009. Long Memory in Oil and Refined Product Markets. The Energy Journal 30: 97–116. [Google Scholar] [CrossRef]
- Davis, Richard A., and William T. M. Dunsmuir. 1996. Maximum Likelihood Estimation for MA(1) processes with a Root on the Unit Circle. Econometric Theory 12: 1–20. [Google Scholar] [CrossRef]
- Davis, Richard A., and Li Song. 2011. Unit Roots in Moving Averages Beyond First Order. Annals of Statistics 39: 3062–91. [Google Scholar] [CrossRef][Green Version]
- Dominicy, Yves, and David Veredas. 2013. The Method of Simulated Quantiles. Journal of Econometrics 172: 235–47. [Google Scholar] [CrossRef][Green Version]
- Dufour, Jean-Marie, Lynda Khalaf, and Marie-Claude Beaulieu. 2003. Exact Skewness and Kurtosis Tests for Multivariate Normality and Goodness of Fit in Multivariate Regressions with Application to Asset Pricing Models. Oxford Bulletin of Economics and Statistics 65: 891–906. [Google Scholar] [CrossRef]
- Dufour, Jean-Marie, Lynda Khalaf, and Marie-Claude Beaulieu. 2010. Finite Sample Diagnostics in Multivariate Regressions with Applications to Asset Pricing Models. Journal of Applied Econometrics 25: 263–85. [Google Scholar] [CrossRef]
- Dufour, Jean-Marie, and Jeong-Ryeol Kurz-Kim. 2010. Exact Inference and Optimal Invariant Estimation for the Stability Parameter of Symmetric α-Stable Distributions. Journal of Empirical Finance 17: 180–94. [Google Scholar] [CrossRef]
- Dufour, Jean-Marie. 2006. Monte Carlo Tests with Nuisance Parameters: A General Approach to Finite-Sample Inference and Nonstandard Asymptotics in Econometrics. Journal of Econometrics 133: 443–78. [Google Scholar] [CrossRef]
- Dufour, Jean-Marie, and Denis Pelletier. 2014. Practical Methods for Modelling Weak VARMA Processes: Identification, Estimation and Specification with a Macroeconomic Application. Available online: https://pdfs.semanticscholar.org/0801/2dbed27e21f9a6f12ca5a50caa12e7425227.pdf (accessed on 2 July 2019). Working Paper.
- Dufour, Jean-Marie, and Olivier Torrès. 2000. Markovian Processes, Two-Sided Autoregressions and Exact Inference for Stationary and Nonstationary Autoregressive Processes. Journal of Econometrics 99: 255–89. [Google Scholar] [CrossRef]
- Dufour, Jean-Marie, and Pascale Valéry. 2006. On a Simple Two-Stage Closed-Form Estimator for a Stochastic Volatility in a General Linear Regression. In Volume 20 (Part A) of Advances in Econometrics: Econometric Analysis of Economic and Financial Time Series. Edited by Thomas B. Fomby and Dek Terrell. Oxford: Elsevier Science, pp. 259–88. [Google Scholar]
- Dufour, Jean-Marie, and Pascale Valéry. 2009. Exact and Assymptotic Test for Possibly Non-Regular Hypothesis on Stochastic Volatility Models. Journal of Econometrics 150: 193–206. [Google Scholar] [CrossRef][Green Version]
- Dridi, Ramdan, Alain Guay, and Eric Renault. 2007. Indirect Inference and Calibration of Dynamic Stochastic General Equilibrium Models. Journal of Econometrics 136: 397–430. [Google Scholar] [CrossRef]
- Energy Information Administration (EIA). 2019. WTI Prices in U.S. Dollars per Barrel Jan.1986-Jun. Available online: eia.gov (accessed on 2 July 2019).
- Forneron, Jean-Jacques, and Senera Ng. 2018. The ABC of Simulation Estimation with Auxiliary Statistics. Journal of Econometrics 205: 112–39. [Google Scholar] [CrossRef]
- French, Kenneth R. 1980. Stocks Returns, and the Weekend Effect. Journal of Financial Economics 8: 55–69. [Google Scholar] [CrossRef]
- Fuleky, Peter, and Eric Zivot. 2014. Indirect Inference Based on the Score. Econometrics Journal 17: 383–93. [Google Scholar] [CrossRef]
- Galbraith, John W., and Victoria Zinde-Walsh. 1994. A Simple, Non-Iterative Estimator for Moving Average Models. Biometrika 81: 143–56. [Google Scholar] [CrossRef]
- Galbraith, John W., and Victoria Zinde-Walsh. 1997. On Some Simple, Autoregression-Based Estimation and Identification Techniques for ARMA Models. Biometrika 84: 685–96. [Google Scholar] [CrossRef]
- Gallant, A. Ronald, and George Tauchen. 1996. Which Moments to Match. Econometric Theory 12: 657–81. [Google Scholar] [CrossRef]
- Genton, Marc G., and Elvezio Ronchetti. 2003. Robust Indirect Inference. Journal of the American Statistical Association 98: 67–76. [Google Scholar]
- Ghysels, Eric, Lynda Khalaf, and Cosmé Vodounou. 2003. Simulation Based Inference in Moving Average Models. Annales D’Economie et Statistique 69: 85–99. [Google Scholar] [CrossRef][Green Version]
- Gil-Alana, Luis A., and Rangan Gupta. 2014. Persistence, and Cycles in Historical Oil Price Data. Energy Economics 45: 511–16. [Google Scholar] [CrossRef]
- Gorodnichenko, Yuriy, Anna Mikusheva, and Serena Ng. 2012. Estimators for Persistent, and Possibly Non-Stationary Data with Classical Properties. Econometric Theory 28: 1003–36. [Google Scholar] [CrossRef]
- Gospodinov, Nikolay. 2002. Bootstrap Based Inference in Models with a Nearly Noninvertible Moving Average Component. Journal of Business and Economic Statistics 20: 254–268. [Google Scholar] [CrossRef]
- Gospodinov, Nikolay, and Serena Ng. 2015. Minimum Distance Estimation of Possibly Non-Invertible Moving Average Models. Journal of Business and Economic Statistics 33: 403–17. [Google Scholar] [CrossRef]
- Gouriéroux, Christian, Alain Monfort, and Eric Renault. 1993. Indirect Inference. Journal of Applied Econometrics 8: S85–118. [Google Scholar] [CrossRef]
- Gouriéroux, Christian, and Alain Monfort. 1996. Simulation-Based Econometric Methods, Core Lectures. Oxford: Oxford University Press. [Google Scholar]
- Gouriéroux, Christian, Peter C. B. Phillips, and Jun Yu. 2010. Indirect Inference for Dynamic Panel Models. Journal of Econometrics 157: 68–77. [Google Scholar] [CrossRef]
- Guerron-Quintana, Pablo, Atsushi Inoue, and Lutz Kilian. 2017. Impulse response matching estimators for DSGE models. Journal of Econometrics 196: 144–55. [Google Scholar] [CrossRef]
- Guay, Alain, and Olivier Scaillet. 2003. Indirect Inference, Nuisance Parameter, and Threshold Moving Average Models. Journal of Business and Economic Statistics 21: 122–32. [Google Scholar] [CrossRef][Green Version]
- Hamilton, James D. 1983. Oil, and the Macroeconomy since World War II. Journal of Political Economy 91: 228–48. [Google Scholar] [CrossRef]
- Hamilton, James D. 1996. This is What Happened to the Oil Price-Macroeconomy Relationship. Journal of Monetary Economics 38: 215–20. [Google Scholar] [CrossRef]
- Hamilton, James D. 2003. What Is an Oil Shock? Journal of Econometrics 113: 363–98. [Google Scholar] [CrossRef]
- Hamilton, James D. 2009. Understanding Crude Oil Prices. The Energy Journal 30: 179–205. [Google Scholar] [CrossRef]
- Hamilton, James D. 2011. Nonlinearities, and the Macroeconomic Effects of Oil Prices. Macroeconomic Dynamics 15: 364–78. [Google Scholar] [CrossRef]
- Hannan, Edward J., and Jorma Rissanen. 1982. Recursive Estimation of Mixed Autoregressive-Moving-Average Order. Biometrika 69: 81–94. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 1999. The Grid Bootstrap, and the Autoregressive Model. Review of Economics, and Statistics 81: 594–607. [Google Scholar] [CrossRef]
- Harvey, Andrew C. 1981. Time Series Models. London: Philip Allan. [Google Scholar]
- Inoue, Atsushi, and Lutz Kilian. 2013. Inference on Impulse Response Functions in Structural VAR Models. Journal of Econometrics 177: 1–13. [Google Scholar] [CrossRef]
- Inoue, Atsushi, and Lutz Kilian. 2016. Joint Confidence Sets for Structural Impulse Responses. Journal of Econometrics 192: 421–32. [Google Scholar] [CrossRef]
- Jordà, Òscar. 2009. Simultaneous Confidence Regions for Impulse Responses. The Review of Economics, and Statistics 91: 629–47. [Google Scholar] [CrossRef]
- Jordà, Òscar, and Massimiliano Marcellino. 2010. Path Forecast Evaluation. Journal of Applied Econometrics 25: 635–62. [Google Scholar] [CrossRef]
- Jordà, Òscar, and Sharon Kozicki. 2011. Estimation, and Inference by the Method of Projection Minimum Distance: An Application to the New Keynesian Hybrid Phillips Curve. International Economic Review 52: 461–87. [Google Scholar] [CrossRef]
- Jordà, Òscar, Malte Knüppel, and Massimiliano Marcellino. 2013. Empirical Simultaneous Confidence Regions for Path-Forecasts. International Journal of Forecasting 29: 456–68. [Google Scholar] [CrossRef]
- Khalaf, Lynda, and Charles J. Saunders. 2019. Monte Carlo Two-Stage Indirect Inference (2SIF) for Autoregressive Panels. Forthcoming: The Journal of Econometrics. [Google Scholar]
- Kilian, Lutz. 2008a. A Comparison of the Effects of Exogenous Oil Supply Shocks on Output, and Inflation in the G7 Countries. Journal of the European Economic Association 6: 78–121. [Google Scholar] [CrossRef]
- Kilian, Lutz. 2008b. The Economic Effects of Energy Price Shocks. Journal of Economic Literature 46: 871–909. [Google Scholar] [CrossRef]
- Kilian, Lutz. 2008c. Exogenous Oil Supply Shocks: How Big Are They, and How Much Do They Matter for the U.S. Economy? Review of Economics, and Statistics 90: 216–40. [Google Scholar] [CrossRef]
- Kilian, Lutz. 2009. Not All Oil Price Shocks Are Alike: Disentangling Demand, and Supply Shocks in the Crude Oil Market. American Economic Review 99: 1053–69. [Google Scholar] [CrossRef]
- Kilian, Lutz. 2014. Oil Price Shocks: Causes, and Consequences. Annual Review of Resource Economics 6: 133–54. [Google Scholar] [CrossRef]
- Kilian, Lutz, and Robert J. Vigfusson. 2017. The Role of Oil Price Shocks in Causing U.S. Recessions. Journal of Money, Credit, and Banking 49: 1747–76. [Google Scholar] [CrossRef]
- Leduc, Sylvain, and Keith Sill. 2004. A Quantitative Analysis of Oil Price Shocks, Systematic Monetary Policy, and Economic Downturns. Journal of Monetary Economics 51: 781–808. [Google Scholar] [CrossRef]
- Lee, Junsoo, John A. List, and Mark C. Strazicich. 2006. Non-Renewable Resource Prices: Deterministic or Stochastic Trends? Journal of Environmental Economic Management 3: 354–70. [Google Scholar] [CrossRef]
- Li, Tong. 2010. Indirect Inference in Structural Econometric Models. Journal of Econometrics 157: 120–28. [Google Scholar] [CrossRef]
- Lubik, Thomas A., and Frank Schorfheide. 2003. Computing Sunspot Equilibria in Linear Rational Expectations Models. Journal of Economic Dynamics & Control 28: 273–85. [Google Scholar]
- Lubik, Thomas A., and Frank Schorfheide. 2004. Testing for Indeterminancy: An Application to U.S. Monetary Policy. The American Economic Review 94: 190–217. [Google Scholar] [CrossRef]
- Lütkepohl, Helmut, Anna Staszewska-Bystrova, and Peter Winker. 2015. Comparison of Methods for Constructing Joint Confidence Bands for Impulse Response Functions. International Journal of Forecasting 31: 782–98. [Google Scholar] [CrossRef]
- Mikusheva, Anna. 2007. Uniform Inference in Autoregressive Models. Econometrica 75: 1411–52. [Google Scholar] [CrossRef]
- Mikusheva, Anna. 2012. One-Dimensional Inference in Autoregressive Models with the Potential Presence of a Unit Root. Econometrica 80: 173–212. [Google Scholar]
- Mikusheva, Anna. 2014. Second Order Expansion of the t-statistic in AR(1) Models. Econometric Theory 31: 426–48. [Google Scholar] [CrossRef]
- Montiel Olea, José Luis, and Mikkel Plagborg-Møller. 2019. Simultaneous Confidence Bands: Theory, Implementation, and an Application to SVARs. Journal of Applied Econometrics 34: 1–17. [Google Scholar] [CrossRef]
- Nelson, Charles R., and Richard Startz. 2007. The Zero-information-limit Condition, and Spurious Inference in Weakly-identified Models. Journal of Econometrics 138: 47–62. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 2014. On Confidence Intervals for Autoregressive Roots, and Predictive Rgressions. Econometrica 82: 1177–95. [Google Scholar]
- Pindyck, Robert S. 1999. The Long Run Eolution of Energy Prices. The Energy Journal 20: 1–27. [Google Scholar] [CrossRef]
- Pindyck, Robert S. 2004. Volatility, and commodity price dynamics. Journal of Futures Markets 24: 1029–47. [Google Scholar] [CrossRef]
- Robins, James M., Aad van der Vaart, and Valérie Ventura. 2000. Asymptotic Distribution of P Values in Composite Null Models. Journal of the American Statistical Association 95: 1143–56. [Google Scholar]
- Ronchetti, Elvezio, and Fabio Trojani. 2001. Robust Inference with GMM Estimators. Journal of Econometrics 101: 37–69. [Google Scholar] [CrossRef]
- Sargan, John D., and Alok Bhargava. 1983. Maximum Likelihood Estimation of Regression Models with First Order Moving Average Errors when the Root Lies on the Unit Circle. Econometrica 51: 799–820. [Google Scholar] [CrossRef]
- Sims, Christopher A. 2001. Solving Linear Rational Expectations Models. Computational Economics 20: 1–20. [Google Scholar] [CrossRef]
- Smith, Anthony A., Jr. 1993. Estimating Nonlinear Time Series Models Using Simulated Vector Autoregressions. Journal of Applied Econometrics 8: S63–84. [Google Scholar] [CrossRef]
- Staszewska-Bystrova, Anna. 2007. Representing Uncertainty About Impulse Response Paths: The Use of Heuristic Optimization Methods. Computational Statistics, and Data Analysis 52: 121–32. [Google Scholar] [CrossRef]
- Staszewska-Bystrova, Anna. 2011. Bootstrap Prediction Bands for Forecast Paths from Vector Autoregressive Models. Journal of Forecasting 30: 721–35. [Google Scholar] [CrossRef]
- Staszewska-Bystrova, Anna. 2013. Modified Scheffé’s Prediction Bands. Journal of Economics, and Statistics 233: 680–90. [Google Scholar] [CrossRef]
- Staszewska-Bystrova, Anna, and Peter Winker. 2013. Constructing Narrowest Pathwise Bootstrap Prediction Bands Using Threshold Accepting. International Journal of Forecasting 29: 221–33. [Google Scholar] [CrossRef]
- Stock, James H. 1991. Confidence Intervals for the Largest Autoregressive Root in Macroeconomic Time Series. Journal of Monetary Economics 28: 435–59. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 1993. A Simple Estimator of Cointegrating Vectors in Higher Order Integrated Systems. Econometrica 61: 783–820. [Google Scholar] [CrossRef]
- US. Bureau of Labor Statistics. 2019. Consumer Price Index for All Urban Consumers: All Items [CPIAUCSL], Index 1982–84=100, retrieved from the Federal Reserve Bank of St. Louis, Economic Data (FRED). Available online: https://fred.stlouisfed.org/series/CPIAUCSL/ (accessed on 5 July 2019).
| 1. | See, for example, Robins et al. (2000); Ronchetti and Trojani (2001); Calzolari et al. (2004); Dridi et al. (2007); Gouriéroux et al. (2010); Li (2010); Dominicy and Veredas (2013); Fuleky and Zivot (2014); Calvet and Czellar (2015); Chaudhuri et al. (2018) and Forneron and Ng (2018). |
| 2. | On simultaneous inference in related contexts see e.g., Jorda (2009); Jorda and Marcellino (2010); Jorda et al. (2013) on simultaneous path forecasts, and recently Montiel et al. (2019). |
| 3. | Throughout this document, size and coverage are used interchangeably; see Andrews and Cheng (2012). |
| 4. | In this regard, our work relates to Dufour and Valéry (2006, 2009) in stochastic volatility models, Dufour and Kurz-Kim (2010) and Beaulieu et al. (2007, 2013, 2014) in models with fat-tailed fundamentals. |
| 5. | |
| 6. | Alternatively, the data can be burned in to induce stationarity. Extensions to the mean-non stationarity framework as in Khalaf and Saunders (2019) is a worthy research direction. |
| 7. | Useful insight beyond the ARMA (1,1) on minimum dimension is found in the literature, in particular, Galbraith and Zinde-Walsh (1997) and more recently Gospodinov and Ng (2015). |
| 8. | This is noteworthy in view of the above cited problems discussed in the literature. |
| 9. | |
| 10. | Lütkepohl et al. (2015) provide an overview and evaluation in terms of coverage of the available literature dedicated to impulse-responses for VAR models and propose a new approach based on adjustments to the Bonferroni bands. |
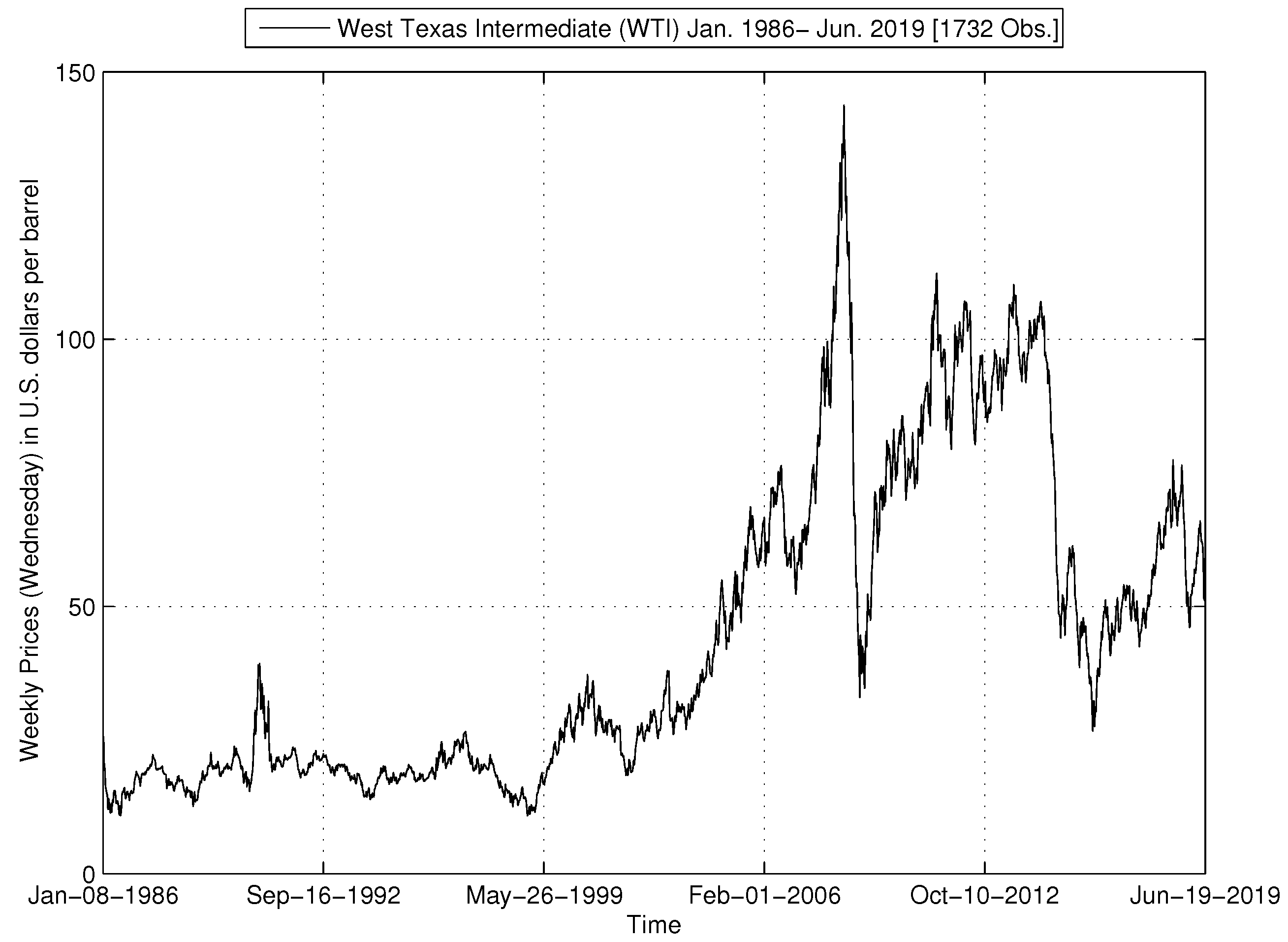
| 11. | Alquist et al. (2013) explain that after mid-1980, due to the U.S. deregulation, the co-movement between the U.S. oil price series, including WTI, refiners acquisition cost for domestically produced oil and for imported crude oil, became stronger. This means that we can take the WIT, since results obtained with other series are expected to be similar due to the high correlation between the various U.S. oil price series. |
| 12. | At the time the series is retrieved, the latest available monthly value corresponds to May, 2019. |
| 13. | The U.S. subprime mortgage crisis triggered an international financial crisis in 2008. According to the U.S. National Bureau of Economics Research (NBER), the U.S. recession is identified in terms of peaks and troughs from the last quarter of 2007 to the second quarter of 2009. |

| SIZE | ||||
|---|---|---|---|---|
| SIM Method | Gaussian MA | Student-t (df = 5) MA | ||
| OLS-Long AR | Simplified | OLS-Long AR | Simplified | |
| T = 50 | 0.046 | 0.040 | 0.043 | 0.038 |
| T = 100 | 0.054 | 0.055 | 0.047 | 0.042 |
| T = 200 | 0.046 | 0.049 | 0.053 | 0.039 |
| MLE | Gaussian MA | Student-t (df = 5) MA | ||
| T = 50 | 0.096 | 0.099 | ||
| T = 100 | 0.054 | 0.062 | ||
| T = 200 | 0.057 | 0.049 | ||
| POWER [SIM Method] | ||||
| T = 50 | Gaussian MA | Student-t (df = 5) MA | ||
| Tested Value | OLS-Long AR | Simplified | OLS-Long AR | Simplified |
| {0.00} | 0.717 | 0.861 | 0.720 | 0.865 |
| {0.30} | 0.322 | 0.364 | 0.302 | 0.370 |
| {0.85} | 0.276 | 0.225 | 0.266 | 0.211 |
| {0.90} | 0.368 | 0.286 | 0.371 | 0.267 |
| {0.96} | 0.436 | 0.324 | 0.430 | 0.302 |
| {0.99} | 0.442 | 0.334 | 0.442 | 0.309 |
| T = 100 | Gaussian MA | Student-t (df = 5) MA | ||
| Tested Value | OLS-Long AR | Simplified | OLS-Long AR | Simplified |
| {0.00} | 0.988 | 0.994 | 0.989 | 0.995 |
| {0.30} | 0.628 | 0.699 | 0.634 | 0.703 |
| {0.85} | 0.611 | 0.476 | 0.623 | 0.470 |
| {0.90} | 0.721 | 0.569 | 0.729 | 0.558 |
| {0.96} | 0.785 | 0.634 | 0.796 | 0.610 |
| {0.99} | 0.790 | 0.640 | 0.806 | 0.618 |
| T = 200 | Gaussian MA | Student-t (df = 5) MA | ||
| Tested Value | OLS-Long AR | Simplified | OLS-Long AR | Simplified |
| {0.00} | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.30} | 0.926 | 0.935 | 0.934 | 0.942 |
| {0.85} | 0.910 | 0.786 | 0.910 | 0.779 |
| {0.90} | 0.960 | 0.869 | 0.967 | 0.862 |
| {0.96} | 0.978 | 0.914 | 0.983 | 0.908 |
| {0.99} | 0.980 | 0.919 | 0.984 | 0.912 |
| SIZE | ||||
|---|---|---|---|---|
| SIM Method | Gaussian MA | Student-t (df = 5) MA | ||
| OLS-Long AR | Simplified | OLS-Long AR | Simplified | |
| T = 50 | 0.052 | 0.045 | 0.048 | 0.041 |
| T = 100 | 0.054 | 0.053 | 0.045 | 0.038 |
| T = 200 | 0.039 | 0.042 | 0.039 | 0.042 |
| MLE | Gaussian MA | Student-t (df = 5) MA | ||
| T = 50 | 0.167 | 0.156 | ||
| T = 100 | 0.294 | 0.229 | ||
| T = 200 | 0.429 | 0.347 | ||
| POWER [SIM Method] | ||||
| T = 50 | Gaussian MA | Student-t (df = 5) MA | ||
| Tested Value | OLS-Long AR | Simplified | OLS-Long AR | Simplified |
| {0.00} | 0.998 | 0.993 | 0.998 | 0.993 |
| {0.30} | 0.948 | 0.854 | 0.961 | 0.842 |
| {0.60} | 0.594 | 0.363 | 0.573 | 0.353 |
| {0.85} | 0.095 | 0.073 | 0.091 | 0.061 |
| {0.90} | 0.061 | 0.054 | 0.059 | 0.049 |
| {0.96} | 0.057 | 0.045 | 0.051 | 0.041 |
| T = 100 | Gaussian MA | Student-t (df = 5) MA | ||
| Tested Value | OLS-Long AR | Simplified | OLS-Long AR | Simplified |
| {0.00} | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.30} | 1.000 | 0.990 | 1.000 | 0.992 |
| {0.60} | 0.918 | 0.676 | 0.916 | 0.690 |
| {0.85} | 0.141 | 0.094 | 0.130 | 0.078 |
| {0.90} | 0.087 | 0.060 | 0.071 | 0.059 |
| {0.96} | 0.059 | 0.053 | 0.045 | 0.040 |
| T = 200 | Gaussian MA | Student-t (df = 5) MA | ||
| Tested Value | OLS-Long AR | Simplified | OLS-Long AR | Simplified |
| {0.00} | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.30} | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.60} | 0.996 | 0.922 | 0.996 | 0.928 |
| {0.85} | 0.204 | 0.099 | 0.196 | 0.124 |
| {0.90} | 0.084 | 0.050 | 0.079 | 0.063 |
| {0.96} | 0.042 | 0.039 | 0.043 | 0.040 |
| SIZE | ||||||
|---|---|---|---|---|---|---|
| SIM Method | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr | |
| T = 50 | 0.056 | 0.053 | 0.038 | 0.041 | 0.049 | 0.033 |
| T = 100 | 0.053 | 0.054 | 0.058 | 0.041 | 0.048 | 0.051 |
| T = 200 | 0.049 | 0.045 | 0.054 | 0.049 | 0.043 | 0.061 |
| MLE | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| MA | AR | Joint | MA | AR | Joint | |
| T = 50 | 0.470 | 0.454 | 0.523 | 0.446 | 0.401 | 0.500 |
| T = 100 | 0.432 | 0.417 | 0.482 | 0.404 | 0.392 | 0.457 |
| T = 200 | 0.414 | 0.414 | 0.470 | 0.370 | 0.371 | 0.445 |
| POWER [SIM Method] | ||||||
| T = 50 | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.430 | 0.225 | 0.181 | 0.418 | 0.229 | 0.174 |
| {0.3, 0.2} | 0.806 | 0.728 | 0.858 | 0.796 | 0.740 | 0.866 |
| {0.3, 0.85} | 0.923 | 0.699 | 0.453 | 0.932 | 0.702 | 0.428 |
| {0.5, 0.5} | 0.956 | 0.866 | 0.981 | 0.958 | 0.858 | 0.986 |
| {0.6, 0} | 0.836 | 0.436 | 0.180 | 0.828 | 0.431 | 0.170 |
| {0.6, 0.85} | 0.985 | 0.878 | 0.880 | 0.992 | 0.884 | 0.880 |
| {0.85, 0.2} | 0.999 | 0.916 | 0.307 | 0.999 | 0.904 | 0.271 |
| {0.85, 0.6} | 1.000 | 0.955 | 0.568 | 1.000 | 0.961 | 0.557 |
| {0.96, 0.5} | 1.000 | 0.961 | 0.481 | 1.000 | 0.963 | 0.471 |
| {0.99, 0.99} | 1.000 | 0.980 | 0.997 | 1.000 | 0.979 | 0.998 |
| T = 100 | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.797 | 0.695 | 0.500 | 0.793 | 0.700 | 0.493 |
| {0.3, 0.2} | 0.980 | 0.998 | 0.991 | 0.981 | 0.999 | 0.990 |
| {0.3, 0.85} | 0.996 | 0.995 | 0.875 | 0.996 | 0.994 | 0.870 |
| {0.5, 0.5} | 0.999 | 1.000 | 0.999 | 1.000 | 1.000 | 0.999 |
| {0.6, 0} | 0.983 | 0.901 | 0.509 | 0.989 | 0.899 | 0.502 |
| {0.6, 0.85} | 1.000 | 1.000 | 0.992 | 1.000 | 1.000 | 0.991 |
| {0.85, 0.2} | 1.000 | 1.000 | 0.727 | 1.000 | 0.999 | 0.727 |
| {0.85, 0.6} | 1.000 | 1.000 | 0.933 | 1.000 | 1.000 | 0.932 |
| {0.96, 0.5} | 1.000 | 1.000 | 0.901 | 1.000 | 1.000 | 0.894 |
| {0.99, 0.99} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| T = 200 | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.984 | 0.979 | 0.887 | 0.987 | 0.983 | 0.894 |
| {0.3, 0.2} | 0.999 | 1.000 | 1.000 | 0.999 | 1.000 | 1.000 |
| {0.3, 0.85} | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 0.996 |
| {0.5, 0.5} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.6, 0} | 0.999 | 0.999 | 0.911 | 1.000 | 0.999 | 0.918 |
| {0.6, 0.85} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.85, 0.2} | 1.000 | 1.000 | 0.994 | 1.000 | 1.000 | 0.992 |
| {0.85, 0.6} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 |
| {0.96, 0.5} | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 0.998 |
| {0.99, 0.99} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| SIZE | ||||||
|---|---|---|---|---|---|---|
| SIM Method | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr | |
| T = 50 | 0.044 | 0.041 | 0.052 | 0.049 | 0.038 | 0.049 |
| T = 100 | 0.049 | 0.041 | 0.053 | 0.049 | 0.035 | 0.048 |
| T = 200 | 0.052 | 0.058 | 0.051 | 0.048 | 0.046 | 0.043 |
| MLE | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| MA | AR | Joint | MA | AR | Joint | |
| T = 50 | 0.140 | 0.060 | 0.171 | 0.119 | 0.060 | 0.153 |
| T = 100 | 0.281 | 0.068 | 0.259 | 0.223 | 0.049 | 0.227 |
| T = 200 | 0.390 | 0.074 | 0.349 | 0.317 | 0.049 | 0.281 |
| POWER [SIM Method] | ||||||
| T = 50 | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.922 | 1.000 | 0.915 | 0.921 | 1.000 | 0.914 |
| {0.3, 0.2} | 0.831 | 1.000 | 0.992 | 0.830 | 1.000 | 0.991 |
| {0.3, 0.85} | 0.609 | 0.979 | 0.331 | 0.615 | 0.985 | 0.332 |
| {0.5, 0.5} | 0.295 | 0.968 | 0.904 | 0.305 | 0.980 | 0.906 |
| {0.5, 0.96} | 0.285 | 0.778 | 0.046 | 0.290 | 0.794 | 0.046 |
| {0.6, 0} | 0.427 | 0.998 | 0.998 | 0.442 | 0.999 | 0.992 |
| {0.6, 0.85} | 0.131 | 0.653 | 0.317 | 0.131 | 0.663 | 0.308 |
| {0.85, 0.2} | 0.017 | 0.763 | 0.980 | 0.020 | 0.772 | 0.986 |
| {0.85, 0.6} | 0.023 | 0.304 | 0.815 | 0.024 | 0.293 | 0.825 |
| {0.96, 0.5} | 0.040 | 0.257 | 0.891 | 0.038 | 0.241 | 0.893 |
| T = 100 | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.997 | 1.000 | 0.994 | 0.997 | 1.000 | 0.995 |
| {0.3, 0.2} | 0.980 | 1.000 | 1.000 | 0.984 | 1.000 | 1.000 |
| {0.3, 0.85} | 0.908 | 1.000 | 0.635 | 0.914 | 1.000 | 0.648 |
| {0.5, 0.5} | 0.690 | 1.000 | 0.993 | 0.701 | 1.000 | 0.994 |
| {0.5, 0.96} | 0.662 | 0.984 | 0.074 | 0.671 | 0.988 | 0.070 |
| {0.6, 0} | 0.826 | 1.000 | 1.000 | 0.824 | 1.000 | 1.000 |
| {0.6, 0.85} | 0.418 | 0.939 | 0.610 | 0.435 | 0.947 | 0.626 |
| {0.85, 0.2} | 0.036 | 0.983 | 1.000 | 0.042 | 0.984 | 1.000 |
| {0.85, 0.6} | 0.035 | 0.508 | 0.976 | 0.033 | 0.531 | 0.973 |
| {0.96, 0.5} | 0.039 | 0.453 | 0.991 | 0.048 | 0.444 | 0.994 |
| T = 200 | Gaussian ARMA | Student-t (df = 5) ARMA | ||||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.3, 0.2} | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| {0.3, 0.85} | 0.991 | 1.000 | 0.922 | 0.992 | 1.000 | 0.921 |
| {0.5, 0.5} | 0.943 | 1.000 | 1.000 | 0.943 | 1.000 | 1.000 |
| {0.5, 0.96} | 0.932 | 1.000 | 0.157 | 0.935 | 1.000 | 0.163 |
| {0.6, 0} | 0.984 | 1.000 | 1.000 | 0.984 | 1.000 | 1.000 |
| {0.6, 0.85} | 0.778 | 0.998 | 0.911 | 0.780 | 0.999 | 0.910 |
| {0.85, 0.2} | 0.121 | 1.000 | 1.000 | 0.100 | 1.000 | 1.000 |
| {0.85, 0.6} | 0.052 | 0.840 | 1.000 | 0.034 | 0.833 | 0.999 |
| {0.96, 0.5} | 0.067 | 0.767 | 1.000 | 0.067 | 0.763 | 1.000 |
| POWER [SIM Method] | |||
|---|---|---|---|
| T = 100 | Gaussian ARMA | ||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.903 | 0.998 | 0.326 |
| {0.3, 0.2} | 0.978 | 0.999 | 0.974 |
| {0.3, 0.85} | 0.994 | 0.999 | 0.310 |
| {0.5, 0.5} | 0.998 | 1.000 | 0.275 |
| {0.5, 0.96} | 1.000 | 1.000 | 0.918 |
| {0.6, 0} | 0.998 | 0.999 | 0.993 |
| {0.6, 0.85} | 1.000 | 1.000 | 0.327 |
| {0.85, 0.2} | 1.000 | 1.000 | 0.862 |
| {0.85, 0.6} | 1.000 | 1.000 | 0.105 |
| {0.96, 0.5} | 1.000 | 1.000 | 0.231 |
| {0.99, 0.99} | 1.000 | 1.000 | 0.987 |
| POWER [SIM Method] | |||
|---|---|---|---|
| T = 100 | Gaussian ARMA | ||
| Tested Pair | OLS-FBLC | OLS-Long AR | AutoCorr |
| {0, 0.6} | 0.635 | 0.931 | 0.962 |
| {0.3, 0.2} | 0.403 | 0.957 | 1.000 |
| {0.3, 0.85} | 0.171 | 0.198 | 0.233 |
| {0.5, 0.5} | 0.066 | 0.130 | 0.959 |
| {0.5, 0.96} | 0.105 | 0.117 | 0.103 |
| {0.6, 0} | 0.056 | 0.733 | 1.000 |
| {0.6, 0.85} | 0.289 | 0.227 | 0.208 |
| {0.85, 0.2} | 0.858 | 0.562 | 0.997 |
| {0.85, 0.6} | 0.930 | 0.814 | 0.898 |
| {0.96, 0.5} | 0.974 | 0.860 | 0.956 |
| {0.99, 0.99} | 0.981 | 0.969 | 0.282 |
| Time Period | Sample | Obs. | Mean | Std. Dev. | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| Jan. 1986–June 2019 | Log of Weekly Nominal Prices | 1732 | −2.8881 × | 0.6582 | 0.6582 | 1.6844 |
| Jan.1986–June 2019 | Log of Monthly Nominal Prices | 402 | 5.0485 × | 0.6566 | 0.2541 | 1.6844 |
| Jan. 1986–May 2019 | Log of Monthly Real Prices | 401 | 9.5241 × | 0.8719 | 0.1165 | 1.5428 |
| Jan. 1986–June 2019 | Weekly Nominal Returns | 1731 | 4.7302 × | 0.05128 | −0.1449 | 5.9181 |
| Jan. 1986–June 2019 | Monthly Nominal Returns | 401 | 6.9216 × | 0.10253 | −0.35965 | 4.9748 |
| Jan. 1986–May 2019 | Monthly Real Returns | 400 | 2.2898 × | 0.10341 | −0.37958 | 5.0612 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalaf, L.; Peraza López, B. Simultaneous Indirect Inference, Impulse Responses and ARMA Models. Econometrics 2020, 8, 12. https://doi.org/10.3390/econometrics8020012
Khalaf L, Peraza López B. Simultaneous Indirect Inference, Impulse Responses and ARMA Models. Econometrics. 2020; 8(2):12. https://doi.org/10.3390/econometrics8020012
Chicago/Turabian StyleKhalaf, Lynda, and Beatriz Peraza López. 2020. "Simultaneous Indirect Inference, Impulse Responses and ARMA Models" Econometrics 8, no. 2: 12. https://doi.org/10.3390/econometrics8020012
APA StyleKhalaf, L., & Peraza López, B. (2020). Simultaneous Indirect Inference, Impulse Responses and ARMA Models. Econometrics, 8(2), 12. https://doi.org/10.3390/econometrics8020012




