Abstract
This work describes a versatile and readily-deployable sensitivity analysis of an ordinary least squares (OLS) inference with respect to possible endogeneity in the explanatory variables of the usual k-variate linear multiple regression model. This sensitivity analysis is based on a derivation of the sampling distribution of the OLS parameter estimator, extended to the setting where some, or all, of the explanatory variables are endogenous. In exchange for restricting attention to possible endogeneity which is solely linear in nature—the most typical case—no additional model assumptions must be made, beyond the usual ones for a model with stochastic regressors. The sensitivity analysis quantifies the sensitivity of hypothesis test rejection p-values and/or estimated confidence intervals to such endogeneity, enabling an informed judgment as to whether any selected inference is “robust” versus “fragile.” The usefulness of this sensitivity analysis—as a “screen” for potential endogeneity issues—is illustrated with an example from the empirical growth literature. This example is extended to an extremely large sample, so as to illustrate how this sensitivity analysis can be applied to parameter confidence intervals in the context of massive datasets, as in “big data”.
Keywords:
robustness; exogeneity; multiple regression; inference; instrumental variables; large samples; big data JEL Classification:
C2; C15
1. Introduction
1.1. Motivation
For many of us, the essential distinction between econometric regression analysis and otherwise-similar forms of regression analysis conducted outside of economics, is the overarching concern shown in econometrics with regard to the model assumptions made in order to obtain consistent ordinary least squares (OLS) parameter estimation and asymptotically valid statistical inference. As Friedman (1953) famously noted (in the context of economic theorizing), it is both necessary and appropriate to make model assumptions—notably, even assumptions which we know to be false—in any successful economic modeling effort: the usefulness of a model, he asserted, inheres in the richness/quality of its predictions rather than in the accuracy of its assumptions. Our contribution here—and in Ashley (2009) and Ashley and Parmeter (2015b), which address similar issues in the context of IV and GMM/2SLS inference using possibly-flawed instruments—is to both posit and operationalize a general proposition that is a natural corollary to Friedman’s assertion: It is perfectly acceptable to make possibly-false (and even very-likely-false) assumptions—if and only if one can and does show that the model results one cares most about are insensitive to the levels of violations in these assumptions that it is reasonable to expect.1
In particular, the present paper proposes a sensitivity analysis for OLS estimation/inference in the presence of unmodeled endogeneity in the explanatory variables of the usual linear multiple regression model. This context provides an ideal setting in which to both exhibit and operationalize a quantification of the “insensitivity” alluded to in the proposition above, because this setting is so very simple. This setting is also attractive in that OLS estimation of multiple regression models with explanatory variables of suspect exogeneity is common in applied economic work. The extension of this kind of sensitivity analysis to more complex—e.g., nonlinear—estimation settings is feasible, but will be laid out in separate work, as it requires a different computational framework, and does not admit the closed-form results obtained (for some cases) here.
The diagnostic analysis proposed here quantifies the sensitivity of OLS hypothesis test rejection p-values (for both multiple and/or nonlinear parameter restrictions)—and also of single-parameter confidence intervals—with respect to possible endogeneity (i.e., non-zero correlations between the explanatory variables and the model errors) in the usual k-variate multiple regression model.
This sensitivity analysis rests on a derivation of the sampling distribution of , the OLS parameter estimator, extended to the case where some or all of the explanatory variables are endogenous to a specified degree. In exchange for restricting attention to possible endogeneity which is solely linear in nature—the most typical case—the derivation of this sampling distribution proceeds in a particularly straightforward way. And under this “linear endogeneity” restriction, no additional model assumptions—e.g., with respect to the third and fourth moments of the joint distribution of the explanatory variables and the model errors—are necessary, beyond the usual assumptions made for any model with stochastic regressors. The resulting analysis quantifies the sensitivity of hypothesis test rejection p-values (and/or estimated confidence intervals) to such linear endogeneity, enabling the analyst to make an informed judgment as to whether any selected inference is “robust” versus “fragile” with respect to likely amounts of endogeneity in the explanatory variables.
We show below that, in the context of the linear multiple regression model, this additional sensitivity analysis is so straightforward an addendum to the usual OLS diagnostic checking which applied economists are already doing—both theoretically, and in terms of the effort required to set up and use our proposed procedure—that analysts can routinely use it. In this regard we see our sensitivity analysis as a general diagnostic “screen” for possibly-important, unaddressed endogeneity issues.
1.2. Relation to Previous Work on OLS Multiple Regression Estimation/Inference
Deficiencies in previous work on the sensitivity of OLS multiple regression estimation/inference with regard to possible endogeneity in the explanatory variables—comprising Ashley and Parmeter (2015a) and Kiviet (2016)—has stimulated us to revise and extend our earlier work on this topic. What is new here is:
- Improved Sampling Distribution Derivation, via a Restriction to “Linear Endogeneity”In response to the critique in Kiviet (2016) of the OLS parameter sampling distribution under endogeneity given in Ashley and Parmeter (2015a), we now obtain this asymptotic sampling distribution, in a particularly straightforward fashion, by limiting the universe of possible endogeneity to solely-linear relationships between the explanatory variables and the model error. In Section 2 we show that the OLS parameter sampling distribution does not then depend on the third and fourth moments of the joint distribution of the explanatory variables and the model errors under this linear-endogeneity restriction. This improvement on the Kiviet and Niemczyk (2007, 2012) and Kiviet (2013, 2016) sampling distribution results—which make no such restriction on the form of endogeneity, but do depend on these higher moments—is crucial to an empirically-usable sensitivity analysis: we see no practical value in a sensitivity analysis which quantifies the impact of untestable exogeneity assumptions only under empirically-inaccessible assumptions with regard to these higher moments. On the other hand, while endogeneity that is linear in form is an intuitively understandable notion—and corresponds to the kind of endogeneity that will ordinarily arise from the sources of endogeneity usually invoked in textbook discussions—this restriction to the sensitivity analysis is itself somewhat limiting; this issue is further discussed in Section 2 below.
- Analytic Results for a Non-Trivial Special CaseWe now obtain closed-form results for the minimal degree of explanatory-variable to model-error correlation necessary in order to overturn any particular hypothesis testing result for a single linear restriction, in the special (one-dimensional) case where the exogeneity of a single explanatory variable is under scrutiny.2
- Simulation-Based Check with Regard to Sample-Length AdequacyBecause the asymptotic bias in depends on , the population variance-covariance matrix of the explanatory variables in the regression model, sampling error in —the usual (consistent) estimator of —does affect the asymptotic distribution of when this estimator replaces in our sensitivity analysis, as pointed out in Kiviet (2016). Our algorithm now optionally uses bootstrap simulation to quantify the impact of this replacement on our sensitivity analysis results.We find this impact to be noticeable, but manageable, in our illustrative empirical example, the classic Mankiw, Romer, and Weil (Mankiw et al. 1992) examination of the impact of human capital accumulation (“”), which uses observations. This example does not necessarily imply that this particular sample length is either necessary or sufficient for the application of this sensitivity analysis to other models and data sets; we consequently recommend performing this simulation-based check (on the adequacy of the sample length for this purpose) at the outset of the sensitivity analysis in any particular regression modeling context.3
- Sensitivity Analysis with Respect to Coefficient Size—Especially for Extremely Large SamplesIn some settings—financial and agricultural economics, for example—analysts’ interest centers on the size of a particular model coefficient rather than on the p-value at which some particular null hypothesis with regard to the model coefficients can be rejected. The estimated size of a model coefficient is generally also a better guide to its economic (as opposed to its statistical) significance—as emphasized by McCloskey and Ziliak (1996).Our sensitivity analysis adapts readily in such cases, to instead depict how the estimated confidence interval for a particular coefficient varies with the vector of correlations between the explanatory variables and the model error term; we denote this is as “parameter-value-centric” sensitivity analysis below. For a one-dimensional analysis, where potential endogeneity is contemplated in only a single explanatory variable, the display of such results is easily embodied in a plot of the estimated confidence interval for this specified regression coefficient versus the single endogeneity-correlation in this setting.We supply two such plots, embodying two such one-dimensional “parameter-value-centric” sensitivity analyses, in Section 4 below; these plots display how the estimated confidence interval for the Mankiw, Romer and Weil (MRW) human capital coefficient (on their “” explanatory variable in our illustrative example) separately varies with the posited endogeneity correlation in each of two selected explanatory variables in the model. Our implementing algorithm itself generalizes easily to multi-dimensional sensitivity analyses—i.e., sensitivity analysis with respect to possible (simultaneous) endogeneity in more than one explanatory variable—and several examples of such two-dimensional sensitivity analysis results, with regard to the robustness/fragility of the rejection p-values for hypothesis tests involving coefficients in the MRW model, are presented in Section 4. We could thus additionally display the results of a two-dimensional “parameter-value-centric” sensitivity analysis for this model coefficient—e.g., plotting how the estimated confidence interval for the MRW human capital coefficient varies with respect to possible simultaneous endogeneity in both of these two MRW explanatory variables—but the display of these confidence interval results would require a three-dimensional plot, which is more troublesome to interpret.4Perhaps the most interesting and important applications of this “parameter-value-centric” sensitivity analysis will arise in the context of models estimated using the extremely large data sets now colloquially referred to as “big data.” In these models, inference in the form of hypothesis test rejection p-values is frequently of limited value, because the large sample sizes in such settings quite often render all such p-values uninformatively small. In contrast, the “parameter-value-centric” version of our endogeneity sensitivity analysis adapts gracefully to such large-sample applications: in these settings each estimated confidence interval will simply shrink to what amounts to a single point, so in such cases the “parameter-value-centric” sensitivity analysis will in essence be simply plotting the asymptotic mean of a key coefficient estimate against posited endogeneity-correlation values. It is, of course, trivial to artificially extend our MRW example to a huge sample and display such a plot for illustrative purposes, and this is done in Section 4 below. But consequential examples of this sort of sensitivity analysis must await the extension of the OLS-inference sensitivity analysis proposed here to the nonlinear estimation procedures typically used in such large-sample empirical work.5
1.3. Preview of the Rest of the Paper
In Section 2 we provide a new derivation of the asymptotic sampling distribution of the OLS structural parameter estimator () for the usual k-variate multiple regression model, where some or all of the explanatory variables are endogenous to a specified degree. This degree of endogeneity is quantified by a given set of covariances between these explanatory variables and the model error term (); these covariances are denoted by the vector . The derivation of the sampling distribution of is greatly simplified by restricting the form of this endogeneity to be solely linear in form, as follows:
We first define a new regression model error term (denoted ), from which all of the linear dependence on the explanatory variables has been stripped out. Thus—under this restriction of the endogeneity to be purely linear in form—this new error term must (by construction) be completely unrelated to the explanatory variables. Hence, with solely-linear endogeneity, must be statistically independent of the explanatory variables. This allows us to easily construct a modified regression equation in which the explanatory variables are independent of the model errors. This modified regression model now satisfies the assumptions of the usual multiple regression model (with stochastic regressors that are independent of the model errors), for which the OLS parameter estimator asymptotic sampling distribution is well known.
Thus, under the linear-endogeneity restriction, OLS estimation of this modified regression model yields unbiased estimation and asymptotically valid inferences on the model’s parameter vector; but these OLS estimates are now, as one might expect, unbiased for a coefficient vector which differs from by an amount depending explicitly on the posited endogeneity covariance vector, . Notably, however, this sampling distribution derivation requires no additional model assumptions beyond the usual ones made for a model with stochastic regressors: in particular, one need not specify any third or fourth moments for the joint distribution of the model errors and explanatory variables, as would be the case if the endogeneity were not restricted to be solely-linear in form.
In Section 3 we show how this sampling distribution for can be used to assess the robustness/fragility of an OLS regression model inference with respect to possible endogeneity in the explanatory variables; this Section splits the discussion into several parts. The first parts of this discussion—Section 3.1 through Section 3.5—describe the sensitivity analysis with respect to how much endogeneity is required in order to “overturn” an inference result with respect to the testing of a particular null hypothesis regarding the structural parameter, , where this null hypothesis has been rejected at some nominal significance level—e.g., —under the assumption that all of the explanatory variables are exogenous. Section 3.6 closes our sensitivity analysis algorithm specification by describing how the sampling distribution for derived in Section 2 can be used to display the sensitivity of a confidence interval for a particular component of to possible endogeneity in the explanatory variables; this is the “parameter-value-centric” sensitivity analysis outlined at the end of Section 1.2. So as to provide a clear “road-map” for this Section, each of these six subsections is briefly described next.
Section 3.1 shows how a specific value for the posited endogeneity covariance vector ()—combined with the sampling distribution of from Section 2—can be used to both recompute the rejection p-value for the specified null hypothesis with regard to and to also convert this endogeneity covariance vector () into the corresponding endogeneity correlation vector, , which is more-interpretable than . This conversion into a correlation vector is possible (for any given value of ) because the sampling distribution yields a consistent estimator of , making the error term in the original (structural) model asymptotically available; this allows the necessary variance of to be consistently estimated.
Section 3.2 operationalizes these two results from Section 3.1 into an algorithm for a sensitivity analysis with regard to the impact (on the rejection of this specified null hypothesis) of possible endogeneity in a specified subset of the k regression model explanatory variables; this algorithm calculates a vector we denote as “,” whose Euclidean length—denoted “” here—is our basic measure of the robustness/fragility of this particular OLS regression model hypothesis testing inference.
The definition of is straightforward: it is simply the shortest endogeneity correlation vector, , for which possible endogeneity in this subset of the explanatory variables suffices to raise the rejection p-value for this particular null hypothesis beyond the specified nominal level (e.g., )—thus overturning the null hypothesis rejection observed under the assumption of exogenous model regressors. Since the sampling distribution derived in Section 2 is expressed in terms of the endogeneity covariance vector (), this implicit search proceeds in the space of the possible values of , using the p-value result from Section 3.1 to eliminate all values still yielding a rejection of the null hypothesis, and using the result corresponding to each non-eliminated value to supply the relevant minimand, .
In Section 3.3 we obtain a closed-form expression for in the (not uncommon) special case of a one-dimensional sensitivity analysis, where only a single explanatory variable is considered possibly-endogenous. This closed-form result reduces the computational burden involved in calculating , by eliminating the numerical minimization over the possible endogeneity covariance vectors; but its primary value is didactic: its derivation illuminates what is going on in the calculation of .
The calculation of is not ordinarily computationally burdensome, even for the general case of multiple possibly-endogenous explanatory variables and tests of complex null hypotheses—with the sole exception of the simulation calculations alluded to in Section 1.2 above. These bootstrap simulations, quantifying the impact of substituting for in the calculation, are detailed in Section 3.4. In practice these simulations are quite easy to do, as they are already coded up as an option in the implementing software, but the computational burden imposed by the requisite set of replications of the calculation can be substantial. In the case of a one-dimensional sensitivity analysis—where the closed-form results are available—these analytic results dramatically reduce the computational time needed for this simulation-based assessment of the extent to which the length of the sample data set is sufficient to support the sensitivity analysis. And our sensitivity results for the illustrative empirical example examined in Section 4 suggest that such one-dimensional sensitivity analyses may frequently suffice. Still, it is fortunate that this simulation-based assessment in practice needs only to be done once, at the outset of one’s work with a particular regression model.
The portion of Section 3 describing the sensitivity analysis with respect to inference in the form of hypothesis testing then concludes with some preliminary remarks, in Section 3.5, as to how one can interpret (and its length, ) in terms of the “fragility” or “robustness” of such a hypothesis test inference. This topic is taken up again in Section 6, at the end of the paper.
Section 3 closes with a description of the implementation of the “parameter-value-centric” sensitivity analysis outlined at the end of Section 1.2. This version of the sensitivity analysis is simply a display of how the confidence interval for any particular component of varies with . Its implementation is consequently a straightforward variation on the algorithm for implementing the hypothesis-testing-centric sensitivity analysis, as the latter already obtains both the sampling distribution of and the value of for any given value of the endogeneity covariance vector, . Thus, each value of chosen yields a point in the requisite display. The results of a univariate sensitivity analysis (where only one explanatory variable is considered to be possibly endogenous, and hence only one component of can be non-zero) are readily displayed in a two-dimensional plot. Multi-dimensional, “parameter-value-centric” sensitivity analysis results are also easy to compute, but these are more challenging to display; in such settings one could, however, still resort to a tabulation of the results, as in Kiviet (2016).
In Section 4 we illustrate the application of this proposed sensitivity analysis to assess the robustness/fragility of the inferences obtained by Mankiw, Romer, and Weil (Mankiw et al. 1992)—denoted “MRW” below—in their influential study of the impact of human capital accumulation on economic growth. This model provides a nice example of the application of our proposed sensitivity analysis procedure, in that the exogeneity of several of their explanatory variables is in doubt, and in that one of their two key null hypotheses is a simple zero-restriction on a single model coefficient and the other is a linear restriction on several of their model coefficients. We find that some of their inferences are robust with respect to possible endogeneity in their explanatory variables, whereas others are fragile. Hypothesis testing was the focus in the MRW study, but this setting also allows us to display how a confidence interval for one of their model coefficients varies with the degree of (linear) endogeneity in a selected explanatory variable, both for the actual MRW sample length () and for an artificially-huge elaboration of their data set.
We view the sensitivity analysis proposed here as a practical addendum to the profession’s usual toolkit of diagnostic checking techniques for OLS multiple regression analysis—in this case as a “screen” for assessing the impact of likely amounts of endogeneity in the explanatory variables. To that end—as noted above—we have written scripts encoding the technique for several popular computing frameworks: and ; Section 5 briefly discusses exactly what is involved in using these scripts.
Finally, in Section 6 we close the paper with a brief summary, and a modest elaboration of our Section 3.5 comments on how to interpret the quantitative (objective) sensitivity results which this proposed technique provides.
2. Sampling Distribution of the OLS Multiple Regression Parameter Estimator With Linearly-Endogenous Covariates
Per the usual k-variate multiple regression modeling framework, we assume that
where the matrix of regressors, X, is with (for simplicity) zero mean and population variance-covariance . Here of the explanatory variables are taken to be “linearly endogenous”—i.e., related to the error term , but in a solely linear fashion—with covariance given by the k-vector .
We next define a random variate which is—by construction—uncorrelated with X:
where it is readily verified that both and equal zero,6 and where we let var() define the scalar .
Solving Equation (2) for and substituting into Equation (1) yields
This is the regression model that one is actually estimating when one regresses Y on X, yielding a realization of . Since the error term () in this equation is constructed to be uncorrelated with X, is a consistent estimator, but for the actual coefficient vector in this model——rather than for . The reader will doubtless recognize the foregoing as the usual textbook derivation that OLS yields an inconsistent estimator of in the presence of endogeneity in the model regressors.
What is needed here, however, is the full asymptotic sampling distribution for , so that rejection p-values for null hypotheses involving and confidence intervals for components of can be computed for non-zero posited amounts of endogeneity in the original model, Equation (1). Kiviet and Niemczyk (2007, 2012) and Kiviet (2013, 2016) derive this sampling distribution, but their result, unfortunately, depends on the third and fourth moments of the joint distribution of (X, ). Absent consistent estimation of , the Equation (1) model error () is not observable, so these moments are not empirically accessible; those sampling distribution results are consequently not useful for implementing our sensitivity analysis.
Instead, we here limit the possible endogeneity considered in the sensitivity analysis to purely linear relationships between the explanatory variables (X) and the Equation (1) model errors, . Under the restriction of solely linear endogeneity, the error term is not just uncorrelated with X: it is actually of X. This result follows directly from the fact that Equation (2) defines as the remainder of the variation in once its linear relationship with X has been removed. Thus, if the relationship between and X is purely linear, then and X must be completely unrelated—i.e., statistically independent.
With X restricted to be linearly endogenous, the implied error term () in the rightmost portion of Equation (3) is consequently independent of the model regressors. So this Equation (3) model is now reduced to the standard stochastic-regression model with (exogenous) regressors that are independent of the model error term, the only difference being that is here an unbiased estimator of rather than of . The asymptotic sampling distribution of is thus well known:7
and this result makes it plain that is itself unbiased and consistent if and only if .
The value of can thus, under this solely-linear endogeneity restriction, be consistently estimated from the OLS fitting errors—using the usual estimator, .8 And the value of in Equation (4) can be consistently estimated from the observed data on the explanatory variables, using the usual sample estimator of the variance-covariance matrix of these variables. We note, however, that—per the discussion in Section 1 above—sampling variation in this estimator of impacts the distribution of —even asymptotically—through its influence on the estimated asymptotic mean implied by Equation (4); this complication is addressed in the implementing algorithm detailed in Section 3 below, using bootstrap simulation.
The restriction here to the special case of solely-linear endogeneity thus makes the derivation of the sampling distribution of almost trivial. But it is legitimate to wonder what this restriction is approximating away, relative to instead—as in Kiviet (2016), say, making an —and empirically inaccessible assumption as to the values of the third and fourth moments of the joint distribution of the variables (X, ). As noted in Section 1.2 above, the forms of endogeneity usually discussed in textbook treatments of endogeneity—i.e., endogeneity due to omitted explanatory variables, due to measurement errors in the explanatory variables, and due to a (linear) system of simultaneous equations; in fact, all lead to endogeneity which is solely-linear in form. But endogeneity in a particular explanatory variable which is arising from its determination as the dependent variable of another equation in a system of nonlinear simultaneous equations will in general not be linear in form. So this restriction is clearly not an empty one. Moreover—in simulating data from a linear regression model—it would be easy to generate nonlinear endogeneity in any particular explanatory variable, by simply adding a nonlinear function of this explanatory variable to the model errors driving the simulations.9
Lastly, we note that (Ashley and Parmeter 2019, p. 12) shows that the sampling distribution of derived above as Equation (4) is equivalent to that given by (Kiviet 2016, Equation 2.7) for the special case where the joint distribution of (X, ) is symmetric with zero excess kurtosis. Thus, joint Gaussianity in (X, )—which, of course, implies linear endogeneity—is sufficient, albeit not necessary, in order to make the two distributional results coincide. As noted above in Section 1.2, however, we see no practical value in a sensitivity analysis which quantifies the impact of untestable exogeneity assumptions on X and only under untestable assumptions with regard to the higher moments of the joint distribution of (X, ). Thus, we would characterize the limitation of this sensitivity analysis to solely-linear endogeneity as a practically necessary—and relatively innocuous—but not empty, restriction.
Finally, it will be useful below to have an expression for , the variance of the error term in Equation (1), so as to provide for the conversion of any posited value for , the k-vector of covariances of X with , into the more-easily-interpretable k-vector of correlations between X and , which will be denoted below.
It follows from Equation (2) that
Dividing both sides of this equation by n and taking expectations yields
It makes sense that exceeds : Where explanatory variables in the original (“structural”) Equation (1) are endogenous—e.g., because of wrongly-omitted variates which are correlated with the included ones—this endogeneity actually improves the fit of the estimated model, Equation (3). This takes place simply because—in the presence of endogeneity—Equation (3) can use sample variation in some of its included variables to “explain” some of the sample variation in . Thus, the actual OLS fitting error () has a smaller variance than does the Equation (1) structural error (), but the resulting OLS parameter estimator () is then inconsistent for the Equation (1) structural parameter, .
Up to this point , the vector of covariances of the k explanatory variables with the structural model errors () has been taken as given. However—absent a consistent estimator of —these structural errors are inherently unobservable, even asymptotically, unless one has additional (exogenous) information not ordinarily available in empirical settings. Consequently is inherently not identifiable. It is, however, possible—quite easy, actually—to quantify the sensitivity of the rejection p-value for any particular null hypothesis involving (or of a confidence interval for any particular component of ) to correlations between the explanatory variables and these unobservable structural errors. The next section describes our algorithm for accomplishing this sensitivity analysis, which is the central result of the present paper.
3. Proposed Sensitivity Analysis Algorithm
3.1. Obtaining Inference Results and the Endogeneity Correlation Vector (), Given the Endogeneity Covariance Vector ()
In implementing the sensitivity analysis proposed here, we presume that the regression model equation given above as Equation (3) has been estimated using OLS, so that the sample data (realizations of Y and X) are available, and have been used to obtain a sample realization of the inconsistent OLS parameter estimator ()—which is actually consistent for —and to obtain a sample realization of the usual estimator of the model error variance estimator, . This error variance estimator provides a consistent estimate of the Equation (3) error variance, , conditional on the values of and .
In addition, the sample length (n) is taken to be sufficiently large that the sampling distribution of has converged to its limiting distribution—derived above as Equation (4)—and that has essentially converged to its probability limit, . In the first parts of this section it is also assumed that n is sufficiently large that the sample estimate need not be distinguished from its probability limit, ; this assumption is relaxed for the bootstrap simulations described below in Section 3.4.
Now assume—for the moment—that a value for , the k-dimensional vector of covariances between the columns of the X matrix and the vector of errors () in Equation (1) is posited and is taken as given; this artificial assumption will be relaxed shortly. Here (in an “ℓ-dimensional sensitivity analysis") ℓ of the explanatory variables are taken to be possibly-endogenous, and hence ℓ components of this posited vector would typically be non-zero.
We presume that the inference at issue—whose sensitivity to possible endogeneity in the model explanatory variables is being assessed—is a particular null hypothesis specifying a given set of linear restrictions on the components of . Based on this posited vector—and the sampling distribution for , derived as Equation (4) above—the usual derivation then yields a test statistic which is asymptotically distributed as F(r, n - k) under this null hypothesis. Thus, the p-value at which this null hypothesis of interest can be rejected is readily calculated, for any given value of the posited vector.10
Equations (3) and (4) together imply a consistent estimator of : , so substitution of this estimator into Equation (1) yields a set of model residuals which are asymptotically equivalent to the vector of structural model errors, . The sample variance of this implied vector then yields , which is a consistent estimate of , the variance of .11
This consistent estimate of the variance of is then combined with the posited covariance vector () and with the consistent sample variance estimates for the k explanatory variables—i.e., with , …, —to yield , a consistent estimate of the corresponding k-vector of correlations between these explanatory variables and the original model errors () in Equation (1).
Thus, the concomitant correlation vector can be readily calculated for any posited covariance vector, . This k-dimensional vector of correlations is worth estimating because it quantifies the (linear) endogeneity posited in each of the explanatory variables in a more intuitively interpretable way than does , the posited vector of covariances between the explanatory variables and the original model errors. We denote the Euclidean length of this implied correlation vector below as “.”
In summary, then, any posited value for —the vector of covariances between the explanatory variables and , the original model errors—yields both an implied rejection p-value for the null hypothesis at issue and also , a consistent estimate of the vector of implied correlations between the k explanatory variables and the original model errors, with Euclidean length .
3.2. Calculation of , the Minimal-Length Endogeneity Correlation Vector Overturning the Hypothesis Test Rejection
The value of the vector is, of course, unknown, so the calculation described above is repeated for a selection M of all possible values can take on, so as to numerically determine the vector which yields the smallest value of the endogeneity correlation vector length () for which the null hypothesis of interest is no longer rejected at the nominal significance level—here taken (for clarity of exposition only) to be —that is already being used. This minimal-length endogeneity correlation vector is denoted by , and its length by . The value of then quantifies the sensitivity of this particular null hypothesis inference to possible endogeneity in any of these ℓ explanatory variables in the original regression model.
Thus, for each of the M vectors selected, the calculation retains the aforementioned correlation vector (), its length (), and the concomitant null hypothesis rejection p-value; these values are then written to one row of a spreadsheet file, if and only if the null hypothesis is no longer rejected with p-value less than . Because the regression model need not be re-estimated for each posited vector, these calculations are computationally inexpensive; consequently, it is quite feasible for M to range up to or even .12
For —i.e., where the exogeneity of at most one or two of the k explanatory variables are taken to be suspect—it is computationally feasible to select the M vectors using a straightforward ℓ-dimensional grid-search over the reasonably-possible vectors. For larger values of ℓ it is still feasible (and, in practice, effective for this purpose) to instead use a Monte-Carlo search over the set of reasonably-possible vectors, as described in Ashley and Parmeter (2015b); in this case the vectors are drawn at random.13
The algorithm described above yields a spreadsheet containing rows, each containing an implied correlation k-vector , its Euclidean length , and its implied null hypothesis rejection p-value—with the latter quantity in each case exceeding the nominal rejection criterion value (e.g., 0.05), by construction. For a sufficiently large value of , this collection of vectors well-approximates an ℓ-dimensional set in the vector space spanned by the ℓ non-zero components of the vector . We denote this as the “No Longer Rejecting” or “NLR” set: the elements of this set are the X-column-to- correlations (exogeneity-assumption flaws) which are sufficient to overturn the 5%-significant null hypothesis rejection observed in the original OLS regression model.14
Simply sorting this spreadsheet on the correlation-vector length then yields the point in the NLR which is closest to the origin—i.e., , the smallest vector which represents a flaw in the exogeneity assumptions sufficient to overturn the observed rejection of the null hypothesis of interest at the 5% level.
The computational burden of calculating as described above—where the impact of the sampling errors in is being neglected—is not large, so that R and Stata code (available from the authors) is generally quite sufficient to the task. But it is illuminating—in Section 3.3 below—to obtain analytically for the not-uncommon special case where —i.e., where just one (the , say) of the k explanatory variables is being taken as possibly-endogenous; in that case only the component () of the vector is non-zero.15
3.3. Closed-Form Result for the Minimal-Length Endogeneity Correlation () Overturning the Hypothesis Test Rejection in the One-Dimensional Case
In this section is obtained in closed form for the special—but not uncommon—case of a one-dimensional () sensitivity analysis, where the impact on the inference of interest is being examined with respect to possible endogeneity in a single one—the —of the k explanatory variables in the regression model. The explicit derivation given here is for a sensitivity analysis with respect to the rejection of the simple null hypothesis that , but this restriction is solely for expositional clarity: an extension of this result to the sensitivity analysis of a null hypothesis specifying a given linear restriction—or set of linear restrictions—on the components of is not difficult, and is indicated in the text below.
In the analysis of it is easy to characterize the two values of for which the null hypothesis is barely rejected at the 5% level: For these two values of the concomitant asymptotic bias induced in —i.e., —must barely suffice to make the magnitude of the relevant estimated t ratio equal its critical value, .
Thus, these two requisite values must each satisfy the equation
where and are the sample realizations of and from OLS estimation of Equation (3) and is the element of the inverse of , the (consistent) sample estimate of . Equation (7) generalizes in an obvious way to a null hypothesis which is a linear restriction on the components of ; this extension merely makes the notation more complicated; for a set of r linear restrictions, the test statistic is—in the usual way—squared and the requisite critical value is then the 0.050 fractile of the F(r, ) distribution.16
Equation (7) yields the two solution values,
Mathematically, there are two solutions to Equation (7) because of the absolute value function. Intuitively, there are two solutions because a larger value for increases the asymptotic bias in the jth component of at rate . Thus—supposing that this component of is (for example) positive—then sufficiently changing in one direction can reduce the value of just enough so that it remains positive and is now just barely significant at the 5% significance level; but changing sufficiently more in this direction will reduce the value of enough so that it becomes sufficiently negative as to again be barely significant at the 5% level.
These two values of lead to two implied values for the single non-zero (mth) component of the implied correlation vector (); is then the one of these two vectors with the smallest magnitude, which magnitude is then:
where the consistent estimate of the variance of defined (along with ) in Section 3.1 above.
3.4. Simulation-Based Check on Sample-Length Adequacy with Regard to Substituting for
The foregoing discussion has neglected the impact of the sampling errors in on the asymptotic distribution of , which was derived as Equation (4) in Section 2 above in terms of the population quantity . Substitution of for in the Equation (4) asymptotic variance expression is asymptotically inconsequential, but Kiviet (2016) correctly points out that this substitution into the expression for the asymptotic mean in Equation (4) has an impact on the distribution of which is not asymptotically negligible. Sampling errors in could hence, in principle, have a notable effect on the values calculated as described above.
So as to gauge the magnitude of these effects on this measure of inference robustness/fragility, our implementing software estimates a standard error for each calculated value, using bootstrap simulation based on the observed X matrix. The size of this estimated standard error for is in effect quantifying the degree to which the sample length (n) is sufficiently large as to support the kind of sensitivity analysis proposed here.17
This standard error calculation is a fairly straightforward application of the bootstrap, which has been amply described in an extensive literature elsewhere, but a few comments are warranted here.18
First, it is essential to simulate new X matrix data “row-wise"—that is choosing the ith row of the newly-simulated X matrix as the jth row of the original X data matrix, where j is chosen randomly from the integers in the interval [1, n]—so as to preserve any correlations between the k explanatory variables in the original data set.
Second, it is important to note that the ordinary (Efron) bootstrap is crucially assuming that the rows of the original X matrix are realizations of IID—which is to say, independently and identically distributed—vectors. The “identically distributed” part of this assumption is essentially already “baked in” to our sensitivity analysis (and into the usual results for stochastic regressions like Equation (1)), at least for the variances of the explanatory variables: otherwise the diagonal elements of are not constants for which the corresponding diagonal elements of could possibly provide consistent estimates. Where the observations in Equation (1) are actually in time-order, the “independently distributed” part of the IID assumption can be problematic: the bootstrap simulation framework is in that setting assuming that each explanatory variable is serially independent, which is frequently not the case with economic time-series data. In this case, however, one could (for really large samples) bootstrap block-wise; or one could readily estimate a k-dimensional VAR model for the rows of the X matrix and bootstrap-simulate out of the resulting k-vector residuals, which are at least (by construction) serially uncorrelated.
That said, it is easy enough in practice to use the bootstrap to simulate replications of X, of , and hence of . The standard deviation of these replicants of is not intended as a means to make precise statistical inferences as to the (population) value of , but it is adequate to meaningfully gauge the degree to which n is sufficiently large that it reasonable to use the values obtained using the original data set in this kind of sensitivity analysis.
The calculation of a single estimate (quantifying the sensitivity analysis of the rejection p-value a particular null hypothesis—even a complicated one—to possible endogeneity in a particular set of explanatory variables) is ordinarily not computationally burdensome. Repeating this calculation times can become time-consuming, however, unless the sensitivity analysis is one-dimensional—i.e., is with respect to possible endogeneity in a single explanatory variable—in which case the closed form results obtained in Section 3.3 above speed up the computations tremendously. For this reason, we envision this simulation-based standard error calculation as something one typically does only occasionally; e.g., at the outset of one’s sensitivity analysis work on a particular regression model, as a check on the adequacy of the sample length to this purpose.
3.5. Preliminary Remarks on the Interpretation of the Length of as Characterizing the Robustness/Fragility of the Inference
The vector is thus practical to calculate for any multiple regression model for which we suspect that one (or a number) of the explanatory variables might be endogenous to some degree. In the special case where there is a single such explanatory variable (), the discussion in Section 3.3—including the explicit result in Equation (9) for the special case where the null hypothesis of interest is a single linear restriction on the vector—yields a closed-form solution for . For , the search over M endogeneity covariance () vectors described in Section 3.2—so as to calculate as the closest point to the origin in the “No Longer Rejecting” set—is easily programmed and is still computationally inexpensive. Either way, it is computationally straightforward to calculate for any particular null hypothesis on the vector; its length () then objectively quantifies the sensitivity of the rejection p-value for this particular null hypothesis to possible endogeneity in these ℓ explanatory variables.
But how, precisely, is one to interpret the value of this estimated value for ? Clearly, if is close to zero—less than around 0.10, say—then only a fairly small amount of explanatory-variable endogeneity suffices to invalidate the original OLS-model rejection of this particular null hypothesis at the user-chosen significance level. One could characterize the statistical inference based on such a rejection as “fragile” with respect to possible endogeneity problems; and one might not want to place much confidence in this inference unless and until one is able to find credibly-valid instruments for the explanatory variables with regard to which inference is relatively fragile.19
In contrast, a large value of —greater than around 0.40, say—indicates that quite a large amount of explanatory-variable endogeneity is necessary in order to invalidate the original OLS-model rejection of this null hypothesis at the at the user-chosen significance level. One could characterize such an inference as “robust” with respect to possible endogeneity problems, and perhaps not worry overmuch about looking for valid instruments in this case.
Notably, inference with respect to one important and interesting null hypothesis might be fragile (or robust) with respect to possible endogeneity in one set of explanatory variables, whereas inference on another key null hypothesis might be differently fragile (or robust)—and with respect to possible endogeneity in a different set of explanatory variables. The sensitivity analysis results thus sensibly depend on the inferential question at issue.
But what about an intermediate estimated value of ? Such a result is indicative of an inference for which the issue of its sensitivity to possible endogeneity issues is still sensibly in doubt. Here the analysis again suggests that one should limit the degree of confidence placed in this null hypothesis rejection, unless and until one is able to find credibly-valid instruments for the explanatory variables which the sensitivity analysis indicates are problematic in terms of potential endogeneity issues. In this instance the sensitivity analysis has not clearly settled the fragility versus robustness issue, but at least it provides a quantification which is communicable to others—and which is objective in the sense that any analyst will obtain the same result. This situation is analogous to the ordinary hypothesis-testing predicament when a particular null hypothesis is rejected with a p-value of, say, 0.07: whether or not to reject the null hypothesis is not clearly resolved based on such a result, but one has at least objectively quantified the weight of the evidence against the null hypothesis.
3.6. Extension to “Parameter-Value-Centric” Sensitivity Analysis
As noted at the end of Section 1.2, in some settings the thrust of the analysis centers on the size of a particular component of rather than on the p-value at which some particular null hypothesis with regard to the components of can be rejected.
In such instances, the sensitivity analysis proposed here actually simplifies: in such a “parameter-value-centric” sensitivity analysis, one merely needs to display how the estimated confidence interval for this particular coefficient varies with , the posited implied vector of endogeneity correlations between the explanatory variables and the model error term.
This variation on the sensitivity analysis described in Section 3.1, Section 3.2, Section 3.3, Section 3.4 and Section 3.5 above is computationally much easier, since it is no longer necessary to choose the endogeneity covariance vector () so as to minimize the length of . Instead—for a selected set of vectors—one merely exploits the sampling distribution derived in Section 2 to both estimate a confidence interval for this particular component of and (per Section 3.1) to convert this value for into the concomitant endogeneity correlation vector, .20 The “parameter-value-centric” sensitivity analysis then simply consists of either plotting or tabulating these estimated confidence intervals against the corresponding values calculated for .
Such a plot is an easily-displayed two-dimensional figure for a one-dimensional sensitivity analysis—i.e., for , where only a single explanatory variable is considered to be possibly-endogenous. For a two-dimensional sensitivity analysis—where and two explanatory variables are taken to be possibly-endogenous—this plot requires the display of a three-dimensional figure; this is feasible, but it is more troublesome to plot and interpret. A graphical display of this kind of sensitivity analysis is infeasible for larger values of ℓ, but one could still tabulate the results.21
The most intriguing aspect of this “parameter-value-centric” approach will arise in the sensitivity analysis—with respect to possible endogeneity issues—of “big data” models, using huge data sets. The p-values for rejecting most null hypotheses in these models are so small as to be uninformative, whereas the confidence values for the key parameter estimates in these models are frequently especially informative because their lengths shrink to become tiny. Thus, the “parameter-value-centric” sensitivity analysis is in this case essentially plotting how the estimated parameters vary with the posited amount of endogeneity correlation. This kind of analysis is potentially quite useful, as it is well-known that there is no guarantee whatever that the explanatory variables in these models are particularly immune to endogeneity problems.
We provide several examples of this kind of sensitivity analysis at the end of the next section, where the applicability and usefulness both kinds of sensitivity analysis are illustrated using a well-known empirical model from the literature on determinants of economic growth. In particular, the “parameter-value-centric” sensitivity analysis results for this model are artificially extended to a huge data set at the end of Section 4 by the simple artifice of noting that the confidence-intervals plots displayed in the “parameter-value-centric” sensitivity analysis shrink in length, essentially to single points, as the sample length becomes extremely large. However, more interesting and consequential examples of the application of “parameter-value-centric” sensitivity analysis to “big data” models must await the extension of the OLS sensitivity analysis proposed here to the nonlinear estimation procedures typically used in such work, as in the Rasmussen et al. (2011) and Arellano et al. (2018) studies cited at the very end of Section 1.2.
4. Revised Sensitivity Analysis Results for the Mankiw, Romer, and Weil Study
Ashley and Parmeter (2015a) provided sensitivity analysis results with regard to statistical inference on the two main hypotheses in the classic Mankiw, Romer, and Weil (Mankiw et al. 1992) study on economic growth: first, that human capital accumulation does impact growth, and second that their main regression model coefficients sum to zero.22 Here these results are updated using the corrected sampling distribution obtained in Section 1 in Equation (4).
For reasons of limited space the reader is referred to Ashley and Parmeter (2015a)—or Mankiw et al. (1992)—for a more complete description of the MRW model. Here we will merely note that the dependent variable in the MRW regression model is real per capita GDP for a particular country, and that the three MRW explanatory variables are the logarithms of the number of years of schooling (",” their measure of human capital accumulation); the real investment rate per unit of output (""); and a catch-all variable (""), capturing population growth, income growth, and depreciation).
Table 1 displays our revised sensitivity analysis results for both of the key MRW hypothesis tests considered in (Tables 1 and 2 in Ashley and Parmeter 2015a). The main changes here—in addition to using the corrected Equation (4) sampling distribution result—are that we now additionally include sensitivity analysis results allowing for possible exogeneity flaws in all three explanatory variables simultaneously, and that we now provide bootstrap-simulated standard error estimates which quantify the uncertainty in each of the values quoted due to sampling variation in .23

Table 1.
Sensitivity analysis results on and from Mankiw, Romer, and Weil (Mankiw et al. 1992). The “” row gives the percentage of bootstrap simulations yielding equal to zero for this null hypothesis.
In Table 1 the analytic results—per Equations (7) and (8)—are used for the three columns in which a single explanatory variable is considered; the results simultaneously considering two or three explanatory variables were obtained using 10,000 Monte Carlo draws. The standard error estimates are in all cases based on 1,000 bootstrap simulations of . Table 1 quotes only the values and not the full ℓ-dimensional vectors because these vectors did not clearly add to the interpretability of the results.24
We first consider the results for both null hypotheses, where the inferential sensitivity is examined with respect to possible endogeneity in one explanatory variable at a time. For these results we find that the MRW inference result with respect to their rejection of (at the 5% level) appears to be quite robust with respect to reasonably likely amounts of endogeneity in and in , but not so clearly robust with respect to possible endogeneity in once one takes into account the uncertainty in the estimate due to likely sampling variation in .
In contrast, the MRW inference result with respect to their concomitant failure to reject at the 5% level appears to be fairly fragile with respect to possible endogeneity in their explanatory variable. In particular, our estimate is just for this case. This estimate is quite small—and is inherently non-negative—so one might naturally worry that its sampling distribution (due to sampling variation in ) might be so non-normal that an estimated standard error could be misleading in this instance. We note, however, that is zero—because this MRW null hypothesis is actually rejected at the 5% level for any posited amount of endogeneity in —fully in of the bootstrapped simulations. We consequently conclude that this estimate is indeed so small that there is quite a decent chance of very modest amounts of endogeneity in overturning the MRW inferential conclusion with regard to this null hypothesis.
With an estimate of (and turning up zero in of the bootstrapped simulations) there is also considerable evidence here that the MRW failure to reject is fragile with respect to possible endogeneity in their explanatory variable; but this result is a bit less compelling. The sensitivity analysis result for this null hypothesis with respect to possible endogeneity in the variate is even less clear: the estimate (of 0.72) is large—indicating robustness to possible endogeneity, but this estimate comes with quite a substantial standard error estimate, indicating that this robustness result is not itself very stable across likely sampling variation in . These two results must be classified as “mixed.”
The and results for these two null hypotheses are not as easy to interpret for this MRW data set: these results appear to be simply reflecting a mixture of the sensitivity results for the corresponding cases, where each of the three explanatory variables is considered individually. And these multidimensional sensitivity results are also computationally a good deal more burdensome to obtain, because they require Monte Carlo or grid searches, rather than following directly from the analytic results in Equations (8) and (9). While it is in principle possible that a consideration of inferential sensitivity with respect to possible endogeneity in several explanatory variables at once might yield fragility-versus-robustness conclusions at variance with those obtained from the corresponding one-dimensional sensitivity analyses for some other data set, we think this quite unlikely for the application of this kind of sensitivity analysis to linear regression models. Consequently, our tentative conclusion is that the one-dimensional () sensitivity analyses are of the greatest practical value here.
In summary, then, this application of the “hypothesis-testing-centric” sensitivity analysis to the MRW study provides a rather comprehensive look at what this aspect of our sensitivity analysis can provide:
- First of all, we did not need to make any additional model assumptions beyond those already present in the MRW study. In particular, our sensitivity analysis does not require the specification of any information with regard to the higher moments of any of the random variables—as in Kiviet (2016, 2018)—although it does restrict attention to linear endogeneity and brings in the issue of sampling variation in .
- Second, we were able to examine the robustness/fragility with respect to possible explanatory variable endogeneity for both of the key MRW inferences, one of which was the rejection of a simple zero-restriction and the other of which was the failure to reject a more complicated linear restriction.25
- Third, we found clear evidence of both robustness and fragility in the MRW inferences, depending on the null hypothesis and on the explanatory variables considered.
- Fourth, we did not—in this data set—find that the multi-dimensional sensitivity analyses (with respect to two or three of the explanatory variables at a time) provided any additional insights not already clearly present in the one-dimensional sensitivity analysis results, the latter of which are computationally very inexpensive because they can use our analytic results.
- And fifth, we determined that the bootstrap-simulated standard errors in the values (arising due to sampling variation in the estimated explanatory-variable variances) are already manageable—albeit not negligible—at the MRW sample length, of . Thus, doing the bootstrap simulations is pretty clearly necessary with a sample of this length; but it also sufficient, in that it suffices to show that this sample is sufficiently long as to yield useful sensitivity analysis results.26
Finally, we apply the “parameter-value-centric” sensitivity analysis described in Section 3.6 to the MRW study. Their paper is fundamentally about the impact of human capital—quantified by the years of schooling variable, “”—on output, so testing the null hypothesis was a crucial concern for them in terms of economic theory. Perhaps more relevant for economic policy-making, however, might be the size of their estimated coefficient on , . Their estimated model yields a confidence interval of [, ] for , but this estimated confidence interval contains in repeated samples with probability only if their model assumptions are all valid. These notably include the assumptions that their most important explanatory variables— and —are both exogenous.
As described in Section 3.6, we calculated how this OLS-estimated confidence interval for varies with possible endogeneity in each of and , and present the results of these one-dimensional “parameter-value-centric” sensitivity analyses below as Figure 1 and Figure 2. Figure 1 graphs how the estimated confidence interval for varies with the concomitant correlation between the model errors and , both of which are jointly generated over a selection of 1000 values for the covariance between the model errors and the variable. Figure 2 analogously graphs how the estimated confidence interval for varies with the concomitant correlation between the model errors and the variable. This correlation, plotted on the horizontal axis, is in each figure the single non-zero component of the endogeneity correlation vector, .
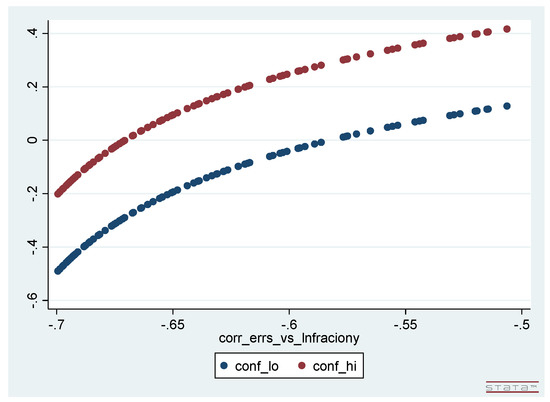
Figure 1.
Estimated confidence interval for graphed against posited correlation between the model errors and .
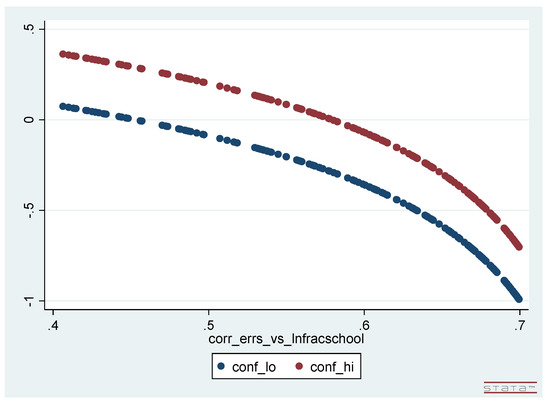
Figure 2.
Estimated confidence interval for graphed against posited correlation between the model errors and .
We note that:
- We could just as easily have used 500 or 5000 endogeneity-covariance values: because (in contrast to the computation of ) these calculations do not involve a numerical minimization, the production of these figures requires only a few seconds of computer time regardless.
- These plots of the upper and lower limits of the confidence intervals are nonlinear—although not markedly so—and the (vertical) length of each interval does depend (somewhat) on the degree of endogeneity-correlation.
- For a two-dimensional, “parameter-value-centric” sensitivity analysis—analogous to the “ & ” column in Table 1 listing our “hypothesis-testing-centric” sensitivity analysis results—the result would be a single three-dimensional plot, displaying (as its height above the horizontal plane) how the confidence interval for varies with the two components of the endogeneity-correlation vector which are now non-zero. In the present (linear multiple regression model) setting, this three-dimensional plot is graphically and computationally feasible, but not clearly more informative than Figure 1 and Figure 2 from the pair of one-dimensional analyses. And for a three-dimensional “parameter-value-centric” sensitivity analysis—e.g., analogous to the “All Three” column in Table 1—it would still be easily feasible to compute and tabulate how the confidence interval for varies with the three components of the endogeneity-correlation vector which are now non-zero; but the resulting four dimensional plot is neither graphically renderable nor humanly visualizable, and a tabulation of these confidence intervals (while feasible to compute and print out) is not readily interpretable.
- One can easily read off from each of these two figures the result of the corresponding one-dimensional, “hypothesis-testing-centric” sensitivity analysis for the null hypothesis —i.e., the value of : One simply observes the magnitude of the endogeneity-correlation value for which the graph of the upper confidence interval limit crosses the horizontal () axis and the magnitude of the endogeneity-correlation value for which the graph of the lower confidence interval limit crosses this axis: is the smaller of these two magnitudes.27
- Finally, if the MRW sample were expanded to be huge—e.g., by repeating the 98 observations on each variable an exceedingly large number times—then the upper and lower limits of the confidence intervals plotted in Figure 1 and Figure 2 would collapse into one another. The plotted confidence intervals in these figures would then essentially become line plots, and each figure would then simply be a plot of the “” component of versus the single non-zero component of the endogeneity correlation vector, .28 Such an expansion is, of course, only notional for an actual data set of modest length, but—in contrast to hypothesis testing in general (and hence to “hypothesis-testing-centric” sensitivity analysis in particular—this feature of the “parameter-value-centric” sensitivity analysis results illustrates how useful this kind of analysis would remain in the context of modeling the huge data sets recently becoming available, where the estimational/inferential distortions arising due to unaddressed endogeneity issues do not diminish as the sample length expands.
5. Implementation Considerations
The sensitivity analysis procedure proposed here is very easy for a user to start up with and utilize, making the “trouble” involved with adopting it, as a routine screen for quantifying the impact of possible endogeneity problems, only a small barrier to its adoption and use. Importantly, the analysis requires no additional assumptions with regard to the regression model at issue, beyond the ones which would ordinarily need to be made in any OLS multiple regression analysis with stochastic regressors. In particular, this sensitivity analysis does not require the user to make any additional assumptions with regard to the higher moments of the joint distribution of the explanatory variables and the model errors.
For most empirical economists the computational implementation of this sensitivity analysis is very straightforward: since and scripts implementing the algorithms are available, these codes can be simply patched into the script that the analyst is likely already using for estimating their model. All that the user needs to provide, then, is a choice as to which of the explanatory variables which are under consideration in the sensitivity analysis as being possibly-endogenous, and a specification of the particular null hypothesis (or of the particular parameter confidence interval) whose robustness or fragility with respect to this possible endogeneity is of interest.29
Our implementing routines can readily handle the “hypothesis-testing-centric” sensitivity analysis with respect to any sort of null hypothesis (simple or compound, linear or nonlinear) for which and can compute a rejection p-value, using whatever kind of standard error estimates (OLS/White-Eicker/HAC) are already being used. For this kind of sensitivity analysis these routines calculate , where is defined in Section 1.3 above to be the minimum-length vector of correlations—between the set of explanatory variables under consideration and the (unobserved) model errors—which suffices to “overturn” the observed rejection (or non-rejection) of the chosen null hypothesis. These implementing scripts can also, optionally, perform the set of bootstrap simulations described in Section 3.4 above, so as to additionally estimate standard errors for the estimates—reflecting the impact of substituting the sample variance-covariance matrix of the explanatory variables () for its population value () in the Equation (4), as described in Section 3.4.)30Alternatively, where the “parameter-value-centric” sensitivity analysis (with respect to a confidence interval for a particular model coefficient) is needed, the implementing software tabulates this estimated confidence interval versus a selection of values, for use in making a plot.
6. Concluding Remarks
Because the “structural” model errors in a multiple regression model—i.e., in Equation (1)—are unobservable, in practice one cannot know (and cannot, even in principle, test) whether or not the explanatory variables in a multiple regression model are or are not exogenous, without making additional (and untestable) assumptions. In contrast, we have shown here that it actually possible to quantitatively investigate whether or not the rejection p-value (with regard to any specific null hypothesis that one is particularly interested in) either is or is not to likely amounts of linear endogeneity in the explanatory variables.
Our approach does restrict the sensitivity analysis to possible endogeneity which is solely linear in form: this restriction to “linear endogeneity” dramatically simplifies the analysis in Section 2 and Section 3. Linear endogeneity in an explanatory variable means that it is related to the unobserved model error, but solely in a linear fashion. The correlations of the explanatory variables with the model error completely capture the endogeneity relationship if and only if the endogeneity is linear; thus—where the endogeneity contemplated is in any case going to be expressed in terms of such correlations—little is lost in restricting attention to linear endogeneity. Moreover—as noted in Section 2 above—all of the usually-discussed sources of endogeneity are, in fact, linear in this sense.31 And the meaning of this restriction is so clearly understandable that the user is in a position to judge its restrictiveness for themself. For our part, we note that it hardly seems likely in practice that endogeneity at a level that is of practical importance will arise which does not engender a notable degree of correlation (i.e., linear relationship) between the explanatory variables and the model error term, so it seems to us quite unlikely that a sensitivity analysis limited to solely-linear possible endogeneity will to any substantial degree underestimate the fragility of one’s OLS inferences with respect to likely amounts of endogeneity.
This paper proposes a flexible procedure for engaging in just such a sensitivity analysis—and one which is so easily implemented in actual practice that it can reasonably serve as a routine “screen” for possible endogeneity problems in linear multiple regression estimation/inference settings.32 This screen produces an objective measure—the calculated “” vector and its Euclidean length “”—which quantifies the sensitivity of the rejection of a chosen, particular null hypothesis (one that presumably is of salient economic interest) to possible endogeneity in the vector of k explanatory variables in the linear multiple regression model of Equation (1). The relative sizes of the components of this vector yield an indication as to which explanatory variables are relatively problematic in terms of endogeneity-related distortion of this particular inference; and this length yields an overall indication as to how “robust” versus “fragile” this particular inference is with respect to possible endogeneity in the explanatory variables considered in the sensitivity analysis.
These quantitative results— and —are completely objective, in the sense that any analyst using the same model and data will replicate precisely these numerical results. And their interpretation, so as to characterize a particular hypothesis test rejection as “robust” versus “fragile,” can in some cases be quite clear-cut. In other cases, these objective results can call out for subjective decision making, as discussed in Section 3.5. But these sensitivity results at the very least provide an objective indication as to the situation that one is in. This inferential predicament is analogous—albeit, the reader is cautioned, not identical—to the commonly-encountered situation where the p-value at which a particular null hypothesis can be rejected is on the margin of the usual, culturally-mediated rejection criterion: This p-value objectively summarizes the weight of the evidence again the null hypothesis, but our decision as to whether or not to reject this null hypothesis is clearly to some degree subjective.
Notably, tests with regard to some null hypothesis restriction (or set of restrictions) on the model parameters may be quite robust, whereas tests of other restrictions may be quite fragile, or fragile with respect to endogeneity in a different explanatory variable. This, too, is useful information which the sensitivity analysis proposed here can provide.
If one or more of the inferences one most cares about are quite robust to likely amounts of correlation between the explanatory variables and the model errors, then one can defend one’s use of OLS inference without further ado. If, in contrast, the sensitivity analysis shows that some of one’s key inferences are fragile with respect to minor amounts of correlation between the explanatory variables and the model errors, then a serious consideration of more sophisticated estimation approaches—such as those proposed in Caner and Morrill (2013), Kraay (2012), Lewbel (2012), or Kiviet (2018)—is both warranted and motivated. Where the sensitivity analysis is indicative of an intermediate level of robustness/fragility in some of the more economically important inferences, then one at least—as noted above—has an objective indication as to the predicament that one is in.
Finally, we note—per the discussion in Section 3.6—that in some settings the analytic interest is focused on the size of a particular structural coefficient, rather than on the p-value at which some particular null hypothesis (with regard to restrictions on the components of the full vector of structural coefficients) can be rejected. In such instances what we have here called “parameter-value-centric” sensitivity analysis is especially useful.
This “parameter-value-centric” sensitivity analysis is a simple variation on the “hypothesis-testing-centric” sensitivity analysis described in Section 3.1, Section 3.2, Section 3.3, Section 3.4 and Section 3.5 above. In Section 3.6 the sampling distribution for the OLS-estimated structural parameter vector derived in Section 2 (for a specified degree of endogeneity-covariance) is used to both obtain a confidence interval for this particular structural coefficient and also to obtain a consistent estimator for the entire vector of structural coefficients. This consistent parameter estimator makes the structural model errors asymptotically available, allowing the specified endogeneity-covariance vector to be converted into the more-interpretable implied endogeneity-correlation vector, denoted above.
Our “parameter-value-centric” sensitivity analysis then simply consists of plotting this estimated confidence interval against . Such plots are easy to make and simple to interpret, so long as only one or two of the explanatory variables are allowed to be possibly endogenous; the empirical example given here (in Section 4) provides several illustrative examples of such plots. These plots are two-dimensional where endogeneity is allowed for in only one explanatory variable; they are three-dimensional where two of the explanatory variables are possibly-endogenous. In the unusual instance where a still higher-dimensional sensitivity analysis seems warranted, such confidence-interval versus plots are impossible to graphically render and visualize, but such results could be tabulated.33
Whereas hypothesis test rejection p-values become increasingly uninformative as the sample length becomes large, the set of confidence intervals produced by our “parameter-value-centric” sensitivity analysis becomes only more informative as the sample length increases.34 We consequently conjecture that this “parameter-value-centric” sensitivity analysis can potentially be of great value in the analysis of the impact of neglected-endogeneity in the increasingly-common empirical models employing huge data sets—e.g., Rasmussen et al. (2011) and Arellano et al. (2018)—once our methodology is extended to the nonlinear estimation methods most commonly used in such settings.
Author Contributions
R.A.A. and C.F.P. share equally in all aspects of the paper: Conceptualization; methodology; software; validation; formal analysis; investigation; resources; data curation; writing–original draft preparation; writing–review and editing; visualization; project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank several anonymous referees for their constructive criticism; and we are also indebted to Kiviet for pointing out (Kiviet 2016) several deficiencies in Ashley and Parmeter (2015a). In response to his critique, we herein provide a substantively fresh approach to this topic. Moreover, because of his effort, we were able to not only correct our distributional result, but also obtain a deeper and more intuitive analysis; the new analytic results obtained here are an unanticipated bonus.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arellano, Manuel, Richard Blundell, and Stephane Bonhomme. 2018. Nonlinear Persistence and Partial Insurance: Income and Consumption Dynamics in the PSID. AEA Papers and Proceedings 108: 281–86. [Google Scholar] [CrossRef]
- Ashley, Richard A. 2009. Assessing the Credibility of Instrumental Variables with Imperfect Instruments via Sensitivity Analysis. Journal of Applied Econometrics 24: 325–37. [Google Scholar] [CrossRef]
- Ashley, Richard A., and Christopher F. Parmeter. 2015a. When is it Justifiable to Ignore Explanatory Variable Endogeneity in a Regression Model? Economics Letters 137: 70–74. [Google Scholar] [CrossRef][Green Version]
- Ashley, Richard A., and Christopher F. Parmeter. 2015b. Sensitivity Analysis for Inference in 2SLS Estimation with Possibly-Flawed Instruments. Empirical Economics 49: 1153–71. [Google Scholar] [CrossRef]
- Ashley, Richard A., and Christopher F. Parmeter. 2019. Sensitivity Analysis of OLS Multiple Regression Inference with Respect to Possible Linear Endogeneity in the the Explanatory Variables. Working Paper. Available online: https://vtechworks.lib.vt.edu/handle/10919/91478 (accessed on 6 October 2019).
- Caner, Mehmet, and Melinda Sandler Morrill. 2013. Violation of Exogeneity: A Joint Test of Structural Parameters and Correlation. Available online: https://4935fa4b-a-bf11e6be-s-sites.googlegroups.com/a/ncsu.edu/msmorrill/files/CanerMorrill_NT (accessed on 4 March 2020).
- Davidson, Russell, and James G. MacKinnon. 1993. Estimation and Inference in Econometrics. New York: Oxford University Press. [Google Scholar]
- Efron, Bradley. 1979. Bootstrapping Methods: Another Look at the Jackknife. Annals of Statistics 7: 1–26. [Google Scholar] [CrossRef]
- Friedman, Milton. 1953. Essays in Positive Economics. Chicago: University of Chicago Press. [Google Scholar]
- Johnston, Jack. 1992. Econometric Methods. New York: McGraw-Hill. [Google Scholar]
- Kiviet, Jan F. 2013. Identification and Inference in a Simultaneous Equation Under Alternative Information Sets and Sampling Schemes. The Econometrics Journal 16: S24–59. [Google Scholar] [CrossRef]
- Kiviet, Jan F. 2016. When is it Really Justifiable to Ignore Explanatory Variable Endogeneity in a Regression Model? Economics Letters 145: 192–95. [Google Scholar] [CrossRef][Green Version]
- Kiviet, Jan F. 2018. Testing the Impossible: Identifying Exclusion Restrictions. Journal of Econometrics. forthcoming. [Google Scholar]
- Kiviet, Jan F., and Jerzy Niemczyk. 2007. The Asymptotic and Finite Sample Distributions of OLS and Simple IV in Simultaneous Equations. Computational Statistics & Data Analysis 51: 3296–318. [Google Scholar]
- Kiviet, Jan F., and Jerzy Niemczyk. 2012. Comparing the Asymptotic and Empirical (Un)conditional Distributions of OLS and IV in a Linear Static Simultaneous Equation. Computational Statistics & Data Analysis 56: 3567–86. [Google Scholar]
- Kraay, Aart. 2012. Instrumental Variables Regression with Uncertain Exclusion Restrictions: A Bayesian Approach. Journal of Applied Econometrics 27: 108–28. [Google Scholar] [CrossRef]
- Leamer, Edward E. 1983. Let’s Take the Con Out of Econometrics. American Economic Reivew 73: 31–43. [Google Scholar]
- Lewbel, Arthur. 2012. Using Heteroscedasticity to Identify and Estimate Mismeasured and Endogenous Regressor Models. Journal of Business and Economic Statistics 30: 67–80. [Google Scholar] [CrossRef]
- Mankiw, N. Gergory, David Romer, and David N. Weil. 1992. A Contribution to the Empirics of Economic Growth. The Quarterly Journal of Economics 107: 407–37. [Google Scholar] [CrossRef]
- McCloskey, Deirdre N., and Stephen T. Ziliak. 1996. The Standard Error of Regressions. Journal of Economic Literature 34: 97–114. [Google Scholar]
- Rasmussen, Lars Hvilsted, Torben Bjerregaard Larsen, Karen Margrete Due, Anne Tønneland, Kim Overvad, and Gergory Y. H. Lip. 2011. Impact of Vascular Disease in Predicting Stroke and Death in Patients with Atrial Fibrillation: The Danish Diet, Cancer and Health Cohort Study. Journal of Thrombosis and Homeostasis 9: 1301–7. [Google Scholar] [CrossRef] [PubMed]
| 1. | See Leamer (1983) for an early recognition of this corollary. |
| 2. | Our results are easily-computable (but not analytic) for the general (multi-dimensional) sensitivity analysis proposed here—where possible (linear) endogeneity in any number of explanatory variables is under consideration, and where what is at issue is either a confidence interval for a single parameter or the null hypothesis rejection p-value for a test of multiple linear (and/or non-linear) restrictions: in that general setting our and implementations then require a bit more in the way of numerical computation. These issues are addressed in Section 3 and Section 5 below. |
| 3. | These simulations do require a non-negligible computational effort, but this calculation needs only to be done once in any particular setting, and is already coded up in the implementation of the algorithm. One might argue that a more wide-ranging initial simulation effort (subsuming this particular calculation) has value in any case, as a check on the degree to which the sample is more broadly sufficiently large for the use of the usual asymptotic inference machinery. |
| 4. | The underlying sensitivity analysis itself extends quite easily to a consideration of more than two possibly-endogeneous explanatory variables; however, the resulting still-higher-dimensional confidence interval plots of this nature would be outright infeasible to visualize. On the other hand, one could in principle resort to tabulating the confidence interval results from such multi-dimensional “parameter-value-centric” sensitivity analyses; Kiviet (2016) has already suggested such a tabulation as a sensitivity analysis display mechanism. |
| 5. | Examples of such work include Rasmussen et al. (2011) on stroke mortality in Danish patients and Arellano et al. (2018) on microeconometric consumption expenditures modeling using the U.S. PSID and the extensive Norwegian population-register administrative data set. |
| 6. | Multiplication of Equation (2) by and taking expectations yields . |
| 7. | E.g., from (Johnston 1992, sct. 9-2), or from many earlier sources. |
| 8. | The asymptotic variance of given by Equation (4) would no longer be valid where var(), but one could in that case use White-Eicker or Newey-West standard error estimates. |
| 9. | Repeatedly simulating data sets on (Y, X, ) in this way would lead to a simulated distribution for (X, ) which could not be jointly Gaussian, and it would lead to a collection of simulated values whose variance would in fact differ as one varied the value of used in the simulation generating mechanism, in the manner predicted by the sampling distribution result given in Kiviet (2016). |
| 10. | Many econometrics programs—e.g., —make it equally easy to calculate analogous rejection p-values for null hypotheses which consist of a specified set of nonlinear restriction on the components of ; so the -based implementation of the sensitivity analysis described here readily extends to tests of nonlinear null hypotheses. |
| 11. | As shown in Section 2, this variance exceeds , the fitting-error variance in the model as actually estimated using OLS, because the inconsistency in the OLS parameter estimate strips out of the estimated model errors the portions of which are—due to the assumed endogeneity—correlated with the columns of X. Note that also follows mathematically from Equation (6), because is positive definite. |
| 12. | The value of M is limited to more like 1000 to 10,000 when (as described in Section 3.4) the entire sensitivity analysis is simulated multiple times so as to quantify the dispersion in generated by the likely sampling errors in . |
| 13. | The resulting value of is itself insensitive to the form of the distribution used to generate the vectors used in such a Monte-Carlo search, so long as this distribution has sufficient dispersion. A multivariate Gaussian distribution was used in Ashley and Parmeter (2015b), but the reader is cautioned that this is a numerical device only: Gaussianity is not being assumed thereby for any random variable in the econometric analysis. |
| 14. | For simplicity of exposition this passage is written for the case where the null hypothesis is rejected in the original OLS model, so that vectors yielding p-values exceeding 0.05 are overturning this observed rejection. Where the original-model inference is instead a failure to reject the null hypothesis, , , and the concomitant rejection p-value are instead written out to the spreadsheet file only when this p-value is less than 0.05. In this case one would instead denote this collection of vectors as the “No Longer Not Rejecting” set; the sensitivity analysis is otherwise the same. |
| 15. | Illumination aside, the substantial computational efficiency improvement afforded by this essentially analytic calculation is quite useful when—in Section 3.4 below—a bootstrap-based simulation is introduced so as to obtain an estimated standard error for , quantifying the dispersion induced in it when one allows for the likely sampling errors in . |
| 16. | |
| 17. | We note that, where n is not adequate to the estimation of in a particular regression setting, then skepticism is also warranted in this setting as to whether the size of n is more broadly inadequate for asymptotic parameter inference work—i.e., estimation of confidence intervals and/or hypothesis test rejection p-values—even aside from concerns with regard to explanatory variable endogeneity. |
| 18. | (Davidson and MacKinnon 1993, pp. 764–65)) provides a brief description of the mechanics of the usual bootstrap and a list of references to this literature, including (of course) Efron (1979). |
| 19. | Perfectly exogenous instruments are generally unavailable also, so it is useful to note again that Ashley and Parmeter (2015b) provides an analogous sensitivity analysis procedure allowing one to quantify the robustness (or fragility) of IV-based inference rejection p-values to likely flaws in the instruments used. |
| 20. | A straightforward rearrangement of Equation (7) yields the confidence interval for the jth component of , where endogeneity is considered possible in the mth explanatory variable and the value of the single non-zero component in the endogeneity covariance vector is . |
| 21. | Such a tabulation was suggested in Kiviet (2016) as a way to display the kind of sensitivity analysis results proposed in Ashley and Parmeter (2015a); his sampling distribution for , as highlighted prior, requires knowledge of the third and fourth moments of the joint distribution of the explanatory variables and the model errors, however. |
| 22. | (Mankiw et al. 1992, p. 421) explicitly indicates that this sum is to equal zero under the null hypothesis: the indication to the contrary in Ashley and Parmeter (2015a) was only a typographical error. |
| 23. | We note that, because of the way his approach frames and tabulates the results, Kiviet’s procedure cannot address scenarios in which either two or more explanatory variables are simultaneously considered to be possibly endogenous. |
| 24. | The full vector is of much greater interest in the analogous sensitivity analysis with respect to the validity of the instruments in IV estimation/inference provided in Ashley and Parmeter (2015b). In that context, the relative fragility of the instruments is very much to the point, as one might well want to drop an instrument which leads to inferential fragility. |
| 25. | The joint null hypothesis that both of these linear restrictions hold could have been examined here also (either using the Monte Carlo algorithm or solving the quadratic polynomial equation which would result from the analog of Equation (7) in that instance), had that been deemed worthwhile in this instance. |
| 26. | These standard error estimates would be smaller—and their estimation less necessary—in substantially larger samples. In substantially smaller samples, however, these bootstrap-simulated standard errors could in principle be so large as to make the sensitivity analysis noticeably less useful; it is consequently valuable that this addendum to the sensitivity analysis allows one to easily check for this. We envision a practitioner routinely obtaining these bootstrap-simulated standard errors for the values. However—because of its computational cost—we see these calculations being done only once or twice: at the outset of the analysis for any particular model and data set, and perhaps again at the very end. |
| 27. | These two crossings correspond to the two solutions for in Equation (8) in Section 3.3. |
| 28. | As derived in Section 3.1 , the consistent estimator of , given the endogeneity covariance vector, . |
| 29. | For completeness, we note that the user also needs to provide a value for M which is sufficiently large that the routine can numerically find the shortest endogeneity-correlation vector reaching the “No Longer Rejecting” set with adequate accuracy and, if needed, the number of bootstrap simulations to be used in estimating standard errors for the estimates. |
| 30. | Three versions of the software are available. One version implements the analytic result derived in Section 3.3 for the value of minimizing the length of ; this version is written for the special case of a null hypothesis which is a single linear restriction and a single possibly-endogenous explanatory variable, but could be fairly easily extended to the testing of more complicated null hypotheses. A second version already allows for the analysis of any kind of null hypothesis—even compound or nonlinear—but still restricts the dimensionality of the sensitivity analysis to possible endogeneity in a single explanatory variable; this script requires a line-search over putative values of —here scalar-valued—but is still very fast. A third version extends the sensitivity analysis to the simultaneous consideration of possible endogoeneity in multiple explanatory variables; this version is a bit more computationally demanding, as it implements either a multi-dimensional grid search or a Monte-Carlo minimization over a range of vectors. |
| 31. | The joint determination of the dependent variable and one or more of the explanatory variables in a set of nonlinear simultaneous equations would yield nonlinear endogeneity, but this is not the kind of simultaneity most usually discussed. |
| 32. | In particular, our procedure readily extends to linear regression models with autocorrelated and/or heteroscedastic errors, and to fixed-effects panel data models. |
| 33. | This kind of tabulation of our sensitivity analysis results was first suggested in Kiviet (2016). |
| 34. | We also note that the “parameter-value-centric” sensitivity analysis eliminates the specification (necessary in the “hypothesis-testing-centric” sensitivity analysis) of any particular value for the significance level. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).