1. Introduction
The notion of ordered fuzzy number (
OFN) is introduced by Kosiński (
Kosiński and Słysz 1993;
Kosiński et al. 2002,
2003) as an extension of the concept of fuzzy number (FN), which is widely interpreted as an imprecise approximation of a real number. They intuitively determine
OFN as FN equipped with information about the location of the approximated number. This additional information is given as orientation of
OFN. For this reason, we can interpret
OFN as an imprecise approximation of a real number which may change in the direction determined by orientation. The monograph (
Prokopowicz et al. 2017) is a competent source of information about the contemporary state of knowledge on
OFN defined by Kosiński. On the other hand,
Kosiński (
2006) has shown that there exist improper
OFNs which cannot be represented by a pair of FNs and its orientation. Then, we cannot to apply any knowledge about fuzzy sets to solve practical problems described by improper
OFN. Therefore, any considerations which use improper
OFN may be not fruitful. For formal reasons, Kosiński’s theory was revised (
Piasecki 2018) in such a way that the revised
OFN definition fully corresponds to the intuitive Kosiński’s definition of
OFN. In this paper, we recall
OFN defined by Kosiński as “Kosiński’s number” which is in line with suggestions given by other researchers (
Prokopowicz 2016;
Prokopowicz and Pedrycz 2015). Moreover, we propose the
OFNs defined in a revised way to be called oriented fuzzy numbers. This proposal has been thoroughly justified in
Piasecki (
2019). In this way, in the concept of
OFNs, we distinguished two of its types: Kosiński’s numbers and oriented fuzzy numbers.
A Japanese candlestick (JC) is a style of financial chart used to describe variability of financial assets’ exchange quotations. Candlestick charts were developed in the 18th century by a Japanese rice trader, Munehisa Homma (
Morris 2006). The JC charting techniques were introduced to the Western world by
Nison (
1991). Among other things, the market quotation changes are described in this way: that any White Candle describes a rise in quotations and any Black Candle describes a fall in quotations. According to the traditional convention, any classical JC is represented by a four-element set of its real numbers: open price, close price, low price, and high price. Some applications of JCs are presented, for example in (
Detollenaere and Mazza 2014;
Fock et al. 2005;
Jasemi et al. 2011;
Marshall et al. 2006;
Kamo and Dagli 2009;
Tsung-Hsun et al. 2012,
2015).
Any original JC charting technique is a graphic tool for recording quotations volatility. Any JC is a very convenient tool for synthetic recording of high-frequency time series of financial data. If we use JCs for the analysis of high-frequency financial data, then then we need their linguistic or numerical representation.
Lee et al. (
2006) proposed to describe some JC attributes by linguistic variables evaluated by linguistic labels which have a meaning depending on the applied pragmatics of the natural language. By its very nature of things, each such description is imprecise information. For this reason,
Zadeh (
1975a,
1975b,
1975c) proposed to describe each linguistic variable by its values defined as a fuzzy subset in the predefined space. Then, these linguistic variables may be transformed with the use of fuzzy set theory.
Lee et al. (
2006) assessed JC attributes by linguistic labels represented by trapezoidal fuzzy numbers. In an analogous way, JCs are described in (
Kamo and Dagli 2009;
Naranjo et al. 2018;
Naranjo and Santos 2019). After (
Herrera and Herrera-Viedma 2000), we can say that an application of imprecise linguistic assessments for decision analysis is very beneficial because it introduces a more flexible framework which allows us to represent the information in a more direct and adequate way when we are unable to express it precisely. Then, all the authors mentioned in this paragraph use linguistic labels representing JC as an input signal for the different systems supporting financial decision-making. The output signals received in this way are very useful.
On the other hand, linguistically described JCs cannot be used for calculating portfolio JC as a sum of their components’ JCs (
Łyczkowska-Hanćkowiak and Piasecki 2018b). This task requires the JCs numerical representation given as their quantified models.
For any security, each quantified JC may be used as such an approximation of its market price that it is additionally equipped with information about this price trend. For these reasons,
Kacprzak et al. (
2013) have described JC by means of Kosiński’s numbers. Kacprzak’s description has a significant disadvantage. There, each Black Candle is described by improper
OFN. So, Kacprzak’s approach is not convenient for financial analysis with JCs use.
The above conclusion justifies remodeling JCs with the use of the revised theory of OFN. The main aim of our paper is to describe JCs by means of oriented fuzzy numbers.
Our approach to represent JCs by
OFNs differs to the approach represented by
Marszałek and Burczyński (
2013a,
2013b,
2014), who define the membership function of candles as some density function. In our opinion, such an approach is not compatible with the essence of the JCs.
Our paper is organized as follows. In
Section 2, we present two kinds of trapezoidal
OFNs: Kosiński’s numbers and oriented fuzzy numbers. At the end of this section, we justify the postulated restricting applications of the oriented fuzzy numbers.
Section 3 contains the main information about JCs. In
Section 4, we briefly discuss Marszałek’s approach and Kacprzak’s approach to modeling JCs by
OFNs.
Section 5 is the main part of our paper. In this section we propose our method of representing JCs by oriented fuzzy numbers. In
Section 6, we determine the imprecise expected return rate by means of JCs models. Next, we show the possibility of application of this return rate for fuzzy portfolio analysis. This section is based on (
Piasecki 2017).
Section 7 presents a simple case study in which the introduced numerical model of JCs is applied for financial portfolio analysis.
Section 8 contains final conclusions.
2. Fuzzy Numbers
The symbol
denotes the family of all fuzzy sets in the real line
. A commonly accepted model of imprecise number is the fuzzy number (FN), generally defined by
Dubois and Prade (
1978) as some kind of fuzzy subset
. Thanks to the results obtained in (
Goetschel and Voxman 1986), any FN can be equivalently defined as follows:
Theorem 1 (Delgado et al. 1998).For any FNthere exists such a non-decreasing sequencethatis determined by its membership functiondescribed by the identity:where the left reference functionand the right reference functionare upper semi-continuous monotonic ones meeting the conditions: Let us note that identity (1) additionally describes the extended notation of numerical intervals, which is used in this work. The family of all FNs is denoted by the symbol
. For any
a FN
is a formal model of linguistic variable “about
”. Understanding the phrase “about
” depends on the applied pragmatics of the natural language. In (
Dubois and Prade 1979), arithmetic operations on FNs are introduced in such a way that they are coherent with the Zadeh’s extension principle. In our paper, we do not apply this arithmetic. Therefore, a description of arithmetic operations on FNs is omitted here.
2.1. Kosiński’s Number
The concept of ordered fuzzy numbers (
OFN) was introduced by Kosiński and his co-writers in the series of papers (
Kosiński and Słysz 1993;
Kosiński et al. 2002,
2003) as an extension of the concept of FN. Thus, any
OFN should be determined with the use of any fuzzy subset in real line
. On the other side, Kosiński has defined
OFN as an ordered pair of functions from the unit interval
into
. This pair is not similar to any fuzzy subset in
. It means that the Kosiński’s proposal of
OFN notion is not an extension of FN. Thus, we can not to accept Kosiński’s original terminology. For this reason, we are agreeing with other scientists (
Prokopowicz 2016;
Prokopowicz and Pedrycz 2015) that the
OFN defined by Kosiński should be called the Kosiński’s number (KN). Let the symbol
denote the pseudo-inversion of monotonic continuous surjection
. KNs are originally defined as follows:
Definition 1. For any sequence, the KNis defined as an ordered pairof monotonic continuous surjections andfulfilling the condition: For any KN
, the function
is called the up-function. Then, the function
is called the down-function. Moreover, for KN
, the number
is called the starting point and the number
is called the ending point. The space of all KNs is denoted by the symbol
. Any sequence
satisfies exactly one of the following conditions:
If the condition (5) is fulfilled, then the KN
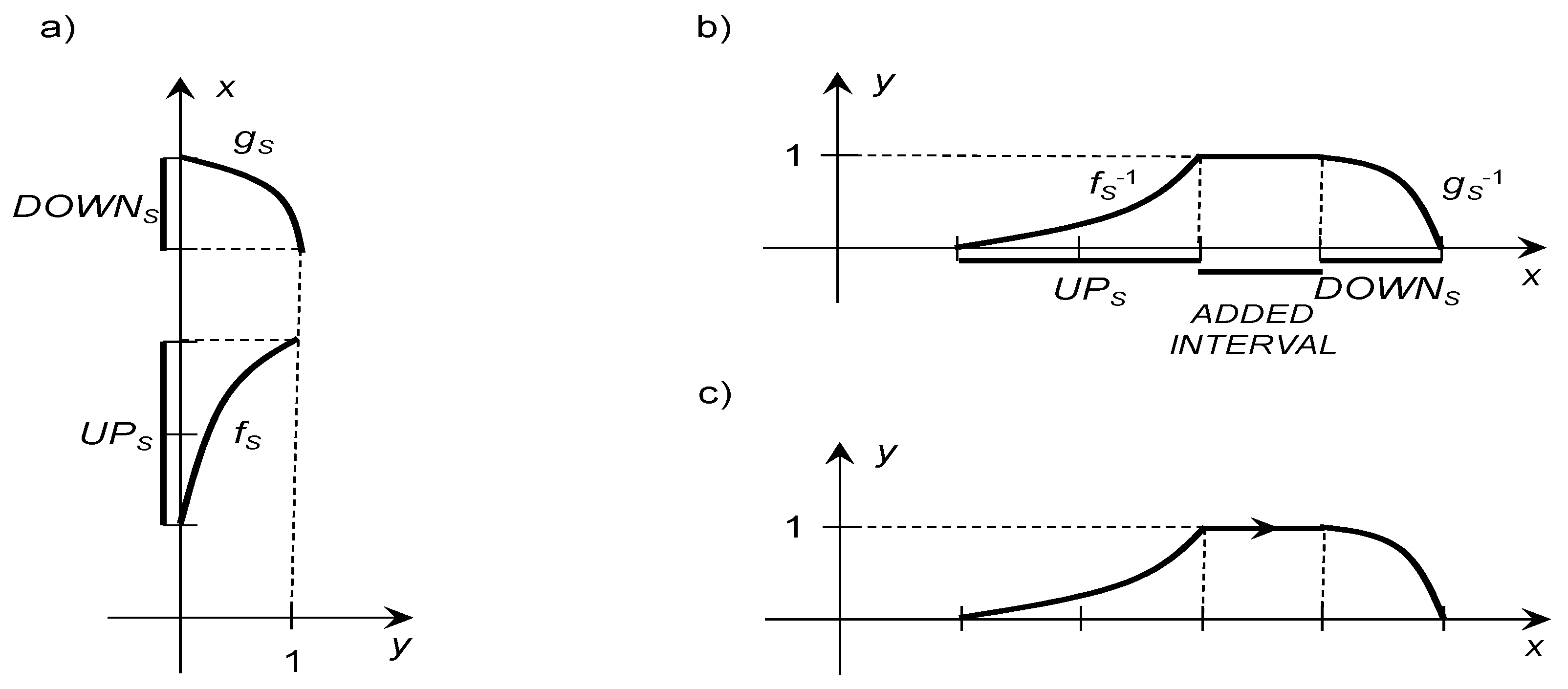
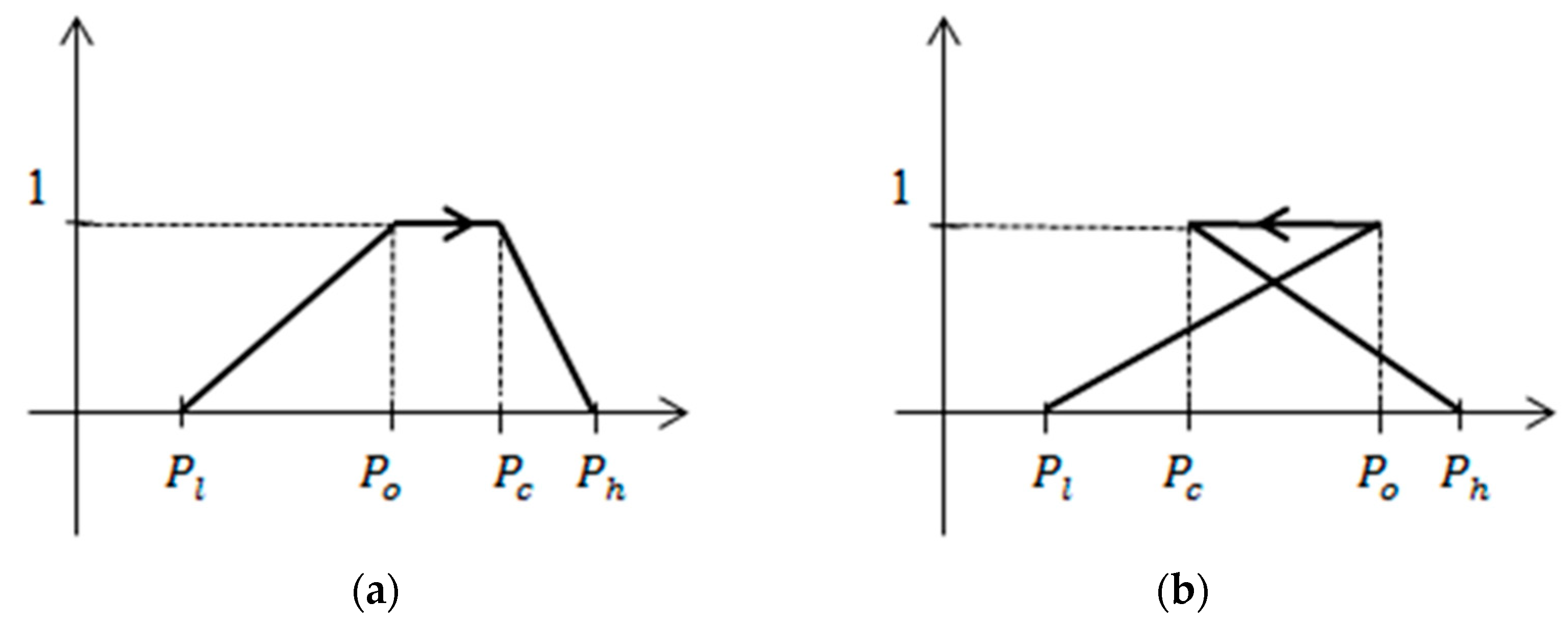
has a positive orientation. For this case, an example of graphs of KN is presented in
Figure 1a. Any positively oriented K’N is interpreted as an imprecise number, which may increase. If the condition (6) is fulfilled, then KN
is negatively oriented. Then, it is interpreted as an imprecise number, which may decrease. For the case (7), KN
represents the interval
.
Theorem 2. For any sequence, the KNis explicitly determined by its membership relationgiven by the identity: The graph of membership function of KN
is presented in
Figure 1b. A membership relation of any KN may be represented by the graph which has an extra arrow from the starting point to the ending one. This arrow denotes the KN orientation, which shows supplementary information about possible changes of the approximated number. The graph of KN membership function with positive orientation is shown in
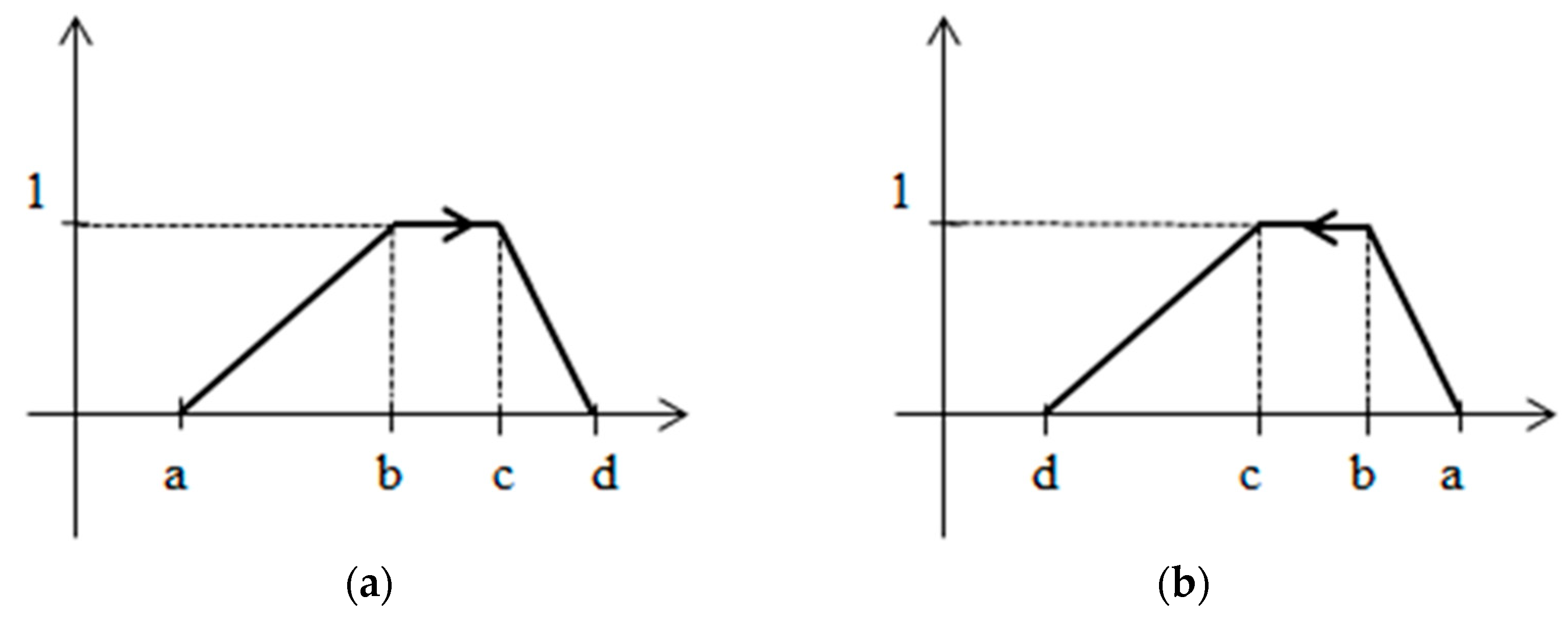
Figure 1c. Next, examples of such graphs are presented in
Figure 2.
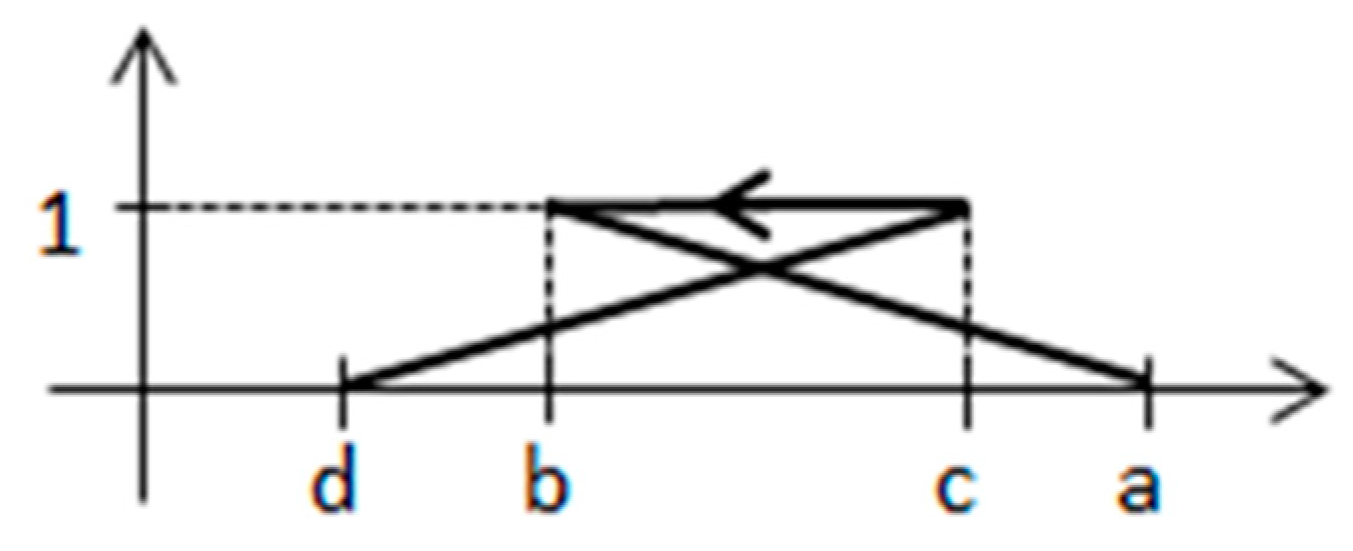
If the sequence
is not monotonic, then the membership relation
is not a function. Then, this membership relation cannot be considered as a membership function of any fuzzy set. Therefore, for any non-monotonic sequence
, the KN
is called an improper one (
Kosiński 2006). An example of a membership relation of a negatively oriented improper KN is presented in
Figure 3. The remaining KNs are called proper ones. Some examples of proper KNs were presented in
Figure 2.
Kosiński et al. (
2002,
2003) determined arithmetic operators for KNs as an extension of results obtained for FNs in (
Goetschel and Voxman 1986). In our paper, we do not apply this arithmetic. Therefore, a description of arithmetic operations on FNs is omitted here.
Because in this paper we restrict our main considerations to the case of trapezoidal numbers, we will take into account the following definition:
Definition 2. For any sequence, the trapezoidal KN (TrKN)is defined as KN determined by its membership relationgiven by the identity: The symbol
denotes the space of all TrKNs. Some examples of membership relations of TrKN are presented in
Figure 2 and
Figure 3.
The “dot multiplication”
defined for any pair
by the identity:
The “Kosiński’s addition”
defined for any pair
by the identity:
The determining “dot multiplication” is coherent with the Zadeh’s extension principle. On the other hand, “Kosiński’s addition” is not coherent with the Zadeh’s extension principle. In (
Kosiński 2006) it is shown that there exist such pairs of proper TrKNs that their Kosiński’s sum is an improper one. This is the main reason why Kosiński’s theory of
OFNs was revised in (
Piasecki 2018).
2.2. Oriented Fuzzy Numbers
Only in the case of any monotonic sequence may the membership relation be interpreted as a membership function . Thus, we distinguish the following kind of proper OFN.
Definition 3. (
Piasecki 2018)
For any monotonic sequence , the oriented fuzzy number (OFN) is the pair of orientation and fuzzy set described by membership function given by the identity:where the starting function and the ending function are upper semi-continuous monotonic ones meeting the conditions (3) and The symbol
denotes the space of all OFNs. Any OFN is a proper KN and any proper KN is OFN. Therefore, we have
. The positive and negative orientations of OFN are determined in the same way as for the case of KN. The interpretation of a OFN orientation is identical to the interpretation of a KN orientation. For the family of all positively oriented OFNs and the family of all negatively oriented OFN, we respectively denote by the symbols
and
. For any OFN
, the condition (7) implies that:
Then, the OFN
describes the real number
which is not oriented. Summing up, we see that:
We restrict our main considerations to the case of trapezoidal OFN, defined as follows:
Definition 4. For any monotonic sequence, the trapezoidal OFN (TrOFN)is defined as OFN determined with use its membership functiongiven by identity (9).
The symbol
denotes the space of all TrOFNs. In our considerations, we will only use the arithmetic operators determined for TrOFN. Then, the“Kosiński addition”
is replaced by “addition”
defined for any pair
by the identity:
The space
is closed under the addition
(
Piasecki 2018). Moreover, sums obtained by using the addition
are the best approximation of sums obtained by means of the Kosiński’s addition
(
Piasecki 2018). The restrictions imposed in Definition 4 allow that TrOFNs may be analyzed with use of the fuzzy set theory. On the other hand, these methods of analysis are not applicable for TrKNs. Therefore, if we intend to apply trapezoidal
OFNs for any additive model, then we should restrict our considerations to the use of the additive semigroup
. This principle is shortly called the postulate restricting applications to the use of TrOFNs. It is very important restriction because we have many additive models of real-world problems. For example, financial portfolio analysis is an additive model.
Furthermore, the addition
is not commutative. It implies that any multiple sum determined by
may be dependent on its summands’ ordering (
Piasecki 2018). For this reason, the assumed order of performing multiple additions may require additional justifications.
For any OFN, the “dot multiplication” operator is determined by the identity (10). As we know, the “dot multiplication” is coherent to the Zadeh’s extension principle. Therefore, using this principle, we can extend the “dot multiplication” operator to any unary operator linked to monotonic function . This extension is determined in the following way:
If TrOFN
is represented by its membership function
, then the membership function
of OFN
is given by the identity:
While discussing the results obtained, we will also refer to the disorientation map
determined in (
Piasecki 2019) as follows:
3. Japanese Candlesticks
We understand the term “security” as an authorization to receive a future financial revenue, payable to a certain maturity. Japanese Candlestick (JC) is a kind of financial chart used to describe the volatility of a fixed security quotation. The JC charting techniques are perfectly described by
Nison (
1991). The basic elements of JC charting techniques are the descriptions of a single JC.
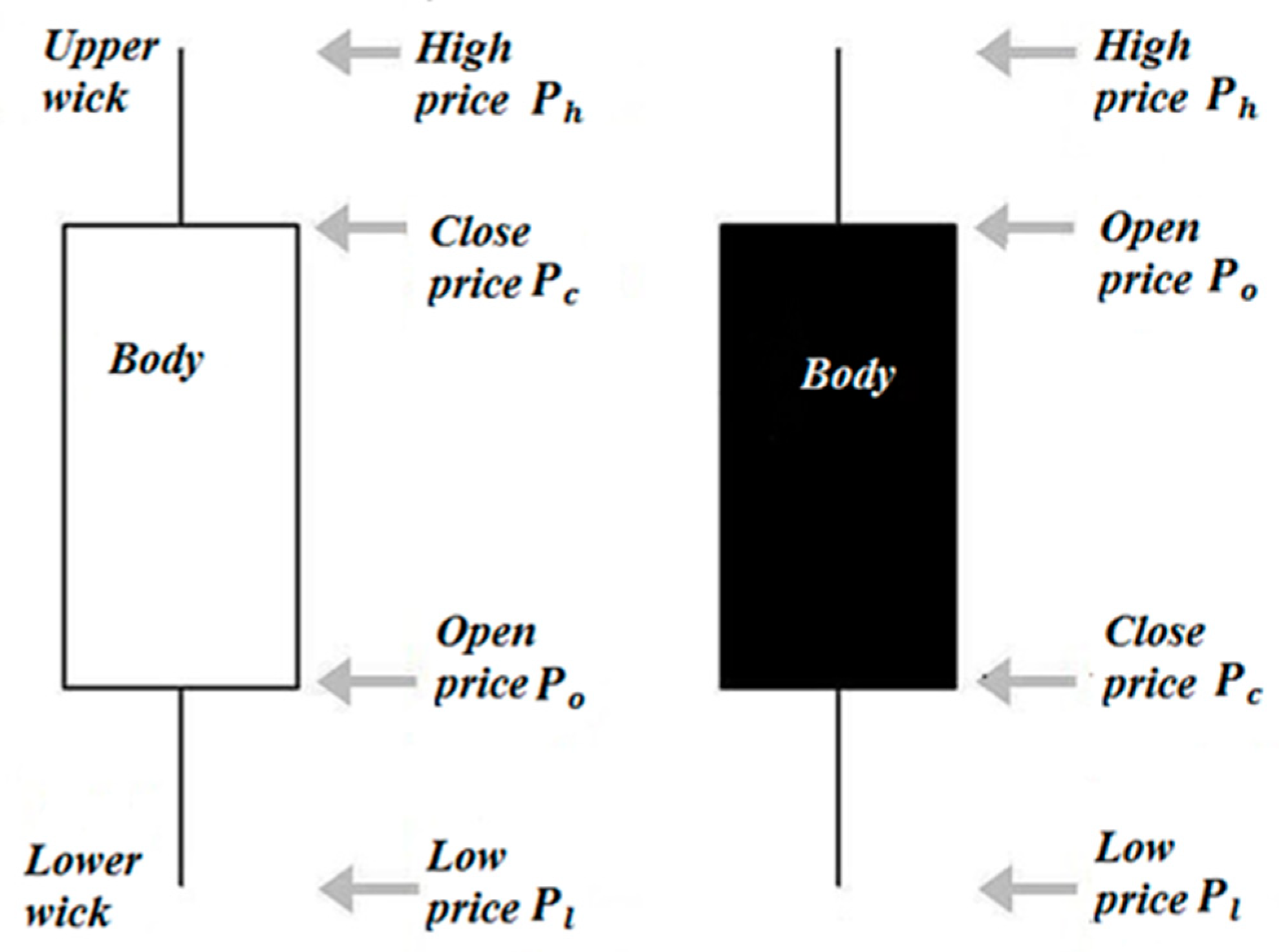
Let fixed security be given as . For the assumed time period , the volatility of the security quotations are described by the function . Then, JC represents four important pieces of information about quotations:
The high price and the low price together are called extreme prices. In brokerage house reports, each JC is usually described by the data set of reported prices. In general, JCs are optional composed of:
The body determined as a rectangle between the open price and the closed price.
The upper wick determined as the line between the body and the high price.
The lower wick determined as the line between the body and the low price.
The body illustrates the opening and closing trades. We can note the following cases here:
If the condition (23) is met, then the candle body is white. Then, the JC is called White Candle or White Spinning. Any Black Candle may be considered as a bullish signal, i.e., a forecast of an increase in quotations. If the condition (24) is satisfied, then the candle body is black. Then, the JC is called Black Candle or Black Spinning. Any Black Candle may be considered as a bearish signal, i.e., a forecast of a decline in quotations. The general case of a White Candle and a Black Candle are presented in the
Figure 4.
Any JC need not have either a body or a wick. If a JC fulfills the condition (25) then it does not have a body. Such a JC is called a Doji. We distinguish the following main kinds of Doji:
Doji Star is a JC fulfilling the condition:
Dragonfly Doji is a JC fulfilling the condition:
Gravestone Doji is a JC fulfilling the condition:
Four Price Doji is a JC fulfilling the condition:
These kinds of Doji are presented in
Figure 5.
Example 1. During the session on the Warsaw Stock Exchange (WSE) on July 23, 2019, we observed quotations of the following companies: Assecopol (ACP), CYFRPLSAT (CPS), ENERGA (ENG), JSW (JSW), KGHM (KGH), LOTOS (LTS), ORANGEPL (OPL), PGE(PGE), PKOBP (PKO). For each observed company, the results of our observations are recorded in Table 1 as reported price sets. Each reported price set may be graphically presented by the JC mentioned in the last column of Table 1. Furthermore, we see that the quotations of ACP are assigned with a White Candle without a lover wick. In addition, all extreme prices are marked here with stars. The notions of earlier and later extreme prices are explained in Section 5. 5. Representation of Japanese Candlesticks by Trapezoidal Oriented Fuzzy Numbers (TrOFN)
In above section, we conclude that any JC should be represented by TrOFN. That is why we are reconsidering the fixed JC,
. Let
be reported by the data set
of reported prices. Then,
may be represented by a TrOFN
where a sequence
is a monotonic permutation of all reported prices. Moreover, it is obvious that the TrOFN
should be oriented from open price
to close price
. It means that in a general case, any sequence
contains the subsequence
. From dependences (19)–(22), we get:
We see that in a general case, the starting point and ending point are extreme prices. Therefore, any may be be represented only by a TrOFN where the sequence is such a permutation of extreme prices that the sequence is monotonic. Looking for a universal method for determining the permutation , in the first step, we will change the identification of extreme prices.
The orientation from open price,
, to close price,
may be determined unambiguously only for the case when
has a body. It is equivalent to the condition:
If the extreme price,
is closer to the open price,
than to the close price,
then the price,
is called the back price. In other words, the extreme price,
is called the back price if it fulfills the condition:
In this way, for the White Candle, the back price,
is equal to the low price,
and for the Black Candle, the back price,
is equal to the high price,
. If the extreme price,
is closer to the close price,
than to the open price,
then the price,
is called face price. In other words, the extreme price,
is called the face price if it fulfills the condition:
In this way, for the White Candle, the face price,
is equal to the high price,
and for the Black Candle, the face price,
is equal to the low price,
. Thanks to condition (36), the back price,
and the face price,
are determined explicitly. With this reinterpretation of extreme prices, we get a modernized model of JCs which have a body. The general cases of a White Candle and a Black candle are presented in
Figure 7.
The sequence
is the unique monotonic permutation of reported prices which contains the subsequence
. For this reason, we propose to describe the Japanese Candle,
by the TrOFN,
. Then, any White Candle is represented by positively oriented TrOFN determined by the membership function presented in
Figure 8a. In this representation, any Black Candle is described by negatively oriented TrOFN determined by the membership function presented in
Figure 8b.
Now, we consider the case (25) when the considered is a Doji. Then, the inequality (35) implies that for any permutation of extreme prices, the sequence is monotonic. Then Doji may be represented by a TrOFN, where the subsequence is any permutation of extreme prices. On the other hand, in line with (5) and (6), the orientation of can only be determined as orientation from the starting point to the ending point. Furthermore, for any Doji, the back price, and the face price, are not explicitly determined. Thus, the orientation of TrOFN representing any Doji cannot be defined as the direction from a back price, to a face price, . For these reasons, we propose to present any Doji by TrOFN with orientation from the earlier extreme price, to the later extreme price, .
The kinds of extreme prices mentioned above are determined in the following way. At the beginning, we assign each quotation
the last moment
of its observation defined by the identity:
Let us consider now the case when:
Then, the earlier extreme price,
and later extreme price,
we define as follows:
In this way, we interpret extreme prices as an earlier or later one. With this reinterpretation of extreme prices, we get a modernized model of Doji. The general cases Doji Stars are presented in
Figure 9.
We propose to describe any Doji by TrOFN,
. Then, the Doji Star presented in
Figure 9a is described by the positively oriented TrOFN,
. The Doji Star presented in
Figure 9b is described by the negatively oriented TrOFN,
. These representations of Doji are determined by their membership functions presented in
Figure 10.
For any Dragonfly Doji we have:
Thus, any Dragonfly Doji is represented by positively oriented TrOFN,
. This positive orientation is consistent with the common belief that any Dragonfly Doji could signal a potential bullish reversal of market quotations. The Dragonfly Doji modernized model is shown in
Figure 11a.
For any Gravestone Doji we have:
Therefore, any Gravestone Doji is represented by negatively oriented TrOFN,
. This negative orientation is consistent with the common belief that any Gravestone Doji could signal a potential bearish reversal of market quotations. The Gravestone Doji modernized model is shown in
Figure 11b.
If the condition (40) is not satisfied, then we get:
This case corresponds to the Four Price Doji, the modernized model of which is presented in
Figure 11c. Any Four Price Doji is described by the TrOFN,
which is not oriented.
It is very easy to check that all types of Japanese candles omitted in the above specification are only special cases of the discussed candles.
Example 3. We describe each Japanese candle observed in Example 1 by TrOFN determined by means of the method proposed by us. The quotations ACP and OPL are assigned with White Candles represented by TrOFNs in the form. The quotations of CPS, JSW, KGH, LTS, and PGE OPL are assigned with Black Candles represented by TrOFNs in the form. The quotations ENG and PKO are assigned with Doji Star. Therefore, we should determine an earlier extreme priceand a later onefor both companies.The results of this search are shown in Table 1. For ENG, we getand. Therefore, the quotations of ENG are assigned to Doji Star represented by TrOFN in the form. For PKO, we obtainand. Therefore, the quotations of PKO are assigned to Doji Star represented by TrOFN in the form. Obtained representations are presented in Table 2. All positively oriented TrOFNs are indicated in green. All negatively oriented TrOFNs are indicated in blue. In summary, any JC can be represented by TrOFN:
where the sequence
is such a permutation of extreme prices
that it is determined by conditions (37) and (38) or by (42) and (43), or by (46).
Any security may be evaluated by a present value (PV) generally defined as a current equivalent value of payments at a fixed point in time (
Piasecki 2012). It is commonly accepted that the PV of a future cash flow can be imprecise. The natural consequence of this approach is estimating PV with FNs. A detailed description of the evolution of this particular model can be found, for example in (
Łyczkowska-Hanćkowiak and Piasecki 2018a). If an imprecisely estimated PV is additionally equipped with a forecast of its closest changes, then it is called oriented PV (OPV). It is obvious that any OPV should be represented by an OFN
.
Let us take into account the fixed security
. If the volatility of its quotations is characterized by JC (47) then we can determine its OPV as follows:
Then, the OPV membership function
is determined by condition (9). Some applications of such an approximated OPV are given in
Section 6 and
Section 7.
6. Oriented Expected Return Determined by Japanese Candlestick
Let us assume that the time horizon of an investment is fixed. Then, the security considered here is determined by two values:
Anticipated FV and
Assessed PV .
The basic characteristic of benefits from owning this security is a return rate
given by the identity:
In the general case, if , then the function: is a decreasing function of PV and an increasing function of FV. Moreover, in the special case, we have here:
In this section, we restrict our considerations to the case of any simple return rate given by condition (50). Thanks to this, our considerations will be more clear. However, the results obtained can be easily generalized to the case of generalized return rate given by condition (49).
The security
is an authorization to receive future financial revenue, payable to a certain maturity. The value of this revenue is interpreted as the anticipated FV of the security. According to the uncertainty theory introduced by
Von Mises (
1962) and
Kaplan and Barish (
1967), for anyone unknown to us, the future state of affairs is uncertain. The Mises–Kaplan uncertainty is a result of our lack of knowledge about the future state of affairs. Yet, in the researched case, we can point out this particular time in the future, in which the considered state of affairs will already be known to the observer. Behind (
Kolmogorov 1933,
1956;
Von Mises 1957;
Von Lambalgen 1996;
Caplan 2001), we will accept that this is a sufficient condition for modeling the uncertainty with probability.
Above is justified in detail that FV is a random variable
. The set,
, is a set of elementary states,
of the financial market. In a classical approach to the problem of return rate estimation, a security PV is identified with the observed market price,
. Thus, the return rate is a random variable determined by identity:
In practice of financial markets analysis, the uncertainty risk is usually described by probability distribution of return rate determined by condition (52). Nowadays, we have an extensive knowledge about this subject. Let us assume that the mentioned probability distribution is given by cumulative distribution function
. We assume that the expected value,
of this distribution exists. Moreover, let us note that we have:
Let us now consider the case when PV is imprecisely estimated by OPV
determined by conditions (47) and (48). Then, it is represented by its membership function
given by identities:
and (9). Then, the Zadeh’s extension principle, (50) and (52), imply that a return rate is a fuzzy probabilistic set (
Hirota 1981) represented by its membership function
as follows:
The membership function,
of an expected return rate,
is calculated as:
According to conditions (9) and (54), the Formula (56) can be transformed into:
Finally, we get that expected return rate is equal to OFN
, given as follows:
where,
The above determined expected return rate,
is an example of the oriented expected return rate (
Piasecki 2017). We see that the expected return rate is not TrOFN. Moreover, the identities (48) and (58) show that JC and the expected return rate determined by it always have opposite orientations. Therefore, we can say:
In theory and practice of finance, both of these facts are well known. This observation proves that the extension of the fuzzy models of imprecise PV and return rate to the case of oriented fuzzy models is the appropriate direction for the development of fuzzy finance theory.
Example 4. During the session on the Warsaw Stock Exchange on 23 July, 2019, we observed quotations of ORANGEPL. The volatility of these quotations is characterized by JC
. Then, in agreement with condition (48), the ORANGEPL OPV is equal to positively oriented: The expected quarterly return rate from ORANGEPL is determined by the broker’s office as follows:. We determined the ORANGEPL market priceas open price on 24 July, 2019. From conditions (58)–(60), we get that expected return rate is equal to the negatively oriented OFNgiven as follows:where, Finally, using the disorientation map (34), we calculate fuzzy expected return rate,in the following way: 8. Summary
It is a well-known fact that JCs are a very convenient tool for synthetic recording of high-frequency time series of financial data. We have shown that each JC may be explicitly represented by such a TrOFN that its orientation is always consistent with the closest quotations’ changes predicted by the represented JC. The positive orientation of JC representation always means a bullish signal. The negative orientation of JC representation is always a bearish signal. The proposed JC numerical model distinguishes all JC types. In addition, the use of this model does not cause a loss of information about the represented JC. Therefore, the JC representation described here can be recommended as a numerical tool for analyzing high-frequency financial data.
The proposed JC numerical model highlights the imprecision of capital market assessments. In the case of economics and finance, this imprecision is a natural state of affairs. Therefore, we can conclude that the proposed model reflects the essence of information about the observed capital market well. On the other hand, a fuzzy set is a commonly used imprecise information model. The replacement of Kacprzak’s model by our model means that we can apply the whole fuzzy sets theory to the analysis of JCs. To our best knowledge, the JC fuzzy numerical model proposed by us is a unique one which is coherent with fuzzy set theory. Some possibilities of application of the usual fuzzy set theory are shown. In a special case, we can use methods dedicated to OFNs.
We showed a simple application of our JC model for financial portfolio analysis. The results obtained have the possibility of further application in any financial analysis. It proves that the JC model proposed by us is applicable for financial analysis.
Each JC chart is a finite sequence of JCs describing the volatility of fixed security quotation in an assumed period of time. Financial practitioners distinguish JC patterns defined as such families of short JC sequences similar to a given reference pattern, which they believe can predict a particular quotations’ movement. Using the results obtained in this work, we can recognize any JC chart as a sequence of TrOFNs. Therefore, our model can be used for recognition of JC patterns on a current JC chart. The above remark well justifies the need for further research into determining known reference patterns.
Moreover, our JC model should be used to test high-frequency financial data systems to determine the optimal time horizon described by a single JC. We recommend this research field as a very promising area of scientific considerations and discussion.
The directions of future research described above are very general. We can also suggest more detailed directions of future research. An interesting problem here is the use of the JC numerical model to determine the orientation of behavioral present value (
Piasecki 2011;
Piasecki and Siwek 2015;
Łyczkowska-Hanćkowiak 2017). Another interesting problem is the use of our numerical JC model as a premise in the models described in (
Marszałek and Burczyński 2013a,
2013b,
2014). Then, we can compare the effects of the application of our numerical JC model with the effects of the application of Marszałek’s fuzzy candles.