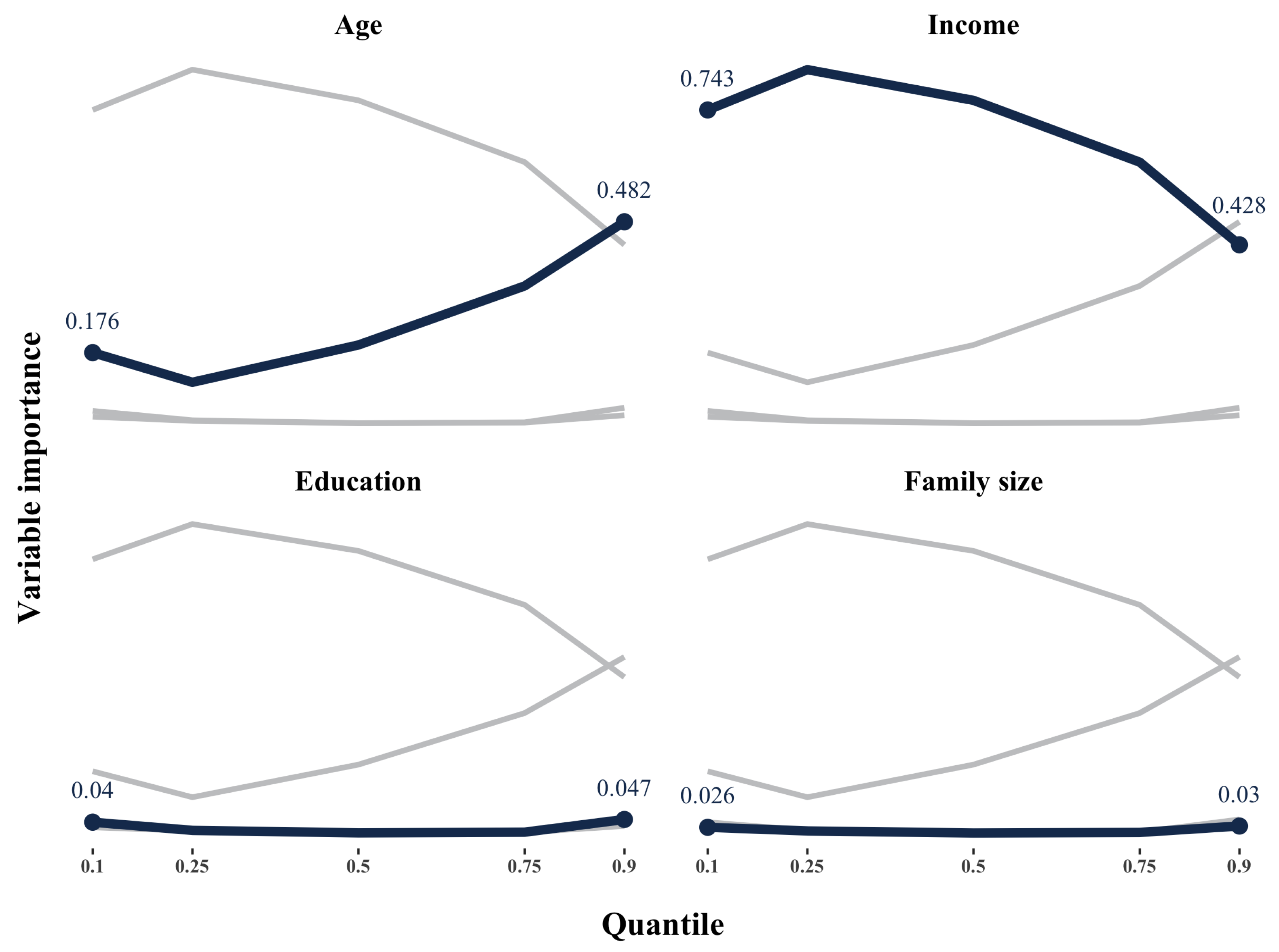
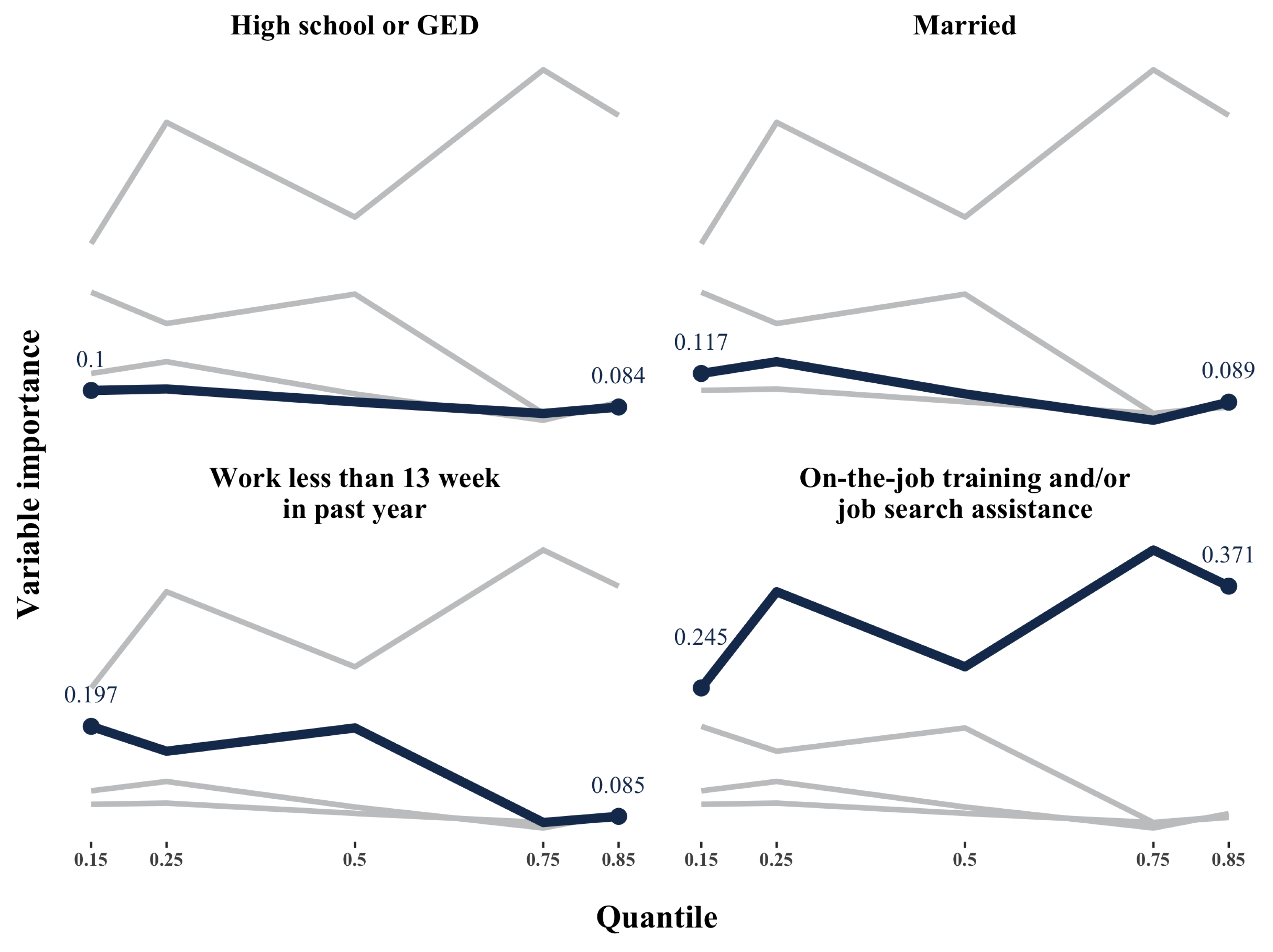
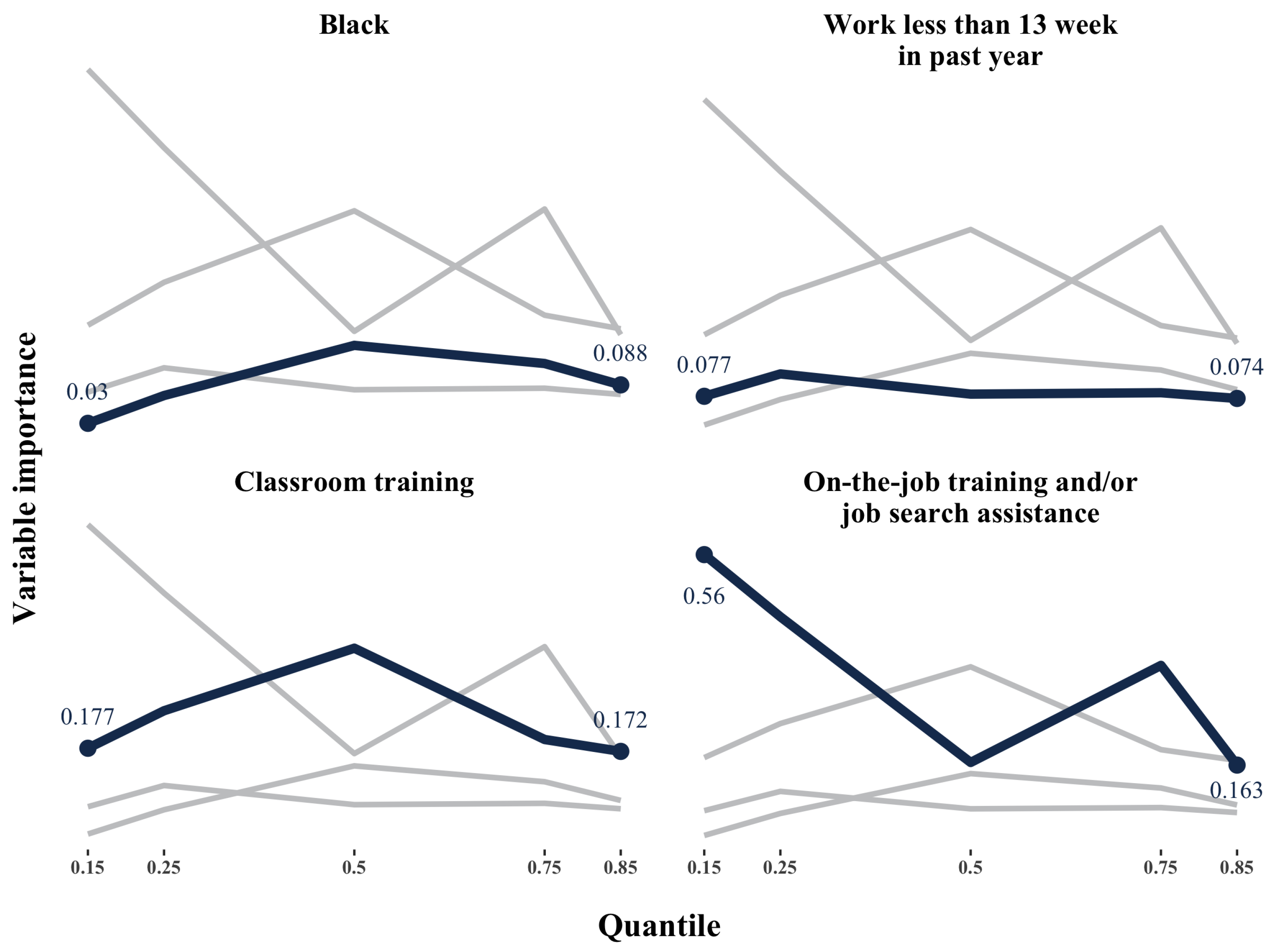
Appendix A.2. The Doubly Robust Estimation for Causal Forests
Athey and Wager (
2019) and their
grf R package implement a variant of doubly robust AIPW estimators for causal forests. Specifically, for estimating average treatment effect, their doubly robust estimator is shown as follows.
where
is the conditional average treatment effect estimator based on causal forest,
is the conditional average treatment effect estimator adjusted by inverse probability weighting,
and
are the estimators of
and
which are based on random forest with honest splitting, and the average treatment effect estimator
is simply the sample average of those adjusted conditional average treatment effect estimates.
Glynn and Quinn (
2009) provide some evidence that the doubly robust estimator performs better in terms of efficiency than inverse probability weighting estimators, matching estimators, and regression estimators. To explore how adapting the doubly robust method in the causal forest estimator affects the efficiency and accuracy, we follow their DGP designs and conduct Monte Carlo experiments with different degree of confoundedness. In the simulation,
, and
are covariates following
,
D is the treatment variable,
Y is the outcome variable, and
is the disturbance which follows
. Two data generating processes are considered. Degree of confoundedness are modeled in three levels: low, moderate, and severe.
Table A1.
Simulation setting.
Table A1.
Simulation setting.
| | Outcome (control) | Outcome (treatment) |
| Simple DGP | | |
| Complicate DGP | | |
| Degree of confoundedness | True treatment assignment probabilities |
| Low | |
| Moderate | |
| Severe | |
With three different sample sizes,
, and 1000, three degrees of confoundedness, and two DGP settings, the Monte Carlo results are tabulated in
Table A2. The results confirm that the causal forest with doubly robust estimation indeed has efficiency gains over the conventional causal forest.
Table A2.
Finite-sample performance: causal forests with doubly robust estimation.
Table A2.
Finite-sample performance: causal forests with doubly robust estimation.
| | | Linear DGP | Nonlinear DGP |
|---|
| | | Causal forest | Causal forest with
doubly robust | Causal forest | Causal forest with
doubly robust |
|---|
| Sample size | Confoundedness degree | RMSE | RMSE | RMSE | RMSE |
|---|
| 250 | low | 0.3730 | 0.1693 | 0.7542 | 0.3147 |
| 250 | moderate | 0.4200 | 0.2099 | 0.9295 | 0.3914 |
| 250 | severe | 0.4562 | 0.2218 | 1.0205 | 0.3997 |
| 500 | low | 0.3206 | 0.1081 | 0.6911 | 0.1855 |
| 500 | moderate | 0.3634 | 0.1417 | 0.8711 | 0.2320 |
| 500 | severe | 0.4107 | 0.1497 | 0.9529 | 0.2505 |
| 1000 | low | 0.2745 | 0.0717 | 0.6041 | 0.1124 |
| 1000 | moderate | 0.3244 | 0.1008 | 0.7755 | 0.1540 |
| 1000 | severe | 0.3742 | 0.1098 | 0.8919 | 0.1709 |
Appendix A.5. Identifying Restrictions and Regularity Conditions for the GRF-IVQR
Following
Chernozhukov and Hansen (
2008), we consider the instrumental variable quantile regression characterizing the structural relationship:
where
Y is the scalar outcome variable of interest.
U is a scalar random variable (rank variable) that aggregates all of the unobserved factors affecting the structural outcome equation.
D is a vector of endogenous variables determined by .
V is a vector of unobserved disturbances determining D and correlated with U.
Z is a vector of instrumental variables.
X is a vector of included control variables.
The one-dimensional rank variable and the rank similarity (rank preservation) condition imposed on the outcome equation play an important role in identifying the quantile treatment effect. To derive the standard error of the IVQR estimator, the following assumptions are needed as well.
Assumption CH1. are iid defined on the probability space and have compact support.
Assumption CH2. For the given τ, is in the interior of the parameter space.
Assumption CH3. Density is bounded by a constant a.s.
Assumption CH4. at has full rank for each θ in Θ, for .
Assumption CH5. has full rank at .
Assumption CH6. The function is one-to-one over parameter space.
Assumptions CH1–CH6 are compatible with those imposed in
Athey et al. (
2019); for example, both sets of assumptions do not apply to time-series data.
Assumption ATW1 (Lipschitz x-signal). For fixed values of , we assume that is Lipschitz continuous in x.
Assumption ATW2 (Smooth identification). When x is fixed, we assume that the M-function is twice continuously differentiable in with a uniformly bounded second derivative, and that is invertible for all , with .
Assumption ATW3 (Lipschitz
-variogram).
The score functions have a continuous covariance structure. Writing γ for the worst-case variogram and for the Frobenius norm, then for some , Assumption ATW4 (Regularity of ). The ψ-functions can be written as , such that λ is Lipschitz-continuous in , is a univariate summary of , and is any family of monotone and bounded functions.
Assumption ATW5 (Existence of solutions). We assume that, for any weights with , the estimating equation returns a minimizer taht at least approximately solves the estimating equation , for some constant .
Assumption ATW6 (Convexity). The score function is a negative sub- gradient of a convex function, and the expected score is the negative gradient of a strongly convex function.
Given Assumptions ATW1-ATW6, the Theorems 3 and 5 of
Athey et al. (
2019) guarantee that the GRF estimator achieves consistency and asymptotic normality. In what follows, we check each assumptions for the proposed GRF-IVQR estimator.
Observe that the score function of the IVQR
In
Chernozhukov and Hansen (
2008), the moment functions are conditional on
. For simplicity, we write conditional functions as
when considering splitting in
within the framework of generalized random forests.
Checking Assumption ATW1. Thus the expected score function
We want the conditional cumulative distribution function is Lipschitz continuous. Since every function with bounded first derivatives is Lipschitz, we need the conditional density is bounded. Assumption CH3 states that the conditional density is bounded by a constant a.s.. In particular, is a density of a convolution of a continuous random variable and a discrete random variable, we also need the continuous variable not to be degenerate.
Checking Assumption ATW2. We want V is invertible and therefore needs to be invertible. In addition, the conditional density is required to have continuous uniformly bounded first derivative. If is continuously differentiable, then its first derivative is uniformly bounded. Those conditions are implied by Assumptions CH4 and CH5. Thus is invertible as well.
Checking Assumption ATW3. Taylor expansion implies the following approximation of
.
Since the conditional probability density function is bounded, there exists a
, such that
Checking Assumption ATW4. The score function can be written as
where
Checking Assumption ATW5. Since Assumption ATW5 is used to ensure the existence of solutions, it is required.
Checking Assumption ATW6. With a V-shaped check function of the instrumental variable quantile regression, the corresponding score function is a negative subgradient of a convex function, and the expected score function is a negative gradient of a strongly convex function. Therefore, Assumption ATW6 holds.
Corollary.(Consistency and asymptotic normality of the GRF-IVQR estimator) Given Assumptions ATW1-6, Assumptions CH1-6, and Theorems 3 and 5 of Athey et al. (2019), the GRF-IVQR is consistent and asymptotically normal: The variance estimatorwhere and are consistent estimators for the and respectively.