Estimation of FAVAR Models for Incomplete Data with a Kalman Filter for Factors with Observable Components
Abstract
1. Introduction
2. Mathematical Background
2.1. Parameter Ambiguity and Identification Restrictions
2.2. Estimation and Model Selection for Complete Panel Data
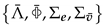 with
with 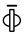 is then obtained by maximizing the expected log-likelihood
is then obtained by maximizing the expected log-likelihood
2.3. Kalman Filter and Smoother
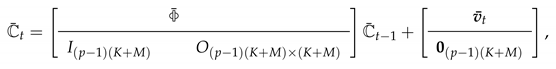
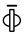 instead of the loadings matrix .5 As usual for KF, we assume known model parameters in (13)–(15) and define the filtration: , for collecting all observations up to time . Then, covers the overall sample . For the hidden factor moments, we set: , and . Analogously, we shorten means and covariance matrices of and , respectively, conditioned on . Algorithm A1 summarizes the adapted KF with factor estimates obtained by PCA as starting values. Note, the KS is not influenced by the observed factor components as shown in Ramsauer (2017).
instead of the loadings matrix .5 As usual for KF, we assume known model parameters in (13)–(15) and define the filtration: , for collecting all observations up to time . Then, covers the overall sample . For the hidden factor moments, we set: , and . Analogously, we shorten means and covariance matrices of and , respectively, conditioned on . Algorithm A1 summarizes the adapted KF with factor estimates obtained by PCA as starting values. Note, the KS is not influenced by the observed factor components as shown in Ramsauer (2017).2.4. EM-Algorithm for Incomplete Panel Data
3. Monte Carlo Simulation
4. Empirical Application
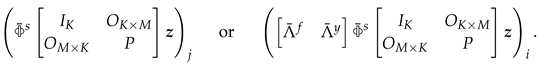
5. Conclusions and Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| bp | basis point |
| DFM | Dynamic Factor Model |
| EM | Expectation-Maximization Algorithm |
| FAVAR | Factor-Augmented Vector Autoregression Model |
| FEVD | Forecast Error Variance Decomposition |
| FEDFUNDS | Effective Federal Funds Rate |
| FX | Foreign Exchange |
| GDP | Gross Domestic Product |
| iid | identically and independently distributed |
| IRF | Impulse Response Function |
| KF | Kalman Filter |
| KS | Kalman Smoother |
| MC | Monte Carlo |
| MLE | Maximum-Likelihood Estimation |
| NSA | Not Seasonally Adjusted |
| OLS | Ordinary Least Squares Regression |
| PCA | Principal Component Analysis |
| SA | Seasonally Adjusted |
| UK | United Kingdom |
| UNRATE | Unemployment Rate |
| URL | Uniform Resource Locator |
| US | United States |
| USD | United States Dollar |
| VAR | Vector Autoregression Model |
Appendix A. Algorithms
| Algorithm A1: Kalman Filter for FAVARs with complete panel data |
 |
| Algorithm A2: Estimation of FAVARs with constraints for incomplete panel data |
 |
Appendix B. Simulation Results
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 0.49 | 0.49 | 0.48 | 0.49 | 0.49 | 0.49 | 0.48 | 0.50 | 0.49 | 0.49 | 0.49 | 0.50 |
| 80 | 800 | 0.49 | 0.49 | 0.50 | 0.49 | 0.50 | 0.49 | 0.48 | 0.50 | 0.49 | 0.49 | 0.49 | 0.48 |
| 100 | 600 | 0.49 | 0.50 | 0.50 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 |
| 100 | 800 | 0.50 | 0.50 | 0.49 | 0.49 | 0.49 | 0.50 | 0.49 | 0.49 | 0.49 | 0.49 | 0.50 | 0.50 |
| 120 | 600 | 0.50 | 0.49 | 0.50 | 0.50 | 0.50 | 0.49 | 0.48 | 0.50 | 0.50 | 0.49 | 0.50 | 0.48 |
| 120 | 800 | 0.49 | 0.50 | 0.49 | 0.50 | 0.49 | 0.49 | 0.50 | 0.49 | 0.49 | 0.49 | 0.49 | 0.49 |
| 80 | 600 | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 | 0.73 | 0.74 | 0.74 | 0.73 | 0.73 |
| 80 | 800 | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 | 0.74 | 0.73 | 0.74 | 0.74 | 0.73 | 0.73 |
| 100 | 600 | 0.75 | 0.76 | 0.76 | 0.75 | 0.76 | 0.75 | 0.75 | 0.75 | 0.76 | 0.75 | 0.75 | 0.74 |
| 100 | 800 | 0.75 | 0.76 | 0.75 | 0.75 | 0.75 | 0.75 | 0.75 | 0.74 | 0.75 | 0.75 | 0.75 | 0.74 |
| 120 | 600 | 0.76 | 0.77 | 0.76 | 0.76 | 0.77 | 0.77 | 0.76 | 0.76 | 0.77 | 0.77 | 0.76 | 0.75 |
| 120 | 800 | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 | 0.75 | 0.76 | 0.76 | 0.75 | 0.75 |
| 80 | 600 | 0.55 | 0.56 | 0.57 | 0.56 | 0.56 | 0.56 | 0.56 | 0.56 | 0.55 | 0.56 | 0.56 | 0.55 |
| 80 | 800 | 0.56 | 0.56 | 0.56 | 0.56 | 0.55 | 0.56 | 0.55 | 0.56 | 0.55 | 0.55 | 0.55 | 0.55 |
| 100 | 600 | 0.57 | 0.56 | 0.57 | 0.56 | 0.56 | 0.57 | 0.56 | 0.56 | 0.56 | 0.57 | 0.57 | 0.56 |
| 100 | 800 | 0.56 | 0.56 | 0.57 | 0.57 | 0.56 | 0.57 | 0.57 | 0.56 | 0.56 | 0.56 | 0.56 | 0.55 |
| 120 | 600 | 0.57 | 0.57 | 0.57 | 0.58 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.56 |
| 120 | 800 | 0.56 | 0.57 | 0.57 | 0.57 | 0.57 | 0.56 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.56 |
| 80 | 600 | 0.79 | 0.79 | 0.79 | 0.78 | 0.79 | 0.79 | 0.78 | 0.78 | 0.79 | 0.79 | 0.78 | 0.77 |
| 80 | 800 | 0.79 | 0.79 | 0.78 | 0.78 | 0.79 | 0.79 | 0.78 | 0.78 | 0.79 | 0.79 | 0.78 | 0.78 |
| 100 | 600 | 0.80 | 0.80 | 0.80 | 0.79 | 0.80 | 0.80 | 0.80 | 0.80 | 0.81 | 0.81 | 0.79 | 0.79 |
| 100 | 800 | 0.81 | 0.80 | 0.80 | 0.80 | 0.81 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.79 | 0.79 |
| 120 | 600 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 0.81 | 0.80 | 0.81 | 0.81 | 0.80 | 0.80 |
| 120 | 800 | 0.82 | 0.82 | 0.81 | 0.81 | 0.82 | 0.81 | 0.81 | 0.80 | 0.81 | 0.81 | 0.81 | 0.80 |
| 80 | 600 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 |
| 80 | 800 | 0.65 | 0.65 | 0.65 | 0.65 | 0.66 | 0.66 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 |
| 100 | 600 | 0.66 | 0.66 | 0.66 | 0.65 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.65 | 0.66 |
| 100 | 800 | 0.67 | 0.66 | 0.66 | 0.67 | 0.66 | 0.66 | 0.66 | 0.65 | 0.66 | 0.66 | 0.66 | 0.66 |
| 120 | 600 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.66 | 0.66 | 0.67 | 0.67 | 0.66 | 0.66 |
| 120 | 800 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.66 | 0.67 | 0.67 | 0.67 | 0.66 |
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 0.46 | 0.46 | 0.45 | 0.46 | 0.46 | 0.46 | 0.45 | 0.44 | 0.46 | 0.47 | 0.45 | 0.43 |
| 80 | 800 | 0.47 | 0.46 | 0.47 | 0.46 | 0.47 | 0.47 | 0.45 | 0.45 | 0.47 | 0.46 | 0.43 | 0.43 |
| 100 | 600 | 0.46 | 0.47 | 0.48 | 0.46 | 0.47 | 0.47 | 0.44 | 0.40 | 0.47 | 0.47 | 0.41 | 0.40 |
| 100 | 800 | 0.48 | 0.48 | 0.46 | 0.47 | 0.46 | 0.47 | 0.44 | 0.41 | 0.46 | 0.47 | 0.43 | 0.40 |
| 120 | 600 | 0.48 | 0.47 | 0.48 | 0.47 | 0.48 | 0.47 | 0.42 | 0.42 | 0.48 | 0.46 | 0.42 | 0.40 |
| 120 | 800 | 0.47 | 0.48 | 0.47 | 0.48 | 0.47 | 0.47 | 0.45 | 0.40 | 0.47 | 0.46 | 0.42 | 0.42 |
| 80 | 600 | 0.68 | 0.67 | 0.67 | 0.66 | 0.68 | 0.67 | 0.65 | 0.63 | 0.68 | 0.67 | 0.64 | 0.56 |
| 80 | 800 | 0.68 | 0.67 | 0.67 | 0.66 | 0.68 | 0.67 | 0.66 | 0.63 | 0.68 | 0.67 | 0.64 | 0.57 |
| 100 | 600 | 0.70 | 0.69 | 0.69 | 0.67 | 0.70 | 0.69 | 0.67 | 0.63 | 0.70 | 0.69 | 0.66 | 0.56 |
| 100 | 800 | 0.69 | 0.69 | 0.68 | 0.68 | 0.70 | 0.69 | 0.68 | 0.63 | 0.70 | 0.69 | 0.66 | 0.57 |
| 120 | 600 | 0.71 | 0.70 | 0.70 | 0.69 | 0.71 | 0.71 | 0.69 | 0.63 | 0.71 | 0.70 | 0.66 | 0.56 |
| 120 | 800 | 0.71 | 0.70 | 0.70 | 0.70 | 0.71 | 0.70 | 0.69 | 0.65 | 0.71 | 0.70 | 0.66 | 0.57 |
| 80 | 600 | 0.38 | 0.37 | 0.37 | 0.35 | 0.38 | 0.37 | 0.35 | 0.31 | 0.38 | 0.37 | 0.33 | 0.29 |
| 80 | 800 | 0.38 | 0.38 | 0.36 | 0.35 | 0.38 | 0.36 | 0.34 | 0.31 | 0.37 | 0.36 | 0.32 | 0.29 |
| 100 | 600 | 0.41 | 0.39 | 0.38 | 0.37 | 0.41 | 0.39 | 0.36 | 0.31 | 0.40 | 0.38 | 0.33 | 0.30 |
| 100 | 800 | 0.40 | 0.39 | 0.38 | 0.37 | 0.40 | 0.39 | 0.36 | 0.31 | 0.40 | 0.38 | 0.33 | 0.30 |
| 120 | 600 | 0.42 | 0.41 | 0.40 | 0.39 | 0.42 | 0.41 | 0.36 | 0.31 | 0.42 | 0.40 | 0.33 | 0.28 |
| 120 | 800 | 0.41 | 0.41 | 0.40 | 0.39 | 0.42 | 0.40 | 0.37 | 0.31 | 0.42 | 0.40 | 0.34 | 0.29 |
| 80 | 600 | 0.75 | 0.74 | 0.74 | 0.73 | 0.75 | 0.74 | 0.73 | 0.69 | 0.75 | 0.74 | 0.73 | 0.65 |
| 80 | 800 | 0.75 | 0.74 | 0.73 | 0.73 | 0.75 | 0.75 | 0.73 | 0.69 | 0.75 | 0.74 | 0.72 | 0.66 |
| 100 | 600 | 0.77 | 0.76 | 0.76 | 0.74 | 0.76 | 0.76 | 0.74 | 0.70 | 0.77 | 0.76 | 0.72 | 0.65 |
| 100 | 800 | 0.77 | 0.76 | 0.75 | 0.75 | 0.77 | 0.76 | 0.75 | 0.71 | 0.76 | 0.76 | 0.73 | 0.67 |
| 120 | 600 | 0.78 | 0.78 | 0.76 | 0.76 | 0.78 | 0.77 | 0.74 | 0.70 | 0.78 | 0.77 | 0.73 | 0.65 |
| 120 | 800 | 0.78 | 0.78 | 0.77 | 0.76 | 0.78 | 0.77 | 0.75 | 0.71 | 0.78 | 0.77 | 0.74 | 0.66 |
| 80 | 600 | 0.54 | 0.52 | 0.52 | 0.51 | 0.55 | 0.54 | 0.50 | 0.47 | 0.54 | 0.52 | 0.50 | 0.45 |
| 80 | 800 | 0.54 | 0.52 | 0.53 | 0.52 | 0.55 | 0.54 | 0.49 | 0.48 | 0.55 | 0.52 | 0.50 | 0.47 |
| 100 | 600 | 0.56 | 0.55 | 0.53 | 0.52 | 0.56 | 0.54 | 0.51 | 0.47 | 0.56 | 0.54 | 0.48 | 0.45 |
| 100 | 800 | 0.57 | 0.55 | 0.55 | 0.54 | 0.55 | 0.55 | 0.52 | 0.46 | 0.55 | 0.54 | 0.50 | 0.45 |
| 120 | 600 | 0.57 | 0.57 | 0.56 | 0.55 | 0.57 | 0.57 | 0.50 | 0.45 | 0.58 | 0.55 | 0.49 | 0.42 |
| 120 | 800 | 0.57 | 0.57 | 0.55 | 0.55 | 0.57 | 0.57 | 0.52 | 0.46 | 0.57 | 0.56 | 0.49 | 0.43 |
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 0.46 | 0.46 | 0.45 | 0.46 | 0.46 | 0.46 | 0.46 | 0.47 | 0.46 | 0.47 | 0.46 | 0.46 |
| 80 | 800 | 0.47 | 0.46 | 0.47 | 0.47 | 0.47 | 0.47 | 0.46 | 0.47 | 0.47 | 0.46 | 0.46 | 0.45 |
| 100 | 600 | 0.46 | 0.48 | 0.48 | 0.46 | 0.47 | 0.47 | 0.47 | 0.46 | 0.47 | 0.47 | 0.47 | 0.46 |
| 100 | 800 | 0.48 | 0.48 | 0.47 | 0.47 | 0.46 | 0.47 | 0.46 | 0.47 | 0.46 | 0.47 | 0.47 | 0.47 |
| 120 | 600 | 0.48 | 0.47 | 0.48 | 0.48 | 0.48 | 0.47 | 0.46 | 0.47 | 0.48 | 0.47 | 0.48 | 0.46 |
| 120 | 800 | 0.47 | 0.48 | 0.47 | 0.48 | 0.47 | 0.47 | 0.48 | 0.47 | 0.47 | 0.47 | 0.47 | 0.46 |
| 80 | 600 | 0.68 | 0.67 | 0.67 | 0.66 | 0.68 | 0.68 | 0.66 | 0.66 | 0.68 | 0.67 | 0.66 | 0.64 |
| 80 | 800 | 0.68 | 0.67 | 0.67 | 0.66 | 0.68 | 0.67 | 0.67 | 0.66 | 0.68 | 0.67 | 0.66 | 0.64 |
| 100 | 600 | 0.70 | 0.69 | 0.69 | 0.68 | 0.70 | 0.69 | 0.68 | 0.67 | 0.70 | 0.69 | 0.68 | 0.66 |
| 100 | 800 | 0.69 | 0.69 | 0.68 | 0.68 | 0.70 | 0.69 | 0.69 | 0.67 | 0.70 | 0.69 | 0.68 | 0.66 |
| 120 | 600 | 0.71 | 0.71 | 0.70 | 0.69 | 0.71 | 0.71 | 0.70 | 0.69 | 0.71 | 0.71 | 0.69 | 0.67 |
| 120 | 800 | 0.71 | 0.71 | 0.70 | 0.70 | 0.71 | 0.70 | 0.70 | 0.68 | 0.71 | 0.70 | 0.69 | 0.67 |
| 80 | 600 | 0.38 | 0.38 | 0.38 | 0.37 | 0.38 | 0.38 | 0.38 | 0.37 | 0.38 | 0.39 | 0.38 | 0.36 |
| 80 | 800 | 0.38 | 0.39 | 0.38 | 0.37 | 0.38 | 0.38 | 0.37 | 0.37 | 0.37 | 0.38 | 0.37 | 0.36 |
| 100 | 600 | 0.41 | 0.40 | 0.40 | 0.39 | 0.41 | 0.40 | 0.39 | 0.39 | 0.40 | 0.40 | 0.40 | 0.38 |
| 100 | 800 | 0.40 | 0.40 | 0.39 | 0.39 | 0.40 | 0.40 | 0.40 | 0.39 | 0.40 | 0.39 | 0.39 | 0.38 |
| 120 | 600 | 0.42 | 0.42 | 0.42 | 0.41 | 0.42 | 0.42 | 0.41 | 0.41 | 0.42 | 0.42 | 0.42 | 0.39 |
| 120 | 800 | 0.41 | 0.41 | 0.41 | 0.41 | 0.42 | 0.41 | 0.41 | 0.41 | 0.42 | 0.42 | 0.42 | 0.39 |
| 80 | 600 | 0.75 | 0.74 | 0.74 | 0.73 | 0.75 | 0.74 | 0.74 | 0.73 | 0.75 | 0.74 | 0.74 | 0.72 |
| 80 | 800 | 0.75 | 0.74 | 0.74 | 0.73 | 0.75 | 0.75 | 0.74 | 0.72 | 0.75 | 0.75 | 0.73 | 0.72 |
| 100 | 600 | 0.77 | 0.76 | 0.76 | 0.74 | 0.76 | 0.76 | 0.76 | 0.75 | 0.77 | 0.77 | 0.75 | 0.74 |
| 100 | 800 | 0.77 | 0.76 | 0.76 | 0.75 | 0.77 | 0.76 | 0.76 | 0.75 | 0.76 | 0.76 | 0.75 | 0.74 |
| 120 | 600 | 0.78 | 0.78 | 0.76 | 0.77 | 0.78 | 0.78 | 0.77 | 0.76 | 0.78 | 0.78 | 0.76 | 0.75 |
| 120 | 800 | 0.78 | 0.78 | 0.77 | 0.76 | 0.78 | 0.77 | 0.77 | 0.76 | 0.78 | 0.78 | 0.77 | 0.76 |
| 80 | 600 | 0.54 | 0.53 | 0.53 | 0.53 | 0.55 | 0.55 | 0.53 | 0.53 | 0.54 | 0.53 | 0.54 | 0.53 |
| 80 | 800 | 0.54 | 0.53 | 0.54 | 0.53 | 0.55 | 0.54 | 0.52 | 0.54 | 0.55 | 0.53 | 0.54 | 0.54 |
| 100 | 600 | 0.56 | 0.55 | 0.54 | 0.53 | 0.56 | 0.55 | 0.55 | 0.55 | 0.56 | 0.55 | 0.54 | 0.54 |
| 100 | 800 | 0.57 | 0.56 | 0.56 | 0.56 | 0.55 | 0.56 | 0.55 | 0.53 | 0.55 | 0.55 | 0.55 | 0.54 |
| 120 | 600 | 0.57 | 0.57 | 0.57 | 0.57 | 0.57 | 0.58 | 0.56 | 0.56 | 0.58 | 0.57 | 0.56 | 0.55 |
| 120 | 800 | 0.57 | 0.57 | 0.56 | 0.56 | 0.57 | 0.58 | 0.57 | 0.56 | 0.57 | 0.57 | 0.56 | 0.56 |
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 0.92 | 0.91 | 0.91 | 0.91 | 0.92 | 0.91 | 0.90 | 0.90 | 0.92 | 0.91 | 0.90 | 0.89 |
| 80 | 800 | 0.92 | 0.91 | 0.91 | 0.91 | 0.92 | 0.91 | 0.91 | 0.90 | 0.92 | 0.91 | 0.90 | 0.89 |
| 100 | 600 | 0.93 | 0.93 | 0.92 | 0.92 | 0.93 | 0.92 | 0.92 | 0.91 | 0.93 | 0.92 | 0.91 | 0.91 |
| 100 | 800 | 0.93 | 0.93 | 0.92 | 0.92 | 0.93 | 0.92 | 0.92 | 0.91 | 0.93 | 0.92 | 0.91 | 0.91 |
| 120 | 600 | 0.94 | 0.94 | 0.93 | 0.93 | 0.94 | 0.94 | 0.93 | 0.92 | 0.94 | 0.94 | 0.92 | 0.92 |
| 120 | 800 | 0.94 | 0.94 | 0.93 | 0.93 | 0.94 | 0.94 | 0.93 | 0.92 | 0.94 | 0.94 | 0.92 | 0.92 |
| 80 | 600 | 0.83 | 0.81 | 0.81 | 0.79 | 0.83 | 0.82 | 0.81 | 0.79 | 0.83 | 0.82 | 0.80 | 0.77 |
| 80 | 800 | 0.82 | 0.82 | 0.80 | 0.80 | 0.83 | 0.82 | 0.81 | 0.80 | 0.83 | 0.82 | 0.80 | 0.77 |
| 100 | 600 | 0.84 | 0.84 | 0.83 | 0.82 | 0.85 | 0.84 | 0.82 | 0.82 | 0.85 | 0.84 | 0.82 | 0.80 |
| 100 | 800 | 0.85 | 0.84 | 0.83 | 0.82 | 0.85 | 0.84 | 0.84 | 0.82 | 0.85 | 0.84 | 0.83 | 0.80 |
| 120 | 600 | 0.86 | 0.85 | 0.85 | 0.84 | 0.87 | 0.86 | 0.84 | 0.83 | 0.87 | 0.86 | 0.84 | 0.81 |
| 120 | 800 | 0.87 | 0.86 | 0.85 | 0.84 | 0.87 | 0.85 | 0.85 | 0.83 | 0.87 | 0.86 | 0.84 | 0.81 |
| 80 | 600 | 0.76 | 0.76 | 0.75 | 0.73 | 0.77 | 0.75 | 0.73 | 0.72 | 0.77 | 0.76 | 0.73 | 0.68 |
| 80 | 800 | 0.78 | 0.75 | 0.75 | 0.73 | 0.77 | 0.76 | 0.74 | 0.73 | 0.77 | 0.75 | 0.73 | 0.69 |
| 100 | 600 | 0.79 | 0.77 | 0.77 | 0.75 | 0.79 | 0.78 | 0.76 | 0.75 | 0.78 | 0.78 | 0.76 | 0.71 |
| 100 | 800 | 0.79 | 0.78 | 0.78 | 0.75 | 0.79 | 0.78 | 0.78 | 0.74 | 0.80 | 0.78 | 0.76 | 0.71 |
| 120 | 600 | 0.81 | 0.80 | 0.77 | 0.78 | 0.80 | 0.79 | 0.78 | 0.77 | 0.80 | 0.79 | 0.77 | 0.72 |
| 120 | 800 | 0.81 | 0.80 | 0.79 | 0.77 | 0.81 | 0.80 | 0.79 | 0.77 | 0.81 | 0.80 | 0.78 | 0.73 |
| 80 | 600 | 0.85 | 0.84 | 0.83 | 0.82 | 0.85 | 0.84 | 0.83 | 0.82 | 0.85 | 0.84 | 0.83 | 0.80 |
| 80 | 800 | 0.85 | 0.84 | 0.83 | 0.82 | 0.85 | 0.84 | 0.83 | 0.82 | 0.85 | 0.84 | 0.83 | 0.81 |
| 100 | 600 | 0.86 | 0.86 | 0.85 | 0.84 | 0.86 | 0.85 | 0.85 | 0.84 | 0.87 | 0.86 | 0.85 | 0.83 |
| 100 | 800 | 0.87 | 0.86 | 0.86 | 0.85 | 0.87 | 0.86 | 0.85 | 0.85 | 0.87 | 0.86 | 0.85 | 0.83 |
| 120 | 600 | 0.88 | 0.87 | 0.87 | 0.86 | 0.87 | 0.87 | 0.87 | 0.85 | 0.88 | 0.87 | 0.86 | 0.85 |
| 120 | 800 | 0.88 | 0.88 | 0.87 | 0.86 | 0.88 | 0.87 | 0.87 | 0.86 | 0.88 | 0.88 | 0.86 | 0.85 |
| 80 | 600 | 0.79 | 0.79 | 0.77 | 0.76 | 0.79 | 0.78 | 0.77 | 0.76 | 0.79 | 0.78 | 0.77 | 0.75 |
| 80 | 800 | 0.80 | 0.79 | 0.78 | 0.77 | 0.80 | 0.79 | 0.79 | 0.77 | 0.80 | 0.79 | 0.77 | 0.76 |
| 100 | 600 | 0.81 | 0.81 | 0.80 | 0.78 | 0.81 | 0.80 | 0.79 | 0.78 | 0.81 | 0.80 | 0.79 | 0.77 |
| 100 | 800 | 0.82 | 0.81 | 0.81 | 0.79 | 0.82 | 0.81 | 0.80 | 0.79 | 0.82 | 0.82 | 0.80 | 0.78 |
| 120 | 600 | 0.83 | 0.82 | 0.81 | 0.81 | 0.83 | 0.82 | 0.81 | 0.80 | 0.83 | 0.82 | 0.81 | 0.79 |
| 120 | 800 | 0.84 | 0.83 | 0.82 | 0.81 | 0.84 | 0.83 | 0.82 | 0.81 | 0.84 | 0.83 | 0.82 | 0.79 |
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 1.88 | 1.86 | 1.88 | 1.85 | 1.88 | 1.86 | 1.87 | 1.81 | 1.88 | 1.84 | 1.82 | 1.80 |
| 80 | 800 | 1.86 | 1.86 | 1.84 | 1.84 | 1.83 | 1.84 | 1.87 | 1.81 | 1.85 | 1.85 | 1.85 | 1.85 |
| 100 | 600 | 1.91 | 1.87 | 1.85 | 1.90 | 1.88 | 1.89 | 1.86 | 1.87 | 1.88 | 1.88 | 1.85 | 1.86 |
| 100 | 800 | 1.86 | 1.85 | 1.90 | 1.86 | 1.91 | 1.86 | 1.89 | 1.85 | 1.91 | 1.87 | 1.84 | 1.83 |
| 120 | 600 | 1.89 | 1.92 | 1.87 | 1.87 | 1.90 | 1.91 | 1.92 | 1.85 | 1.90 | 1.91 | 1.85 | 1.90 |
| 120 | 800 | 1.91 | 1.89 | 1.89 | 1.87 | 1.91 | 1.89 | 1.85 | 1.87 | 1.91 | 1.89 | 1.87 | 1.87 |
| 80 | 600 | 1.12 | 1.10 | 1.10 | 1.07 | 1.12 | 1.10 | 1.10 | 1.08 | 1.12 | 1.10 | 1.09 | 1.06 |
| 80 | 800 | 1.12 | 1.11 | 1.09 | 1.08 | 1.12 | 1.11 | 1.10 | 1.09 | 1.12 | 1.11 | 1.09 | 1.07 |
| 100 | 600 | 1.12 | 1.11 | 1.10 | 1.09 | 1.12 | 1.11 | 1.10 | 1.09 | 1.12 | 1.11 | 1.10 | 1.07 |
| 100 | 800 | 1.13 | 1.11 | 1.11 | 1.10 | 1.13 | 1.12 | 1.11 | 1.10 | 1.13 | 1.12 | 1.11 | 1.08 |
| 120 | 600 | 1.13 | 1.11 | 1.11 | 1.10 | 1.13 | 1.12 | 1.11 | 1.10 | 1.13 | 1.12 | 1.11 | 1.08 |
| 120 | 800 | 1.14 | 1.12 | 1.12 | 1.11 | 1.14 | 1.13 | 1.11 | 1.11 | 1.14 | 1.13 | 1.11 | 1.08 |
| 80 | 600 | 1.38 | 1.35 | 1.31 | 1.31 | 1.37 | 1.34 | 1.31 | 1.29 | 1.39 | 1.34 | 1.31 | 1.23 |
| 80 | 800 | 1.39 | 1.35 | 1.34 | 1.31 | 1.39 | 1.36 | 1.34 | 1.31 | 1.39 | 1.36 | 1.32 | 1.25 |
| 100 | 600 | 1.39 | 1.37 | 1.35 | 1.32 | 1.40 | 1.37 | 1.35 | 1.33 | 1.39 | 1.37 | 1.33 | 1.26 |
| 100 | 800 | 1.41 | 1.38 | 1.36 | 1.33 | 1.41 | 1.38 | 1.37 | 1.32 | 1.41 | 1.38 | 1.35 | 1.29 |
| 120 | 600 | 1.43 | 1.39 | 1.36 | 1.35 | 1.41 | 1.39 | 1.37 | 1.34 | 1.41 | 1.39 | 1.34 | 1.29 |
| 120 | 800 | 1.44 | 1.40 | 1.38 | 1.35 | 1.42 | 1.41 | 1.39 | 1.35 | 1.43 | 1.41 | 1.36 | 1.29 |
| 80 | 600 | 1.07 | 1.07 | 1.05 | 1.04 | 1.07 | 1.07 | 1.06 | 1.05 | 1.07 | 1.07 | 1.05 | 1.04 |
| 80 | 800 | 1.07 | 1.07 | 1.06 | 1.06 | 1.07 | 1.07 | 1.06 | 1.06 | 1.07 | 1.06 | 1.06 | 1.04 |
| 100 | 600 | 1.08 | 1.07 | 1.06 | 1.06 | 1.08 | 1.07 | 1.06 | 1.05 | 1.07 | 1.07 | 1.07 | 1.05 |
| 100 | 800 | 1.07 | 1.07 | 1.07 | 1.06 | 1.08 | 1.07 | 1.07 | 1.06 | 1.08 | 1.07 | 1.07 | 1.05 |
| 120 | 600 | 1.08 | 1.07 | 1.08 | 1.07 | 1.08 | 1.07 | 1.07 | 1.06 | 1.08 | 1.07 | 1.07 | 1.06 |
| 120 | 800 | 1.08 | 1.08 | 1.07 | 1.07 | 1.08 | 1.08 | 1.08 | 1.06 | 1.09 | 1.08 | 1.07 | 1.06 |
| 80 | 600 | 1.22 | 1.22 | 1.19 | 1.17 | 1.21 | 1.20 | 1.19 | 1.17 | 1.22 | 1.21 | 1.18 | 1.15 |
| 80 | 800 | 1.22 | 1.22 | 1.20 | 1.18 | 1.22 | 1.21 | 1.22 | 1.18 | 1.22 | 1.22 | 1.18 | 1.16 |
| 100 | 600 | 1.23 | 1.22 | 1.22 | 1.20 | 1.23 | 1.22 | 1.21 | 1.19 | 1.23 | 1.22 | 1.22 | 1.17 |
| 100 | 800 | 1.23 | 1.23 | 1.21 | 1.18 | 1.24 | 1.22 | 1.22 | 1.21 | 1.25 | 1.24 | 1.21 | 1.18 |
| 120 | 600 | 1.24 | 1.22 | 1.22 | 1.21 | 1.24 | 1.22 | 1.23 | 1.21 | 1.24 | 1.23 | 1.22 | 1.20 |
| 120 | 800 | 1.25 | 1.23 | 1.23 | 1.22 | 1.26 | 1.23 | 1.22 | 1.23 | 1.25 | 1.24 | 1.23 | 1.20 |
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 1.99 | 1.97 | 2.01 | 1.98 | 1.99 | 1.97 | 2.01 | 2.03 | 1.99 | 1.95 | 2.01 | 2.06 |
| 80 | 800 | 1.97 | 1.98 | 1.95 | 1.96 | 1.93 | 1.95 | 2.00 | 2.01 | 1.96 | 1.97 | 2.07 | 2.09 |
| 100 | 600 | 2.00 | 1.96 | 1.94 | 2.00 | 1.97 | 1.99 | 2.08 | 2.25 | 1.97 | 1.99 | 2.21 | 2.27 |
| 100 | 800 | 1.95 | 1.93 | 2.00 | 1.96 | 2.01 | 1.95 | 2.09 | 2.20 | 2.00 | 1.98 | 2.11 | 2.25 |
| 120 | 600 | 1.96 | 2.00 | 1.95 | 1.96 | 1.97 | 2.00 | 2.24 | 2.21 | 1.97 | 2.04 | 2.18 | 2.28 |
| 120 | 800 | 1.99 | 1.97 | 1.98 | 1.95 | 1.98 | 1.97 | 2.08 | 2.31 | 1.98 | 2.02 | 2.18 | 2.19 |
| 80 | 600 | 1.22 | 1.22 | 1.22 | 1.20 | 1.22 | 1.21 | 1.23 | 1.26 | 1.22 | 1.22 | 1.24 | 1.39 |
| 80 | 800 | 1.22 | 1.22 | 1.20 | 1.20 | 1.22 | 1.22 | 1.23 | 1.27 | 1.22 | 1.23 | 1.25 | 1.37 |
| 100 | 600 | 1.20 | 1.21 | 1.20 | 1.21 | 1.22 | 1.21 | 1.23 | 1.30 | 1.22 | 1.22 | 1.25 | 1.43 |
| 100 | 800 | 1.22 | 1.22 | 1.22 | 1.21 | 1.23 | 1.22 | 1.23 | 1.29 | 1.23 | 1.22 | 1.27 | 1.40 |
| 120 | 600 | 1.22 | 1.21 | 1.21 | 1.20 | 1.22 | 1.22 | 1.23 | 1.31 | 1.22 | 1.22 | 1.28 | 1.44 |
| 120 | 800 | 1.23 | 1.22 | 1.21 | 1.21 | 1.23 | 1.22 | 1.23 | 1.29 | 1.23 | 1.23 | 1.26 | 1.43 |
| 80 | 600 | 2.02 | 2.04 | 2.04 | 2.10 | 1.99 | 2.03 | 2.12 | 2.33 | 2.02 | 2.05 | 2.22 | 2.33 |
| 80 | 800 | 2.03 | 2.00 | 2.07 | 2.10 | 2.03 | 2.09 | 2.17 | 2.39 | 2.06 | 2.07 | 2.28 | 2.36 |
| 100 | 600 | 1.95 | 1.97 | 2.01 | 2.01 | 1.95 | 1.98 | 2.15 | 2.39 | 1.93 | 2.03 | 2.28 | 2.37 |
| 100 | 800 | 1.96 | 1.99 | 2.04 | 2.05 | 1.98 | 1.99 | 2.17 | 2.36 | 1.96 | 2.06 | 2.28 | 2.39 |
| 120 | 600 | 1.94 | 1.94 | 1.92 | 1.97 | 1.91 | 1.94 | 2.16 | 2.48 | 1.90 | 1.98 | 2.30 | 2.59 |
| 120 | 800 | 1.95 | 1.98 | 1.99 | 1.99 | 1.93 | 1.99 | 2.16 | 2.50 | 1.92 | 2.00 | 2.27 | 2.53 |
| 80 | 600 | 1.12 | 1.13 | 1.12 | 1.12 | 1.13 | 1.14 | 1.14 | 1.19 | 1.12 | 1.13 | 1.14 | 1.23 |
| 80 | 800 | 1.13 | 1.13 | 1.13 | 1.13 | 1.12 | 1.13 | 1.14 | 1.19 | 1.13 | 1.13 | 1.15 | 1.21 |
| 100 | 600 | 1.13 | 1.13 | 1.12 | 1.13 | 1.13 | 1.13 | 1.15 | 1.20 | 1.12 | 1.13 | 1.18 | 1.27 |
| 100 | 800 | 1.12 | 1.13 | 1.14 | 1.14 | 1.13 | 1.13 | 1.14 | 1.20 | 1.14 | 1.14 | 1.16 | 1.25 |
| 120 | 600 | 1.13 | 1.13 | 1.14 | 1.13 | 1.12 | 1.13 | 1.16 | 1.21 | 1.13 | 1.13 | 1.18 | 1.30 |
| 120 | 800 | 1.12 | 1.13 | 1.13 | 1.13 | 1.12 | 1.13 | 1.16 | 1.20 | 1.14 | 1.14 | 1.17 | 1.29 |
| 80 | 600 | 1.47 | 1.50 | 1.48 | 1.48 | 1.45 | 1.45 | 1.54 | 1.62 | 1.46 | 1.51 | 1.54 | 1.66 |
| 80 | 800 | 1.47 | 1.52 | 1.48 | 1.49 | 1.47 | 1.48 | 1.59 | 1.61 | 1.46 | 1.52 | 1.54 | 1.62 |
| 100 | 600 | 1.45 | 1.47 | 1.50 | 1.52 | 1.45 | 1.48 | 1.56 | 1.68 | 1.46 | 1.50 | 1.65 | 1.72 |
| 100 | 800 | 1.44 | 1.48 | 1.47 | 1.45 | 1.48 | 1.48 | 1.55 | 1.70 | 1.49 | 1.51 | 1.61 | 1.73 |
| 120 | 600 | 1.44 | 1.44 | 1.46 | 1.47 | 1.45 | 1.44 | 1.61 | 1.80 | 1.44 | 1.49 | 1.65 | 1.86 |
| 120 | 800 | 1.46 | 1.46 | 1.49 | 1.47 | 1.47 | 1.45 | 1.57 | 1.78 | 1.46 | 1.49 | 1.67 | 1.84 |
| Stock | Stock/Flow (Average) | Stock/Change in Flow (Average) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ratio of missing data | ratio of missing data | ratio of missing data | |||||||||||
| N | T | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% | 0% | 5% | 10% | 15% |
| 80 | 600 | 1.99 | 1.96 | 2.00 | 1.96 | 1.99 | 1.97 | 1.98 | 1.92 | 1.99 | 1.96 | 1.94 | 1.93 |
| 80 | 800 | 1.97 | 1.97 | 1.94 | 1.94 | 1.93 | 1.95 | 1.99 | 1.92 | 1.96 | 1.96 | 1.98 | 1.98 |
| 100 | 600 | 2.00 | 1.95 | 1.93 | 1.98 | 1.97 | 1.98 | 1.96 | 1.98 | 1.97 | 1.97 | 1.95 | 1.98 |
| 100 | 800 | 1.95 | 1.93 | 1.99 | 1.94 | 2.01 | 1.95 | 1.98 | 1.95 | 2.00 | 1.97 | 1.94 | 1.94 |
| 120 | 600 | 1.96 | 1.99 | 1.95 | 1.95 | 1.97 | 1.99 | 2.00 | 1.95 | 1.97 | 1.99 | 1.93 | 2.01 |
| 120 | 800 | 1.99 | 1.97 | 1.97 | 1.94 | 1.98 | 1.97 | 1.93 | 1.97 | 1.98 | 1.97 | 1.96 | 1.98 |
| 80 | 600 | 1.22 | 1.21 | 1.21 | 1.20 | 1.22 | 1.21 | 1.22 | 1.21 | 1.22 | 1.21 | 1.20 | 1.21 |
| 80 | 800 | 1.22 | 1.22 | 1.20 | 1.20 | 1.22 | 1.22 | 1.22 | 1.21 | 1.22 | 1.22 | 1.21 | 1.22 |
| 100 | 600 | 1.20 | 1.21 | 1.20 | 1.21 | 1.22 | 1.21 | 1.21 | 1.21 | 1.22 | 1.21 | 1.20 | 1.21 |
| 100 | 800 | 1.22 | 1.22 | 1.22 | 1.21 | 1.23 | 1.22 | 1.22 | 1.21 | 1.23 | 1.22 | 1.22 | 1.21 |
| 120 | 600 | 1.22 | 1.21 | 1.21 | 1.20 | 1.22 | 1.21 | 1.21 | 1.21 | 1.22 | 1.21 | 1.22 | 1.21 |
| 120 | 800 | 1.23 | 1.21 | 1.22 | 1.21 | 1.23 | 1.22 | 1.21 | 1.22 | 1.23 | 1.22 | 1.21 | 1.20 |
| 80 | 600 | 2.02 | 1.99 | 1.94 | 1.99 | 1.99 | 1.97 | 1.95 | 1.95 | 2.02 | 1.96 | 1.94 | 1.89 |
| 80 | 800 | 2.03 | 1.95 | 2.00 | 1.99 | 2.03 | 2.02 | 2.00 | 1.98 | 2.06 | 1.99 | 2.01 | 1.94 |
| 100 | 600 | 1.95 | 1.92 | 1.93 | 1.89 | 1.95 | 1.93 | 1.94 | 1.92 | 1.93 | 1.94 | 1.90 | 1.84 |
| 100 | 800 | 1.96 | 1.95 | 1.96 | 1.95 | 1.98 | 1.94 | 1.96 | 1.90 | 1.96 | 1.98 | 1.95 | 1.89 |
| 120 | 600 | 1.94 | 1.90 | 1.85 | 1.88 | 1.91 | 1.88 | 1.88 | 1.85 | 1.90 | 1.89 | 1.85 | 1.86 |
| 120 | 800 | 1.95 | 1.94 | 1.92 | 1.89 | 1.93 | 1.93 | 1.92 | 1.87 | 1.92 | 1.92 | 1.87 | 1.89 |
| 80 | 600 | 1.12 | 1.13 | 1.12 | 1.12 | 1.13 | 1.13 | 1.12 | 1.13 | 1.12 | 1.13 | 1.12 | 1.12 |
| 80 | 800 | 1.13 | 1.13 | 1.13 | 1.13 | 1.12 | 1.12 | 1.12 | 1.13 | 1.13 | 1.12 | 1.12 | 1.12 |
| 100 | 600 | 1.13 | 1.13 | 1.12 | 1.13 | 1.13 | 1.12 | 1.12 | 1.12 | 1.12 | 1.12 | 1.14 | 1.12 |
| 100 | 800 | 1.12 | 1.13 | 1.13 | 1.13 | 1.13 | 1.13 | 1.12 | 1.13 | 1.14 | 1.13 | 1.13 | 1.12 |
| 120 | 600 | 1.13 | 1.12 | 1.14 | 1.13 | 1.12 | 1.12 | 1.13 | 1.12 | 1.13 | 1.12 | 1.13 | 1.13 |
| 120 | 800 | 1.12 | 1.13 | 1.12 | 1.13 | 1.12 | 1.13 | 1.13 | 1.13 | 1.14 | 1.13 | 1.12 | 1.13 |
| 80 | 600 | 1.47 | 1.48 | 1.45 | 1.44 | 1.45 | 1.43 | 1.45 | 1.43 | 1.46 | 1.47 | 1.43 | 1.42 |
| 80 | 800 | 1.47 | 1.51 | 1.45 | 1.45 | 1.47 | 1.46 | 1.50 | 1.43 | 1.46 | 1.50 | 1.42 | 1.42 |
| 100 | 600 | 1.45 | 1.46 | 1.47 | 1.47 | 1.45 | 1.46 | 1.45 | 1.43 | 1.46 | 1.46 | 1.47 | 1.42 |
| 100 | 800 | 1.44 | 1.46 | 1.45 | 1.42 | 1.48 | 1.46 | 1.45 | 1.47 | 1.49 | 1.48 | 1.45 | 1.43 |
| 120 | 600 | 1.44 | 1.43 | 1.43 | 1.43 | 1.45 | 1.41 | 1.45 | 1.44 | 1.44 | 1.44 | 1.43 | 1.44 |
| 120 | 800 | 1.46 | 1.45 | 1.47 | 1.44 | 1.47 | 1.44 | 1.43 | 1.44 | 1.46 | 1.46 | 1.45 | 1.43 |
Appendix C. Underlying Data
| Real output and income | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 1. | IPFINAL* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Final Products (Market Group), Index 2012=100, SA, delay of 0 months, fred/IPFINAL (https://fred.stlouisfed.org/series/IPFINAL) |
| IPCONGD* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Consumer Goods, Index 2012=100, SA, delay of 0 months, fred/IPCONGD (https://fred.stlouisfed.org/series/IPCONGD) | |
| 3. | IPDCONGD* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Durable Consumer Goods, Index 2012=100, SA, delay of 0 months, fred/IPDCONGD (https://fred.stlouisfed.org/series/IPDCONGD) |
| 4. | IPNCONGD* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Nondurable Consumer Goods, Index 2012=100, SA, delay of 0 months, fred/IPNCONGD (https://fred.stlouisfed.org/series/IPNCONGD) |
| 5. | IPBUSEQ* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Business Equipment, Index 2012=100, SA, delay of 0 months, fred/IPBUSEQ (https://fred.stlouisfed.org/series/IPBUSEQ) |
| 6. | IPMAT* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Materials, Index 2012=100, SA, delay of 0 months, fred/IPMAT (https://fred.stlouisfed.org/series/IPMAT) |
| 7. | IPB53100N* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Durable goods materials, Index 2012=100, NSA, delay of 0 months, fred/IPB53100N (https://fred.stlouisfed.org/series/IPB53100N) |
| 8. | IPB53200N* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production: Nondurable Goods Materials, Index 2012=100, NSA, delay of 0 months, fred/IPB53200N (https://fred.stlouisfed.org/series/IPB53200N) |
| 9. | IPMANSICS* | 1959:01-2015:10 | m | 1 | 5 | Industrial Production: Manufacturing (SIC), Index 2012=100, SA, delay of 0 months, fred/IPMANSICS (https://fred.stlouisfed.org/series/IPMANSICS) |
| 10. | INDPRO* | 1959:01–2015:10 | m | 1 | 5 | Industrial Production Index, Index 2012=100, SA, delay of 0 months, fred/INDPRO (https://fred.stlouisfed.org/series/INDPRO) |
| 11. | CUMFNS* | 1959:01–2015:10 | m | 1 | 1 | Capacity Utilization: Manufacturing (SIC), Percent of Capacity, SA, delay of 0 months, fred/CUMFNS (https://fred.stlouisfed.org/series/CUMFNS) |
| 12. | NAPM* | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: PMI Composite Index, Index, SA, delay of 0 months, fred/NAPM (https://fred.stlouisfed.org/series/NAPM) |
| 13. | NAPMPI* | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: Production Index, Index, SA, delay of 0 months, fred/NAPMPI (https://fred.stlouisfed.org/series/NAPMPI) |
| 14. | RPI* | 1959:01–2015:10 | m | 1 | 5 | Real Personal Income, billions of chained 2009 USD, SA Annual Rate, delay of 0 months, fred/RPI (https://fred.stlouisfed.org/series/RPI) |
| 15. | W875RX1* | 1959:01–2015:10 | m | 1 | 5 | Real Personal Income Excluding Current Transfer Receipts, billions of chained 2009 USD, SA annual rate, delay of 0 months, fred/W875RX1 (https://fred.stlouisfed.org/series/W875RX1) |
| Employment and hours | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 16. | CE16OV* | 1959:01–2015:10 | m | 1 | 5 | Civilian Employment, thousands of persons, SA, delay of 0 months, fred/CE16OV (https://fred.stlouisfed.org/series/CE16OV) |
| UNRATE* | 1959:01–2015:10 | m | 1 | 1 | Civilian Unemployment Rate, percent, SA, delay of 0 months, fred/UNRATE (https://fred.stlouisfed.org/series/UNRATE) | |
| 18. | UEMPMEAN* | 1959:01–2015:10 | m | 1 | 5 | Average (Mean) Duration of Unemployment, Weeks, SA, delay of 0 months, fred/UEMPMEAN (https://fred.stlouisfed.org/series/UEMPMEAN) |
| 19. | UEMPLT5* | 1959:01–2015:10 | m | 1 | 5 | Number of Civilians Unemployed for Less Than 5 Weeks, thousands of persons, SA, delay of 0 months, fred/UEMPLT5 (https://fred.stlouisfed.org/series/UEMPLT5) |
| 20. | UEMP5TO14* | 1959:01–2015:10 | m | 1 | 5 | Number of Civilians Unemployed for 5 to 14 Weeks, thousands of persons, SA, delay of 0 months, fred/UEMP5TO14 (https://fred.stlouisfed.org/series/UEMP5TO14) |
| 21. | UEMP15OV* | 1959:01–2015:10 | m | 1 | 5 | Number of Civilians Unemployed for 15 Weeks and Over, thousands of persons, SA, delay of 0 months, fred/UEMP15OV (https://fred.stlouisfed.org/series/UEMP15OV) |
| 22. | UEMP15T26* | 1959:01–2015:10 | m | 1 | 5 | Number of Civilians Unemployed for 15 to 26 Weeks, thousands of persons, SA, delay of 0 months, fred/UEMP15T26 (https://fred.stlouisfed.org/series/UEMP15T26) |
| PAYEMS* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Total Nonfarm Payrolls, thousands of persons, SA, delay of 0 months, fred/PAYEMS (https://fred.stlouisfed.org/series/PAYEMS) | |
| 24. | USPRIV* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Total Private Industries, thousands of persons, SA, delay of 0 months, fred/USPRIV (https://fred.stlouisfed.org/series/USPRIV) |
| 25. | USGOOD* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Goods-Producing Industries, Thousands of Persons, SA, delay of 0 months, fred/USGOOD (https://fred.stlouisfed.org/series/USGOOD) |
| 26. | CES1021000001* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Mining and Logging: Mining, thousands of persons, SA, delay of 0 months, fred/CES1021000001 (https://fred.stlouisfed.org/series/CES1021000001) |
| 27. | USCONS* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Construction, thousands of persons, SA, delay of 0 months, fred/USCONS (https://fred.stlouisfed.org/series/USCONS) |
| 28. | MANEMP* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Manufacturing, thousands of persons, SA, delay of 0 months, fred/MANEMP (https://fred.stlouisfed.org/series/MANEMP) |
| 29. | DMANEMP* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Durable Goods, thousands of persons, SA, delay of 0 months, fred/DMANEMP (https://fred.stlouisfed.org/series/DMANEMP) |
| 30. | NDMANEMP* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Nondurable Goods, thousands of persons, SA, delay of 0 months, fred/NDMANEMP (https://fred.stlouisfed.org/series/NDMANEMP) |
| 31. | CES0800000001* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Private Service-Providing, thousands of persons, SA, delay of 0 months, fred/CES0800000001 (https://fred.stlouisfed.org/series/CES0800000001) |
| 32. | USTPU* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Trade, Transportation and Utilities, thousands of persons, SA, delay of 0 months, fred/USTPU (https://fred.stlouisfed.org/series/USTPU) |
| 33. | USWTRADE* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Wholesale Trade, thousands of persons, SA, delay of 0 months, fred/USWTRADE (https://fred.stlouisfed.org/series/USWTRADE) |
| USFIRE* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Financial Activities, thousands of persons, SA, delay of 0 months, fred/USFIRE (https://fred.stlouisfed.org/series/USFIRE) | |
| 35. | USPBS* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Professional and Business Services, thousands of persons, SA, delay of 0 months, fred/USPBS (https://fred.stlouisfed.org/series/USPBS) |
| 36. | USGOVT* | 1959:01–2015:10 | m | 1 | 5 | All Employees: Government, thousands of persons, SA, delay of 0 months, fred/USGOVT (https://fred.stlouisfed.org/series/USGOVT) |
| 37. | AWHMAN* | 1959:01–2015:10 | m | 1 | 1 | Average Weekly Hours of Production and Nonsupervisory Employees: Manufacturing, Hours, SA, delay of 0 months, fred/AWHMAN (https://fred.stlouisfed.org/series/AWHMAN) |
| AWOTMAN* | 1959:01–2015:10 | m | 1 | 1 | Average Weekly Overtime Hours of Production and Nonsupervisory Employees: Manufacturing, Hours, SA, delay of 0 months, fred/AWOTMAN (https://fred.stlouisfed.org/series/AWOTMAN) | |
| 39. | NAPMEI* | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: Employment Index, Index, SA, delay of 0 months, fred/NAPMEI (https://fred.stlouisfed.org/series/NAPMEI) |
| Consumption | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| PCE* | 1959:01–2015:10 | m | 1 | 5 | Personal Consumption Expenditures, billions of USD, SA annual rate, delay of 0 months, fred/PCE (https://fred.stlouisfed.org/series/PCE) | |
| 41. | PCEDG* | 1959:01–2015:10 | m | 1 | 5 | Personal Consumption Expenditures: Durable Goods, billions of USD, SA annual rate, delay of 0 months, fred/PCEDG (https://fred.stlouisfed.org/series/PCEDG) |
| 42. | PCEND* | 1959:01–2015:10 | m | 1 | 5 | Personal Consumption Expenditures: Nondurable Goods, billions of USD, SA annual rate, delay of 0 months, fred/PCEND (https://fred.stlouisfed.org/series/PCEND) |
| 43. | PCES* | 1959:01–2015:10 | m | 1 | 5 | Personal Consumption Expenditures: Services, billions of USD, SA annual rate, delay of 0 months, fred/PCES (https://fred.stlouisfed.org/series/PCES) |
| Housing starts and sales | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 44. | HOUST | 1959:01–2015:10 | m | 1 | 4 | Housing Starts: Total: New Privately Owned Housing Units Started, thousands of units, SA annual rate, delay of 0 months, fred/HOUST (https://fred.stlouisfed.org/series/HOUST) |
| 45. | HOUSTNE | 1959:01–2015:10 | m | 1 | 4 | Housing Starts in Northeast Census Region, thousands of units, SA annual rate, delay of 0 months, fred/HOUSTNE (https://fred.stlouisfed.org/series/HOUSTNE) |
| 46. | HOUSTMW | 1959:01–2015:10 | m | 1 | 4 | Housing Starts in Midwest Census Region, thousands of units, SA annual Rate, delay of 0 months, fred/HOUSTMW (https://fred.stlouisfed.org/series/HOUSTMW) |
| 47. | HOUSTS | 1959:01–2015:10 | m | 1 | 4 | Housing Starts in South Census Region, thousands of units, SA annual rate, delay of 0 months, fred/HOUSTS (https://fred.stlouisfed.org/series/HOUSTS) |
| 48. | HOUSTW | 1959:01–2015:10 | m | 1 | 4 | Housing Starts in West Census Region, thousands of units, SA annual rate, delay of 0 months, fred/HOUSTW (https://fred.stlouisfed.org/series/HOUSTW) |
| 49. | PERMITNSA | 1959:01–2015:10 | m | 1 | 4 | New Private Housing Units Authorized by Building Permits, thousands of units, NSA, delay of 0 months, fred/PERMITNSA (https://fred.stlouisfed.org/series/PERMITNSA) |
| Real inventories, orders, and unfilled orders | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 50. | NAPMII | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: Inventories Index, Index, NSA, delay of 0 months, fred/NAPMII (https://fred.stlouisfed.org/series/NAPMII) |
| 51. | NAPMNOI | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: New Orders Index, Index, SA, delay of 0 months, fred/NAPMNOI (https://fred.stlouisfed.org/series/NAPMNOI) |
| 52. | NAPMSDI | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: Supplier Deliveries Index, Index, SA, delay of 0 months, fred/NAPMSDI (https://fred.stlouisfed.org/series/NAPMSDI) |
| Stock prices | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 53. | FSPCOM | 1959:01–2015:10 | m | 1 | 5 | S&P’s Common Stock Price Index: Composite, delay of 0 months, http://www.econ.yale.edu/~shiller/data/ie_data.xls |
| 54. | FSDXP | 1959:01–2015:10 | m | 1 | 1 | S&P’s Composite Common Stock: Dividend Yield, delay of 0 months, http://www.econ.yale.edu/~shiller/data/ ie_data.xls |
| 55. | FSPXE | 1959:01–2015:10 | m | 1 | 1 | S&P’s Composite Common Stock: Price-Earnings Ratio, delay of 0 months, http://www.econ.yale.edu/∼shiller/data/ie_data.xls |
| Foreign exchange rates | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 56. | EXSZUS | 1959:01–2015:10 | m | 1 | 5 | Switzerland / US Foreign Exchange Rate, Swiss Francs to One USD, NSA, delay of 0 months, fred/EXSZUS (https://fred.stlouisfed.org/series/EXSZUS) |
| 57. | EXJPUS | 1959:01–2015:10 | m | 1 | 5 | Japan / US Foreign Exchange Rate, Japanese Yen to One USD, NSA, delay of 0 months, fred/EXJPUS (https://fred.stlouisfed.org/series/EXJPUS) |
| 58. | EXUSUK | 1959:01–2015:10 | m | 1 | 5 | US / UK Foreign Exchange Rate, USDs to One British Pound, NSA, delay of 0 months, fred/EXUSUK (https://fred.stlouisfed.org/series/EXUSUK) |
| 59. | EXCAUS | 1959:01–2015:10 | m | 1 | 5 | Canada / US Foreign Exchange Rate, Canadian Dollars to One USD, NSA, delay of 0 months, fred/EXCAUS (https://fred.stlouisfed.org/series/EXCAUS) |
| Interest rates | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 60. | TB3MS | 1959:01–2015:10 | m | 1 | 1 | 3-Month Treasury Bill: Secondary Market Rate, percent, NSA, delay of 0 months, fred/TB3MS (https://fred.stlouisfed.org/series/TB3MS) |
| 61. | TB6MS | 1959:01–2015:10 | m | 1 | 1 | 6-Month Treasury Bill: Secondary Market Rate, percent, NSA, delay of 0 months, fred/TB6MS (https://fred.stlouisfed.org/series/TB6MS) |
| 62. | GS1 | 1959:01–2015:10 | m | 1 | 1 | 1-Year Treasury Constant Maturity Rate, percent, NSA, delay of 0 months, fred/GS1 (https://fred.stlouisfed.org/series/GS1) |
| 63. | GS5 | 1959:01–2015:10 | m | 1 | 1 | 5-Year Treasury Constant Maturity Rate, percent, NSA, delay of 0 months, fred/GS5 (https://fred.stlouisfed.org/series/GS5) |
| 64. | GS10 | 1959:01–2015:10 | m | 1 | 1 | 10-Year Treasury Constant Maturity Rate, percent, NSA, delay of 0 months, fred/GS10 (https://fred.stlouisfed.org/series/GS10) |
| 65. | AAA | 1959:01–2015:10 | m | 1 | 1 | Moody’s Seasoned Aaa Corporate Bond Yield, percent, NSA, delay of 0 months, fred/AAA (https://fred.stlouisfed.org/series/AAA) |
| 66. | BAA | 1959:01–2015:10 | m | 1 | 1 | Moody’s Seasoned Baa Corporate Bond Yield, percent, NSA, delay of 0 months, fred/BAA (https://fred.stlouisfed.org/series/BAA) |
| 67. | TB3SMFFM | 1959:01–2015:10 | m | 1 | 1 | 3-Month Treasury Bill Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/TB3SMFFM (https://fred.stlouisfed.org/series/TB3SMFFM) |
| 68. | TB6SMFFM | 1959:01–2015:10 | m | 1 | 1 | 6-Month Treasury Bill Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/TB6SMFFM (https://fred.stlouisfed.org/series/TB6SMFFM) |
| 69. | T1YFFM | 1959:01–2015:10 | m | 1 | 1 | 1-Year Treasury Constant Maturity Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/T1YFFM (https://fred.stlouisfed.org/series/T1YFFM) |
| 70. | T5YFFM | 1959:01–2015:10 | m | 1 | 1 | 5-Year Treasury Constant Maturity Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/T5YFFM (https://fred.stlouisfed.org/series/T5YFFM) |
| 71. | T10YFFM | 1959:01–2015:10 | m | 1 | 1 | 10-Year Treasury Constant Maturity Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/T10YFFM (https://fred.stlouisfed.org/series/T10YFFM) |
| 72. | AAAFFM | 1959:01–2015:10 | m | 1 | 1 | Moody’s Seasoned Aaa Corporate Bond Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/AAAFFM (https://fred.stlouisfed.org/series/AAAFFM) |
| 73. | BAAFFM | 1959:01–2015:10 | m | 1 | 1 | Moody’s Seasoned Baa Corporate Bond Minus Federal Funds Rate, percent, NSA, delay of 0 months, fred/BAAFFM (https://fred.stlouisfed.org/series/BAAFFM) |
| Money and credit quantity aggregates | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 74. | M1SL | 1959:01–2015:10 | m | 1 | 5 | M1 Money Stock, billions of USD, SA, delay of 0 months, fred/M1SL (https://fred.stlouisfed.org/series/M1SL) |
| 75. | M2SL | 1959:01–2015:10 | m | 1 | 5 | M2 Money Stock, billions of USD, SA, delay of 0 months, fred/M2SL (https://fred.stlouisfed.org/series/M2SL) |
| 76. | TOTRESNS | 1959:01–2015:10 | m | 1 | 5 | Total Reserves of Depository Institutions, billions of USD, NSA, delay of 0 months, fred/TOTRESNS (https://fred.stlouisfed.org/series/TOTRESNS) |
| 77. | BUSLOANS | 1959:01–2015:10 | m | 1 | 5 | Commercial and Industrial Loans, All Commercial Banks, billions of USD, SA, delay of 0 months, fred/BUSLOANS (https://fred.stlouisfed.org/series/BUSLOANS) |
| 78. | NONREVSL | 1959:01–2015:10 | m | 1 | 5 | Total Nonrevolving Credit Owned and Securitized, Outstanding, billions of USD, SA, delay of 0 months, fred/NONREVSL (https://fred.stlouisfed.org/series/NONREVSL) |
| Price indices | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 79. | NAPMPRI | 1959:01–2015:10 | m | 1 | 1 | ISM Manufacturing: Prices Index, Index, NSA, delay of 0 months, fred/NAPMPRI (https://fred.stlouisfed.org/series/NAPMPRI) |
| 80. | PPIFGS* | 1959:01–2015:10 | m | 1 | 5 | Producer Price Index by Commodity for Finished Goods, Index 1982=100, SA, delay of 0 months, fred/PPIFGS (https://fred.stlouisfed.org/series/PPIFGS) |
| PPIFCG* | 1959:01–2015:10 | m | 1 | 5 | Producer Price Index by Commodity for Finished Consumer Goods, Index 1982=100, SA, delay of 0 months, fred/PPIFCG (https://fred.stlouisfed.org/series/PPIFCG) | |
| 82. | PPIITM* | 1959:01–2015:10 | m | 1 | 5 | Producer Price Index by Commodity Intermediate Materials: Supplies and Components, Index 1982=100, SA, delay of 0 months, fred/PPIITM (https://fred.stlouisfed.org/series/PPIITM) |
| PPICRM* | 1959:01–2015:10 | m | 1 | 5 | Producer Price Index by Commodity for Crude Materials for Further Processing, Index 1982=100, SA, delay of 0 months, fred/PPICRM (https://fred.stlouisfed.org/series/PPICRM) | |
| 84. | CPIAUCSL* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: All Items, Index 1982–1984=100, SA, delay of 0 months, fred/CPIAUCSL (https://fred.stlouisfed.org/series/CPIAUCSL) |
| 85. | CPIAPPSL* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: Apparel, Index 1982–1984=100, SA, delay of 0 months, fred/CPIAPPSL (https://fred.stlouisfed.org/series/CPIAPPSL) |
| 86. | CPITRNSL* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: Transportation, Index 1982–1984=100, SA, delay of 0 months, fred/CPITRNSL (https://fred.stlouisfed.org/series/CPITRNSL) |
| 87. | CPIMEDSL* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: Medical Care, Index 1982–1984=100, SA, delay of 0 months, fred/CPIMEDSL (https://fred.stlouisfed.org/series/CPIMEDSL) |
| 88. | CUSR0000SAC* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: Commodities, Index 1982–1984=100, SA, delay of 0 months, fred/CUSR0000SAC (https://fred.stlouisfed.org/series/CUSR0000SAC) |
| 89. | CUSR0000SAD* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: Durables, Index 1982–1984=100, SA, delay of 0 months, fred/CUSR0000SAD (https://fred.stlouisfed.org/series/CUSR0000SAD) |
| 90. | CUSR0000SAS* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: Services, Index 1982–1984=100, SA, delay of 0 months, fred/CUSR0000SAS (https://fred.stlouisfed.org/series/CUSR0000SAS) |
| CPILFESL* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: All Items Less Food and Energy, Index 1982–1984=100, SA, delay of 0 months, fred/CPILFESL (https://fred.stlouisfed.org/series/CPILFESL) | |
| 92. | CUSR0000SA0L2* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: All items less shelter, Index 1982–1984=100, SA, delay of 0 months, fred/CUSR0000SA0L2 (https://fred.stlouisfed.org/series/CUSR0000SA0L2) |
| 93. | CUSR0000SA0L5* | 1959:01–2015:10 | m | 1 | 5 | Consumer Price Index for All Urban Consumers: All items less medical care, Index 1982–1984=100, SA, delay of 0 months, fred/CUSR0000SA0L5 (https://fred.stlouisfed.org/series/CUSR0000SA0L5) |
| Average hourly earnings | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 94. | CES2000000008* | 1959:01–2015:10 | m | 1 | 5 | Average Hourly Earnings of Production and Nonsupervisory Employees: Construction, USD per Hour, SA, delay of 0 months, fred/CES2000000008 (https://fred.stlouisfed.org/series/CES2000000008) |
| 95. | CES3000000008* | 1959:01–2015:10 | m | 1 | 5 | Average Hourly Earnings of Production and Nonsupervisory Employees: Manufacturing, USD per Hour, SA, delay of 0 months, fred/CES3000000008 (https://fred.stlouisfed.org/series/CES3000000008) |
| Miscellaneous | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 96. | MEI | 1959:01–2015:10 | m | 1 | 1 | Composite Leading Indicators, Amplitude Adjusted, delay of 0 months, http://stats.oecd.org/Index.aspx? DataSetCode=MEI_CLI |
| Mixed-frequency time series | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 97. | EXGEUS | 1971:01–2001:12 | m | 1 | 5 | Germany / US Foreign Exchange Rate, German Deutsche Marks to One USD, NSA, delay of 0 months, fred/EXGEUS (https://fred.stlouisfed.org/series/EXGEUS) |
| 98. | EXFRUS | 1971:01–2001:12 | m | 1 | 5 | France / US Foreign Exchange Rate, French Francs to One USD, NSA, delay of 0 months, fred/EXFRUS (https://fred.stlouisfed.org/series/EXFRUS) |
| 99. | EXITUS | 1971:01–2001:12 | m | 1 | 5 | Italy / US Foreign Exchange Rate, Italian Lire to One USD, NSA, delay of 0 months, fred/EXITUS (https://fred.stlouisfed.org/series/EXITUS) |
| 100. | EXUSEU | 1999:01–2015:10 | m | 1 | 5 | US / Euro Foreign Exchange Rate, USDs to One Euro, NSA, delay of 0 months, fred/EXUSEU (https://fred.stlouisfed.org/series/EXUSEU) |
| 101. | GDP | 1959:01–2015:10 | q | 2 | 5 | Gross Domestic Product, billions of USD, SA annual rate, delay of 0 months, fred/GDP (https://fred.stlouisfed.org/series/GDP) |
| 102. | W068RCQ027SBEA | 1960:01–2015:10 | q | 2 | 5 | Government Total Expenditures, billions of USD, SA annual rate, delay of 0 months, fred/W068RCQ027SBEA (https://fred.stlouisfed.org/series/W068RCQ027SBEA) |
| 103. | IMPGSC1 | 1959:01–2015:10 | q | 2 | 5 | Real Imports of Goods and Services, billions of Chained 2009 USD, SA annual rate, delay of 0 months, fred/IMPGSC1 (https://fred.stlouisfed.org/series/IMPGSC1) |
| 104. | EXPGSC1 | 1959:01–2015:10 | q | 2 | 5 | Real Exports of Goods and Services, billions of Chained 2009 USD, SA annual rate, delay of 0 months, fred/EXPGSC1 (https://fred.stlouisfed.org/series/EXPGSC1) |
| 105. | WALCL | 2002:12–2015:10 | m | 1 | 5 | All Federal Reserve Banks - Total Assets, Eliminations from Consolidation, millions of USD, NSA, delay of 0 months, fred/WALCL (https://fred.stlouisfed.org/series/WALCL) |
| 106. | MBST | 2002:12–2015:10 | m | 1 | 5 | Mortgage-backed securities held by the Federal Reserve: All Maturities, millions of USD, NSA, delay of 0 months, fred/MBST (https://fred.stlouisfed.org/series/MBST) |
| 107. | TREAST | 2002:12–2015:10 | m | 1 | 5 | US Treasury securities held by the Federal Reserve: All Maturities, millions of USD, NSA, delay of 0 months, fred/TREAST (https://fred.stlouisfed.org/series/TREAST) |
| 108. | WRESBAL | 1984:01–2015:10 | m | 1 | 5 | Reserve Balances with Federal Reserve Banks, billions of USD, NSA, delay of 0 months, fred/WRESBAL (https://fred.stlouisfed.org/series/WRESBAL) |
| Observed variables | ||||||
| No. | Series ID | Time Span | Freq. | Type | Trans. | Series Description |
| 109. | CURRCIR | 1959:01–2015:10 | m | 1 | 5 | Currency in Circulation, billions of USD, NSA, delay of 0 months, fred/CURRCIR (https://fred.stlouisfed.org/series/CURRCIR) |
| 110. | AMBSL | 1959:01–2015:10 | m | 1 | 5 | St. Louis Adjusted Monetary Base, billions of USD, SA, delay of 0 months, fred/AMBSL (https://fred.stlouisfed.org/series/AMBSL) |
| 111. | FEDFUNDS | 1959:01–2015:10 | m | 1 | 1 | Effective Federal Funds Rate, percent, NSA, delay of 0 months, fred/FEDFUNDS (https://fred.stlouisfed.org/series/FEDFUNDS) |
Appendix D. Impulse Response Functions
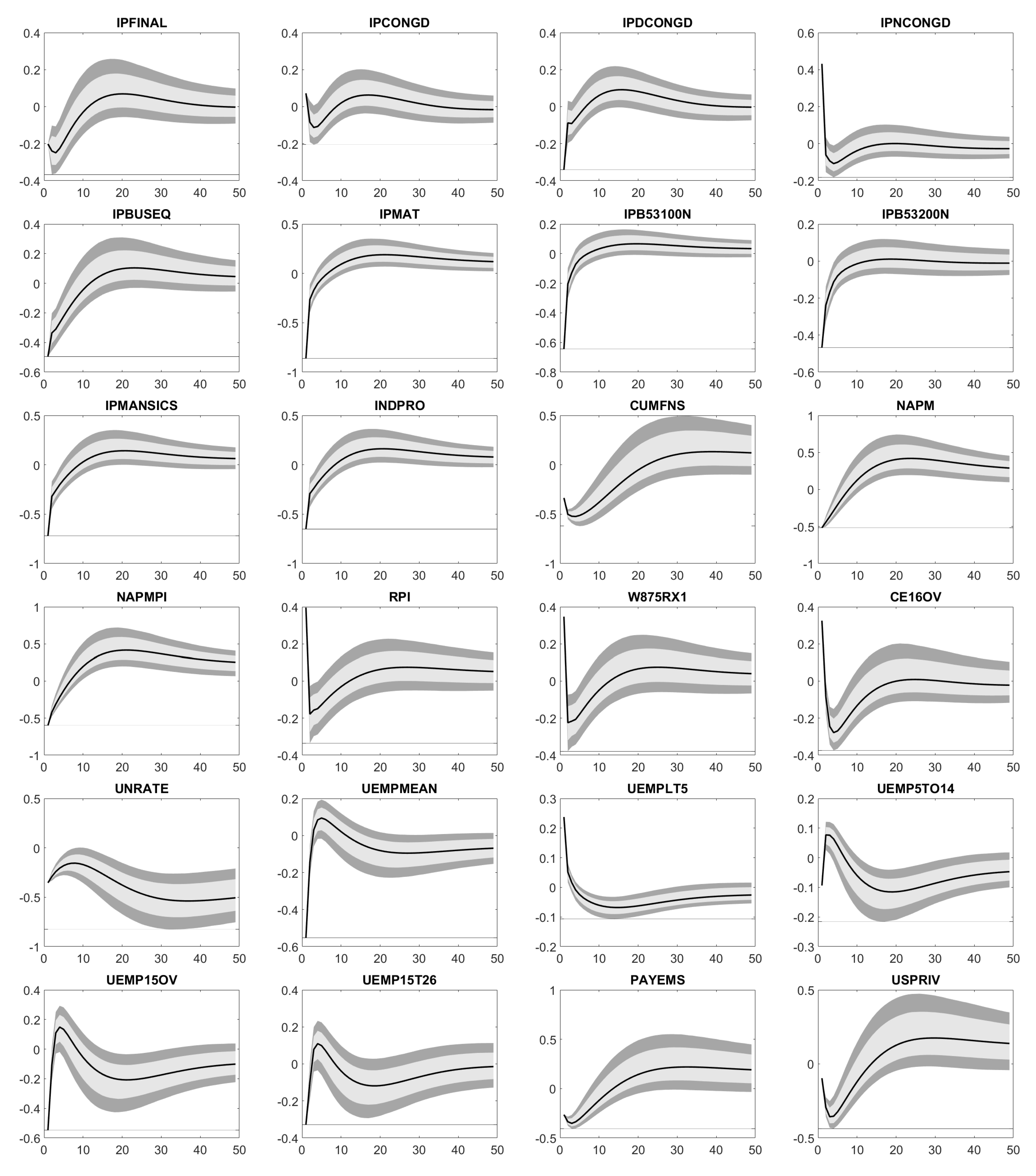
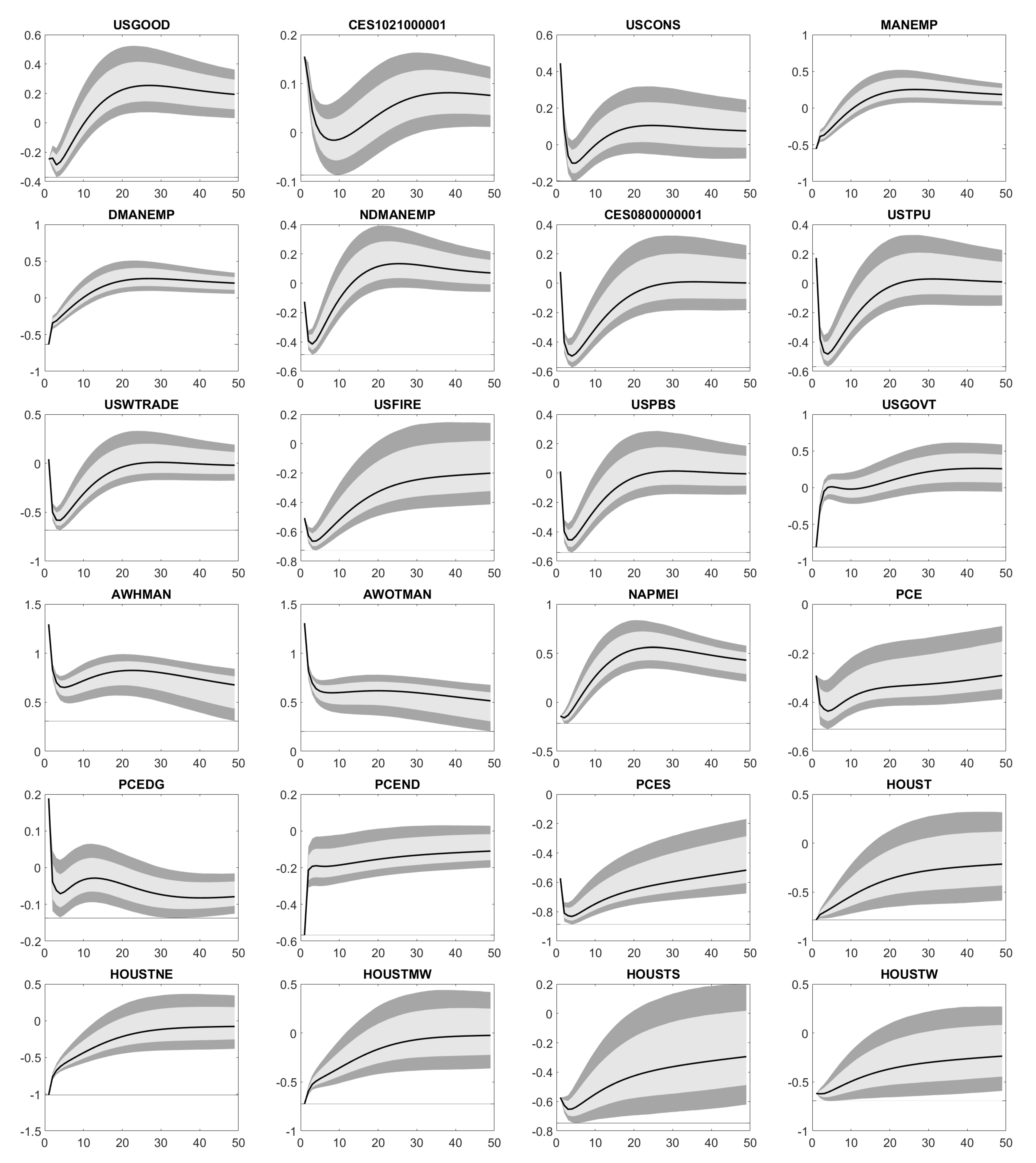
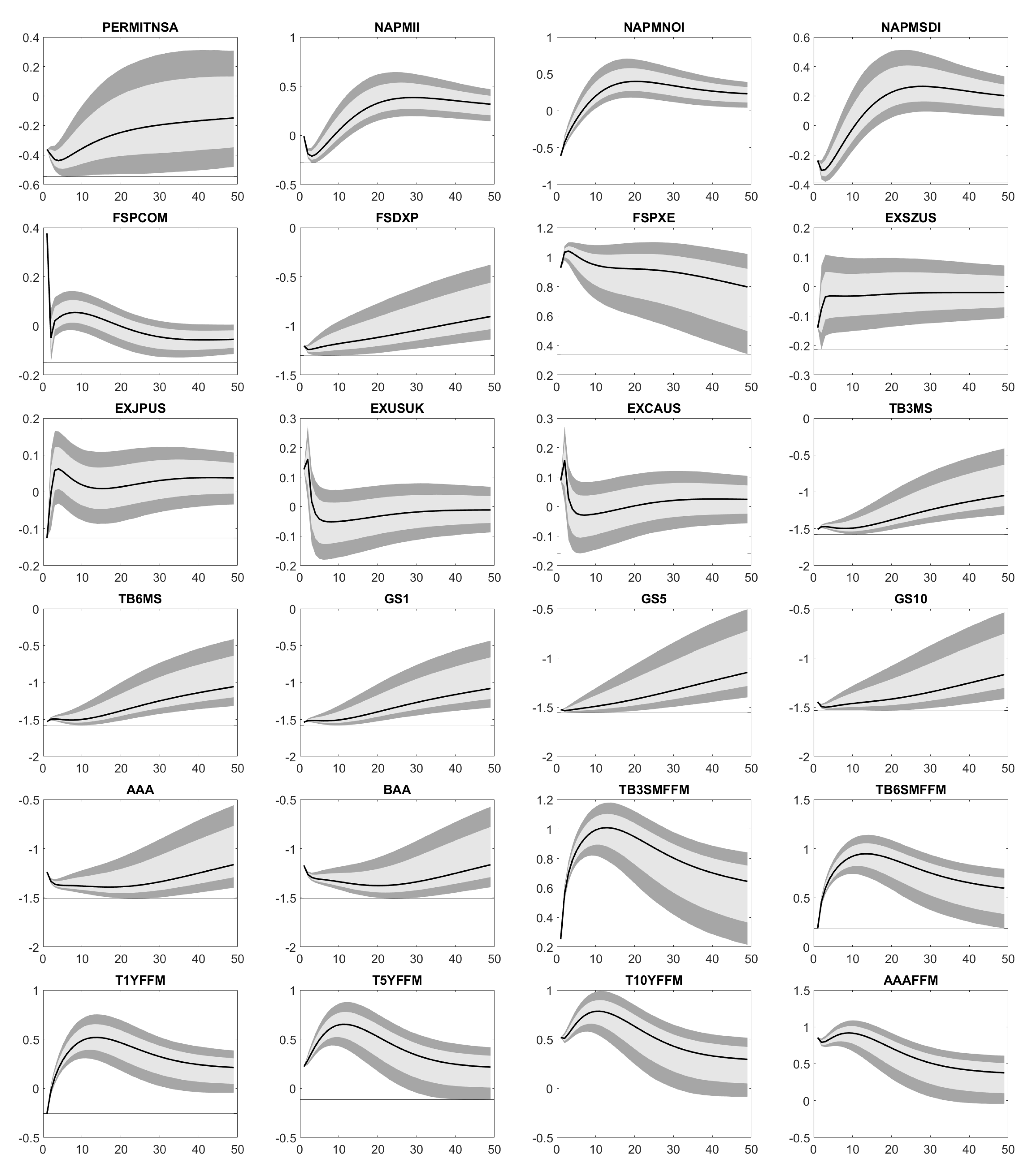
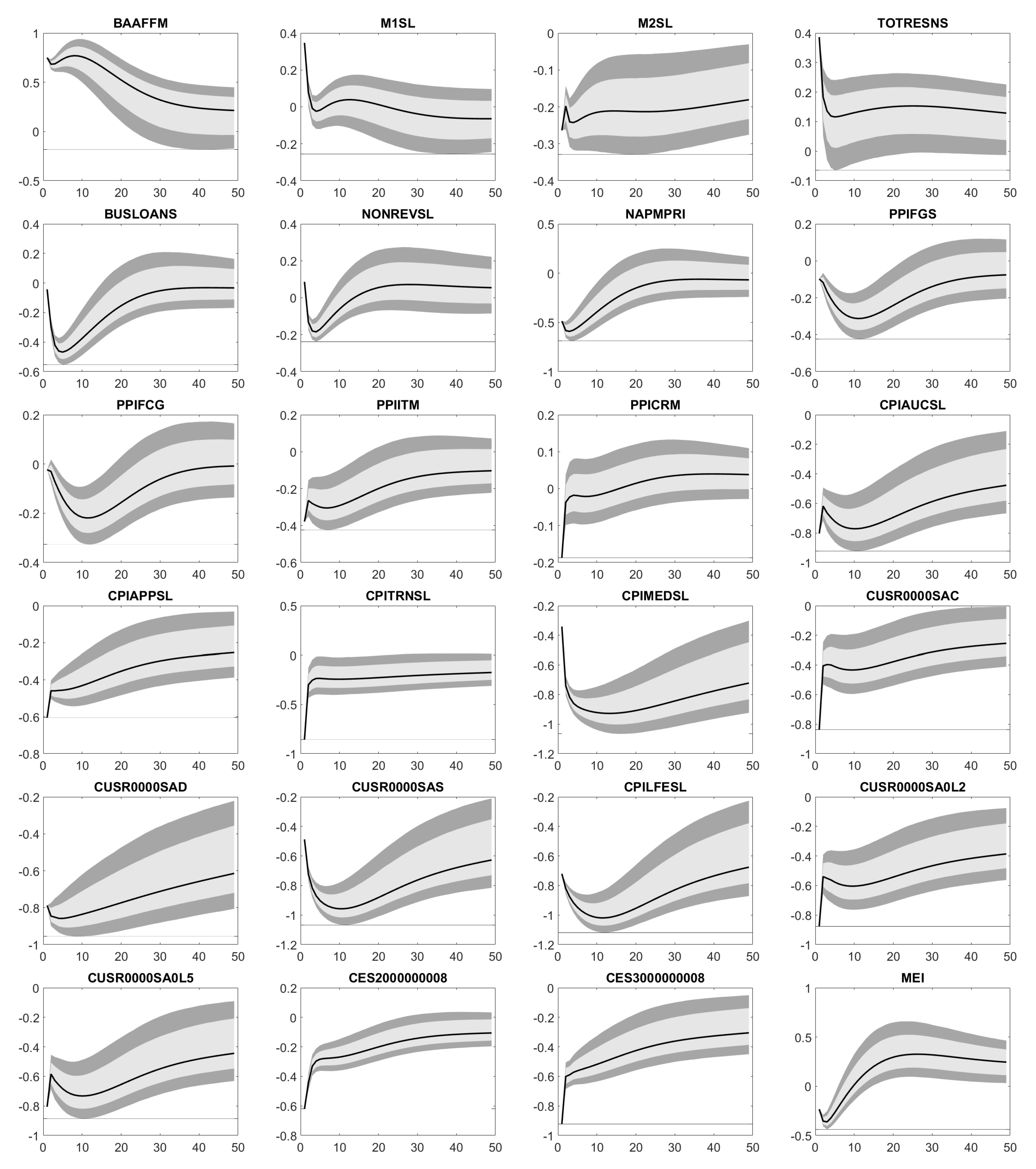
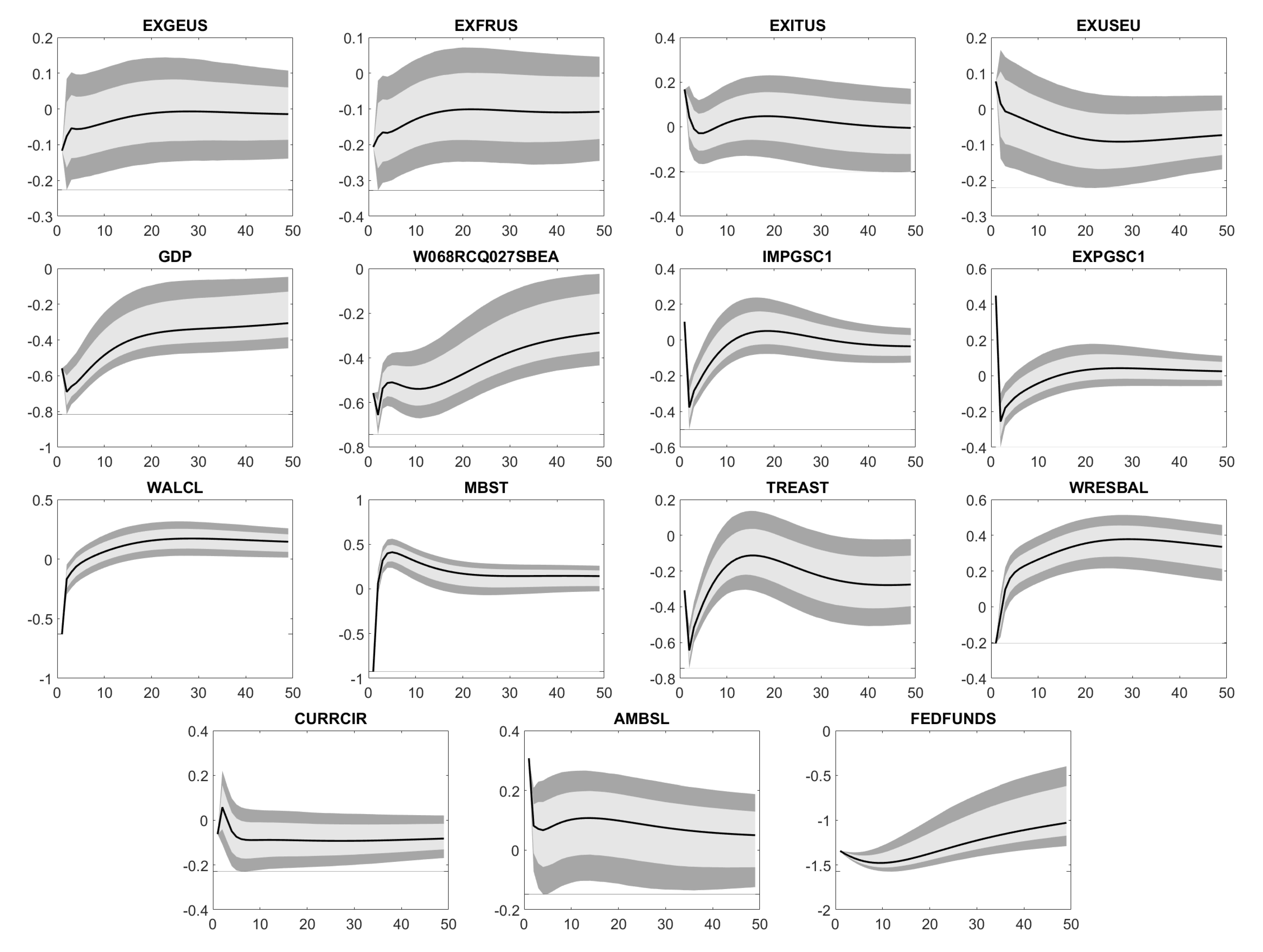
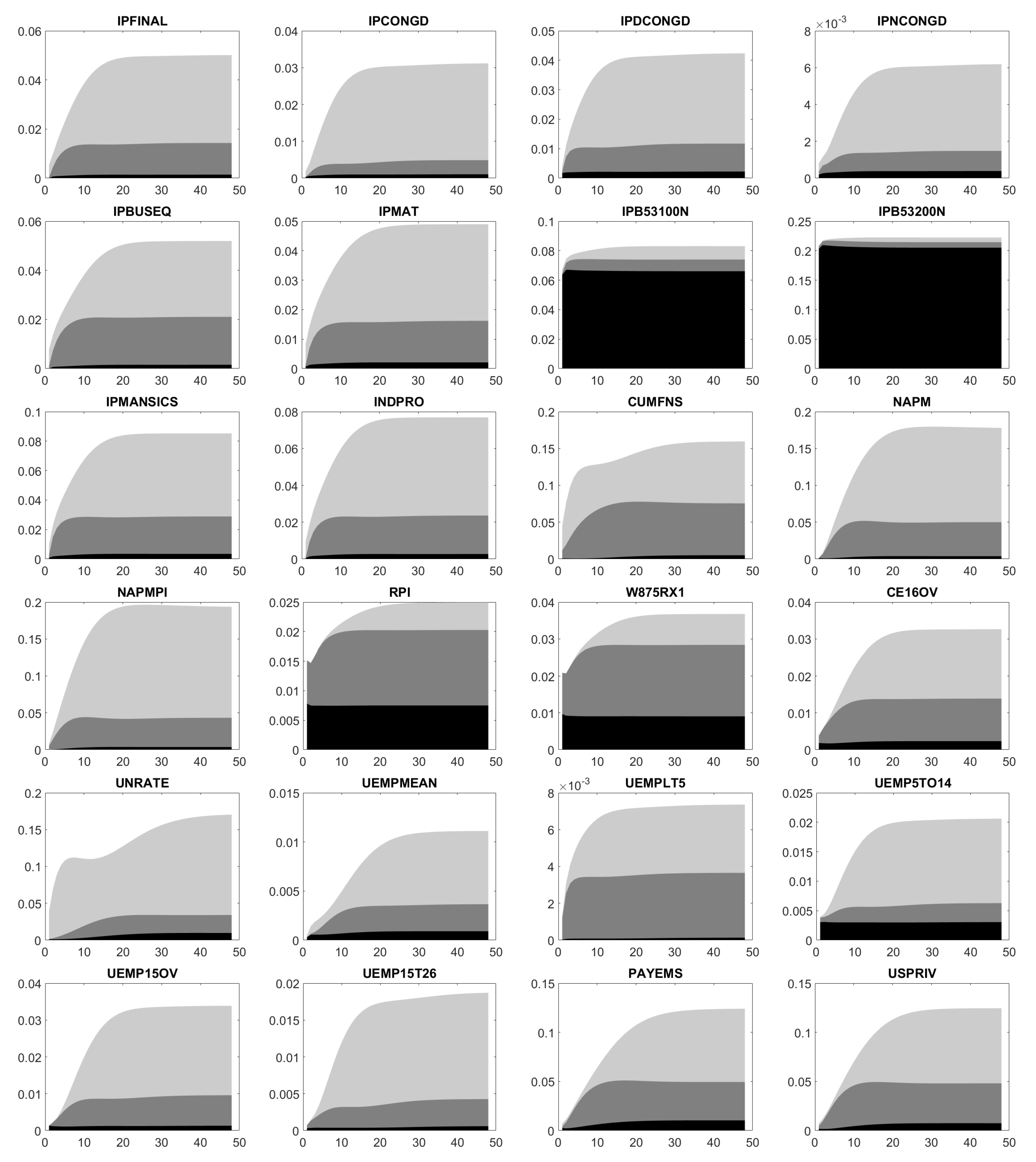
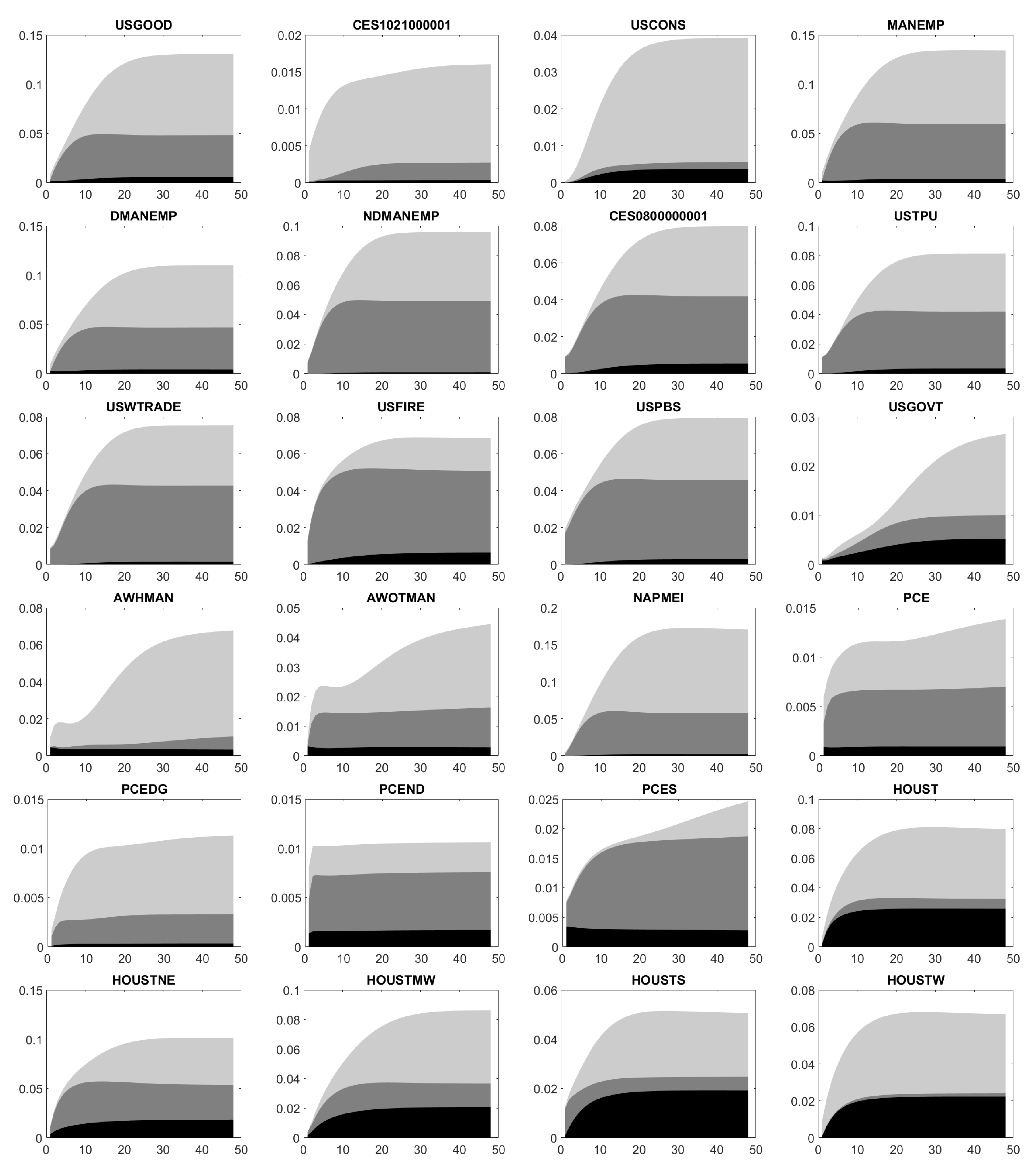
Appendix E. Forecast Error Variance Decomposition
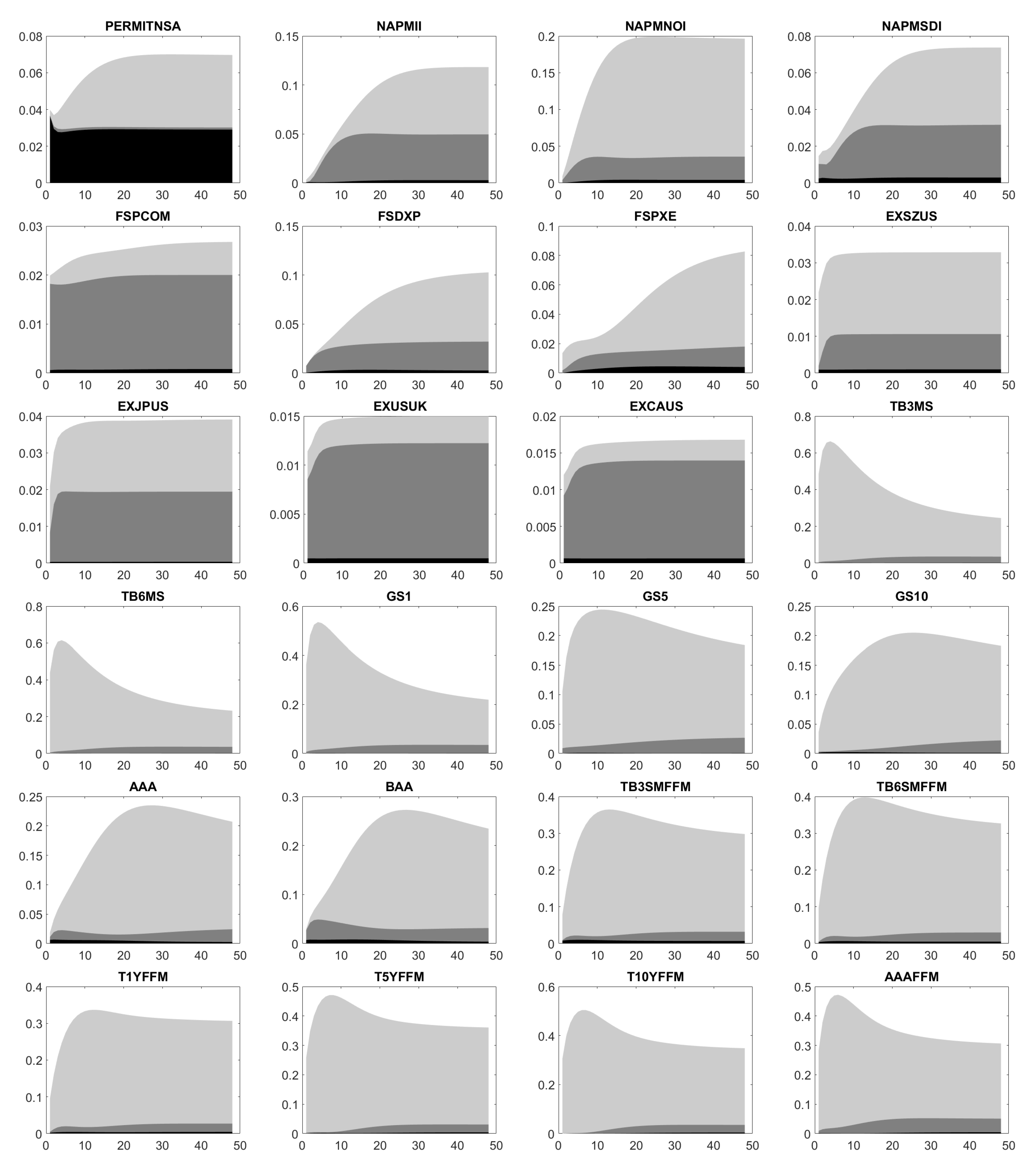
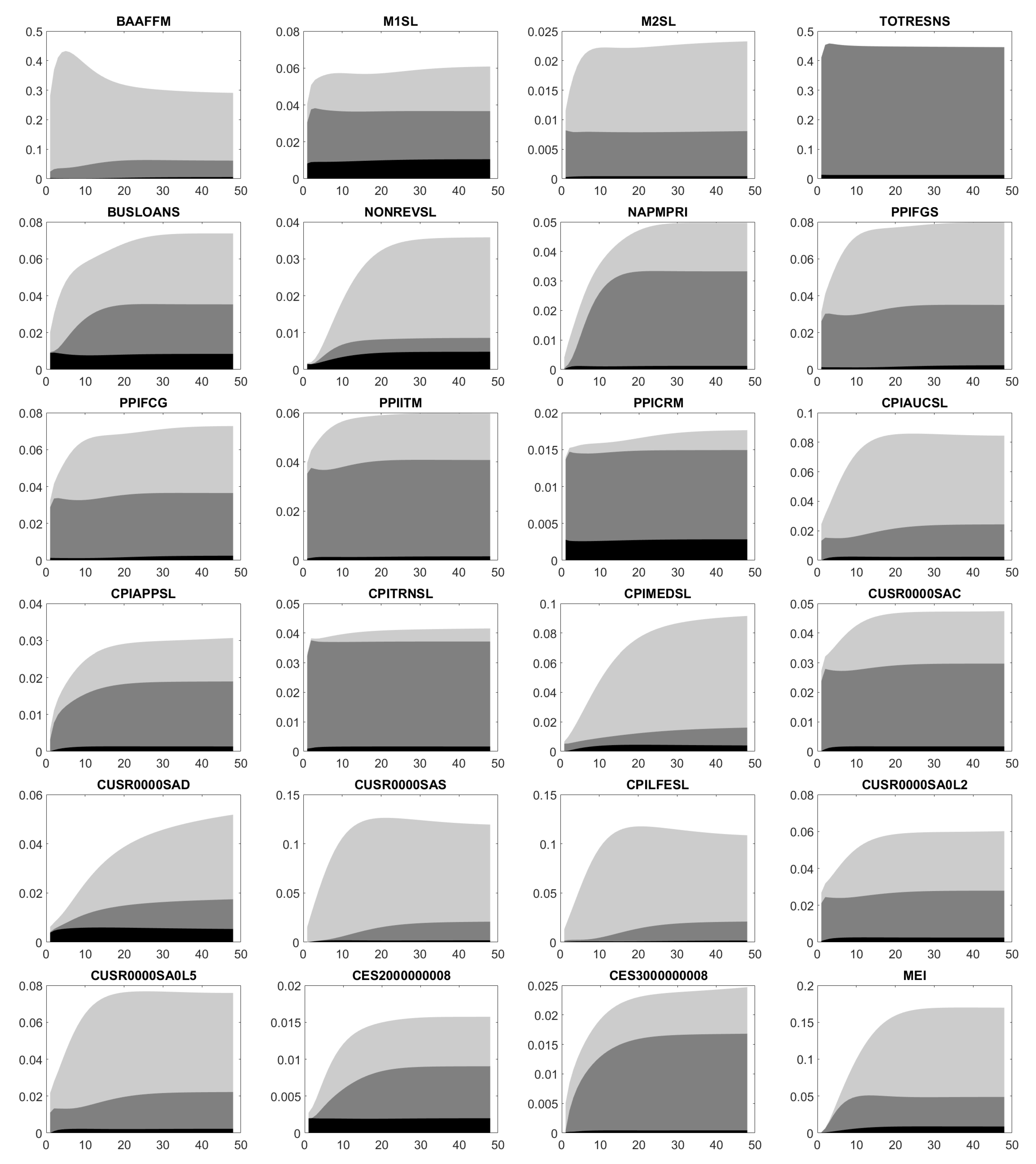
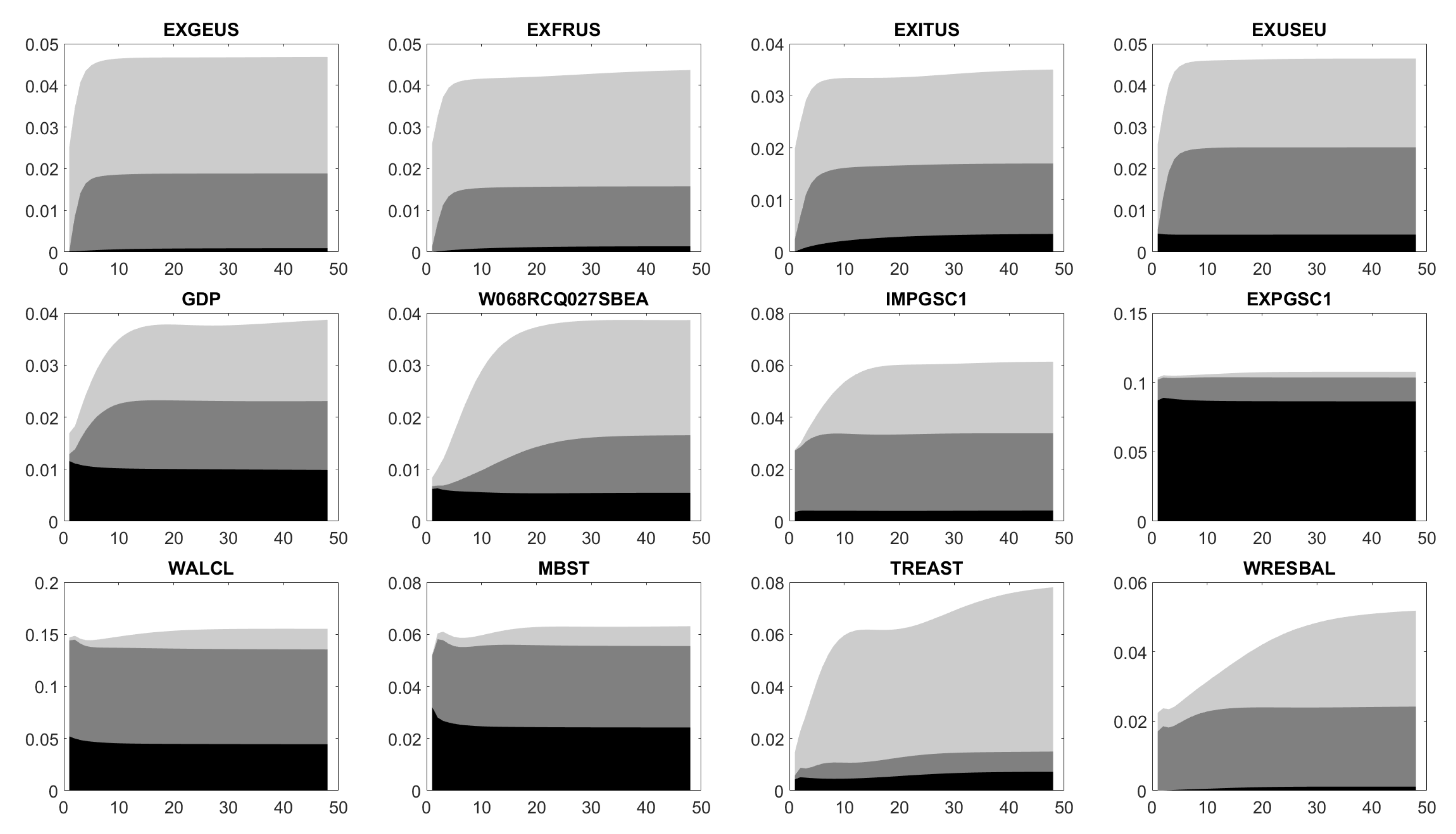
References
- Bai, Jushan, Kunpeng Li, and Lina Lu. 2015. Estimation and inference of FAVAR models. Journal of Business & Economic Statistics 34: 620–41. [Google Scholar]
- Bai, Jushan, and Serena Ng. 2002. Determining the number of factors in approximate factor models. Econometrica 70: 191–221. [Google Scholar] [CrossRef]
- Bai, Jushan, and Serena Ng. 2008. Large dimensional factor analysis. Foundations and Trends® in Econometrics 3: 89–163. [Google Scholar] [CrossRef]
- Ball, Laurence, and David Romer. 1990. Real rigidities and the non-neutrality of money. Review of Economic Studies 57: 183–203. [Google Scholar] [CrossRef]
- Bańbura, Marta, Domenico Giannone, Michele Modugno, and Lucrezia Reichlin. 2013. Now-casting and the real-time data flow. In Handbook of Economic Forecasting. Edited by G. Elliott and A. Timmermann. Amsterdam: Elsevier, vol. 2, pp. 195–237. [Google Scholar]
- Bańbura, Marta, Domenico Giannone, and Lucrezia Reichlin. 2010. Large bayesian vector auto regressions. Journal of Applied Econometrics 25: 71–92. [Google Scholar] [CrossRef]
- Bańbura, Marta, Domenico Giannone, and Lucrezia Reichlin. 2011. Nowcasting. In The Oxford Handbook on Economic Forecasting. Part II. Data Issues. Edited by M. Clements and D. Hendry. Oxford: Oxford University Press, pp. 193–224. [Google Scholar]
- Bańbura, Marta, and Michele Modugno. 2014. Maximum likelihood estimation of factor models on datasets with arbitrary pattern of missing data. Journal of Applied Econometrics 29: 133–60. [Google Scholar] [CrossRef]
- Bekiros, Stelios, and Alessia Paccagnini. 2014. Bayesian forecasting with small and medium scale factor-augmented vector autoregressive DSGE models. Computational Statistics and Data Analysis 71: 298–323. [Google Scholar] [CrossRef]
- Bekiros, Stelios, and Alessia Paccagnini. 2015. Macroprudential policy and forecasting using hybrid DSGE models with financial frictions and state space Markov-switching TVP-VARS. Macroeconomic Dynamics 19: 1565–92. [Google Scholar] [CrossRef]
- Benkwitz, Alexander, Helmut Lütkepohl, and Jürgen Wolters. 1999. Comparison of bootstrap confidence intervals for impulse responses of German monetary systems. In Interdisciplinary Research Project 373: Quantification and Simulation of Economic Processes. Discussion Paper No. 1999/29. Berlin: Humboldt University of Berlin. [Google Scholar] [CrossRef]
- Bernanke, Ben, and Alan Blinder. 1992. The federal funds rate and the channels of monetary transmission. The American Economic Review 82: 901–21. [Google Scholar]
- Bernanke, Ben, Jean Boivin, and Piotr Eliasz. 2005. Measuring the effects of monetary policy: A factor-augmented vector autoregressive (FAVAR) approach. The Quarterly Journal of Economics 120: 387–422. [Google Scholar]
- Boivin, Jean, and Marc Giannoni. 2008. Global Forces and Monetary Policy Effectiveness. Working Paper No. 13736. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Boivin, Jean, Marc Giannoni, and Dalibor Stevanovic. 2010. Monetary Transmission in a Small Open Economy: More Data, Fewer Puzzles. Working Paper. New York: Columbia University. [Google Scholar]
- Bork, Lasse. 2009. Estimating US Monetary Policy Shocks Using a Factor-Augmented Vector Autoregression: An EM Algorithm Approach. Available online: http://ssrn.com/abstract=1358876 (accessed on 14 July 2019).
- Bork, Lasse. 2015. A Large-Dimensional Factor Analysis of the Federal Reserve’s Large-Scale Asset Purchases. Working Paper. Aalborg: Aalborg University. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2618378 (accessed on 14 July 2019).
- Bork, Lasse, Hans Dewachter, and Romain Houssa. 2010. Identification of Macroeconomic Factors in Large Panels. Working Paper No. 2010/10. Namur: Center for Research in the Economics of Development. [Google Scholar]
- Carr, Jack, and Michael Darby. 1981. The role of money supply shocks in the short-run demand for money. Journal of Monetary Economics 8: 183–99. [Google Scholar] [CrossRef][Green Version]
- Dempster, Arthur, Nan Laird, and Donald Rubin. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 39: 1–38. [Google Scholar] [CrossRef]
- Doz, Catherine, Domenico Giannone, and Lucrezia Reichlin. 2012. A quasi-maximum likelihood approach for large, approximate dynamic factor models. The Review of Economics and Statistics 94: 1014–24. [Google Scholar] [CrossRef]
- Ellis, Colin, Haroon Mumtaz, and Pawel Zabczyk. 2014. What lies beneath? A time-varying FAVAR model for the UK transmission mechanism. The Economic Journal 124: 668–99. [Google Scholar] [CrossRef]
- Golub, Gene, and Charles Van Loan. 1996. Matrix Computations. Baltimore: Johns Hopkins University Press. [Google Scholar]
- Grandmont, Jean-Michel, and Yves Younes. 1972. On the role of money and the existence of a monetary equilibrium. The Review of Economic Sudies 39: 355–72. [Google Scholar] [CrossRef]
- Hallin, Marc, and Roman Liška. 2007. Determining the number of factors in the general dynamic factor model. Journal of the American Statistical Association 102: 603–17. [Google Scholar] [CrossRef]
- Hamilton, James Douglas. 1994. Time Series Analysis. Princeton: Princeton University Press. [Google Scholar]
- Kilian, Lutz. 1998. Small-sample confidence intervals for impulse response functions. Review of Economics and Statistics 80: 218–30. [Google Scholar] [CrossRef]
- Levhari, David, and Don Patinkin. 1968. The role of money in a simple growth model. The American Economic Review 58: 713–53. [Google Scholar]
- Mankiw, N. Gregory. 2010. Macroeconomics. New York: Worth Publishers. [Google Scholar]
- Mankiw, N. Gregory. 2014. Principles of Economics. Boston: Cengage Learning. [Google Scholar]
- Marcellino, Massimiliano, and Vasja Sivec. 2016. Monetary, fiscal and oil shocks: Evidence based on mixed frequency structural FAVARs. Journal of Econometrics 193: 335–48. [Google Scholar] [CrossRef]
- Mariano, Roberto, and Yasutomo Murasawa. 2003. A new coincident index of business cycles based on monthly and quarterly series. Journal of Applied Econometrics 18: 427–43. [Google Scholar] [CrossRef]
- Mariano, Roberto, and Yasutomo Murasawa. 2010. A coincident index, common factors, and monthly real GDP. Oxford Bulletin of Economics and Statistics 72: 27–46. [Google Scholar] [CrossRef]
- Minsky, Hyman. 1993. On the non-neutrality of money. Federal Reserve Bank of New York Quarterly Review 18: 77–82. [Google Scholar]
- Ramsauer, Franz. 2017. Estimation of Factor Models with Incomplete Data and Their Applications. Ph.D. dissertation, Technical University of Munich, Munich, Germany. Available online: https://mediatum.ub.tum.de/680900?sortfield0=-year-accepted&sortfield1=&show_id=1349701 (accessed on 14 July 2019).
- Rubin, Donald, and Dorothy Thayer. 1982. EM algorithms for ML factor analysis. Psychometrika 47: 69–76. [Google Scholar] [CrossRef]
- Schumacher, Christian, and Jörg Breitung. 2008. Real-time forecasting of German GDP based on a large factor model with monthly and quarterly data. International Journal of Forecasting 24: 386–98. [Google Scholar] [CrossRef]
- Serletis, Apostolos, and Zisimos Koustas. 1998. International evidence on the neutrality of money. Journal of Money, Credit and Banking 30: 1–25. [Google Scholar] [CrossRef]
- Shumway, Robert, and David Stoffer. 1982. An approach to time series smoothing and forecasting using the EM algorithm. Journal of Time Series Analysis 3: 253–64. [Google Scholar] [CrossRef]
- Sims, Christopher. 1992. Interpreting the macroeconomic time series facts: The effects of monetary policy. European Economic Review 36: 975–1000. [Google Scholar] [CrossRef]
- Stock, James, and Mark Watson. 1999. Diffusion Indices. Working Paper No. 6702, rev. ed. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Stock, James, and Mark Watson. 2002a. Forecasting using principal components from a large number of predictors. Journal of the American Statistical Association 97: 1167–79. [Google Scholar] [CrossRef]
- Stock, James, and Mark Watson. 2002b. Macroeconomic forecasting using diffusion indexes. Journal of Business & Economic Statistics 20: 147–62. [Google Scholar]
- Watson, Mark, and Robert Engle. 1983. Alternative algorithms for the estimation of dynamic factor, mimic and varying coefficient regression models. Journal of Econometrics 23: 385–400. [Google Scholar] [CrossRef]
- Wu, C. F. Jeff. 1983. On the convergence properties of the EM algorithm. The Annals of Statistics 11: 95–103. [Google Scholar] [CrossRef]
- Wu, Jing Cynthia, and Fan Dora Xia. 2014. Measuring the Macroeconomic Impact of Monetary Policy at the Zero Lower Bound. Technical Report. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Yamamoto, Yohei. 2012. Bootstrap Inference for Impulse Response Functions in Factor-Augmented Vector Autoregressions. Hi-Stat Discussion Paper. Kunitachi: Hitotsubashi University. [Google Scholar]
| 1. | Distinction between stock, flow or change in flow variables. |
| 2. | Of course, there are exceptions from this statement such as Bańbura et al. (2010). |
| 3. | In the scope of a MC simulation study in Section 3, we show scenarios, where our estimation approach is superior. |
| 4. | Alternatively, the information criteria of Bai and Ng (2002, 2008) or Hallin and Liška (2007) enable model selection. |
| 5. | |
| 6. | For signal , let the integers count the high-frequency periods between two successive observations. Then, captures when the j-th observation is made. For stock variables, the observations match with their artificial counterparts, that is, we have: . For flow variables, the observations either represent the sum or the average of the artificial elements of the respective low-frequency period. Hence, the sum version obeys: . The average formulation satisfies: . For change in flow variables, the change in two consecutive observations is traced back to a linear combination of the changes in the artificial time series. As before, a sum and average version exist. For the latter it holds: . By contrast, the sum version requires the equality for all to derive a similar result. To verify this requirement we assume and obtain: . Since the last term is the signal itself, the observed change does not consist of a pure combination of high-frequency changes. By similar reasoning the same holds for any . |
| 7. | We regard the four quarterly growth rates as sum versions of flow variables, while all other time series serve as stock variables. For the 107 monthly time series there is no distinction between stock, flow and change in flow variables. Although some time series start at a later point in time, for example, the USD-EUR FX, or are discontinued, for example, the German Mark-USD FX, there are no intermediately missing observations. |
| No. | Bork (2009) | Our Data (Ticker) |
|---|---|---|
| 1 | Industrial production: manufacturing (1992 = 100, SA) | PAYEMS |
| 2 | Unemploy. by duration: average (mean) duration in weeks (SA) | CPILFESL |
| 3 | Purchasing managers’ index (SA) | PPIFCG |
| 4 | Avg. weekly hrs. of prod. wkrs.: mfg., overtime hrs. (SA) | UNRATE |
| 5 | CPI-u: commodities (82–84 = 100, SA) | USFIRE |
| 6 | Employment: ratio; help-wanted ads: no. unemployed clf | IPCONGD |
| 7 | Capacity util rate: manufac., total (% of capacity, SA) (frb) | AWOTMAN |
| 8 | Pers cons exp (chained)—tot. dur. (bil 96$, SAAR) | PCE |
| 9 | Industrial production: total index (1992 = 100, SA) | PPICRM |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramsauer, F.; Min, A.; Lingauer, M. Estimation of FAVAR Models for Incomplete Data with a Kalman Filter for Factors with Observable Components. Econometrics 2019, 7, 31. https://doi.org/10.3390/econometrics7030031
Ramsauer F, Min A, Lingauer M. Estimation of FAVAR Models for Incomplete Data with a Kalman Filter for Factors with Observable Components. Econometrics. 2019; 7(3):31. https://doi.org/10.3390/econometrics7030031
Chicago/Turabian StyleRamsauer, Franz, Aleksey Min, and Michael Lingauer. 2019. "Estimation of FAVAR Models for Incomplete Data with a Kalman Filter for Factors with Observable Components" Econometrics 7, no. 3: 31. https://doi.org/10.3390/econometrics7030031
APA StyleRamsauer, F., Min, A., & Lingauer, M. (2019). Estimation of FAVAR Models for Incomplete Data with a Kalman Filter for Factors with Observable Components. Econometrics, 7(3), 31. https://doi.org/10.3390/econometrics7030031




