Abstract
Most empirical work in the social sciences is based on observational data that are often both incomplete, and therefore unrepresentative of the population of interest, and affected by measurement errors. These problems are very well known in the literature and ad hoc procedures for parametric modeling have been proposed and developed for some time, in order to correct estimate’s bias and obtain consistent estimators. However, to our best knowledge, the aforementioned problems have not yet been jointly considered. We try to overcome this by proposing a parametric approach for the estimation of the probabilities of misclassification of a binary response variable by incorporating them in the likelihood of a binary choice model with sample selection.
1. Introduction
Most empirical work in the social sciences is based on observational data that are often incomplete, and therefore unrepresentative of the population of interest, and/or affected by measurement errors.
There are many types of selection mechanisms that result in a non-random sample. Some of them are due to sample design, while others depend on the behavior of the units being sampled, other than non-response or attrition. In the first case, data are usually missing on all the variables of interest; for example, in estimating a saving function for all the families of a given country, a bias would arise if only families whose household head shows certain characteristics were sampled. However, when causes of missingness are appropriately exogenous, using a sub-sample has no serious consequences.
In the second case, instead, there is a self-selection of the sample units and data availability on a key variable depends on the behavior of the units about another variable. The classical example is that of the linear wage equation where we want to estimate the expected wage of an individual using a set of exogenous characteristics (gender, age, education, etc.). The key problem is that, in regressing wages on the characteristics of employed individuals, we are not making inferences for the population as a whole. In fact, those in employment are a selected sample of the population and their wages are higher than those not in the labor force would have. Hence, the results will tend to be biased and inconsistent (sample selection bias). To avoid this problem, we need to take into account the selection mechanism by which an individual decides to take a job and then receives a wage.
As is well known, Heckman (1979) proposed a useful framework for handling estimation when the sample is subject to a selection mechanism, trying to correct for non-randomly selected data in a two-model hierarchy where, on the first level, a binary selection equation determines whether a particular observation will be available for the second level (outcome equation). In the original framework, the dependent variable in the outcome equation (the wage equation in the above example) is continuous and can be explained by a linear regression model with a normal random component. In addition to the output equation, a selection equation describes the selection rule by means of a binary choice model (probit).
The original Heckman’s model was extended in many directions and a survey would be beyond the scope of this paper, but the interested reader can refer to the works of Vella (1998) and Lee (2007). To our purposes, the relevant framework is the one where both the output and the selection equations are defined as a binary choice model (Dubin and Rivers 1989). The likelihood function takes into account the selection mechanism and allows for consistent estimates of the parameters of interest (i.e., the coefficients of the selection and the outcome equations and the correlation coefficient of the two processes).
In many disciplines, however, binary data are frequently misclassified. Misclassification of a binary variable means that an observation with a true value of 0 is observed as 1 or an observation that is truly a 1 is observed as a 0. This mistake could easily happen, for example, during an interview if the respondent misunderstands the question or the interviewer simply checks the wrong box. In employment analysis, tenure responses can be measured with errors because respondents have poor recall or confuse a change in position with an actual job change (Hausman et al. 1998); in this framework, evidence from validation studies (e.g., (Mellow and Sider 1983)) suggests that 20 percent of one-digit occupational choices are misclassified. Finally, as underlined by the social psychology literature, respondents tend to over-report socially desirable behaviors and under-report socially undesirable ones (Loftus 1975). For example, in surveys on voting behavior, some respondents state that they have voted, while they did not. Empirical evidence of this behavior was provided by Katz and Katz (2010): using auxiliary information from the American National Elections, they discovered that, depending on the election year, between 13.6% and 24.6% of the respondents claiming to have voted did in fact not vote according to the public records.
This kind of misreporting might become even more frequent when the response variable refers to characteristics subjected to a moral judgment; it is the case, for example, of the dependent variable considered in the application discussed in Section 4 (having, or not, carried out some undeclared activities), but also when the dependent variable refers to one’s attitude to tax evasion, racism, drug or games addiction, and religious belief.
Ignoring the presence of misclassification is not trivial; in fact, when traditional estimation methods (e.g., logit or probit) are used in binary choice contexts with a misclassified dependent variable, the resulting estimates are inconsistent.
Previous work on misclassified dependent variables in discrete choice models follows two approaches. In the first, supplemental data are used to verify the accuracy of responses. In the work of Chua and Fuller (1987), a parametric model that incorporates all possible misclassification of a J-level outcome variable is developed. This approach has been seldom used because it is very data demanding, as a minimum of three independent sets of survey responses obtained by re-interviewing the original respondents are required. A similar approach, based on a conditional logit procedure, was proposed by Poterba and Summers (1995). It also incorporates all possible misclassification and the estimation of the misclassification probabilities is done by analyzing the divergences between interview and re-interview outcomes.
Other authors have taken a different path to deal with misclassification, using parametric models. In particular, Hausman et al. (1998) and Abrevaya and Hausman (1999) incorporated the probability of misclassification directly into the estimation procedure. They considered a parametric model for a binary response variable with two types of misclassification; these unknown misclassification probabilities are estimated parametrically and simultaneously with the usual coefficients of the binary choice model. More recently, Sullivan (2009) proposed a model that corrects for misclassification in occupational choices and measurement error in occupation-specific work experience, when direct evidence on the validity of individuals’ self-reported occupations is unavailable. This model consists of two sub-models that are estimated jointly by simulated maximum likelihood: one explains the occupational choice, and the other the extent of misclassification in occupational data. However, this proposal is specific for the study of the determinants of occupational choices and for estimating the effects of occupation-specific human capital on wages. On the contrary, Hausman et al.’s proposal is quite general and applicable in several contexts. Therefore, we start from their work, incorporating the other source of inconsistency coming from sample selection. We use a parametric approach to simultaneously estimate the parameters of the selection and of the outcome equations, the correlation between them and the probabilities of misclassification.
2. The Model
Let us first introduce some notations and briefly illustrate the sample selection framework with a binary choice model for both the selection and the output equations (Dubin and Rivers 1989).
We start with two observable binary variables: the dependent variable of the outcome equation Y and the one of the selection equation S. They can be seen as the observable proxies of two latent (unobservable) variables, and , characterizing the output and the selection equations respectively. The model, in its general form, is:
where is a vector of exogenous variables (namely, for and for ), containing all the relevant covariates, and are the vectors of regression coefficients, and and are the disturbances, assumed in general related with . Note that for the model in Equations (1a) and (1b) to be identified, we can rely either on nonlinearity (typically assuming a joint normality of ) or on an exclusion restriction that translate in a non-full overlapping of and ; that is, the covariates of the selection and outcome equations must differ for at least one variable. The latter condition is necessary only when there are reasons to doubt that the nonlinearity holds.
We can now define the observable binary variables and as:
The p.d.f. of are Bernoulli, with probability of success depending on the parameters and , respectively.
The model in Equation (3) defines the mechanism which governs the censoring process: we can observe if and only if . On the contrary, if , will be missing. Note that the selection mechanism affects the estimates only when is nonzero.
In the general case with nonzero , if we were to estimate the parameters of Equation (1a) without considering the selection process (Equation (1b)), that is omitting information about , a problem of inconsistency would arise (see, for example, (Cameron and Trivedi 2005), for further details).
The appropriate likelihood function for the model in Equations (1a) and (1b) is:
where is the vector of parameters to be estimated, and the function gives the probability that an observation is uncensored.
Now, if we assume that:
and put , we can compute the probabilities and the joint probabilities in Equation (4) as follows:
where and are c.d.f. of the univariate and the bivariate normal, respectively.
Now, let us suppose that can be misclassified, that is some true ones are observed as zeros, and some true zeros are observed as ones. It follows that what we observe can differ from the true proxy of the response variable of the outcome equation. Let us denote as the observed binary variable affected by error, and as the true response variable of Equation (2). Following Hausman et al. (1998), we assume that the probability of misclassification depends on the value of , but is otherwise independent of the covariates if conditioned on . To be more specific, we set the following misclassification probabilities:
with .
The probability that a true zero is misclassified as a one is given by ; the probability that a true one is misclassified as a zero is given by . The stochastic mechanism that determines the values of the observed dependent variable becomes:
where is the homologous of in Equations (7) and (8).
Obviously, we can put:
To estimate the entire vector of parameters, , we have to extend the likelihood function in Equation (4) bearing in mind that the observed values of the dependent variable in the outcome equation are misclassified. Rewriting the likelihood function by plugging Equations (11) and (12) into Equation (4) and considering the assumption in Equation (5), we get the following likelihood function:
3. Simulation Results
In this section, we present Monte Carlo simulations done to evaluate finite sample performances of the proposed model. We consider the following generating model:
For the outcome equation, we mimic Hausman et al. (1998); in particular, is drawn from a lognormal, is a dummy variable equal to one with probability and is a uniform . In addition, the vector of parameters is identical to theirs. For the selection equation, we have drawn both and from a standard normal distribution. The choice of in is to ensure a medium and low amount of censored data (approximately 30% and 5%, respectively).
We performed 200 replications with samples of size . We chose and the following pairs of misclassification probabilities: and .
We compared four models: the simple probit, a model that corrects for sample selection only (named SS in the following), a model that corrects for misclassification only (MIS) and a model that corrects for both sample selection and misclassification (MIS-SS).
The results, reported in Table 1, Table 2,Table 3 and Table 4, allow evaluating the models’ performances by comparing the average estimates and mean squared error (MSE) as well as the coverages of the confidence intervals. MIS-SS has very good values for all indicators, along all simulation settings. In the following, we focus on the parameters of the outcome equation, being those of main interest.

Table 1.
Monte Carlo simulation results: average values of estimates, coverage of confidence intervals and MSEs. Data generating scheme: , , ; censored observations approximately 5%.

Table 2.
Monte Carlo simulation results: average values of estimates, coverage of confidence intervals and MSEs. Data generating scheme: , ; , ; censored observations approximately 5%.

Table 3.
Monte Carlo simulation results: average values of estimates, coverage of confidence intervals and MSEs. Data generating scheme: , , ; censored observations approximately 30%.

Table 4.
Monte Carlo simulation results: average values of estimates, coverage of confidence intervals and MSEs. Data generating scheme: , ; , ; censored observations approximately 30%.
With regards to probit estimates, in accordance with Hausman et al. (1998), we find biased estimates. In particular, the average relative bias1, spans from 0.1% to 42% of the parameter true value, depending on the coefficient and on data generating schemes. As expected, the probit model performance improves with low levels of misclassification and censoring.
Correcting for sample selection (SS) induces the relative bias under 13%, no matter the value of , if the misclassification probabilities are low; in the other cases, the bias spans from 6% to 44%.
When correcting for misclassification (MIS), the relative bias considerably reduces (around 5%) only if is moderate. However, as expected, when the correlation between the outcome and the selection equation errors is higher, the bias reaches 15–20% with a peak of over 50% for the intercept.
Correcting for both types of error leads to an improvement in estimation: the MIS-SS model bias spans from 0.04% to 12% of the parameter true value, outperforming all others.
Looking at the coverages, MIS-SS is almost always the best model when the misclassification probabilities are both at 2%. When the misclassification probabilities raise ( and ), MIS dominates all models, but MIS-SS is the second best; furthermore, the performance of MIS-SS improves as the censoring percentage increases.
Similar considerations partially apply to the MSEs, although the evaluations are more difficult as the results are more diversified across the parameters space.
4. Application on Real Data: Estimating the Effect of Tax Morale on Undeclared Work in Southern European Countries
According to EU definition, undeclared work is any paid activities that are lawful as regard their nature, but not declared to the public authorities. It is therefore referable as a special form of tax evasion, perpetrated by the employers. Tax compliance decisions have always been of great interest to researchers and policy makers. In a seminal work of Allingham and Sandmo (1972), tax evasion is modeled as a portfolio choice made by a rational individual: he/she maximizes the expected utility of the tax evasion gamble, weighing the benefits of a successful cheating against the costs arising from detection and punishment. In this light, deterrence policies are seen as the key elements to increase tax compliance.
The main shortcoming of the Allingham and Sadmo model is that it predicts a much higher tax evasion level than that actually observed in real economic systems (Torgler 2001b; Torgler 2001a). The high levels of tax compliance registered around the world suggested that there are factors other than the economic ones (e.g., audit probabilities, tax rates, penalty rates, and income) that matter as much if not more. Hence, tax morale has emerged as one important determinant of tax behavior. The term “tax morale” was introduced by Schmölders (1960) back in 1960 who defined it as “the attitude of a group or the whole population of taxpayers regarding the question of accomplishment or neglect of their tax duties; it is anchored in citizens’ tax mentality and in their consciousness to be citizens, which is the base of their inner acceptance of tax duties and acknowledgment of the sovereignty of the state”.
Despite the definition of Schmölders, tax morale is still a debated concept with different meanings. Some authors (Braithwaite and Ahmed 2005; Feld and Frey 2002) perceive it as the “internalized obligation to pay tax”, while others (Alm and Torgler 2006) as the “intrinsic motivation” to pay taxes.
One of the most used methods to elicit tax morale is through surveys. Respondents are presented with compliant/non-compliant situations whose acceptability have to be assessed according to their system of beliefs. It is the case of the Eurobarometer survey No. 402 conducted in 2013 to unravel the attitudes of European citizens towards and their involvement in undeclared activities. We downsized the original sample of 27,563 adults aged 15 years or older to those living in one of the seven southern European countries (Portugal, Malta, Italy, Spain, Cyprus, Greece and Croatia). The size of the sub-sample is 6039 units. Interviews were either administered face-to-face or as CAPI (computer assisted personal interview).
To assess the effect of different tax moral dimensions, we used a statistical model whose observed dependent variable assumes value 1 if the interviewed answered yes to the question “Apart from a regular employment, have you yourself carried out any undeclared paid activities in the last 12 months?”, and 0 otherwise. The set of controls of the outcome equation were identified in accordance to the existing literature (Williams and Horodnic 2015a; Williams and Horodnic 2015b; Williams and Horodnic 2017). These include:
- Female: A dummy variable with value 1 for women and 0 for men.
- Age: A quantitative variable indicating the age of the respondent when interviewed.
- Urban: A dummy variable with value 1 if the respondent lives in a town of any size, and 0 otherwise.
- Children: A quantitative variable indicating the number of children less than 10 years old living in the household.
- Occupation: A categorical variable that states if the respondent is either unemployed, self-employed, employed, retired or inactive.
- Financial problems: A categorical variable grouping individuals by their difficulties in paying bills. The values are “most of the time”, “from time to time” and “almost never/never”.
- Country: A categorical variable whose levels correspond to each of the seven EU States belonging to the southern area.
- Detection risk: A categorical variable stating if the individual perceives a very high, fairly high, fairly small or very small probability of being detected when perpetrating fraudulent behavior.
- Expected sanction: A categorical variable with three levels corresponding to what the individual believes the sanction would be if caught in fraudulent behavior. The levels are: “Tax or social security contributions”, “Tax or social security contributions plus a fine”, and “Prison”.
- Tax moral: A set of three continuous variables each capturing one specific dimension of the general concept.
To be more specific regarding tax morale, we considered the following three dimensions: (1) business-level macro behaviors (TM1); (2) individual-level micro behaviors (TM2); and (3) explicit fraudulent behavior (TM3).
Each oh these dimensions is measured aggregating several corresponding elementary indicators through the arithmetic mean (in this way, we assume that the elementary indicators used for each dimension are substitutable; see Nardo et al. (2008)). In particular, TM1 considers the interviewed opinions on the following situations: “A firm is hired by a private household for work and it does not report the payment received in return to tax or social security institutions”, “A firm is hired by another firm for work and it does not report its activity to tax or social security institutions”, and “A firm hires a private person and all or a part of the salary paid to him/her is not officially registered”. TM2 is computed from the statements: “Someone uses public transport without a valid ticket” and “A private person is hired by a private household for work and he/she does not report the payment received in return to tax or social security institutions although it should be reported”. TM3 averages the opinions about “Someone receives welfare payments without entitlement” and “Someone evades taxes by not or only partially declaring income”. Each statement scores on a 10-point Likert scale, where 1 means that the behavior is absolutely unacceptable and 10 means absolutely acceptable. Consequently, by construction, each hypothesized dimension ranges itself from 1 to 10 and the lower is the index, the higher is the tax morale.
The first source of bias comes from the censoring due to non-responses on the dependent variable (around 5% of the interviewed refused to answer the question about their involvement in paid undeclared activities) and the second is about the concrete possibility that people actually employed off-the-book are reluctant to admit it and could have answered “No, I’m not employed off-the-book” when in fact they are.
At the same time, we believe unlikely the opposite kind of misclassification (that is, a person not employed off-the-book answering yes), thus we expect a very low value (if not zero) for the probability .
If we would ignore the censoring mechanism and the fact that and might be nonzero, the probability of observing an off-the-book worker (see Equation (11)) would be wrongly estimated. In such a situation, the reference model is a simple probit.
To cope with censoring, we specified a selection equation considering all the covariates that may influence non-response. Some covariates are in common with the outcome equation but one is included only in the selection equation. This latter variable is the the respondent cooperation, which is a four-level score the interviewer uses to asses the respondent’s willingness to cooperate during the interview2, whereas the ones in common are female, age, tax-morale, detection risk and country.
We present in Table 5 the results from a probit model and the model described in Section 2. First, we can note that the two models produce coherent estimates, consistent with other findings in the literature3, according to which the typical individual involved in undeclared work activities is a young unemployed male, who has financial difficulties in paying the household bills most of the time, lives in an urban area, has a very low perception of detection risk, his/her expected sanction for a fraudulent behavior is prison and there are no kids in the household. Now, however, not all the estimates are statistically significant. This is the case of urban area, presence of kids, detection risk (for model MIS-SS only we obtained weak significance), and expected sanctions.

Table 5.
Estimates of the drivers of participation in undeclared activities.
Referring to tax morale, coherently with our expectations, in both models, the probability of participation in undeclared work decreases as the level of morality increases. However, we may observe that tax morale variables could be endogenous, since unobservables affecting the propensity to be an undeclared worker also affect the level of tax morale indicators. Nonetheless, this problem goes far beyond the scope of the present work and we intend to address it in the future. In the context of the southern countries, however, the most significant drivers are the two dimensions related to individual level behavior. It is important to underline that tax morale variables could be endogenous, since unobservables affecting the propensity to be an undeclared worker also affect the level of tax morale indicators. Nonetheless, this problem goes far beyond the scope of the present work and we intend to address it in the future.
Referring to country effect, it emerges that almost all the southern countries are similar with respect to the behaviors on undeclared activities; the only exceptions are Croatia and Spain, where the probability of undeclared work becomes higher.
Some final considerations refer to the supplementary parameters of MIS-SS specification, which allow managing not only the problem of the bias arising from the presence of missing data in the dependent variable, but also the problem of its misclassification. In fact, as already observed, it is reasonable to think that respondents could be somewhat reticent in declaring themselves as undeclared workers and, consequently, there is a lack in measuring the prevalence of the phenomenon.
In particular, coherently with our expectations of very low or zero probability that a non-undeclared worker answer to be undeclared, estimates are approximately zero. On the contrary, estimates are very high (although not highly significant) and this result confirms that there is a share of population that declares to have not worked off-the-book when in fact they did, also consistently with expectations.
As is known, in applied problems, a useful tool to evaluate model performance is the confusion matrix, which allows the computation of percent correct prediction. Unfortunately, when the data are misclassified, the measure is unreliable. However, in our application, this is partially true. In fact, as the estimated is roughly zero, it follows that , and therefore it makes sense to compare the percent correct predictions that a worker is undeclared, under the two models. As shown in Figure 1, no matter the cutoff, the percent correct predictions from MIS-SS always dominates probit.
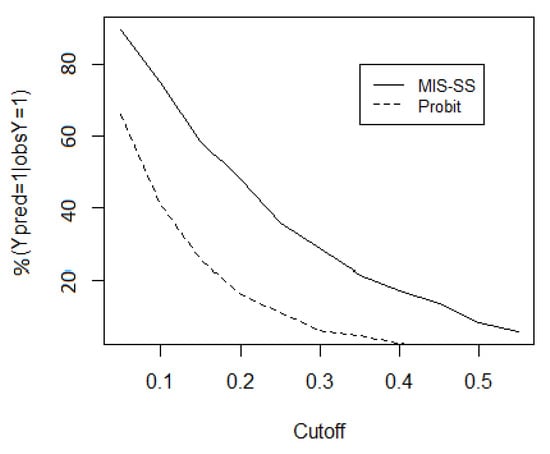
Figure 1.
Percent correct predictions of undeclared workers.
Finally, we note that the p-values of the MIS-SS estimates are higher than probit. A possible reason is that, when accounting for selection bias and misclassification, the degrees of freedom reduces and an increase in sample size should be needed (Hug 2010).
5. Conclusions
In this paper, we propose a method for estimating the regression coefficients in binary response models with sample selection and the dependent variable affected by measurement errors. We derived the likelihood function analytically and we found that it is a weighted version of the Heckman’s likelihood, where the weights account for the probability of misclassification of the dependent variable.
A simulation study highlighted that the performances of the point estimators are very satisfactory compared to the existing estimators that allow managing each problem at a time, or to the benchmark probit model. Actually, parameter estimates from our model outperform both those from sample selection model and those from Hausman et al.’s (Hausman et al. 1998) proposal.
The results obtained in an empirical analysis referring to undeclared work give strength to our proposal. Actually, even if it is impossible to assess the global goodness of fit in presence of misclassified data, in our application, we could compare the percent correct predictions for undeclared workers. Our model clearly outperforms probit. Another point that adds strength to our proposal is that, for all covariates included in the model, we obtained parameter estimates coherent with the existing literature.
Future research will be devoted, first, to disentangling the effects coming from the two sources of bias, verifying the existence of a possible offsetting. Secondly, we will extend MIS-SS model by introducing a misclassification problem in the selection equation as well. A third extension could be the specification of the misclassification probabilities as a function of some covariates. Another interesting direction for future research could refer to the problems arising from measurement errors in the covariates of the outcome equation, which currently is well known for intrinsically introducing an endogeneity issue.
Author Contributions
The authors contributed equally to the work.
Funding
Sapienza University, grant number 00041_19_RDB_ATENEO2018_AREZZO.
Conflicts of Interest
Authors declare no conflict of interest.
References
- Abrevaya, Jason, and Jerry A. Hausman. 1999. Semiparametric estimation with mismeasured dependent variables: An application to duration models for unemployment spells. Annals of Economics and Statistics, 243–75. [Google Scholar] [CrossRef]
- Allingham, Michael, and Agnar Sandmo. 1972. Income tax evasion: A theoretical analysis. Journal of Public Economics 1: 323–38. [Google Scholar] [CrossRef]
- Alm, James, and Benno Torgler. 2006. Culture differences and tax morale in the united states and in europe. Journal of Economic Psychology 27: 224–46. [Google Scholar] [CrossRef]
- Braithwaite, Valerie, and Eliza Ahmed. 2005. A threat to tax morale: The case of australian higher education policy. Journal of Economic Psychology 25: 523–40. [Google Scholar] [CrossRef]
- Cameron, A. Colin, and Pravin K. Trivedi. 2005. Microeconometrics: Methods and Applications. New York: Cambridge University Press. [Google Scholar]
- Chua, Tin Chiu, and Wayne A. Fuller. 1987. A model for multinomial response error applied to labor flows. Journal of the American Statistical Association 82: 46–51. [Google Scholar] [CrossRef]
- Dubin, Jeffrey A., and Douglas Rivers. 1989. Selection bias in linear regression, logit and probit models. Sociological Methods & Research 18: 360–90. [Google Scholar]
- Feld, Lars P., and Bruno S. Frey. 2002. Trust breeds trust: How taxpayers and treated. Economics of Governance 2: 87–99. [Google Scholar] [CrossRef]
- Hausman, Jerry A., Jason Abrevaya, and Fiona M. Scott-Morton. 1998. Misclassification of the dependent variable in a discrete-response setting. Journal of Econometrics 87: 239–69. [Google Scholar] [CrossRef]
- Heckman, James J. 1979. Sample selection bias as a specification error. Econometrica 47: 153–62. [Google Scholar] [CrossRef]
- Hug, Simon. 2010. The effect of misclassifications in probit models: Monte carlo simulations and applications. Political Analysis 18: 78–102. [Google Scholar] [CrossRef]
- Katz, Jonathan N., and Gabriel Katz. 2010. Correcting for survey misreports using auxiliary information with an application to estimating turnout. American Journal of Political Science 54: 815–35. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 2007. Self-Selection. In A Companion to Theoretical Econometrics. Edited by Badi H. Baltagi. Oxford: Blackwell Publishing Ltd., Chapter 18. pp. 383–409. [Google Scholar]
- Loftus, Elizabeth F. 1975. Reconstructing memory: The incredible eyewitness. Jurimetrics Journal 15: 188–93. [Google Scholar]
- Mellow, Wesley, and Hal Sider. 1983. Accuracy of response in labor market surveys: Evidence and implications. Journal of Labor Economics 1: 331–44. [Google Scholar] [CrossRef]
- Nardo, M., M. Saisana, A. Saltelli, S. Tarontola, A. Hoffman, and Enrico Giovannini. 2008. Handbook on Constructing Composite Indicators: Methodology and User Guide. Paris: OECD. [Google Scholar]
- Poterba, James, and Lawrence Summers. 1995. Unemployment benefits and labor market transitions: A multinomial logit model with errors in classification. The Review of Economics and Statistics 77: 207–16. [Google Scholar] [CrossRef]
- Schmölders, Gunter. 1960. Das Irrationale in der öffentlichen Finanzwirtschaft: Probleme der Finanzpsychologie. Rowohlts Deutsche Enzyklopädie: Staats- und Wirtschaftswissenschaften. Rowohlt. [Google Scholar]
- Sullivan, Paul. 2009. Estimation of an occupational choice model when occupations are misclassified. The Journal of Human Resources 44: 495–535. [Google Scholar] [CrossRef][Green Version]
- Torgler, Benno. 2001a. Is tax evasion never justifiable? Journal of Public Finance and Public Choice 20: 143–68. [Google Scholar]
- Torgler, Benno. 2001b. What do we know about tax morale and tax compliance? International Review of Economics and Business 48: 395–419. [Google Scholar]
- Vella, Francis. 1998. Estimating models with sample selection bias: A survey. The Journal of Human Resources 33: 127–69. [Google Scholar] [CrossRef]
- Williams, Colin C., and Ioana A. Horodnic. 2017. Evaluating the policy approaches for tackling undeclared work in the european union. Environment and Planning C: Politics and Space 35: 916–36. [Google Scholar] [CrossRef]
- Williams, Colin C., and Ioana A. Horodnic. 2015a. Evaluating the prevalence of the undeclared economy in central and eastern europe: An institutional asymmetry perspective. European Journal of Industrial Relations 21: 389–406. [Google Scholar] [CrossRef]
- Williams, Colin C., and Ioana A. Horodnic. 2015b. Rethinking the marginalisation thesis: An evaluation of the socio-spatial variations in undeclared work in the european union. Employee Relations 37: 48–65. [Google Scholar] [CrossRef]
| 1 | For each replication k, we compute the following relative difference between the estimate and the parameter value ; afterward, we average over the number of replications. |
| 2 | The variable “respondent cooperation” guarantees that the model is identified even if the assumption of normality does not hold, because it makes . |
| 3 | The association between tax morale and the participation in undeclared activities is well known in the literature and was already observed in Europe using Eurobarometer data on all European countries (Williams and Horodnic 2017). |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).