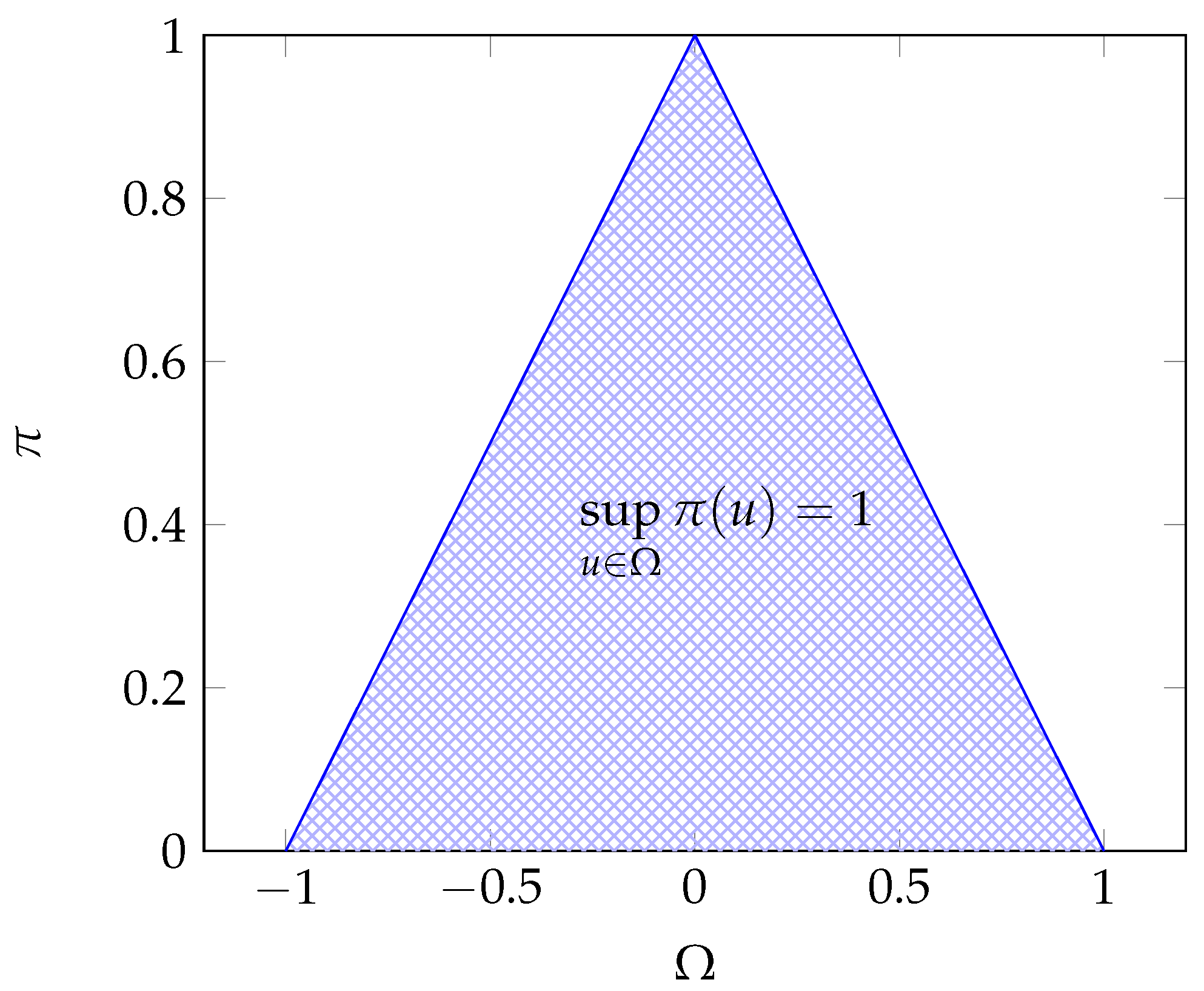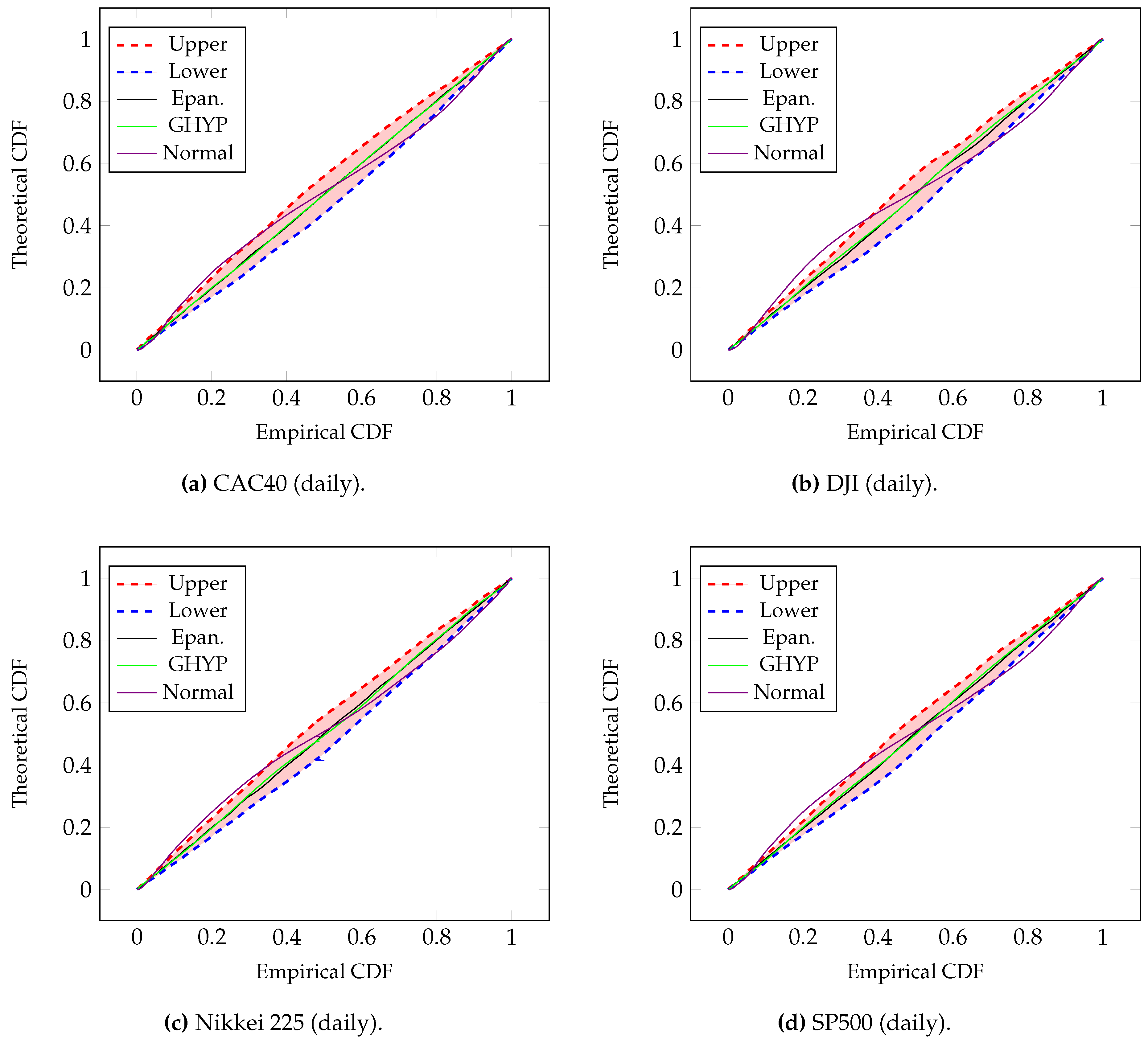1. Introduction
Controlling financial risk is an important issue for financial institutions. For the necessity of risk management, the first task is to measure risk. Value-at-Risk (VaR) is probably the most widely used risk measurement in financial institutions. It has made its way into the Basel II Capital-Adequacy framework. VaR is an estimate of the largest loss over a specified time horizon at a particular probability level. For example, if the daily VaR of an investment portfolio is
$10 million with a
confidence level, this means that we can be
confident that the portfolio will not lose more than
$10 million over the next day. In a more formal way, the VaR of a portfolio at a probability level
can be defined as
McNeil et al. (
2005, p. 38).
where
X is a random variable representing daily percent return for a total stock index with Cumulative Distribution Function (CDF)
. As
McNeil et al. (
2005) point out, VaR is simply a quantile of the corresponding loss distribution, which makes its computation easy. Various methods have been proposed in the relevant literature to compute the VaR. Each method differs in the methodology used, the hypotheses, and the way the models are implemented. A highly questionable fact is that each method leads to different results. Thus the choice of computational method is likely to have a large impact on the way a financial institution manages its credit portfolio.
The most commonly used approach is the nonparametric Historical Simulation (HS) method described in
Linsmeier and Pearson (
1997). It is based on the empirical CDF of the historically simulated returns by attributing an equal probability weight to each day’s return. The HS approach is easy to implement but suffers from two major drawbacks: First, the success of the approach depends on the ability to collect a large series of data; second, this is an unconditional model and thus we need a number of extreme scenarios in the historical record to provide more informative estimates of the tail of the loss distribution
McNeil et al. (
2005). Moreover, estimates of extreme quantiles are inefficient since extrapolation beyond past observations is impossible. To avoid these drawbacks, several parametric and nonparametric approaches have been developed. For example,
Butler and Schachter (
1998) propose the kernel estimators in conjunction with the historical simulation method. Also,
Charpentier and Oulidi (
2010) calculate the VaR by using several nonparametric estimators based on Beta kernel. This study shows that those estimators improve the efficiency of traditional ones, not only for light tailed, but also heavy tailed distributions.
Numerous recent VaR models are referred to as parametric. From the point of view of the risk manager, estimate VaR assuming normal distribution of asset returns is inappropriate and lead to underestimate the left tail at low probability level. For this reason, most recent research papers deal with going beyond the normal model and attempt to capture the related phenomena of heavy and long tails and asymmetric form of the returns series. EVT (Extreme Value Theory) and the so-called GHYP (Generalized HYPerbolic) distributions are among the most widely used. The main advantage of hypothesizing a GHYP distribution is its ability to account for the statistical properties of financial market data such as volatility clustering, asymmetry and heavy-tail phenomena (see
McNeil et al. (
2005) for an introduction and
Paolella and Polak (
2015) for a recent application).
Kuester et al. (
2006) use an EVT-based approach and focuses on the long tails of the return distribution.
Braione and Scholtes (
2016) study the performance of forecasting VaR under different parametric distributional assumptions and show the predominance and the predictive ability for the skewed and heavy-tailed distributions in the univariate case. The main drawback of using a parametric model is the high dependency of the obtained method to the hypothesized distribution model. To lower this dependency, some authors have proposed a group of semiparametric methods that are based on extreme value theory. These methods have been successfully used by financial analysts in estimating VaR
Danielsson and De Vries (
2000). However, all the above mentioned attempts have the common weakness of a low robustness to modelling leading to variations in the VaR estimation. To enable this method to be used in a prudent manner, it would be of instrumental interest to estimate the variation of the computed VaR w.r.t. the modelling. Some attempts have been proposed to achieve such a goal. For example,
Butler and Schachter (
1998) propose a method to measure the precision of a VaR estimate.
Jorion (
1996) suggests that VaR always be reported with confidence intervals and shows that it is possible to improve the efficiency of VaR estimates using their standard errors.
Kupiec (
1995) proposes a method for quantifying the uncertainty, in the estimated VaR, induced by the fact that the return distribution is unknown.
Pritsker (
1997) proposes to estimate a standard error by using a Monte Carlo VaR analysis.
In this paper, we propose a completely new approach to estimate the variations in the VaR induced by choosing a particular model in a kernel-based approach. The idea is that an estimate of the CDF of the daily percent return can be used to compute the VaR as suggested by Equation (
1). Such an estimate can be obtained by using a kernel-based approach
Silvermann (
1986). In Kernel Density Estimation (KDE), the role of the kernel is to achieve an interpolation to lower the impact of sampling on the obtained estimation. Roughly speaking, it smoothes the empirical CDF. However, as in the above mentioned methods, there is a systematic bias induced by the choice of the kernel used to estimate the CDF. Our proposal is to focus on the new nonparametric approach developed by
Loquin and Strauss (
2008a) to estimate the CDF. This approach makes use of the ability of a new kind of interpolating kernel, called
maxitive kernel, to represent a convex set of conventional kernels—that we call
summative kernels Loquin and Strauss (
2008b). Within this approach, the estimate of the CDF is interval-valued. Such an interval-valued estimate of the CDF, also called a p-box
Destercke et al. (
2007), is the convex set of all the CDF that would have been computed by using the convex set of conventional summative kernel represented by the maxitive kernel. We show that this approach can advantageously be used to compute with accuracy the corresponding convex set of kernel-based VaR estimates. This approach has advantages over Monte Carlo based approaches since its complexity is comparable to that of classical kernel estimation. Moreover, within this approach the bounds are exact while Monte Carlo approaches provide an inner estimation of those bounds.
This paper is structured as follows.
Section 2 reviews some nonparametric and parametric approaches and bootstrap methods used to compute the confidence interval of VaR. In
Section 3, we introduce the empirical distribution function and the kernel cumulative estimator based on summative kernel. We define in
Section 4 the maxitive kernel, which forms the basis of our approach, and it is shown how an interval-valued estimation of VaR, based on maxtive kernel, can be derived that has relevant properties in this context.
Section 5 presents and discusses our empirical findings. Firstly, we show how the choice of kernel function affects the VaR estimates. Secondly, we investigate the performance of the interval-valued proposed in this paper by comparing it to three very competitive approaches: The simple Normal VaR, the HS VaR, and the GHYP VaR. Finally,
Section 6 concludes this paper with some further remarks.
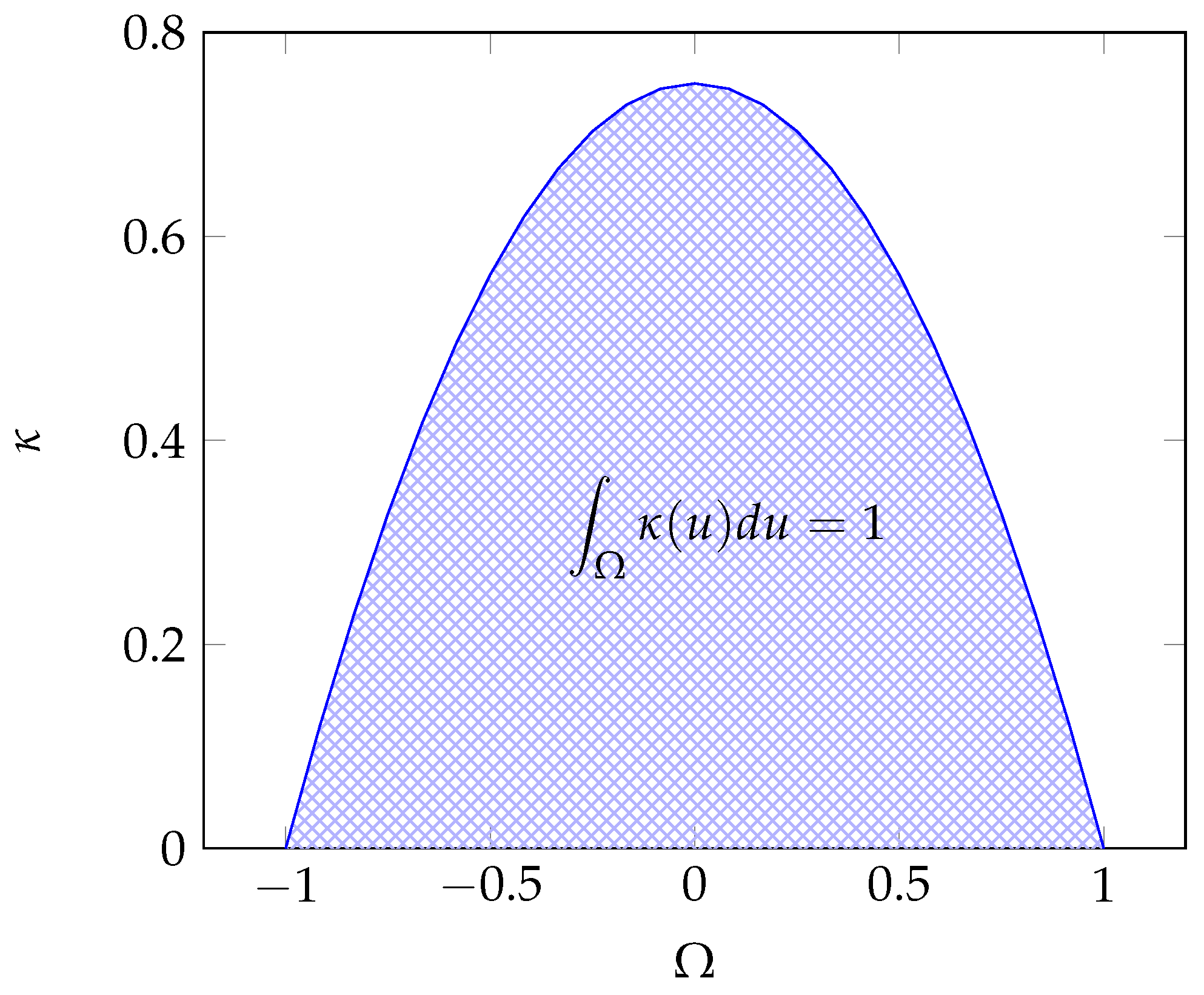
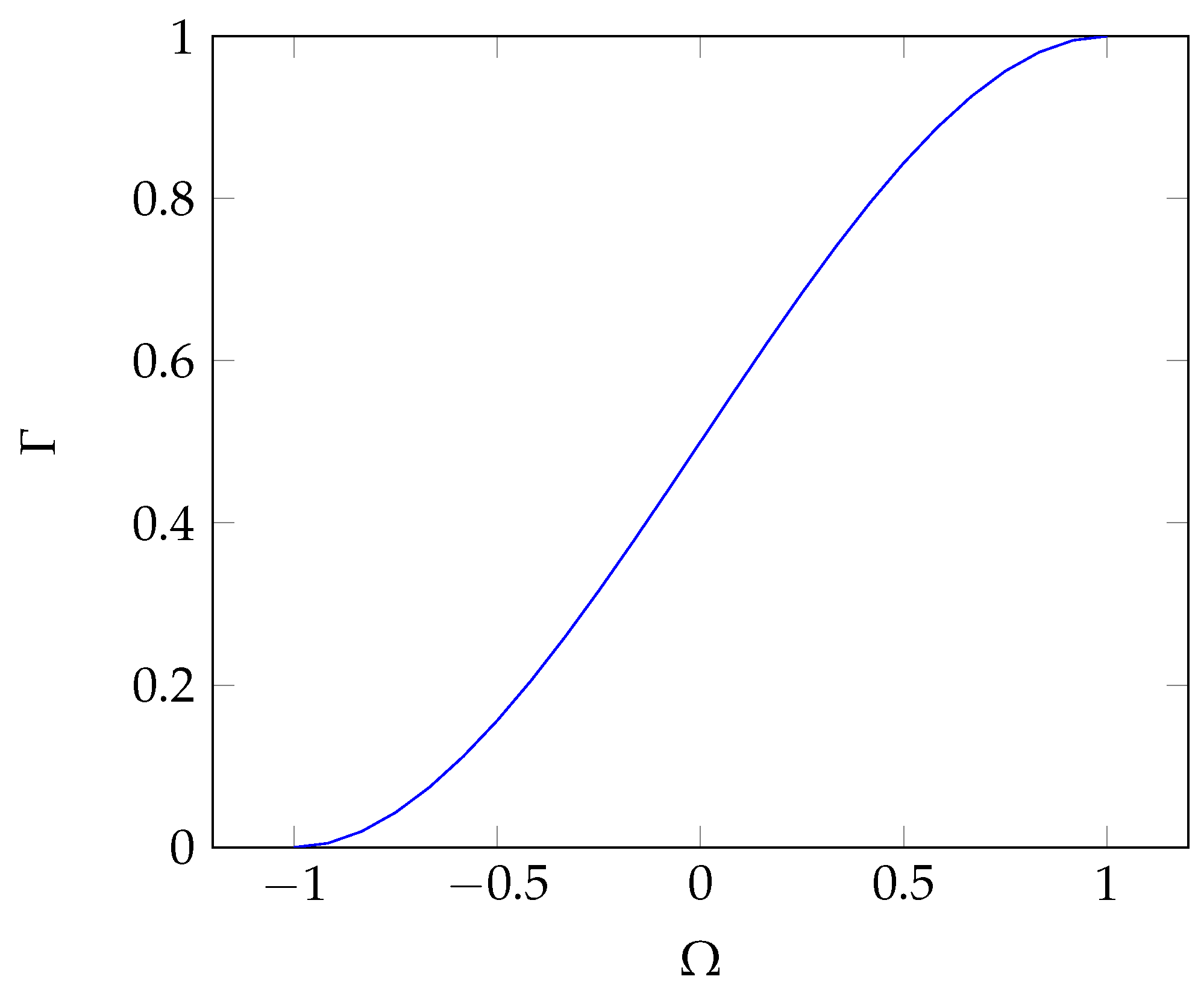
Throughout this paper, we consider that the observations belong to a convex and compact subset (universe) of , called the reference set. is the collection of all measurable subsets of . It naturally contains the empty set and is closed under complementation and countable unions. Then is a measurable space. Let be the set of functions defined on with values in .
5. Experiment: Empirical Results
5.1. Data and Experimental Process
The data used in the present study consisted of daily closing prices collected between January 2010 and December 2016 for four stock indexes from developed countries: S&P500, DJI, Nikkei225, and CAC40. The daily close prices were converted to daily log-returns. We took the first differences of the natural logarithm of the daily prices. For an observed price
, the corresponding one-day log-return on day
t was defined by:
.
Table 1 contains descriptive statistics for the sample return of the four considered stock indexes. We observed that the returns were negatively skewed and characterized by heavy tails since the kurtoses were significantly greater than 3. The series had a distribution with tails that were significantly fatter than those of normal distribution. The Jarque-Bera test also indicated that hypothesizing the four data to be normally distributed can be rejected with a very low significance level.
Due to these properties, the normal distribution would be an inappropriate model for calculating the daily VaR—as mentioned in the introduction. We thus rather envisage a nonparametric asymmetric approach based on kernel estimation of the CDF. However, as previously mentioned, estimating the VaR using a kernel based approach can be highly biased, since the choice of the kernel has an important impact on assessing the VaR estimate at a given probability level.
In this section, we propose to gauge this impact by estimating the VaR at a several probability levels with different types of kernels, whose bandwidths have been adapted to the available datasets. We confirmed that no kernel can be considered as optimal in this context and show that the new maxitive interval-valued nonparametric approach we propose leads to a more cautious behavior when applied to real data. In fact, the bounds of the interval-valued estimate of the VaR, for a given probability level, can be instrumental in applications such as reserve requirements for banks. We then show that this approach allows discarding some parametric approaches since they are not adapted to heavy tailed data like those we consider.
5.2. Nonparametric Estimate of the VaR: Comparing Summative and Maxitive Approaches
In this experiment, we have considered estimating the VaR for low probability levels—namely at levels lower than
—for each of the four datasets. In the first experiment, we have focused on DJI and Nikkei225 indexes. The CDF(s) have been estimated by considering four of the most used summative kernels whose bandwidth have been adapted using the rule of thumb method: Epanechnikov, normal, biweight, and triweight (linear)—see
Silvermann (
1986) for their analytical expressions.
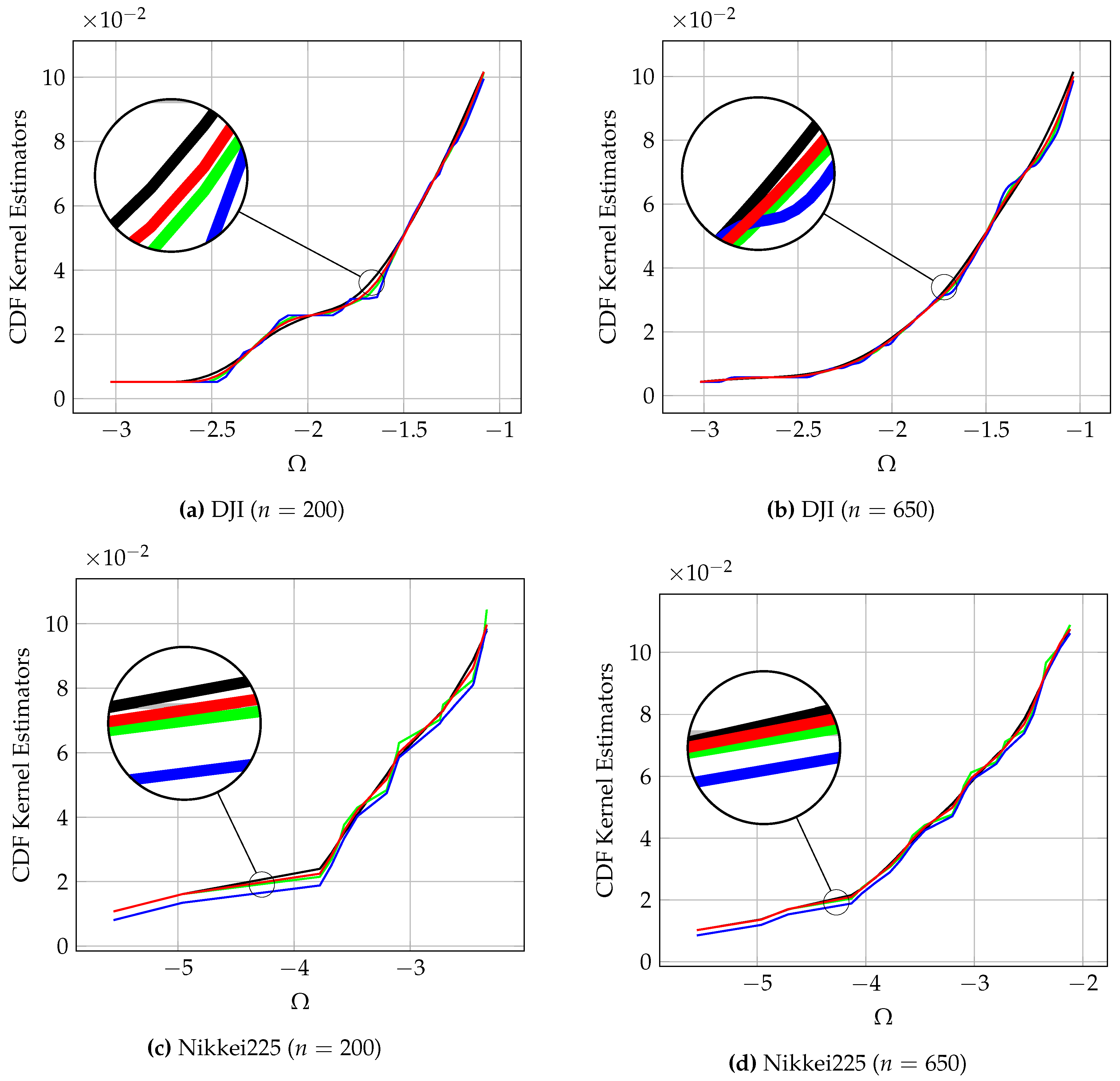
Figure 4 illustrates the impact of the kernel choice in the VaR estimation. This impact is more marked with high volatility stocks (Nikkei225). For example, referring to
Figure 4a, it can be seen that the VaR estimate based on the Epanechnikov kernel is absolutely greater than the one based on the normal kernel at the probability level of
while the opposite situation occurs at the probability level of
. Referring to each plots of
Figure 4, it is obvious that no kernel can be seen as always providing the upper or lower valued CDF. Since the CDF curves intersect each other for different probability levels then the risk of bias in the VaR estimate is relatively great, especially when the number of observations in the data set is low—compare
Figure 4b–d. In this context, no kernel function can be considered as more or less conservative than the others. Also, other indexes would have produced similar results.
This first experiment shows that the high dependence of the CDF estimate to the chosen kernel shape can highly impact and bias the VaR estimate. The goal of the second experiment aims to show that none of the four considered kernel can be considered as optimal in this context. This experiment needs a ground truth which is not available. A resampling methodology was carried out to estimate such a ground truth. This methodology consists of five steps:
Step 1: Fit a GARCH model to the four stock returns data. The fitted model considered for the returns
is a AR(1)
1- GARCH(1,1) given by:
where
is the return value at time
t,
is a standard Normal random variable and
n is the sample size (
and 1500). The conditional mean
, is assumed to follow an AR(1) model given by:
. By definition
is serially uncorrelated with mean zero, but a time varying conditional variance equal to
. The three positive parameters
,
,
and the two parameters
,
are, respectively, the parameters of the GARCH(1,1) and the AR(1) models. The ML method provides a systematic way to adjust the parameters of the model to give the best fit.
Table 2 lists the fitted models for each daily stock returns data.
Step 2: Generate 1000 simulated samples from each returns data using the coefficients obtained from the above fitted models. The main reason behind proposing GARCH models to simulate our real data is the dependence properties and the volatility phenomena of stock returns; see
Engle (
1982).
In a first step, we generate an i.i.d series, , by the random generator in MATLAB (R2010a) and another series . The random numbers sampled were all assumed to be normally distributed with expectation zero and unit variance. Then, the innovations for the GARCH series have been obtained via the equation . Finally the generation of from the AR(1) process is straightforward. Therefore we run the series for 1500 and 200 times in each of the 1000 simulated samples.
Step 3: Calculate the VaR estimates for each sample data generated in step two using the 4 kernel functions. These VaRs are calculated at five chosen levels of probability (, , , , ) with 2 times horizons ( and ).
Step 4: Assess the performance of each kernel function by comparing their VaRs with the empirical VaRs. The performance criterion we examine is the mean square error (MSE), i.e.,:
where
is a vector of quantiles obtained from the simulated samples.
Step 5: Tabulate the results that lead us to some important conclusions.
The results of the MSE of each
(%) VaR estimates are reported in
Table 3 and
Table 4. From
Table 3 and
Table 4, for S&P500, the best kernel function that estimate the VaR at level of
and
is the Epanechnikov kernel, while the Normal kernel is the best at
probabilities level. For Nikkei225, it seems that the Normal perform better than the other kernel functions. For DJI, the Epanechnikov kernel is more accurate to estimate the VaR, while for CAC40 the Normal and is matched more accurately. From
Table 4, when
, it appears that the Biwieight and Epanechnikov kernel are more likely to estimate VaR more accurately at several probability levels. However, the performance of kernel functions rapidly declines as
n and
get smaller.
The simulations results showed that, for large sample sizes (here ), all kernel functions are consistent estimators, i.e., MSE values are close to 0. On the other hand, MSE values are larger for the smaller sample size (here ). This demonstrates that choosing a particular kernel, when the sample size is low, is risky. Therefore a coherent interval-valued of VaR as we propose is likely to provide a more careful decision in this context.
5.3. Interval Estimation of Value-at-Risk and Some Numerical Comparisons
Here we apply the maxitive kernel estimator presented in
Section 4.3 to obtain the lower and upper bound for VaR corresponding to each four stock indexes for three probability levels (
). To obtain the optimal bounds for the VaR, the bandwidth has been, once again, chosen using the most popular methods such as biased cross-validation method and plug-in method presented in
Section 3.3. As shown in
Table 5, the maximum available bandwidth is taken to insure that all kernel estimators are inside the interval given by the maxitive kernel estimator. In order to examine the performance of the maxitive kernel estimation method, we divide the data into three samples: the first sample corresponds to data with 6 year time horizons, the second sample is chosen with time horizons of 3 years and the third correspond to one year time horizon. In a first step, after choosing the best-fit distribution from the family of GHYP distribution by using the AIC
2 criteria, we compute the VaR across the candidate distribution. Next, we compute the VaR confidence interval based on these three distributions using the bias-corrected and accelerated (BCa) bootstrap method. Finally, we compare our proposed maxitive interval-valued with those based on the bootstrap technique under different samples sizes. So far, the bootstrap confidence interval of VaR for the three distributions: GHYP, Normal, and HS are presented together in
Table 6,
Table 7 and
Table 8. With these punctual VaRs at hand for comparison purposes, we evaluate the performance of our approach. In this section, we have chosen to illustrate our results and to discuss the benefit of our approach in two ways. In
Table 6,
Table 7 and
Table 8, we show the explicit results for the minimum and maximum value, as well as the width of the interval estimation of VaR for several probability levels between
and
.
Figure 5 shows the PP-plots, i.e., the
of all models against the
. Based on the numerical results we can formulate several conclusions: Evidently, the lower and upper bounds increase with the probability level
. However, it is important to note that the intervals estimation of VaRs for the two indexes
Nikkei225 and
CAC40 are larger than those of
DJI and
S&P500 indexes. Note also that the influence of the volatility stock market is much more important than the influence of the sample size. Also, the widths of maxitive VaR intervals are rather tight than those derived from the GHYP, HS, and normal distributions. For example, for the short time horizon 1 year with the high volatility stock (Nikkei225) and at the
of probability level the width of the interval-valued of VaR is
while the widths of the BCa (
) confidence interval based on HS, normal, and GHYP distributions are respectively
,
, and
respectively (See
Table 6). Furthermore, we can remark that the maxitive interval-valued estimation of the VaR is on the left side of the normal VaR and this shows the ability of our approach to model very dangerous financial risks while the normal distribution is not consistent with tail-thickness and right tail risk. This results indicate that our approach is more accurate and informative especially for the smaller sample size.
Next, in order to inspect the goodness-of-fit of the used models a graphical tool (PP-plot) is constructed (
Figure 5) to compare the empirical cumulative function to the fitted cumulative functions. This plot confirms that the Epanechnikov kernel function and the GHYP distribution give a good global fit for the 4 returns data. The points of the PP-plot are close to the 45 degree line and they also lie within the interval estimation using maxitive kernel.
In contrast, from the same figure, the PP-plot of the normal cumulative function against the empirical cumulative function shows that the left end pattern is above the 45 degree line and the right end is below it. Thus, the normal distribution underestimates the VaR at low probability level. This is due to the fact that the normal distribution ignores the presence of fat tails in the actual distribution. Based on these results, we can conclude that the GHYP and the maxitive kernel method provide a better fit than a normal distribution to market return data. Thus, the maxitive kernel method seems to be a good choice to estimate the risk for VaR.
6. Conclusions
Using an estimate of the Value-at-Risk (VaR) based on a small-sized sample may pose a risk to financial application due to the high dependence of this VaR estimate to the computation method. In fact, computing a VaR estimate can be performed in many ways including parametric and nonparametric approaches. We have shown, with experiments based on daily closing prices data of four stock indexes, that no method can be said to be optimal to achieve this estimate. Moreover, the bias induced by choosing a particular method is particularly sensitive for estimates based on small samples. In this paper, we have presented a new method for computing the VaR which highly differs from its competitors in the sense that it is interval-valued. This interval-valued VaR estimate is the set of all estimates that could have been obtained, with the same data sample, by using a set of kernel-based estimation methods. In our experiments, we noted that the output of parametric methods, like the GHYP VaR estimate, always belong to the interval-valued VaR we propose while others, like the normal VaR estimate, do not. It appears that VaR estimates belonging to the interval-valued VaR estimate we propose are likely to be less risky than those that do not. Moreover, a wide interval-valued VaR estimate is a marker of a high risk for a trader since it reflects thick tails, pronounced skewness, and excess kurtosis of financial asset price returns.
The interval-valued estimation, based on maxitive kernel, that we propose in this paper is a convex envelope of the kernel VaR estimation. Although the VaR is probably one of the most popular tool in risk management, an alternative measure for Value-at-Risk which satisfied the conditions for a coherent risk measure has been proposed (see e.g.,
Rockafellar and Uryasev 2000;
Artzner et al. 1999). This risk measure is called Expected Shortfall (ES; also known as conditional VaR or average VaR). Indeed, the Basel Committee published, in January 2016
Basel Committee on Banking Supervision (
2016), revised standards for minimum capital requirements for market risk which include a shift from Value-at-Risk to expected shortfall as the preferred risk measure. Then, the future research should be conducted into finding an
interval-valued estimation of ES, based on maxitive kernel, and to compare it with the
interval-valued estimation of VaR and the ES for many distributions. In this regard,
Broda and Paolella (
2011) presents easily-computed expressions for evaluating the expected shortfall for numerous distributions which are now commonly used for modelling asset returns. Another interesting avenue of research would be to construct a
CoVaR interval combining GARCH model with maxitive kernel.