Micro-Macro Connected Stochastic Dynamic Economic Behavior Systems
Abstract
1. Introduction
1.1. A Micro Based Information Theoretic Approach
1.2. Looking Ahead
2. Self-Organized Economic Behavior-Entropy Connection
3. The Cressie-Read Minimum Power Divergence Family
3.1. Reformulated Moment Based Model Econometric Example
3.2. A Markov Process with Discrete State and Time
4. Entropy Based Micro State Income Distributions
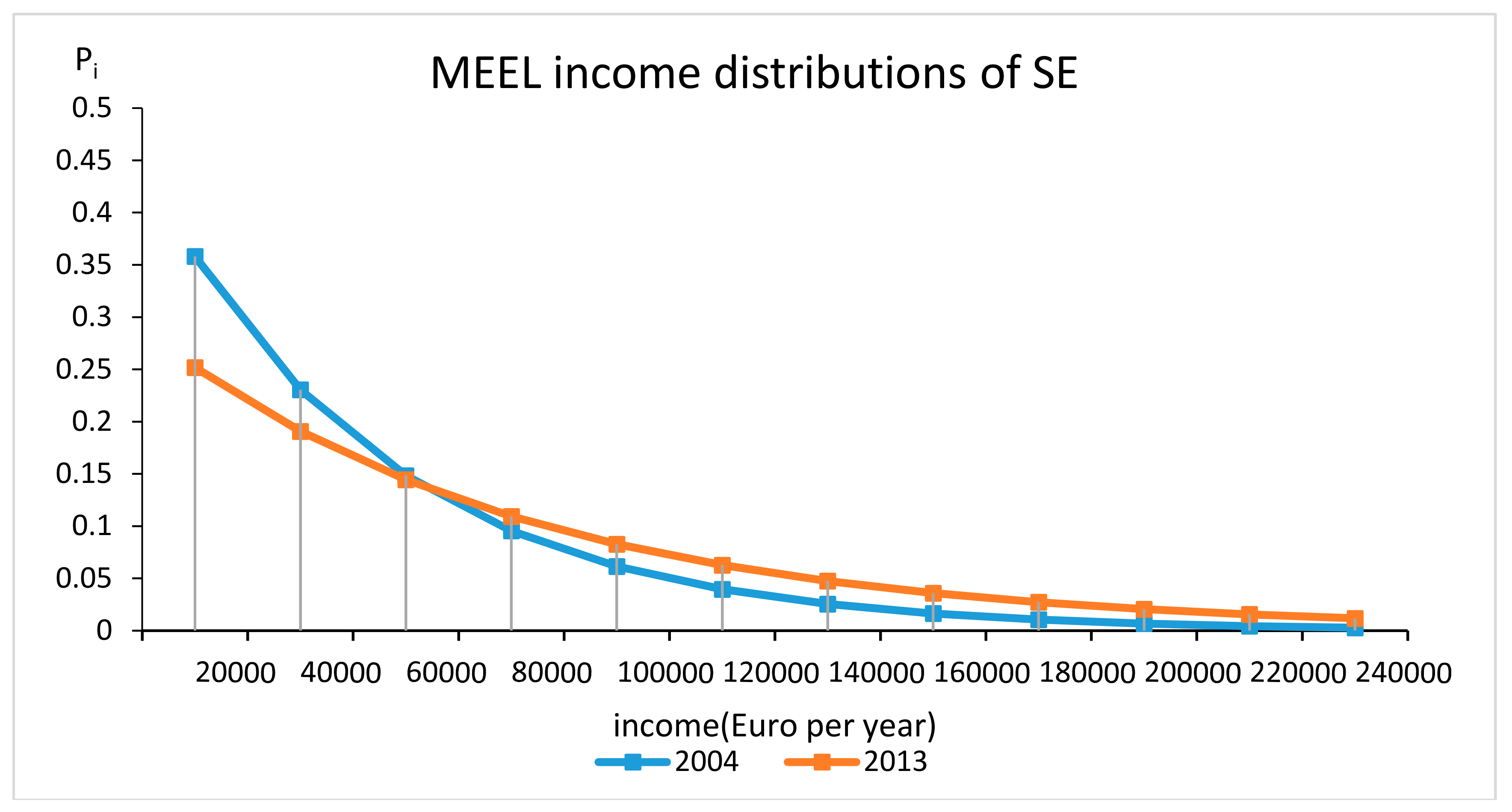
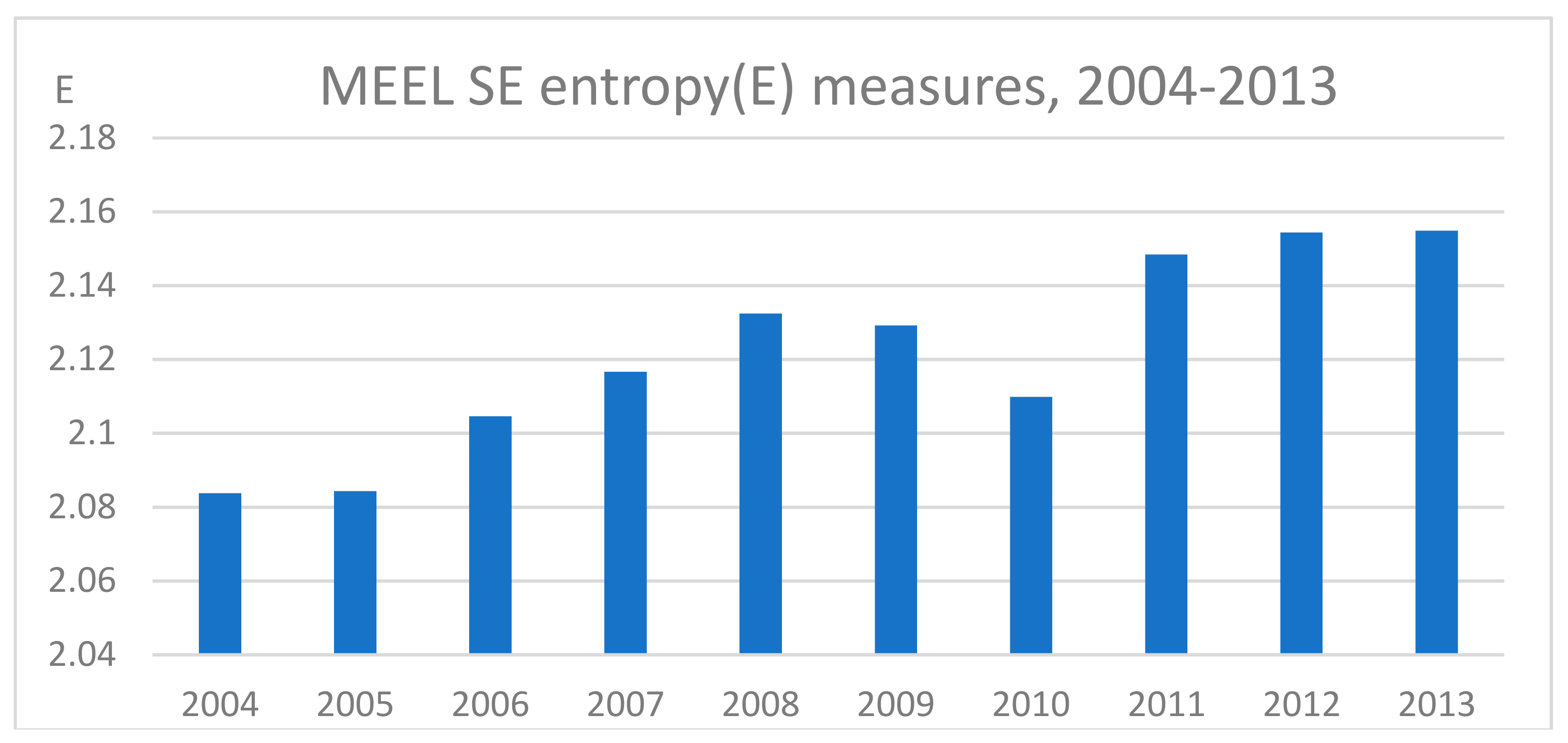
5. An Empirical Example
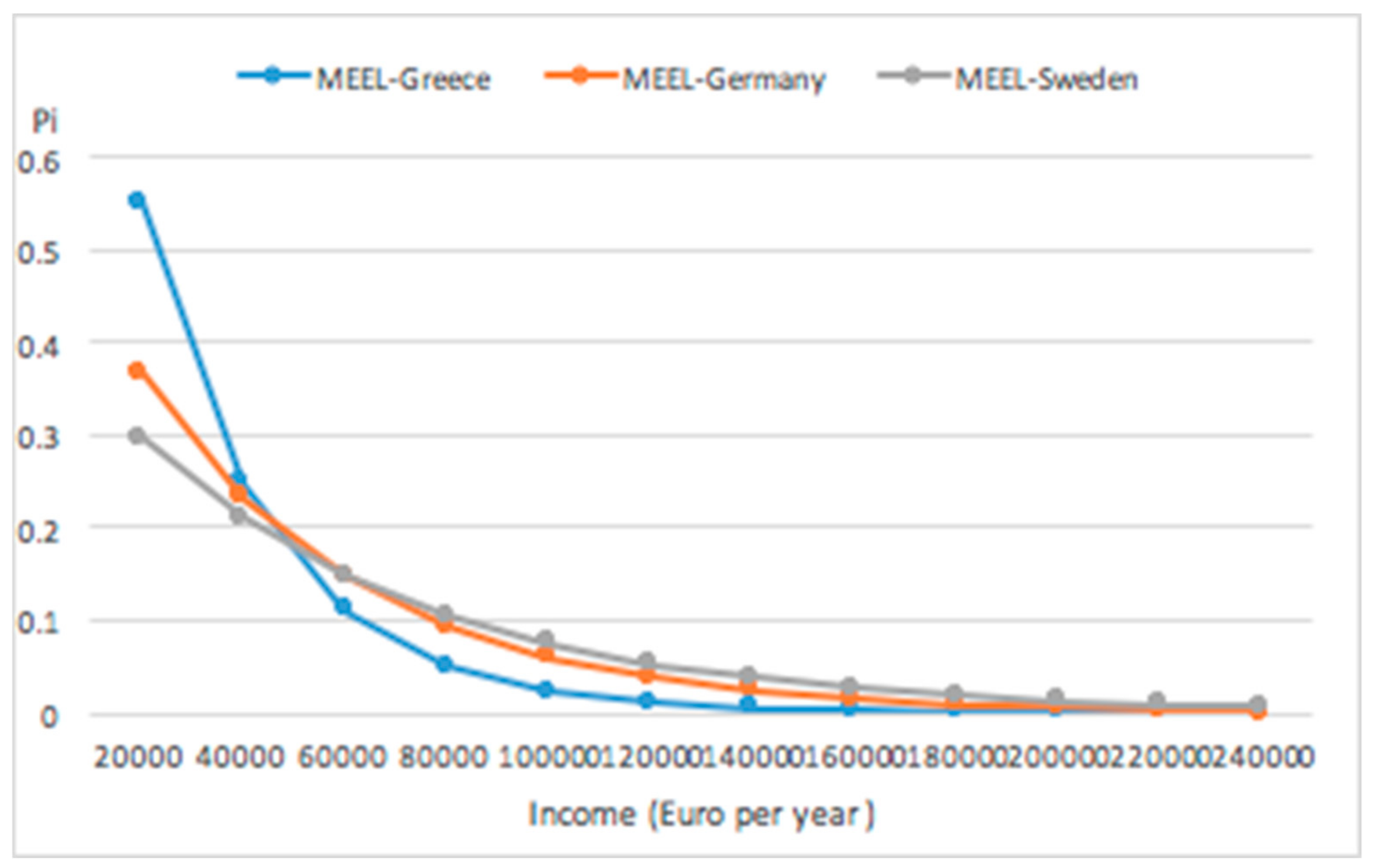
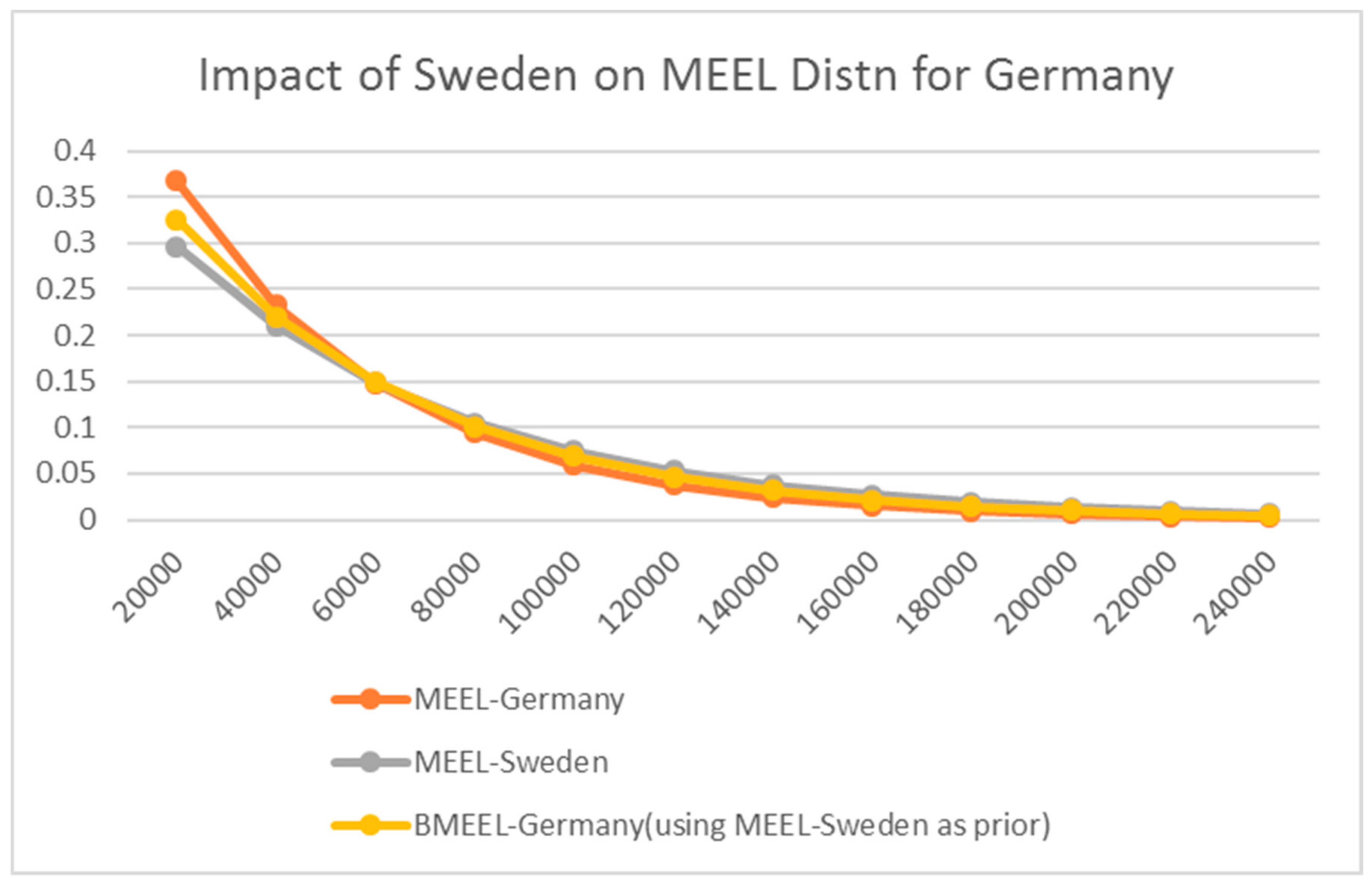
6. An Entropic Prior
A Transitional Prior Application
7. Related Literature Review
7.1. Network Information Recovery
7.2. Agent Based Models
8. Summing Up and Looking Ahead
Funding
Acknowledgments
Conflicts of Interest
References
- Bargigli, Leonardo, and Gabriele Tedeschi. 2014. Interaction in Agent Based Economics: A survey of the Network Approach. Physica A 399: 1–15. [Google Scholar] [CrossRef]
- Bargigli, Leonardo, Andrea Lionetto, and Stefano Viaggiu. 2013. A Statistical Equilibrium Representation of Markets as Complex Networks. Journal of Statistical Physics 165: 351–70. [Google Scholar] [CrossRef]
- Bhattacharya, Rabi, and Mukul Majumdar. 2007. Random Dynamical Systems: Theory and Applications. Cambridge: Cambridge University Press. [Google Scholar]
- Bruun, Charlotte. 2003. The Economy as an Agent-based Whole-Simulating Schumpeterian Dynamics. Industry and Innovation 10: 475–91. [Google Scholar] [CrossRef]
- Cho, Wendy, and George Judge. 2014. An Information Theoretic Approach to Network Tomography. Applied Econometric Letters 97: 201–7. [Google Scholar] [CrossRef]
- Cressie, Noel, and Timothy Read. 1984. Multinomial Goodness of Fit tests. Journal of the Royal Statistical Society Series B 4: 440–64. [Google Scholar]
- Gallager, Robert G. 2014. Stochastic Processes: Theory for Applications. Cambridge: Cambridge University Press. [Google Scholar]
- Gatti, Domenico Delli, Edoardo Gaffeo, and Mauro Gallegati. 2010. Complex Agent-Based Macroeconomics: A Manifesto for a New Paradigm. Journal of Economic Interaction and Coordination 5: 111–35. [Google Scholar] [CrossRef]
- Georgescu-Roegen, Nicholas. 1971. The Entropy Law and the Economic Process. Harvard: Harvard University Press. [Google Scholar]
- Gibbs, J. Willard. 1902. Elementary Principles in Statistical Mechanics. New York: Charles Scribner. [Google Scholar]
- Gomes, Orlando. 2014. Complex Networks in Macroeconomics. In Applied and Computational Mathematics. vol. 3, p. e138. [Google Scholar] [CrossRef]
- Good, Irving. 1963. Maximum Entropy for Hypothesis Formulation, Especially for Multidimensional Contingency Tables. The Annals of Mathematical Statistics 34: 911–34. [Google Scholar] [CrossRef]
- Gorban, Alexander N., Pavel A. Gorban, and George Judge. 2010. Entropy: The Markov Ordering Approach. Entropy 12: 1145–93. [Google Scholar] [CrossRef]
- Hendry, David, and John Muellbauer. 2018. The Future of Macroeconomics: Macro Theory and Models at the Bank of England. Oxford Review of Economic Policy 34: 287–328. [Google Scholar] [CrossRef]
- Jaynes, Edwin T. 1957a. Information Theory and Statistical Mechanics. Physics Review 106: 620–30. [Google Scholar] [CrossRef]
- Jaynes, Edwin T. 1957b. Information Theory and Statistical Mechanics. Physics Review 106: 171–90. [Google Scholar] [CrossRef]
- Jaynes, Edwin T. 1978. Where Do We Stand on Maximum Entropy? In The Maximum Entropy Formalism. Edited by Raphael D. Levine and Myron Tribus. Cambridge: MIT Press, pp. 15–118. [Google Scholar]
- Jaynes, Edwin T., and G. Larry Bretthorst. 2003. Probability Theory: The Logic of Science. Cambridge: Cambridge University Press. [Google Scholar]
- Judge, George. 2015. Entropy Maximization as a Basis for Information Recovery in Dynamic Economic Behavioral Systems. Econometrics 3: 91–100. [Google Scholar] [CrossRef]
- Judge, George. 2016. Econometric Information Recovery in Behavioral Networks. Econometrics 4: 38. [Google Scholar] [CrossRef]
- Judge, George G., and Ron C. Mittelhammer. 2011. An Information Theoretic Approach to Econometrics. Cambridge: Cambridge University Press. [Google Scholar]
- Judge, George G., and Ron C. Mittelhammer. 2012. Implications of the Cressie-Read Family of Additive Divergences for Information Recovery. Entropy 14: 2427–38. [Google Scholar] [CrossRef]
- Kullback, Solomon. 1959. Information Theory and Statistics. New York: John Wiley. [Google Scholar]
- Kullback, Solomon, and Richard Leibler. 1951. On Information and Sufficiency. The Annals of Mathematical Statistics 22: 79–86. [Google Scholar] [CrossRef]
- Miller, Douglas J., and George Judge. 2015. Information Recovery in a Dynamic Statistical Markov Model. Econometrics 3: 187–98. [Google Scholar] [CrossRef]
- Qian, Hong. 2000. Relative entropy: Free energy associated with equilibrium fluctuations and nonequilibrium deviations. Physical Review E 63: 042103. [Google Scholar] [CrossRef]
- Qian, Hong, and George Judge. 2014. Econometric Information Recovery in Stochastic Dynamic Systems. Working Paper. Berkeley: University of California. [Google Scholar]
- Read, Timothy R., and Noel A. Cressie. 1988. Goodness of Fit Statistics for Discrete Multivariate Data. New York: Springer. [Google Scholar]
- Rovelli, Carlo. 2018. The Order of Time. New York: Riverhead Books. [Google Scholar]
- Shannon, Claude Elwood. 1948. A Mathematical Theory of Communications. Bell Systems Technical Journal 27: 379–423. [Google Scholar] [CrossRef]
- Squartini, Tiziano, Enrico Ser-Giacomi, Diego Garlaschelli, and George Judge. 2015. Information Recovery in Behavioral Networks. PLoS ONE 10: e01277. [Google Scholar] [CrossRef]
- Stiglitz, Joseph. 2018. Where Modern Macroeconomics Went Wrong. Oxford Review of Economic Policy 34: 70–106. [Google Scholar]
- Tesfatsion, Leigh, and Kenneth Judd. 2006. Agent Based Computational Economics: A Constructive Approach to Economic Theory. Amsterdam: Elsevier. [Google Scholar]
- Villas-Boas, Sofia B., Qiuzi Fu, and George Judge. 2018. Entropy Based European Income Distributions and Inequality Measures. Physica A 514: 686–98. [Google Scholar] [CrossRef]
- Wagner, Richard. 2012. A Macro Economy as an Ecology of Plans. Journal of Economic Behavior and Organization 82: 433–44. [Google Scholar] [CrossRef]
- Wissner-Gross, Alexander D., and Cameron E. Freer. 2013. Causal Entropic Forces. Physical Review Letters 110: 167802. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Judge, G. Micro-Macro Connected Stochastic Dynamic Economic Behavior Systems. Econometrics 2018, 6, 46. https://doi.org/10.3390/econometrics6040046
Judge G. Micro-Macro Connected Stochastic Dynamic Economic Behavior Systems. Econometrics. 2018; 6(4):46. https://doi.org/10.3390/econometrics6040046
Chicago/Turabian StyleJudge, George. 2018. "Micro-Macro Connected Stochastic Dynamic Economic Behavior Systems" Econometrics 6, no. 4: 46. https://doi.org/10.3390/econometrics6040046
APA StyleJudge, G. (2018). Micro-Macro Connected Stochastic Dynamic Economic Behavior Systems. Econometrics, 6(4), 46. https://doi.org/10.3390/econometrics6040046



