On the Stock–Yogo Tables
Abstract
:1. Introduction
2. An Analytic Development of Stock–Yogo
- The practitioner chooses a value for , e.g., , if an asymptotic relative bias of less than 10% is deemed acceptable.
- Given and , is obtained on solving (8).
- Given , critical values for F can be determined, which are proportional to those of the non-central chi-squared distribution as specified in (4).
- The null of weak instruments is then rejected for sufficiently large values of the first-stage F-statistic, and we conclude that is no larger than the value chosen in Step 1 above.
3. Some Further Consequences of Theorem 1
4. Some Monte Carlo Results
5. -Values
6. Multiple Endogenous Regressors
7. The Wisdom of Hindsight: Some Historical Remarks
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Expectation of a Particular Function of Normal Random Variables
Appendix B. Analysis of Table 1
Appendix B.1. Preliminaries
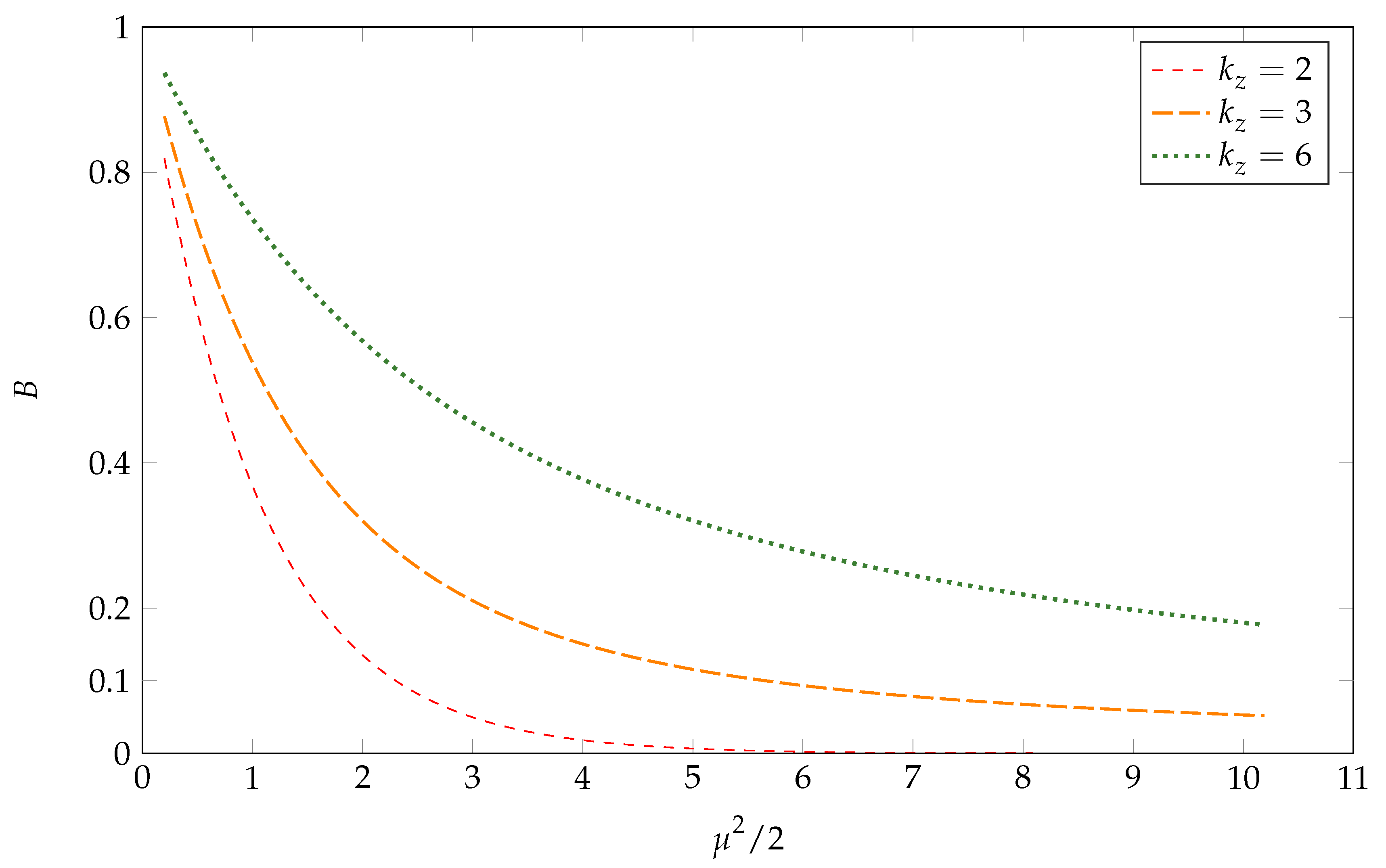
Appendix B.2. The Consequence of Varying B for Fixed
Appendix C. Some Remarks on Computational Aspects
Appendix D. Some Remarks on the Just-Identified Scalar Case

| B | ||||||||
|---|---|---|---|---|---|---|---|---|
| −0.01 | −0.05 | −0.10 | −0.20 | |||||
| mean | std dev | mean | std dev | mean | std dev | mean | std dev | |
| 1.4949 | 0.0086 | 1.4988 | 0.0086 | 1.4993 | 0.0086 | 1.4996 | 0.0087 | |
| 0.9954 | 0.1003 | 0.9753 | 0.2327 | 0.9495 | 0.4389 | 0.8936 | 6.0492 | |
| F | 104.11 | 20.411 | 24.429 | 9.8352 | 14.821 | 7.5732 | 9.1757 | 5.8671 |
| −0.0092 | −0.0496 | −0.1011 | −0.2130 | |||||
| 103.06 | 23.412 | 13.830 | 8.198 | |||||
| cv F | 139.17 | 42.035 | 28.769 | 20.323 | ||||
| rej freq F | 0.0496 | 0.0507 | 0.0485 | 0.0489 | ||||
Appendix E. Derivation of the O() Term in (16)
References
- Angrist, Joshua D., and Jörn-Steffen Pischke. 2009. Mostly Harmless Econometrics. An Empiricist’s Companion. Princeton and Oxford: Princeton University Press. [Google Scholar]
- Baum, Christopher F., Mark E. Schaffer, and Steven Stillman. 2010. ivreg2: Stata Module for Extended Instrumental Variables/2SLS, GMM and AC/HAC, LIML, and k-Class Regression. Boston College Department of Economics, Statistical Software Components S425401. Available online: http://ideas.repec.org/c/boc/bocode/s425401.html (accessed on 26 August 2015).
- Buse, Adolf. 1992. The bias of instrumental variables estimators. Econometrica 60: 173–80. [Google Scholar] [CrossRef]
- Chao, John, and Norman R. Swanson. 2007. Alternative approximations of the bias and MSE of the IV estimator under weak identification with an application to bias correction. Journal of Econometrics 137: 515–55. [Google Scholar] [CrossRef]
- Cohen, Jonathan D. 1988. Noncentral Chi-Square: Some observations on recurrence. The American Statistician 42: 120–22. [Google Scholar] [CrossRef]
- Constantine, A. Graham. 1963. Some non-central distribution problems in multivariate analysis. Annals of Mathematical Statistics 34: 1270–85. [Google Scholar] [CrossRef]
- Cragg, John G., and Stephen G. Donald. 1993. Testing identifiability and specification in instrument variable models. Econometric Theory 9: 222–40. [Google Scholar] [CrossRef]
- Das Gupta, Somesh, and Michael D. Perlman. 1974. Power of the noncentral F-test: Effect of additional variates on Hotelling’s T2-test. Journal of the American Statistical Association 69: 174–80. [Google Scholar]
- Davis, A. William. 1979. Invariant polynomials with two matrix arguments extending the zonal polynomials: Applications to multivariate distribution theory. Annals of the Institute of Statistical Mathematics 31 Pt A: 465–85. [Google Scholar] [CrossRef]
- Dufour, Jean-Marie. 1997. Some impossibility theorems in econometrics with applications to structural and dynamic models. Econometrica 65: 1365–87. [Google Scholar] [CrossRef]
- Forchini, Giovanni, and Grant H. Hillier. 2003. Conditional inference for possibly unidentified structural equations. Econometric Theory 19: 707–43. [Google Scholar] [CrossRef]
- Hale, Christopher, Roberto S. Mariano, and John G. Ramage. 1980. Finite sample analysis of misspecification in simultaneous equation models. Journal of the American Statistical Association 75: 418–27. [Google Scholar] [CrossRef]
- Herz, Carl S. 1955. Bessel functions of matrix argument. Annals of Mathematics 61: 474–523. [Google Scholar] [CrossRef]
- Hillier, Grant H., Raymond Kan, and Xiaolu Wang. 2009. Computationally efficient recursions for top-order invariant polynomials with applications. Econometric Theory 25: 211–42. [Google Scholar] [CrossRef]
- Hillier, Grant H., Raymond Kan, and Xiaolu Wang. 2014. Generating functions and short recursions, with applications to the moments of quadratic forms in noncentral normal vectors. Econometric Theory 30: 436–73. [Google Scholar] [CrossRef]
- Hillier, Grant H., Terrence W. Kinal, and Virendra K. Srivastava. 1984. On the moments of ordinary least squares and instrumental variables estimators in a general structural equation. Econometrica 52: 185–202. [Google Scholar] [CrossRef]
- James, Alan T. 1961. Zonal polynomials of the real positive definite symmetric matrices. Annals of Mathematics 74: 456–69. [Google Scholar] [CrossRef]
- James, Alan T. 1964. Distributions of matrix variates and latent roots derived from normal samples. The Annals of Mathematical Statistics 35: 475–501. [Google Scholar] [CrossRef]
- Johansson, Fredrik. 2016. Computing Hypergeometric Functions Rigorously. Available online: https://hal.inria.fr/hal-01336266v2 (accessed on 15 September 2016).
- Kinal, Terrence W. 1980. The existence of moments of k-class estimators. Econometrica 49: 241–49. [Google Scholar] [CrossRef]
- Kleibergen, Frank. 2002. Pivotal statistics for testing structural parameters in instrumental variables regression. Econometrica 70: 1781–803. [Google Scholar] [CrossRef]
- Knight, John L. 1982. A note on finite sample analysis of misspecification in simultaneous equation models. Economics Letters 9: 275–79. [Google Scholar] [CrossRef]
- MathWorks. 2016. MATLAB and Statistics Toolbox Release 2016b. Natick: The MathWorks Inc. [Google Scholar]
- Muirhead, Robb J. 1982. Aspects of Multivariate Statistical Theory. New York: John Wiley and Sons, Inc. [Google Scholar]
- National Institute of Standards and Technology (NIST). 2015. Digital Library of Mathematical Functions; Edited by Frank W. J. Olver, Adri B. Olde Daalhuis, Daniel W. Lozier, Barry I. Schneider, Ronald F. Boisvert, Charles W. Clark, Bruce R. Miller and Bonita V. Saunders. Release 1.0.10 of 2015-08-07; Gaithersburg: NIST. Available online: http://dlmf.nist.gov/ (accessed on 10 August 2015).
- Nelson, Charles R., and Richard Startz. 1990a. The distribution of the instrumental variables estimator and its t-ratio when the instrument is a poor one. Journal of Business 63 Pt 2: S125–40. [Google Scholar] [CrossRef]
- Nelson, Charles R., and Richard Startz. 1990b. Some further results on the exact small sample properties of the instrumental variable estimator. Econometrica 58: 967–76. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 1980. The exact distribution of instrumental variable estimators in an equation containing n + 1 endogenous variables. Econometrica 48: 861–78. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 1983a. Exact small sample theory in the simultaneous equations model. In Handbook of Econometrics, Volume I. Edited by Zvi Griliches and Michael D. Intriligator. Amsterdam: North Holland, Chapter 8. pp. 449–516. [Google Scholar]
- Phillips, Peter C. B. 1983b. Marginal densities of instrumental variable estimators in the general single equation case. Advances in Econometrics 2: 24. [Google Scholar]
- Phillips, Peter C. B. 1989. Partially identified econometric models. Econometric Theory 5: 181–240. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 2016. Inference in near-singular regression. Advances in Econometrics 36: 461–86. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 2017. Reduced forms and weak instrumentation. Econometric Reviews 36: 818–39. [Google Scholar] [CrossRef]
- Phillips, Peter C. B, and Wayne Y. Gao. 2017. Structural inference from reduced forms with many instruments. Journal of Econometrics 199: 96–116. [Google Scholar] [CrossRef]
- Richardson, David H. 1968. The exact distribution of a structural coefficient estimator. Journal of the American Statistical Association 63: 1214–26. [Google Scholar] [CrossRef]
- Richardson, David H., and De-Min Wu. 1971. A note on the comparison of ordinary and two-stage least squares estimators. Econometrica 39: 973–81. [Google Scholar] [CrossRef]
- Sanderson, Eleanor, and Frank Windmejer. 2016. A weak instrument F-test in linear IV models with multiple endogenous variables. Journal of Econometrics 190: 212–21. [Google Scholar] [CrossRef] [PubMed]
- Skeels, Christopher L. 1995. Instrumental variables estimation in misspecified single equations. Econometric Theory 11: 498–529. [Google Scholar] [CrossRef]
- Skeels, Christopher L., and Frank Windmeijer. 2016. On the Stock–Yogo Tables. Discussion Paper 16/679. Bristol: Department of Economics, University of Bristol. [Google Scholar]
- Slater, Lucy J. 1960. Confluent Hypergeometric Functions. Cambridge: Cambridge University Press. [Google Scholar]
- Slater, Lucy J. 1966. Generalized Hypergeometric Functions. Cambridge: Cambridge University Press. [Google Scholar]
- Staiger, Douglas, and James H. Stock. 1997. Instrumental variables regression with weak instruments. Econometrica 65: 557–86. [Google Scholar] [CrossRef]
- StataCorp. 2015. Stata Statistical Software: Release 14. College Station: StataCorp LP. [Google Scholar]
- Stock, James H., and Motohiro Yogo. 2005. Testing for weak instruments in linear IV regression. In Identification and Inference for Econometric Models: Essays in Honor of Thomas Rothenberg. Edited by Donald W. K. Andrews and James H. Stock. Cambridge: Cambridge University Press, Chapter 5. pp. 80–108. [Google Scholar]
- Wasserstein, Ronald L., and Nicole A. Lazar. 2016. The ASA’s statement on p-values: Context, process, and purpose. The American Statistician 70: 129–33. [Google Scholar] [CrossRef]
| 1. | Much of the later literature has focussed less on testing for the presence of weak instruments and more on the development of techniques that are robust to the presence of weak instruments. |
| 2. | A heuristically appealing aspect of using the first-stage F-statistic as a measure of instrument weakness, in the case of a single endogenous regressor, is its consistency with the well-known Staiger–Stock rule of thumb. Staiger and Stock (1997), p. 557, suggested that instruments be deemed weak if the first-stage F is less than 10. SY (pp. 101–2) observe that 10 corresponds closely to their tabulated critical values for a 5% test that the relative bias is 10% for all values of , and concluded that ‘this provides a formal, and not unreasonable, testing interpretation of the the Staiger–Stock rule of thumb.’ |
| 3. | Through the use of more extensive simulation results than those used originally by SY, we are able to support the proposition that the numerical approximation errors inherent in the computation of our analytical results are less than those contained in the original SY tables. |
| 4. | Some references specify the non-centrality parameter for a non-central chi-squared distribution as , whereas others specify it as . We have adopted the former convention here. |
| 5. | The exact details of these arguments can be found in SY and will not be repeated here. |
| 6. | We thank an anonymous referee for bringing this subtlety to our attention. For a more complete discussion of this point, we refer the reader to the discussion of (Chao and Swanson 2007, pp. 518–19) and the references cited therein. |
| 7. | It should be noted that the proof provided is not the only one possible and we would like to thank helpful referees for drawing various alternatives to our attention. For example, in an elegant paper, Chao and Swanson (2007), Proposition 3.1 and Lemma 3.3, respectively, derive local to zero approximations for each of and , from whence derivation of the ratio is straightforward. Similarly, there are finite sample papers in the literature from which it would be possible to start a proof along the lines of the one presented but at a more advanced point (see, for example, Forchini and Hillier 2003, Equation B.13). However, we favour the proof presented for two reasons. First, it is a direct continuation of the developments of Stock and Yogo (2005), Equation 3.1, and the discussion immediately thereafter. Second, when viewed in the correct light, there are much earlier antecedents that take precedence over the two mentioned here. We discuss this further in Section 6. |
| 8. | |
| 9. | We have also computed simulated critical values from 20,000 random draws as in SY, but repeating the exercise 1000 times. The resulting mean critical values are virtually identical to those in Table 1, with the maximum difference being 0.02. |
| 10. | Theorem 2 is similar in spirit to Das Gupta and Perlman (1974), p. 180, Remark 4.1, although they only address the numerator of the ratio in Equation (5). Consequently, Das Gupta and Perlman are silent on the relative magnitudes of and which, in essence, is the content of Theorem 2. |
| 11. | The complete set of assumptions are presented in SY (Section 2.4). |
| 12. | |
| 13. | Make the substitutions for , respectively, in Hillier et al. (1984), Equation (30). |
| 14. | Please note that the definition of adopted here is slightly different from the definitions used in either Hillier et al. (1984) and SY. |
| 15. | |
| 16. | The zonal polynomials appearing in (14) adopt a normalisation due to Constantine (1963), which typically leads to more compact expressions than do the polynomials originally proposed by James (1961). |
| 17. | Some progress towards addressing the computational aspects of these polynomials has been made by Hillier et al. (2009, 2014). |
| 18. | Although the derivation of (15) is straightforward, this is less true for (16). A derivation of the terms in (16) that are in addition to those in (15) is provided in Appendix E. |
| 19. | Similarly, in the proof of Theorem A1, we established that was unbounded when . |
| 20. |
| 0.01 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | |
|---|---|---|---|---|---|---|---|
| 2 | 11.57 | 9.02 | 7.85 | 7.14 | 6.61 | 6.19 | 5.83 |
| 3 | 46.32 | 13.76 | 9.18 | 7.52 | 6.60 | 5.96 | 5.49 |
| 4 | 63.10 | 16.72 | 10.23 | 7.91 | 6.67 | 5.88 | 5.32 |
| 5 | 72.55 | 18.27 | 10.78 | 8.11 | 6.71 | 5.82 | 5.19 |
| 6 | 78.59 | 19.19 | 11.08 | 8.21 | 6.70 | 5.75 | 5.09 |
| 7 | 82.75 | 19.79 | 11.25 | 8.25 | 6.67 | 5.69 | 5.01 |
| 8 | 85.78 | 20.20 | 11.36 | 8.26 | 6.64 | 5.63 | 4.93 |
| 9 | 88.07 | 20.49 | 11.42 | 8.25 | 6.60 | 5.58 | 4.87 |
| 10 | 89.86 | 20.70 | 11.46 | 8.24 | 6.56 | 5.52 | 4.81 |
| 11 | 91.30 | 20.86 | 11.49 | 8.22 | 6.53 | 5.48 | 4.76 |
| 12 | 92.47 | 20.99 | 11.50 | 8.20 | 6.49 | 5.43 | 4.71 |
| 13 | 93.43 | 21.08 | 11.50 | 8.17 | 6.46 | 5.39 | 4.67 |
| 14 | 94.25 | 21.16 | 11.50 | 8.15 | 6.42 | 5.36 | 4.63 |
| 15 | 94.94 | 21.22 | 11.49 | 8.13 | 6.39 | 5.32 | 4.59 |
| 16 | 95.54 | 21.26 | 11.49 | 8.11 | 6.36 | 5.29 | 4.56 |
| 17 | 96.05 | 21.30 | 11.48 | 8.08 | 6.34 | 5.26 | 4.53 |
| 18 | 96.50 | 21.33 | 11.46 | 8.06 | 6.31 | 5.23 | 4.50 |
| 19 | 96.09 | 21.35 | 11.45 | 8.04 | 6.29 | 5.21 | 4.47 |
| 20 | 97.25 | 21.37 | 11.44 | 8.02 | 6.26 | 5.18 | 4.45 |
| 21 | 97.56 | 21.39 | 11.43 | 8.00 | 6.24 | 5.16 | 4.43 |
| 22 | 97.84 | 21.40 | 11.41 | 7.98 | 6.22 | 5.14 | 4.40 |
| 23 | 98.09 | 21.41 | 11.40 | 7.96 | 6.20 | 5.12 | 4.38 |
| 24 | 98.32 | 21.41 | 11.39 | 7.94 | 6.18 | 5.10 | 4.36 |
| 25 | 98.53 | 21.42 | 11.38 | 7.93 | 6.16 | 5.08 | 4.35 |
| 26 | 98.71 | 21.42 | 11.36 | 7.91 | 6.15 | 5.06 | 4.33 |
| 27 | 98.88 | 21.42 | 11.35 | 7.90 | 6.13 | 5.05 | 4.31 |
| 28 | 99.04 | 21.42 | 11.34 | 7.88 | 6.11 | 5.03 | 4.30 |
| 29 | 99.18 | 21.42 | 11.32 | 7.87 | 6.10 | 5.02 | 4.28 |
| 30 | 99.31 | 21.42 | 11.31 | 7.85 | 6.08 | 5.00 | 4.27 |
| 0.05 | 0.10 | 0.20 | 0.30 | |
|---|---|---|---|---|
| 3 | 0.15 | −0.10 | −0.14 | −0.10 |
| 4 | 0.13 | 0.04 | 0.04 | 0.02 |
| 5 | 0.10 | 0.05 | 0.06 | 0.06 |
| 6 | 0.09 | 0.04 | 0.06 | 0.06 |
| 7 | 0.07 | 0.04 | 0.06 | 0.07 |
| 8 | 0.05 | 0.03 | 0.05 | 0.06 |
| 9 | 0.04 | 0.04 | 0.05 | 0.05 |
| 10 | 0.04 | 0.03 | 0.05 | 0.05 |
| 11 | 0.04 | 0.01 | 0.03 | 0.04 |
| 12 | 0.02 | 0.02 | 0.04 | 0.04 |
| 13 | 0.02 | 0.02 | 0.03 | 0.04 |
| 14 | 0.02 | 0.02 | 0.03 | 0.04 |
| 15 | 0.01 | 0.02 | 0.03 | 0.04 |
| 16 | 0.02 | 0.01 | 0.03 | 0.03 |
| 17 | 0.01 | 0.01 | 0.02 | 0.03 |
| 18 | 0.01 | 0.02 | 0.02 | 0.03 |
| 19 | 0.01 | 0.01 | 0.02 | 0.04 |
| 20 | 0.01 | 0.01 | 0.02 | 0.03 |
| 21 | 0.00 | 0.01 | 0.02 | 0.03 |
| 22 | 0.00 | 0.01 | 0.02 | 0.03 |
| 23 | 0.00 | 0.01 | 0.02 | 0.03 |
| 24 | 0.00 | 0.01 | 0.02 | 0.03 |
| 25 | 0.00 | 0.00 | 0.02 | 0.02 |
| 26 | 0.00 | 0.01 | 0.01 | 0.02 |
| 27 | 0.00 | 0.01 | 0.01 | 0.03 |
| 28 | 0.00 | 0.02 | 0.02 | 0.02 |
| 29 | 0.00 | 0.01 | 0.01 | 0.03 |
| 30 | 0.00 | 0.01 | 0.01 | 0.02 |
| B | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.05 | 0.10 | 0.20 | |||||
| mean | std dev | mean | std dev | mean | std dev | mean | std dev | |
| 1.4950 | 0.0086 | 1.4989 | 0.0087 | 1.4994 | 0.0087 | 1.4997 | 0.0087 | |
| 1.0054 | 0.0998 | 1.0241 | 0.2222 | 1.0506 | 0.3161 | 1.1025 | 0.4276 | |
| F | 34.713 | 6.7626 | 8.0336 | 3.1828 | 4.7849 | 2.3952 | 3.0948 | 1.8630 |
| rel bias | 0.0108 | 0.0482 | 0.1014 | 0.2052 | ||||
| 33.674 | 7.0445 | 3.7754 | 2.0902 | |||||
| cv F | 46.316 | 13.765 | 9.1815 | 6.5960 | ||||
| rej freq F | 0.0515 | 0.0505 | 0.0508 | 0.0511 | ||||
| mean | std dev | mean | std dev | mean | std dev | mean | std dev | |
| 1.4996 | 0.0087 | 1.4997 | 0.0087 | 1.4997 | 0.0087 | 1.4998 | 0.0087 | |
| 1.0056 | 0.4398 | 1.0256 | 0.7195 | 1.0519 | 0.9651 | 1.0981 | 1.1404 | |
| F | 5.6124 | 3.1989 | 4.0004 | 2.6492 | 3.2963 | 2.3746 | 2.6011 | 2.0502 |
| rel bias | 0.0111 | 0.0513 | 0.1039 | 0.1962 | ||||
| 4.6052 | 2.9957 | 2.3026 | 1.6094 | |||||
| cv F | 11.572 | 9.0232 | 7.8521 | 6.6087 | ||||
| rej freq F | 0.0509 | 0.0507 | 0.0505 | 0.0498 | ||||
| 0.01 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | |
|---|---|---|---|---|---|---|---|
| 02 | 04.605 | 02.996 | 2.303 | 1.897 | 1.609 | 1.386 | 1.204 |
| 03 | 33.674 | 07.045 | 3.775 | 2.677 | 2.090 | 1.706 | 1.426 |
| 04 | 50.000 | 10.000 | 5.000 | 3.329 | 2.483 | 1.960 | 1.599 |
| 05 | 59.799 | 11.793 | 5.784 | 3.774 | 2.761 | 2.144 | 1.724 |
| 06 | 66.332 | 12.991 | 6.315 | 4.081 | 2.958 | 2.277 | 1.816 |
| 07 | 70.998 | 13.848 | 6.696 | 4.304 | 3.102 | 2.375 | 1.885 |
| 08 | 74.498 | 14.491 | 6.982 | 4.472 | 3.212 | 2.450 | 1.938 |
| 09 | 77.221 | 14.992 | 7.205 | 4.604 | 3.298 | 2.510 | 1.980 |
| 10 | 79.398 | 15.392 | 7.384 | 4.709 | 3.367 | 2.558 | 2.014 |
| 11 | 81.180 | 15.720 | 7.531 | 4.796 | 3.424 | 2.597 | 2.043 |
| 12 | 82.665 | 15.993 | 7.653 | 4.868 | 3.471 | 2.630 | 2.066 |
| 13 | 83.922 | 16.224 | 7.756 | 4.929 | 3.511 | 2.658 | 2.086 |
| 14 | 84.999 | 16.423 | 7.845 | 4.981 | 3.546 | 2.682 | 2.104 |
| 15 | 85.932 | 16.594 | 7.922 | 5.027 | 3.576 | 2.703 | 2.119 |
| 16 | 86.749 | 16.745 | 7.989 | 5.067 | 3.602 | 2.721 | 2.132 |
| 17 | 87.470 | 16.877 | 8.048 | 5.102 | 3.626 | 2.738 | 2.144 |
| 18 | 88.110 | 16.995 | 8.101 | 5.133 | 3.646 | 2.752 | 2.154 |
| 19 | 88.683 | 17.101 | 8.148 | 5.161 | 3.665 | 2.765 | 2.163 |
| 20 | 89.199 | 17.196 | 8.191 | 5.186 | 3.681 | 2.777 | 2.172 |
| 21 | 89.666 | 17.281 | 8.229 | 5.209 | 3.697 | 2.787 | 2.179 |
| 22 | 90.090 | 17.360 | 8.264 | 5.230 | 3.710 | 2.797 | 2.186 |
| 23 | 90.477 | 17.431 | 8.296 | 5.249 | 3.723 | 2.806 | 2.193 |
| 24 | 90.833 | 17.496 | 8.326 | 5.266 | 3.734 | 2.814 | 2.198 |
| 25 | 91.159 | 17.556 | 8.353 | 5.282 | 3.745 | 2.821 | 2.204 |
| 26 | 91.461 | 17.612 | 8.377 | 5.297 | 3.755 | 2.828 | 2.209 |
| 27 | 91.740 | 17.663 | 8.400 | 5.311 | 3.764 | 2.834 | 2.213 |
| 28 | 91.999 | 17.711 | 8.422 | 5.323 | 3.772 | 2.840 | 2.217 |
| 29 | 92.241 | 17.755 | 8.442 | 5.335 | 3.780 | 2.846 | 2.221 |
| 30 | 92.466 | 17.797 | 8.460 | 5.346 | 3.787 | 2.851 | 2.225 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skeels, C.L.; Windmeijer, F. On the Stock–Yogo Tables. Econometrics 2018, 6, 44. https://doi.org/10.3390/econometrics6040044
Skeels CL, Windmeijer F. On the Stock–Yogo Tables. Econometrics. 2018; 6(4):44. https://doi.org/10.3390/econometrics6040044
Chicago/Turabian StyleSkeels, Christopher L., and Frank Windmeijer. 2018. "On the Stock–Yogo Tables" Econometrics 6, no. 4: 44. https://doi.org/10.3390/econometrics6040044
APA StyleSkeels, C. L., & Windmeijer, F. (2018). On the Stock–Yogo Tables. Econometrics, 6(4), 44. https://doi.org/10.3390/econometrics6040044





