Foreign Workers and the Wage Distribution: What Does the Influence Function Reveal?
Abstract
1. Introduction
2. Methods
2.1. Gâteaux Derivatives for Changes in Covariate Distributions
2.2. Influence Functions
2.3. Estimation by Influence Function Regression
3. Data
4. Results
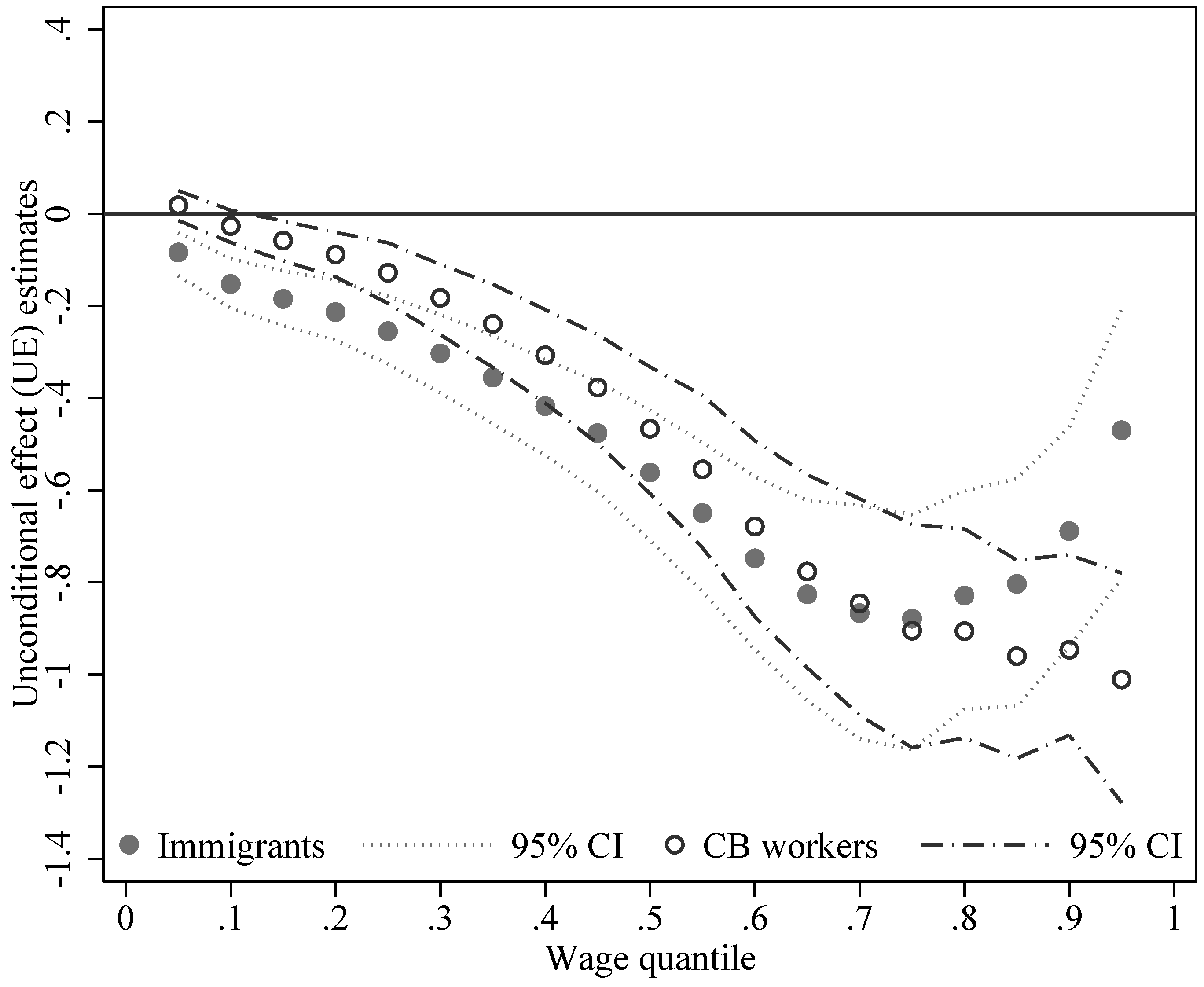
4.1. Unconditional Impacts: UE Estimates
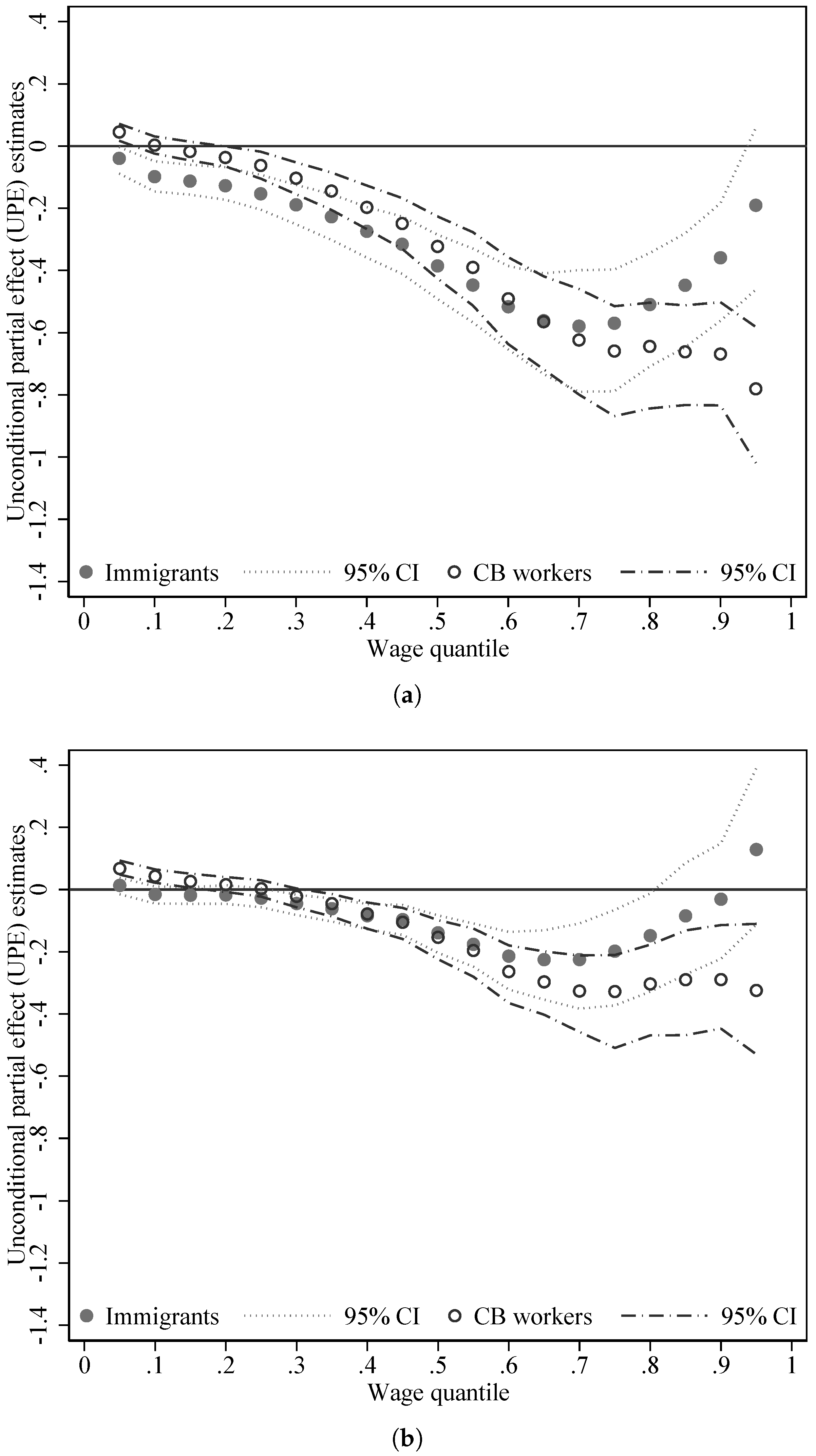
4.2. Accounting for Human Capital and Job Characteristics: UPE Estimates
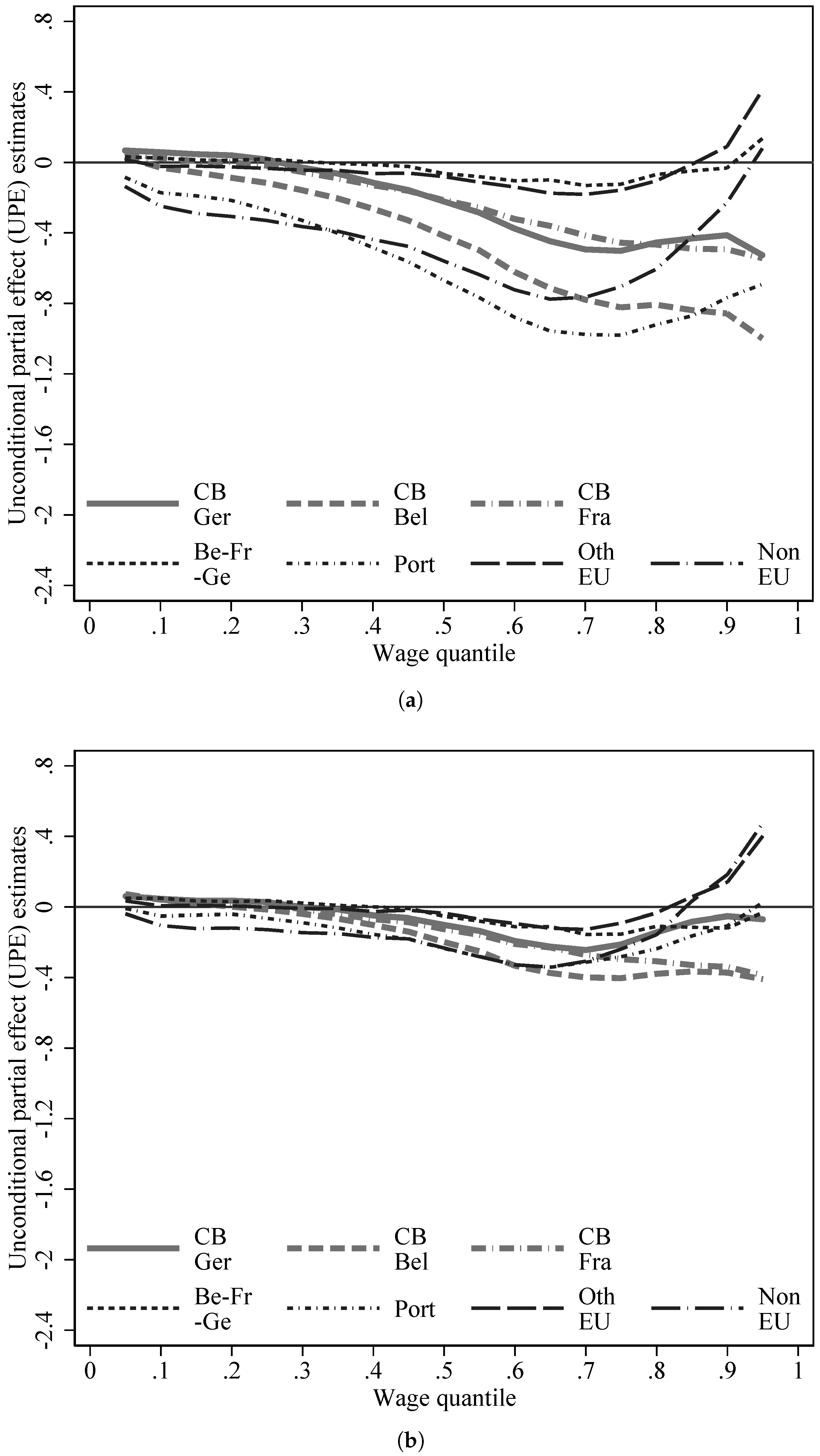
4.3. Impacts by Disaggregate Nationality Groups
5. Summary and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Proofs
Appendix B. Detailed Influence Function Regression Results
| Aggregate Nationality Groups | Disaggregate Nationality Groups | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||||||||
| Immigrant worker | −0.154 | * | −0.102 | * | −0.018 | ||||||||
| Cross-border worker | −0.027 | 0.002 | 0.042 | * | |||||||||
| Be-Fr-Ge resident | 0.018 | 0.024 | 0.049 | * | |||||||||
| Portuguese resident | −0.258 | * | −0.178 | * | −0.056 | * | |||||||
| Other EU resident | −0.045 | * | −0.023 | 0.006 | |||||||||
| Non-EU resident | −0.314 | * | −0.250 | * | −0.107 | * | |||||||
| German CB | 0.031 | 0.059 | * | 0.047 | * | ||||||||
| French CB | −0.073 | * | −0.031 | 0.039 | * | ||||||||
| Belgian CB | 0.016 | 0.021 | 0.039 | * | |||||||||
| Female | −0.187 | * | −0.121 | * | −0.185 | * | −0.119 | * | |||||
| Age | 0.434 | * | 0.385 | * | 0.425 | * | 0.384 | * | |||||
| Age squared/100 | −0.005 | * | −0.004 | * | −0.005 | * | −0.004 | * | |||||
| Secondary education | 0.130 | * | 0.008 | 0.100 | * | 0.002 | |||||||
| Tertiary education | 0.304 | * | 0.066 | 0.245 | * | 0.053 | |||||||
| Job tenure | 0.186 | * | 0.148 | * | 0.191 | * | 0.152 | * | |||||
| Job tenure squared/100 | −0.004 | * | −0.003 | * | −0.004 | * | −0.003 | * | |||||
| Manager | 0.008 | 0.006 | |||||||||||
| 10–49 employees in firm | 0.033 | 0.035 | |||||||||||
| 50–249 employees in firm | 0.041 | 0.042 | |||||||||||
| 500–999 employees in firm | −0.070 | −0.069 | |||||||||||
| 1000+ employees in firm | 0.021 | 0.023 | |||||||||||
| Part time contract | −0.074 | * | −0.074 | * | |||||||||
| Industry/Manufacture | −0.086 | * | −0.087 | * | |||||||||
| Construction | −0.069 | * | −0.060 | ||||||||||
| Wholesale | −0.268 | * | −0.267 | * | |||||||||
| Hotel/Restaurant | −0.374 | * | −0.372 | * | |||||||||
| Trans/Comm | −0.050 | −0.050 | |||||||||||
| Finance | −0.064 | * | −0.067 | * | |||||||||
| Real estate | −0.159 | * | −0.157 | * | |||||||||
| Managerial | 0.452 | * | 0.435 | * | |||||||||
| Professional | 0.488 | * | 0.471 | * | |||||||||
| Associate professional | 0.505 | * | 0.488 | * | |||||||||
| Clerk | 0.493 | * | 0.477 | * | |||||||||
| Service worker | 0.301 | * | 0.289 | * | |||||||||
| Craft and trade worker | 0.380 | * | 0.371 | * | |||||||||
| Manufacturers | 0.386 | * | 0.376 | * | |||||||||
| Constant | 1.042 | * | 0.005 | −0.132 | 1.042 | * | 0.057 | −0.111 | |||||
| Aggregate Nationality Groups | Disaggregate Nationality Groups | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||||||||
| Immigrant worker | −0.564 | * | −0.390 | * | −0.142 | * | |||||||
| Cross-border worker | −0.468 | * | −0.325 | * | −0.155 | * | |||||||
| Be-Fr-Ge resident | −0.025 | −0.064 | −0.052 | ||||||||||
| Portuguese resident | −0.989 | * | −0.677 | * | −0.241 | * | |||||||
| Other EU resident | −0.138 | * | −0.081 | −0.037 | |||||||||
| Non-EU resident | −0.751 | * | −0.562 | * | −0.234 | * | |||||||
| German CB | −0.384 | * | −0.222 | * | −0.100 | * | |||||||
| French CB | −0.594 | * | −0.419 | * | −0.201 | * | |||||||
| Belgian CB | −0.290 | * | −0.219 | * | −0.128 | * | |||||||
| Female | −0.020 | −0.134 | * | −0.018 | −0.129 | * | |||||||
| Age | 0.851 | * | 0.564 | * | 0.820 | * | 0.559 | * | |||||
| Age squared/100 | −0.010 | * | −0.006 | * | −0.010 | * | −0.006 | * | |||||
| Secondary education | 0.429 | * | 0.033 | 0.331 | * | 0.016 | |||||||
| Tertiary education | 1.285 | * | 0.194 | * | 1.092 | * | 0.165 | * | |||||
| Job tenure | 0.415 | * | 0.286 | * | 0.427 | * | 0.295 | * | |||||
| Job tenure squared/100 | −0.004 | * | −0.004 | * | −0.005 | * | −0.004 | * | |||||
| Manager | 0.216 | * | 0.212 | * | |||||||||
| 10-49 employees in firm | −0.054 | −0.054 | |||||||||||
| 50-249 employees in firm | −0.026 | −0.026 | |||||||||||
| 500-999 employees in firm | −0.001 | 0.003 | |||||||||||
| 1000+ employees in firm | 0.160 | 0.165 | |||||||||||
| Part time contract | 0.071 | * | 0.069 | * | |||||||||
| Industry/Manufacture | −0.223 | * | −0.222 | * | |||||||||
| Construction | −0.522 | * | −0.502 | * | |||||||||
| Wholesale | −0.527 | * | −0.521 | * | |||||||||
| Hotel/Restaurant | −0.519 | * | −0.509 | * | |||||||||
| Trans/Comm | −0.137 | −0.141 | |||||||||||
| Finance | 0.031 | 0.024 | |||||||||||
| Real estate | −0.324 | * | −0.310 | * | |||||||||
| Managerial | 1.017 | * | 0.972 | * | |||||||||
| Professional | 1.153 | * | 1.112 | * | |||||||||
| Associate professional | 1.033 | * | 0.992 | * | |||||||||
| Clerk | 0.644 | * | 0.607 | * | |||||||||
| Service worker | 0.258 | * | 0.233 | * | |||||||||
| Craft and trade worker | 0.328 | * | 0.309 | * | |||||||||
| Manufacturers | 0.265 | * | 0.239 | * | |||||||||
| Constant | 1.939 | * | −0.589 | * | −0.066 | 1.939 | * | −0.417 | * | −0.009 | |||
| Aggregate Nationality Groups | Disaggregate Nationality Groups | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||||||||
| Immigrant worker | −0.718 | * | −0.378 | * | −0.031 | ||||||||
| Cross-border worker | −0.986 | * | −0.699 | * | −0.301 | * | |||||||
| Be-Fr-Ge resident | 0.338 | −0.034 | −0.123 | ||||||||||
| Portuguese resident | −1.652 | * | −0.809 | * | −0.108 | ||||||||
| Other EU resident | 0.124 | 0.093 | 0.147 | ||||||||||
| Non-EU resident | −0.604 | * | −0.239 | 0.193 | |||||||||
| German CB | −0.725 | * | −0.430 | * | −0.055 | ||||||||
| French CB | −1.284 | * | −0.895 | * | −0.386 | * | |||||||
| Belgian CB | −0.616 | * | −0.519 | * | −0.352 | * | |||||||
| Female | −0.268 | * | −0.380 | * | −0.262 | * | −0.377 | * | |||||
| Age | 0.543 | * | −0.108 | 0.485 | * | −0.130 | |||||||
| Age squared/100 | −0.000 | 0.006 | * | 0.000 | 0.006 | * | |||||||
| Secondary education | 1.029 | * | 0.297 | * | 0.890 | * | 0.284 | * | |||||
| Tertiary education | 4.034 | * | 1.220 | * | 3.768 | * | 1.202 | * | |||||
| Job tenure | 0.654 | * | 0.302 | * | 0.679 | * | 0.325 | * | |||||
| Job tenure squared/100 | −0.006 | 0.002 | −0.007 | 0.002 | |||||||||
| Manager | 0.787 | * | 0.793 | * | |||||||||
| 10-49 employees in firm | −0.147 | −0.153 | |||||||||||
| 50-249 employees in firm | −0.034 | −0.030 | |||||||||||
| 500-999 employees in firm | 0.213 | 0.227 | |||||||||||
| 1000+ employees in firm | 0.063 | 0.081 | |||||||||||
| Part time contract | 0.507 | * | 0.503 | * | |||||||||
| Industry/Manufacture | −0.888 | * | −0.881 | * | |||||||||
| Construction | −0.896 | * | −0.883 | * | |||||||||
| Wholesale | −0.704 | * | −0.685 | * | |||||||||
| Hotel/Restaurant | −0.826 | * | −0.809 | * | |||||||||
| Trans/Comm | −0.278 | −0.301 | |||||||||||
| Finance | −0.228 | −0.231 | |||||||||||
| Real estate | −1.087 | * | −1.051 | * | |||||||||
| Managerial | 4.910 | * | 4.891 | * | |||||||||
| Professional | 2.221 | * | 2.208 | * | |||||||||
| Associate professional | 1.024 | * | 1.001 | * | |||||||||
| Clerk | 0.054 | 0.035 | |||||||||||
| Service worker | 0.165 | 0.158 | |||||||||||
| Craft and trade worker | 0.129 | 0.119 | |||||||||||
| Manufacturers | −0.046 | −0.059 | |||||||||||
| Constant | 3.879 | * | 0.116 | 2.136 | * | 3.879 | * | 0.384 | 2.195 | * | |||
| Aggregate Nationality Groups | Disaggregate Nationality Groups | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||||||||
| Immigrant worker | −7.58 | −6.97 | −1.91 | ||||||||||
| Cross-border worker | −14.17 | * | −13.52 | * | −6.76 | ||||||||
| Be-Fr-Ge resident | 3.91 | −6.84 | −6.37 | ||||||||||
| Portuguese resident | −19.42 | * | −10.56 | * | −1.41 | ||||||||
| Other EU resident | −0.32 | −4.95 | −2.66 | ||||||||||
| Non-EU resident | 5.42 | 5.98 | 11.51 | ||||||||||
| German CB | −10.72 | * | −10.41 | −3.62 | |||||||||
| French CB | −17.66 | * | −15.51 | * | −7.27 | * | |||||||
| Belgian CB | −10.20 | * | −11.92 | * | −8.23 | * | |||||||
| Female | −5.25 | * | −10.38 | −5.20 | * | −10.42 | |||||||
| Age | −36.81 | * | −42.57 | * | −37.43 | * | −42.97 | * | |||||
| Age squared/100 | 0.60 | * | 0.61 | * | 0.60 | * | 0.62 | * | |||||
| Secondary education | 10.50 | * | 2.55 | 9.65 | * | 2.67 | |||||||
| Tertiary education | 63.31 | * | 31.23 | * | 61.75 | * | 31.52 | * | |||||
| Job tenure | 10.92 | * | 7.59 | 11.27 | * | 7.80 | |||||||
| Job tenure squared/100 | −0.42 | * | −0.25 | −0.42 | * | −0.25 | |||||||
| Manager | 2.43 | 2.67 | |||||||||||
| 10–49 employees in firm | 0.31 | 0.13 | |||||||||||
| 50–249 employees in firm | 12.25 | 12.34 | |||||||||||
| 500–999 employees in firm | 1.31 | 1.49 | |||||||||||
| 1000+ employees in firm | −1.79 | −1.61 | |||||||||||
| Part time contract | 20.26 | * | 20.21 | * | |||||||||
| Industry/Manufacture | −22.51 | −22.34 | |||||||||||
| Construction | −23.64 | * | −23.79 | * | |||||||||
| Wholesale | −14.48 | −14.22 | |||||||||||
| Hotel/Restaurant | −16.43 | −16.51 | |||||||||||
| Trans/Comm | −15.91 | −16.27 | |||||||||||
| Finance | −21.29 | −21.07 | |||||||||||
| Real estate | −25.67 | −25.33 | |||||||||||
| Managerial | 103.07 | * | 104.00 | * | |||||||||
| Professional | 18.75 | 19.77 | |||||||||||
| Associate professional | 7.13 | 7.93 | |||||||||||
| Clerk | 1.31 | 2.10 | |||||||||||
| Service worker | −0.39 | 0.11 | |||||||||||
| Craft and trade worker | 2.85 | 3.29 | |||||||||||
| Manufacturers | 0.59 | 1.16 | |||||||||||
| Constant | 41.24 | * | 72.65 | * | 101.35 | * | 41.24 | * | 74.77 | * | 101.11 | * | |
| Aggregate Nationality Groups | Disaggregate Nationality Groups | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 1 | Model 2 | Model 3 | ||||||||
| Immigrant worker | −0.0003 | −0.0004 | 0.0002 | ||||||||||
| Cross-border worker | −0.0054 | * | −0.0053 | * | −0.0030 | * | |||||||
| Be-Fr-Ge resident | 0.0029 | −0.0019 | −0.0026 | ||||||||||
| Portuguese resident | −0.0046 | * | −0.0012 | 0.0007 | |||||||||
| Other EU resident | 0.0027 | 0.0006 | 0.0007 | ||||||||||
| Non-EU resident | 0.0060 | * | 0.0058 | * | 0.0057 | * | |||||||
| German CB | −0.0044 | * | −0.0043 | * | −0.0013 | ||||||||
| French CB | −0.0066 | * | −0.0059 | * | −0.0034 | * | |||||||
| Belgian CB | −0.0040 | * | −0.0047 | * | −0.0036 | * | |||||||
| Female | −0.0006 | −0.0023 | −0.0006 | −0.0023 | |||||||||
| Age | −0.0192 | * | −0.0213 | * | −0.0194 | * | −0.0215 | * | |||||
| Age squared/100 | 0.0003 | * | 0.0003 | * | 0.0003 | * | 0.0003 | * | |||||
| Secondary education | 0.0033 | * | 0.0012 | 0.0032 | * | 0.0013 | |||||||
| Tertiary education | 0.0254 | * | 0.0126 | * | 0.0253 | * | 0.0129 | * | |||||
| Job tenure | 0.0012 | −0.0002 | 0.0014 | −0.0001 | |||||||||
| Job tenure squared/100 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | |||||||||
| Manager | 0.0028 | * | 0.0029 | * | |||||||||
| 10–49 employees in firm | −0.0003 | −0.0004 | |||||||||||
| 50–249 employees in firm | 0.0022 | 0.0022 | |||||||||||
| 500–999 employees in firm | 0.0017 | 0.0018 | |||||||||||
| 1000+ employees in firm | −0.0009 | −0.0008 | |||||||||||
| Part time contract | 0.0067 | * | 0.0067 | * | |||||||||
| Industry/Manufacture | −0.0060 | −0.0060 | |||||||||||
| Construction | −0.0056 | −0.0058 | |||||||||||
| Wholesale | −0.0003 | −0.0002 | |||||||||||
| Hotel/Restaurant | −0.0007 | −0.0007 | |||||||||||
| Trans/Comm | −0.0028 | −0.0029 | |||||||||||
| Finance | −0.0043 | −0.0042 | |||||||||||
| Real estate | −0.0073 | * | −0.0071 | * | |||||||||
| Managerial | 0.0398 | * | 0.0403 | * | |||||||||
| Professional | 0.0018 | 0.0023 | |||||||||||
| Associate professional | −0.0051 | −0.0047 | |||||||||||
| Clerk | −0.0085 | * | −0.0081 | * | |||||||||
| Service worker | −0.0034 | * | −0.0031 | * | |||||||||
| Craft and trade worker | −0.0054 | * | −0.0052 | * | |||||||||
| Manufacturers | −0.0072 | * | −0.0069 | * | |||||||||
| Constant | 0.0311 | * | 0.0534 | * | 0.0679 | * | 0.0311 | * | 0.0538 | * | 0.0677 | * | |
References
- Adsera, Alicia, and Barry Chiswick. 2007. Are there gender and country of origin differences in immigrant labor market outcomes across European destinations? Journal of Population Economics 20: 495–526. [Google Scholar] [CrossRef]
- Amétépé, Fofo, and Claudia Hartmann-Hirsch. 2011. An outstanding positioning of migrants and nationals: The case of Luxembourg. Population Review 50: 195–217. [Google Scholar]
- Annaert, Jean-Luc. 2004. A bright spot in the heart of Europe: What can we learn from the Luxembourg success story? ECFIN Country Focus 1: 15. [Google Scholar]
- Blau, Francine D., and Lawrence M. Kahn. 2012. Immigration and the distribution of incomes. NBER Working Paper 18515. Cambridge, MA, USA.: National Bureau of Economic Research. [Google Scholar]
- Borjas, George J. 1985. Assimilation, changes in cohort quality, and the earnings of immigrants. Journal of Labor Economics 3: 463–89. [Google Scholar] [CrossRef]
- Borjas, George J. 1995. Assimilation and changes in cohort quality revisited: What happened to immigration earnings in the 1980s? Journal of Labor Economics 13: 201–45. [Google Scholar] [CrossRef] [PubMed]
- Borjas, George J. 1999. Heaven’s Door. Princeton: Princeton University Press. [Google Scholar]
- Borjas, George J. 2003. The labor demand curve is downward sloping: Reexamining the impact of immigration on the labor market. NBER Working Paper 9755. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Card, David. 1990. The impact of the mariel boatlift on the Miami labor market. Industrial and Labor Relations Review 43: 245–57. [Google Scholar] [CrossRef]
- Card, David. 2009. Immigration and inequality. American Economic Review 99: 1–21. [Google Scholar] [CrossRef]
- Carrasco, Raquel, Juan F. Jimeno, and A. Carolina Ortega. 2008. The effect of immigration on the labor market performance of native-born workers: Some evidence for Spain. Journal of Population Economics 21: 627–48. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, Ivan Fernandez-Val, and Blaise Melly. 2013. Inference on counterfactual distributions. Econometrica 81: 2205–68. [Google Scholar] [CrossRef]
- Chiswick, Barry R. 1978. The effect of americanization on the earnings of foreign-born men. Journal of Political Economy 86: 897–921. [Google Scholar] [CrossRef]
- Deville, Jean-Claude. 1999. Variance estimation for complex statistics and estimators: Linearization and residual techniques. Survey Methodology 25: 193–203. [Google Scholar]
- Dugger, Daniel, and Peter J. Lambert. 2014. The 1913 paper of René Gâteaux, upon which the modern-day influence function is based. Journal of Economic Inequality 12: 149–52. [Google Scholar] [CrossRef]
- Dustmann, Christian, Tommaso Frattini, and Ian P. Preston. 2013. The effect of immigration along the distribution of wages. Review of Economic Studies 80: 145–73. [Google Scholar] [CrossRef]
- Efron, Bradley. 1981. Nonparametric standard errors and confidence intervals. The Canadian Journal of Statistics/La Revue Canadienne de Statistique 9: 139–58. [Google Scholar] [CrossRef]
- Essama-Nssah, Boniface, and Peter J. Lambert. 2012. Influence functions for policy impact analysis. In Inequality, Mobility and Segregation: Essays in Honor of Jacques Silber (Research on Economic Inequality, Volume 20). Edited by John A. Bishop and Rafael Salas. Bingley: Emerald Group Publishing, chp. 6. pp. 135–59. [Google Scholar]
- Fernholz, Luisa Turrin. 1983. von Mises Calculus For Statistical Functionals. Number 19 in Lecture Notes in Statistics. New York: Springer-Verlag. [Google Scholar]
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2007. Unconditional quantile regressions. Technical Working Paper 339. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2009. Unconditional quantile regressions. Econometrica 77: 953–73. [Google Scholar]
- Friedberg, Rachel M. 2001. The impact of mass migration on the Israeli labor market. Quarterly Journal of Economics 116: 1373–408. [Google Scholar] [CrossRef]
- Fusco, Alessio, Philippe Van Kerm, Aigul Alieva, Luna Bellani, Fanny Etienne-Robert, Anne-Catherine Guio, Iryna Kyzyma, Kristell Leduc, Philippe Liégeois, Maria Noel Pi Alperin, and et al. 2014. Luxembourg: Has inequality grown enough to matter? In Changing Inequalities and Societal Impacts in Rich Countries: Thirty Countries Experiences. Edited by Brian Nolan, Wiemer Salverda, Daniele Checchi, Ive Marx, Abigail McKnight, István György Tóth and Herman van de Werfhorst. Oxford: Oxford University Press. [Google Scholar]
- Gâteaux, René. 1913. Sur les fonctionnelles continues et les fonctionnelles analytiques. Comptes Rendus de l’Académie des Sciences de Paris 157: 325–27. Translation published as (2014) ‘A note on continuous functionals and analytic functions’. "Rediscovered classics" series. Journal of Economic Inequality 12: 153–55. [Google Scholar]
- Grossman, Jean Baldwin. 1982. The substitutability of natives and immigrants in production. Review of Economics and Statistics 64: 596–603. [Google Scholar] [CrossRef]
- Hampel, Frank R. 1974. The influence curve and its role in robust estimation. Journal of the American Statistical Association 69: 383–93. [Google Scholar] [CrossRef]
- Hampel, Frank R., Elvezio M. Ronchetti, Peter J. Rousseeuw, and Werner A. Stahel. 1986. Robust Statistics: The Approach Based on Influence Functions. Wiley series in Probability and Statistics; Hoboken: John Wiley and Sons, Inc. [Google Scholar]
- Huber, Peter J. 1981. Robust Statistics. Wiley series in Probability and Statistics; Hoboken: John Wiley and Sons, Inc. [Google Scholar]
- Manacorda, Marco, Alan Manning, and Jonathan Wadsworth. 2012. The impact of immigration on the structure of wages: Theory and evidence from Britain. Journal of the European Economic Association 10: 120–51. [Google Scholar] [CrossRef]
- Müller, Tobias, and José Ramirez. 2009. Wage inequality and segregation between native and immigrant workers in Switzerland: Evidence using matched employee-employer data. In Occupational and Residential Segregation (Research on Economic Inequality, Volume 17). Edited by Yves Flückiger, Sean F. Reardon and Jacques Silber. Bingley: Emerald Group Publishing, pp. 205–43. [Google Scholar]
- OECD. 2012. OECD Economic Surveys: Luxembourg 2012. Paris: OECD Publishing. [Google Scholar]
- Ottaviano, Gianmarco I. P., and Giovanni Peri. 2012. Rethinking the effect of immigration on wages. Journal of the European Economic Association 10: 152–97. [Google Scholar] [CrossRef]
- Rothe, Christoph. 2010. Nonparametric estimation of distributional policy effects. Journal of Econometrics 155: 56–70. [Google Scholar] [CrossRef]
- Saigo, Hiroshi, Jun Shao, and Randy R. Sitter. 2001. A repeated half-sample bootstrap and balanced repeated replications for randomly imputed data. Survey Methodology 27: 189–96. [Google Scholar]
- Shorrocks, Anthony F. 1984. Inequality decomposition by population subgroups. Econometrica 52: 1369–85. [Google Scholar] [CrossRef]
- StataCorp. 2015. Stata Statistical Software: Release 14. College Station: StataCorp LP. [Google Scholar]
- STATEC. 2009. La structure des salaires en 2006. Bulletin du STATEC 1–2009, STATEC Institut national de la statistique et des études économiques, Luxembourg. Available online: http://www.statistiques.public.lu/catalogue-publications/bulletin-Statec/2009/PDF-Bulletin-1-2009.pdf (accessed on 3 September 2018).
- Van Kerm, Philippe. 2013. Repeated half-sample bootstrap resampling. Paper presented at United Kingdom Stata Users’ Group Meetings 2013, London, UK, 12–13 September 2013; Available online: https://ideas.repec.org/p/boc/usug13/10.html (accessed on 3 September 2018).
- Van Kerm, Philippe, Seunghee Yu, and Chung Choe. 2017. Decomposing quantile wage gaps: A conditional likelihood approach. Journal of the Royal Statistical Society: Series C (Applied Statistics) 65: 507–27. [Google Scholar] [CrossRef]
| 1. | The equilibrium impacts of immigration on the distribution of native workers wages remains a debated topic. They crucially depend on the degree of complementarity or substitutability between foreign and native labour—and this may vary by occupation and skill groups—so net impacts are not unambiguous. In the United States for instance, while Grossman (1982), Card (1990) or, more recently, Card (2009) and Ottaviano and Peri (2012) show that the impact of immigration on native wages is small or negligible, Borjas (1999, 2003) find that immigration lowers the wage of competing native workers. Manacorda et al. (2012) and Dustmann et al. (2013) show that the impact of immigration on wages in the UK is heterogeneous across the distribution: the overall effect on native wages is positive as a combination of a negative effect at lower percentiles of the distribution but a positive effect at higher percentiles. No or small positive impacts have been identified in Spain and Israel (Carrasco et al. 2008; Friedberg 2001). |
| 2. | See Van Kerm et al. (2017) for a study of the anatomy of wage differentials between natives and foreign workers using alternative approaches. |
| 3. | See http://www.statistiques.public.lu/stat/TableViewer/tableView.aspx?ReportId=12916 (accessed 2018-08-30). |
| 4. | Please note that Theorem 1 in Firpo et al. (2009) integrates the recentered influence function defined as . Our expression in terms of the influence function is equivalent since in the recentered influence function expression of the theorem can be differenced away. |
| 5. | The unconditional partial effect is labelled a ‘policy effect’ in Rothe (2010) or a ‘counterfactual effect’ in Chernozhukov et al. (2013). |
| 6. | Estimates based on several other relative inequality measures were also examined (quantile group shares ratios, the standard deviation of log wage, generalized entropy measures) and lead to similar conclusions. They are not reported here but are available on request. |
| 7. | Most noticeably, civil servants and agricultural sector workers are excluded from the sampling frame. These sectors employ only few foreign workers (in particular cross-border workers). |
| 8. | RIF regression calculations were done with the statistical software Stata (version 14.2) (StataCorp 2015) and the user-written package for Stata rifreg available from Nicole Fortin at http://faculty.arts.ubc.ca/nfortin/datahead.html. Bootstrap confidence intervals for the UE and UPE estimates were constructed on the basis of 1,000 replications from a repeated half-sample bootstrap resampling scheme (Saigo et al. 2001) and account for the two-stage design of the survey (see Section 3). We use the rhsbsample Stata user-written package for generating the replication weights (Van Kerm 2013). Pointwise confidence intervals are based on the bias-corrected percentile method (Efron 1981). |
| 9. | Formally, the approximation is the leading term of a von Mises expansion of functional differences (Fernholz 1983; Hampel 1974):
|
| 10. | Endogenous selection is likely at play here with high wage workers from Belgium, France or Germany affording the potential costs of migrating into Luxembourg. |
| 11. | Please note that estimates of general equilibrium effects of immigration available for other countries are in fact generally small (Blau and Kahn 2012; Card 2009), although of course these findings may not necessarily apply to the Luxembourg case. |
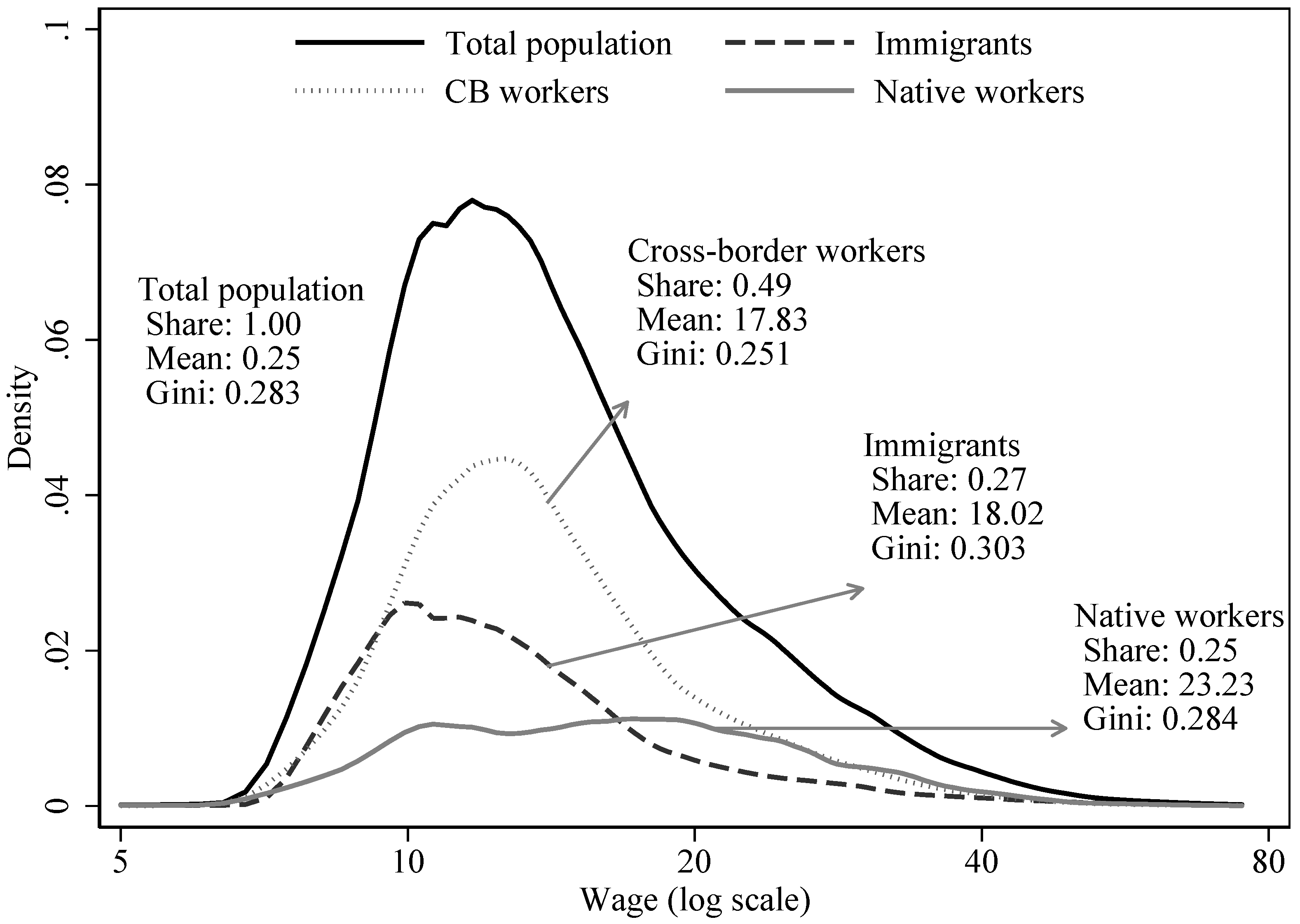

| Luxembourg | Immigrant | Cross-Border | |
|---|---|---|---|
| Nationals | Workers | Workers | |
| Employment share | 0.25 | 0.27 | 0.49 |
| Mean and selected percentiles (€) | |||
| Mean | 23.2 | 18.0 | 17.8 |
| 10th percentile (P10) | 10.7 | 9.1 | 10.2 |
| 25th percentile (P25) | 14.5 | 10.9 | 12.0 |
| Median (P50) | 20.3 | 13.9 | 14.9 |
| 75th percentile (P75) | 27.9 | 20.1 | 20.4 |
| 90th percentile (P90) | 37.0 | 31.6 | 28.8 |
| Measures of dispersion and inequality | |||
| Standard deviation | 15.3 | 13.2 | 10.3 |
| Gini coefficient | 0.284 | 0.303 | 0.251 |
| P90/P10 ratio | 3.5 | 3.5 | 2.8 |
| P50/P10 ratio | 1.9 | 1.5 | 1.5 |
| P90/P50 ratio | 1.8 | 2.3 | 1.9 |
| Luxembourg | Immigrant | Cross-Border | |
|---|---|---|---|
| Nationals | Workers | Workers | |
| Luxembourg | 1.00 | – | – |
| Belgian | – | 0.08 | 0.22 |
| French | – | 0.13 | 0.50 |
| German | – | 0.05 | 0.22 |
| Portuguese | – | 0.47 | 0.01 |
| Other EU | – | 0.18 | 0.04 |
| Non-EU | – | 0.10 | 0.01 |
| Female | 0.39 | 0.38 | 0.32 |
| Age | 39.90 | 37.63 | 37.20 |
| Primary educ. or less (ref.) | 0.11 | 0.24 | 0.08 |
| Secondary education | 0.80 | 0.62 | 0.80 |
| Tertiary education | 0.08 | 0.14 | 0.12 |
| Years at current employer | 11.82 | 6.32 | 5.59 |
| Manager | 0.17 | 0.14 | 0.14 |
| 10–49 employees in firm | 0.24 | 0.32 | 0.27 |
| 50–249 employees in firm | 0.24 | 0.30 | 0.35 |
| 250–499 employees in firm (ref.) | 0.11 | 0.13 | 0.14 |
| 500–999 employees in firm | 0.08 | 0.11 | 0.11 |
| 1000+ employees in firm | 0.33 | 0.14 | 0.13 |
| Part time contract | 0.18 | 0.15 | 0.13 |
| Industry/Manufacture | 0.17 | 0.10 | 0.18 |
| Construction | 0.05 | 0.21 | 0.14 |
| Wholesale | 0.12 | 0.10 | 0.13 |
| Hotel/Restaurant | 0.01 | 0.06 | 0.03 |
| Trans/Comm | 0.16 | 0.07 | 0.09 |
| Finance | 0.17 | 0.16 | 0.17 |
| Real estate | 0.08 | 0.18 | 0.19 |
| Education, Health & Other not-for-profit (ref.) | 0.24 | 0.11 | 0.08 |
| Managerial | 0.07 | 0.06 | 0.04 |
| Professional | 0.10 | 0.09 | 0.12 |
| Associate professional | 0.23 | 0.13 | 0.18 |
| Clerk | 0.23 | 0.11 | 0.15 |
| Service worker | 0.09 | 0.10 | 0.11 |
| Craft and trade worker | 0.13 | 0.21 | 0.20 |
| Manufacturers | 0.08 | 0.09 | 0.13 |
| Low skilled and laborer (ref.) | 0.08 | 0.20 | 0.07 |
| Number of observations | 7537 | 8367 | 15105 |
| UE | UPE | |||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2a | Model 2b | Model 3a | Model 3b | ||
| Variance | ||||||
| Immigrant worker | −7.58 | −6.97 | −7.92 | −1.91 | −1.16 | |
| (6.75) | (7.85) | (8.59) | (4.83) | (3.53) | ||
| Cross-border worker | −14.17 | −13.52 | −14.57 | −6.76 | −5.31 | |
| (6.20) | (7.29) | (7.85) | (4.30) | (2.59) | ||
| Gini coefficient | ||||||
| Immigrant worker | −0.0003 | −0.0004 | −0.0007 | 0.0002 | 0.0006 | |
| (0.0016) | (0.0017) | (0.0019) | (0.0012) | (0.0011) | ||
| Cross-border worker | −0.0054 | −0.0053 | −0.0053 | −0.0030 | −0.0021 | |
| (0.0015) | (0.0015) | (0.0017) | (0.0010) | (0.0008) | ||
| Percentile ratio P90/P10 | ||||||
| Immigrant worker | −0.022 | −0.005 | −0.009 | 0.003 | 0.010 | |
| (0.014) | (0.013) | (0.013) | (0.011) | (0.012) | ||
| Cross-border worker | −0.091 | −0.071 | −0.068 | −0.044 | −0.026 | |
| (0.013) | (0.011) | (0.011) | (0.010) | (0.010) | ||
| Percentile ratio P50/P10 | ||||||
| Immigrant worker | −0.032 | −0.023 | −0.024 | −0.012 | −0.012 | |
| (0.005) | (0.005) | (0.004) | (0.003) | (0.003) | ||
| Cross-border worker | −0.043 | −0.033 | −0.032 | −0.022 | −0.020 | |
| (0.005) | (0.005) | (0.004) | (0.004) | (0.003) | ||
| Percentile ratio P90/P50 | ||||||
| Immigrant worker | 0.028 | 0.027 | 0.026 | 0.017 | 0.021 | |
| (0.011) | (0.009) | (0.009) | (0.007) | (0.007) | ||
| Cross-border worker | −0.002 | −0.002 | −0.001 | 0.001 | 0.009 | |
| (0.011) | (0.010) | (0.009) | (0.007) | (0.007) | ||
| UE | UPE | |||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2a | Model 2b | Model 3a | Model 3b | ||
| Variance | ||||||
| Be-Fr-Ge resident | 3.91 | −6.84 | −3.91 | −6.37 | −4.74 | |
| (9.31) | (11.77) | (10.57) | (9.33) | (5.34) | ||
| Portuguese resident | −19.42 | −10.56 | −20.31 | −1.41 | −13.45 | |
| (7.13) | (6.95) | (8.83) | (3.03) | (3.79) | ||
| Other EU resident | −0.32 | −4.95 | −7.33 | −2.66 | −4.42 | |
| (8.02) | (9.42) | (9.25) | (6.52) | (4.23) | ||
| Non-EU resident | 5.42 | 5.98 | 0.63 | 11.51 | 3.58 | |
| (5.33) | (5.09) | (6.85) | (5.60) | (8.46) | ||
| German CB | −10.72 | −10.41 | −11.22 | −3.62 | −1.77 | |
| (6.63) | (7.76) | (8.29) | (5.40) | (4.47) | ||
| French CB | −17.66 | −15.51 | −17.82 | −7.27 | −8.71 | |
| (6.62) | (7.56) | (8.34) | (4.05) | (2.95) | ||
| Belgian CB | −10.20 | −11.92 | −12.07 | −8.23 | −4.32 | |
| (5.24) | (6.57) | (6.68) | (4.08) | (2.22) | ||
| Gini coefficient | ||||||
| Be-Fr-Ge resident | 0.0029 | −0.0019 | −0.0006 | −0.0026 | −0.0016 | |
| (0.0019) | (0.0023) | (0.0021) | (0.0018) | (0.0012) | ||
| Portuguese resident | −0.0046 | −0.0012 | −0.0063 | 0.0007 | −0.0061 | |
| (0.0019) | (0.0018) | (0.0019) | (0.0010) | (0.0010) | ||
| Other EU resident | 0.0027 | 0.0006 | −0.0003 | 0.0007 | −0.0003 | |
| (0.0022) | (0.0024) | (0.0022) | (0.0018) | (0.0013) | ||
| Non-EU resident | 0.0060 | 0.0058 | 0.0047 | 0.0057 | 0.0050 | |
| (0.0021) | (0.0020) | (0.0026) | (0.0018) | (0.0028) | ||
| German CB | −0.0044 | −0.0043 | −0.0037 | −0.0013 | −0.0001 | |
| (0.0016) | (0.0017) | (0.0019) | (0.0014) | (0.0016) | ||
| French CB | −0.0066 | −0.0059 | −0.0067 | −0.0034 | −0.0039 | |
| (0.0016) | (0.0016) | (0.0018) | (0.0010) | (0.0008) | ||
| Belgian CB | −0.0040 | −0.0047 | −0.0046 | −0.0036 | −0.0019 | |
| (0.0014) | (0.0015) | (0.0015) | (0.0010) | (0.0007) | ||
| UE | UPE | |||||
|---|---|---|---|---|---|---|
| Model 1 | Model 2a | Model 2b | Model 3a | Model 3b | ||
| Percentile ratio P90/P10 | ||||||
| Be-Fr-Ge resident | 0.028 | −0.011 | 0.001 | −0.029 | −0.011 | |
| (0.016) | (0.013) | (0.013) | (0.013) | (0.012) | ||
| Portuguese resident | −0.082 | −0.023 | −0.091 | 0.007 | −0.082 | |
| (0.019) | (0.018) | (0.017) | (0.013) | (0.015) | ||
| Other EU resident | 0.027 | 0.017 | 0.013 | 0.013 | 0.009 | |
| (0.021) | (0.019) | (0.018) | (0.018) | (0.016) | ||
| Non-EU resident | 0.042 | 0.058 | 0.042 | 0.055 | 0.067 | |
| (0.026) | (0.023) | (0.028) | (0.020) | (0.028) | ||
| German CB | −0.083 | −0.063 | −0.046 | −0.021 | −0.004 | |
| (0.015) | (0.013) | (0.017) | (0.014) | (0.021) | ||
| French CB | −0.106 | −0.081 | −0.084 | −0.052 | −0.048 | |
| (0.014) | (0.012) | (0.012) | (0.010) | (0.011) | ||
| Belgian CB | −0.068 | −0.059 | −0.059 | −0.048 | −0.026 | |
| (0.013) | (0.011) | (0.011) | (0.011) | (0.010) | ||
| Percentile ratio P50/P10 | ||||||
| Be-Fr-Ge resident | −0.005 | −0.010 | −0.009 | −0.013 | −0.009 | |
| (0.004) | (0.004) | (0.004) | (0.004) | (0.005) | ||
| Portuguese resident | −0.059 | −0.040 | −0.048 | −0.015 | −0.023 | |
| (0.008) | (0.007) | (0.008) | (0.005) | (0.007) | ||
| Other EU resident | −0.007 | −0.005 | −0.004 | −0.005 | −0.002 | |
| (0.005) | (0.004) | (0.004) | (0.004) | (0.004) | ||
| Non-EU resident | −0.026 | −0.017 | −0.024 | −0.007 | −0.011 | |
| (0.009) | (0.008) | (0.008) | (0.007) | (0.006) | ||
| German CB | −0.044 | −0.032 | −0.030 | −0.018 | −0.022 | |
| (0.007) | (0.006) | (0.006) | (0.004) | (0.005) | ||
| French CB | −0.048 | −0.038 | −0.036 | −0.027 | −0.022 | |
| (0.006) | (0.005) | (0.005) | (0.004) | (0.004) | ||
| Belgian CB | −0.032 | −0.025 | −0.027 | −0.019 | −0.021 | |
| (0.005) | (0.004) | (0.004) | (0.004) | (0.004) | ||
| Percentile ratio P90/P50 | ||||||
| Be-Fr-Ge resident | 0.025 | 0.006 | 0.012 | −0.001 | 0.004 | |
| (0.009) | (0.008) | (0.008) | (0.008) | (0.008) | ||
| Portuguese resident | 0.024 | 0.037 | 0.004 | 0.025 | −0.023 | |
| (0.017) | (0.014) | (0.015) | (0.009) | (0.012) | ||
| Other EU resident | 0.026 | 0.017 | 0.013 | 0.014 | 0.008 | |
| (0.012) | (0.011) | (0.010) | (0.011) | (0.010) | ||
| Non-EU resident | 0.060 | 0.059 | 0.058 | 0.043 | 0.057 | |
| (0.014) | (0.012) | (0.015) | (0.011) | (0.016) | ||
| German CB | 0.004 | 0.002 | 0.011 | 0.010 | 0.026 | |
| (0.012) | (0.010) | (0.012) | (0.008) | (0.014) | ||
| French CB | −0.004 | −0.002 | −0.006 | 0.002 | −0.002 | |
| (0.013) | (0.011) | (0.010) | (0.008) | (0.008) | ||
| Belgian CB | −0.001 | −0.004 | −0.002 | −0.006 | 0.010 | |
| (0.009) | (0.009) | (0.009) | (0.007) | (0.007) | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choe, C.; Van Kerm, P. Foreign Workers and the Wage Distribution: What Does the Influence Function Reveal? Econometrics 2018, 6, 41. https://doi.org/10.3390/econometrics6030041
Choe C, Van Kerm P. Foreign Workers and the Wage Distribution: What Does the Influence Function Reveal? Econometrics. 2018; 6(3):41. https://doi.org/10.3390/econometrics6030041
Chicago/Turabian StyleChoe, Chung, and Philippe Van Kerm. 2018. "Foreign Workers and the Wage Distribution: What Does the Influence Function Reveal?" Econometrics 6, no. 3: 41. https://doi.org/10.3390/econometrics6030041
APA StyleChoe, C., & Van Kerm, P. (2018). Foreign Workers and the Wage Distribution: What Does the Influence Function Reveal? Econometrics, 6(3), 41. https://doi.org/10.3390/econometrics6030041





