Decomposing Wage Distributions Using Recentered Influence Function Regressions
Abstract
1. Introduction
2. The Decomposition Problem and Shortcomings of Existing Methods
3. Identification of General Composition and Structure Effects
3.1. Wage Structure and Composition Effects
3.2. The RIF Regressions
3.3. Interpreting the Decomposition
3.3.1. Composition Effects
3.3.2. Wage Structure Effect
4. Estimation and Inference
4.1. First Stage Estimation
4.2. Second Stage Estimation
4.3. Examples
4.3.1. Quantiles and Interquantile Ranges
4.3.2. Variance
4.3.3. The Gini coefficient
5. Empirical Application: Changes in Male Wage Inequality between 1988 and 2016
5.1. RIF-Regressions
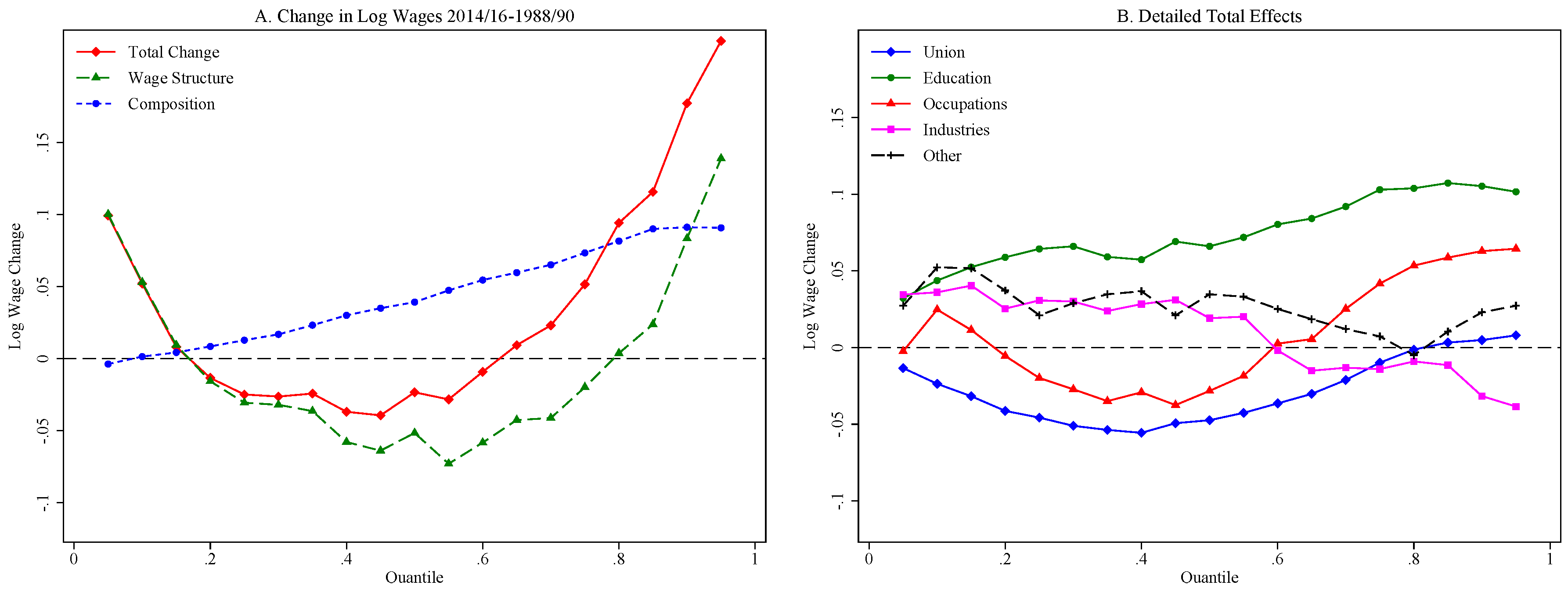
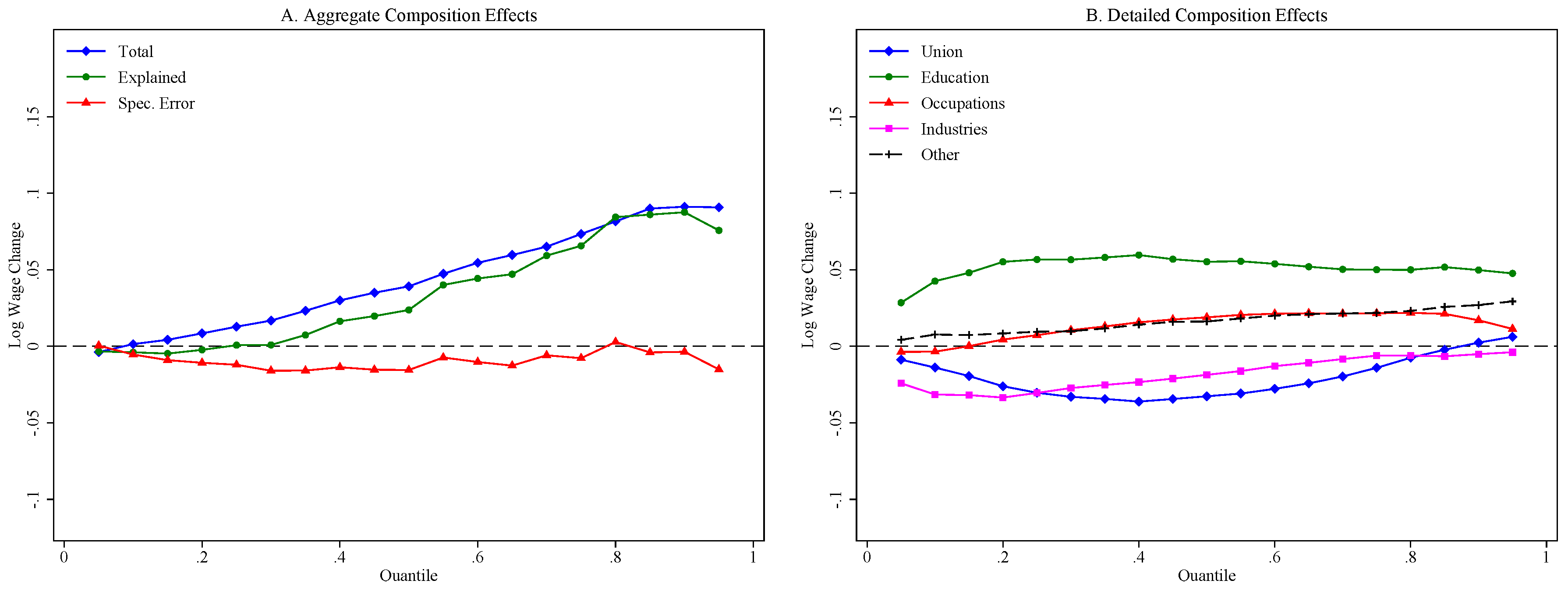
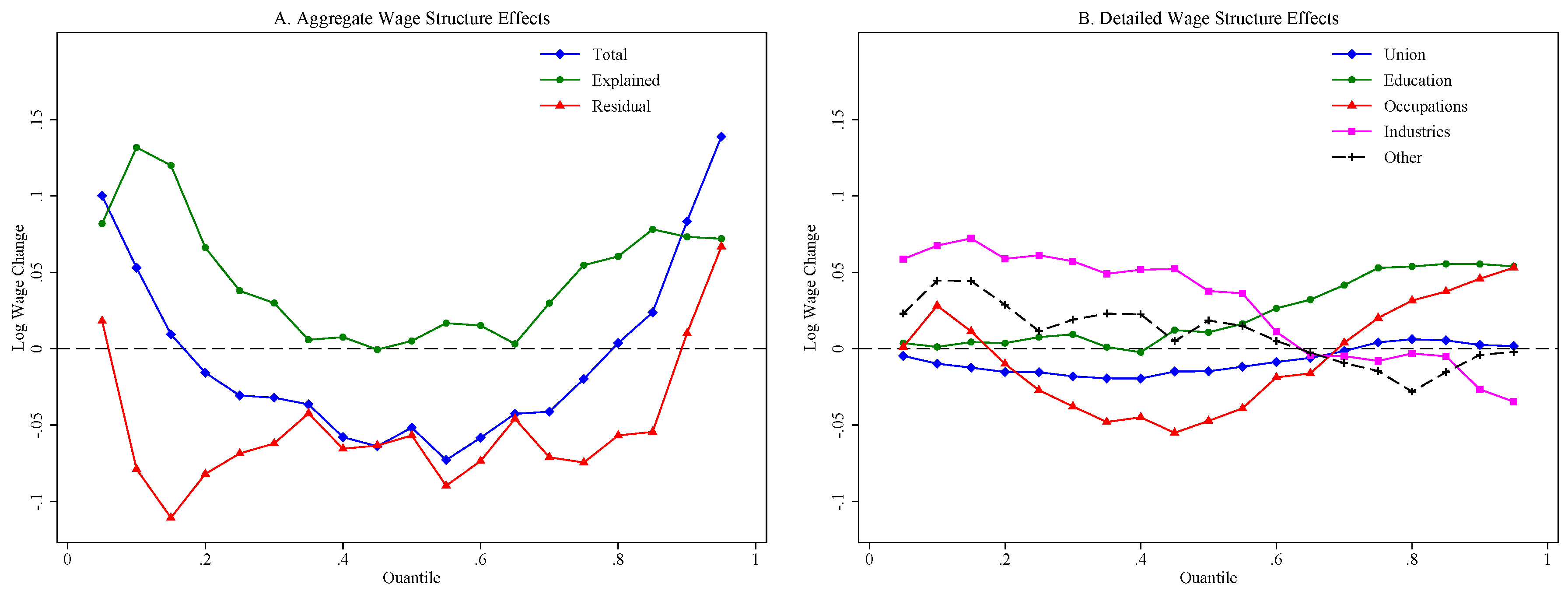
5.2. Decomposition Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Tables
| Years: | 1988/90 | 2014/16 | Difference |
|---|---|---|---|
| Log wages | 2.860 | 2.901 | 0.041 |
| Std of log wages | 0.579 | 0.622 | 0.043 |
| Union covered | 0.223 | 0.127 | −0.095 |
| Non-white | 0.134 | 0.186 | 0.052 |
| Non-Married | 0.388 | 0.457 | 0.068 |
| Age | 36.204 | 39.882 | 3.677 |
| Education | |||
| Primary | 0.059 | 0.034 | −0.025 |
| Some HS | 0.118 | 0.054 | −0.064 |
| High School | 0.381 | 0.307 | −0.074 |
| Some College | 0.202 | 0.275 | 0.072 |
| College | 0.139 | 0.218 | 0.078 |
| Post-grad | 0.101 | 0.113 | 0.012 |
| Occupations | |||
| Upper Management | 0.082 | 0.080 | −0.002 |
| Lower Management | 0.040 | 0.068 | 0.028 |
| Engineers & Computer Occ. | 0.061 | 0.081 | 0.019 |
| Other Scientists | 0.014 | 0.010 | −0.004 |
| Social Support Occ. | 0.052 | 0.061 | 0.009 |
| Lawyers & Doctors | 0.010 | 0.015 | 0.005 |
| Health Treatment Occ. | 0.010 | 0.019 | 0.009 |
| Clerical Occ. | 0.066 | 0.068 | 0.002 |
| Sales Occ. | 0.086 | 0.085 | −0.001 |
| Insur. & Real Estate Sales | 0.007 | 0.006 | −0.001 |
| Financial Sales | 0.003 | 0.002 | −0.001 |
| Service Occ. | 0.107 | 0.149 | 0.042 |
| Primary Occ. | 0.026 | 0.011 | −0.015 |
| Construction & Repair Occ. | 0.164 | 0.155 | −0.009 |
| Production Occ. | 0.141 | 0.086 | −0.055 |
| Transportation Occ. | 0.086 | 0.060 | −0.026 |
| Truckers | 0.045 | 0.041 | −0.004 |
| Industries | |||
| Agriculture, Mining | 0.033 | 0.026 | −0.007 |
| Construction | 0.097 | 0.101 | 0.005 |
| Hi-Tech Manufac | 0.102 | 0.066 | −0.037 |
| Low-Tech Manufac | 0.137 | 0.087 | −0.050 |
| Wholesale Trade | 0.051 | 0.033 | −0.018 |
| Retail Trade | 0.105 | 0.113 | 0.008 |
| Transportation & Utilities | 0.086 | 0.079 | −0.008 |
| Information except Hi-Tech | 0.018 | 0.012 | −0.006 |
| Financial Activities | 0.047 | 0.058 | 0.011 |
| Hi-Tech Services | 0.035 | 0.064 | 0.029 |
| Business Services | 0.051 | 0.065 | 0.014 |
| Education & Health Services | 0.097 | 0.113 | 0.016 |
| Personal Services | 0.081 | 0.127 | 0.046 |
| Public Admin | 0.058 | 0.054 | −0.005 |
| Public Sector | 0.149 | 0.126 | −0.024 |
| Code Sources: | 2010 Census SOC | 1980 SOC |
|---|---|---|
| Occupations | ||
| Upper Management | 10–200, 430 | 1–13, 19 |
| Lower Management | 200–950 | 14–18, 20–37, 473–476 |
| Engineers & Computer Occ. | 1000–1560 | 43–68, 213–218, 229 |
| Other Scientists | 1600–1960 | 69–83, 166–173, 223–225, 235 |
| Social Support Occ. | 2000–2060, 2140–2960 | 113–165, 174–177, 183–199, 228, 234 |
| Lawyers & Doctors | 2100–2110, 3010, 3060 | 84–85, 178–179 |
| Health Treatment Occ. | 3000, 3030–3050, 3110–3540 | 86–106, 203–208 |
| Clerical Occ. | 5000–5940 | 303–389 |
| Sales Occ. | 4700–4800, 4830–4900, 4930–4965 | 243–252, 256–285 |
| Insur. & Real Estate Sales | 4810,4920 | 253–254 |
| Financial Sales | 4820 | 255 |
| Service Occ. | 3600–4650 | 430–470 |
| Primary Occ. | 6000–6130 | 477–499 |
| Construction & Repair Occ. | 6200–7620 | 503–617, 863–869 |
| Production Occ. | 7700–8960 | 633–799, 873, 233 |
| Transportation Occ. | 9000–9120, 9140–9750 | 803, 808–859, 876–889, 226–227 |
| Truck Drivers | 9130 | 804–806 |
| Industries | ||
| Agriculture, Mining | 170–490 | 10–50 |
| Construction | 770 | 60 |
| Hi-Tech Manufac | 2170–2390, 3180, 3360–3690, 3960 | 180–192, 210–212, 310, 321–322, 340–372 |
| Low-Tech Manufac | 1070–2090, 2470–3170, 3190–3290, 3770–3890, 3970–3990 | 100–162, 200–201,220–301, 311–320, 331–332, 380–392 |
| Wholesale Trade | 4070–4590 | 500–571 |
| Retail Trade | 4670–5790 | 580–640, 642–691 |
| Transportation & Utilities | 570–690, 6070–6390 | 400–432, 460–472 |
| Information except Hi-Tech | 6470–6480, 6570–6670, 6770–6780 | 171–172, 852 |
| Financial Activities | 6870–7190 | 700–712 |
| Hi-Tech Services | 6490, 6675–6695, 7290–7460 | 440–442, 732–740, 882 |
| Business Services | 7270–7280, 7470–7790 | 721–731, 741–791, 890, 892 |
| Education & Health Services | 7860–8470 | 812–851, 860–872, 891 |
| Personal Services | 8560–9290 | 641, 750–802, 880–881 |
| Public Admin | 9370–9590 | 900–932 |
Appendix B. Supplemental Material
Appendix B.1. Details of Weighting Functions Estimation
Appendix B.1.1. Estimating the Weights
Appendix B.1.2. Estimating the Distributional Statistics
Appendix B.1.3. Parametric Propensity Score Estimation
Appendix B.1.4. Nonparametric Propensity Score Estimation
Appendix B.2. Asymptotic Distribution
Appendix B.2.1. The Asymptotic Distribution of Plug-In Estimators
Appendix B.3. Proofs
References
- Acemoglu, Daron, and David H. Autor. 2011. Skills, Tasks, and Technologies: Implications for Employment and Earnings. In Handbook of Labor Economics. Edited by Orley Ashenfelter and David Card. Amsterdam: North-Holland, vol. IV.B, pp. 1043–172. [Google Scholar]
- Alvaredo, Facundo, Anthony B. Atkinson, Thomas Piketty, and Emmanuel Saez. 2013. The Top 1 Percent in International and Historical Perspective. Journal of Economic Perspectives 27: 3–20. [Google Scholar] [CrossRef]
- Autor, David H., and David Dorn. 2013. The Growth of Low-Skill Service Jobs and the Polarization of the US Labor Market. American Economic Review 103: 1553–97. [Google Scholar] [CrossRef]
- Autor, David H., David Dorn, Gordon H. Hanson, and Jae Song. 2014. Trade Adjustment: Worker-level Evidence. Quarterly Journal of Economics 129: 1799–860. [Google Scholar] [CrossRef]
- Autor, David H., David Dorn, and Gordon H. Hanson. 2015. Untangling Trade and Technology: Evidence from Local Labour Markets. Economic Journal 125: 621–46. [Google Scholar] [CrossRef]
- Autor, David H., Lawrence F. Katz, and Melissa S. Kearney. 2005. Rising Wage Inequality: The Role of Composition and Prices. NBER Working paper No. 11628. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Autor, David H., Lawrence F. Katz, and Melissa S. Kearney. 2006. The Polarization of the U.S. Labor Market. American Economic Review 96: 189–94. [Google Scholar] [CrossRef]
- Autor, David H., Frank Levy, and Richard J. Murnane. 2003. The Skill Content Of Recent Technological Change: An Empirical Exploration. Quarterly Journal of Economics 118: 1279–333. [Google Scholar] [CrossRef]
- Barsky, Robert, John Bound, Kerwin Kofi Charles, and Joseph P. Lupton. 2002. Accounting for the Black-White Wealth Gap: A Nonparametric Approach. Journal of the American Statistical Association 97: 663–73. [Google Scholar] [CrossRef]
- Bento, Antonio, Kenneth Gillingham, and Kevin Roth. 2017. The Effect of Fuel Economy Standards on Vehicle Weight Dispersion and Accident Fatalitiesc. NBER Working paper No. w23340. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Blinder, Alan. 1973. Wage Discrimination: Reduced Form and Structural Estimates. Journal of Human Resources 8: 436–55. [Google Scholar] [CrossRef]
- Brochu, Pierre, David A. Green, Thomas Lemieux, and James Townsend. 2017. The Minimum Wage, Turnover, and the Shape Effects of Wage Distribution. In Mimeo. Vancouver: University of British Columbia. [Google Scholar]
- Card, David. 1992. The Effects of Unions on the Distribution of Wages: Redistribution or Relabelling? NBER Working paper No. 4195. Cambridge, MA, USA: National Bureau of Economic Research. [Google Scholar]
- Cattaneo, Matias D., Michael Jansson, and Xinwei Ma. 2017. Simple Local Polynomial Density Estimators. In Mimeo. Berkeley: UC Berkeley. [Google Scholar]
- Chamberlain, Gary. 1994. Quantile Regression Censoring and the Structure of Wages. In Advances in Econometrics. Edited by Christopher Sims. New York: Elsevier. [Google Scholar]
- Chernozhukov, Victor, Ivan Fernandez-Val, and Blaise Melly. 2013. Inference on Counterfactual Distributions. Econometrica 81: 2205–68. [Google Scholar]
- Chen, Xiaohong, Han Hong, and Alessandro Tarozzi. 2008. Semiparametric Efficiency in GMM Models with Auxiliary Data. The Annals of Statistics 36: 808–43. [Google Scholar] [CrossRef]
- Choe, Chung, and Philippe Van Kerm. 2014. Foreign Workers and the Wage Distribution: Where Do They Fit in? Technical Report 2014-02. Esch-sur-Alzette: Luxembourg Institute of Socio-Economic Research. [Google Scholar]
- Cowell, Frank, and Maria-Pia Victoria-Feser. 1996. Robustness Properties of Inequality Measures. Econometrica 64: 77–101. [Google Scholar] [CrossRef]
- DiNardo, John, Nicole M. Fortin, and Thomas Lemieux. 1996. Labor Market Institutions and the Distribution of Wages, 1973–1992: A Semiparametric Approach. Econometrica 64: 1001–44. [Google Scholar] [CrossRef]
- Eeckhout, Jan, Roberto Pinheiro, and Kurt Schmidheiny. 2014. Spatial sorting. Journal of Political Economy 122: 554–620. [Google Scholar] [CrossRef]
- Essama-Nssah, Boniface, and Peter J. Lambert. 2012. Influence functions for policy impact analysis. In Inequality, Mobility and Segregation: Essays in Honor of Jacques Silber. Edited by John A. Bishop and Rafael Salas. Cheltenham: Emerald Group Publishing Limited, chp. 6. pp. 135–59. [Google Scholar]
- Firpo, Sergio. 2007. Efficient Semiparametric Estimation of Quantile Treatment Effects. Econometrica 75: 259–76. [Google Scholar] [CrossRef]
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2007. Decomposing Wage Distributions using Recentered Influence Functions Regressions. In Mimeo. Vancouver: University of British Columbia. [Google Scholar]
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2009. Unconditional Quantile Regressions. Econometrica 77: 953–973. [Google Scholar]
- Firpo, Sergio, Nicole M. Fortin, and Thomas Lemieux. 2011. Occupational Tasks and Changes in the Wage Structure. In Mimeo. Vancouver: University of British Columbia. [Google Scholar]
- Firpo, Sergio, and Cristine Pinto. 2016. Identification and Estimation of Distributional Impacts of Interventions Using Changes in Inequality Measures. Journal of Applied Econometrics 31: 457–86. [Google Scholar] [CrossRef]
- Fortin, Nicole, Thomas Lemieux, and Sergio Firpo. 2011. Decomposition Methods in Economics. In Handbook of Labor Economics. Edited by Orley Ashenfelter and David Card. Amsterdam: North-Holland, vol. IV.A, pp. 1–102. [Google Scholar]
- Fortin, Nicole, and Thomas Lemieux. 2016. Inequality and Changes in Task Prices: Within and between Occupation Effects? In Income Inequality, Causes and Consequences (Research in Labor Economics, Vol. 43). Edited by Lorenzo Cappellari, Solomon W. Polachek and Konstantinos Tatsiramos. Cheltenham: Emerald Group Publishing Limited, pp. 195–226. [Google Scholar]
- Freeman, Richard B. 1980. Unionism and the Dispersion of Wages. Industrial and Labor Relations Review 34: 3–23. [Google Scholar] [CrossRef]
- Freeman, Richard B. 1993. How Much has Deunionization Contributed to the Rise of Male Earnings Inequality? In Uneven Tides: Rising Income Inequality in America. Edited by Sheldon Danziger and Peter Gottschalk. New York: Russell Sage Foundation, pp. 133–63. [Google Scholar]
- Gâteaux, René. 1913. Sur les fonctionnelles continues et les fonctionnelles analytiques. Comptes Rendus de l’Académie des Sciences-Series I—Mathematics 157: 325–27. [Google Scholar]
- Gardeazabal, Javier, and Arantza Ugidos. 2004. More on the Identification in Detailed Wage Decompositions. Review of Economics and Statistics 86: 1034–57. [Google Scholar] [CrossRef]
- Gradín, Carlos. 2016. Why Is Income inequality so High in Spain? In Income Inequality Around the World (Research in Labor Economics, Vol. 44). Edited by Lorenzo Cappellari, Solomon W. Polachek and Konstantinos Tatsiramos. Cheltenham: Emerald Group Publishing Limited, pp. 109–77. [Google Scholar]
- Hampel, Frank R. 1974. The Influence Curve and Its Role in Robust Estimation. Journal of the American Statistical Association 60: 383–93. [Google Scholar] [CrossRef]
- Heckman, James J. 1990. Varieties of Selection Bias. American Economic Review 80: 313–18. [Google Scholar]
- Heckman, James J., Hidehiko Ichimura, and Petra Todd. 1997. Matching as an Econometric Evaluation Estimator. Review of Economic Studies 65: 261–94. [Google Scholar] [CrossRef]
- Heckman, James J., Hidehiko Ichimura, Jeffrey A. Smith, and Petra Todd. 1998. Characterizing Selection Bias Using Experimental Data. Econometrica 66: 1017–98. [Google Scholar] [CrossRef]
- Heckman, James J., and Richard Robb. 1985. Alternative Methods for Evaluating the Impact of Interventions: An Overview. Journal of Econometrics 30: 239–67. [Google Scholar] [CrossRef]
- Heckman, James J., and Richard Robb. 1986. Alternative Methods for Solving the Problem of Selection Bias in Evaluating the Impact of Treatments on Outcomes. In Drawing Inference from Self-Selected Samples. Edited by Howard Wainer. New York: Springer, pp. 63–107. [Google Scholar]
- Hirano, Keisuke, Guido W. Imbens, and Geert Ridder. 2003. Efficient Estimation of Average Treatment Effects Using the Estimated Propensity Score. Econometrica 71: 1161–89. [Google Scholar] [CrossRef]
- Jann, Ben. 2008. The Oaxaca-Blinder Decomposition for Linear Regression Models. Stata Journal 8: 435–79. [Google Scholar]
- Juhn, Chinhui, Kevin Murphy, and Brooks Pierce. 1993. Wage Inequality and the Rise in Returns to Skill. Journal of Political Economy 101: 410–42. [Google Scholar] [CrossRef]
- Kline, Patrick. 2011. Oaxaca-Blinder as a Reweighting Estimator. American Economic Review 101: 532–37. [Google Scholar] [CrossRef]
- Koenker, Roger. 2005. Quantile Regression. Cambridge: Cambridge University Press. [Google Scholar]
- Koenker, Roger, and Gilbert Bassett, Jr. 1978. Regression Quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Lemieux, Thomas. 2002. Decomposing Changes in Wage Distributions: A Unified Approach. Canadian Journal of Economics 35: 646–88. [Google Scholar] [CrossRef]
- Lemieux, Thomas. 2006a. Post-secondary Education and Increasing Wage Inequality. American Economic Review 96: 195–99. [Google Scholar] [CrossRef]
- Lemieux, Thomas. 2006b. Increasing Residual Wage Inequality: Composition Effects, Noisy Data, or Rising Demand for Skill? American Economic Review 96: 461–98. [Google Scholar] [CrossRef]
- Lemieux, Thomas. 2008. The Changing Nature of Wage Inequality. Journal of Population Economics 21: 21–48. [Google Scholar] [CrossRef]
- Machado, José A. F., and José Mata. 2005. Counterfactual Decomposition of Changes in Wage Distributions Using Quantile Regression. Journal of Applied Econometrics 20: 445–65. [Google Scholar] [CrossRef]
- Melly, Blaise. 2005. Decomposition of Differences in Distribution Using Quantile Regression. Labour Economics 12: 577–1990. [Google Scholar] [CrossRef]
- Monti, Anna Clara. 1991. The Study of the Gini Concentration Ratio by Means of the Influence Function. Statistica 51: 561–77. [Google Scholar]
- Oaxaca, Ronald. 1973. Male-Female Wage Differentials in Urban Labor Markets. International Economic Review 14: 693–709. [Google Scholar] [CrossRef]
- Oaxaca, Ronald, and Michael R. Ransom. 1999. Identification in Detailed Wage Decompositions. Review of Economics and Statistics 81: 154–57. [Google Scholar] [CrossRef]
- Rosenbaum, Paul R., and Donald B. Rubin. 1983. The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika 70: 41–55. [Google Scholar] [CrossRef]
- Rosenbaum, Paul R., and Donald B. Rubin. 1984. Reducing Bias in Observational Studies Using Subclassification on the Propensity Score. Journal of the American Statistical Association 79: 516–24. [Google Scholar] [CrossRef]
- Rothe, Christoph. 2010. Nonparametric Estimation of Distributional Policy Effects. Journal of Econometrics 155: 56–70. [Google Scholar] [CrossRef]
- Rothe, Christoph. 2012. Partial Distributional Policy Effects. Econometrica 80: 2269–301. [Google Scholar]
- Rothe, Christoph. 2015. Decomposing the Composition Effect. Journal of Business Economics and Statistics 33: 323–37. [Google Scholar] [CrossRef]
- Von Mises, Richard. 1947. On the Asymptotic Distribution of Differentiable Statistical Functions. The Annals of Mathematical Statistics 18: 309–48. [Google Scholar] [CrossRef]
- White, Halbert. 1980. Using Least Squares to Approximate Unknown Regression Functions. International Economic Review 21: 149–70. [Google Scholar] [CrossRef]
- Yun, Myeong-Su. 2005. A simple Solution to the Identification Problem in Detailed Wage Decompositions. Economic Inquiry 43: 766–72. [Google Scholar] [CrossRef]
| 1 | Recentered influence functions have since been derived for a host of inequality measures by Essama-Nssah and Lambert (2012). |
| 2 | Eeckhout et al. (2014) compare the CFM approach to the RIF-regressions approach to decompose the skill distributions across large and small cities in terms of education, occupations, and industries, focusing on the bottom and top decile. Bento et al. (2017) provide a useful comparison of local kernel regressions, conditional quantile regressions, and RIF regressions in the context of a Monte-Carlo simulation of the effect of fuel economy standards on the distribution of vehicle weight. |
| 3 | |
| 4 | The federal minimum wage has declined substantially (in real terms) over time and is now superseeded by higher state minimum wages in most states. As a result, the effect of state and federal minimum wages would need to be modeled over of a range of wages. This task is beyond the scope of the current paper. |
| 5 | Consider, for instance, the contribution of increasing returns to education to changes in mean wages over time in the case where workers are either high school graduates or college graduates. In the case where high school is the base group, is a dummy variable indicating that the worker is a college graduate, and and are the effect of college on wages in years and 1. If returns to college increase over time (), then the contribution of education to the wage structure effect, , is positive, where is the share of college graduates. If we use instead college as the base group, then is negative, where represents the share of high school () and represents the effect of high school (). Thus, whether changes in returns to schooling contribute positively or negatively to the change in mean wages critically depends on the choice of the base group. |
| 6 | As we show below, our goal is to estimate a counterfactual mean wage that would prevail if workers in Group 1 were paid under the wage structure of Group 0. Under the linearity assumption, this is equal to , a term that appears in both the wage structure and composition effect. The problem is that, when linearity does not hold, the counterfactual mean wage is not be equal to . |
| 7 | |
| 8 | We discuss the case of reweighting in more detail below. In the case where the conditional expectation is estimated non-parametrically, a whole different procedure would have to be used to separate the wage structure into the contribution of each covariate. For instance, average derivative methods could be used to estimate an effect akin to the coefficients used in standard decompositions. Unfortunately, these methods are difficult to use in practice, and would not be helpful in dividing up the composition effect into the contribution of each individual covariate. |
| 9 | We sometimes refer to the functional simply as In the Oaxaca–Blinder decomposition discussed earlier, the parameter equals the mean () and is the total difference in mean wages. |
| 10 | See, for instance, Rosenbaum and Rubin (1983, 1984), Heckman et al. (1997) and Heckman et al. (1998). |
| 11 | This rules out selection into Group 1 or 0 based on unobservables. |
| 12 | This is not a restrictive assumption when looking at changes in the wage distribution over time. Problems could arise, however, in gender wage gap decompositions where some of the detailed occupations are only held by men or by women. |
| 13 | See also Firpo and Pinto (2016). |
| 14 | Note that, even if and , the result from Result 2 is unaffected. The intuition is that, since () have a joint distribution, we can use the available information on that distribution to reweight the effect of the ’s on Y. |
| 15 | This finding is closely linked to the well-known fact that estimates of marginal effects estimated using a linear probability model tend to be very similar, in practice, to those obtained using a probit, logit, or another flexible non-linear discrete response model. |
| 16 | In the case of the mean, another rationale for using a linear model comes from Kline (2011), who notes that the OB decomposition remains valid even when the regression function is non-linear as long as the reweighting factor is well approximated by a linear odds ratio model. Unfortunately, this property does not hold for distributional statistics besides the mean. |
| 17 | In the case of the mean, several procedures have been suggested as potential solutions to the base group problem. They typically involve creating an artificial base group with the average observed characteristics in the population (see, e.g., Yun 2005). As this choice is as arbitrary as other choices of base group, and arguably harder to interpret, especially across studies, it does not really solve the base group problem. See Fortin et al. (2011) for a more complete discussion. In Footnote 29, we also discuss some issues with previous attempts (Firpo et al. 2007) using a normalization approach to the base group. |
| 18 | In practice, we simply use the Stata integ command. |
| 19 | This technological change explanation was first suggested by Autor et al. (2003). It also implies that the wages of both skilled (e.g., doctors) and unskilled (e.g., truck drivers) non-routine jobs, at the top and low end of the wage distribution, increased relative to those of “routine” workers in the middle of the wage distribution. |
| 20 | Autor et al. (2005) used the Machado and Mata (2005) method to decompose changes at each quantile into a “price” (wage structure) and “quantity” (composition) effect. They did not further consider, however, the contribution of each individual covariate to the wage structure effect, except for separating the contribution of (all) covariates from the residual change in inequality. See also Lemieux (2002) for a similar decomposition based on a reweighting procedure. |
| 21 | Table A2 gives the details of the occupation and industry categories used. |
| 22 | Several cross-validation tools suggested tuning parameters in that range, but the graphs were indistinguishable. In addition to the reweighting factors discussed in Section 3 and Section 4, we also use CPS sample weights throughout the empirical analysis. In practice, this means that we multiply the relevant reweighting factor with CPS sample weight. |
| 23 | See Brochu et al. (2017) for a more precise modeling of the effect of minimum wages on the distribution of wages. |
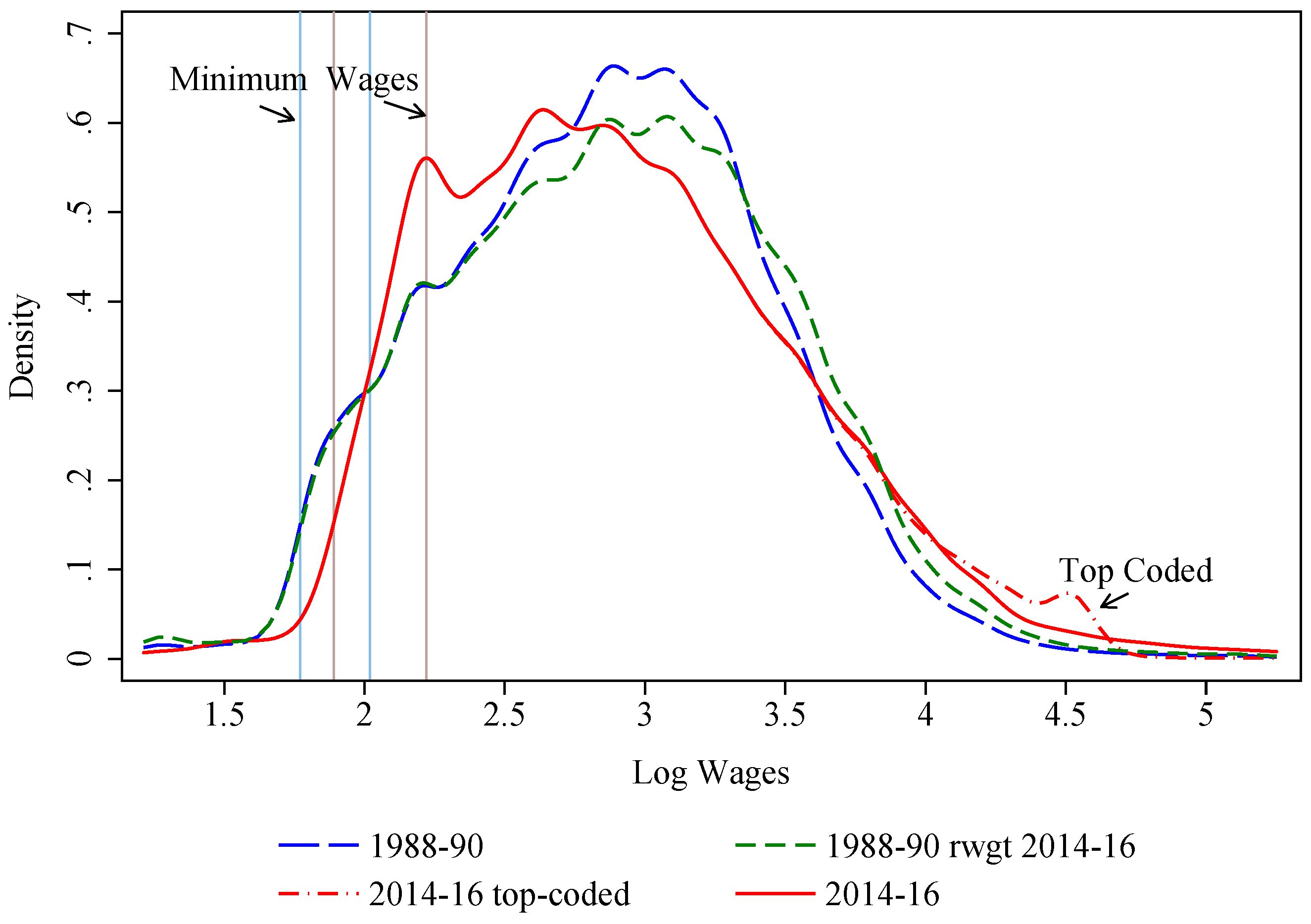
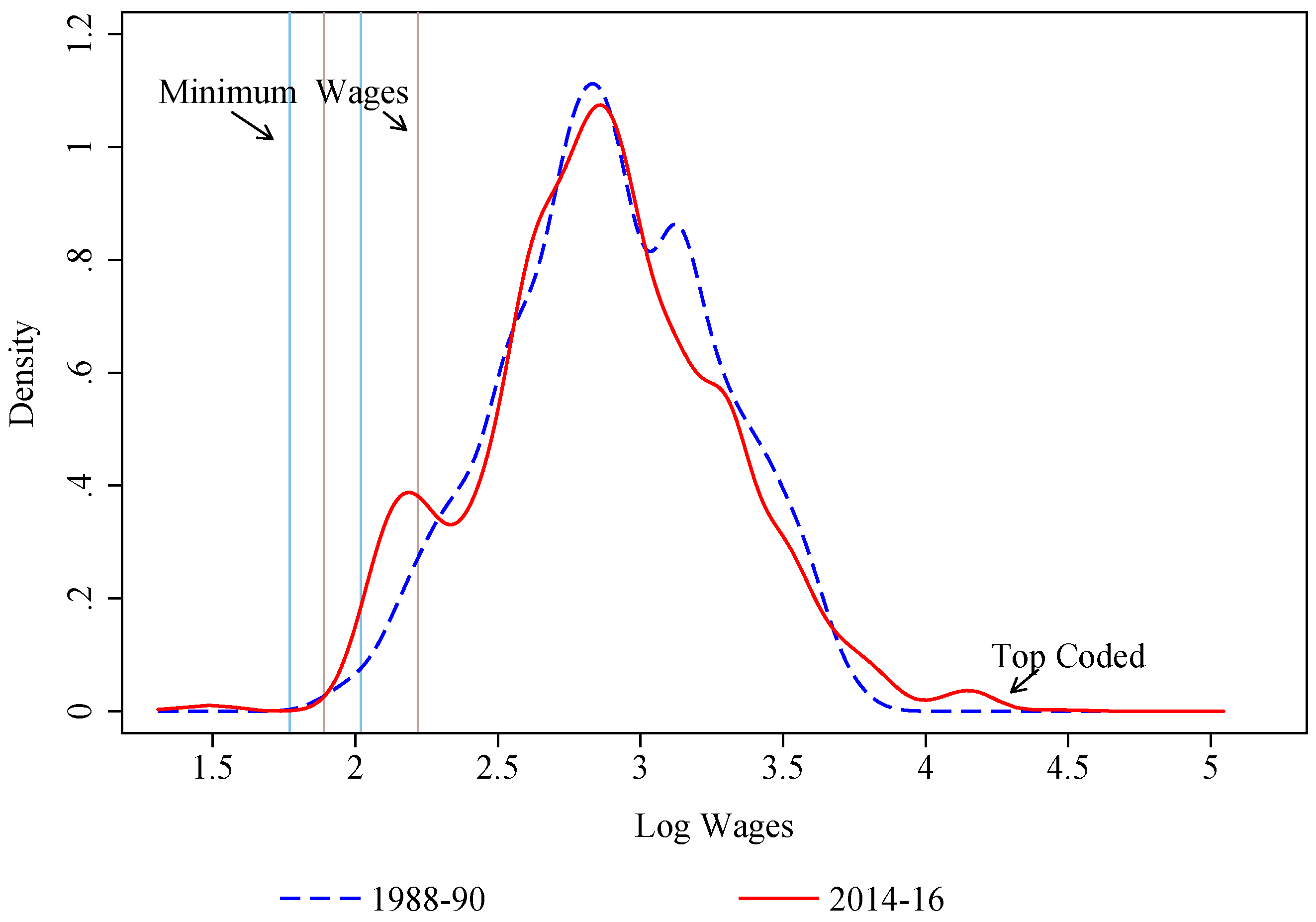
| 24 | Weekly earnings are top-coded at $1923 in 1988–1990 and $2884 in 2014–2016. The latter is substantially lower in constant dollars. Furthermore, the top-code is even higher in relative terms because of the substantial growth in real wages at the top end of the distribution. |
| 25 | A large fraction of workers top-coded at $2884 a week work 40 h a week, which yields an hourly wage rate of $72.1. Applying the 1.4 adjustment factor increases the wage to $100.9, or about $92.5 in dollars of 2010. This precisely matches the spike in Figure 1 since log(92.5) = 4.53. |
| 26 | Deflating wages with monthly CPI while combining several years of data helps mitigate the issue of heaping. |
| 27 | There are only 5–6 women in this category, which highlights the need of using different base groups for men and women. |
| 28 | In nominal terms, the mode of the distributions is around $10.00/h in 1988–1990 and around $19.00/h in 2014–2016. In 1988–1990, there is a second local peak around $12.00/h, while, in 2014–2016, the second lower local peak is around $10.00/h. |
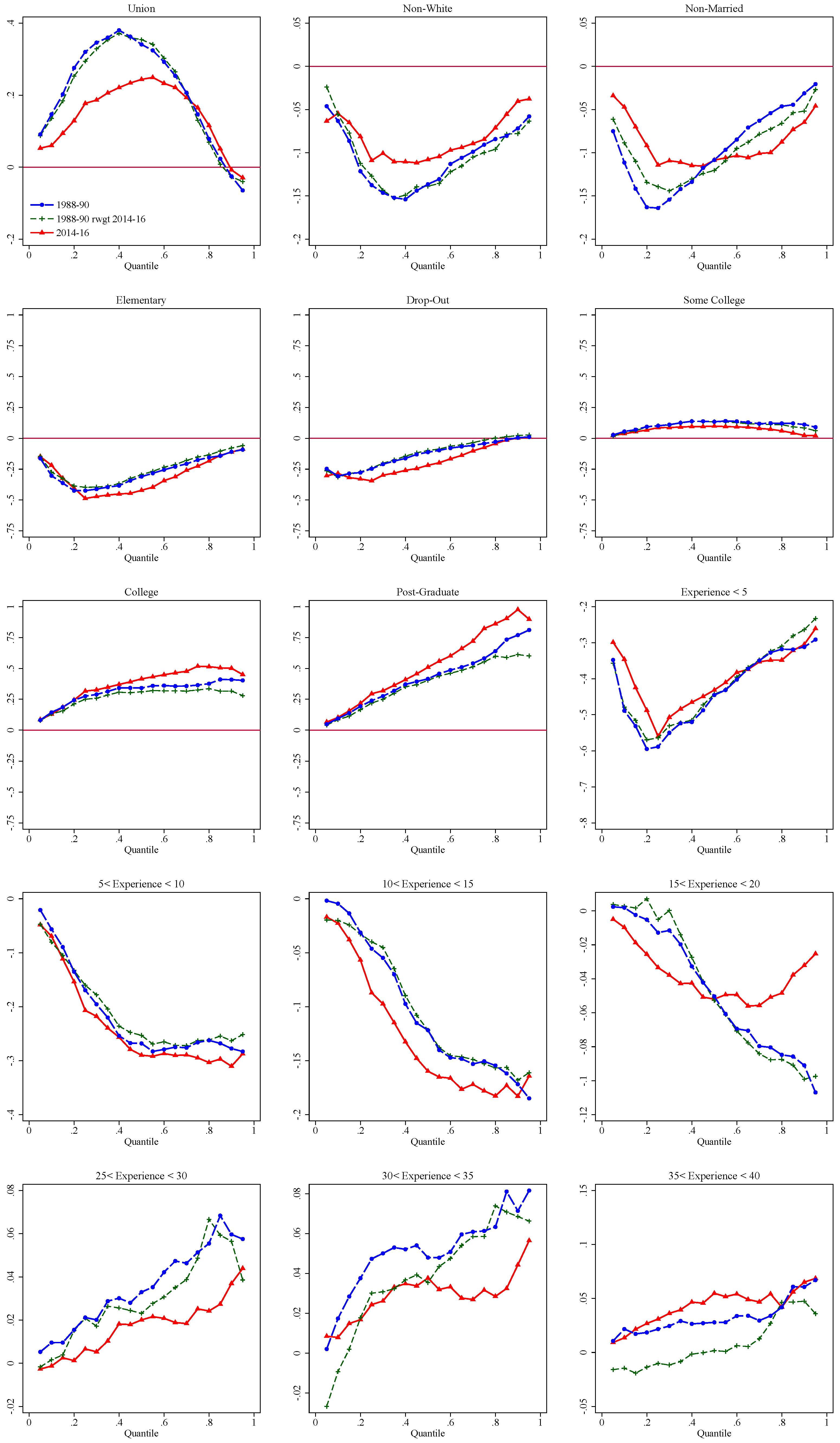
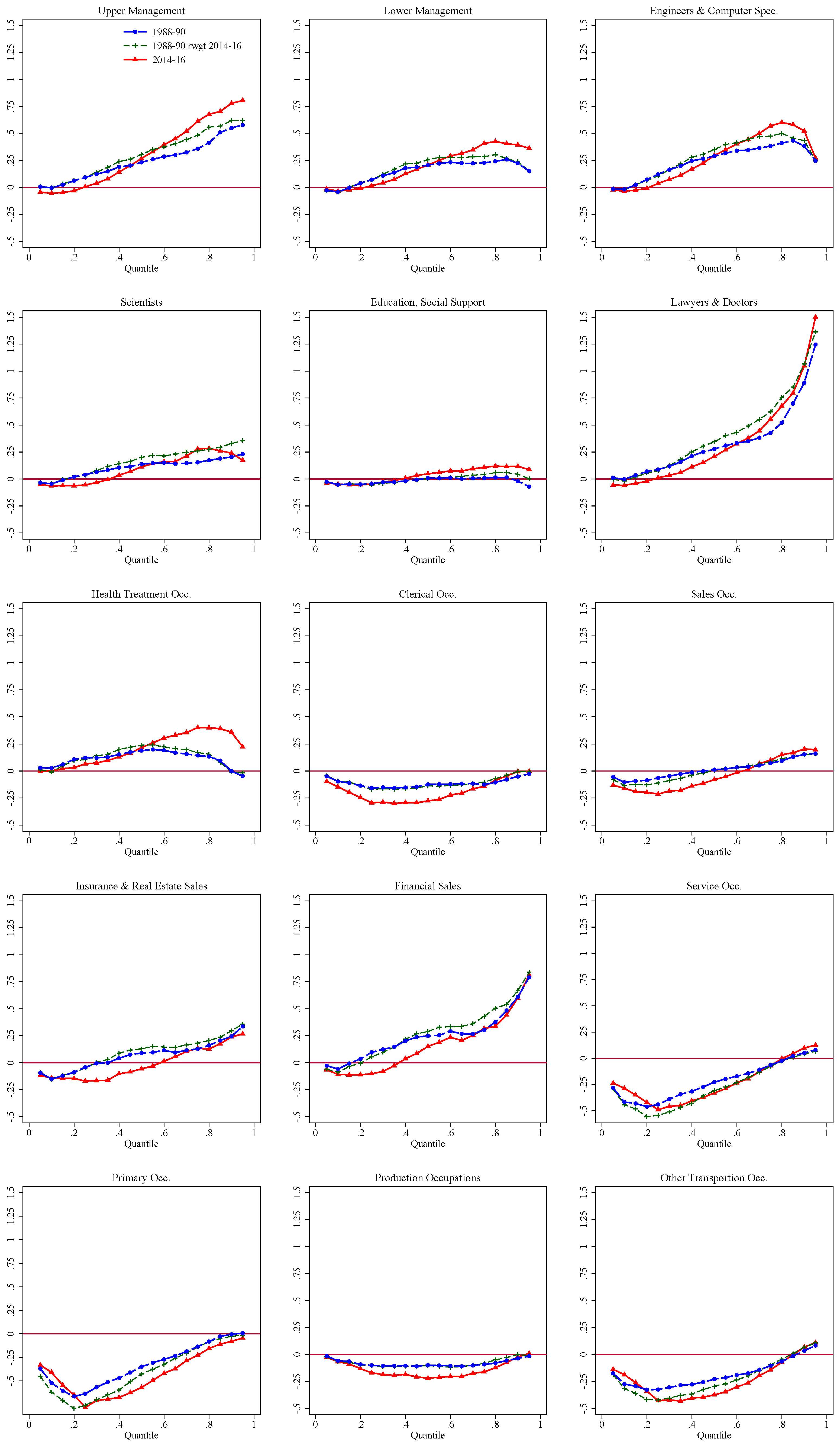
| 29 | In Firpo et al. (2007), we used a mixed approach for the base group normalizing the coefficients of the occupation and industry dummies. That approach, although superficially attractive, has the important disadvantage of limiting the explanatory power of the variables whose coefficients are constrained. As a result, in this earlier version of the paper, very little of the changes in inequality were attributable to occupations and industries. |
| 30 | As argued in FFL, the different relative strength of between and within effects at different quantiles explain the inverse U-shaped effect of unions. This is in sharp contrast with the effect of unions found estimated using conditional quantile regressions which captures only within-group effects and declines monotonically over the wage distribution (Chamberlain 1994). |
| 31 | The logit specification also includes a full set of interaction between experience and education, union status and education, union status and experience, between education and occupations, and experience and industries. |
| 32 | This stands in sharp contrast with the situation that prevailed in the 1980s when the corresponding curve was positively sloped as wage dispersion increased at all points of the distribution (Juhn et al. 1993). |
| 33 | The effect of each set of factors is obtained by summing up the contribution of the relevant covariates. For example, the effect for “education” is the sum of the effect of each of the five education categories shown in Table 1. Showing the effect of each individual dummy separately would be cumbersome and harder to interpret. |
| 34 | In practice, we use the popular Jann (2008) “oaxaca" Stata ado file and obtain bootstrapped standard errors over the entire procedure given the statistics and the RIF are estimated values. We opted for boostrapped instead of analytical standard errors by simplicity. Computation of analytical standard errors would involve estimation of different functionals, increasing the degree of complexity of the estimation step, whereas bootstrapped standard errors, although being potentially computationally more demanding are typically simpler to implement. |
| 35 | Adding more terms in the specification of the reweighting function helps reducing the reweighting error. This has to be balanced with issues of common support, as more terms may lead to more perfect predictions, an undesirable outcome. As we discuss below, the specification we use yields a very small reweighting error. |
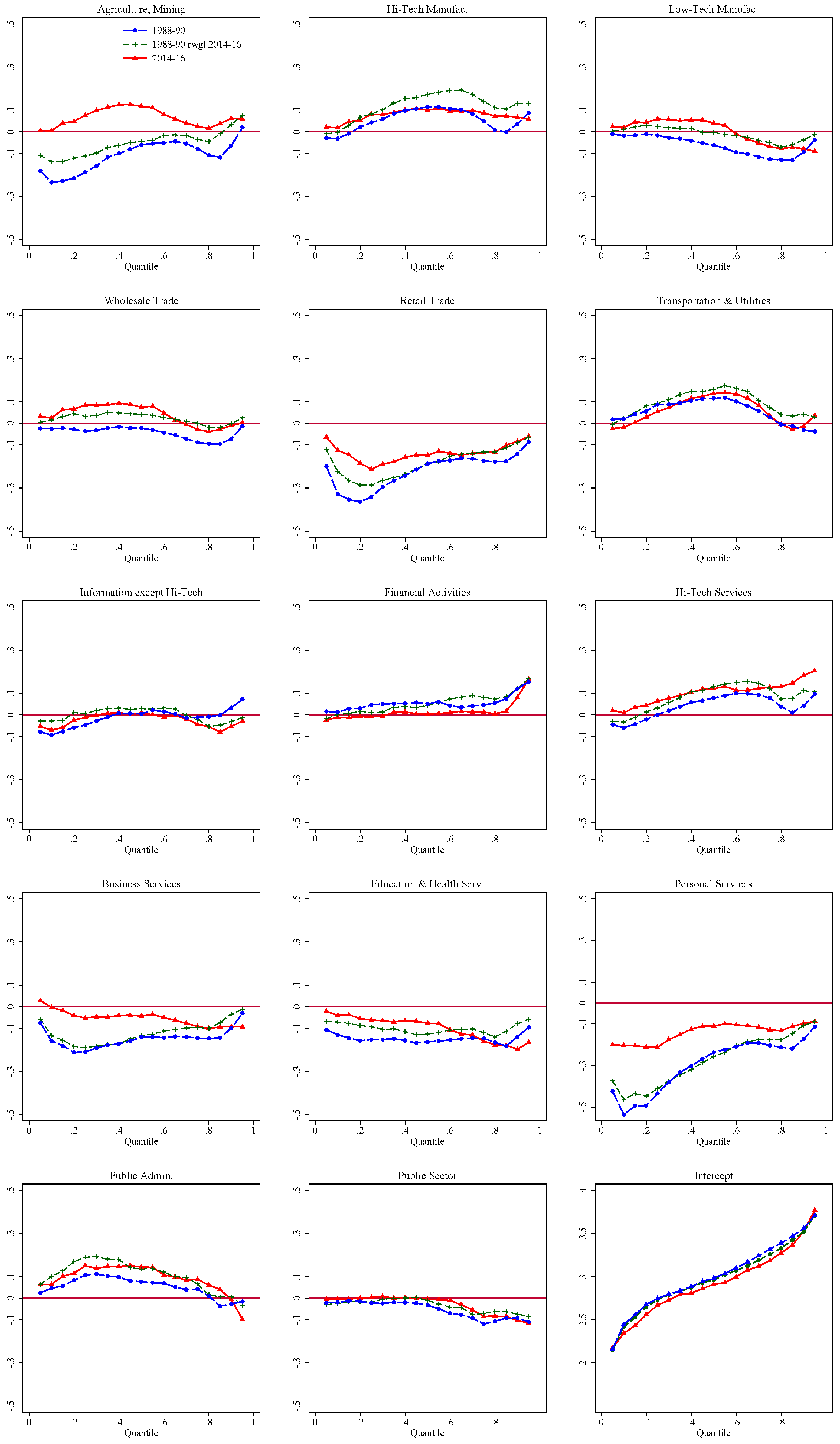
| Years: | 1988/90 | 2014/16 | ||||
|---|---|---|---|---|---|---|
| Quantiles: | 10 | 50 | 90 | 10 | 50 | 90 |
| Explanatory Variables | ||||||
| Union covered | 0.146 | 0.343 | −0.025 | 0.058 | 0.240 | −0.008 |
| (0.003) | (0.005) | (0.004) | (0.003) | (0.006) | (0.007) | |
| Non-white | −0.063 | −0.137 | −0.072 | −0.053 | −0.106 | −0.041 |
| (0.006) | (0.005) | (0.005) | (0.004) | (0.004) | (0.006) | |
| Non-Married | −0.111 | −0.109 | −0.031 | −0.046 | −0.107 | −0.064 |
| (0.004) | (0.003) | (0.004) | (0.003) | (0.004) | (0.005) | |
| Education (High School omitted) | ||||||
| Primary | −0.301 | −0.312 | −0.109 | −0.212 | −0.415 | −0.110 |
| (0.011) | (0.006) | (0.005) | (0.01) | (0.009) | (0.006) | |
| Some HS | −0.305 | −0.112 | 0.005 | −0.275 | −0.215 | 0.002 |
| (0.007) | (0.005) | (0.003) | (0.008) | (0.007) | (0.004) | |
| Some College | 0.055 | 0.135 | 0.112 | 0.036 | 0.098 | 0.023 |
| (0.005) | (0.004) | (0.005) | (0.004) | (0.005) | (0.004) | |
| College | 0.143 | 0.343 | 0.410 | 0.125 | 0.409 | 0.493 |
| (0.005) | (0.005) | (0.008) | (0.004) | (0.006) | (0.009) | |
| Post-grad | 0.094 | 0.418 | 0.772 | 0.099 | 0.502 | 0.962 |
| (0.006) | (0.006) | (0.013) | (0.004) | (0.008) | (0.017) | |
| Potential Experience (20 ≤ Experience < 25 omitted) | ||||||
| Experience < 5 | −0.486 | −0.448 | −0.312 | −0.335 | −0.425 | −0.301 |
| (0.009) | (0.006) | (0.008) | (0.007) | (0.007) | (0.011) | |
| 5 ≤ Experience < 10 | −0.056 | −0.270 | −0.278 | −0.067 | −0.285 | −0.306 |
| (0.006) | (0.006) | (0.008) | (0.005) | (0.007) | (0.011) | |
| 10 ≤ Experience < 15 | −0.005 | −0.122 | −0.172 | −0.022 | −0.157 | −0.182 |
| (0.005) | (0.006) | (0.008) | (0.004) | (0.006) | (0.011) | |
| 15 ≤ Experience < 20 | 0.002 | −0.051 | −0.091 | −0.009 | −0.051 | −0.034 |
| (0.005) | (0.005) | (0.008) | (0.004) | (0.006) | (0.012) | |
| 25 ≤ Experience < 30 | 0.010 | 0.033 | 0.060 | −0.001 | 0.020 | 0.036 |
| (0.006) | (0.006) | (0.01) | (0.004) | (0.006) | (0.012) | |
| 30 ≤ Experience < 35 | 0.017 | 0.048 | 0.071 | 0.008 | 0.037 | 0.042 |
| (0.006) | (0.006) | (0.011) | (0.004) | (0.007) | (0.012) | |
| 35 ≤ Experience < 40 | 0.022 | 0.028 | 0.061 | 0.013 | 0.054 | 0.062 |
| (0.007) | (0.008) | (0.012) | (0.004) | (0.007) | (0.013) | |
| Experience ≥ 40 | 0.068 | 0.020 | −0.010 | 0.030 | 0.058 | −0.013 |
| (0.008) | (0.008) | (0.009) | (0.005) | (0.007) | (0.012) | |
| R−square | 0.253 | 0.359 | 0.206 | 0.182 | 0.353 | 0.202 |
| No. of observations | 268,494 | 236,296 | ||||
| Years: | 1988/90 | 2014/16 | 1988/90 | 2014/16 |
|---|---|---|---|---|
| Inequality Measures | Variance of Log Wages | Gini | ||
| Estimated Values: | 0.341 | 0.418 | 0.330 | 0.396 |
| Explanatory Variables | ||||
| Constant | 0.203 | 0.205 | 0.261 | 0.290 |
| (0.004) | (0.006) | (0.002) | (0.002) | |
| Union covered | −0.075 | −0.040 | −0.067 | −0.039 |
| (0.002) | (0.004) | (0.001) | (0.001) | |
| Non-white | −0.002 | 0.005 | 0.006 | 0.005 |
| (0.003) | (0.004) | (0.001) | (0.001) | |
| Non-Married | 0.039 | 0.001 | 0.022 | 0.008 |
| (0.002) | (0.004) | (0.001) | (0.001) | |
| Education (High School omitted) | ||||
| Primary | 0.074 | 0.073 | 0.051 | 0.057 |
| (0.004) | (0.006) | (0.002) | (0.002) | |
| Some HS | 0.104 | 0.129 | 0.048 | 0.063 |
| (0.003) | (0.005) | (0.001) | (0.001) | |
| Some College | 0.028 | −0.001 | 0.006 | −0.006 |
| (0.003) | (0.003) | (0.002) | (0.003) | |
| College | 0.121 | 0.166 | 0.053 | 0.061 |
| (0.005) | (0.005) | (0.002) | (0.001) | |
| Post-grad | 0.301 | 0.401 | 0.157 | 0.177 |
| (0.007) | (0.01) | (0.003) | (0.002) | |
| Potential Experience (20 ≤ Experience < 25 omitted) | ||||
| Experience < 5 | 0.047 | 0.027 | 0.031 | 0.021 |
| (0.004) | (0.007) | (0.002) | (0.002) | |
| 5 ≤ Experience < 10 | −0.098 | −0.093 | −0.036 | −0.030 |
| (0.005) | (0.007) | (0.002) | (0.002) | |
| 10 ≤ Experience < 15 | −0.078 | −0.070 | −0.035 | −0.028 |
| (0.004) | (0.007) | (0.002) | (0.002) | |
| 15 ≤ Experience < 20 | −0.050 | −0.006 | −0.026 | 0.003 |
| (0.005) | (0.008) | (0.002) | (0.002) | |
| 25 ≤ Experience < 30 | 0.023 | 0.024 | 0.012 | 0.014 |
| (0.006) | (0.008) | (0.002) | (0.002) | |
| 30 ≤ Experience < 35 | 0.022 | 0.017 | 0.008 | 0.007 |
| (0.006) | (0.008) | (0.002) | (0.002) | |
| 35 ≤ Experience < 40 | 0.015 | 0.022 | 0.008 | 0.008 |
| (0.007) | (0.008) | (0.003) | (0.002) | |
| Experience ≥ 40 | −0.031 | −0.012 | −0.015 | −0.005 |
| (0.005) | (0.008) | (0.003) | (0.002) | |
| Occupations (Construction & Repair Occ. omitted) | ||||
| Upper Management | 0.235 | 0.415 | 0.132 | 0.203 |
| (0.007) | (0.011) | (0.003) | (0.002) | |
| Lower Management | 0.090 | 0.200 | 0.027 | 0.080 |
| (0.008) | (0.009) | (0.003) | (0.002) | |
| Engineers & Computer Occ. | 0.107 | 0.202 | 0.013 | 0.054 |
| (0.006) | (0.009) | (0.003) | (0.002) | |
| Other Scientists | 0.081 | 0.134 | 0.025 | 0.068 |
| (0.011) | (0.027) | (0.005) | (0.006) | |
| Social Support Occ. | −0.001 | 0.065 | −0.012 | 0.012 |
| (0.007) | (0.009) | (0.003) | (0.003) | |
| Lawyers & Doctors | 0.524 | 0.637 | 0.337 | 0.363 |
| (0.027) | (0.032) | (0.010) | (0.008) | |
| Health Treatment Occ. | −0.020 | 0.115 | −0.035 | 0.011 |
| (0.0101) | (0.012) | (0.005) | (0.005) | |
| Clerical Occ. | 0.013 | 0.069 | 0.017 | 0.044 |
| (0.004) | (0.005) | (0.002) | (0.002) | |
| Explanatory Variables | ||||
| Occupations (cnt.) | ||||
| Sales Occ. | 0.088 | 0.177 | 0.043 | 0.084 |
| (0.005) | (0.008) | (0.002) | (0.002) | |
| Insur. & Real Estate Sales | 0.208 | 0.197 | 0.152 | 0.105 |
| (0.031) | (0.038) | (0.011) | (0.010) | |
| Financial Sales | 0.525 | 0.409 | 0.429 | 0.219 |
| (0.06) | (0.076) | (0.018) | (0.014) | |
| Service Occ. | 0.188 | 0.208 | 0.101 | 0.107 |
| (0.004) | (0.005) | (0.002) | (0.002) | |
| Primary Occ. | 0.226 | 0.222 | 0.114 | 0.127 |
| (0.008) | (0.015) | (0.004) | (0.004) | |
| Production Occ. | 0.004 | 0.020 | 0.011 | 0.028 |
| (0.003) | (0.005) | (0.001) | (0.002) | |
| Transportation Occ. | 0.119 | 0.145 | 0.079 | 0.094 |
| (0.004) | (0.006) | (0.002) | (0.002) | |
| Truckers | 0.015 | 0.042 | 0.030 | 0.040 |
| (0.004) | (0.006) | (0.002) | (0.002) | |
| Industries (Construction omitted) | ||||
| Agriculture, Mining | 0.079 | 0.013 | 0.036 | −0.001 |
| (0.008) | (0.012) | (0.003) | (0.003) | |
| Hi-Tech Manufac | 0.018 | 0.014 | −0.001 | 0.002 |
| (0.005) | (0.009) | (0.002) | (0.002) | |
| Low-Tech Manufac | −0.037 | −0.053 | −0.011 | −0.019 |
| (0.004) | (0.007) | (0.002) | (0.002) | |
| Wholesale Trade | −0.012 | −0.027 | 0.001 | −0.006 |
| (0.006) | (0.012) | (0.002) | (0.003) | |
| Retail Trade | 0.060 | 0.016* | 0.038 | 0.023 |
| (0.005) | (0.007) | (0.002) | (0.002) | |
| Transportation & Utilities | 0.013 | −0.029 | −0.005 | −0.019 |
| (0.005) | (0.007) | (0.002) | (0.002) | |
| Information except Hi-Tech | −0.001 | 0.055 | −0.010 | 0.041 |
| (0.008) | (0.019) | (0.003) | (0.005) | |
| Financial Activities | 0.065 | 0.064 | 0.052 | 0.053 |
| (0.009) | (0.013) | (0.004) | (0.003) | |
| Hi-Tech Services | 0.048 | 0.071 | 0.018 | 0.035 |
| (0.008) | (0.01) | (0.004) | (0.003) | |
| Business Services | 0.018 | −0.042 | 0.019 | −0.014 |
| (0.005) | (0.008) | (0.002) | (0.002) | |
| Education & Health Services | −0.008 | −0.064 | −0.001 | −0.018 |
| (0.006) | (0.008) | (0.003) | (0.002) | |
| Personal Services | 0.136 | 0.054 | 0.051 | 0.023 |
| (0.006) | (0.006) | (0.002) | (0.002) | |
| Public Admin | −0.038 | −0.071 | −0.036 | −0.029 |
| (0.007) | (0.011) | (0.003) | (0.003) | |
| Public Sector | −0.058 | −0.055 | −0.030 | −0.048 |
| (0.005) | (0.007) | (0.002) | (0.002) | |
| R-squared | 0.115 | 0.087 | 0.048 | 0.025 |
| No. of observations | 268,492 | 236,287 | 268,492 | 236,287 |
| Inequality Measures | 90–10 | 50–10 | 90–50 | Variance (× 100) | Gini (× 100) |
|---|---|---|---|---|---|
| Total Change | 0.125 | −0.075 | 0.201 | 7.775 | 6.599 |
| Composition | 0.089 | 0.037 | 0.052 | 4.163 | 1.966 |
| Wage Structure | 0.037 | −0.112 | 0.149 | 3.612 | 4.633 |
| Composition Effects: | |||||
| Union | 0.016 | −0.019 | 0.035 | 0.713 | 0.639 |
| Other | 0.019 | 0.008 | 0.011 | 0.984 | 0.473 |
| Education | 0.009 | 0.013 | −0.005 | 0.665 | 0.207 |
| Occupation | 0.019 | 0.022 | −0.002 | 0.672 | 0.112 |
| Industry | 0.026 | 0.013 | 0.013 | 1.128 | 0.536 |
| Wage Structure Effects: | |||||
| Union | 0.014 | −0.002 | 0.015 | 0.442 | 0.360 |
| Other | −0.048 | −0.034 | −0.014 | −0.983 | −0.161 |
| Education | 0.015 | 0.008 | 0.007 | 1.444 | 0.188 |
| Occupation | 0.057 | −0.066 | 0.123 | 5.664 | 2.423 |
| Industry | −0.079 | −0.048 | −0.031 | −3.212 | −1.044 |
| Constant | 0.079 | 0.030 | 0.049 | 0.257 | 0.287 |
| Total Effects: | |||||
| Union | 0.030 | −0.021 | 0.051 | 1.156 | 0.998 |
| Other | −0.029 | −0.026 | −0.003 | 0.001 | 0.312 |
| Education | 0.024 | 0.022 | 0.002 | 2.110 | 0.395 |
| Occupation | 0.076 | −0.045 | 0.121 | 6.336 | 2.534 |
| Industry | −0.054 | −0.036 | −0.018 | −2.084 | −0.508 |
| Inequality Measures | 90–10 | 50–10 | 90–50 | Variance (× 100) | Gini (× 100) |
|---|---|---|---|---|---|
| Total Change | 0.125 | −0.075 | 0.201 | 7.775 | 6.599 |
| Composition | 0.090 | 0.038 | 0.052 | 4.193 | 1.966 |
| Wage Structure | 0.030 | −0.105 | 0.135 | 3.149 | 4.402 |
| Composition Effects: | |||||
| Union | 0.016 | −0.019 | 0.035 | 0.712 | 0.638 |
| Other | 0.019 | 0.009 | 0.011 | 1.007 | 0.481 |
| Education | 0.007 | 0.013 | −0.005 | 0.600 | 0.173 |
| Occupation | 0.020 | 0.022 | −0.002 | 0.719 | 0.129 |
| Industry | 0.026 | 0.013 | 0.014 | 1.155 | 0.546 |
| Specification Error | 0.002 | −0.010 | 0.012 | −0.308 | 0.175 |
| Wage Structure Effects: | |||||
| Union | 0.012 | −0.005 | 0.017 | 0.338 | 0.220 |
| Other | −0.049 | −0.026 | −0.023 | −0.871 | −0.068 |
| Education | 0.054 | 0.010 | 0.045 | 2.303 | 1.183 |
| Occupation | 0.018 | −0.075 | 0.093 | 2.872 | 1.416 |
| Industry | −0.094 | −0.030 | −0.064 | −3.852 | −1.306 |
| Constant | 0.089 | 0.022 | 0.067 | 2.359 | 2.957 |
| Reweighting Error | 0.003 | 0.002 | 0.001 | 0.125 | 0.057 |
| Total Effects: | |||||
| Union | 0.029 | −0.024 | 0.052 | 1.050 | 0.857 |
| Other | −0.029 | −0.018 | −0.012 | 0.135 | 0.413 |
| Education | 0.062 | 0.022 | 0.039 | 2.903 | 1.356 |
| Occupation | 0.038 | −0.053 | 0.091 | 3.591 | 1.545 |
| Industry | −0.068 | −0.017 | −0.051 | −2.697 | −0.760 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Firpo, S.P.; Fortin, N.M.; Lemieux, T. Decomposing Wage Distributions Using Recentered Influence Function Regressions. Econometrics 2018, 6, 28. https://doi.org/10.3390/econometrics6020028
Firpo SP, Fortin NM, Lemieux T. Decomposing Wage Distributions Using Recentered Influence Function Regressions. Econometrics. 2018; 6(2):28. https://doi.org/10.3390/econometrics6020028
Chicago/Turabian StyleFirpo, Sergio P., Nicole M. Fortin, and Thomas Lemieux. 2018. "Decomposing Wage Distributions Using Recentered Influence Function Regressions" Econometrics 6, no. 2: 28. https://doi.org/10.3390/econometrics6020028
APA StyleFirpo, S. P., Fortin, N. M., & Lemieux, T. (2018). Decomposing Wage Distributions Using Recentered Influence Function Regressions. Econometrics, 6(2), 28. https://doi.org/10.3390/econometrics6020028




