Structural Break Tests Robust to Regression Misspecification
Abstract
1. Introduction
2. Unconditional Mean and Variance Break Tests
- (i)
- and ;
- (ii)
- for some , and is -near epoch dependent of size on , i.e., with where , and is either ϕ-mixing of size or α-mixing of size .7
- (i)
- , for some ; and
- (ii)
- , for some .
3. Conditional Mean and Variance Break Tests
3.1. Correct Specification
- (i)
- , and , two positive definite (pd) matrices of constants; and
- (ii)
- for some , and is -near epoch dependent of size on , and is either ϕ-mixing of size or α-mixing of size .
3.2. Dynamic Misspecification
- (i)
- , , a pd matrix of constants;
- (ii)
- for some , and is -near epoch dependent of size on either an ϕ-mixing process of size or an α-mixing process of size ;
- (iii)
- , where is the null matrix; and
- (iv)
- , a pd matrix of constants.
- (i)
- If is constructed under heteroskedasticity,
- (ii)
- Let . If is constructed under homoskedasticity, then the result in (i) holds, with .
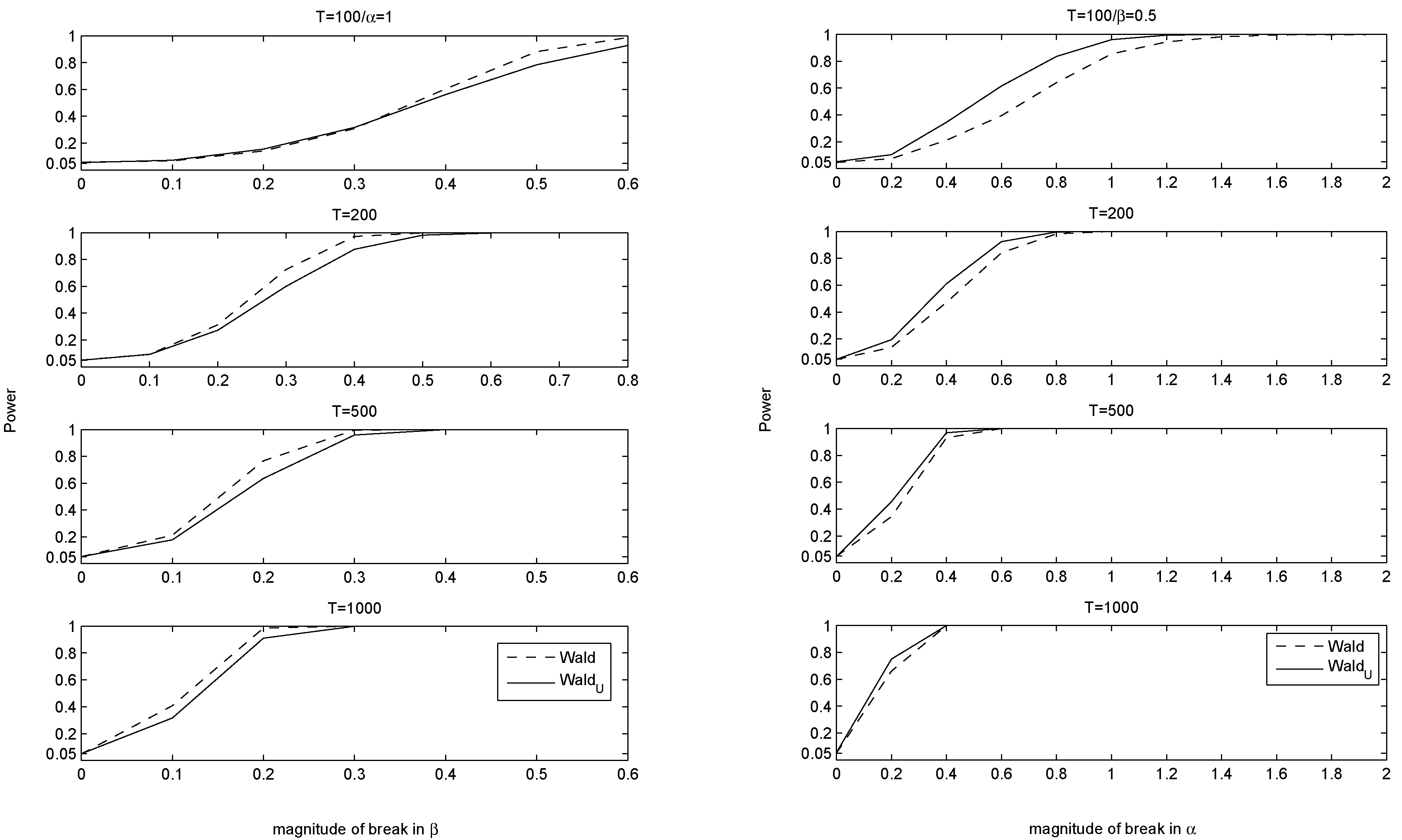
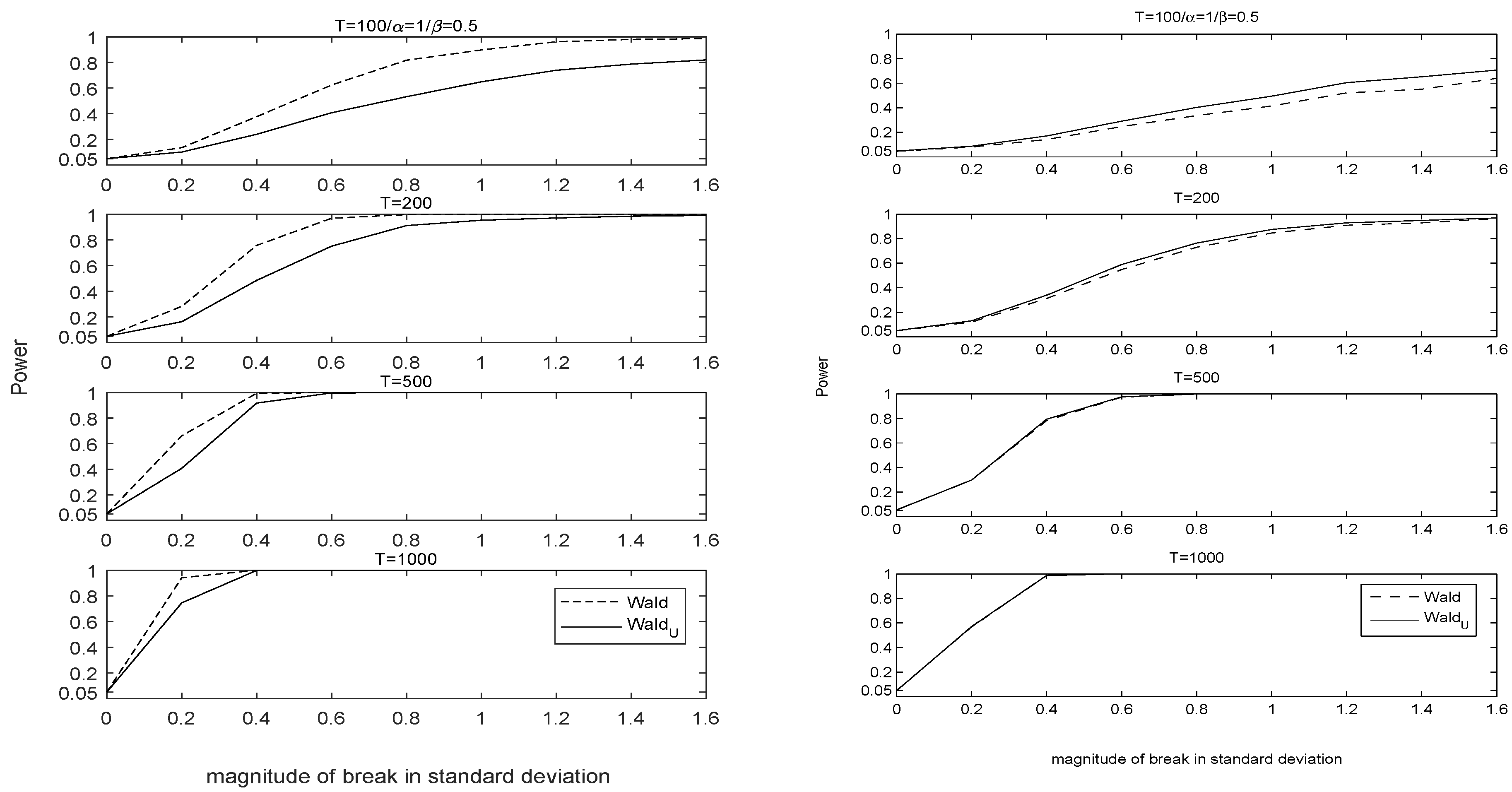
4. Simulation Results
4.1. Correct Specification and Various Misspecifications
4.2. Dynamic Misspecification
5. Empirical Illustrations
5.1. Unemployment Rate
5.2. Industrial Production Growth
5.3. Interest Rates
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proofs of Theorems 1–3
References
- Altansukh, Gantungalag. 2013. International Inflation Linkages and Forecasting in the Presence of Structural Breaks. PhD thesis, University of Manchester, Manchester, UK. Available online: https://www.research.manchester.ac.uk/portal/files/54550450/FULL_TEXT.PDF (accessed on 1 May 2015).
- Andreou, Elena, and Eric Ghysels. 2002. Detecting multiple breaks in financial market volatility dynamcis. Journal of Applied Econometrics 17: 579–600. [Google Scholar] [CrossRef]
- Andrews, Donald W. K. 1991. Heteroskedasticity and autocorrelation consistent covariance matrix estimation. Econometrica 59: 817–58. [Google Scholar] [CrossRef]
- Andrews, Donald W. K. 1993. Tests for parameter instability and structural change with unknown change point. Econometrica 61: 821–56. [Google Scholar] [CrossRef]
- Andrews, Donald W. K. 2003. Tests of parameter instability and structural change with unkown change point: A corrigendum. Econometrica 71: 395–97. [Google Scholar] [CrossRef]
- Andrews, Donald W. K., and Werner Ploberger. 1994. Optimal tests when a nuisance parameter is present only under the alternative. Econometrica 62: 1383–414. [Google Scholar] [CrossRef]
- Aue, Alexander, and Lajos Horvath. 2012. Structural breaks in time series. Journal of Time Series Analysis 34: 1–16. [Google Scholar] [CrossRef]
- Bai, Jushan, Haiqiang Chen, Terence Tai-Leung Chong, and Seraph Xin Wang. 2008. Generic consistency of the break-point estimators under specification errors in a multiple-break model. Econometrics Journal 11: 287–307. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 1998. Estimating and testing linear models with multiple structural changes. Econometrica 66: 47–78. [Google Scholar] [CrossRef]
- Bataa, Erdenebat, Denise Osborn, Marianne Sensier, and Dick van Dijk. 2013. Structural breaks in the international dynamics of inflation. Review of Economics and Statistics 95: 646–59. [Google Scholar] [CrossRef]
- Benigno, Pierpaolo, Luca Antonio Ricci, and Paolo Surico. 2015. Unemployment and productivity in the long run: The role of macroeconomic volatility. The Review of Economics and Statistics 97: 698–709. [Google Scholar] [CrossRef]
- Cho, Cheol-Keun, and Timothy J. Vogelsang. 2014. Fixed-b Inference for Testing Structural Change in a Time Series Regression. Working Paper. Available online: https://msu.edu/ tjv/cho-vogelsang.pdf (accessed on 1 May 2016).
- Chong, Terence Tai-Leung. 2003. Generic consistency of the break-point estimator under specification errors. Econometrics Journal 6: 167–92. [Google Scholar] [CrossRef]
- Davidson, James. 1994. Stochastic Limit Theory. Oxford: Oxford University Press. [Google Scholar]
- Diebold, Francis X., and Atsushi Inoue. 2001. Long memory and regime switching. Journal of Econometrics 105: 131–59. [Google Scholar] [CrossRef]
- Elliott, Graham, and Ulrich K. Müller. 2007. Confidence sets for the date of a single break in linear time series regressions. Journal of Econometrics 141: 1196–218. [Google Scholar] [CrossRef]
- Eo, Junjong, and James Morley. 2015. Likelihood-ratio-based confidence sets for the timing of structural breaks. Quantitative Economics 6: 463–97. [Google Scholar] [CrossRef]
- Garcia, Rene, and Pierre Perron. 1996. An analysis of the real interest rate under regime shifts. The Review of Economics and Statistics 78: 111–25. [Google Scholar] [CrossRef]
- Hall, Alastair R., Sanggohn Han, and Otilia Boldea. 2012. Inference regarding multiple structural changes in linear models with endogenous regressors. Journal of Econometrics 170: 281–302. [Google Scholar] [CrossRef] [PubMed]
- Hansen, Bruce E. 1991. GARCH(1,1) processes are near epoch dependent. Economics Letters 36: 181–86. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 2000. Testing for structural change in conditional models. Journal of Econometrics 97: 93–115. [Google Scholar] [CrossRef]
- Jurado, Kyle, Sydney C. Ludvigson, and Serena Ng. 2014. Measuring uncertainty. American Economic Review 105: 1177–216. [Google Scholar] [CrossRef]
- Kejriwal, Mohitosh. 2009. Tests for a mean shift with good size and monotonic power. Economic Letters 102: 78–82. [Google Scholar] [CrossRef]
- Kurozumi, Eiji, and Purevdorj Tuvaandorj. 2011. Model selection criteria in multivariate models with multiple structural changes. Journal of Econometrics 164: 218–38. [Google Scholar] [CrossRef]
- McConnell, Margaret M., and Gabriel Perez-Quiros. 2000. Output fluctuations in the United States: What has changed since the early 1980’s? American Economic Review 90: 1464–76. [Google Scholar] [CrossRef]
- McKitrick, Ross R., and Timothy J. Vogelsang. 2014. Hac robust trend comparisons among climate series with possible level shifts. Environmetrics 25: 528–47. [Google Scholar] [CrossRef]
- Müller, Ulrich K., and Mark W. Watson. 2017. Low-frequency econometrics. In Advances in Economics and Econometrics: Eleventh World Congress of the Econometric Society. Edited by Bo Honoré, Ariel Pakes, Monika Piazzesi and Larry Samuelson. Cambridge: Cambridge University Press, Volume II, pp. 53–94. [Google Scholar]
- Newey, Whitney K., and Kenneth D. West. 1994. Automatic lag selection in covariance matrix estimation. Review of Economic Studies 61: 631–53. [Google Scholar] [CrossRef]
- Perron, Pierre. 1989. The great crash, the oil price shock, and the unit root hypothesis. Econometrica 57: 1361–401. [Google Scholar] [CrossRef]
- Perron, Pierre, and Tomoyoshi Yabu. 2009. Testing for shifts in trend with an integrated or stationary noise component. Journal of Business and Economic Statistics 27: 369–96. [Google Scholar] [CrossRef]
- Pitarakis, Jean-Yves. 2004. Least squares estimation and tests of breaks in mean and variance under misspecification. Econometrics Journal 7: 32–54. [Google Scholar] [CrossRef]
- Ploberger, Werner, and Walter Krämer. 1992. The CUSUM test with OLS residuals. Economnetrica 60: 271–85. [Google Scholar] [CrossRef]
- Qu, Zhongjun, and Pierre Perron. 2007. Estimating and testing structural changes in multivariate regressions. Econometrica 75: 459–502. [Google Scholar] [CrossRef]
- Rapach, David E., and Mark E. Wohar. 2005. Regime changes in international real interest rates: Are they a monetary phenomenon? Journal of Money, Credit and Banking 37: 887–906. [Google Scholar] [CrossRef]
- Sayginsoy, Özgen, and Timothy J. Vogelsang. 2011. Testing for a shift in trend at an unknown date: A fixed-b analysis of heteroskedasticity autocorrelation robust OLS-based tests. Econometric Theory 27: 992–1025. [Google Scholar] [CrossRef]
- Sensier, Marianne, and Dick van Dijk. 2004. Testing for volatility changes in U.S. macroeconomic time series. The Review of Economics and Statistics 86: 833–39. [Google Scholar] [CrossRef]
- Smallwood, Aaron D. 2016. A Monte Carlo investigation of unit root tests and long memory in detecting mean reversion in i(0) regime switching, structural break, and nonlinear data. Econometric Reviews 35: 986–1012. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2002. Has the business cycle changed and why? NBER Macroeconomics Annual 17: 159–218. [Google Scholar] [CrossRef]
- Vogelsang, Timothy J. 1997. Wald-type tests for detecting breaks in the trend function of a dynamic time series. Econometric Theory 13, 818–48. [Google Scholar] [CrossRef]
- Vogelsang, Timothy J. 1998. Trend function hypothesis testing in the presence of serial correlation. Econometrica 66: 123–48. [Google Scholar] [CrossRef]
- Vogelsang, Timothy J. 1999. Sources of nonmonotonic power when testing for a shift in mean of a dynamic time series. Journal of Econometrics 88: 283–99. [Google Scholar] [CrossRef]
- Vogelsang, Timothy J., and Pierre Perron. 1998. Additional tests for a unit root allowing for a break in the trend function at an unknown time. International Economic Review 39: 1073–1100. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey M., and Halbert White. 1988. Some invariance principles and central limit theorems for dependent heterogeneous processes. Econometric Theory 4: 210–30. [Google Scholar] [CrossRef]
| 1 | There are a few notable exceptions. For example, Rapach and Wohar (2005) directly tested and found multiple unconditional mean shifts in international interest rates and inflation using the Bai and Perron (1998) tests. Elliott and Müller (2007) and Eo and Morley (2015) considered in their simulations a break in the unconditional mean (and variance) of a time series. Their focus was on constructing confidence sets with good coverage for small and large breaks, by inverting structural break tests. Recently, Müller and Watson (2017) proposed new methods for detecting low-frequency mean or trend changes. Our paper is different as it highlights the properties of the existing sup Wald test for a break in the unconditional and conditional mean and variance of a time series. |
| 2 | Non-stationary processes with a trend break and unit root errors, whose first-differences exhibit mean shifts with stationary errors, have been analyzed in many papers. However, as Vogelsang (1998, 1999) showed, to recover monotonic power, testing the first-differenced series for a mean shift is better than testing the level series for a trend shift. |
| 3 | The only case where our test has comparatively low power to the conditional mean test is in a correctly specified dynamic model with an intercept very close to zero. This case is further discussed in Section 3. |
| 4 | |
| 5 | Even though UM tests are not routinely used, they are a special case of the HAC-adjusted conditional break-point test in, e.g., Bai and Perron (1998), when the only regressor is an intercept. In addition, a CUSUM (cumulative sum) variant of this test for iid data is in Pitarakis (2004). As shown in Appendix A, proof of Theorem 1, for unconditional break tests, there is an explicit asymptotic relationship between the CUSUM test and the sup Wald test. However, as the Appendix shows, the conclusion of the two tests based on asymptotic critical values is in general different. Since there is strong evidence for the non-monotonic power of the CUSUM test (see, e.g., Vogelsang 1999), the paper focuses on the sup Wald test instead. |
| 6 | Note that a break in the expected absolute value of a demeaned series is not the same as a variance break only under certain conditions. |
| 7 | Here, stands for the -norm, and stands for the Euclidean norm. |
| 8 | For a proof that the most common GARCH model, GARCH(1,1), is near-epoch dependent and therefore fits our assumptions, see (Hansen 1991). |
| 9 | Simulation evidence for this statement is available from the authors upon request. |
| 10 | |
| 11 | The weights mentioned in Newey and West (1994) are set equal to one as usual for scalar cases. |
| 12 | Here, “⇒” indicates weak convergence in the Skorohod metric. |
| 13 | The simulation section shows that the CM tests are severely oversized with dynamic misspecification. |
| 14 | We extend the notation to denote stacking in a vector all columns of A, then all columns of B, one by one, in order, even when do not have the same number of rows, and we let . |
| 15 | Overspecifying the number of lags or regressors is not a problem, as the coefficients on the additional regressors or lags will converge to zero. |
| 16 | This was also mentioned in (Chong 2003), in the comments after their Theorem 3. |
| 17 | A formal proof of this statement can be found in (Hall et al. 2012, Supplemental Appendix, page 23.) |
| 18 | The unconditional mean and variance sup Wald tests require a long-run variance estimator. We report the Newey and West (1994) HAC estimator with the data dependent bandwidth therein and the Bartlett kernel, as explained in detail in Section 2. The Andrews (1991) fixed bandwidth HAC estimator leads to slightly worse performance across all tests and designs; results are available upon request from the authors. |
| 19 | For a static DGP with i.i.d. errors (DGP3, detailed below), we report the power of the tests based on asymptotic critical values rather than size-adjusted powers, because the size distortions are minor. |
| 20 | The size-adjusted powers are computed as follows: for a DGP under the alternative of one break, we take the parameter values after the break, and use these parameter values for generating the DGP under the null, which will have the same sample size as the DGP under the alternative. We simulate this null DGP and take the 95% quantile of the empirical distribution of a test statistic as the empirical critical value to be used. We then simulate the corresponding DGP under the alternative, and calculate the empirical rejection frequency using the corresponding empirical critical values. Note that, by construction, all size-adjusted power plots start at 5%, which is the corresponding empirical rejection frequency for a DGP under the null of no break using its simulated empirical 95% critical values. |
| 21 | Only for the static model in DGP3, we used 2000 simulations because they were sufficient to get accurate Monte Carlo results. |
| 22 | Note that, for DGP1, the unconditional mean of is equal to . If is close to zero regardless of t, the UM test will, by design, have little power for a break in the slope . Therefore, if a slope break is the only break of interest, it should be tested directly via the CM test for partial structural change in slopes. |
| 23 | Note that we do not plot size-adjusted powers for this DGP, and we only do so in general for correctly specified models. |
| 24 | The results are very similar for the UA and CA tests and they are available upon request. |
| 25 | Other types of model misspecifications may also affect the size and power of the (CM and CV) structural break tests. Analyzing them is beyond the scope of this paper, but further results regarding these misspecifications can be found in (Chong 2003; Pitarakis 2004), among others. |
| 26 | For one test in Table 10, the critical values are not available because this test entails 26 parameters, while critical values are available, to our knowledge, only for maximum 20 parameters. However, from (Andrews 2003), it is evident that the critical values are strictly increasing in the number of parameters, so it is reasonable to assume that the critical values for 26 parameters should be above the critical values for 20 parameters. |
| 27 | The means are: for the unemployment rate, for the interest rate, and for the industrial production growth. For the power of the UM test, the means themselves are not important as long as they are non-zero, and as long as the t-statistics for these means (also known as signal-noise ratios) reject the null hypothesis of a zero mean. |
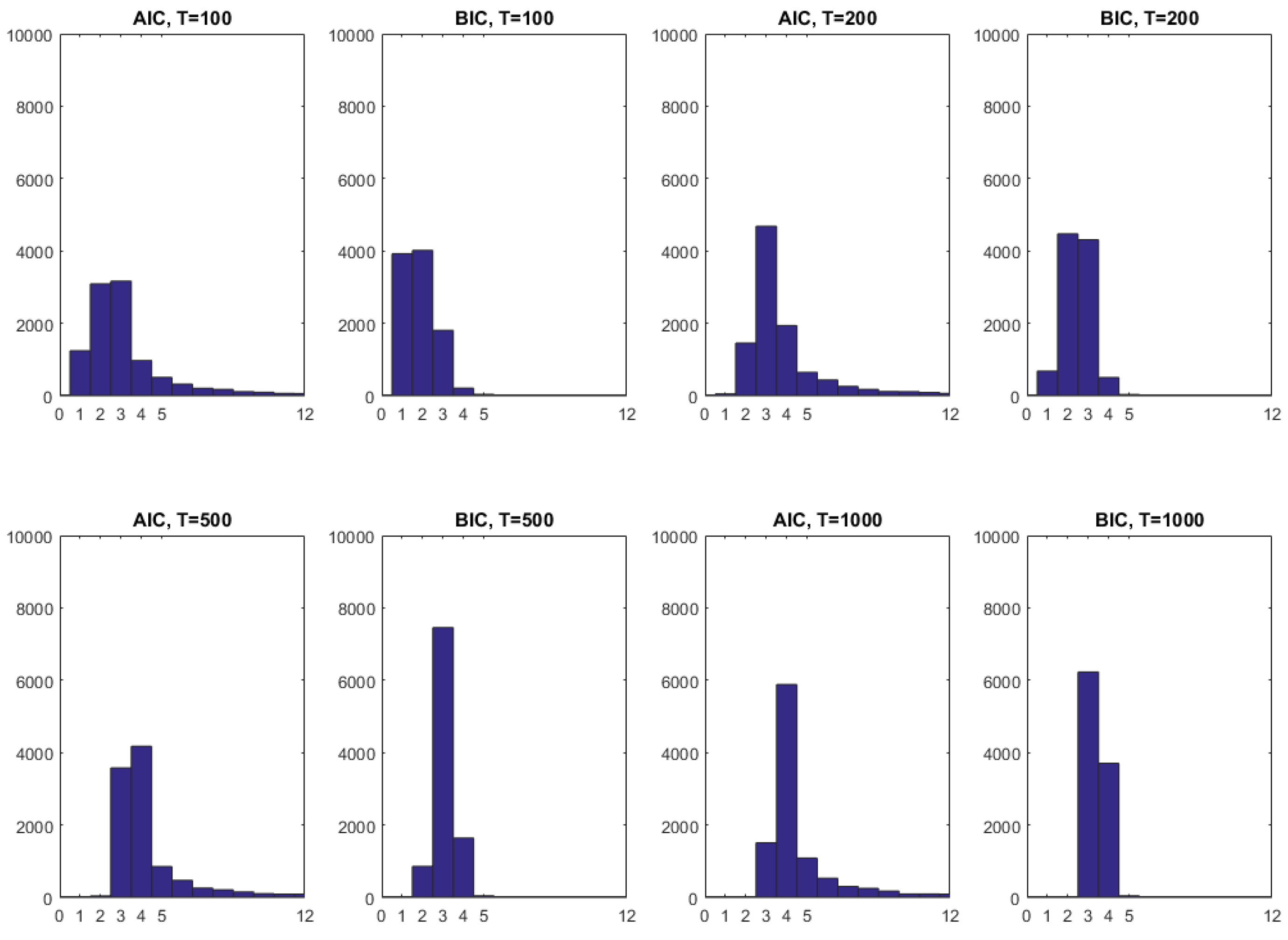
| 28 | Note that, in this case, the AIC and BIC with a maximum number of 30 lags picks the same number of lags as when a maximum of 12 lags is imposed. |
| 29 | In addition, note that the test statistic is known in statistics as a “weighted version” of the CUSUM test—see (Aue and Horvath 2012, p. 5). |










| DGP | Trim | Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T = 100 | 200 | 500 | 1000 | 100 | 200 | 500 | 1000 | ||||
| DGP1—AR(1) model, iid errors | 15% | 1 | 0.1 | 0.034 | 0.040 | 0.047 | 0.052 | 0.067 | 0.056 | 0.050 | 0.050 |
| 0.2 | 0.039 | 0.047 | 0.054 | 0.056 | 0.078 | 0.060 | 0.050 | 0.051 | |||
| 0.3 | 0.040 | 0.048 | 0.053 | 0.057 | 0.082 | 0.063 | 0.056 | 0.052 | |||
| 0.4 | 0.044 | 0.055 | 0.056 | 0.056 | 0.091 | 0.064 | 0.058 | 0.048 | |||
| 0.5 | 0.052 | 0.052 | 0.062 | 0.060 | 0.107 | 0.068 | 0.063 | 0.050 | |||
| 0.6 | 0.061 | 0.058 | 0.070 | 0.065 | 0.120 | 0.079 | 0.055 | 0.058 | |||
| 0.7 | 0.082 | 0.072 | 0.075 | 0.069 | 0.141 | 0.092 | 0.062 | 0.058 | |||
| DGP3—static model, iid errors | 15% | 1 | 0.1 | 0.067 | 0.052 | 0.060 | 0.050 | 0.075 | 0.063 | 0.059 | 0.041 |
| 0.2 | 0.073 | 0.053 | 0.049 | 0.043 | 0.086 | 0.052 | 0.054 | 0.047 | |||
| 0.3 | 0.067 | 0.056 | 0.054 | 0.052 | 0.083 | 0.062 | 0.049 | 0.049 | |||
| 0.4 | 0.084 | 0.055 | 0.049 | 0.052 | 0.091 | 0.058 | 0.042 | 0.052 | |||
| 0.5 | 0.061 | 0.053 | 0.058 | 0.051 | 0.070 | 0.056 | 0.061 | 0.051 | |||
| 0.6 | 0.058 | 0.058 | 0.046 | 0.054 | 0.080 | 0.056 | 0.044 | 0.052 | |||
| 0.7 | 0.073 | 0.056 | 0.056 | 0.055 | 0.081 | 0.059 | 0.054 | 0.048 | |||
| 0.8 | 0.063 | 0.060 | 0.047 | 0.048 | 0.079 | 0.059 | 0.051 | 0.048 | |||
| 0.9 | 0.069 | 0.062 | 0.055 | 0.050 | 0.092 | 0.065 | 0.050 | 0.052 | |||
| DGP 4—static model, AR(1) errors | 15% | 1 | 0.1 | 0.063 | 0.055 | 0.067 | 0.064 | 0.115 | 0.107 | 0.090 | 0.098 |
| 0.3 | 0.065 | 0.061 | 0.066 | 0.062 | 0.113 | 0.111 | 0.090 | 0.100 | |||
| 0.5 | 0.063 | 0.060 | 0.063 | 0.059 | 0.122 | 0.109 | 0.091 | 0.106 | |||
| 0.7 | 0.060 | 0.061 | 0.070 | 0.060 | 0.111 | 0.113 | 0.104 | 0.109 | |||
| 0.9 | 0.064 | 0.061 | 0.065 | 0.065 | 0.109 | 0.106 | 0.086 | 0.099 | |||
| DGP | Estimated Model | Trim | Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T = 100 | 200 | 500 | 1000 | 100 | 200 | 500 | 1000 | |||||
| DGP2—AR(4), iid errors | AR(1) | 15% | 1 | 0.1 | 0.157 | 0.114 | 0.114 | 0.088 | 0.427 | 0.463 | 0.486 | 0.508 |
| 0.2 | 0.191 | 0.131 | 0.132 | 0.102 | 0.493 | 0.509 | 0.531 | 0.560 | ||||
| 0.3 | 0.231 | 0.171 | 0.174 | 0.130 | 0.554 | 0.579 | 0.606 | 0.616 | ||||
| DGP2—AR(4), iid errors | AR(2) | 15% | 1 | 0.1 | 0.157 | 0.113 | 0.114 | 0.088 | 0.419 | 0.371 | 0.336 | 0.332 |
| 0.2 | 0.190 | 0.131 | 0.131 | 0.103 | 0.455 | 0.378 | 0.344 | 0.336 | ||||
| 0.3 | 0.230 | 0.170 | 0.173 | 0.129 | 0.496 | 0.421 | 0.374 | 0.358 | ||||
| DGP3—static model, iid errors | AR(1) | 15% | 1 | 0.1 | 0.067 | 0.052 | 0.060 | 0.050 | 0.067 | 0.054 | 0.053 | 0.046 |
| 0.2 | 0.073 | 0.053 | 0.049 | 0.043 | 0.067 | 0.054 | 0.047 | 0.049 | ||||
| 0.3 | 0.067 | 0.056 | 0.054 | 0.052 | 0.070 | 0.056 | 0.048 | 0.056 | ||||
| 0.4 | 0.084 | 0.055 | 0.049 | 0.052 | 0.070 | 0.053 | 0.048 | 0.052 | ||||
| 0.5 | 0.061 | 0.053 | 0.058 | 0.051 | 0.065 | 0.055 | 0.051 | 0.051 | ||||
| 0.6 | 0.058 | 0.058 | 0.046 | 0.054 | 0.074 | 0.053 | 0.049 | 0.051 | ||||
| 0.7 | 0.073 | 0.056 | 0.056 | 0.055 | 0.067 | 0.055 | 0.049 | 0.048 | ||||
| 0.8 | 0.063 | 0.060 | 0.047 | 0.048 | 0.073 | 0.054 | 0.050 | 0.051 | ||||
| 0.9 | 0.069 | 0.062 | 0.055 | 0.050 | 0.065 | 0.053 | 0.053 | 0.052 | ||||
| DGP4—static model, AR(1) errors | instead of | 15% | 1 | 0.1 | 0.063 | 0.055 | 0.067 | 0.064 | 0.207 | 0.165 | 0.111 | 0.121 |
| 0.3 | 0.065 | 0.061 | 0.066 | 0.062 | 0.204 | 0.158 | 0.120 | 0.125 | ||||
| 0.5 | 0.063 | 0.060 | 0.063 | 0.059 | 0.211 | 0.162 | 0.121 | 0.131 | ||||
| 0.7 | 0.060 | 0.061 | 0.070 | 0.060 | 0.209 | 0.160 | 0.127 | 0.128 | ||||
| 0.9 | 0.064 | 0.061 | 0.065 | 0.065 | 0.216 | 0.173 | 0.137 | 0.143 | ||||
| DGP | Trim | Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T = 100 | 200 | 500 | 1000 | 100 | 200 | 500 | 1000 | ||||
| DGP1—AR(1) model, iid errors | 15% | 1 | 1 | 0.042 | 0.052 | 0.051 | 0.059 | 0.0753 | 0.0570 | 0.050 | 0.048 |
| 1.2 | 0.042 | 0.047 | 0.051 | 0.050 | 0.0730 | 0.0533 | 0.050 | 0.048 | |||
| 1.4 | 0.039 | 0.046 | 0.050 | 0.056 | 0.0754 | 0.0584 | 0.050 | 0.052 | |||
| 1.6 | 0.040 | 0.043 | 0.052 | 0.054 | 0.0745 | 0.0517 | 0.053 | 0.047 | |||
| 1.8 | 0.040 | 0.045 | 0.052 | 0.055 | 0.0735 | 0.0543 | 0.053 | 0.051 | |||
| 2.0 | 0.040 | 0.047 | 0.052 | 0.054 | 0.0775 | 0.0572 | 0.053 | 0.052 | |||
| 2.2 | 0.041 | 0.044 | 0.054 | 0.057 | 0.0768 | 0.0592 | 0.050 | 0.051 | |||
| 2.4 | 0.043 | 0.049 | 0.054 | 0.055 | 0.0774 | 0.0595 | 0.051 | 0.048 | |||
| 2.6 | 0.043 | 0.047 | 0.052 | 0.052 | 0.0738 | 0.0581 | 0.049 | 0.048 | |||
| DGP4—static model, AR(1) errors | 15% | 1 | 1 | 0.041 | 0.051 | 0.052 | 0.057 | 0.076 | 0.067 | 0.059 | 0.060 |
| 1.2 | 0.041 | 0.049 | 0.053 | 0.055 | 0.075 | 0.067 | 0.060 | 0.058 | |||
| 1.4 | 0.042 | 0.048 | 0.053 | 0.058 | 0.076 | 0.066 | 0.060 | 0.060 | |||
| 1.6 | 0.039 | 0.047 | 0.056 | 0.054 | 0.071 | 0.064 | 0.063 | 0.056 | |||
| 1.8 | 0.041 | 0.048 | 0.056 | 0.053 | 0.077 | 0.066 | 0.063 | 0.057 | |||
| 2.0 | 0.043 | 0.048 | 0.055 | 0.057 | 0.076 | 0.062 | 0.063 | 0.061 | |||
| 2.2 | 0.039 | 0.049 | 0.058 | 0.052 | 0.073 | 0.064 | 0.063 | 0.056 | |||
| 2.4 | 0.042 | 0.053 | 0.056 | 0.054 | 0.075 | 0.072 | 0.061 | 0.057 | |||
| 2.6 | 0.045 | 0.048 | 0.053 | 0.057 | 0.072 | 0.061 | 0.058 | 0.060 | |||
| DGP | Estimated Model | Trim | Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T = 100 | 200 | 500 | 1000 | 100 | 200 | 500 | 1000 | |||||
| DGP2—AR(4) model, iid errors | AR(1) | 15% | 1 | 1 | 0.057 | 0.064 | 0.075 | 0.063 | 0.110 | 0.107 | 0.124 | 0.121 |
| 1.2 | 0.061 | 0.063 | 0.072 | 0.065 | 0.112 | 0.102 | 0.118 | 0.129 | ||||
| 1.4 | 0.059 | 0.068 | 0.072 | 0.065 | 0.116 | 0.112 | 0.119 | 0.129 | ||||
| 1.6 | 0.062 | 0.061 | 0.072 | 0.063 | 0.116 | 0.100 | 0.118 | 0.125 | ||||
| 1.8 | 0.055 | 0.056 | 0.073 | 0.067 | 0.113 | 0.104 | 0.120 | 0.125 | ||||
| 2 | 0.057 | 0.064 | 0.068 | 0.062 | 0.119 | 0.106 | 0.115 | 0.123 | ||||
| 2.2 | 0.060 | 0.063 | 0.077 | 0.064 | 0.118 | 0.099 | 0.119 | 0.122 | ||||
| 2.4 | 0.057 | 0.063 | 0.075 | 0.067 | 0.108 | 0.108 | 0.121 | 0.125 | ||||
| 2.6 | 0.062 | 0.065 | 0.074 | 0.065 | 0.111 | 0.113 | 0.116 | 0.125 | ||||
| DGP1—AR(1) model, iid errors | AR(4) | 15% | 1 | 1 | 0.042 | 0.052 | 0.051 | 0.059 | 0.075 | 0.054 | 0.047 | 0.047 |
| 1.2 | 0.042 | 0.047 | 0.051 | 0.050 | 0.075 | 0.052 | 0.048 | 0.046 | ||||
| 1.4 | 0.039 | 0.046 | 0.050 | 0.056 | 0.070 | 0.054 | 0.049 | 0.050 | ||||
| 1.6 | 0.040 | 0.043 | 0.052 | 0.054 | 0.079 | 0.052 | 0.049 | 0.046 | ||||
| 1.8 | 0.040 | 0.045 | 0.052 | 0.055 | 0.076 | 0.051 | 0.049 | 0.050 | ||||
| 2 | 0.040 | 0.047 | 0.052 | 0.054 | 0.075 | 0.056 | 0.050 | 0.050 | ||||
| 2.2 | 0.041 | 0.044 | 0.054 | 0.057 | 0.073 | 0.051 | 0.047 | 0.049 | ||||
| 2.4 | 0.043 | 0.049 | 0.054 | 0.055 | 0.074 | 0.053 | 0.048 | 0.046 | ||||
| 2.6 | 0.043 | 0.047 | 0.052 | 0.052 | 0.076 | 0.055 | 0.047 | 0.046 | ||||
| DGP3—static model, iid errors | AR(1) | 15% | 1 | 1 | 0.030 | 0.033 | 0.041 | 0.047 | 0.077 | 0.057 | 0.051 | 0.051 |
| 1.2 | 0.030 | 0.032 | 0.040 | 0.048 | 0.076 | 0.058 | 0.048 | 0.053 | ||||
| 1.4 | 0.029 | 0.032 | 0.043 | 0.047 | 0.075 | 0.055 | 0.055 | 0.051 | ||||
| 1.6 | 0.028 | 0.032 | 0.041 | 0.044 | 0.072 | 0.054 | 0.049 | 0.050 | ||||
| 1.8 | 0.028 | 0.033 | 0.039 | 0.049 | 0.071 | 0.054 | 0.047 | 0.053 | ||||
| 2 | 0.029 | 0.037 | 0.040 | 0.048 | 0.074 | 0.061 | 0.049 | 0.054 | ||||
| 2.2 | 0.029 | 0.033 | 0.040 | 0.043 | 0.080 | 0.057 | 0.049 | 0.045 | ||||
| 2.4 | 0.026 | 0.036 | 0.039 | 0.044 | 0.069 | 0.058 | 0.048 | 0.049 | ||||
| 2.6 | 0.029 | 0.032 | 0.045 | 0.045 | 0.074 | 0.055 | 0.056 | 0.050 | ||||
| DGP4—static model, AR(1) errors | instead of | 15% | 1 | 1 | 0.041 | 0.051 | 0.052 | 0.057 | 0.075 | 0.064 | 0.059 | 0.058 |
| 1.2 | 0.041 | 0.049 | 0.053 | 0.055 | 0.074 | 0.063 | 0.058 | 0.055 | ||||
| 1.4 | 0.042 | 0.048 | 0.053 | 0.058 | 0.073 | 0.064 | 0.058 | 0.058 | ||||
| 1.6 | 0.039 | 0.047 | 0.056 | 0.054 | 0.071 | 0.063 | 0.063 | 0.057 | ||||
| 1.8 | 0.041 | 0.048 | 0.056 | 0.053 | 0.070 | 0.064 | 0.060 | 0.059 | ||||
| 2 | 0.043 | 0.048 | 0.055 | 0.057 | 0.076 | 0.065 | 0.058 | 0.059 | ||||
| 2.2 | 0.039 | 0.049 | 0.058 | 0.052 | 0.069 | 0.064 | 0.063 | 0.054 | ||||
| 2.4 | 0.042 | 0.053 | 0.056 | 0.054 | 0.075 | 0.067 | 0.060 | 0.052 | ||||
| 2.6 | 0.045 | 0.048 | 0.053 | 0.057 | 0.075 | 0.060 | 0.057 | 0.058 | ||||
| DGP 2: AR(4) Model: | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 0.153 | 0.563 | 0.468 | 0.309 | 0.246 | 0.292 | 0.346 | 0.447 | 0.536 | 0.661 | |||
| 0.178 | 0.714 | 0.515 | 0.332 | 0.271 | 0.323 | 0.377 | 0.465 | 0.558 | 0.676 | |||
| 0.221 | 0.849 | 0.577 | 0.373 | 0.300 | 0.354 | 0.407 | 0.500 | 0.592 | 0.699 | |||
| 0.110 | 0.612 | 0.464 | 0.243 | 0.151 | 0.140 | 0.154 | 0.169 | 0.184 | 0.215 | |||
| 0.134 | 0.774 | 0.527 | 0.265 | 0.168 | 0.149 | 0.160 | 0.180 | 0.200 | 0.230 | |||
| 0.170 | 0.893 | 0.585 | 0.292 | 0.182 | 0.165 | 0.178 | 0.198 | 0.217 | 0.245 | |||
| 0.121 | 0.660 | 0.492 | 0.210 | 0.109 | 0.082 | 0.083 | 0.088 | 0.092 | 0.095 | |||
| 0.131 | 0.813 | 0.545 | 0.214 | 0.105 | 0.077 | 0.076 | 0.082 | 0.085 | 0.087 | |||
| 0.170 | 0.924 | 0.606 | 0.243 | 0.119 | 0.086 | 0.086 | 0.094 | 0.095 | 0.101 | |||
| 0.087 | 0.682 | 0.501 | 0.190 | 0.097 | 0.064 | 0.061 | 0.067 | 0.067 | 0.066 | |||
| 0.099 | 0.838 | 0.569 | 0.203 | 0.097 | 0.065 | 0.065 | 0.069 | 0.069 | 0.070 | |||
| 0.119 | 0.944 | 0.614 | 0.217 | 0.096 | 0.066 | 0.063 | 0.064 | 0.065 | 0.065 | |||
| DGP 2: AR(4) Model: | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 0.084 | 0.233 | 0.157 | 0.235 | 0.275 | 0.254 | 0.306 | 0.399 | 0.498 | 0.624 | |||
| 0.143 | 0.315 | 0.219 | 0.335 | 0.383 | 0.272 | 0.327 | 0.421 | 0.513 | 0.637 | |||
| 0.214 | 0.405 | 0.305 | 0.454 | 0.516 | 0.295 | 0.355 | 0.455 | 0.542 | 0.656 | |||
| 0.106 | 0.239 | 0.139 | 0.191 | 0.203 | 0.122 | 0.127 | 0.152 | 0.164 | 0.191 | |||
| 0.168 | 0.342 | 0.221 | 0.315 | 0.327 | 0.128 | 0.137 | 0.163 | 0.183 | 0.208 | |||
| 0.242 | 0.455 | 0.326 | 0.453 | 0.479 | 0.138 | 0.148 | 0.172 | 0.194 | 0.226 | |||
| 0.138 | 0.262 | 0.149 | 0.193 | 0.187 | 0.076 | 0.081 | 0.088 | 0.091 | 0.096 | |||
| 0.191 | 0.365 | 0.221 | 0.300 | 0.293 | 0.071 | 0.072 | 0.075 | 0.079 | 0.084 | |||
| 0.279 | 0.509 | 0.351 | 0.469 | 0.467 | 0.077 | 0.078 | 0.086 | 0.084 | 0.091 | |||
| 0.072 | 0.266 | 0.138 | 0.171 | 0.164 | 0.060 | 0.063 | 0.062 | 0.062 | 0.062 | |||
| 0.077 | 0.385 | 0.224 | 0.312 | 0.303 | 0.063 | 0.062 | 0.063 | 0.065 | 0.069 | |||
| 0.092 | 0.539 | 0.357 | 0.475 | 0.460 | 0.063 | 0.063 | 0.063 | 0.066 | 0.068 | |||
| Moments/Models | Trimming | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|---|
| Unconditional Mean sup Wald tests: | |||||
| 10% | 9.585 * | 9.11 | 0.892 | Oct-08 | |
| 5% | 9.585 | 9.71 | 0.892 | - | |
| Conditional Mean sup Wald tests: | |||||
| AR(1) | 10% | 11.408 | 12.17 | 0.419 | - |
| 5% | 15.494 * | 12.80 | 0.929 | Nov-10 | |
| AR(4) | 10% | 14.736 | 18.86 | 0.139 | - |
| 5% | 38.485 * | 19.57 | 0.911 | Dec-09 | |
| AR(5)—BIC | 10% | 18.205 | 20.81 | 0.121 | - |
| 5% | 36.777 * | 21.53 | 0.928 | Nov-10 | |
| AR(6)—AIC | 10% | 25.214 * | 22.62 | 0.880 | Apr-08 |
| 5% | 31.279 * | 23.41 | 0.928 | Nov-10 | |
| AR(12) | 10% | 30.343 | 32.76 | 0.879 | - |
| 5% | 56.090 * | 33.63 | 0.949 | Jan-12 | |
| DL(1) with macro factors—BIC | 10% | 13.935 | 16.91 | 0.451 | - |
| 5% | 18.612 * | 17.54 | 0.949 | Mar-09 | |
| DL(7) with macro factors—AIC | 10% | 19.665 | 37.43 | 0.619 | - |
| 5% | 25.653 | 38.35 | 0.934 | - | |
| DL(12) with uncertainty factors—AIC/BIC | 10% | 150.259 * | 32.76 | 0.173 | Mar-70 |
| 5% | 1826 * | 33.63 | 0.941 | Jan-09 | |
| Moments | Test | Trimming | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|---|---|
| Macro Factor | ||||||
| E() | 10% | 2.646 | 9.11 | 0.281 | - | |
| 5% | 2.646 | 9.71 | 0.281 | - | ||
| Macro Uncertainty Factor | ||||||
| E() | 10% | 5.214 | 9.11 | 0.898 | - | |
| 5% | 6.295 | 9.71 | 0.921 | - | ||
| Macro Factor | ||||||
| () | 10% | 4.277 | 9.11 | 0.898 | - | |
| 5% | 10.181 * | 9.71 | 0.935 | Jul-08 | ||
| Macro Uncertainty Factor | ||||||
| () | 10% | 4.969 | 9.11 | 0.898 | - | |
| 5% | 8.317 | 9.71 | 0.928 | - | ||
| Moments/Models | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|
| Unconditional Variance sup Wald tests: | ||||
| 5.011 | 9.11 | 0.447 | - | |
| Conditional Variance sup Wald tests: | ||||
| AR(1) | 15.278 * | 9.11 | 0.476 | Feb-86 |
| AR(4) | 11.948 * | 9.11 | 0.471 | Feb-86 |
| AR(5)—BIC | 13.024 * | 9.11 | 0.469 | Feb-86 |
| AR(6)—AIC | 17.660 * | 9.11 | 0.468 | Feb-86 |
| AR(12) | 14.753 * | 9.11 | 0.457 | Feb-86 |
| DL(1) with macro factors—BIC | 15.098 * | 9.11 | 0.275 | May-74 |
| DL(7) with macro factors—AIC | 15.044 * | 9.11 | 0.259 | Apr-74 |
| DL(12) with uncertainty factors—AIC/BIC | 6.375 | 9.11 | 0.415 | - |
| Moments/Models | Trimming | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|---|
| Unconditional Mean sup Wald tests: | |||||
| 10% | 3.191 | 9.11 | 0.252 | - | |
| 5% | 3.191 | 9.71 | 0.252 | - | |
| Conditional Mean sup Wald tests: | |||||
| AR(1) | 10% | 13.949 * | 12.17 | 0.401 | Jan-82 |
| 5% | 28.948 * | 12.80 | 0.933 | Feb-11 | |
| AR(3)—BIC | 10% | 19.147 * | 16.91 | 0.399 | Jan-82 |
| 5% | 22.813 * | 17.54 | 0.922 | Jul-10 | |
| AR(4) | 10% | 25.432 * | 18.86 | 0.398 | Jan-82 |
| 5% | 25.432 * | 19.57 | 0.398 | Jan-82 | |
| AR(5)—AIC | 10% | 28.486 * | 20.81 | 0.397 | Jan-82 |
| 5% | 28.486 * | 21.53 | 0.397 | Jan-82 | |
| AR(12) | 10% | 35.846 * | 32.76 | 0.392 | Feb-82 |
| 5% | 37.517 * | 33.63 | 0.924 | Sep-10 | |
| DL(12) with macro factors—AIC/BIC | 10% | 32.600 | >43.47 | 0.102 | - |
| 5% | 36.215 | >44.46 | 0.060 | - | |
| DL(1) with uncertainty factors—BIC | 10% | 11.632 | 12.17 | 0.539 | - |
| 5% | 26.729 * | 12.80 | 0.948 | May-09 | |
| DL(5) with uncertainty factors—AIC | 10% | 17.761 | 20.81 | 0.254 | - |
| 5% | 20.115 | 21.53 | 0.935 | - | |
| Moments/Models | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|
| Unconditional Variance sup Wald tests: | ||||
| 5.535 | 9.11 | 0.437 | - | |
| Conditional Variance sup Wald tests: | ||||
| AR(1) | 10.164 * | 9.11 | 0.437 | Jan-84 |
| AR(3)—BIC | 12.535 * | 9.11 | 0.433 | Jan-84 |
| AR(4) | 13.302 * | 9.11 | 0.413 | Jan-83 |
| AR(5)—AIC | 12.168 * | 9.11 | 0.411 | Jan-83 |
| AR(12) | 10.495 * | 9.11 | 0.398 | Jan-83 |
| DL(12) with macro factors—AIC/BIC | 8.267 | 9.11 | 0.442 | - |
| DL(1) with uncertainty factors—BIC | 13.318 * | 9.11 | 0.455 | Jan-84 |
| DL(5) with uncertainty factors—AIC | 10.938 * | 9.11 | 0.448 | Jan-84 |
| Moments/Models | Trimming | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|---|
| Unconditional Mean sup Wald tests: | |||||
| 10% | 15.797 * | 9.11 | 0.752 | Apr-01 | |
| 5% | 15.797* | 9.71 | 0.752 | Apr-01 | |
| Conditional Mean sup Wald tests: | |||||
| AR(1) | 10% | 57.077 * | 12.17 | 0.893 | Dec-08 |
| 5% | 57.077 * | 12.80 | 0.893 | Dec-08 | |
| AR(4) | 10% | 54.459 * | 18.86 | 0.893 | Dec-08 |
| 5% | 54.459 * | 19.57 | 0.893 | Dec-08 | |
| AR(9)—BIC | 10% | 125.086 * | 27.77 | 0.892 | Dec-08 |
| 5% | 125.086 * | 28.64 | 0.892 | Dec-08 | |
| AR(12)—AIC | 10% | 129.647 * | 32.76 | 0.891 | Dec-08 |
| 5% | 129.647 * | 33.63 | 0.891 | Dec-08 | |
| DL(1) with macro factors—AIC/BIC | 10% | 8.081 | 16.91 | 0.409 | - |
| 5% | 25.995 * | 17.54 | 0.934 | Jun-08 | |
| DL(1) with uncertainty factors—AIC/BIC | 10% | 850.945 * | 12.17 | 0.791 | Apr-01 |
| 5% | 1840 * | 12.80 | 0.942 | Jan-09 | |
| Moments/Models | Statistic Value | Critical Value | Break Fraction | Break Date |
|---|---|---|---|---|
| Unconditional Variance sup Wald tests: | ||||
| 4.852 | 9.11 | 0.409 | - | |
| Conditional Variance sup Wald tests: | ||||
| AR(1) | 21.591 * | 9.11 | 0.410 | Sep-82 |
| AR(4) | 24.721 * | 9.11 | 0.407 | Oct-82 |
| AR(9)—BIC | 20.799 * | 9.11 | 0.394 | Aug-82 |
| AR(12)—AIC | 23.787 * | 9.11 | 0.388 | Aug-82 |
| DL(1) with macro factors—AIC/BIC | 12.637 * | 9.11 | 0.433 | Aug-82 |
| DL(1) with uncertainty factors—AIC/BIC | 9.678 * | 9.11 | 0.428 | Aug-82 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abi Morshed, A.; Andreou, E.; Boldea, O. Structural Break Tests Robust to Regression Misspecification. Econometrics 2018, 6, 27. https://doi.org/10.3390/econometrics6020027
Abi Morshed A, Andreou E, Boldea O. Structural Break Tests Robust to Regression Misspecification. Econometrics. 2018; 6(2):27. https://doi.org/10.3390/econometrics6020027
Chicago/Turabian StyleAbi Morshed, Alaa, Elena Andreou, and Otilia Boldea. 2018. "Structural Break Tests Robust to Regression Misspecification" Econometrics 6, no. 2: 27. https://doi.org/10.3390/econometrics6020027
APA StyleAbi Morshed, A., Andreou, E., & Boldea, O. (2018). Structural Break Tests Robust to Regression Misspecification. Econometrics, 6(2), 27. https://doi.org/10.3390/econometrics6020027




