1. Introduction
In this paper, we consider the problem of inference for an index functional T, i.e., quantities of interest that can be written as a function of the data generating model. Given a sample and an associated distribution F such that one can assume that , we are interested in computing confidence intervals or proceeding with hypothesis testing for . For that, there exists many different approaches that are based on either or , where is the empirical distribution (hence leading to a nonparametric approach) and is a parametric model for which needs to be estimated from the sample (hence leading to a parametric approach).
As a leading example, we consider
T to be an inequality index and
F an income distribution. Inequality indices are welfare indices which can be very generally written in the following quasi-additively decomposable form (see
Cowell and Victoria-Feser (
2002,
2003) for the original formal setting)
where
is piecewise differentiable in
. The generalized entropy family of inequality indices given by
is obviously obtained by setting
For example, the cases
and
are given by
with
being the Mean Logarithmic Deviation (see
Cowell and Flachaire 2015) and
being the Theil index. A notable exception to the class in (
1) is the Gini coefficient which can be expressed in several forms, such as
with
, the cumulative income functional. Inference on
can be done in several manners:
The (nonparametric) bootstrap is a distribution-free approach that allows to derive the sample distribution of
from which quantiles (for confidence intervals) and variance (for testing) can be estimated; for application to inequality indices, see e.g.,
Mills and Zandvakili (
1997) and
Biewen (
2002).
A parametric (and asymptotic) approach, given a chosen parametric model for the data generating model, consists in first consistently estimating , say , then considering its asymptotic properties such as its variance and derive the corresponding asymptotic variance of using e.g., the delta method (based on a first order Taylor series expansion).
A parametric (finite sample) approach, given a chosen parametric model for the data generating model, consists in first consistently estimating , say , then using parametric bootstrap to derive the sample distribution of from which quantiles (for confidence intervals) and variance (for testing) can be estimated.
Refinements and combinations of these approaches.
While most would agree that the fully parametric and asymptotic approach based on the delta method cannot provide as accurate inference as the other methods, it is not clear that avoiding the specification of a parametric model is the way to go. Indeed, for example,
Cowell and Flachaire (
2015) notice that nonparametric bootstrap inference on inequality indices is sensitive to the exact nature of the upper tail of the income distribution, in that bootstrap inference is expected to perform reasonably well in moderate and large samples, unless the tails are quite heavy. Similar conclusions are also drawn in
Davidson and Flachaire (
2007);
Cowell and Flachaire (
2007);
Davidson (
2009);
Davidson (
2010) and
Davidson (
2012). This has for example motivated
Schluter and van Garderen (
2009) and
Schluter (
2012), using the results of
Hall (
1992), to propose normalizing transformations of inequality measures using Edgeworth expansions, to adjust asymptotic Gaussian approximations.
Alternatively,
Davidson and Flachaire (
2007) and
Cowell and Flachaire (
2007) consider a semi-parametric bootstrap, where bootstrap samples are generated from a distribution which combines a parametric estimate of the upper tail, namely the Pareto distribution, with a nonparametric estimate the other part of the distribution. We note that modelling the upper tail with a parametric model is common in instances were not only the interest lies in the upper tail itself but also where the data are sparse. For example, in finance, determination of the value at risk or expected shortfall is central to portfolio management, and in insurance, it is important to estimate probabilities associated with given levels of losses. A critical challenge is then to select the threshold from which the upper tail is modelled parametrically (see for example
Danielsson et al. 2001;
Guillou and Hall 2001;
Beirlant et al. 2002;
Dupuis and Victoria-Feser 2006 and the references therein).
Cowell and Flachaire (
2015) propose to use a another type of semi-parametric approach by which a mixture of lognormal distributions is first considered and then data are generated from the estimated mixture. A mixture of lognormal distributions to model the data can be thought of as a compromise between fully parametric and nonparametric estimation. The use of mixtures for income distribution estimation can be found for example in
Flachaire and Nuñez (
2007) and the references in
Cowell and Flachaire (
2015).
Through a simulation study,
Cowell and Flachaire (
2015), Table 7, compare the actual coverage probabilities of 95% confidence intervals for the Theil index, using, as data generating models, the lognormal distribution and the Singh-Maddala (SM) distribution (
Singh and Maddala 1976), with varying parameters to increase the heaviness of the tail. The different methods cited above are compared.
Cowell and Flachaire (
2015) conclude that, in the presence of very heavy-tailed distributions, even if significant improvements can be obtained on the fully asymptotic and the standard bootstrap methods, none of the alternative methods provides very good results overall.
Moreover,
Cowell and Flachaire (
2015) do not consider a parametric bootstrap and this has motivated the present paper. Namely, we study the behaviour of coverage probabilities associate to the index functional
using a parametric bootstrap based on samples generated from
(i.e., Approach 4). A parametric model introduces a form of smoothness into the inferential procedure which can lead to more accurate inference. This is for example a fundamental argument for modelling the upper tail with a Pareto distribution. Specifying a parametric distribution for the data generating process can be considered as an additional risk of introducing “error” in the inferential procedure. With income distributions, common wisdom however suggests that some parametric models are sufficiently flexible to encompass most of the data generating processes observed with real data. For example, the four parameters generalized beta distribution of second kind (GB2) proposed by (
McDonald 1984), which encompasses the generalized gamma, the Singh-Maddala and Dagum distribution (
Dagum 1977) (see also
McDonald and Xu 1995), can be considered as sufficiently general to model income data. If this is not the case, then one would wonder if the lack of flexibility of a general four parameter model is not due to a spurious amount of observations, and hence consider a robust estimation approach as proposed and motivated in
Cowell and Victoria-Feser (
1996), see also (
Cowell and Victoria-Feser 2000).
In this paper, as an alternative to the classical Maximum Likelihood Estimator (MLE), we propose a
Target Matching Estimator (TME), a member of the class of Generalized Method of Moments (GMM) estimators (
Hansen 1982), where one of the “moments” is the targeted inequality index
T. It has the advantage that for inference on
T, the scale parameter does not need to be estimated (and hence can be set to an arbitrary value), so that the estimation exercise is simpler in that the optimization is performed in a smaller dimension. We derive its asymptotic properties and compare them to the MLE when targeting
. As illustrated in a simulation study, it turns out that the finite sample coverage probabilities obtained from a parametric bootstrap based on this alternative estimator are far more accurate than the ones computed with other methods, especially with heavy tailed income distributions.
2. A Target Matching Estimator
Recall that we are interested in making inference on an inequality index
T and we assume that the sample data are generated from a (sufficiently general) parametric mode
,
. We let
be a vector of statistics of length
q, where the first element is the statistic of interest and the remaining
elements are additional statistics. We denote by
the sample vector of statistics and by
its expectation at the model
, for a fixed sample size
n. Assuming that the mapping
is bijective, a GMM estimator can be defined as
where
is positive definite
matrix of weights, possibly estimated from the sample (in that case one assumes that it converges to a non-stochastic quantity), used to adjust the statistical efficiency of
. If
cannot be obtained in an analytically tractable form, one can use instead
, or alternatively, use Monte Carlo simulations to approximate
, leading to a Simulated Method of Moments (SMM) estimator (
McFadden 1989) given by
where
and
is the
b-th vector of statistics obtained on pseudo-values simulated from
. If the number of simulation
B is infinite, then the estimators in (
6) and (
7) are equivalent, otherwise the latter is (asymptotically) less efficient.
It is computationally advantageous to have an analytic expression for
and thus prefer this approximation over
. However, in finite samples, the bias on
using
may be more important than the one resulting from using
(see
Guerrier et al. 2018). An other approach, considered for example by
Arvanitis and Demos (
2015), is to directly approximate
with expansions on analytical functions.
Given that the interest here is to make inference about a functional
T, one also needs to consider a suitable choice for the (additional) statistics in
. Obviously one needs to choose a number of statistics at least as large as the number of parameter in the assumed model, i.e.,
. If these statistics are sufficient, then
. Moreover,
T may depend only on
of the elements of
, and for this purpose, the whole estimation of
maybe an unnecessary burden. Let
where
, of dimension
is the vector of parameters that (uniquely) determines
T whereas
, of dimension
, is the vector of “nuisance parameters” that do not influence
T. Then, instead of solving (
6) or (
7), we propose to consider a
Target Matching Estimator (TME) defined as
It is known that in an homogeneous system the asymptotic covariance of
is not influenced by the weighting matrix
(supposedly independent from
) as long as
is a positive-definite matrix. Since we consider the case when the dimension of the statistics and the parameters of interest are the same, i.e.,
, taking the identity matrix for
, and assuming that the minimum of the quadratic function is attained in the interior of the parameter space
, we then have that (
8) can be equivalently written as
The generalized entropy family of measures and the Gini index are scale invariant whereas the models
usually suggested in the literature (
Kleiber and Kotz 2003) are parametrised with a scale component. Indeed, let
, an element of
, denote the scale parameter, then with the linear property of the expectation,
in (
2) is invariant to any transformation
. The same statement is true for the Gini coefficient. This is not surprising as scale-invariance is indeed one of the required property of inequality indices. We hence have
, so that
is
without the scale parameter
. Note that
may be useful in situations where the analytical form of
is not available.
More generally, suppose we are in the situation where
T is such that
and
. Also suppose that the statistics
are chosen such that
and
,
,
, then (
8) provides a suitable estimator for inference on
T. For scale invariant inequality measures
T, any statistics of the form
is also scale-invariant. This is also true with a logarithmic transformation as
Finally, for the choice of
, one can consider the GB2 (see
Section 4) which is sufficiently general to encompass real data situations with income data (
Bandourian et al. 2002). Alternatively, as suggested for example in
Cowell and Flachaire (
2015), one can also consider the SM distribution.
In the simulation
Section 4 we propose suitable statistics
that are used in (
8). Given these statistics
and an assumed data generating model
, inference about
T, using the parametric bootstrap, is obtained using Algorithm 1.
| Algorithm 1: TME-percentile confidence interval |
![Econometrics 06 00022 i001 Econometrics 06 00022 i001]() |
Note that if
is used instead of
in (
8), the last step of the optimization leading to
readily delivers
.
3. Asymptotic Properties
We now look at the asymptotic distribution of the TME in (
8). Since
is fixed but
is estimated by matching some statistics
, a crucial question is on whether
is more efficient than say
, the estimator that we would have obtained by the MLE on the whole vector
. In order to answer this question consider a setting in which the regular conditions for the MLE
to be square root-
n consistent are met. In this case, we let
denotes the Fisher information matrix evaluated at the point
, we have
This setting is clearly not the weakest possible in theory for our analysis and may be further relaxed. We do not attempt to pursue the weakest possible conditions to avoid overly technical treatments in establishing the theoretical result given in this section.
Theorem 1. Let be compact. Suppose that the point is in the interior of . Suppose that is the expectation of when n is large. If satisfies a central limit theorem with covariance matrix Ξ
, the mapping is bijective, continuously once differentiable in an open neighborhood of the point and the derivative is nonsingular at the point , then Compared to the MLE, the additional condition that the statistics
satisfy a central limit theorem is mild and generally met in practice for sample moments and the inequality indices considered here. The results on the delta method and the continuous mapping theorem of
Phillips (
2012) may be employed to refine Theorem 1 to the case where the known function
is replaced by the function evaluated by simulation
.
The asymptotic covariance matrix of
, given in Theorem 1 by
, is proportional to the inverse of the derivative of the expectation of the statistics with respect to
and the asymptotic covariance matrix of the statistics. The choice of statistics should then be guided by their sensitivity to
and their variability at the model. The same argument is found in
Heggland and Frigessi (
2004).
If the statistics
are sufficient, then the asymptotic covariance matrix of
is equivalent to the asymptotic covariance matrix of the MLE conditionally on
fixed. From the properties of the normal distribution, we have asymptotically that
where
,
denotes the partition of
corresponding to
,
for
and
for the covariances between
and
. Thus, the estimator
obtained from (
8) has a smaller variance than the unconditional MLE by a factor
. In particular, this gain could by substantial if
has a large variance. On the other hand, the gain would be null if
and
are independent as their covariances
.
Choosing “good” statistics
remains a difficult task: sufficient statistics with appropriate data reduction and with the property of being independent (asymptotically) from
may be hard to find.
Heggland and Frigessi (
2004) suggest a graphical procedure based on simulation to find statistics “sensitive enough” to the parameter of interest. In a similar context,
Gallant and Tauchen (
1996) propose to use the likelihood score function of a model “close” to the one of interest as statistics. In the present context, it could be a probability model parametrised by
only. There are however no guarantee that such a model exists, and if it does, it might be not unique.
4. Simulation Study
We consider here two parametric distributions, namely the four parameters GB2 and the three parameters SM distributions. We compare the coverage probabilities provided by the parametric bootstrap using on the one hand the MLE and on the other hand the TME approach presented in
Section 2 (using Algorithm 1) to the nonparametric bootstrap for the GB2. We also compare the coverage probabilities assuming a SM data generating process, to a variance stabilizing transform of the index proposed by
Schluter (
2012) (Varstab), the semi-parametric approach of
Davidson and Flachaire (
2007) and
Cowell and Flachaire (
2007) (Semip) and when mixtures of lognormal distributions are used to fit the density as proposed in
Cowell and Flachaire (
2015).
The GB2 has density function
where
is the beta function,
b is the scale parameter,
a,
p and
q are shape parameters. Note that here we consider
a to be positive, yet, the distribution of the inverse may be obtained by allowing
a to be negative (
McDonald and Xu 1995). Suppose we are interested in the Theil index defined in (
4), the population index, with
, is given by
where
is the gamma function and
is the digamma function. Clearly the Theil index is scale invariant, so that we set
and
.
The population values of the statistics
in (
9) are given by
and the ones for
in (
10), for
, are given by
where
is the polygamma function, i.e., the
m-th derivative of the digamma function
.
As is done in
Cowell and Flachaire (
2015), we consider the SM distribution with density
and corresponding population statistics
T,
and
,
, given by
where
is the Apéry’s constant.
Under the GB2, for generating the data, we set
,
and
. For the TME, we choose the vector of statistics to be
with
the Theil index and
given in (
10). We fix the value of the scale parameter to the arbitrary value of one (
) in Algorithm 1. We repeat the experiment
times and set the number of bootstrap replicates to
.
To solve for
in (
8) or for the MLE, we use the classical quasi-Newton optimization algorithm with starting values obtained from the differential evolution heuristic (
Storn and Price 1997), in order to mimic a real situation in which the true parameter’s values are unknown.
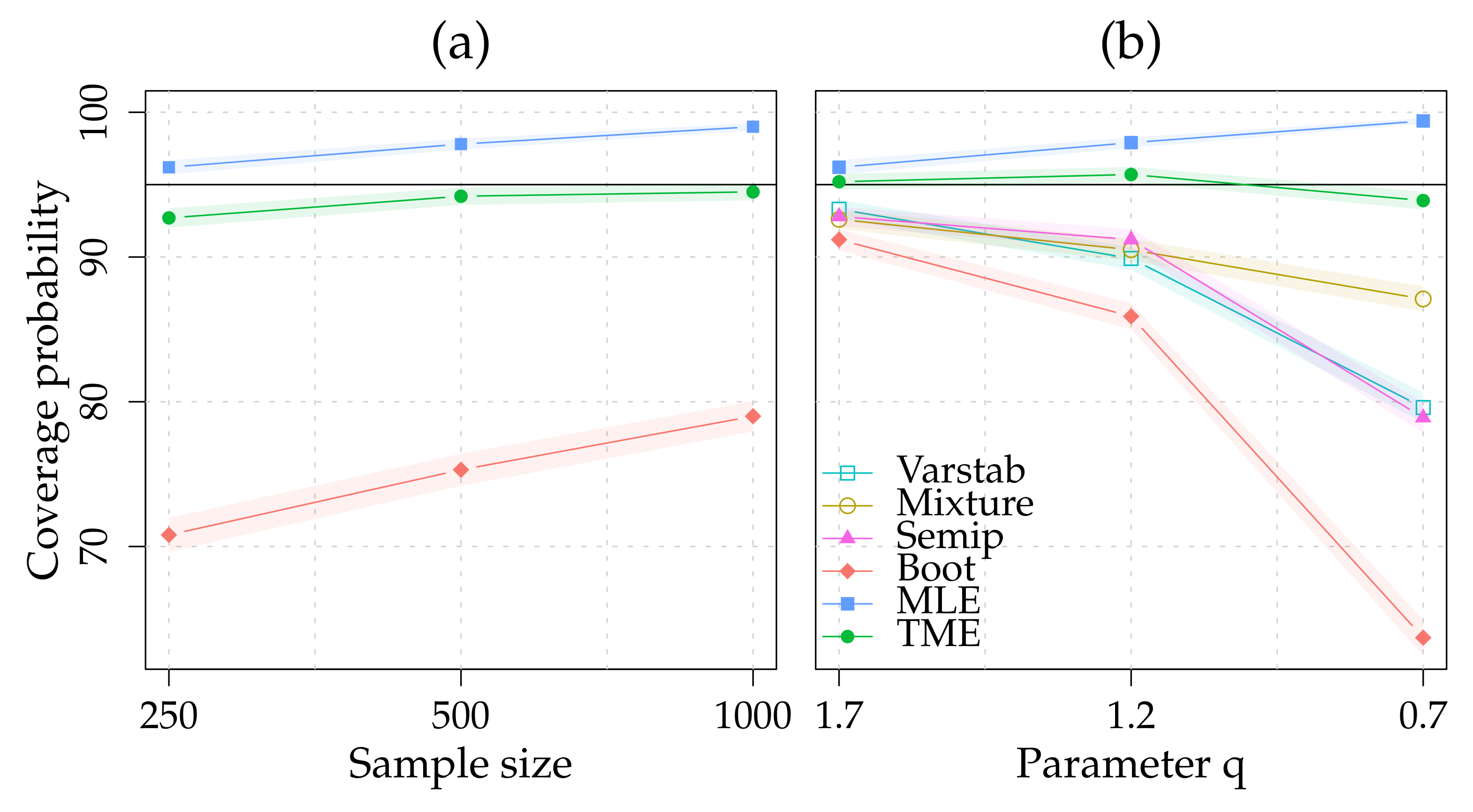
In
Table 1, we report the performances of the three approaches with respect to a nominal confidence level of 95% for the three sample sizes. As already shown in the literature (see e.g.,
Cowell and Flachaire 2015), we find poor performance for the nonparametric bootstrap (Boot), far from the nominal confidence level. The parametric bootstrap using the MLE provides reasonable finite sample coverage that are nevertheless conservatives. On the other hand, the performance of parametric bootstrap using the TME is overall satisfactory, with enhanced performance when sample size increases.
In
Table 2, we replicate the simulation study in (
Cowell and Flachaire 2015, Table 6.6), and report the values for
Varstab,
Semip and
Mixture. We have
,
and set
with
the Theil index and
given in (
10). We fix the value of the scale parameter to the arbitrary value of one (
) in Algorithm 1. We repeat the experiment
times and set the number of bootstrap replicates to
. The results reported in
Table 2 are also presented graphically in
Figure 1. Both parametric approaches present finite sample coverage probabilities that are far more accurate than the other approaches, especially in the heavy tail case. As with the GB2, the parametric bootstrap based on the MLE tends to provide conservative coverage probabilities.
5. Conclusions
In this paper, we study the finite sample accuracy of confidence intervals built via parametric bootstrap. We also propose a GMM estimator, the TME, that targets the quantity of interest, namely the considered inequality index. Its primary advantage is that the scale parameter of the assumed parametric model does not need to be estimated to perform parametric bootstrap, since inequality measures are scale invariant. The theoretical result and the simulation study suggest that this feature provides an advantage over the parametric bootstrap using the MLE and also over other established simulation-based inferential methods.
As noted by an anonymous referee, an important point that has not been directly assessed is the specification robustness, i.e., the properties of the proposed method when the assumed general model is not the exact one. This point deserves more (formal) investigation that we leave for further research.
On the more practical side, although this study is limited to two income distributions and one inequality index, the methodology presented here can be extended to other settings in a relative straightforward manner. For example, it is possible to extend the TME to include trimmed inequality indices since it suffices to use the trimmed version of
T in
. If trimming is done for robustness purposes as proposed in
Cowell and Victoria-Feser (
2003), then the other statistics in
should also be robust (see also
Victoria-Feser 2000). This is the case, for example, with trimmed moments.