Using the GB2 Income Distribution
Abstract
:1. Introduction
2. Inequality and Poverty Measures from the GB2 Distribution
2.1. Inequality Measures
2.1.1. Gini Coefficient
2.1.2. Generalized Entropy Measures
2.1.3. Atkinson Index
2.1.4. Pietra Index
2.1.5. Quintile Share Ratio
2.2. Poverty Measures
2.3. Measures of Pro-Poor Growth
3. Estimation
3.1. Estimation with Single Observations
3.2. Estimation with Grouped Data
4. Applications
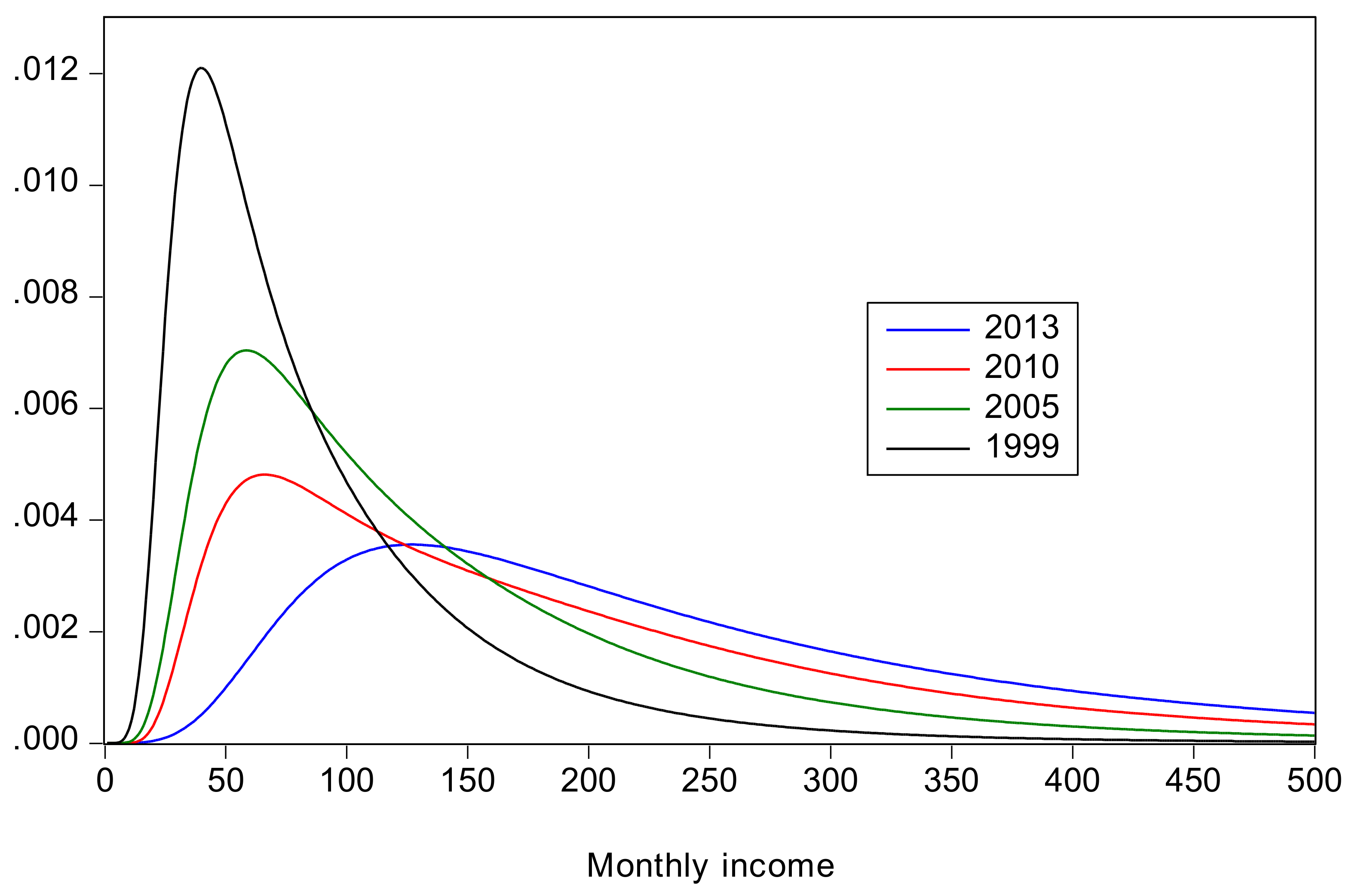
- All inequality measures indicate that inequality increased from 1999 to 2010, and then declined from 2010 to 2013. The recent decline is attributable to a decline in rural inequality; there was an increase in urban inequality in the same period. Also, there is no clear conclusion about how rural inequality changed from 1999 to 2005; the Gini and suggest a slight decrease, whereas QSR, and Pietra suggest a slight increase.
- Inequality is much greater in the combined distribution than in its components, reflecting the large discrepancy in mean incomes between the rural and urban areas. Within inequality remains greater than between inequality, however.
- The changes in inequality have been accompanied by large increases in mean income and large decreases in poverty. The decline in poverty was particularly dramatic for rural China where the headcount ratio declined from 57% in 1999 to 3.7% in 2013. Poverty in rural China is uniformly greater than that in urban China.
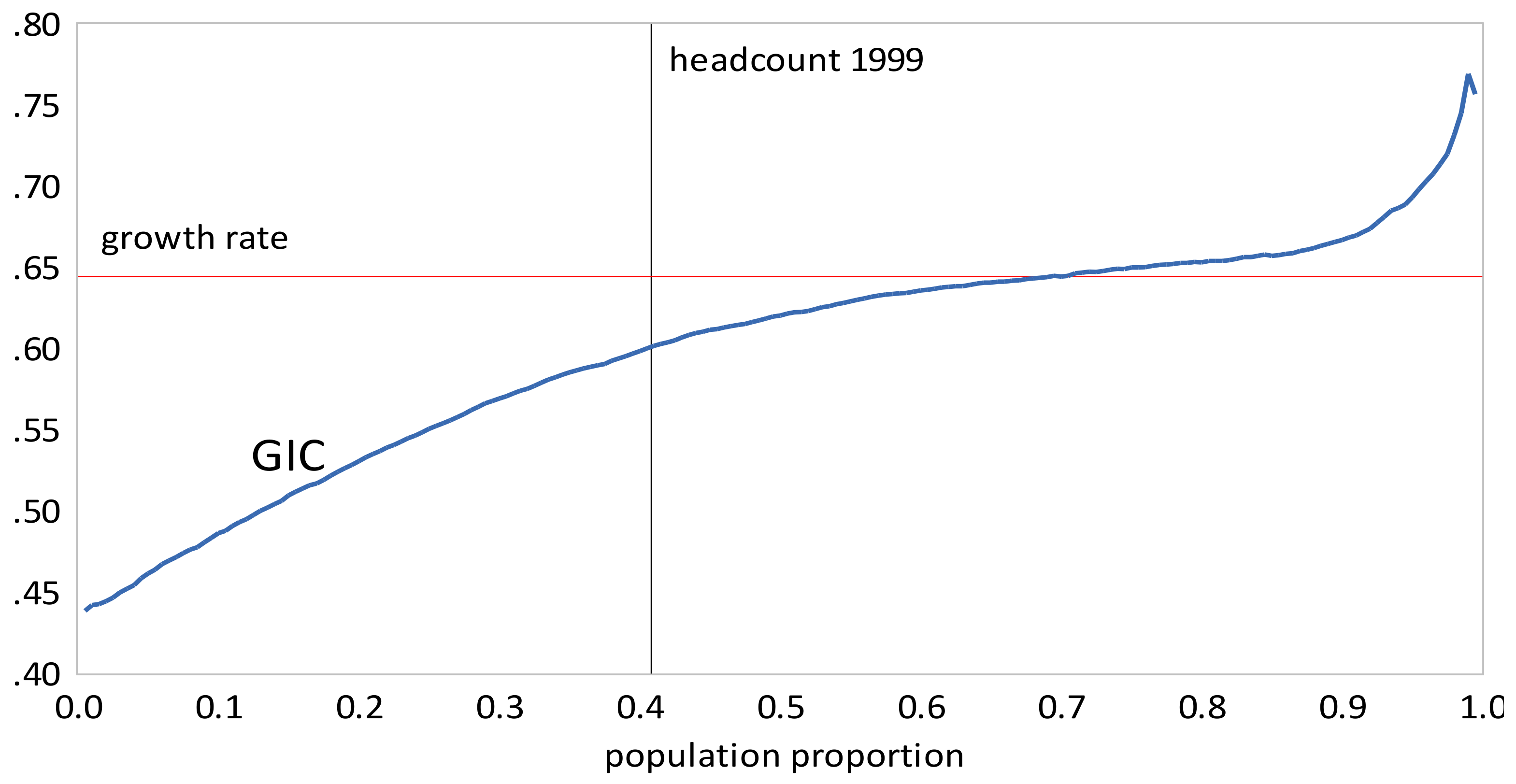
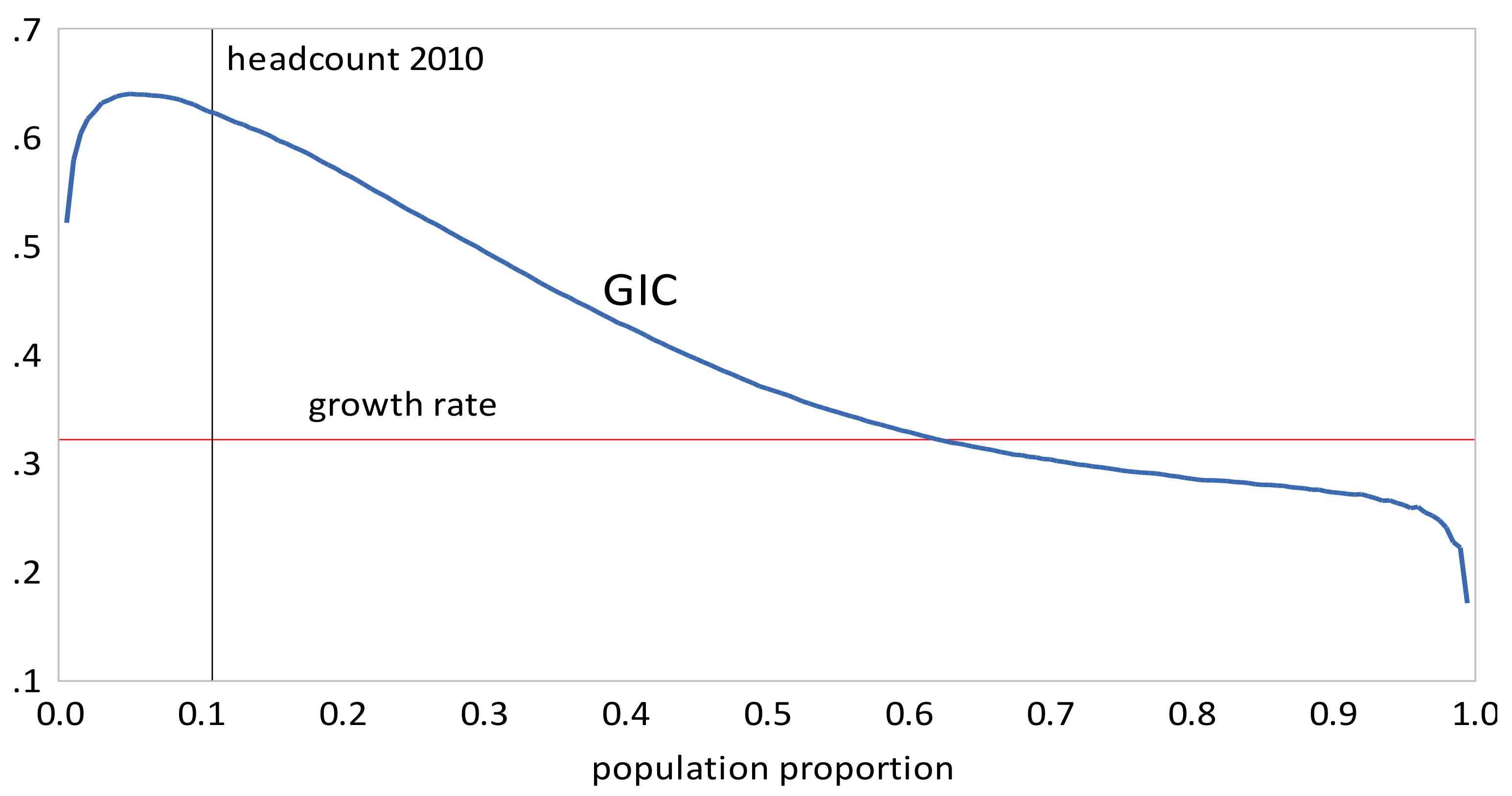
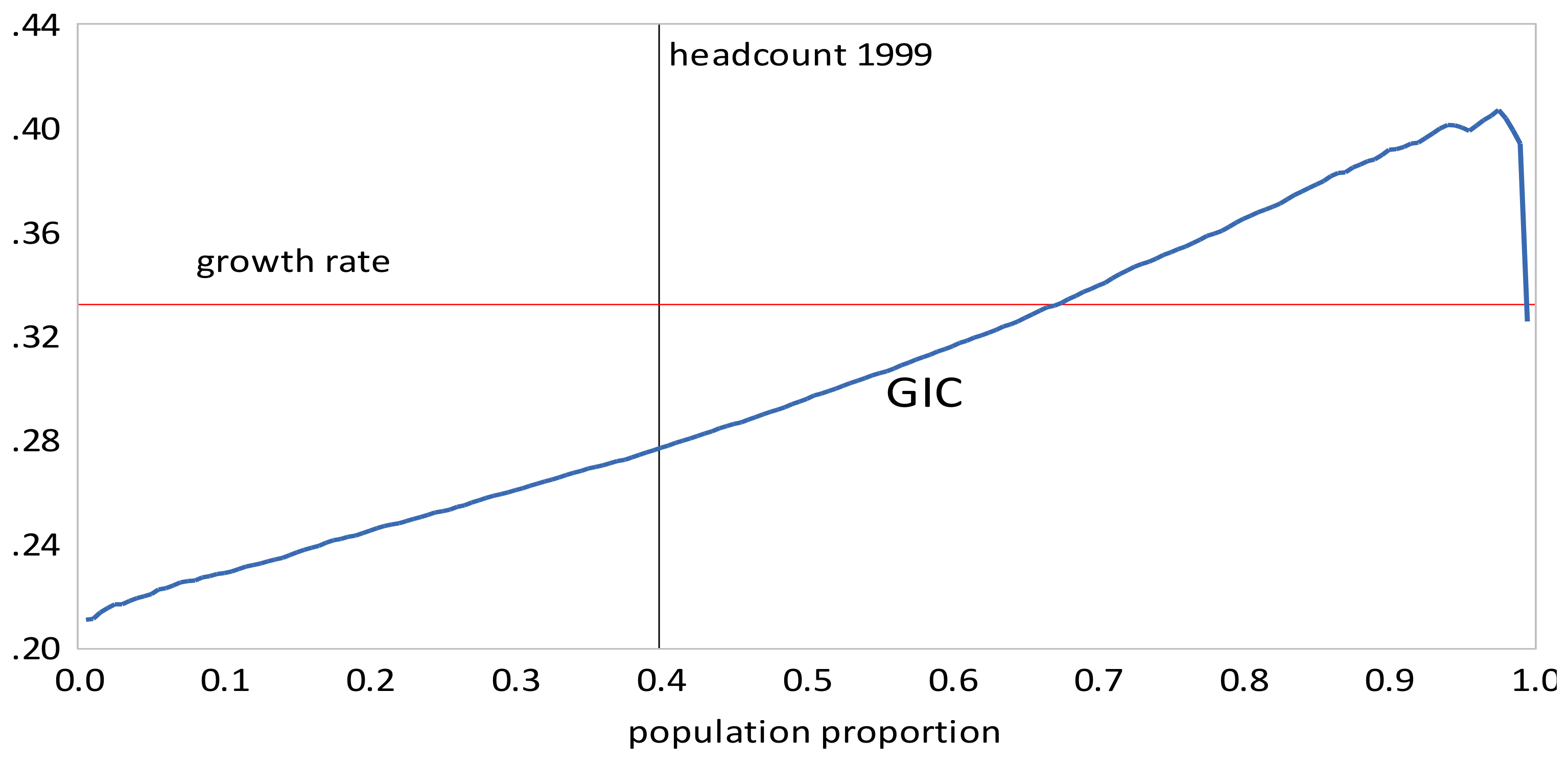
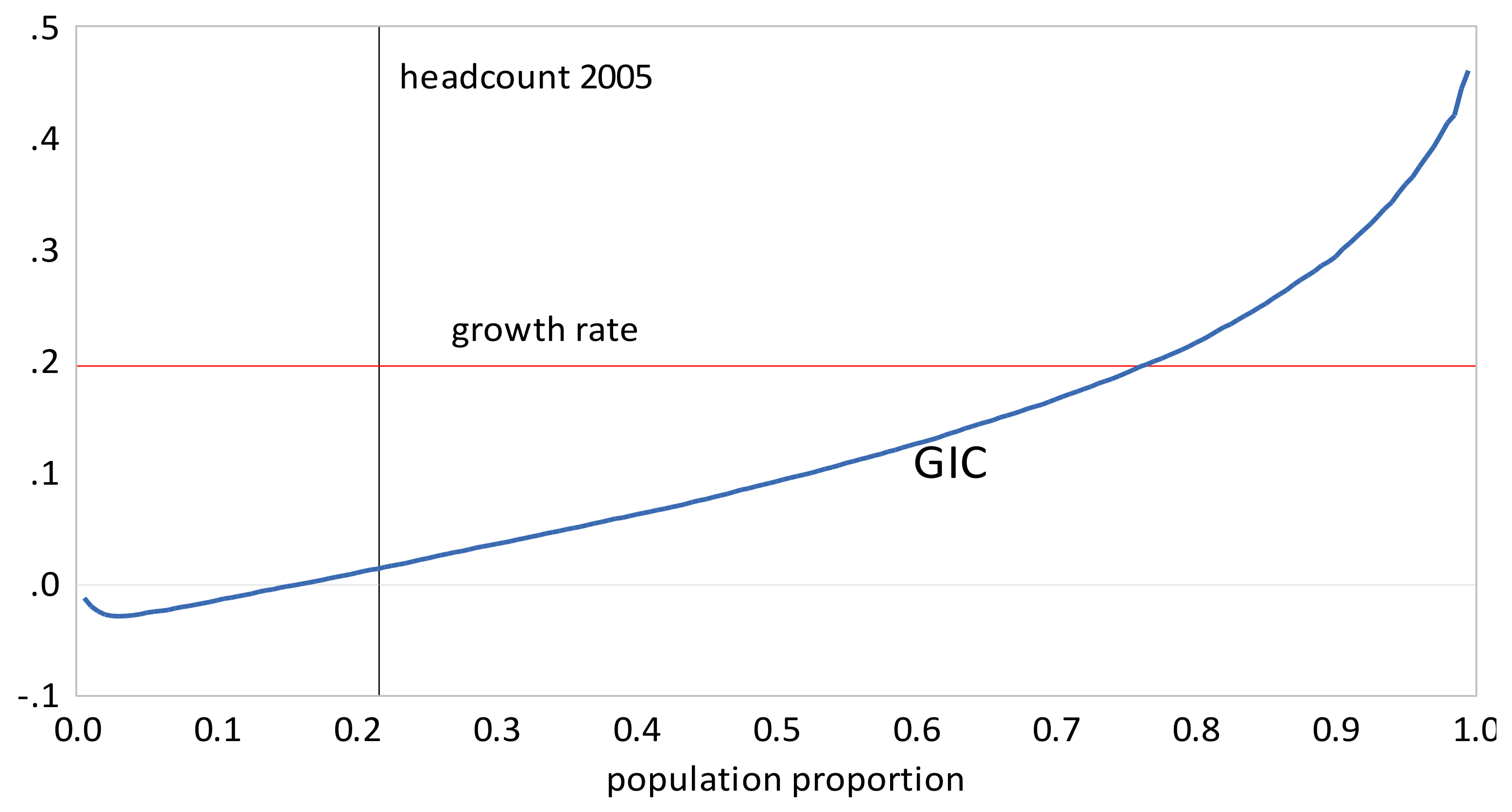
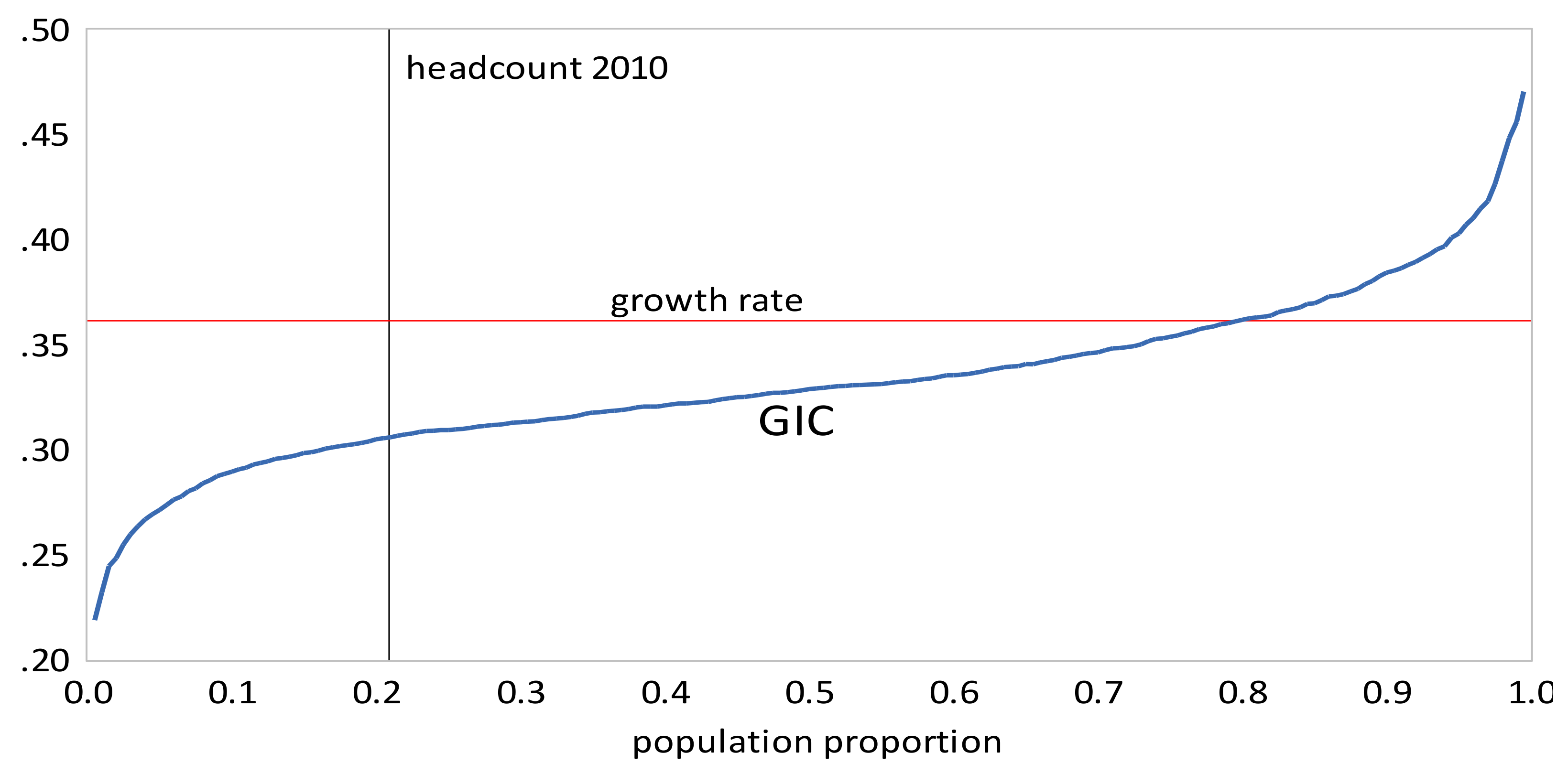
- The GIC curves show that, from 1999 to 2010, growth has favored the rich more than the poor, but from 2010 to 2013, growth has strongly favored the poor relative to the rich, a result consistent with the decline in inequality over this period. The scalar measures of pro-poor growth are also consistent with this observation. Growth has favured the poor in an absolute sense from 1999 to 2010 , , , and in a relative sense after 2010 , , .
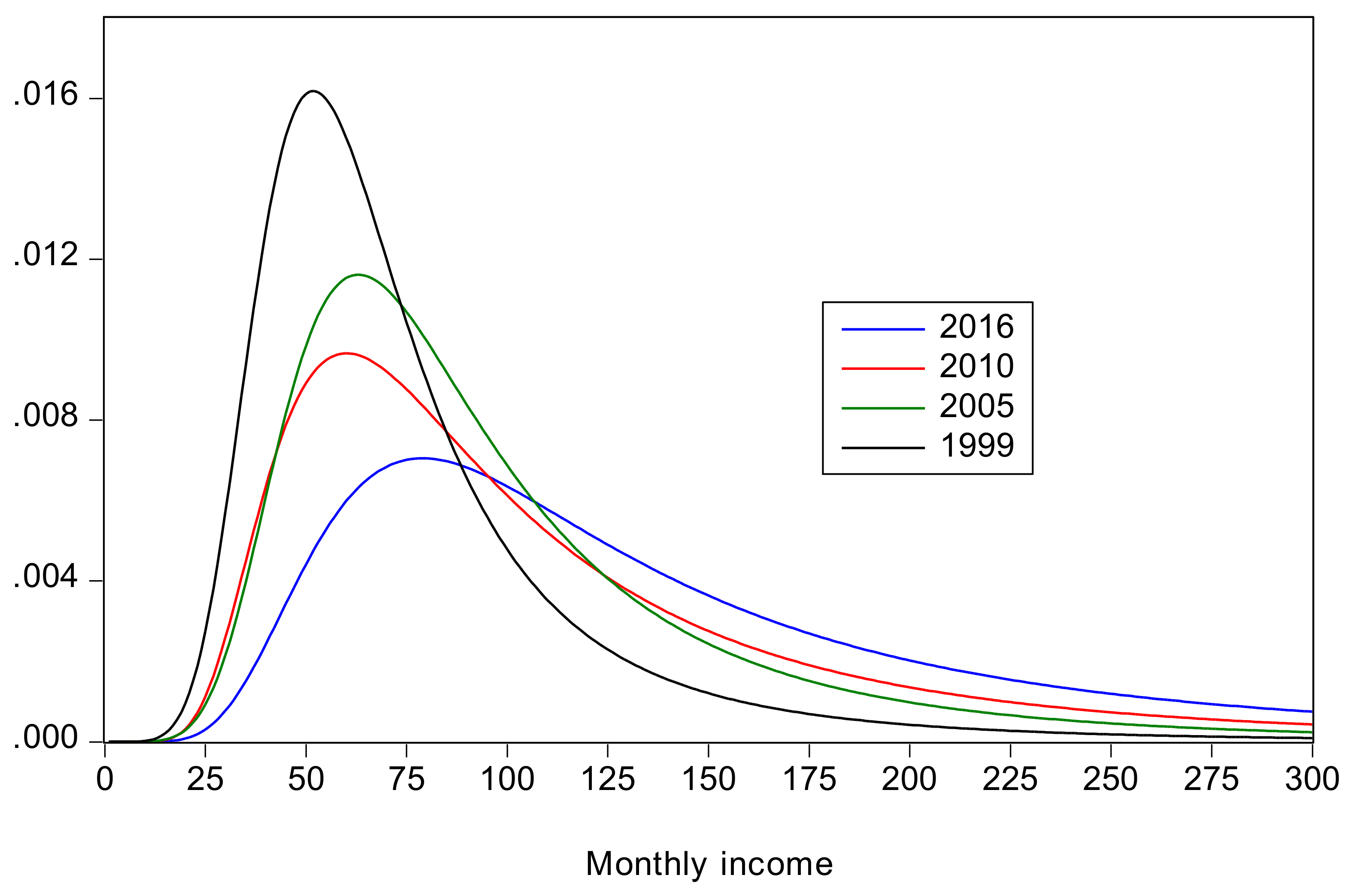
- Urban inequality changed very little from 1999 to 2005, increased dramatically from 2005 to 2010, and then increased more moderately from 2010 to 2016. Rural inequality increased from 1999 to 2010, but declined thereafter. The combined results reflect these changes, with increasing inequality overall, but with Gini coefficients approximately the same in 2010 and 2016.
- Poverty declined from 1999 to 2005, remained roughly constant from 2005 to 2010, when there were large increases in inequality, and then declined again from 2010 to 2016. From 2005 to 2010 a decline in urban poverty was offset by an increase in rural poverty.
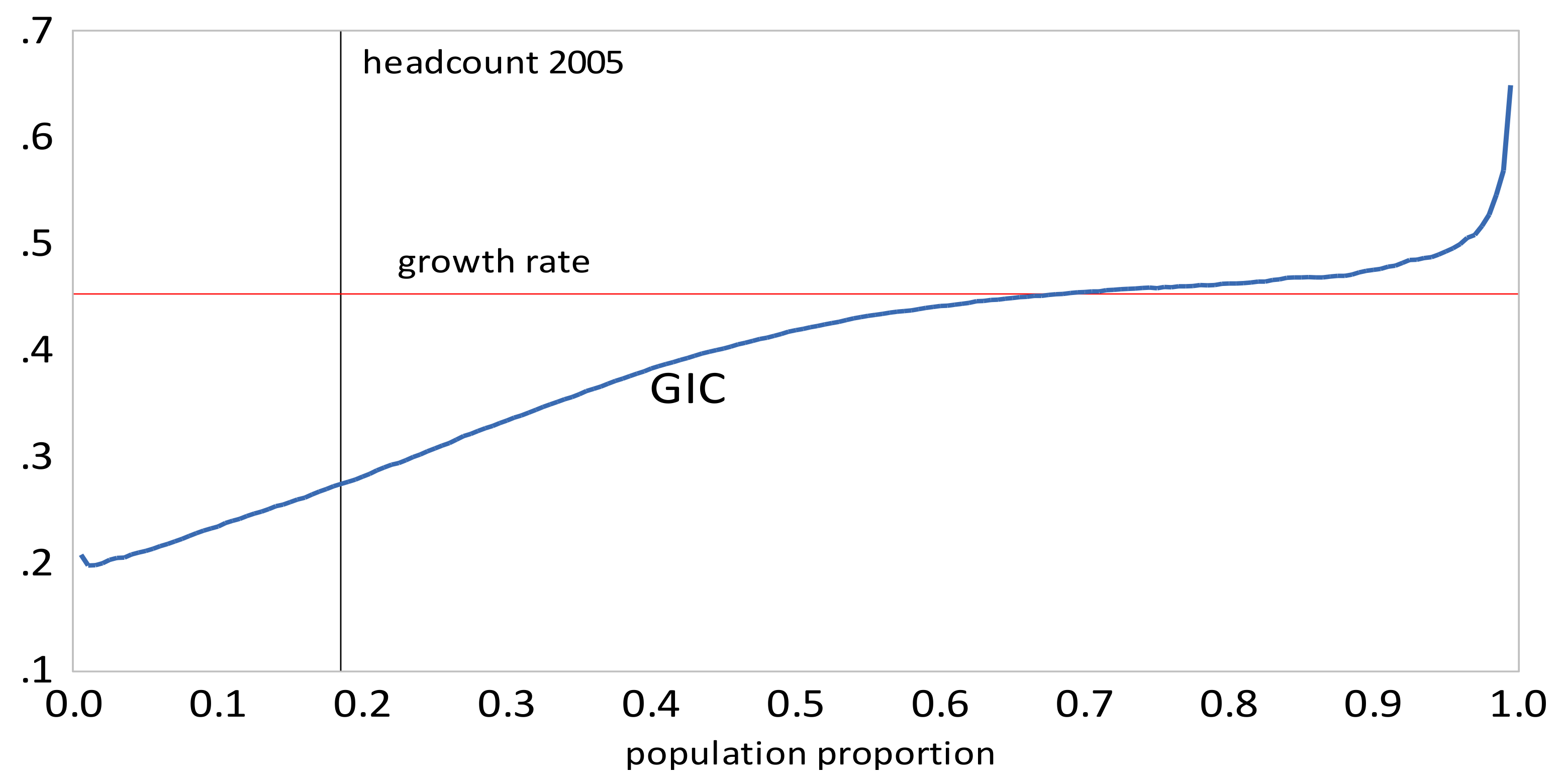
- The GIC curves show that growth has favored the rich relative to the poor in all time intervals. From 2005 to 2010 the poor faired very badly; the growth rate for the bottom 15% of the population was negative. This period was also one where the growth in mean incomes was low relative to that in the other two periods. The scalar pro-poor growth measures are in line with the conclusions from the GIC curves. Growth was absolutely but not relatively pro-poor in the first and third time intervals; in the second interval it was not absolutely pro-poor according to the RC measure, and only slightly absolutely pro-poor using the KP measure.
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Biewen, Martin, and Stephen P. Jenkins. 2005. A Framework for the Decomposition of Poverty Differences with an Application to Poverty Differences between Countries. Empirical Economics 30: 331–58. [Google Scholar] [CrossRef]
- Bordley, Robert F., James B. McDonald, and Anand Mantrala. 1997. Something New, Something Old: Parametric Models for the Size of Distribution of Income. Journal of Income Distribution 6: 91–103. [Google Scholar]
- Butler, Richard J., and James B. McDonald. 1986. Income Inequality in the U.S.: 1948–80. Research in Labor Economics 8: 85–140. [Google Scholar]
- Butler, Richard J., and James B. McDonald. 1989. Using Incomplete Moments to Measure Inequality. Journal of Econometrics 42: 109–20. [Google Scholar] [CrossRef]
- Chotikapanich, Duangkamon, ed. 2008. Modeling Income Distributions and Lorenz Curves. New York: Springer. [Google Scholar]
- Chotikapanich, Duangkamon, William Griffiths, Wasana Karunarathne, and D. S. Prasada Rao. 2013. Calculating Poverty Measures from the Generalized Beta Income Distribution. Economic Record 89: 48–66. [Google Scholar] [CrossRef]
- Chotikapanich, Duangkamon, William E. Griffiths, and D. S. Prasada Rao. 2007. Estimating and Combining National Income Distributions Using Limited Data. Journal of Business and Economic Statistics 25: 97–109. [Google Scholar] [CrossRef]
- Chotikapanich, Duangkamon, William E. Griffiths, D. S. Prasada Rao, and Vicar Valencia. 2012. Global Income Distributions and Inequality, 1993 and 2000: Incorporating Country-level Inequality Modeled with Beta Distributions. The Review of Economics and Statistics 94: 52–73. [Google Scholar] [CrossRef]
- Cummins, John, Georges Dionne, James McDonald, and B. Michael Pritchett. 1990. Applications of the GB2 Family of Distributions in Modeling Insurance Loss Processes. Insurance: Mathematics and Economics 9: 257–72. [Google Scholar] [CrossRef]
- Duclos, Jean-Yves, and Audrey Verdier-Chouchane. 2010. Analyzing Pro-Poor Growth in Southern Africa: Lessons from Mauritius and South Africa. Working Papers Series No. 115. Tunis: African Development Bank. [Google Scholar]
- Feng, Shuaizhang, Richard Burkhauser, and J. S. Butler. 2006. Levels and Long-Term Trends in Earnings Inequality: Overcoming Current Population Survey Censoring Problems Using the GB2 Distribution. Journal of Business and Economic Statistics 24: 57–62. [Google Scholar] [CrossRef]
- Foster, James, Joel Greer, and Erik Thorbecke. 1984. A Class of Decomposable Poverty Measures. Econometrica 52: 761–66. [Google Scholar] [CrossRef]
- Graf, Monique. 2009. An Efficient Algorithm for the Computation of the Gini Coefficient of the Generalised Beta Distribution of the Second Kind. In JSM Proceedings, Business and Economic Statistics Section. Alexandria: American Statistical Association, pp. 4835–43. [Google Scholar]
- Graf, Monique, and Desislava Nedyalkova. 2014. Modeling of Income and Indicators of Poverty and Social Exclusion Using the Generalized Beta Distribution of the Second Kind. Review of Income and Wealth 60: 821–42. [Google Scholar] [CrossRef]
- Greene, William H. 2012. Econometric Analysis, 7th ed. New York: Prentice Hall. [Google Scholar]
- Griffiths, William, and Gholamreza Hajargasht. 2015. On GMM Estimation of Distributions from Grouped Data. Economics Letters 126: 122–26. [Google Scholar] [CrossRef]
- Hajargasht, Gholamreza, and William E. Griffiths. 2013. Pareto-Lognormal Distributions: Inequality, Poverty, and Estimation from Grouped Income Data. Economic Modelling 33: 593–604. [Google Scholar] [CrossRef]
- Hajargasht, Gholamreza, William E. Griffiths, Joseph Brice, D. S. Prasada Rao, and Duangkamon Chotikapanich. 2012. Inference for Income Distributions Using Grouped Data. Journal of Business of Economic Statistics 30: 563–76. [Google Scholar] [CrossRef]
- Jenkins, Stephen P. 2009. Distributionally-Sensitive Inequality Indices and the GB2 Income Distribution. Review of Income and Wealth 55: 392–98. [Google Scholar] [CrossRef]
- Jones, Andrew M., James Lomas, and Nigel Rice. 2014. Applying Beta-Type Size Distributions to Healthcare Cost Regressions. Journal of Applied Econometrics 29: 649–70. [Google Scholar] [CrossRef]
- Kakwani, Nanak, and Ernesto M. Pernia. 2000. What is Pro-Poor Growth. Asian Development Review 18: 1–16. [Google Scholar]
- Kakwani, Nanak, Shahidur R. Khandker, and Hyun Son. 2004. Pro-Poor Growth: Concepts and Measurement with Country Case Studies. Working Paper No. 1. Brasilia: International Poverty Centre, United Nations Development Programme. [Google Scholar]
- Kleiber, Christian, and Samuel Kotz. 2003. Statistical Size Distributions in Economics and Actuarial Sciences. New York: John Wiley and Sons. [Google Scholar]
- McDonald, James B. 1984. Some Generalized Functions for the Size Distribution of Income. Econometrica 52: 647–63. [Google Scholar] [CrossRef]
- McDonald, James B., and Michael Ransom. 2008. The Generalized Beta Distribution as a Model for the Distribution of Income: Estimation of Related Measures of Inequality. In Modeling Income Distributions and Lorenz Curves. Edited by Duangkamon Chotikapanich. New York: Springer, pp. 147–66. [Google Scholar]
- McDonald, James B., Jeff Sorensen, and Patrick A. Turley. 2011. Skewness and Kurtosis Properties of Income Distribution Models. Review of Income and Wealth 59: 360–74. [Google Scholar] [CrossRef]
- McDonald, James B., and Yexiao J. Xu. 1995. A generalization of the beta distribution with applications. Journal of Econometrics 66: 133–52, Erratum in Journal of Econometrics 69: 427–28. [Google Scholar] [CrossRef]
- Parker, Simon C. 1999. The Generalized Beta as a Model for the Distribution of Earnings. Economics Letters 62: 197–200. [Google Scholar] [CrossRef]
- Quintano, Claudio, and Antonella D’Agostino. 2006. Studying Inequality in Income Distribution of Single-Person Households in Four Developed Countries. Review of Income and Wealth 52: 525–46. [Google Scholar] [CrossRef]
- Ravallion, Martin, and Shaohua Chen. 2003. Measuring Pro-Poor Growth. Economics Letters 78: 93–99. [Google Scholar] [CrossRef]
- Sarabia, José María, and Vanesa Jordá. 2014. Explicit Expressions of the Pietra Index for the Generalized Function for the Size Distribution of Income. Physica A 416: 582–89. [Google Scholar] [CrossRef]
- Sarabia, José María, Vanesa Jordá, and Lorena Remuzgo. 2017. The Theil Indices in Parametric Families of Income Distributions—A Short Review. Review of Income and Wealth 63: 867–80. [Google Scholar] [CrossRef]
- Sen, Amartya K. 1976. Poverty: An Ordinal Approach to Measurement. Econometrica 44: 219–31. [Google Scholar] [CrossRef]
- Theil, Henri. 1967. Economics and Information Theory. Amsterdam: North Holland. [Google Scholar]
- Watts, Harold W. 1968. An Economic Definition of Poverty. In On Understanding Poverty. Edited by Daniel P. Moyniham. New York: Basic Books, pp. 316–29. [Google Scholar]
| 1 | McDonald and Xu (1995) and McDonald and Ransom (2008) also consider a five-parameter generalized beta distribution which nests the GB2 and a GB1 distribution. |
| 2 | The Singh-Maddala distribution is also commonly known as the Burr distribution, and has been described using a variety of other names. See (Kleiber and Kotz 2003, p. 198). |
| 3 | See, for example, (Butler and McDonald 1989). |
| 4 | See McDonald and Ransom (2008) or Jenkins (2009) for derivations. Equation (4) in Jenkins (2009) should read . Sarabia et al. (2017) give details of the Theil indices for a wide range of distributions including the GB2. |
| 5 | It may be better to describe the estimators that minimize and as minimum distance estimators rather than GMM estimators because the “moment condition” for is plim not . The asymptotic distribution is the same, however. See, for example, (Greene 2012, chp. 13). |
| 6 | The version of the data that was used was downloaded on 9 March 2018 at http://iresearch.worldbank.org/PovcalNet/povOnDemand.aspx. |
| 7 | See (McDonald and Xu 1995, p. 139). |
| Country/Year | a | b | p | q | Population (Millions) | ||
|---|---|---|---|---|---|---|---|
| China rural | |||||||
| 2013 | 1.5806 | 101.3579 | 3.8613 | 2.1609 | 190.23 | 635.69 | |
| 2010 | 1.2063 | 21.4069 | 11.6780 | 2.2025 | 131.52 | 697.21 | |
| 2005 | 1.3443 | 32.0352 | 7.0416 | 2.3558 | 100.07 | 749.35 | |
| 1999 | 2.0243 | 30.1693 | 3.3733 | 1.3113 | 67.78 | 815.97 | |
| China urban | |||||||
| 2013 | 1.6455 | 261.4467 | 2.3392 | 1.9792 | 373.92 | 721.69 | |
| 2010 | 1.8842 | 187.8696 | 2.3745 | 1.5884 | 306.81 | 658.50 | |
| 2005 | 1.8294 | 144.7708 | 2.4059 | 1.7919 | 217.11 | 554.37 | |
| 1999 | 1.6302 | 95.0994 | 3.2433 | 2.5261 | 134.70 | 436.77 | |
| Indonesia rural | |||||||
| 2016 | 2.0275 | 55.8739 | 3.8536 | 1.3660 | 129.11 | 118.90 | |
| 2010 | 2.1389 | 36.6977 | 4.4602 | 1.2132 | 96.63 | 121.45 | |
| 2005 | 2.7720 | 52.1883 | 2.5501 | 1.1926 | 85.84 | 122.57 | |
| 1999 | 3.0994 | 49.6466 | 2.0371 | 1.2727 | 67.62 | 123.52 | |
| Indonesia urban | |||||||
| 2016 | 0.7417 | 0.0010 | 25,914.0 | 4.0699 | 208.00 | 142.22 | |
| 2010 | 0.9107 | 0.0094 | 15,488.0 | 3.2802 | 156.25 | 121.08 | |
| 2005 | 2.0275 | 55.8746 | 3.8535 | 1.3660 | 129.11 | 104.15 | |
| 1999 | 2.0737 | 35.6598 | 4.7873 | 1.2719 | 96.37 | 85.10 | |
| Country/Year | Gini | QSR | I(0) | I(1) | Pietra | |
|---|---|---|---|---|---|---|
| China rural | ||||||
| 2013 | 0.3349 | 5.4526 | 0.1903 | 0.2086 | 0.2424 | |
| 2010 | 0.3959 | 7.1456 | 0.2664 | 0.3189 | 0.2901 | |
| 2005 | 0.3519 | 5.8464 | 0.2097 | 0.2375 | 0.2563 | |
| 1999 | 0.3638 | 5.6579 | 0.2083 | 0.2495 | 0.2545 | |
| China urban | ||||||
| 2013 | 0.3735 | 6.5286 | 0.2291 | 0.2454 | 0.2628 | |
| 2010 | 0.3540 | 5.9757 | 0.2126 | 0.2370 | 0.2545 | |
| 2005 | 0.3436 | 5.7017 | 0.1992 | 0.2163 | 0.2460 | |
| 1999 | 0.3185 | 4.9247 | 0.1649 | 0.1731 | 0.2246 | |
| China combined | ||||||
| 2013 | 0.4010 | 8.1998 | 0.2659 | 0.2864 | 0.2874 | |
| 2010 | 0.4323 | 9.5593 | 0.3274 | 0.3451 | 0.3155 | |
| 2005 | 0.4052 | 6.4547 | 0.2796 | 0.2979 | 0.2959 | |
| 1999 | 0.3941 | 4.5101 | 0.2495 | 0.2683 | 0.2825 | |
| Indonesia rural | ||||||
| 2016 | 0.3343 | 5.2640 | 0.1912 | 0.2270 | 0.2442 | |
| 2010 | 0.3502 | 5.2808 | 0.1962 | 0.2412 | 0.2480 | |
| 2005 | 0.2756 | 3.9165 | 0.1275 | 0.1448 | 0.1980 | |
| 1999 | 0.2352 | 3.3989 | 0.1002 | 0.1087 | 0.1746 | |
| Indonesia urban | ||||||
| 2016 | 0.4154 | 7.9453 | 0.2920 | 0.3409 | 0.3044 | |
| 2010 | 0.4070 | 6.7226 | 0.2493 | 0.2930 | 0.2818 | |
| 2005 | 0.3444 | 5.2640 | 0.1912 | 0.2270 | 0.2442 | |
| 1999 | 0.3368 | 5.2471 | 0.1939 | 0.2370 | 0.2467 | |
| Indonesia combined | ||||||
| 2016 | 0.4027 | 7.6873 | 0.2737 | 0.3286 | 0.2963 | |
| 2010 | 0.4042 | 6.5792 | 0.2513 | 0.3013 | 0.2842 | |
| 2005 | 0.3297 | 4.6841 | 0.1776 | 0.2117 | 0.2357 | |
| 1999 | 0.2959 | 4.0104 | 0.1539 | 0.1879 | 0.2169 | |
| Country/Year | |||||||
|---|---|---|---|---|---|---|---|
| China combined | |||||||
| 2013 | 0.2659 | 0.2109 | 0.0550 | 0.2864 | 0.2340 | 0.0523 | |
| 2010 | 0.3274 | 0.2399 | 0.0875 | 0.3451 | 0.2622 | 0.0829 | |
| 2005 | 0.2796 | 0.2053 | 0.0743 | 0.2979 | 0.2244 | 0.0735 | |
| 1999 | 0.2495 | 0.1932 | 0.0563 | 0.2683 | 0.2101 | 0.0582 | |
| Indonesia combined | |||||||
| 2016 | 0.2737 | 0.2461 | 0.0276 | 0.3286 | 0.3019 | 0.0267 | |
| 2010 | 0.2513 | 0.2227 | 0.0286 | 0.3013 | 0.2732 | 0.0281 | |
| 2005 | 0.1776 | 0.1568 | 0.0208 | 0.2117 | 0.1910 | 0.0207 | |
| 1999 | 0.1539 | 0.1385 | 0.0154 | 0.1879 | 0.1723 | 0.0156 | |
| Country/Year | HC | FGT(1) | FGT(2) | SEN | |
|---|---|---|---|---|---|
| China rural | |||||
| 2013 | 0.0374 | 0.0070 | 0.0021 | 0.0099 | |
| 2010 | 0.2042 | 0.0489 | 0.0171 | 0.0713 | |
| 2005 | 0.2998 | 0.0786 | 0.0296 | 0.1057 | |
| 1999 | 0.5702 | 0.1907 | 0.0844 | 0.2568 | |
| China urban | |||||
| 2013 | 0.0077 | 0.0017 | 0.0006 | 0.0020 | |
| 2010 | 0.0085 | 0.0017 | 0.0005 | 0.0023 | |
| 2005 | 0.0294 | 0.0062 | 0.0021 | 0.0088 | |
| 1999 | 0.1064 | 0.0233 | 0.0080 | 0.0324 | |
| China combined | |||||
| 2013 | 0.0216 | 0.0042 | 0.0013 | 0.0083 | |
| 2010 | 0.1079 | 0.0256 | 0.0089 | 0.0496 | |
| 2005 | 0.1848 | 0.0478 | 0.0179 | 0.0901 | |
| 1999 | 0.4084 | 0.1324 | 0.0577 | 0.2289 | |
| Indonesia rural | |||||
| 2016 | 0.1267 | 0.0243 | 0.0073 | 0.0348 | |
| 2010 | 0.3033 | 0.0700 | 0.0234 | 0.0995 | |
| 2005 | 0.2917 | 0.0613 | 0.0193 | 0.0883 | |
| 1999 | 0.4647 | 0.1117 | 0.0385 | 0.1526 | |
| Indonesia urban | |||||
| 2016 | 0.0649 | 0.0122 | 0.0035 | 0.0174 | |
| 2010 | 0.1142 | 0.0221 | 0.0065 | 0.0313 | |
| 2005 | 0.1267 | 0.0243 | 0.0073 | 0.0353 | |
| 1999 | 0.3031 | 0.0700 | 0.0234 | 0.0941 | |
| Indonesia combined | |||||
| 2016 | 0.0931 | 0.0177 | 0.0052 | 0.0345 | |
| 2010 | 0.2089 | 0.0461 | 0.0150 | 0.0863 | |
| 2005 | 0.2159 | 0.0443 | 0.0138 | 0.0828 | |
| 1999 | 0.3988 | 0.0947 | 0.0324 | 0.1659 | |
| Country/Year | Growth Rate | Growth Rate for the Poor (RC) | KP | PEGR |
|---|---|---|---|---|
| China | ||||
| 2010–2013 | 0.3218 | 0.6245 | 1.4251 | 0.3245 |
| 2005–2010 | 0.4536 | 0.2331 | 0.6503 | 0.2839 |
| 1999–2005 | 0.6446 | 0.5281 | 0.8702 | 0.4504 |
| Indonesia | ||||
| 2010–2016 | 0.3614 | 0.2836 | 0.8622 | 0.2414 |
| 2005–2010 | 0.1956 | –0.0107 | 0.0709 | 0.0079 |
| 1999–2005 | 0.3323 | 0.2449 | 0.8049 | 0.2575 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chotikapanich, D.; Griffiths, W.E.; Hajargasht, G.; Karunarathne, W.; Rao, D.S.P. Using the GB2 Income Distribution. Econometrics 2018, 6, 21. https://doi.org/10.3390/econometrics6020021
Chotikapanich D, Griffiths WE, Hajargasht G, Karunarathne W, Rao DSP. Using the GB2 Income Distribution. Econometrics. 2018; 6(2):21. https://doi.org/10.3390/econometrics6020021
Chicago/Turabian StyleChotikapanich, Duangkamon, William E. Griffiths, Gholamreza Hajargasht, Wasana Karunarathne, and D. S. Prasada Rao. 2018. "Using the GB2 Income Distribution" Econometrics 6, no. 2: 21. https://doi.org/10.3390/econometrics6020021
APA StyleChotikapanich, D., Griffiths, W. E., Hajargasht, G., Karunarathne, W., & Rao, D. S. P. (2018). Using the GB2 Income Distribution. Econometrics, 6(2), 21. https://doi.org/10.3390/econometrics6020021





