A Multivariate Kernel Approach to Forecasting the Variance Covariance of Stock Market Returns
Abstract
:1. Introduction
2. Background
2.1. Notation and Terminology
2.2. Approaches to Modelling the VCM
2.3. The Role of Predictor Variables
3. Riskmetrics and HAR Models Interpreted as Kernel (Similarity) Based Forecasts
4. Methodology
4.1. Calculation of Realised Variance Covariance Matrices
4.2. Kernel Approach to Forecasting
4.3. Cross Validation Optimisation of Kernel Bandwidths
4.3.1. Cross-Validation Criterion and Setup
4.3.2. Practical Implementation
- For each of the p variables considered for inclusion in the multivariate kernel, apply cross validation to obtain the optimal bandwidth when only that variable is included in the kernel estimator. These are referred to as univariate optimised bandwidths .
- Compare the forecasting performance of the univariate optimised bandwidths from Step 1, , against from a simple moving average forecast model. Any of the p variables that fail to improve on the rolling average forecast performance by at least 1% are eliminated at this stage as it is considered to have little value for forecasting. We are left with variables used as weighting variables.
- Estimate the multivariate optimised bandwidths for the variables that are not eliminated in Step 2 by minimising the cross validation criterion in Equation (9). As opposed to Step 1 this optimisation is done simultaneously over all bandwidths.
5. Data
5.1. Stock Data
5.2. Weighting Variables
5.2.1. Matrix Comparison Variables
5.2.2. Economic Variables
6. Empirical Framework
6.1. Variations of Kernel Forecasting Models
6.2. Competing Forecasting Models
6.3. Model Confidence Sets
7. Analysis-Kernel Weights and Variables
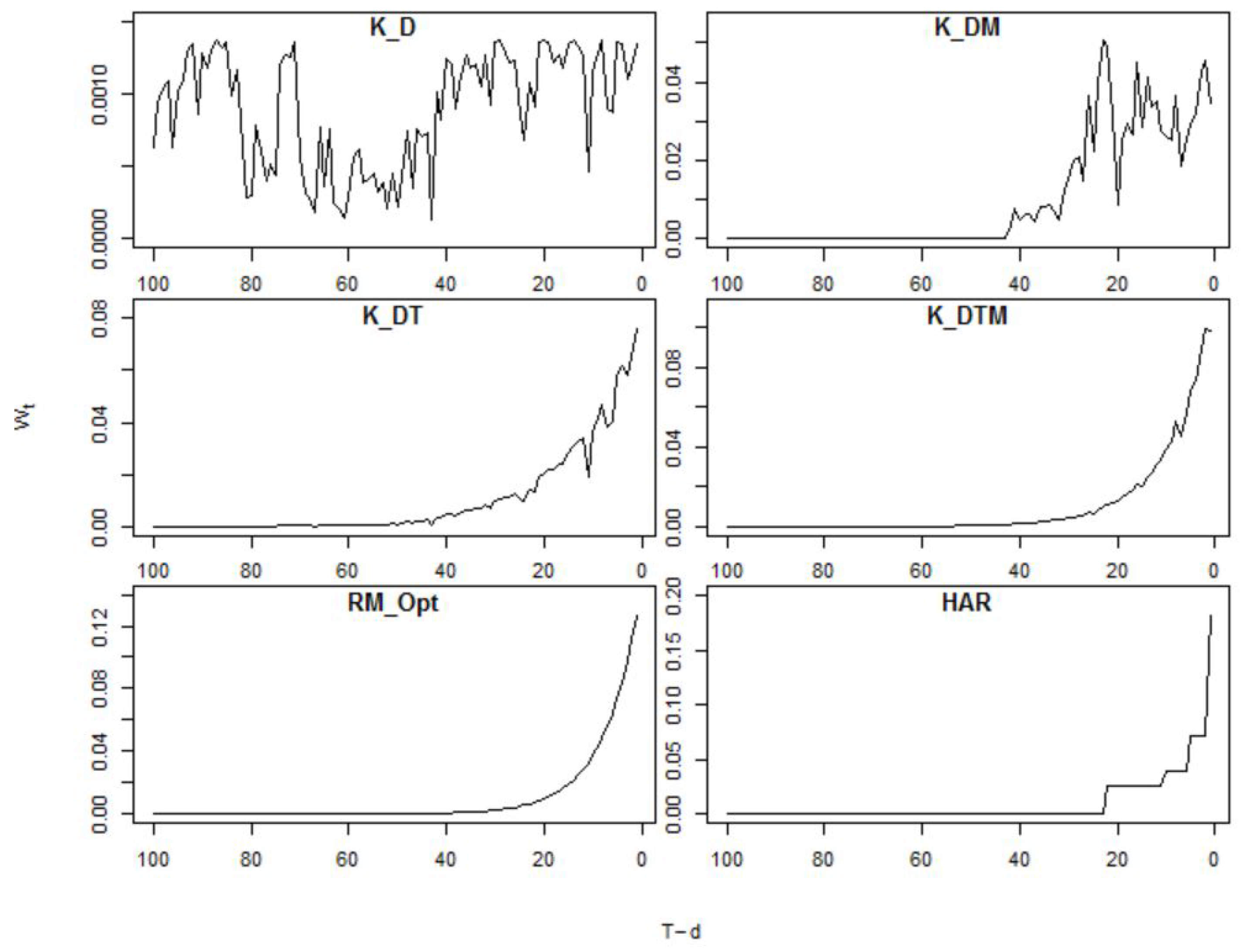
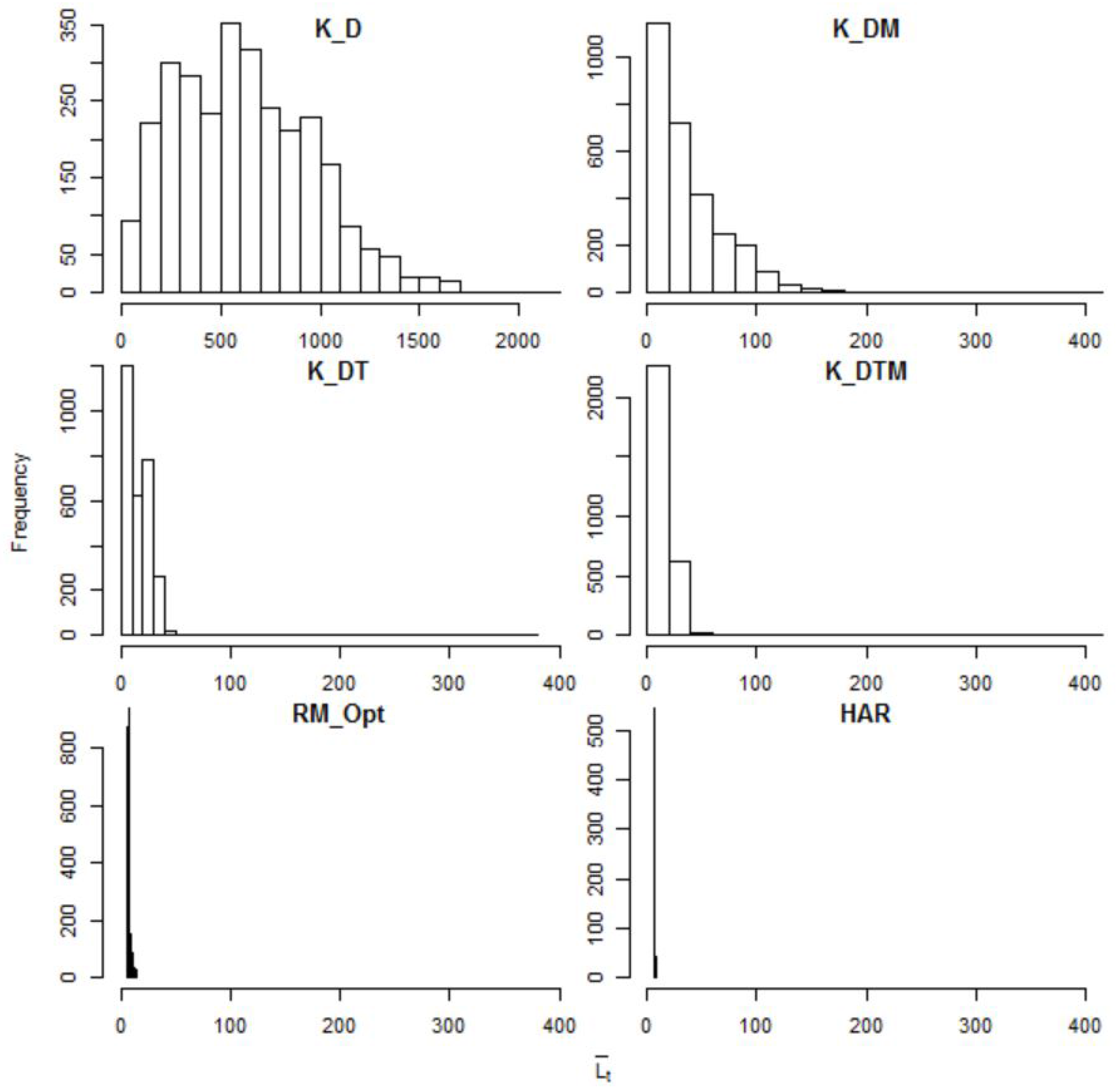
7.1. Kernel Weights
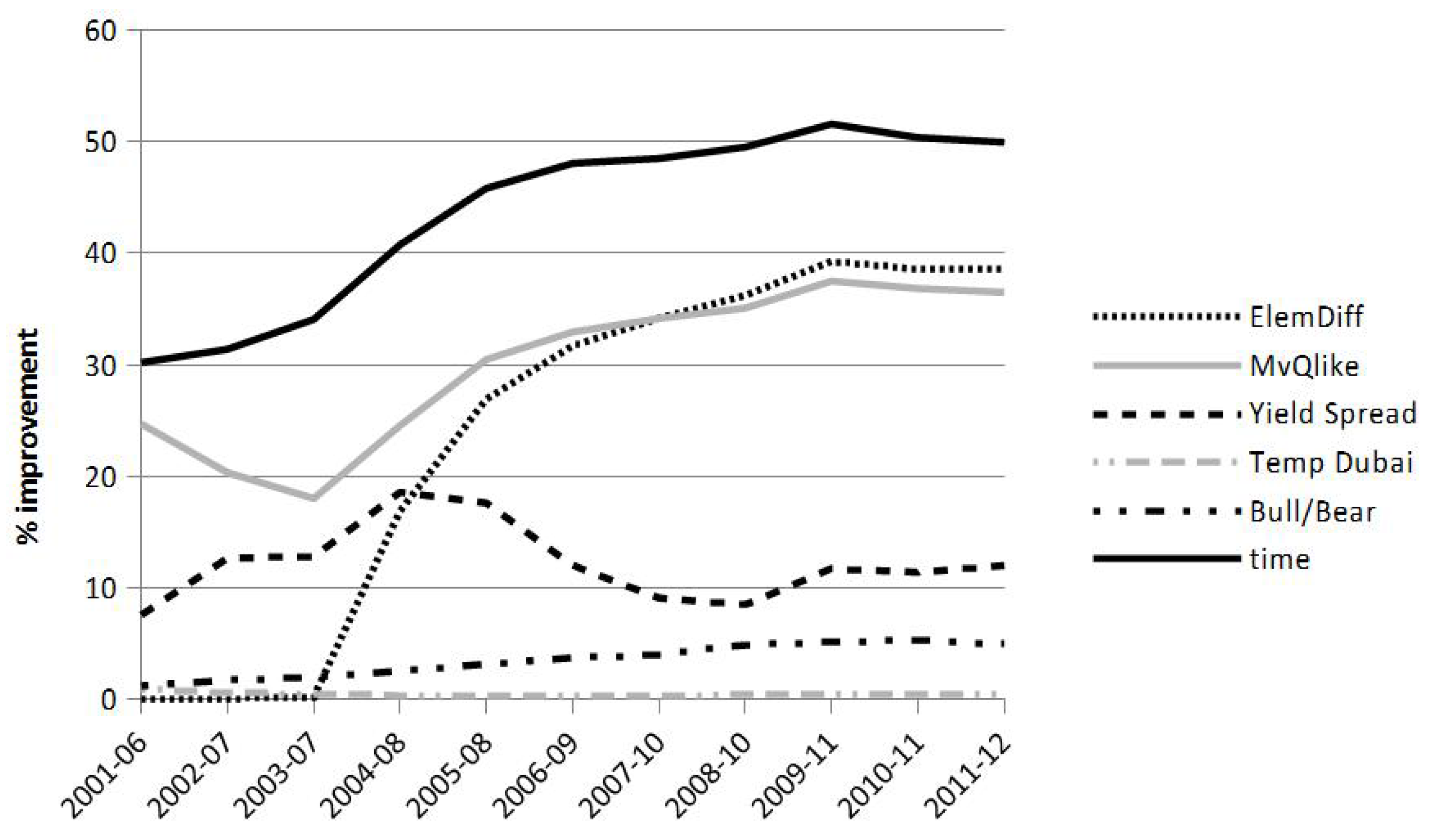
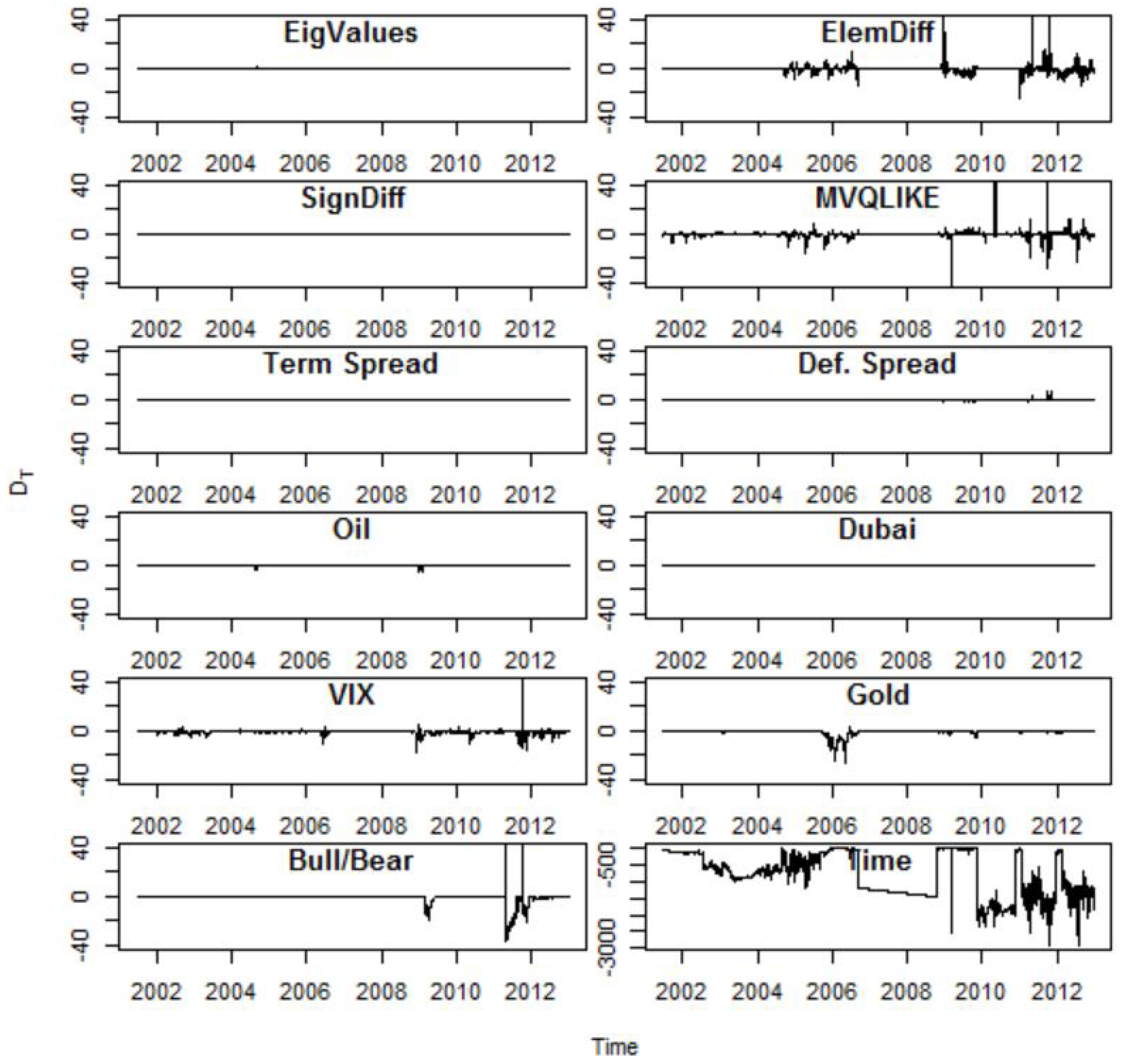
7.2. Weighting Variables
8. Analysis-Forecast Evaluation
8.1. Full-Sample Results
8.2. Sub-Sample Analysis
8.3. Results Summary
9. Conclusions and Outlook
Author Contributions
Conflicts of Interest
Appendix A. List of Stocks
| Symbol | Company | NAICS Sector |
|---|---|---|
| AA | Alcoa Inc | Manufacturing |
| AXP | American Express | Finance and Insurance |
| BA | Boeing | Manufacturing (Aerospace) |
| BAC | Bank of America | Finance and Insurance |
| BMY | Bristol-Myers Squibb | Manufacturing (Pharmaceutical) |
| CL | Colgate-Palmolive | Manufacturing (Householdand Personal Products) |
| DD | DuPont | Manufacturing (Agricultural) |
| DIS | Walt Disney | Information |
| GD | General Dynamics | Manufacturing (Aircraft) |
| GE | General Electric | Manufacturing |
| IBM | International Business Machines Corporation | Services |
| JNJ | Johnson & Johnson | Manufacturing (Pharmaceutical) |
| JPM | JPMorgan Chase | Finance and Insurance |
| KO | The Coca-Cola Company | Manufacturing (Beverages) |
| MCD | McDonald’s Corporation | Food Servics |
| MMM | 3M Company | Manufacturing (Medical) |
| PEP | PepsiCo | Manufacturing (Beverages) |
| PFE | Pfizer Inc | Manufacturing (Pharmaceutical) |
| TYC | Tyco International | Services (Security Systems) |
| WFC | Wells Fargo | Finance and Insurance |
References
- Aït-Sahalia, Yacine, and Michael W. Brandt. 2001. Variable selection for portfolio choice. The Journal of Finance 56: 1297–351. [Google Scholar] [CrossRef]
- Aitchison, J., and C. G. G. Aitken. 1976. Multivariate binary discrimination by the kernel method. Biometrika 63: 413–20. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Peter Reinhard Hansen, Asger Lunde, and Neil Shephard. 2009. Realized kernals in parctice: Trades and quotes. Econometrics Journal 12: C1–C32. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Peter Reinhard Hansen, Asger Lunde, and Neil Shephard. 2012. Multivariate realised kernals: Consistent positive semi-definite estimators of the covariation of equity prices with noise and non-synchronous trading. Journal of Econometrics 162: 149–69. [Google Scholar] [CrossRef]
- Bauer, Gregory H., and Keith Vorkink. 2011. Forecasting multivariate realized stock market volatility. Journal of Econometrics 160: 93–101. [Google Scholar] [CrossRef]
- Becker, Ralf, Adam Clements, Mark Doolan, and Stan Hurn. 2014. Selecting volatility forecasting models for portfolio allocation purposes. International Journal of Forecasting 31: 849–61. [Google Scholar] [CrossRef]
- Blair, Bevan J., Ser-Huang Poon, and Stephen J. Taylor. 2001. Forecasting S&P 100 volatility: The incremental information content of implied volatilities and high-frequency index returns. Journal of Econometrics 105: 5–26. [Google Scholar]
- Bowman, Adrian W. 1984. An alternative method of cross-validation for the smoothing of density estimates. Biometrika 71: 353–60. [Google Scholar] [CrossRef]
- Bowman, Adrian W. 1997. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations. Oxford: Clarendon Press. [Google Scholar]
- Caporin, Michael, and Massimiliano McAleer. 2012. Robust Ranking Multivariate GARCH Models by Problem Dimension: An Empirical Evaluation. Working Paper No. 815. Kyoto, Japan: Institute of Economic Research, Kyoto University. [Google Scholar]
- Campbell, John Y. 1987. Stock returns and the term structure. Journal of Financial Econometrics 18: 373–99. [Google Scholar] [CrossRef]
- Campbell, John Y., Martin Lettau, Burton G. Malkiel, and Yexiao Xu. 2001. Have individual stocks become more volatile? An empirical exploration of idiosyncratic risk. The Journal of Finance 56: 1–43. [Google Scholar] [CrossRef]
- Christensen, Kim, Silja Kinnebrock, and Mark Podolskij. 2010. Pre-averaging estimators of the ex-post covariance matrix in noisy diffusion models with non-synchronous data. Journal of Econometrics 159: 116–33. [Google Scholar] [CrossRef]
- Clements, Adam E., Stan Hurn, and Ralf Becker. 2011. Semi-Parametric Forecasting of Realized Volatility. Studies in Nonlinear Dynamics & Econometrics 15: 1–21. [Google Scholar]
- Chiriac, Roxana, and Valeri Voev. 2011. Modelling and forecasting multivariate realized volatility. Journal of Applied Econometrics 26: 922–47. [Google Scholar] [CrossRef]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 1–23. [Google Scholar] [CrossRef]
- Engle, Robert F., Eric Ghysels, and Bumjean Sohn. 2013. Stock market volatility and macroeconomic fundamentals. The Review of Economics and Statistics 95: 776–97. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kevin Sheppard. 2001. Theoretical and Empirical Properties of Dynamic Conditional Correlation Multivariate GARCH. NBER Working Paper No. 8554. Cambridge, MA, USA: NBER. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 1989. Business conditions and expected returns on stocks and bonds. Journal of Financial Economics 25: 23–49. [Google Scholar] [CrossRef]
- Fleming, Jeff, Chris Kirby, and Barbara Ostdiek. 2003. The economic value of volatility timing using ’realized’ volatility. Journal of Financial Economics 67: 473–509. [Google Scholar] [CrossRef]
- Gijbels, Itzhak, Alun Lloyd Pope, and M. P. Wand. 1999. Understanding exponential smoothing via kernel regression. Journal of the Royal Statistical Society 61: 39–50. [Google Scholar] [CrossRef]
- Gilboa, Itzhak, Offer Lieberman, and David Schmeidler. 2006. Empirical similarity. The Review of Economics and Statistics 88: 433–44. [Google Scholar] [CrossRef]
- Gilboa, Itzhak, Offer Lieberman, and David Schmeidle. 2011. A similarity-based approach to prediction. Journal of Econometrics 162: 124–31. [Google Scholar] [CrossRef]
- Golosnoy, Vasyl, Alain Hamid, and Yarema Okhrin. 2014. The empirical similarity approach for volatility prediction. Journal of Banking & Finance 40: 321–29. [Google Scholar] [CrossRef]
- Golosnoy, Vasyl, Alain Hamid, and Yarema Okhrin. 2012. The conditional autoregressive Wishart model for multivariate stock market volatility. Journal of Econometrics 167: 211–23. [Google Scholar] [CrossRef]
- Hamilton, James D., and Gang Lin. 1996. Stock market volatility and the business cycle. Journal of Applied Econometrics 11: 573–93. [Google Scholar] [CrossRef]
- Hamilton, James D. 1996. This is what happened to the oil price-macroeconomy relationship. Journal of Monetary Economics 38: 215–20. [Google Scholar] [CrossRef]
- Hansen, R. P., and A. Lunde. 2007. MULCOM 1.00, Econometric toolkit for multiple comparisons. (Packaged with Mulcom package). Unpublished. [Google Scholar]
- Hansen, Peter Reinhard, Asger Lunde, and James M. Nason. 2003. Choosing the best volatility models: the model confidence set approach. Oxford Bulletin of Economics and Statistics 65: 839–61. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 1989. Time-varying conditional covariance in tests of asset pricing models. Journal of Financial Economics 24: 289–317. [Google Scholar] [CrossRef]
- Harvey, Campbell R. 1991. The Specification Of Conditional Expectations. Working Paper. Durham, NC, USA: Duke University. [Google Scholar]
- Heiden, Moritz D. 2015. Pitfalls of the Cholesky Decomposition for Forecasting Multivariate Volatility. Available online: http://ssrn.com/abstract=2686482 (accessed on 29 September 2017).
- J.P. Morgan. 1996. Riskmetrics Technical Document, 4th ed. New York: J.P. Morgan. [Google Scholar]
- Laurent, Sébastien, Jeroen V. K. Rombouts, and Francesco Violante. 2012. On the forecasting accuracy of multivariate GARCH models. Journal of Applied Econometrics 27: 934–55. [Google Scholar] [CrossRef]
- Laurent, Sébastien, Jeroen V. K. Rombouts, and Francesco Violante. 2013. On loss functions and ranking forecasting performances of multivariate volatility models. Journal of Econometrics 173: 1–10. [Google Scholar] [CrossRef]
- Li, Qi, and Jeffrey S. Racine. 2007. Nonparametric Econometrics Theory and Practice. Oxford: Princeton University Press. [Google Scholar]
- Moskowitz, Tobias J. 2003. An analysis of covariance risk and pricing anomalies. The Review of Financial Studies 16: 417–57. [Google Scholar] [CrossRef]
- Pagan, Adrian R., and Kirill A. Sossounov. 2003. A simple framework for analysing bull and bear markets. Journal of Applied Econometrics 18: 23–46. [Google Scholar] [CrossRef]
- Patton, Andrew J., and Kevin Sheppard. 2009. Evaluating volatility and correlation forecasts. In Handbook of Financial Time Series. Edited by Torben Gustav Andersen, Richard A. Davis, Jens-Peter Kreib and Thomas V. Mikosch. Berlin: Springer Verlag. [Google Scholar]
- Poon, Ser-Huang, and Clive W. J. Granger. 2003. Forecasting volatility in financial markets: A review. Journal of Economic Literature 41: 478–539. [Google Scholar] [CrossRef]
- Rudemo, Mats. 1982. Empirical choice of histograms and kernel density estimators. Scandinavian Journal of Statistics 9: 65–78. [Google Scholar]
- Sadorsky, Perry. 1999. Oil price shocks and stock market activity. Energy Economics 21: 449–69. [Google Scholar] [CrossRef]
- Schwert, G. William. 1989. Why does stock market volatility change over time. The Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Silvennoinen, Annastiina, and Timo Teräsvirta. 2009. Multivariate GARCH Models. In Handbook of Financial Time Series. Edited by Torben Gustav Andersen, Richard A. Davis, Jens-Peter Kreib and Thomas V. Mikosch. Berlin: Springer. [Google Scholar]
- Silverman, Bernard W. 1986. Density Estimation for Statistics and Data Analysis. London: Chapman & Hall. [Google Scholar]
- Sjaastad, Larry A., and Fabio Scacciavillani. 1996. The price of gold and the exchange rate. Journal of International Money and Finance 15: 79–97. [Google Scholar] [CrossRef]
- Wand, M. P., and M. C. Jones. 1995. Kernel Smoothing. London: Chapman & Hall. [Google Scholar]
- Whitelaw, Robert F. 1994. Time variations and covariations in the expectation and volatility of stock market returns. The Journal of Finance 49: 515–41. [Google Scholar] [CrossRef]
| 1 | The HAR approach has not been applied to forecasting the full variance-covariance matrix. To do so would require a range of possible transformations to ensure positive definiteness, which leads to a deterioration in forecast performance. |
| 2 | In practice the HAR model will deliver a decreasing step-function, although it could also produce non-decreasing step functions. |
| 3 | Please refer to the discussion of the literature in Barndorff-Nielsen et al. (2011) for more information on recent developments in this area. |
| 4 | The scale matrix is the conditional expectation of the rVCM. |
| 5 | Gijbels et al. (1999) show that the Riskmetrics approach can be interpreted as a kernel approach in which weights on historical observations are determined by the lag at which a realization was observed. See Section 3. |
| 6 | Below this is abbreviated as QLIKE. |
| 7 | More accurately this is a half kernel as it is zero for etc. |
| 8 | As different assets will trade at different irregular intervals, intra-day returns require synchronisation. The synchronisation used here is the refresh-time synchronisation as described in Barndorff-Nielsen et al. (2011). There you will also find information on a necessary end-point correction (jittering) that has been applied to obtain this synchronised intra-day return vector. |
| 9 | The computations of the MVRK were done using the “realized_multivariate_kernel” function of Kevin Sheppard’s MFE Toolbox for MATLAB https://www.kevinsheppard.com/MFE_Toolbox. |
| 10 | The following empirical analysis was repeated with an alternative estimator, using intra-daily 5 min return data. None of the results reported in this paper changes qualitatively when using this alternative estimator. Some results that use this alternative estimator for the rVCM are reported in Section 8. |
| 11 | In this paper we restrict our applied analysis to the case where however in general there is no reason why the approach should not be extended to multi-day forecasts, although this requires consideration of the impact and inclusion of overnight returns in the construction of realized VCMs. |
| 12 | We normalise continuous variables before applying the kernel function. |
| 13 | Using rather than a realized VCM. |
| 14 | This measure has been successfully used in the forecast evaluation literature, e.g., in Laurent et al. (2013), and is sometimes called the Stein distance measure. |
| 15 | The following argument is, for notational ease, made for 1 period ahead forecasts but the extension to d period forecasts is straight forward. |
| 16 | We set , which means that every forecast used in cross-validation is based on a minimum of 300 observations. |
| 17 | In order to gauge the size of this threshold 1000 random variables were simulated which were subsequently considered as potential weighting variables (and there ) calculated. As it turns out a threshold of 1% would eliminate virtually all of these irrelevant random variables. We also applied a more conservative threshold of 2% but results remained virtually unchanged and are therefore not reported. Despite this the threshold is essentially ad-hoc and it is envisaged that future research may improve on this aspect of the proposed methodology. |
| 18 | Wharton Research Data Services (WRDS) was used in preparing this paper. This service and the data available thereon constitute valuable intellectual property and trade secrets of WRDS and/or its third-party suppliers. |
| 19 | The data cleaning advice provided in Barndorff-Nielsen et al. (2009) is followed. |
| 20 | The realized correlation matrices are calculated from where is a diagonal matrix with on the ith diagonal element and is the element of . |
| 21 | Difference between 1 and 10 year maturity treasury yield curve rates for US treasury issued bonds, see http://www.treasury.gov/resource-center/data-chart-center/interest-rates/Pages/TextView.aspx?data=yield. |
| 22 | Difference between yields on Moody’s Aaa and Baa rated corporate bonds. Data obtained from https://research.stlouisfed.org/fred2/categories/119. |
| 23 | Gold price is Gold Fixing price in London Bullion Market, 3:00 pm London time, from https://research.stlouisfed.org/fred2/series/GOLDPMGBD228NLBM#. Oil price is crude oil brent, price per barrel. Obtained from datastream, with the identifier OILBREN. |
| 24 | While all these variables are available on a daily frequency, the methodology can easily handle lower frequency data such as Industrial Production and inflation measures which were used to model slow moving stock market volatility by Engle et al. (2013). |
| 25 | While, of course, bull and bear markets are not synonymous with booms and recessions, we feel that the use of the more narrow definition of a stock market state is justified for the problem at hand. The algorithm identifies bull and bear periods based on monthly data, daily data is often too noisy to support identification of broad trends. As a result once the algorithm identifies a month as belonging to a bull/bear period all of the constituent days are also assumed to belong to this period. |
| 26 | Data used here is closing price of the S&P500 index for the last day of the month. |
| 27 | Daily observations of the CBOE volatility index, data obtained from: http://www.cboe.com/micro/vix/historical.aspx. |
| 28 | Temperature data was obtained from the University of Dayton’s daily temperature archive. See http://academic.udayton.edu/kissock/http/Weather/. |
| 29 | The cross-validation procedure is repeated for every new forecasting period. |
| 30 | Chiriac and Voev (2011) propose a VARFIMA model rather than the simpler to estimate HAR model although there seems little forecasting improvement from using this different model. |
| 31 | Recall that forecasts of the VCM were labelled as . |
| 32 | It should be noted that the elements of are non-linear combinations of the elements in . Therefore, while this procedure can produce unbiased forecasts for , it will not deliver unbiased forecasts for . While Chiriac and Voev (2011) devise a bias correction strategy they also conclude that it is likely to be practically negligible and hence we refrain from applying this bias correction. The same issue and conclusion are reached in Bauer and Vorkink (2011). |
| 33 | This was also implemented in Chiriac and Voev (2011). |
| 34 | In the below forecast experiments we use the realized VCM, , using a regular 5 min grid of intra-daily returns, in place of as it is a consistent estimator of the unobserved VCM. To establish the robustness of the results we also use the realised multivariate kernel. Some such robustness results will be included in subsequent tables. |
| 35 | We use the mcs function implemented in Kevin Sheppard’s MFE toolbox for MATLAB (https://www.kevinsheppard.com/MFE_Toolbox). |
| 36 | See the definitions in Section 8.1. |
| 37 | |
| 38 | Of course one could allow for longer lag use in a HAR-type model by allowing longer averages than the standard maximum of 22 days. |
| 39 | The results for the variables not shown here, to keep the image readable, are similar to the ones shown. |
| 40 | The temperature was introduced as a sensibility check. In fact, when using the rolling (rather than recursuve) sample scheme, this variable does survive the first elimination step. This could be the seasonal nature of this variable which may pick up some element of local trending in the variance covariance matrix. |
| 41 | This is done keeping all other bandwidths constant. |
| 42 | As our first forecasting period is the 19 June 2001, the first of these sub-samples has somewhat fewer observations, 384, than the others which all have around 500 observations. |
| 43 | These results are available on request. |
| 44 | TMR models model and forecast combinations of elements in the VCM (see e.g., Heiden 2015), whereas kernel and RM approaches essentially forecast each element as a weighted average of that same element. |
| 45 | Note that the QLIKE was used to find the optimal bandwidth parameters for the kernel forecasting models and the RM_Opt. While these were in-sample QLIKE, one may argue that this therefore provides these models with an inherent advantage when evaluated using a QLIKE loss function. Interestingly though, the RM model with fixed bandwidth makes no use of any in-sample QLIKE information and still retains a clear advantage to the HAR models. |
| Label | Short Description |
|---|---|
| K_TDM | Kernel forecasting method with time, matrix distance and macroeconomic information as explanatory variables |
| K_DM | Kernel forecasting method with matrix distance and macroeconomic variables |
| K_TD | Kernel forecasting method time and matrix distance variables |
| K_D | Kernel forecasting method which excludes both time and macroeconomic variables and only includes matrix distance measures |
| HAR_CD | HAR Forecasting method using the Cholesky Decomposition |
| HAR_LOG | HAR Forecasting method using the Matrix Logarithm Decomposition |
| RM | Riskmetrics method using pre-defined values for decay |
| RM_Opt | Riskmetrics using an optimised decay parameter |
| VCM est | RMVK | RVCM | ||||||
|---|---|---|---|---|---|---|---|---|
| Sampling | Rolling | Recursive | Rolling | Recursive | ||||
| Model | QLIKE | MSE | QLIKE | MSE | QLIKE | MSE | QLIKE | MSE |
| K_D | 1 | 0.538 | 0 | 0.46 | 0.1 | 0.896 | 0 | 0.64 |
| K_DM | 0.02 | 0.538 | 0 | 0.3 | 0.896 | 0.01 | 0 | 0.6 |
| K_TDM | 0.53 | 0.538 | 0.047 | 1 | 0 | 0.896 | 0.022 | 1 |
| K_TD | 0.2 | 1 | 1 | 0.77 | 0 | 0.896 | 1 | 0.64 |
| HAR_CD | 0 | 0.986 | 0 | 0.34 | 0 | 1 | 0 | 0.64 |
| HAR_LOG | 0 | 0.243 | 0 | 0.22 | 0 | 0.297 | 0 | 0.26 |
| RM | 0.06 | 0.177 | 0.005 | 0.15 | 0.01 | 0.156 | 0 | 0.14 |
| RM_Opt | 0.06 | 0.986 | 0 | 0.46 | 1 | 0.896 | 0 | 0.64 |
| 2001–2002 | 2003–2004 | 2005–2006 | 2007–2008 | 2009–2010 | 2011–2012 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Av. Loss | Pval | Av. Loss | Pval | Av. Loss | Pval | Av. Loss | Pval | Av. Loss | Pval | Av. Loss | Pval | |
| K_DM | 7.4926 | 0.01 | 7.3289 | 0 | 7.6893 | 0.001 | 11.3613 | 0 | 10.6056 | 0 | 9.8433 | 0.016 |
| K_D | 9.6571 | 0 | 10.2559 | 0 | 7.9274 | 0 | 10.7996 | 0.002 | 10.7521 | 0 | 10.2044 | 0 |
| K_TDM | 7.1727 | 1 | 7.1398 | 1 | 7.3832 | 1 | 9.8082 | 0.008 | 9.5993 | 0.118 | 9.3501 | 0.21 |
| K_TD | 7.2663 | 0.158 | 7.2028 | 0.003 | 7.3833 | 0.997 | 9.4967 | 1 | 9.4073 | 1 | 9.1939 | 1 |
| HAR_CD | 8.1583 | 0.009 | 7.3687 | 0 | 7.5808 | 0 | 11.2403 | 0.002 | 11.067 | 0 | 10.3472 | 0 |
| HAR_LOG | 8.6004 | 0 | 7.9947 | 0 | 8.4708 | 0 | 12.1655 | 0 | 11.6134 | 0 | 11.2819 | 0 |
| RM | 8.0545 | 0.01 | 7.1912 | 0.133 | 7.4499 | 0.184 | 10.6856 | 0.008 | 10.0059 | 0.005 | 9.4448 | 0.21 |
| RM_Opt | 7.2539 | 0.158 | 7.2429 | 0 | 7.4573 | 0.001 | 9.8331 | 0.008 | 9.6222 | 0.118 | 9.4153 | 0.016 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, R.; Clements, A.; O'Neill, R. A Multivariate Kernel Approach to Forecasting the Variance Covariance of Stock Market Returns. Econometrics 2018, 6, 7. https://doi.org/10.3390/econometrics6010007
Becker R, Clements A, O'Neill R. A Multivariate Kernel Approach to Forecasting the Variance Covariance of Stock Market Returns. Econometrics. 2018; 6(1):7. https://doi.org/10.3390/econometrics6010007
Chicago/Turabian StyleBecker, Ralf, Adam Clements, and Robert O'Neill. 2018. "A Multivariate Kernel Approach to Forecasting the Variance Covariance of Stock Market Returns" Econometrics 6, no. 1: 7. https://doi.org/10.3390/econometrics6010007
APA StyleBecker, R., Clements, A., & O'Neill, R. (2018). A Multivariate Kernel Approach to Forecasting the Variance Covariance of Stock Market Returns. Econometrics, 6(1), 7. https://doi.org/10.3390/econometrics6010007





