1. Introduction
We consider the performance of a new method for selecting the appropriate lag order p of an autoregressive (AR) model for the residuals of a linear regression. Our focus is on the small-sample performance as compared to competing methods, and, as such, we concentrate on the underlying small-sample distribution theory employed, instead of considerations of consistency and performance in an asymptotic framework.
The problem of ARMA model specification has a long history, and we omit a literature review, though note the book by
Choi (
1992), dedicated to the topic. Less well documented is the use of small-sample distributional approximations using saddlepoint techniques. Saddlepoint methodology started with the seminal contributions from
Daniels (
1954,
1987) and continued with those from
Barndorff-Nielsen and Cox (
1979),
Skovgaard (
1987),
Reid (
1988),
Daniels and Young (
1991) and
Kolassa (
1996). It has been showcased in the book-length treatments of
Field and Ronchetti (
1990),
Jensen (
1995),
Kolassa (
2006), and
Butler (
2007), the latter showing the enormous variety of problems in statistical inference that are amendable to its use.
In our setting herein, we restrict attention to the stationary setting and do not explicitly consider the unit root case. Time series
is assumed to have distribution
, where
is a full rank,
matrix of exogenous variables and
is the covariance matrix corresponding to a stationary AR(
p) model with parameter vector
. Values
,
,
and
p are fixed but unknown. Below (in
Section 6), we extend to an ARMA framework, such that, in addition, the MA parameters
are unknown, but
q is assumed known.
The two most common approaches used to determine the appropriate AR lag order are (i) assessing the lag at which the sample partial autocorrelation “cuts off”; and (ii) use of popular penalty-based model selection criteria such as AIC and SBC/BIC (see, e.g.,
Konishi and Kitagawa 2008;
Brockwell and Davis 1991, sct. 9.3;
McQuarrie and Tsai 1998;
Burnham and Anderson 2003). As emphasized in
Chatfield (
2001, pp. 31, 91), interpreting a sample correlogram is one of the hardest tasks in time series analysis, and their use for model determination is, at best, difficult, and often involves considerable experience and subjective judgment. The fact that the distribution of the sample autocorrelation function (SACF) and the sample partial ACF (SPACF) of the regression residuals are—especially for smaller sample sizes—highly dependent on the
matrix makes matters significantly more complicated. In comparison, the application of penalty-based model selection criteria is virtually automatic, requiring only the choice of which criteria to use. The criticism that their use involves model estimation and, thus, far more calculation is, with modern computing power, no longer relevant.
A different, albeit seldom used, identification methodology involves sequential testing procedures. One approach sequentially tests
Testing stops when the first hypothesis is rejected (and all remaining are then also rejected). Tests of the
kth null hypothesis can be based on a scaled sum of squared values of the SPACF or numerous variations thereof, all of which are asymptotically
distributed; see
Choi (
1992, chp. 6) and the references therein for a detailed discussion.
The use of sequential testing procedures in this context is not new. For example,
Jenkins and Alevi (
1981) and
Tiao and Box (
1981) propose methods based on the asymptotic distribution of the SPACF under the null of white noise. More generally,
Pötscher (
1983) considers determination of optimal values of
p and
q by a sequence of Lagrange multiplier tests. In particular, for a given choice of maximal orders,
P and
Q, and a chain of
-values
,
, such that either
and
or
and
,
, a sequence of Lagrange-multiplier tests are performed for each possible chain. The optimal orders are obtained when the test does not reject for the first time. As noted by
Pötscher (
1983, p. 876), “strong consistency of the estimators is achieved if the significance levels of all the tests involved tend to zero with increasing [sample] size…”. This forward search procedure is superficially similar to the method proposed herein, and also requires specification of a sequence of significance levels. Our method differs in two important regards. First, near-exact small-sample distribution theory is employed by use of conditional saddlepoint approximations; and second, we explicitly allow for, and account for, a mean term in the form of a regression
.
Besides the inherent problems involved in sequential testing procedures, such as controlling overall type I errors and the possible tendency to over-fit (as in backward regression procedures), the reliance on asymptotic distributions can be detrimental when working with small samples and unknown mean term
. This latter problem could be overcome by using exact small-sample distribution theory and a sequence of point optimal tests in conjunction with some prior knowledge of the AR coefficients; see, e.g.,
King and Sriananthakumar (
2015) and the references therein.
Compared to sequential hypothesis testing procedures, penalty-based model selection criteria have the arguable advantage that there is no model preference via a null hypothesis, and that the order in which calculations are performed is irrelevant (see, for example,
Granger et al. 1995). On the other hand, as is forcefully and elegantly argued in
Zellner (
2001) in a general econometric modeling context, it is worthwhile to have an ordering of possible models in terms of complexity, with higher probabilities assigned to simpler models. Moreover,
Zellner (
2001, sct. 3) illustrates the concept with the choice of ARMA models, discouraging the use of MA components in favor of pure AR processes, even if it entails more parameters, because “counting parameters” is not necessarily a measure of complexity (see also
Keuzenkamp and McAleer 1997, p. 554). This agrees precisely with the general findings of
Makridakis and Hibon (
2000, p. 458), who state “Statistically sophisticated or complex models do not necessarily produce more accurate forecasts than simpler ones”. With such a modeling approach, the aforementioned disadvantages of sequential hypothesis testing procedures become precisely its advantages. In particular, one is able to specify error rates on individual hypotheses corresponding to models of differing complexity.
In this paper, we present a sequential hypothesis testing procedure for computing the lag length that, in comparison to the somewhat ad hoc sequential methods mentioned above, operationalizes the uniformly most powerful unbiased (UMPU) test of
Anderson (
1971, pp. 34–46, 260–76). It makes use of a conditional saddlepoint approximation to the—otherwise completely intractable—distribution of the
mth sample autocorrelation given those of order
. While exact calculation of the required distribution is not possible (not even straightforward via simulation because of the required conditioning),
Section 4 provides evidence that the saddlepoint approximation is, for practical purposes, virtually exact in this context.
The remainder of the paper is outlined as follows.
Section 2 and
Section 3 briefly outline the required distribution theory of the sample autocorrelation function and the UMPU test, respectively.
Section 4 illustrates the performance of the proposed method in the null case of no autocorrelation, while
Section 5 compares the performance of the new and existing order selection methods for several autoregressive structures.
Section 6 proposes an extension of the method to handle AR lag selection in the presence of ARMA disturbances.
Section 7 provides a performance comparison when the Gaussianity assumption is violated.
Section 8 provides concluding remarks.
2. The Distribution of the Autocorrelation Function
Define the
matrix
such that its
-th element is given by
and
denotes the indicator function. Then, for covariance stationary, mean-zero vector
, the ratio of quadratic forms
is the usual estimator of the
lth lag autocorrelation coefficient. The sample autocorrelation function with
m components, hereafter SACF, is then given by vector
with joint density denoted by
.
Recall that a function
is the autocovariance function of a weakly stationary time series if and only if
is even, i.e.,
for all
, and is positive semi-definite. See, e.g.,
Brockwell and Davis (
1991, p. 27) for proof. Next recall that a symmetric matrix is positive definite if and only if all the leading principal minors are positive; see, e.g.,
Abadir and Magnus (
2005, p. 223). As such, the support of
is given by
where
is the band matrix given by
Assume for the moment that there are no regression effects and let
with
, i.e.,
is positive definite. While no tractable expression for
appears to exist, a saddlepoint approximation to the density of
at
is shown in
Butler and Paolella (
1998) to be given by
where
and
with
-th element given by
. Saddlepoint vector
solves
and, in general, needs to be numerically obtained. In the null setting for which
,
, so that the last factor in (
3) is just
. Special cases for which explicit solutions to (
5) exist are given in
Butler and Paolella (
1998).
With respect to the calculation of
corresponding to a stationary, invertible ARMA(
) process, the explicit method in
McLeod (
1975) could be used, though more convenient in matrix-based computing platforms are the matrix expressions given in
Mittnik (
1988) and
Van der Leeuw (
1994). Code for the latter, as well as for computing the CACF test, are available upon request.
The extension of (
3) for use with regression residuals is not immediately possible because the covariance matrix of
is not full rank and a canonical reduction of the residual vector is required. To this end, let
where
is a full rank
matrix of exogenous variables. Denote the OLS residual vector as
, where
. As
is an orthogonal projection matrix, it can be expressed as
, where
is
and such that
and
. Then
where
and
is a
symmetric matrix. For example,
could consist of an orthogonal basis for the
eigenvectors of
corresponding to the unit eigenvalues. By setting
, approximation (
3) becomes valid using
and
in place of
and
, respectively. Note that, in the null case with
,
.
3. Conditional Distributions and UMPU Tests
Anderson (
1971, sct. 6.3.2) has shown for the regression model with circular AR(
m) errors (so
) and the columns of
restricted to Fourier regressors, i.e.,
that the uniformly most powerful unbiased (UMPU) test of AR
versus AR
disturbances rejects for values of
falling sufficiently far out in either tail of the conditional density
where
denotes the observed value of the vector of random variables
. A
p-value can be computed as
, where
Like in the well-studied
case (cf. (
Durbin and Watson 1950,
1971) and the references therein), the optimality of the test breaks down in either the non-circular model and/or with arbitrary exogenous
, but does provide strong motivation for an approximately UMPU test in the general setting considered here. This is particularly so for economic time series, as they typically exhibit seasonal (i.e., cyclical) behavior that can mimic the Fourier regressors in (
8) (
Dubbelman et al. 1978;
King 1985, p. 32).
Following the methodology outlined in
Barndorff-Nielsen and Cox (
1979),
Butler and Paolella (
1998) derive a conditional double saddlepoint density to (
9) computed as the ratio of two single approximations
where
and
are the
and
values, respectively, associated with the
-dimensional saddlepoint
of the denominator determined by
; likewise for
and
, and explicit dependence on
has been suppressed.
Thus,
in (
10) for
can be computed as
where
and
denotes the conditional support of
given
. It is given by
where
and
are such that, for
outside these values,
does not correspond to the ACF of a stationary AR
process. These values can be found as follows: Assume that
lies in the support of the distribution of
. From (
2), the range of support for
is determined by the inequality constraint
. Expressing the determinant in block form,
and, as
by assumption,
ranges over
Letting
,
, and using the fact that
is both symmetric and persymmetric (i.e., symmetric in the northeast-to-southwest diagonal), the range of
is given by
This equation is quadratic in
so that the two ordered roots can be taken as the values for
and
respectively. For
, this yields
; for
,
While computation of (
12) is straightforward, it is preferable to derive an approximation to
similar in spirit to the
Lugannani and Rice (
1980) saddlepoint approximation to the cdf of a univariate random variable. This method begins with the cumulative integral of the conditional saddlepoint density integrated over
as a portion of
, the support of
given
, as specified in the first equality of
A change of variable in the integration from
to
is needed which allows the integration to be rewritten as in the second equality of (
14). Here,
is the standard normal density,
is the remaining portion of the integrand for equality to hold in (
14), and
is the image of
under the mapping
and given in (
16) below. Temme’s approximation approximates the right-hand-side of (
14) and this leads to the expression
for
, where
and
and
denote the cdf and pdf of the standard normal distribution, respectively. Details of this derivation are given in
Butler and Paolella (
1998) and
Butler (
2007, scts. 12.5.1 and 12.5.5).
In general, it is well known that the middle integral in (
14) is less accurate than the normalized ratio in (
12); see
Butler (
2007, eq. 2.4.6). However, quite remarkably, the Temme argument applied to (
14) most often makes (
15) more accurate than the normalized ratio in (
12). A full and definitive answer to the latter tendency remains elusive. However, a partial asymptotic explanation is discussed in
Butler (
2007, sct. 2.3.2). In this setting, both (
15) and (
12) indeed yield very similar results, differing only in the third significant digit. It should be noted that the resulting
p-values, or even the conditional distribution itself, cannot easily be obtained via simulation, so that it is difficult to check the accuracy of (
12) and (
15). In the next two sections, we show a way that lends support to the correctness (and usefulness) of the methods.
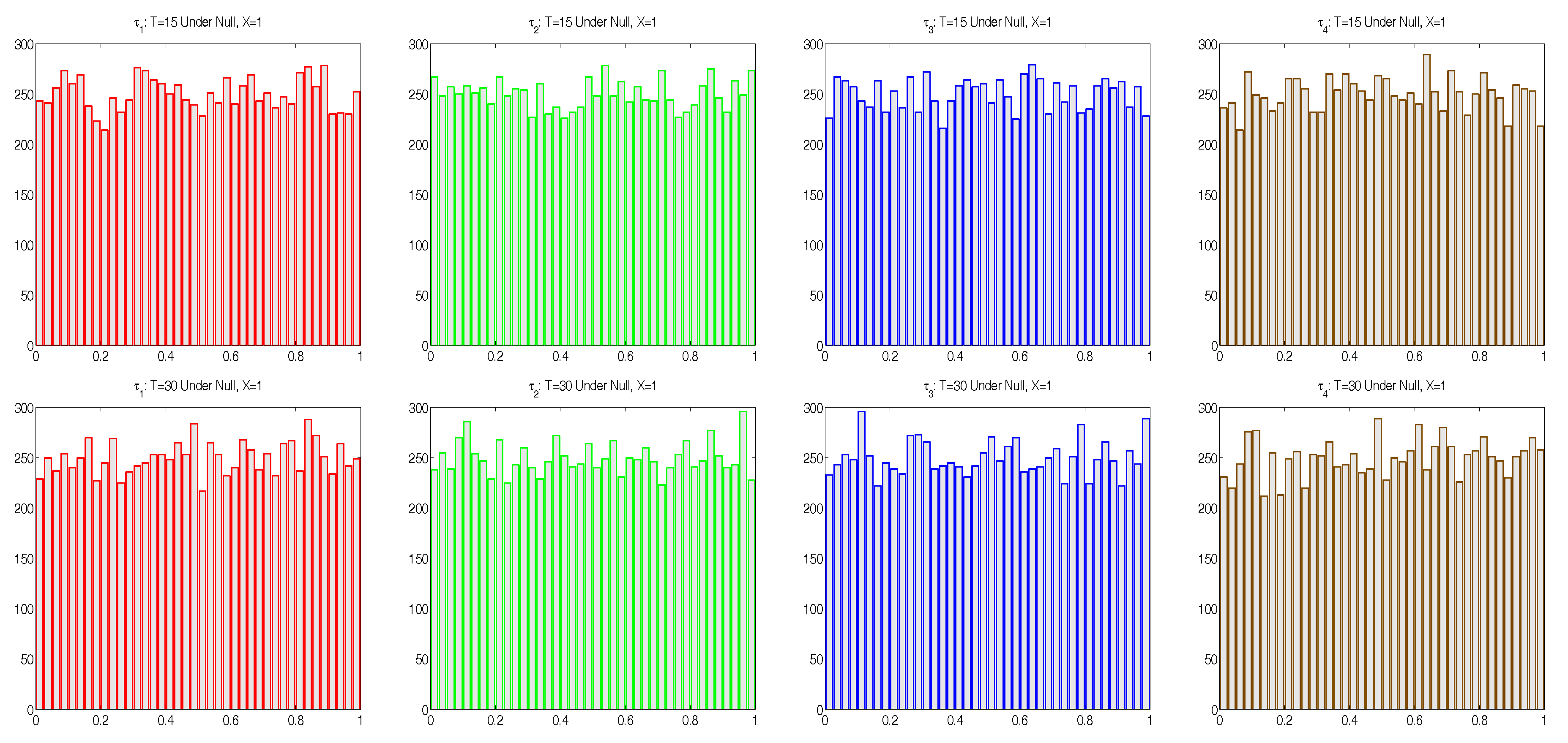
4. Properties of the Testing Procedure Under the Null
We first wish to assess the accuracy of the conditional saddlepoint approximation to (
9) when
in (
6), i.e., there is no autocorrelation in the disturbance terms of the linear model
. In this case, we expect
. This was empirically tested by computing
,
and
in (
10), based on (
15), using observed values
, for
replications of
T-length time series, each consisting of
T independent standard normal simulated random variables,
and
, but with mean removal, i.e., taking
. Histograms of the resulting
, as shown in
Figure 1, are in agreement with the uniform assumption. Furthermore, the absolute sample correlations between each pair of the
were all less than 0.02 for
and less than 0.013 for
.
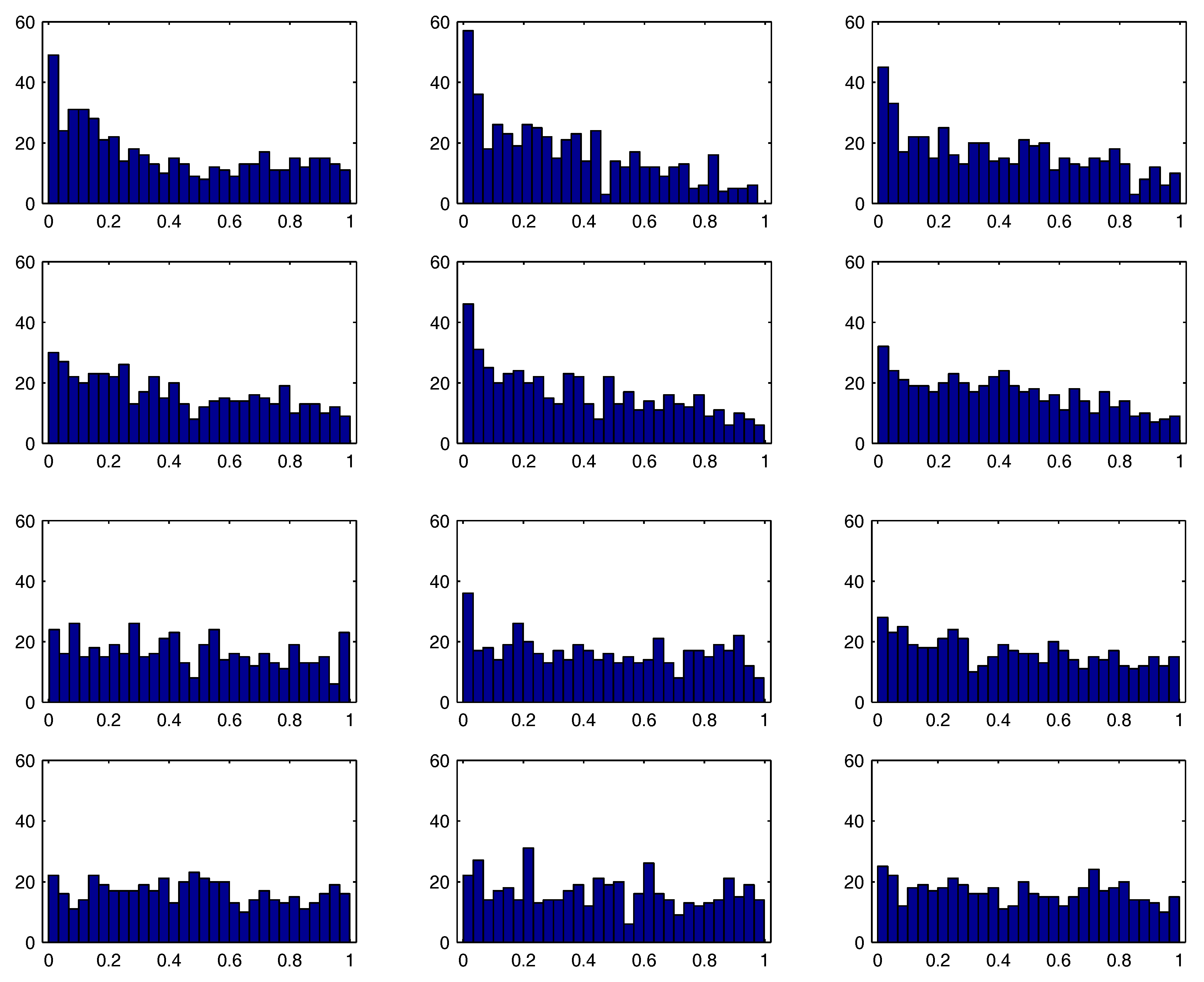
These results are in stark contrast to the empirical distribution of the “
t-statistics” and the associated
p-values of the maximum likelihood estimates (MLEs). For 500 simulated series, the model
,
,
,
, was estimated using exact maximum likelihood with approximate standard errors of the parameters obtained by numerically evaluating the Hessian at the MLE.
Figure 2 shows the empirical distribution of the
, where
is the ratio of the MLE of
to its corresponding approximate standard error,
, and
refers to the cdf of the Student’s
t distribution with
degrees of freedom.
1 The top two rows correspond to
and
; while somewhat better for
, it is clear that the usual distributional assumption on the MLE
t-statistics does not hold. The last two rows correspond to
and
, for which the asymptotic distribution is adequate.
5. Properties of the Testing Procedure Under the Alternative
5.1. Implementation and Penalty-Based Criteria
One way of implementing the
p-values computed from (
15) for selecting the autoregressive lag order
p is to let it be the largest value
such that
or
; or set it to zero if no such extreme
occurs. Hereafter, we refer to this as the
conditional ACF test, or, in short, CACF. The effectiveness of this strategy will clearly be quite dependent on the choices of
m and
c. We will see that it is, unfortunately and like all selection criteria, also highly dependent on the actual, unknown autoregressive coefficients.
Another possible strategy, say, the alternative CACF test, is, for a given c and m, to start with testing an AR(1) specification and check if or . If this is not the case, then one declares the lag order to be . If instead is in the critical region, then one continues to the AR(2) case, inspecting if or . If not, is chosen; and if so, then is computed, etc., continuing sequentially for , stopping when either the null at lag j is not rejected, in which case is returned, or when . Below, we will only investigate the performance of the first strategy. We note that the two strategies will have different small sample properties that clearly depend on the true p and the coefficients of the AR(p) model (as well as the sample size T and choices of m and c). In particular, assuming in both cases that , the alternative CACF test could perform better if m is chosen substantially larger than the true p.
While penalty function methods also require an upper limit
m, the CACF has the extra “tuning parameter”
c that can be seen as either a blessing or a curse. A natural value might be
, so that, under the null of zero autocorrelation,
p assumes a particular wrong value with approximate probability
; and
is chosen approximately with probability
, i.e.,
from the binomial expansion. This value of
c will be used for two of the three comparisons below, while the last one demonstrates that a higher value of
c is advisable.
The CACF will be compared to the use of the following popular penalty-based measures, such that the lag order is chosen based upon the value of
j for which they are minimized:
where
denotes the MLE of the innovation variance and
denotes the number of estimated parameters (not including
, but including
k, the number of regressors). Observe that both our CACF method, and the use of penalty criteria, assume the model regressor matrix is correctly specified, and condition on it, but both methods do not assume that the regression coefficients are known, and instead need to be estimated, along with the autoregressive parameters. Original references and ample discussion of these selection criteria can be found in the survey books of
Choi (
1992, chp. 3),
McQuarrie and Tsai (
1998) and
Konishi and Kitagawa (
2008), as well as
Lütkepohl (
2005) for the vector autoregressive case.
5.2. Comparison with AR(1) Models
For each method, the optimal AR lag orders among the choices
through
were determined for each of 100 simulated mean-zero AR(1) series of length
and AR parameter
, using
,
2 as well as the two regression models, constant (
) and constant-trend (
), where
. For the CACF method, values
and
were used.
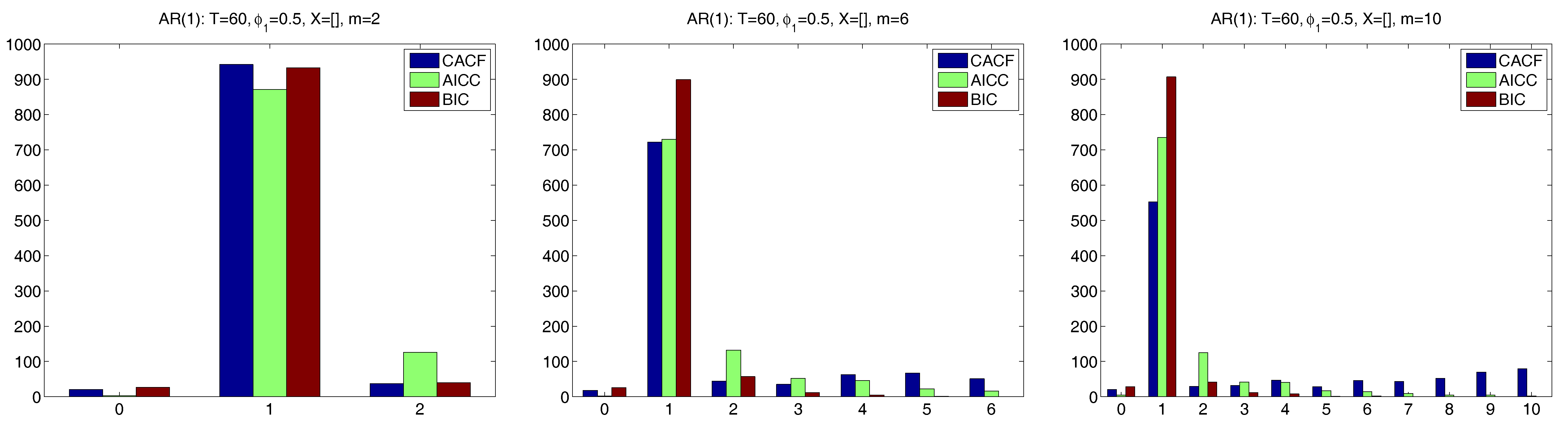
Figure 3 and
Figure 4 show the results for the two regression cases. In both cases, the CACF method dominates in the null model, while for small absolute values of
, the CACF underselects more than the penalty-based criteria. For
, the CACF dominates, though SBC is not far off in the
case. For the constant-trend model, the CACF is clearly preferred. The relative improvement of the CACF performance in the constant-trend model shows the benefit of explicitly taking the regressors into account when computing tail probabilities in (
15) via (
3).
A potential concern with the CACF method is what happens if
m is much larger than the true
p. To investigate this, we stay with the AR(1) example, but consider only the case with
, and use three choices of
m, namely 2, 6 and 10. We first do this with a larger sample size of
and no
matrix, which should convey an advantage to the penalty-based measures relative to CACF. For the former, we use only the AICC and BIC.
Figure 5 shows the results, based on
replications. With
, all three methods are very accurate, with CACF and BIC being about equal with respect to the probability of choosing the correct
p of one, and slightly beating AICC. With
, the BIC dominates. The nature of the CACF methodology is such that, when
m is much larger than
p, the probability of overfitting (choosing
p too high) will increase, according to the choice of
c. With
, this is apparent. In this case, the BIC is superior, also substantially stronger than the more liberal AICC.
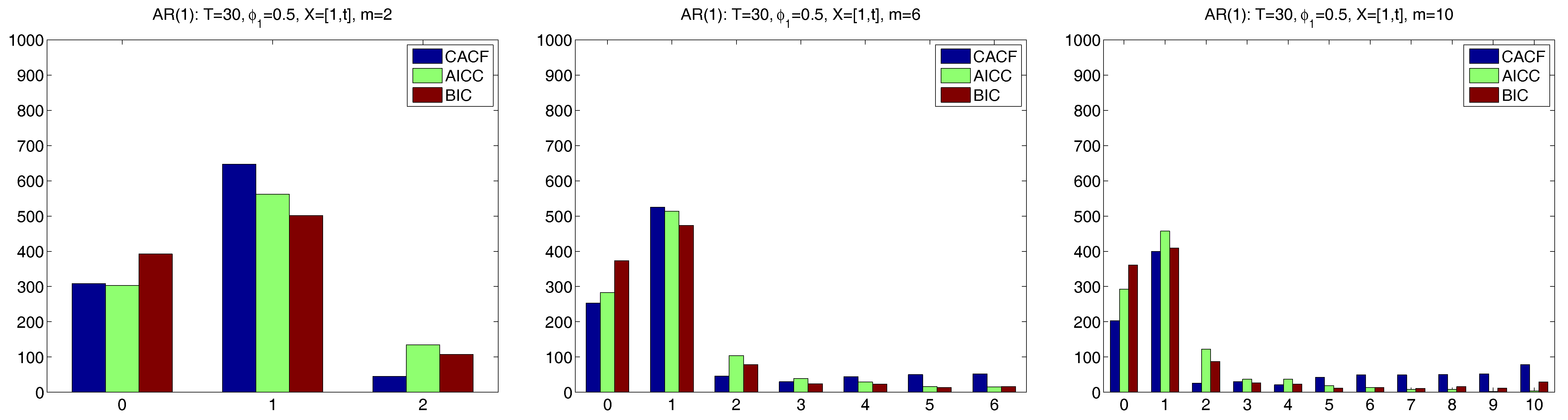
We now conduct a similar exercise, but using conditions for which the CACF method was designed, namely a smaller sample size of
and a more substantial regressor matrix of an intercept and time trend regression, i.e.,
.
Figure 6 shows the results. For
, the CACF clearly outperforms the penalty-based criteria, while for
, which is substantially larger than the true
, the CACF chooses the correct
p with the highest probability of the three selection methods, though the AICC is very close. For the very large
(which, for
, might be deemed inappropriate), CACF and BIC perform about the same with respect to the probability of choosing the correct
p of one, while AICC dominates. Thus, in this somewhat extreme case (with
and
), the CACF still performs competitively, due to its nearly exact small sample distribution theory and the presence of an
matrix.
5.3. Comparison with AR(2) Models
The effectiveness of the simple lag order determination strategy is now investigated for the AR(2) model, but by applying it to cases for which the penalty-based criteria will have a comparative advantage, namely with more observations () and either no regressors or just a constant. We also include the constant-trend case () used above in the AR(1) simulation. Based on 1000 replications, six different AR(2) parameter constellations are considered. As before, the CACF method uses and the highest lag order computed is .
The simulation results of the CACF test are summarized in
Table 1. Some of these results are also given in the collection of more detailed tables in
Appendix A. In particular, they are shown in the top left sections of
Table A1 (corresponds to no
matrix) and
Table A2 (
). There, the magnitude of the roots of the AR(2) polynomial are also shown, labeled as
and
, the latter being omitted to indicate complex conjugate roots (in which case
).
The first model corresponds to the null case , in which the error rate for false selection of p should be (given the use of ) about 5% for each false candidate. This is indeed the case, as the error rate with should be roughly 0.80, as seen in the boldface entries. For the remaining non-null models, quite different lag selection characteristics were observed, with the choice of ranging between 40% and 91% among the five AR(2) models in the known mean case; 33% and 91% in the constant but unknown () case; and 31% and 90% in the constant-trend () case. Observe how, as expected from the small-sample theory, as the matrix increases in complexity, there is relatively little effect on the performance of the method, for a given AR(2) parametrization. However, the choice of the latter does have a very strong impact on its performance. For example, the 5th model is such that the CACF method chooses more often than the correct .
The comparative results using the penalty-based methods are shown in
Table A3 through
Table A7 under the heading “For AR(
p) Models”. We will discuss only the
case in detail. For the null model (i.e.,
), denoted 1.0x, where the “x” indicates that an
matrix was used, the CACF outperforms all other criteria by a wide margin, with
of the runs resulting in
, compared with the 2nd best, SBC, with
. For model 2.0x, all the model selection criteria performed well, with the CACF and SBC resulting in
and
, respectively. Similarly, all criteria performed relatively poorly for models 3.0x and 4.0x, but particularly the CACF, which was worst (with
occurring
and
of the time, respectively), while AICC and HQ were the best and resulted in virtually the same
values for the two models (
and
). Similar results hold for models 5.0x and 6.0x, for which the CACF again performs relatively poorly.
The unfortunate and, perhaps unexpected, fact that the performance of the new method and the penalty-based criteria highly depend on the true model parameters is not new; see, for example,
Rahman and King (
1999) and the references therein.
5.4. Higher Order AR(p) Processes
Clearly, as
p increases, it becomes difficult to cover the whole parameter space in a simulation study. We (rather arbitrarily) consider AR(4) models with parameters
,
,
and
takes on the 6 values
through
, for which the maximum moduli of the roots of the AR polynomial are 0.616, 0.679, 0.747, 0.812, 0.864 and 0.908, respectively. This is done for two sample sizes,
and
and, in an attempt to use a more complicated design matrix that is typical in econometric applications, an
matrix corresponding to an intercept-trend model with structural break, i.e., for
,
As mentioned in the beginning of
Section 5, the choices of
c and
m are not obvious, and ideally would be purely data driven. The optimal value of
m in conjunction with penalty-based criteria is still an open issue; see, for example, the references in
Choi (
1992, p. 72) to work by E. J. Hannan and colleagues. The derivation of a theoretically based optimal choice of
m for the CACF is particularly difficult because the usual appeal to asymptotic arguments is virtually irrelevant in this small-sample setting. At this point, we have little basis for their choices, except to say (precisely as others have) that
m should grow with the sample size.
It is not clear if the optimal value of
c should vary with sample size. What we can say is that its choice depends on the purpose of the analysis. For example, consider the findings of
Fomby and Guilkey (
1978), who demonstrated that, when measuring the performance of
based on mean squared error, the optimal size of the Durbin-Watson test when used in conjunction with a pretest estimator for the AR(1) term should be much higher than the usual
, with
being their overall recommendation. This will, of course, increase the risk of model over-fitting, but that can be somewhat controlled in this context by a corresponding reduction in
m. (Recall that the probability of not rejecting the null hypothesis of no autocorrelation is
under white noise.)
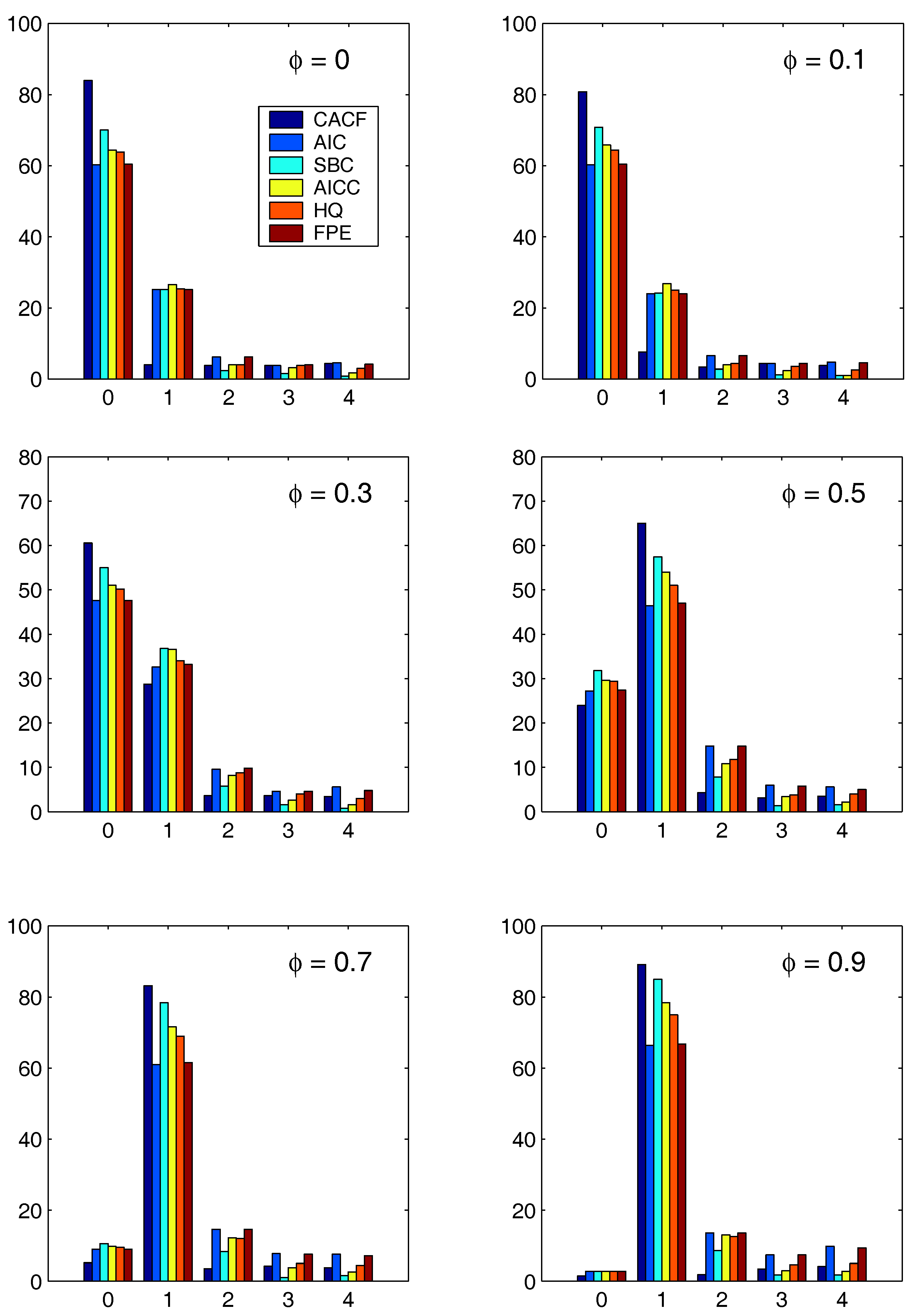
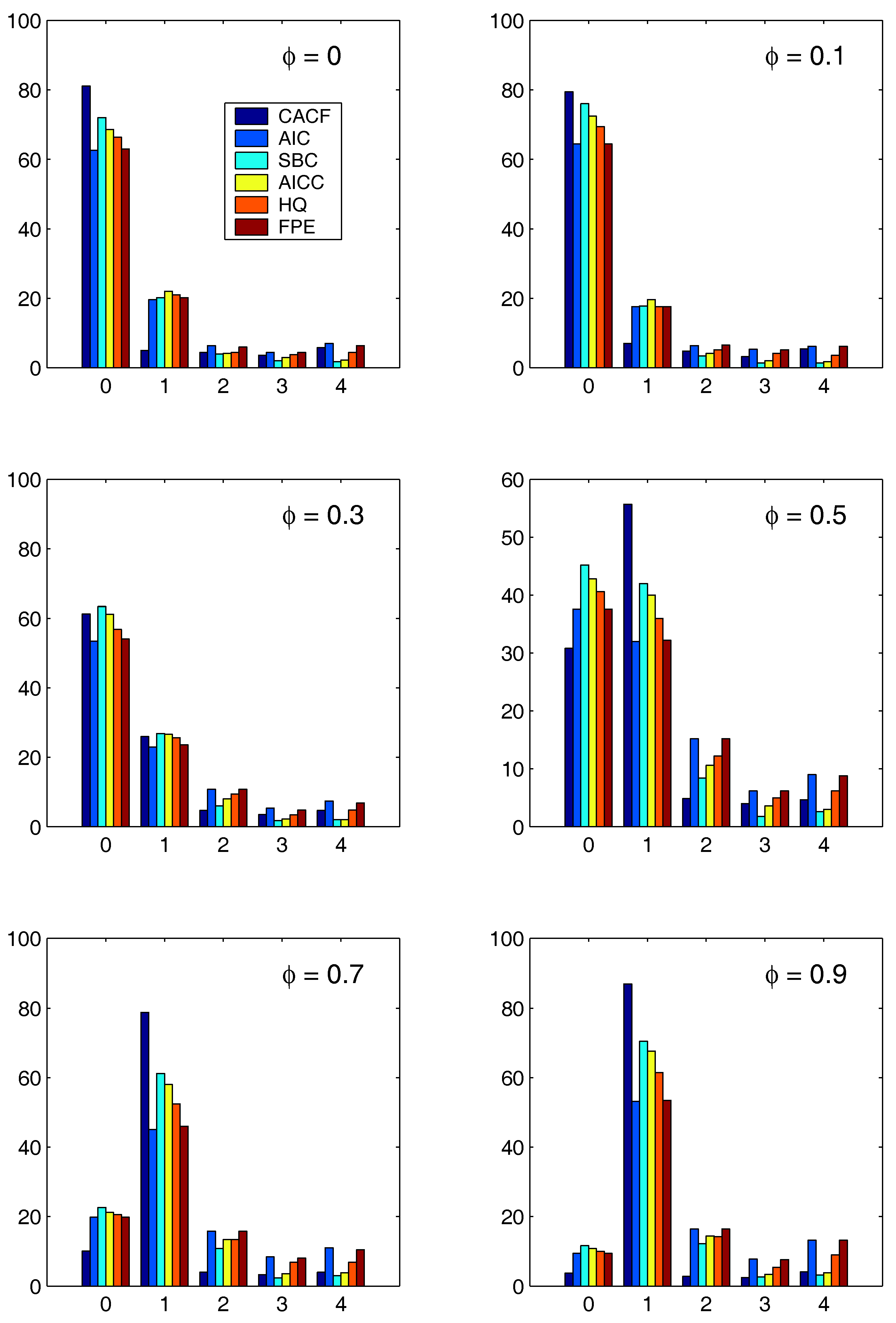
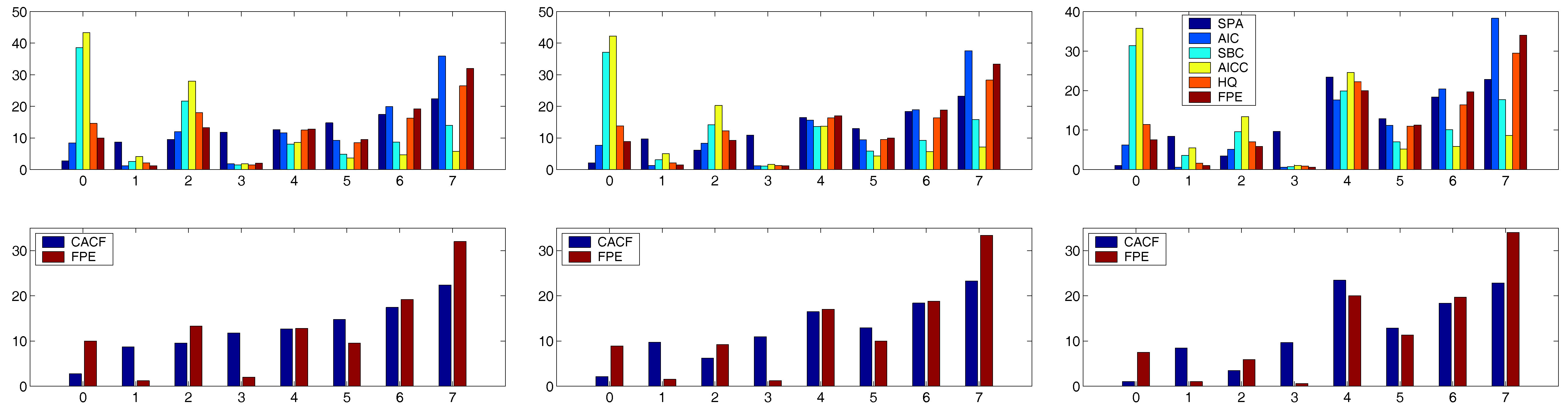
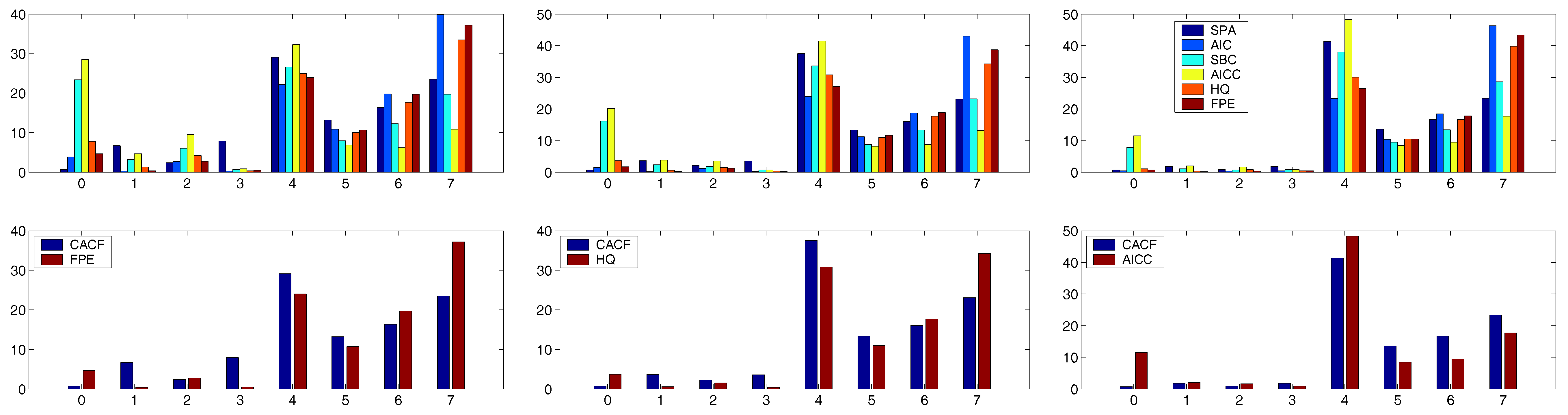
For the trials in the AR(4) case, we take
to provide some room for over-fitting (but which admittedly might be considered somewhat high for only
observations). With this
m, use of
proved to be a good choice for all the runs with
. For this sample size, the top panels of
Figure 7 and
Figure 8 show the outcomes for all criteria for each of the six values of
. For all the criteria, the probability of choosing
increases as
increases in magnitude.
To assist the interpretation of these plots, we computed the simple measures
and
for each criteria. In all six cases, the CACF was the best according to both
and
. The lower panels of
Figure 7 and
Figure 8 show just the CACF and the criteria that was second best according to
. For
, the FPE was the second best, while for
and
, HQ and AICC were second best, respectively.
This is also brought out in
Table 2, which shows the
measures for the two extreme cases
and
. Observe how, in the former, the SBC and AICC perform significantly worse than the other criteria, while for
, they are 2nd and 3rd best. This example clearly demonstrates the utility of the new CACF method, and also emphasizes how the performance of the various penalty-based criteria are highly dependent on the true autoregressive model parameters.
The results for the case were not as unambiguous. For each of the six models, a value of c could be found that rendered the CACF method either the best or a close second best. These ranged from for to for . When using a constant value of c between these two extremes such as , the AIC and FPE performed better for , while SBC and AICC were better for .
5.5. Parsimonious Model Selection
The frequentist order selection methods such as the the sequential one proposed herein and—even more so—the penalty-based methods, have the initial appeal of being objective. However, the infusion of “prior information”, most often in the forms of non-quantitative beliefs and opinions, is ubiquitous when building models with real data; the well-known quote from Edward Leamer (“There are two things you are better off not watching in the making: sausages and econometric estimates”) immediately comes to mind. Indeed, the empirical case studies by
Pankratz (
1983) make clear the desire for parsimonious models and attempt to “downplay” the significance of spikes in the correlograms or
p-values of estimates at higher order lags that are not deemed “sensible”. Moreover, any experienced modeler has a sense, explicit or not, of the maximally acceptable number of model parameters allowed with respect to the available sample size, and is (usually) well aware of the dangers of overfitting.
3Letting the level of a test decrease with increasing sample size is common and good practice in many testing situations; for discussion see
Lehmann (
1958),
Sanathanan (
1974), and
Lehmann (
1986, p. 70). When the level of the test is fixed and the sample size is allowed to increase, the power can increase to unacceptably high values, forcing the type I and type II errors to be out of balance. Indeed, such balance is important in the model selection context, because the consequences of the two error types are not especially different as they would be in the more traditional testing problem. Furthermore, there may be a desire to have the relative values of the two error types reflect the desire for parsimony. In the context of our sequential test procedure, such preferences would suggest using smaller levels when testing for larger lag
m, and increasingly larger levels as the lag order tested becomes smaller. Thus, at each stage of the testing, balance may be achieved between the two types of errors to reflect the desired parsimony.
This frequentist “trap” could be avoided by conducting an explicit Bayesian analysis instead. While genuine Bayesian methods have been pursued (see, for example,
Zellner 1971;
Schervish and Tsay 1988;
Chib 1993;
Le et al. 1996;
Brooks et al. 2003; and the references therein), their popularity is quite limited. The CACF method proposed herein provides a straightforward method of incorporating the preference for low order models, while still being as “objective” as any frequentist hypothesis testing procedure can, for which the size of the test needs to be chosen by the analyst. This is achieved by letting the tuning parameter
c be a vector with different values for different lags. For example, with the AR(4) case considered previously, the optimal choice would be
. While certainly such flexibility could be abused to arrive at virtually any desired model, it makes sense to let the elements of
decrease in a certain manner if there is a preference for low-order parsimonious models. Notice also that, if seasonal effects are expected, then the
vector could also be chosen to reflect this.
To illustrate, we applied the simple linear sequence
to the
case. This resulted in the CACF method being the best for all values of
except the last,
, in which case it was slightly outperformed by the SBC. As was expected, when using (
19) for the time series with
, the CACF remained superior in all cases but by an even larger margin.
6. Mixed ARMA Models
Virtually undisputed in time series modeling is the sizeable increase in difficulty for identifying the orders in the mixed, i.e., ARMA, case. It is interesting to note that, in the multivariate time series case, the theoretical and applied literature is dominated by strict AR models (vector autoregressions), whether for prediction purposes or for causality testing. Under the assumption that the true data generating process does not actually belong to the ARMA class, it can be argued that, for forecasting purposes, purely autoregressive structures will often be adequate, if not preferred; see also
Zellner (
2001) and the references therein. Along these lines, it is also noteworthy that the thorough book on regression and time series model selection by
McQuarrie and Tsai (
1998) only considers order selection for autoregressive models in
both the univariate and multivariate case. Their only use for an MA(1) model is to demonstrate AR lag selection in misspecified models.
Nevertheless, it is of interest to know how the CACF method performs in the presence of mixed models. While the use of penalty-based criteria for mixed model selection is straightforward, it is not readily apparent how the CACF method can be extended to allow for moving average structures. This section presents a way of proceeding.
6.1. Known Moving Average Structure
The middle left and lower left panels of
Table A1 and
Table A2 show the CACF results when using the same AR structure as previously, but with a
known moving average structure, i.e., (
15) is calculated taking
corresponding to an MA(1) model. As with all model results in
Table A1 and
Table A2, the sample size is
. This restrictive assumption allows a clearer comparison of methods without the burden of MA order selection or estimation; this will be relaxed in the next section, so that the added effect of MA parameter estimation can be better seen.
Models 1.5 through 6.5 take the MA parameter to be 0.5, while models 1.9 through 6.9 use . For the null models 1.5 and 1.9, only a slight degradation of performance is seen. For the other models, on average, the probability of selecting increases markedly as increases, drastically so for model 6.
The results can be compared to the entries in
Table A3 through
Table A7 labeled “For ARMA(
p,1) Models”, for which the penalty-based criteria were computed for the five models ARMA(
i,1),
. (Notice that the comparison is not entirely fair because the CACF method has the benefit of knowing the MA polynomial, not just its length.) Consider the
cases first. For the null model 1.5x, the CACF performed as expected under the null hypothesis, with
choices of
and about
for each of the other choices. It was outperformed however by the SBC, with
choices and an ever diminishing probability as
p increases, which agrees with the SBC’s known properties of low model order preference. The
choices for the other criteria were between
(AIC and FPE) and
(HQ). For model 2.5x, in terms of number of
choices, CACF, AIC and FPE were virtually tied with about
, while SBC, HQ and AICC gave
,
and
, respectively. The CACF for models 3.5x and 4.5x performed—somewhat unexpectedly in light of previous results—relatively well: For model 3.5x, CACF resulted in
choices of
, while the SBC was the worst, with
. The others were all about
. Similarly for model 4.5x: CACF (
), AIC (
), SBC (
), AICC (
), HQ (
) and FPE (
). Model 5.5x resulted in (approximately) CACF, AIC and FPE (
), and SBC, AICC and HQ (
). For model 6.5x, the CACF was disasterous, with only
for
, while the other criteria ranged from
(SBC) to
(AIC).
As before, the performance of all the criteria is highly dependent on the true model parameters. However, what becomes apparent from this study is the great disparity in performance: For a particular model, the CACF may rank best and SBC the worst, while for different parameter constellation, precisely the opposite may be the case. That the SBC is often among the best performers agrees with the findings of
Koreisha and Yoshimoto (
1991) and the references therein.
The results for the cases do not differ remarkably from the cases, except that for models 3.9x and 4.9x, all the penalty-based criteria were much closer to (and occasionally slightly better) than the CACF.
6.2. Iterative Scheme for ARMA() Models with q Known
Assume, somewhat more realistically than before, that the regression error terms follow a stationary ARMA(
p,
q) process with
q known, but the actual MA parameters
and
p are not known. A possible method for eliciting
p using the sequential test (
15) is as follows: Iterate the two following steps starting with
: (i) Estimate an ARMA(
) model to obtain
; (ii) Compute
with
corresponding to the MA(
q) model with parameters
, from which
is determined. Iteration stops when
(or
i exceeds some preset value,
I), and
is set as before for a given value of
c. The choice of
m and
c will clearly be critical to the performance of this method; simulation, as detailed next, will be necessary to determine its usefulness.
The right panels of
Table A1 and
Table A2 show the results when applied to the same 500 simulated time series of length
as previously used, but with the aforementioned iterative scheme applied with
and
(also as before),
and
. Unexpectedly, for the null model 1,
was actually chosen more frequently than under the known
cases, for each choice of
. Not surprisingly, for the
cases, the iterative schemes resulted in poorer performance compared to their known
counterparts, with model under-selection (i.e.,
) occurring more frequently, drastically so for models 3 and 4. For
, models 3 and 4 again suffer from under-selection, though less so than with
, while the remaining models exhibit an overall mild improvement in lag order selection. In the
case, performance is about the same whether
is known or not for all 6 models, though for model 6, high over-selection in the
known case is reversed to high under-selection for
not known.
The number of iterations required until convergence and the probability of not converging (given in the column labeled ) also depends highly on the true model parameters; models for which the true AR polynomial roots were smallest exhibited the fastest convergence. Nevertheless, in most cases, one or two iterations were enough, and the probability of non-convergence appears quite low. (The few cases that did not converge were discarded from the analysis.) While certainly undesirable, if the iterative scheme does not converge, it does not mean that the results are not useful. Most often, the iterations bounced back and forth between two choices, from which a decision could be made based on “the subjective desire for parsimony” and/or inspection of the actual p-values, which could be very close to the cutoff values, themselves having been arbitrarily chosen.
To more fairly compare the CACF results with the penalty-based criteria, the latter were evaluated using the 10 models AR(
i), ARMA(
i,1),
, the results of which are in
Table A3 through
Table A7 under the heading “Among both Sets”. To keep the analysis short,
Table 3 presents only the percentage of correct
p choices for two criteria (CACF and the 1st or 2nd best). The CACF was best 6 times, SBC and AICC were each best 5 times, while HQ and FPE were best one time each. It must be emphasized that these numbers are a very rough reduction of the performance data. For example,
Table 3 shows that cases 2.0x and 2.5x were extremely close, while 6.0x, 3.5x, 4.5x, 5.5x, 1.9x were reasonably close. A fair summary appears to be that
In most cases, either the CACF, SBC and AICC will be the best,
Each of these can perform (sometimes considerably) better than the other two for certain parameter constellations,
Each can perform relatively poorly for certain parameter constellations.
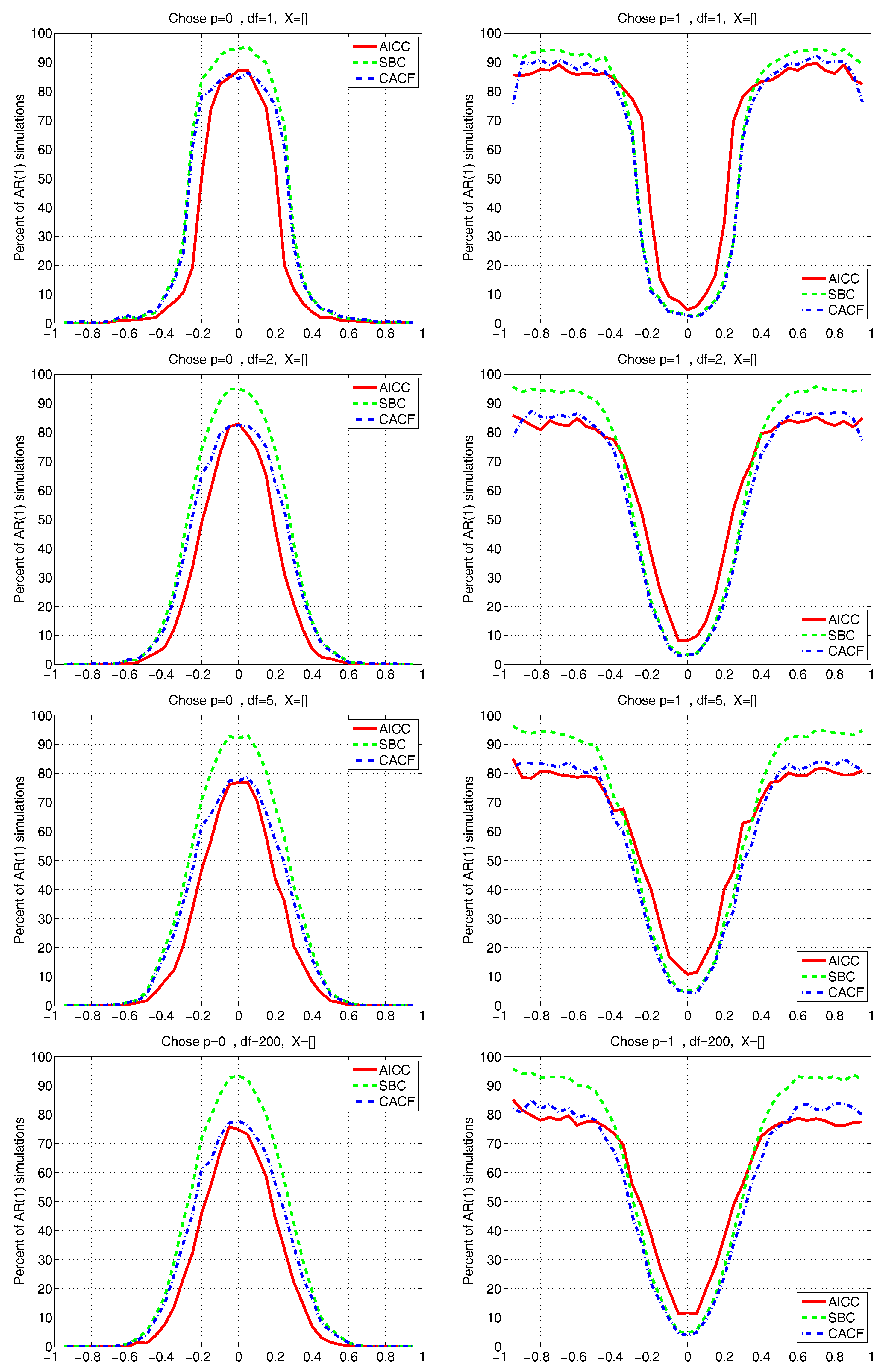
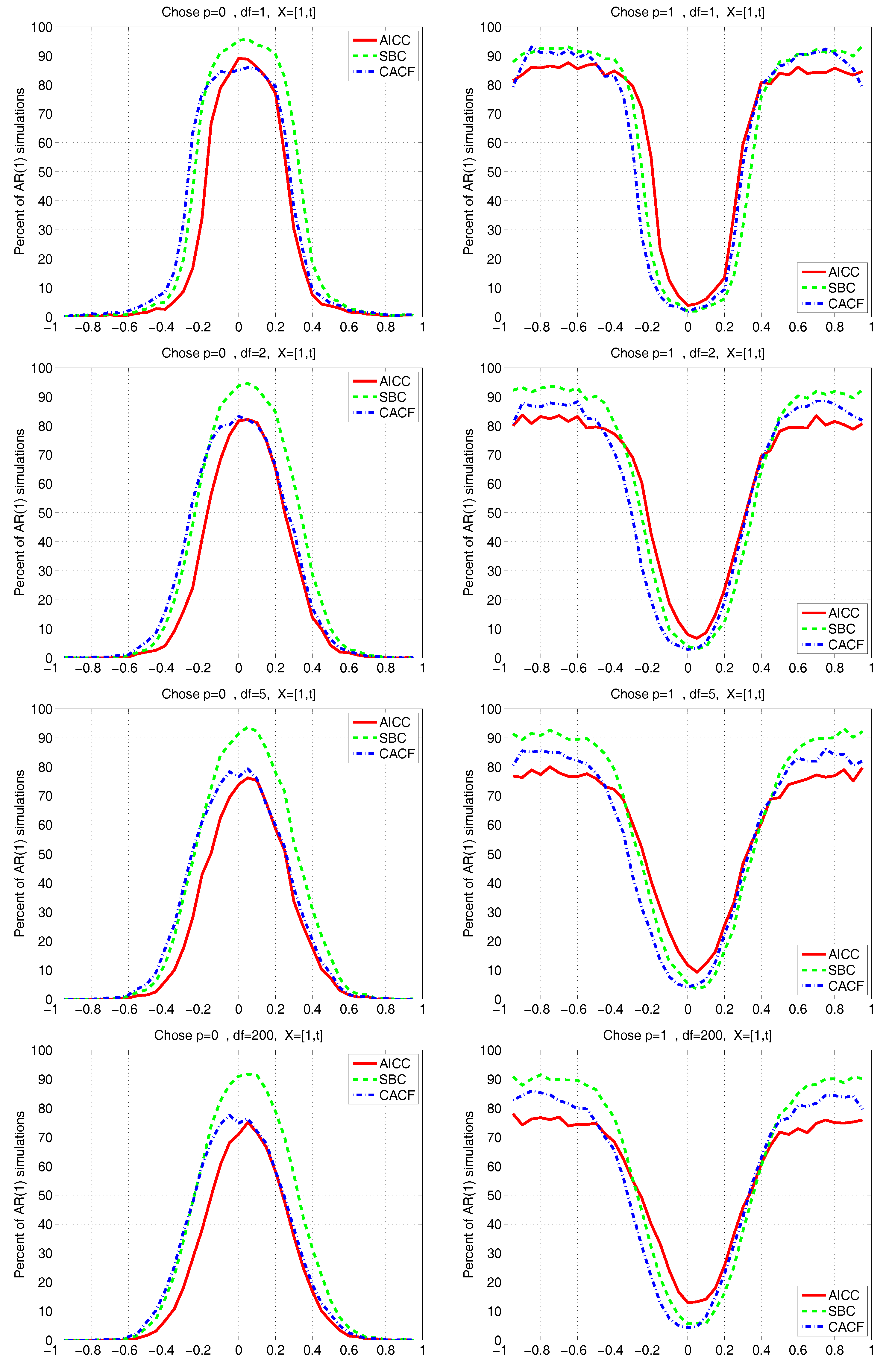
7. Performance in the Non–Gaussian Setting
All our findings above are based on the assumptions that the true model is known to be a linear regression with correctly specified matrix; error terms are from a Gaussian AR(p) process; tuning parameter m is chosen such that ; and parameters p, , , and are fixed but unknown. We now modify this by assuming, similarly, that the true data generating process is , with a stationary AR(1) process, but now such that , , i.e., Student’s t with degrees of freedom, location zero, and scale .
Figure 9 and
Figure 10 depict the results for the CACF, AICC, and SBC methods, having used a grid of
-values, true
, a sample size of
,
,
, and four different values of degrees of freedom parameter
; and
for all methods falsely assuming Gaussianity.
Figure 9 is for the known mean case, while
Figure 10 assumes the constant and time-trend model
.
We see that none of the methods are substantially affected by use of even very heavy-tailed innovation sequences, notably the CACF, which explicitly uses the normality assumption in the small-sample distribution theory. However, note from the top left panel of
Figure 9 (which corresponds to
, or Cauchy innovations) that, for
, instead of
from (
18), the null of
is chosen about 86% of the time, while from the third and fourth rows (for
and
), it is about 78%. This was to be expected: In the non-Gaussian case, (
18) is no longer tenable, as (i) the
are no longer independent; and (ii) their marginal distributions under the null will no longer be precisely (at least up to the accuracy allowed for by the saddlepoint approximation)
. In particular, the latter violation is such that the empirically obtained quantiles of
under the null no longer match their theoretical ones, and, as seen, the probability that
falls outside the range, say,
, is smaller than 0.05. This results in the probability of choosing
when it is true being larger than the nominal of 0.774.
Similarly, the choice of
when
should occur about 5% of the time for the CACF method, but, from the right panels of
Figure 9, it is lower than this, decreasing as
decreases. However, for
, it is already very close to the nominal of 5%. Interestingly, with respect to choosing
, the behavior of the CACF for all choices of
is virtually identical to the AICC near
, while as
grows, the behavior of the CACF coincides with that of the SBC. (Note that this behavior is precisely what we do
not want: Ideally, for
, the method would always choose
, while for
, the method would never choose
.)
Figure 10 is similar to
Figure 9, but having used
. Observe how, for all values of
, unlike the known mean case, the performance of the AICC and SBC is no longer symmetric about
, but the CACF is still virtually symmetric. Fascinatingly, we see from the left panels of
Figure 10 that the CACF probability of choosing
virtually coincides with that of the AICC for
, while for
, it virtually coincides with that of the SBC.
8. Conclusions
We have operationalized the UMPU test for sequential lag order selection in regression models with autoregressive disturbances. This is made possible by using a saddlepoint approximation to the joint density of the sample autocorrelation function based on ordinary least squares residuals from arbitrary exogenous regressors and with an arbitrary (covariance stationary) variance-covariance matrix. Simulation results verify that, compared to the popular penalty-based model selection methods, the new method fairs very well precisely in situations that are both difficult and common in practice: when faced with small samples and an unknown mean term. With respect to the mean term, the superiority of the new method increases as the complexity of the exogenous regressor matrix
increases; this is because the saddlepoint approximation explicitly incorporates the
matrix, differing from the approximation developed in
Durbin (
1980), which only takes account of its size, or the standard asymptotic results for the sample ACF and sample partial ACF, which completely ignore the regressor matrix.
The simulation study also verifies a known (but—we believe—not well-known) fact that the small sample performances of penalty-based criteria such as SBC and (corrected) AIC are highly dependent on the actual autoregressive model parameters. The same result was found to hold true for the new CACF method as well. Autoregressive parameter constellations were found for which CACF was greatly superior to all other methods considered, but also for which CACF ranked among the worst performers. Based on the use of a wide variety of parameter sets, we conclude that the new CACF method, the SBC and the corrected AIC, in that order, are the preferred methods, although, as mentioned, their comparative performance is highly dependent on the true model parameters.
An aspect of the new CACF method that greatly enhances its ability and is not applicable with penalty-based model selection methods is the use of different sizes for the sequential tests. This allows an objective way of incorporating prior notions of preferring low order, parsimoniously parameterized models. This was demonstrated using a linear regression model with AR(4) disturbance terms; the results highly favor the use of the new method in conjunction with a simple, arbitrarily chosen, linear sequence of size values. More research should be conducted into finding optimal, sample-size driven choices of this sequence.
Finally, the method was extended to select the autoregressive order when faced with ARMA disturbances. This was found to perform satisfactorily, both numerically as well as in terms of order selection.
Matlab programs to compute the CACF test and some of the examples in the paper are available from the second author.