Twenty-Two Years of Inflation Assessment and Forecasting Experience at the Bulletin of EU & US Inflation and Macroeconomic Analysis
Abstract
1. Introduction
2. Econometric Background in BIAM Methodology
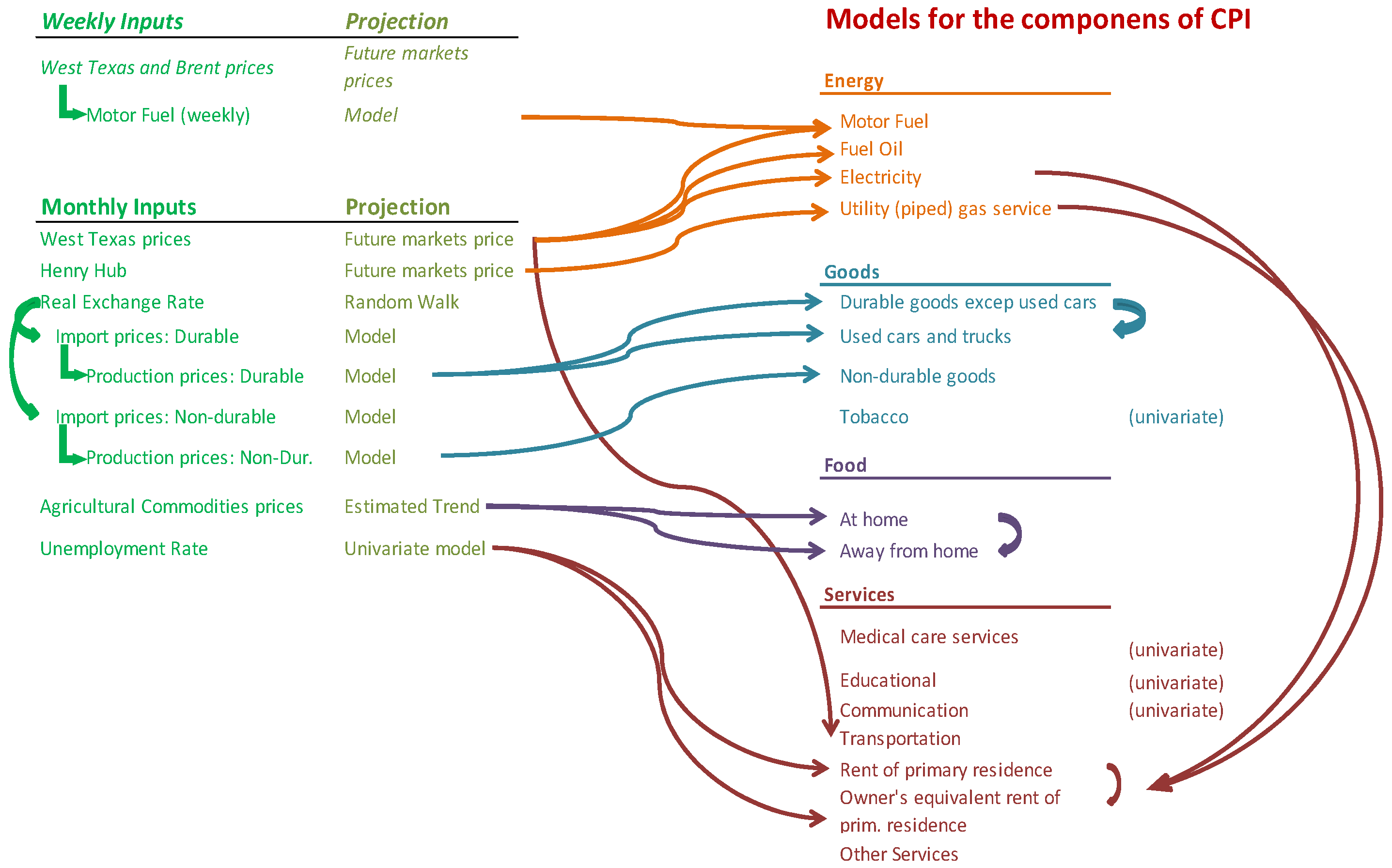
2.1. Indirect Forecasts and Disaggregation
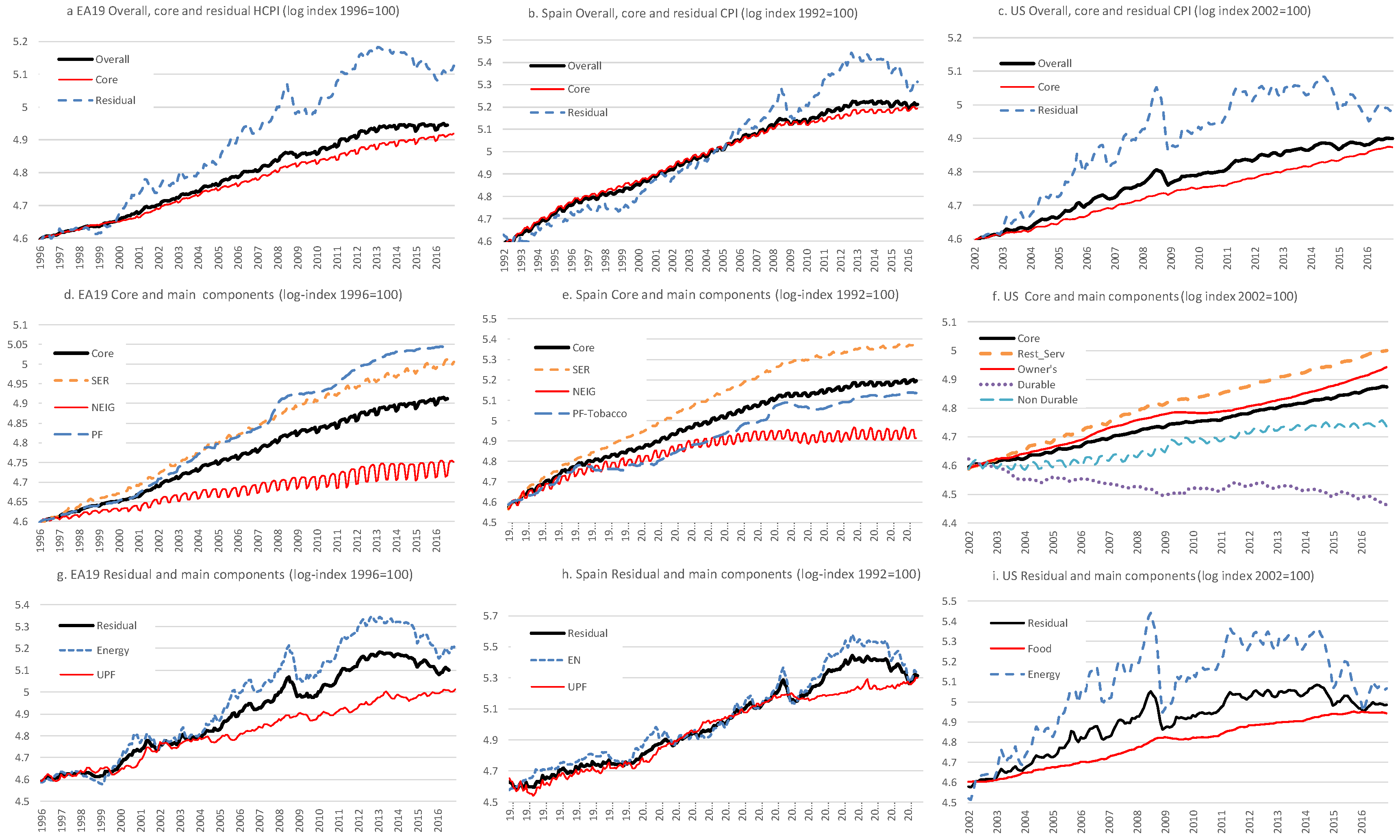
2.2. An Initial Basic Disaggregation
2.3. Criteria for Disaggregation Schemes
2.4. Hierarchical Forecasts
2.5. Intervention Analysis, Outlier Correction and Robust Forecasts. Breaks in Seasonality
2.6. Linking the Forecasts from Leading Indicator Models with Those from Congruent Econometric Models
3. The Assessment of Inflation and Inflation Expectations: An Application of the BIAM Methodology
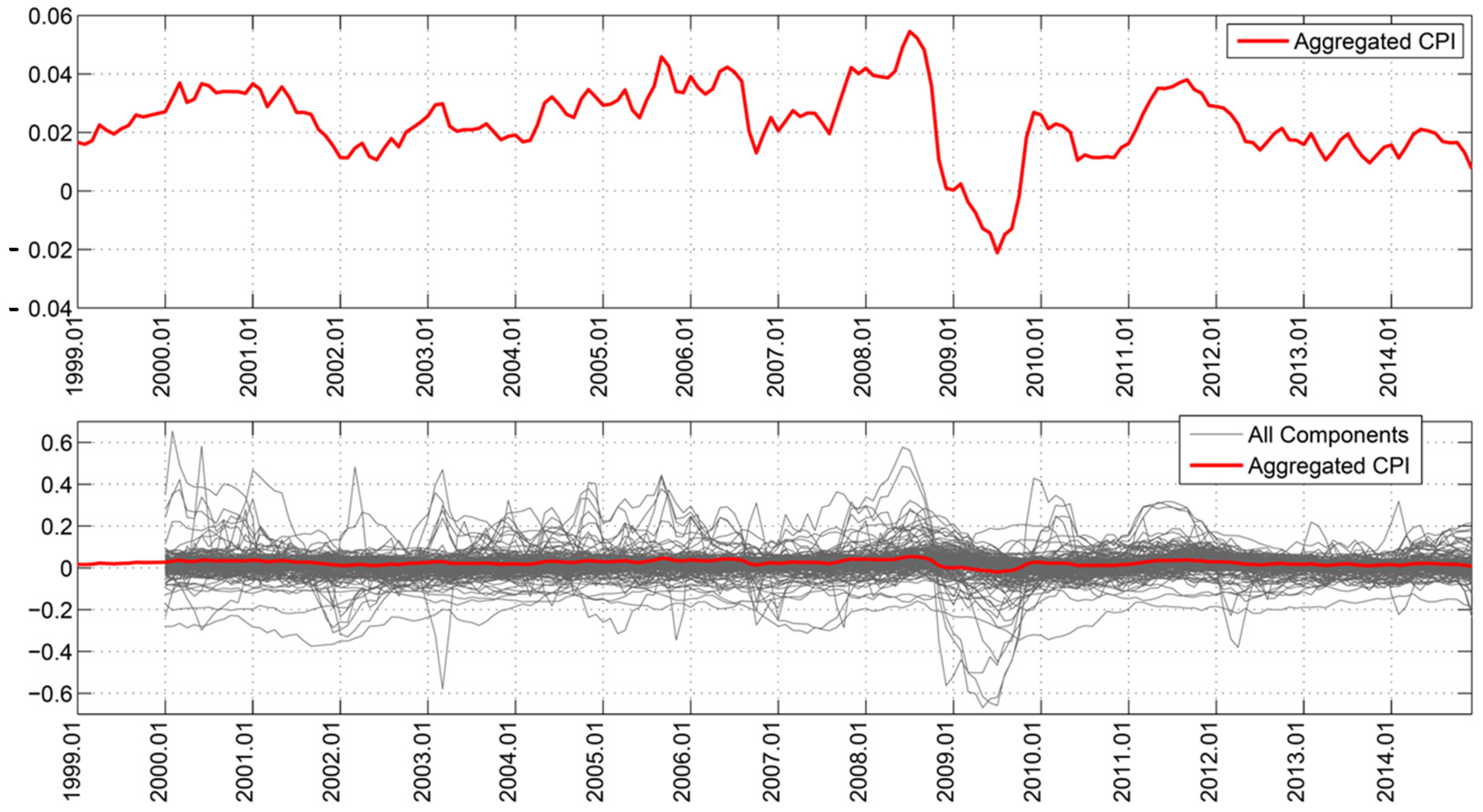
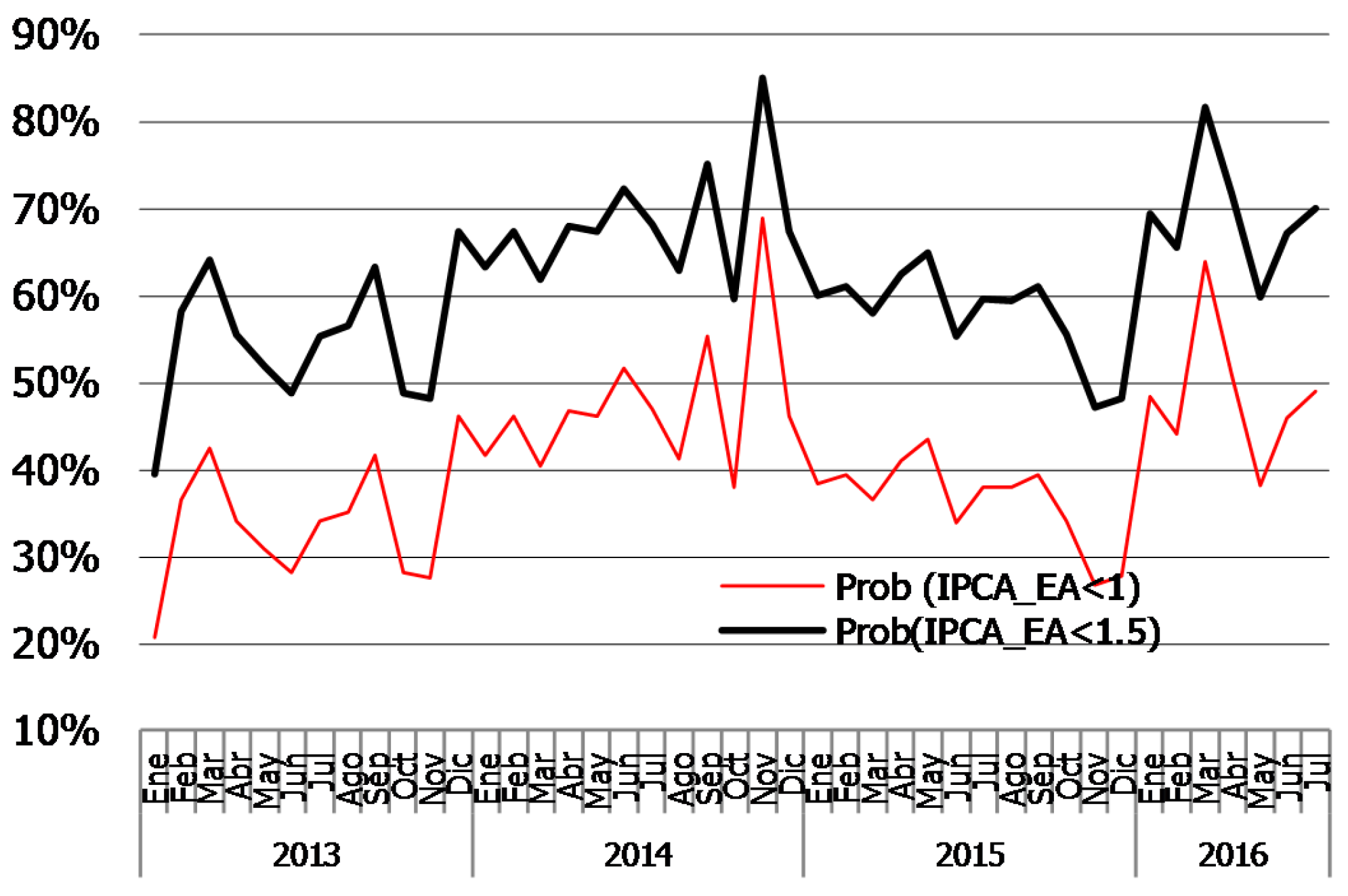
3.1. Evaluating New Data: The Information Content in the Forecast Error
3.2. Updating Forecasts
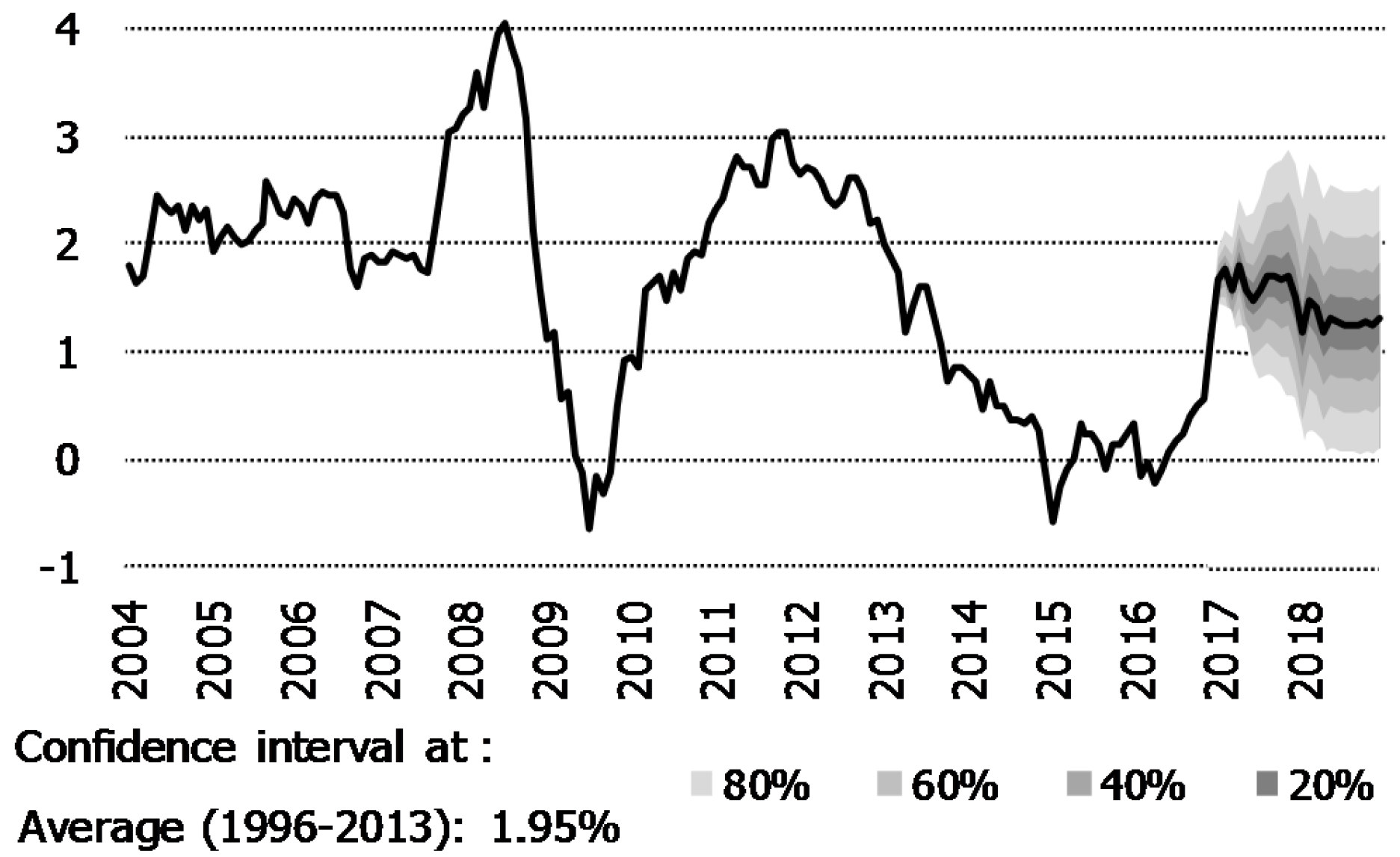
3.3. Using Quantitative Measures of the Uncertainty around the Forecasts
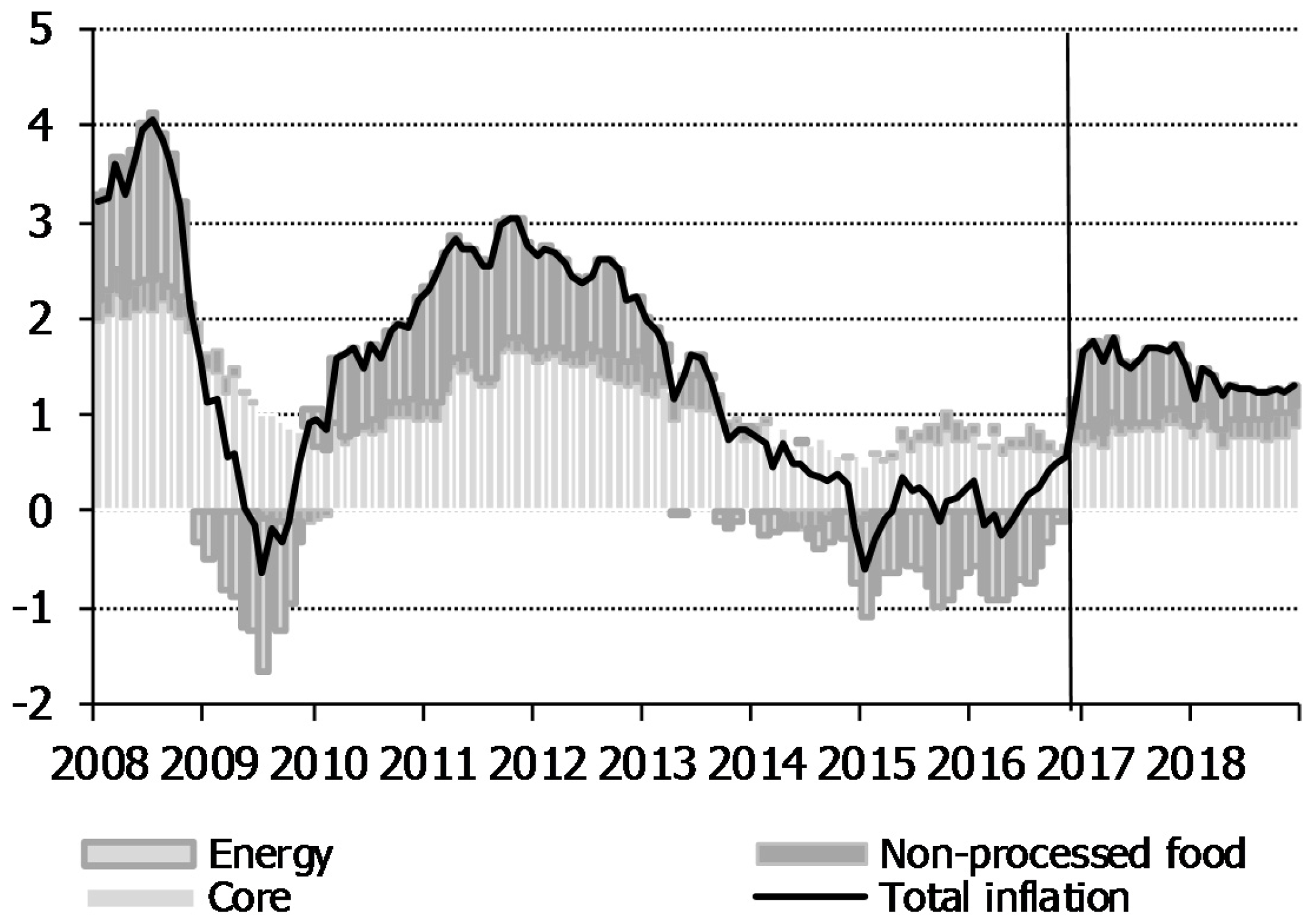
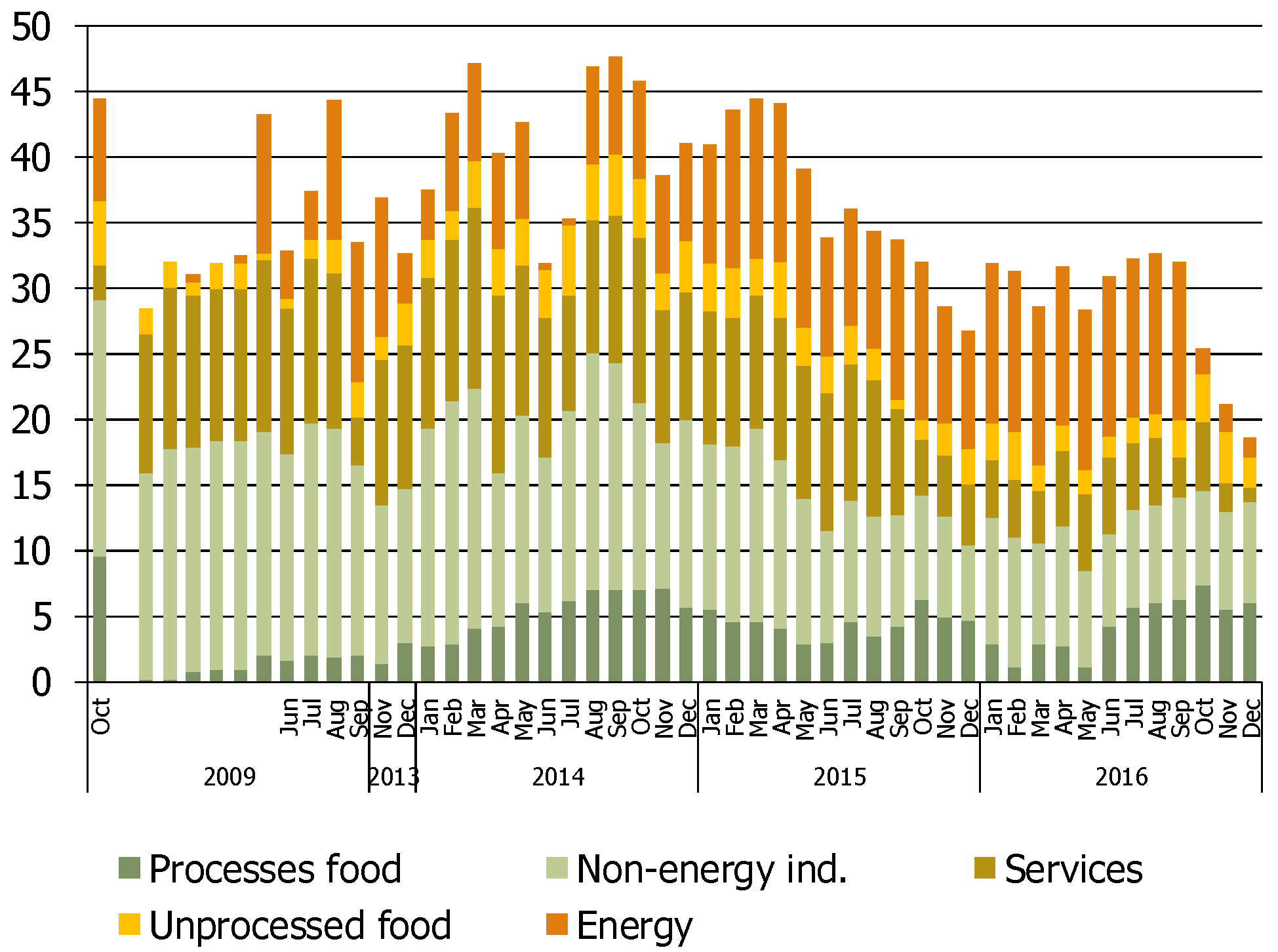
3.4. Use of Detailed Component Forecasts
4. Evaluating Forecasting Performance
BIAM Forecast Comparison with ECB Survey of Professional Forecasters
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aiolfi, Marco, Carlos Capistran, and Allan Timmermann. 2011. Forecast combinations. In The Oxford Handbook of Economic Forecasting. Edited by Michael Clements and David Forbes Hendry. Oxford: Oxford University Press, pp. 355–88. [Google Scholar]
- Altissimo, Filippo, Benoit Mojon, and Paolo Zaffaroni. 2007. Fast micro and slow macro: Can aggregation explain the persistence of inflation? Working Paper No. 2007-02. Federal Reserve of Chicago. [Google Scholar]
- Aron, Janine, and John Muellbauer. 2012. Improving forecasting in an emerging economy, South Africa: Changing trends, long run restrictions and disaggregation. International Journal of Forecasting 28: 456–76. [Google Scholar] [CrossRef]
- Athanasopoulos, George, Roman Ahmed, and Rob J. Hyndman. 2009. Hierarchical forecasts for Australian domestic tourism. International Journal of Forecasting 25: 146–66. [Google Scholar] [CrossRef]
- Bates, John M., and Clive W. J. Granger. 1969. The combination of forecasts. Operational Research Quarterly 20: 451–68. [Google Scholar] [CrossRef]
- Beck, Guenter W., Kirstin Hubrich, and Massimiliano Marcellino. 2011. On the Importance of Sectoral and Regional Shocks for Price-Setting. Working Paper Series 1334, Frankfurt, Germany: European Central Bank. [Google Scholar]
- BIAM 266. 2016. Bulletin of EU&US Inflation and Macroeconomic Analysis. Madrid: Universidad Carlos III de Madrid. Available online: http://www.uc3m.es/biam (accessed on 30 December 2016).
- Bils, Mark, and Peter J. Klenow. 2004. Some evidence on the importance of sticky prices. Journal of Political Economy 112: 947–85. [Google Scholar] [CrossRef]
- Boivin, Jean, Marc P. Giannoni, and Ilian Mihov. 2009. Sticky prices and monetary policy: Evidence from disaggregated us data. The American Economic Review 99: 350–84. [Google Scholar] [CrossRef]
- Bowles Carlos, Roberta Fritz, Véronique Genre, Geoff Kenny, Aidan Meyler, and Tuomas Rautanen. 2007. The ECB Survey of Professional Forecasters (SPF). A Review after Eight Years’ Experience. (Occasional Paper Series 59); Frankfurt, Germany: European Central Bank. [Google Scholar]
- Bowles, Carlos, Roberta Fritz, Véronique Genre, Geoff Kenny, Aidan Mayler, and Tuomas Rautanen. 2010. An Evaluation of the Growth and Unemployment Forecasts in the ECB Survey of Professional Forecasters. OECD Journal: Journal of Business Cycle Measurement and Analysis 2: 63–90. [Google Scholar] [CrossRef]
- Britton, Erik, Paul G. Fisher, and John D. Whitley. 1998. The Inflation Report projections: understanding the fan chart. Bank of England Quarterly Bulletin 38: 30–37. [Google Scholar]
- Carlomagno, Guillermo. 2016. Discovering Common Features in a Large Set of Disaggregates. Methodology, Modelling and Forecasting. Ph.D. dissertation, Statistics Department, Universidad Carlos III, Madrid, Spain, February. [Google Scholar]
- Carlomagno, Guillermo, and Antoni Espasa. 2015a. Discovering Common Trends in a Large Set of Disaggregates: Statistical Procedures and Their Properties. UC3M Working Paper 15-19. Madrid: University Carlos III. [Google Scholar]
- Carlomagno, Guillermo, and Antoi Espasa. 2015b. Forecasting a Large Set of Disaggregates with Common Trends and Outliers. UC3M Working Paper 15-18. Madrid: University Carlos III. [Google Scholar]
- Castle, Jennifer L., Jurgen A. Doornik, David F. Hendry, and Felix Pretis. 2015. Detecting location shifts during model selection by step-indicator saturation. Econometrics 3: 240–64. [Google Scholar] [CrossRef]
- Clark, Todd E. 2006. Disaggregate evidence on the persistence of consumer price inflation. Journal of Applied Econometrics 21: 563–87. [Google Scholar] [CrossRef]
- Clemen, Robert T. 1989. Combining forecasts: A review and annotated bibliography. International Journal of Forecasting 5: 559–83. [Google Scholar] [CrossRef]
- Clements, Michael P., and David F. Hendry. 1993. On the limitations of comparing mean squared forecast errors. Journal of Forecasting 12: 617–37, (With Discussion 669–76). [Google Scholar] [CrossRef]
- Conflitti, Cristina, Christine De Mol, and Domenico Giannone. 2015. Optimal combination of survey forecasts. International Journal of Forecasting 31: 1096–103. [Google Scholar] [CrossRef]
- Cuevas, Angel, Enrique Quilis, and Antoni Espasa. 2015. Quarterly Regional GDP Flash Estimates by Means of Benchmarking and Chain-Linking. Journal of Official Statistics 31: 627–47. [Google Scholar] [CrossRef]
- De Menezes, Lillian M., Derek W. Bunn, and James W. Taylor. 2000. Review of guidelines for the use of combined forecasts. European Journal of Operational Research 120: 190–204. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business & Economic Statistics 20: 134–44. [Google Scholar]
- Doornik, Jurgen A., and David F. Hendry. 2016. Outliers and models selection: Discussion of the paper by Soren Johansen and Bent Nielsen. Scandinavian Journal of Statistics 43: 360–65. [Google Scholar] [CrossRef]
- Dreger, Christian, and Massimiliano Marcellino. 2007. A Macroeconometric Model for the Euro economy. Journal of Policy Modeling 29: 1–13. [Google Scholar] [CrossRef]
- Dreger, Christian. 2002. A Macroeconometric Model for the Euro Area. Halle (IWH), Germany: Institute for Economic Research, manuscript. [Google Scholar]
- ECB. 2014. Fifteen years of the ECB Survey of Professional Forecasters. In ECB Monthly Bulletin. Frankfurt: European Central Bank. [Google Scholar]
- EFN. 2013. EFN Report Economic Outlook for the Euro Area in 2013 and 2014. Available online: http://www.eui.eu/Documents/RSCAS/Research/EFN/Reports/EFN2013/EFN2013autumn.pdf (accessed on 30 September 2017).
- Espasa, Antoni, and Rebeca Albacete. 2007. Econometric modelling for short-term inflation forecasting in the euro area. Journal of Forecasting 26: 303–16. [Google Scholar] [CrossRef]
- Espasa, Antoni, and M. Llanos Matea. 1991. Underlying Inflation in the Spanish Economy: Estimation and Methodology. Working Paper 91-30. Madrid, Spain: Department of Economics, Universidad Carlos III, November, Italian translation published in Note Economiche. vol. XXI, No. 3, 477–93. [Google Scholar]
- Espasa, Antoni, and Iván Mayo-Burgos. 2013. Forecasting aggregates and disaggregates with common features. International Journal of Forecasting 29: 718–32. [Google Scholar] [CrossRef]
- Espasa, Antoni, Ascensión Molina, and Eva Ortega. 1984. Forecasting the Rate of Inflation by Means of the Consumer Price Index. Working paper 8416. Paper presented at the Fourth International Symposium on Forecasting, London, UK; Banco de España, Madrid, Spain. [Google Scholar]
- Espasa, Antoni, M. Llanos Matea, and M. Cruz Manzano. 1987. La inflación subyacente en la economía española: Estimación y metodología. In Boletín Económico. Madrid: Banco de España. [Google Scholar]
- Espasa, Antoni, Eva Senra, and Rebeca Albacete. 2002a. Forecasting inflation in the European Monetary Union: A disaggregated approach by countries and by sectors. The European Journal of Finance 8: 402–21. [Google Scholar] [CrossRef]
- Espasa, Antoni, Pilar Poncela, and Eva Senra. 2002. Forecasting Monthly US Consumer Price Indexes through a Disaggregated I (2) Analysis. Working Paper 02-03. Madrid: University Carlos III. [Google Scholar]
- Genre Véronique, Geoff Kenny, Aida Meyler, and Allan Timmermann. 2013. Combining expert forecasts: Can anything beat the simple average? International Journal of Forecasting 29: 108–21. [Google Scholar] [CrossRef]
- Hendry, David F. 2006. Robustifying forecasts from equilibrium-correction systems. Journal of Econometrics 135: 399–426. [Google Scholar] [CrossRef]
- Hendry, David. F., and Jurgen A. Doornik. 2014. Empirical Model Discovery and Theory Evaluation. Cambridge: MIT Press. [Google Scholar]
- Hendry, David F., and Kirstin Hubrich. 2011. Combining disaggregate forecasts or combining disaggregate information to forecast an aggregate. Journal of Business & Economic Statistics 29: 216–27. [Google Scholar]
- Hyndman, Rob J., Roman Ahmed, George Athanasopoulos, and Han Lin Shang. 2011. Optimal combination forecasts for hierarchical time series. Computational Statistics & Data Analysis 55: 2579–89. [Google Scholar]
- Imbs, Jean, Haroon Mumtaz, Morten O. Ravn, and Helene Rey. 2005. PPP strikes back: Aggregation and the real exchange rate. The Quarterly Journal of Economics 120: 1–43. [Google Scholar]
- Johansen, Soren, and Bent Nielsen. 2016. Asymptotic theory of outlier detection algorithms for linear time series regression models. Scandinavian Journal of Statistics 43: 321–48. [Google Scholar] [CrossRef]
- Juselius, Katarina. 2015. Haavelmo’s probability approach and the cointegrated VAR. Econometric Theory 31: 213–32. [Google Scholar] [CrossRef]
- Lorenzo, Fernando. 1997. Modelización de la Inflación con fines de Predicción y Diagnóstico. Ph.D. dissertation, Department of Statistics and Econometrics, Universidad Carlos III, Madrid, Spain, September. [Google Scholar]
- Lunnemann, Patrick, and Thomas Y. Mathä. 2004. How persistent is disaggregate inflation? An analysis across EU 15 countries and HICP sub-indices. ECB Working Paper 415. Frankfurt, Germany: European Central Bank. [Google Scholar]
- Lütkepohl, Helmut. 1987. Forecasting Aggregated Vector ARMA Processes. Berlin: Springer-Verlag. [Google Scholar]
- Minguez, Román, and Antoni Espasa. 2006. A Time Series Disaggregated Model to Forecast GDP in the Eurozone. In Growth and Cycle in the Eurozone. Edited by Gian Luigi Mazzi and Giovanni Savio. Basingstoke: Palgrave, chp. 17. pp. 213–20. [Google Scholar]
- Newbold, Paul, and David I. Harvey. 2002. Forecast combination and encompassing. In A Companion to Economic Forecasting. Edited by Michael P. Clements and David F. Hendry. Hoboken: Wiley, pp. 268–83. [Google Scholar]
- Osborn, Denise, and Michael P. Clements. 2002. Unit root versus deterministic representations of seasonality for forecasting. In A Companion to Economic Forecasting. Edited by Michael P. Clements and David F. Hendry. Malden: Blackwell Publishers. [Google Scholar]
- Osborn, Denise, Saeed Heravi, and Chris R. Birchenhall. 1999. Seasonal unit roots and forecasts of two-digit European industrial production. International Journal of Forecasting 15: 27–47. [Google Scholar] [CrossRef]
- Peach, Richard W., Robert Rich, and Alexis Antonaides. 2004. The historical and recent behaviour of goods and services inflation. FRBNY Economic Policy Review 10: 19–31. [Google Scholar]
- Peach, Richard W., Robert Rich, and M. Hendry Linder. 2013. The parts are more than the whole: separating goods and services to predict core inflation. Current Issues in Economic and Finance 19: 1–8. [Google Scholar]
- Pino, Gabriel, Juan de Dios Tena, and Antoni Espasa. 2016. Geographical disaggregation of sectoral inflation. Econometric modelling of the Euro area and Spanish economies. Applied Economics 48: 799–815. [Google Scholar] [CrossRef]
- Poncela, Pilar, and Eva Senra. 2017. Measuring uncertainty and assessing its predictive power in the euro area. Empirical Economics 53: 165–82. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 2004. Combination forecasts of output growth in a seven-country data set. Journal of Forecasting 23: 405–30. [Google Scholar] [CrossRef]
- Timmermann, Allan. 2006. Forecast combinations. In Handbook of Economic Forecasting. Edited by Graham Elliott, Clive Granger and Allan Timmermann. Amsterdam: Elsevier, vol. 1, pp. 135–96. [Google Scholar]
- Wallis, Kenneth F. 1999. Asymmetric density forecasts of inflation and the Bank of England’s fan chart. National Institute Economic Review 167: 106–12. [Google Scholar] [CrossRef]
- Wallis, Kenneth F. 2011. Combining forecasts—Forty years later. Applied Financial Economics 21: 33–41. [Google Scholar] [CrossRef]
| 1 | In general, this assignment is approximated because some basic components might include prices corresponding to two different basic sub-aggregates, for instance, NEIG and SERV. Nevertheless, when this is the case, the prices inside the basic component belong mostly to one basic sub-aggregate. |
| 2 | We are grateful to Ángel Sánchez for preparing this figure. |
| Economic | Important differences in accessing to information on quality and prices of products on the different markets. |
| Different possibilities of incorporating technology. | |
| Competition in the sector. | |
| Stocking availability. | |
| Dependency on foreign prices and trade. | |
| Changing in habits or preferences. | |
| Institutional | Different regulations on indirect taxes. |
| Existence of administered prices. | |
| Special markets, like electricity. | |
| Statistical | Different trend. |
| Different seasonality. | |
| Different breaks and outliers. | |
| Different persistence. | |
| Non-linearity in the conditional means. | |
| Possibility of including leading indicators in the conditional means. |
| Disaggregates | Weight 2016 | Average | Standard Deviation |
|---|---|---|---|
| Euro Area (Sample: Jan 1997–Aug 2016) | |||
| CPI | 1000.00 | 1.72 | 0.93 |
| Core | 828.53 | 1.54 | 0.53 |
| Processed Food (PF) | 97.38 | 1.73 | 1.60 |
| Tobacco (T) | 23.88 | 4.95 | 2.28 |
| Non Energy Industrial Goods (NEIG) | 265.45 | 0.68 | 0.40 |
| Services (SER) | 441.82 | 1.99 | 0.58 |
| Residual | 171.47 | 2.52 | 3.87 |
| Unprocessed Food (UPF) | 74.07 | 2.01 | 2.04 |
| Energy (EN) | 97.4 | 2.96 | 6.60 |
| Spain (Sample: Jan 1993–Aug 2016) | |||
| CPI | 1000.00 | 2.55 | 1.6 |
| Core | 815.13 | 2.48 | 1.39 |
| Processed Food (PF) | 125.05 | 2.24 | 2.28 |
| Tobacco (T) | 144.8 | 7.02 | 4.84 |
| Non Energy Industrial Goods (NEIG) | 271.03 | 1.4 | 1.46 |
| Services (SER) | 399.3 | 3.23 | 1.69 |
| Residual | 184.87 | 2.96 | 4.67 |
| Unprocessed Food (UPF) | 70.3 | 2.82 | 3.05 |
| Energy (EN) | 114.57 | 3.08 | 7.69 |
| US (Sample: Jan 2003–Dec 2016) | |||
| CPI | 1000.00 | 2.06 | 1.38 |
| Core | 79.20 | 1.87 | 0.44 |
| Non Energy Commodities less Food | 19.60 | 0.08 | 1.08 |
| Durables | 9.60 | ࢤ0.88 | 1.51 |
| Non Durables | 10.00 | 0.99 | 1.08 |
| Non Energy Services | 59.60 | 2.54 | 0.69 |
| Owner´s equivalent rent of primary | 23.10 | 2.28 | 0.94 |
| Other Services | 36.40 | 2.76 | 0.64 |
| Residual | 20.80 | 2.68 | 5.53 |
| Food | 14.00 | 2.44 | 1.51 |
| Energy | 6.80 | 3.17 | 13.45 |
| Basic Sub-Aggregates | Weights 2015 | Observed | Forecasts | Confidence Intervals * |
|---|---|---|---|---|
| Processed Food | 122.72 | 0.09 | 0.09 | ±0.38 |
| Tobacco | 23.94 | 0.04 | 0.47 | |
| Processed food excluding tobacco | 98.78 | 0.10 | 0.02 | |
| Non-energy Industrial goods | 266.60 | 0.64 | 0.65 | ±0.21 |
| Services | 427.76 | −0.18 | −0.12 | ±0.14 |
| Core | 817.08 | 0.13 | 0.15 | ±0.13 |
| Non-processed food | 74.85 | −0.03 | 0.84 | ±0.72 |
| Energy | 108.07 | 1.60 | 1.30 | ±0.86 |
| Residual | 182.92 | 0.88 | 1.07 | ±0.57 |
| Overall | 1000.00 | 0.25 | 0.31 | ±0.12 |
| Core | Residual | Total HICP | 80 % Confidence Interval | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Processed Food Excluding Tobacco | Tobacco | Non Energy Industrial Goods | Services | Total CORE | 80 % Confidence Interval | Non Processed Food | Energy | Total Residual | ||||||
| Weights 2016 | 9.9% | 2.4% | 26.7% | 42.8% | 81.7% | 7.5% | 10.8% | 18.3% | ||||||
| Annual Average | ||||||||||||||
| 2015 | 0.0 | 3.0 | 0.3 | 1.2 | 0.8 | 1.6 | −6.8 | −3.4 | 0.0 | |||||
| 2016 | 0.1 | 2.3 | 0.4 | 1.1 | 0.8 | 1.4 | −5.1 | −2.3 | 0.2 | |||||
| 2017 | 0.1 | 2.3 | 0.3 | 1.2 | 1.0 | ± | 0.33 | 1.9 | 6.7 | 4.7 | 1.6 | ± | 0.65 | |
| 2018 | 1.4 | 4.0 | 0.5 | 1.0 | 1.0 | ± | 0.42 | 2.6 | 2.9 | 2.8 | 1.3 | ± | 0.80 | |
| ANNUAL RATES (year-on-year rates) | ||||||||||||||
| 2016 | July | 0.0 | 2.4 | 0.4 | 1.2 | 0.8 | 2.9 | −6.7 | −2.7 | 0.2 | ||||
| August | 0.0 | 2.3 | 0.3 | 1.1 | 0.8 | 2.5 | −5.6 | −2.2 | 0.2 | |||||
| September | 0.0 | 2.3 | 0.3 | 1.1 | 0.8 | 1.1 | −3.0 | −1.3 | 0.4 | |||||
| October | 0.1 | 2.3 | 0.3 | 1.1 | 0.7 | 0.2 | −0.9 | −0.4 | 0.5 | |||||
| November | 0.3 | 2.3 | 0.3 | 1.1 | 0.8 | 0.7 | −1.1 | −0.3 | 0.6 | |||||
| December | 0.3 | 2.5 | 0.3 | 1.3 | 0.9 | 2.1 | 2.6 | 2.4 | 1.1 | |||||
| 2017 | January | 0.3 | 2.9 | 0.3 | 1.2 | 0.8 | ± | 0.13 | 2.6 | 7.7 | 5.5 | 1.7 | ± | 0.14 |
| February | 0.5 | 3.1 | 0.2 | 1.3 | 0.9 | ± | 0.19 | 2.6 | 8.2 | 5.8 | 1.8 | ± | 0.27 | |
| March | 0.7 | 3.2 | 0.2 | 1.0 | 0.8 | ± | 0.24 | 2.2 | 7.6 | 5.2 | 1.6 | ± | 0.38 | |
| April | 0.7 | 3.1 | 0.3 | 1.5 | 1.1 | ± | 0.28 | 2.1 | 7.9 | 5.3 | 1.8 | ± | 0.50 | |
| May | 1.1 | 2.7 | 0.3 | 1.3 | 1.0 | ± | 0.33 | 1.6 | 6.3 | 4.2 | 1.6 | ± | 0.60 | |
| June | 1.2 | 2.8 | 0.4 | 1.2 | 1.0 | ± | 0.37 | 1.8 | 5.0 | 3.7 | 1.5 | ± | 0.70 | |
| July | 1.4 | 3.2 | 0.4 | 1.2 | 1.0 | ± | 0.42 | 1.1 | 6.3 | 4.1 | 1.6 | ± | 0.79 | |
| August | 1.4 | 3.3 | 0.4 | 1.2 | 1.0 | ± | 0.47 | 1.0 | 7.7 | 4.8 | 1.7 | ± | 0.88 | |
| September | 1.6 | 3.4 | 0.2 | 1.2 | 1.0 | ± | 0.53 | 2.1 | 7.0 | 4.9 | 1.7 | ± | 0.97 | |
| October | 1.6 | 3.9 | 0.4 | 1.2 | 1.1 | ± | 0.57 | 2.1 | 5.7 | 4.2 | 1.7 | ± | 1.04 | |
| November | 1.4 | 4.1 | 0.4 | 1.2 | 1.1 | ± | 0.61 | 2.1 | 6.4 | 4.6 | 1.7 | ± | 1.11 | |
| December | 1.5 | 4.2 | 0.5 | 1.2 | 1.1 | ± | 0.65 | 1.6 | 4.9 | 3.5 | 1.5 | ± | 1.17 | |
| 2018 | January | 1.5 | 4.2 | 0.3 | 1.0 | 0.9 | ± | 0.68 | 1.6 | 2.7 | 2.3 | 1.2 | ± | 1.23 |
| … | … | … | … | … | … | … | … | … | … | |||||
| December | 1.3 | 3.9 | 0.4 | 1.2 | 1.1 | ± | 0.69 | 3.0 | 2.1 | 2.4 | 1.3 | ± | 1.25 | |
| CPI | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Overall CPI | Confidence Intervals at 80% Level | CORE CPI | Confidence Intervals at 80% Level | PCE CORE | MB-PCE | ||||
| Weights 2016 | 100% | 79.2% | |||||||
| Annual Average | |||||||||
| 2015 | 0.12 | 1.83 | 1.4 | 1.0 | |||||
| 2016 | 1.26 | ± | 0.01 | 2.21 | ± | 0.01 | 1.7 | 1.4 | |
| 2017 | 2.13 | ± | 0.54 | 2.22 | ± | 0.23 | 1.8 | 1.8 | |
| 2018 | 1.97 | ± | 0.65 | 2.27 | ± | 0.30 | 2.0 | 1.9 | |
| ANNUAL RATES (year-on-year rates) | |||||||||
| 2016 | July | 0.8 | 2.2 | 1.6 | 0.8 | ||||
| August | 1.1 | 2.3 | 1.7 | 0.8 | |||||
| September | 1.5 | 2.2 | 1.7 | 1.0 | |||||
| October | 1.6 | 2.1 | 1.8 | 1.2 | |||||
| November | 1.69 | 2.11 | 1.65 | 1.50 | |||||
| December | 2.03 | ± | 0.11 | 2.18 | ± | 0.09 | 1.71 | 1.50 | |
| 2017 | January | 2.3 | ± | 0.35 | 2.2 | ± | 0.16 | 1.6 | 1.9 |
| February | 2.8 | ± | 0.57 | 2.1 | ± | 0.21 | 1.6 | 2.0 | |
| March | 2.4 | ± | 0.69 | 2.2 | ± | 0.26 | 1.8 | 2.3 | |
| April | 2.0 | ± | 0.74 | 2.2 | ± | 0.30 | 1.7 | 2.3 | |
| May | 1.8 | ± | 0.79 | 2.1 | ± | 0.32 | 1.7 | 2.3 | |
| June | 1.8 | ± | 0.83 | 2.2 | ± | 0.34 | 1.8 | 2.3 | |
| July | 1.9 | ± | 0.89 | 2.3 | ± | 0.34 | 1.8 | 2.3 | |
| August | 2.1 | ± | 0.94 | 2.2 | ± | 0.35 | 1.8 | 2.3 | |
| September | 2.1 | ± | 0.96 | 2.3 | ± | 0.36 | 1.9 | 2.3 | |
| October | 2.2 | ± | 0.97 | 2.3 | ± | 0.39 | 1.9 | 2.3 | |
| November | 2.1 | ± | 0.98 | 2.3 | ± | 0.43 | 2.0 | 2.3 | |
| December | 2.1 | ± | 1.01 | 2.3 | ± | 0.43 | 2.0 | 2.3 | |
| 2018 | January | 2.0 | ± | 1.04 | 2.3 | ± | 0.42 | 2.0 | 2.3 |
| … | … | … | … | … | … | … | |||
| December | 2.0 | ± | 1.07 | 2.3 | ± | 0.41 | 2.0 | 2.3 | |
| Item | Weight (%) | 2016 | 2017 | Item | Weight (%) | 2016 | 2017 | Item | Weight (%) | 2016 | 2017 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NON-ENERGY IND. GOODS (NEIG) | 26.42 | 0.6 | 0.6 | PROCESSED FOOD AND TOBACCO (PF) | 15.13 | 0.2 | 0.2 | SERVICES (SERV) | 39.67 | 1.1 | 1.0 |
| Men’s outerwear | −0.05 | −1.4 | 1.4 | Rice | −0.94 | 1.2 | −1.8 | Maint. & rep. srv. | 0.28 | 1.9 | 0.4 |
| Men’s underwear | 0.09 | −1.1 | 2.4 | Flours & cereals | -0.34 | −0.2 | 0.2 | Ot. srv. related to vehicles | −0.04 | 0.6 | −1.4 |
| Women’s outerwear | −0.15 | −1.7 | 0.2 | Bread | −0.03 | −0.1 | −0.4 | Railway transport | 0.49 | 1.3 | 0.8 |
| Women’s underwear | 0.09 | −0.9 | 2.1 | Pastry goods, cakes etc. | −0.01 | 0.5 | 0.4 | Road transport | 0.17 | 1.4 | −0.1 |
| Child. & inf. garments | −0.02 | −1.7 | 1.0 | Farin.-based prd. | −0.16 | 0.9 | −1.8 | Air transport | 0.06 | −2.7 | 0.1 |
| Men’s footwear | 0.01 | 1.0 | 1.3 | Delicat. type meat prd. | 0.00 | −0.1 | −0.4 | Ot. transport srv. | 0.55 | −0.6 | 2.2 |
| Women’s footwear | 0.10 | 1.0 | 1.8 | Processed meat prd. | −0.08 | 0.5 | 0.3 | Insur. con. with transport | 0.18 | 3.6 | 2.6 |
| Child. & inf. footwear | 0.01 | 0.9 | 1.4 | Preser. & proc. fish | 0.00 | 1.8 | 3.0 | Rest, bars, coffee bars etc. | 0.13 | 1.0 | 1.1 |
| Motor vehicles | −0.12 | 3.6 | 2.9 | Milk | −0.52 | −3.2 | −1.5 | Hotels & ot. lodgings | 0.02 | 2.6 | 3.4 |
| Ot. vehicles | 0.00 | 1.7 | 0.1 | ot. dairy prd. | −0.33 | 0.1 | −0.9 | Package holidays | −0.46 | −1.3 | −0.5 |
| Spare parts & maint | 0.13 | −1.8 | −0.6 | Cheeses | −0.02 | 0.2 | 0.2 | Higher education | 0.33 | −0.1 | 0.7 |
| Mat. f maint. & rep. dw. | 0.14 | −0.4 | 0.0 | Preser. Fruits & dri. Fru. | −0.14 | 4.2 | 0.4 | Postal srv. | 0.45 | 1.5 | 1.4 |
| Water supply | 0.21 | −0.4 | 0.7 | Dried pulses & veg. | −0.08 | 7.4 | 3.5 | Telephone srv. | −0.04 | 2.3 | 1.2 |
| Furniture | 0.11 | −0.1 | 0.3 | Frozen & preser. veg. | −0.10 | 1.1 | −0.4 | Rentals f housing | 0.11 | −0.8 | 0.0 |
| Ot. Equip. | 0.04 | 1.1 | 0.8 | Sugar | −0.90 | −0.3 | −2.5 | Srv. maint./ rep. of the dw. | 0.04 | −0.2 | 0.6 |
| Hhold textiles | 0.02 | −1.3 | −1.1 | Choco. & confec. | −0.01 | 1.4 | 0.4 | Sewerage collection | 0.30 | 1.1 | 0.9 |
| Refr.,w. mach. & dishw. | −0.18 | −3.6 | −3.6 | Ot. food prd. | 0.02 | 0.2 | −0.4 | Out. Hosp. & param. srv. | 0.14 | 0.5 | 1.4 |
| Cookers & ovens | −0.16 | −0.6 | −1.7 | Coffee, coc. & infus. | −0.01 | −0.1 | −0.1 | Dental srv. | 0.13 | 0.9 | 0.7 |
| Heating & air cond. | 0.07 | −0.4 | −0.5 | Min. waters. drinks etc. | −0.23 | 1.8 | 0.3 | Hospital srv. | −0.08 | −2.1 | −1.3 |
| Ot. hhold app. | 0.05 | −1.6 | −1.7 | Spirits & liqueurs | 0.17 | 0.2 | 1.4 | Medical insurances | 0.56 | 4.4 | 4.1 |
| Glass.,crock. & cutlery | 0.19 | 0.0 | 0.6 | Wines | −0.08 | 1.0 | 0.5 | Recreational & sporting srv. | 0.11 | 1.0 | 1.5 |
| Ot. kitchen uten. & furn. | 0.22 | 0.5 | 0.2 | Beer | 0.07 | 0.5 | 1.0 | Cultural srv. | 0.16 | 0.4 | 0.6 |
| Tools & acc. f h. & gard. | 0.23 | −0.4 | −0.2 | Tobacco | 1.50 | 0.4 | 1.3 | Education | 0.21 | 0.9 | 1.1 |
| Cleaning hhold art. | −0.08 | −0.3 | 0.1 | Butter & margarine | −0.16 | −0.6 | 1.3 | Rep. of footwear | 0.35 | 1.4 | 0.6 |
| Ot. non-dur. hhold art. | 0.11 | 0.4 | 0.8 | Oils | −0.28 | 10.0 | −0.7 | Dom. Serv /ot. hhold srv. | 0.19 | 0.6 | −0.6 |
| Med. & ot. pharma prd. | −0.53 | −1.8 | −1.3 | NON-PROC.FOOD (NPF) | 15.13 | 1.4 | 1.6 | Insur. Con. with dw. | 0.36 | 3.1 | 2.1 |
| Therapeutic app. & eq. | 0.00 | −1.5 | −0.2 | Beef | 0.05 | 0.3 | 0.5 | Personal care srv. | 0.14 | 0.9 | 0.3 |
| Equip. sound & pict. | −0.86 | −5.6 | −5.8 | Pork | −0.21 | −1.5 | 0.2 | Social srv. | 0.25 | 0.7 | 0.6 |
| Photo & cinema eq | −1.40 | −3.0 | −8.9 | Sheep meat | −0.31 | −0.7 | 0.2 | ot. insurances | 0.26 | 2.9 | 2.7 |
| Info proc. Eq | −0.61 | −9.9 | −10.4 | Poultry | −0.40 | −1.9 | −0.2 | Financial srv. | 0.51 | 0.0 | −0.3 |
| Recording media | −0.01 | −3.7 | −0.9 | Ot. meats & n-meat ed. | −0.26 | 1.7 | 2.2 | Ot. srv. | 0.06 | 0.4 | 1.5 |
| Games & toys | −0.25 | −3.7 | −3.5 | Fresh fish | 0.13 | 4.3 | 1.7 | Rep. of hhold app. | 0.29 | 0.2 | 0.3 |
| Ot. Recr. & sport. art. | −0.01 | −2.2 | −0.1 | Crustaceans & molluscs | 0.32 | 4.9 | 4.1 | ENERGY (ENE) | 12.14 | −8.6 | 13.7 |
| Plants, flow. & pets | 0.21 | 0.9 | 1.4 | Eggs | −0.03 | −0.5 | −1.3 | Electricity & gas | 0.42 | −9.9 | 17.1 |
| Books | 0.12 | 0.3 | 0.4 | Fresh fruits | −0.12 | 5.5 | −0.8 | ot. fuels | 2.47 | −16.3 | 28.4 |
| Newspapers & mag. | 0.26 | 1.2 | 3.3 | Fresh pulses & veg. | 0.13 | 0.0 | 6.4 | Fuels & lubricants | 1.69 | −7.1 | 10.4 |
| Stationery mat. | 0.17 | 0.4 | 0.7 | Potat. & proc. prd. | 0.76 | 12.5 | −0.4 | ||||
| Personal care art. | 0.00 | −1.4 | −0.6 | ||||||||
| Jewel, clocks & watches | 1.25 | 1.9 | 3.4 | ||||||||
| Ot. art. f pers. use | 0.04 | −1.2 | 0.6 | ||||||||
| 2016 | 2017 | Forec.> CPI + 80% RMSE | |||||||||
| Forecast CPI | −0.2 | 2.2 | Forec.= CPI + − 80% RMSE | ||||||||
| RMSE 80% | 0.0 | 1.2 | Forec.< CPI − 80% RMSE | ||||||||
| Monthly Forecasts | Sample Standard Deviation | MFE | RMSFE | Ratio RMSFE/Standard Deviation | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 12 | 1 | 6 | 12 | 1 | 6 | 12 | ||
| Euro Area | ||||||||||
| CPI | 0.99 | 0.00 | 0.04 | 0.11 | 0.12 | 0.57 | 0.94 | 0.12 | 0.58 | 0.95 |
| Core | 0.56 | − 0.01 | −0.03 | −0.07 | 0.10 | 0.29 | 0.52 | 0.18 | 0.52 | 0.93 |
| Processed Food (PF) | 1.45 | −0.01 | 0.05 | 0.13 | 0.26 | 0.86 | 1.49 | 0.18 | 0.59 | 1.03 |
| Non Energy Industrial Goods (NEIG) | 0.42 | 0.00 | −0.05 | −0.12 | 0.19 | 0.34 | 0.54 | 0.45 | 0.81 | 1.29 |
| Services (SER) | 0.61 | −0.02 | −0.06 | −0.12 | 0.15 | 0.31 | 0.51 | 0.25 | 0.51 | 0.84 |
| Residual | 4.09 | 0.05 | 0.52 | 1.10 | 0.65 | 2.56 | 3.81 | 0.16 | 0.63 | 0.93 |
| Unprocessed Food (UPF) | 2.11 | 0.00 | 0.17 | 0.26 | 0.66 | 1.60 | 2.34 | 0.31 | 0.76 | 1.11 |
| Energy (EN) | 6.60 | 0.13 | 0.94 | 1.92 | 1.01 | 4.32 | 6.14 | 0.15 | 0.65 | 0.93 |
| Spain | ||||||||||
| CPI | 1.59 | −0.01 | −0.04 | −0.06 | 0.15 | 0.86 | 1.33 | 0.09 | 0.54 | 0.84 |
| Core | 1.11 | −0.02 | −0.12 | −0.29 | 0.14 | 0.52 | 0.90 | 0.13 | 0.47 | 0.81 |
| Processed Food (PF) | 1.7 | −0.02 | 0.05 | 0.06 | 0.34 | 1.18 | 1.96 | 0.20 | 0.69 | 1.15 |
| Non Energy Industrial Goods (NEIG) | 1.08 | −0.01 | −0.15 | −0.37 | 0.25 | 0.63 | 0.95 | 0.23 | 0.58 | 0.88 |
| Services (SER) | 1.39 | −0.04 | −0.20 | −0.43 | 0.17 | 0.54 | 0.91 | 0.12 | 0.39 | 0.66 |
| Residual | 5.22 | 0.02 | 0.37 | 1.05 | 0.60 | 3.23 | 4.51 | 0.11 | 0.62 | 0.86 |
| Unprocessed Food (UPF) | 2.88 | 0.03 | 0.04 | −0.10 | 0.92 | 2.04 | 2.85 | 0.32 | 0.71 | 0.99 |
| Energy (EN) | 8.65 | 0.00 | 0.76 | 1.87 | 0.62 | 5.75 | 7.99 | 0.07 | 0.67 | 0.92 |
| US | ||||||||||
| CPI | 1.02 | −0.01 | −0.01 | 0.14 | 0.09 | 0.59 | 0.74 | 0.09 | 0.58 | 0.72 |
| Core | 0.29 | 0.00 | 0.01 | 0.03 | 0.08 | 0.26 | 0.33 | 0.27 | 0.88 | 1.14 |
| Non Energy Commodities less Food | 0.92 | 0.00 | 0.10 | 0.36 | 0.17 | 0.59 | 0.76 | 0.18 | 0.64 | 0.82 |
| Durables | 1.16 | −0.02 | 0.18 | 0.59 | 0.22 | 0.97 | 1.08 | 0.19 | 0.84 | 0.93 |
| Non Durables | 0.85 | 0.02 | 0.03 | 0.13 | 0.23 | 0.53 | 0.81 | 0.28 | 0.62 | 0.95 |
| Non Energy Services | 0.42 | 0.00 | −0.02 | −0.09 | 0.07 | 0.22 | 0.32 | 0.17 | 0.52 | 0.75 |
| Owner’s equivalent rent of primary res. | 0.72 | 0.00 | 0.05 | −0.18 | 0.06 | 0.29 | 0.37 | 0.09 | 0.41 | 0.52 |
| Other Services | 0.3 | 0.00 | 0.00 | −0.03 | 0.11 | 0.28 | 0.42 | 0.37 | 0.92 | 1.40 |
| Residual | 4.52 | −0.07 | −0.08 | 0.51 | 0.25 | 2.14 | 2.93 | 0.06 | 0.47 | 0.65 |
| Food | 1.29 | −0.02 | −0.02 | 0.21 | 0.18 | 0.71 | 1.20 | 0.14 | 0.55 | 0.93 |
| Energy | 10.42 | −0.14 | −0.19 | 0.88 | 0.59 | 5.45 | 7.30 | 0.06 | 0.52 | 0.70 |
| Forecast Statistics and Time Span | 1 Year Ahead | 2 Years Ahead | Ratio BIAM/ ECB-SPF | |||
|---|---|---|---|---|---|---|
| Quarterly Forecasts | BIAM | ECB-SPF | BIAM | ECB-SPF | 1 Year Ahead | 2 Years Ahead |
| Mean Squared Forecast Error (MFE) | ||||||
| 1999Q4–2016Q4 | 0.77 | 0.82 | 0.85 | 0.94 | 0.94 | 0.90 |
| 1999Q4–2007Q4 | 0.24 | 0.31 | 0.46 | 0.53 | 0.75 | 0.88 |
| 2008Q1–2016Q4 | 1.26 | 1.29 | 1.31 | 1.46 | 0.98 | 0.90 |
| Root Mean Squared Forecast Error (RMSFE) | ||||||
| 1999Q4–2016Q4 | 0.88 | 0.91 | 0.92 | 0.97 | 0.97 | 0.95 |
| 1999Q4–2007Q4 | 0.49 | 0.56 | 0.68 | 0.73 | 0.87 | 0.94 |
| 2008Q1–2016Q4 | 1.12 | 1.13 | 1.14 | 1.21 | 0.99 | 0.95 |
| Mean Absolute Forecast Error (MAFE) | ||||||
| 1999Q4–2016Q4 | 0.68 | 0.73 | 0.70 | 0.79 | 0.93 | 0.89 |
| 1999Q4–2007Q4 | 0.38 | 0.47 | 0.60 | 0.66 | 0.81 | 0.91 |
| 2008Q1–2016Q4 | 0.96 | 0.96 | 0.97 | 1.06 | 1.00 | 0.91 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espasa, A.; Senra, E. Twenty-Two Years of Inflation Assessment and Forecasting Experience at the Bulletin of EU & US Inflation and Macroeconomic Analysis. Econometrics 2017, 5, 44. https://doi.org/10.3390/econometrics5040044
Espasa A, Senra E. Twenty-Two Years of Inflation Assessment and Forecasting Experience at the Bulletin of EU & US Inflation and Macroeconomic Analysis. Econometrics. 2017; 5(4):44. https://doi.org/10.3390/econometrics5040044
Chicago/Turabian StyleEspasa, Antoni, and Eva Senra. 2017. "Twenty-Two Years of Inflation Assessment and Forecasting Experience at the Bulletin of EU & US Inflation and Macroeconomic Analysis" Econometrics 5, no. 4: 44. https://doi.org/10.3390/econometrics5040044
APA StyleEspasa, A., & Senra, E. (2017). Twenty-Two Years of Inflation Assessment and Forecasting Experience at the Bulletin of EU & US Inflation and Macroeconomic Analysis. Econometrics, 5(4), 44. https://doi.org/10.3390/econometrics5040044





