1. Introduction
Elliott (1998) and
Cavanagh et al. (1995) investigated the test on a coefficient of a cointegrating relation in the presence of a near unit root in a bivariate cointegrating regression. They show convincingly that when inference on the coefficient is performed as if the process has a unit root, then the size distortion is serious, see top panel of
Figure A1 for a reproduction of their results. This paper analyses the
p-dimensional cointegrated VAR model with
r cointegrating relations under local alternatives
where
are
and
is i.i.d.
. It is assumed that
and
are known
matrices of rank
and
c is
and an unknown parameter, such that the model allows for a whole matrix,
of near unit roots. We consider below the likelihood ratio test,
for a given value of
calculated as if
that is, as if we have a CVAR with rank
The properties of the test
can be very bad, when the actual data generating process (DGP) is a slight perturbation of the process generated by the model specified by
. The matrix
describes a surface in the space of
matrices of dimension
. Therefore a model is formulated that in some particular “directions”, given by the matrix
has a small perturbation of the order of
and
extra parameters,
c, that are used to describe the near unit roots.
A similar model could be suggested for near unit roots in the
model, see
Di Iorio et al. (2016), but this will not be attempted here.
The model (
1) contains as a special case the DGP used for the simulations in
Elliott (1998), whe the errors are i.i.d. Gaussian and no deterministic components are present. The likelihood ratio test,
for
equal to a given value, is derived assuming that
and analyzed when in fact near unit roots are present,
. The parameters
and
can be estimated consistently, but
c cannot, and this is what causes the bad behaviour of
The matrix
is an invertible function of the
parameters
see Lemma 1, so that the Gaussian maximum likelihood estimator in model (
1) is least squares, and their limit distributions are found in Theorem 2. The main contribution of this paper, however, is a simulation study for the bivariate VAR with
,
It is shown that two of the methods introduced by
McCloskey (2017, Theorems Bonf and Bonf -Adj), for allowing the critical value for
to depend on the estimator of
give a much better solution to inference on
in the case of a near unit root. The results of
McCloskey (2017) also allow for multivariate parameters and for more complex adjustments, but in the present paper we focus for the simulations on the case with
and
so there is only one parameter in
c. In case
the matrix
is linear in
and for
it has an extra unit root. Therefore there is a near unit root for
, and we choose the vector
such
corresponds to the non-explosive near unit roots of interest.
The assumption that
and
are known is satisfied under the null, in the DGP analyzed by Elliott, see (
15) and (16). This is of course convenient, because
as free parameters, are not estimable.
Let
denote the parameters
and
and let
and
denote the maximum likelihood estimators in model (
1). For a given
(here
or
the quantile
is defined by
. Simulations show that the quantile is increasing in
and solving the inequality for
a
confidence interval,
is defined for
c. For given
(here
or
the quantile
is defined by
and
McCloskey (2017) suggests replacing the critical value
by the stochastic critical value
or introducing the optimal
by solving the equation
for a given nominal size
(here 10%).
These methods are explained and implemented by a simulation study, and it is shown that they offer a solution to the problem of inference on in the presence of a near unit root.
3. Critical Value Adjustment for Test on in the CVAR with near Unit Roots
3.1. Bonferroni Bounds
In this section the method of
McCloskey (2017, Theorem Bonf) is illustrated by a number of simulation experiments. The simulations are performed with data generated by a bivariate model (
1), where
and
The direction
is chosen such that
The test
for a given value of
is calculated assuming
, see (
6). The simulations of
Elliott (1998), see
Section 3.3, show that there may be serious size distortions of the test, depending on the value of
c and
, if the test is based on the quantiles from the asymptotic
distribution.
The methods of
McCloskey (2017) consists in this case of replacing the
critical value with a stochastic critical value depending on
in order to control the rejection probability under the null hypothesis.
Let
and let
denote the probability measure corresponding to the parameters
The method consists of finding the
quantile of
see (5) with
replaced by
, as defined by
for
or
say, and the
quantile
of
as defined by
for
or
say.
By simulation for given
and a grid of given of values
the quantiles
and
are determined. It turns out, that both
and
are increasing in
see
Figure A2. Therefore, a solution
can be found such that
This gives a
confidence interval
for
c, based on the estimator
. Note that for
it holds by monotonicity of
that
such that
but we also have
such that
In the paper from
McCloskey (2017) it is proved under suitable conditions that we have the much stronger result
Thus, the limiting rejection probability, for given of the test on calculated as if but replacing the quantile by the estimated stochastic quantile lies between and In the simulations we set and , so that the limiting rejection probability is bounded by
Note that
is replaced by the consistent estimator
It obviously simplifies matters that in all the examples we simulate, it turns out that
is approximately linear and increasing in
and
is approximately quadratic and increasing in
c for the relevant values of
c, see
Figure A2.
3.2. Adjusted Bonferroni Bounds
McCloskey (2017, Theorem Bonf-Adj) suggests determining by simulation on a grid of values of
c and
the quantitity
It turns out that
is monotone in
and we can determine for a given nominal size
(here 10%)
The Adjusted Bonferroni quantile is then
and we find
The result of
McCloskey (2017, Theorem Bonf-Adj) is that under suitable assumptions
where we illustrate the upper bound.
3.3. The Simulation Study of Elliott (1998)
The DGP is defined by the equations,
It is assumed that
are i.i.d.
with
and the initial values are
The data
are generated from (
15) and (16), and the test statistic
for the hypothesis
is calculated using (
6).
The DGP defined by (
15) and (16) is contained in model (
1) for
. Note that
such that
where the sign on
has been chosen such that
Finally
and
and therefore
For the process is and is stationary, and if is close to zero, has a near unit root.
Applying Corollary 1 to the DGP (
15) and (16), the expectation of the test statistic
is found to be
which increases approximately linearly in
Based on
simulations of errors
,
, the data
, are constructed from the DGP for each combination of the parameters
where
indicates the interval from
a to
c with step
b. Based on each simulation,
and the test
for
are calculated.
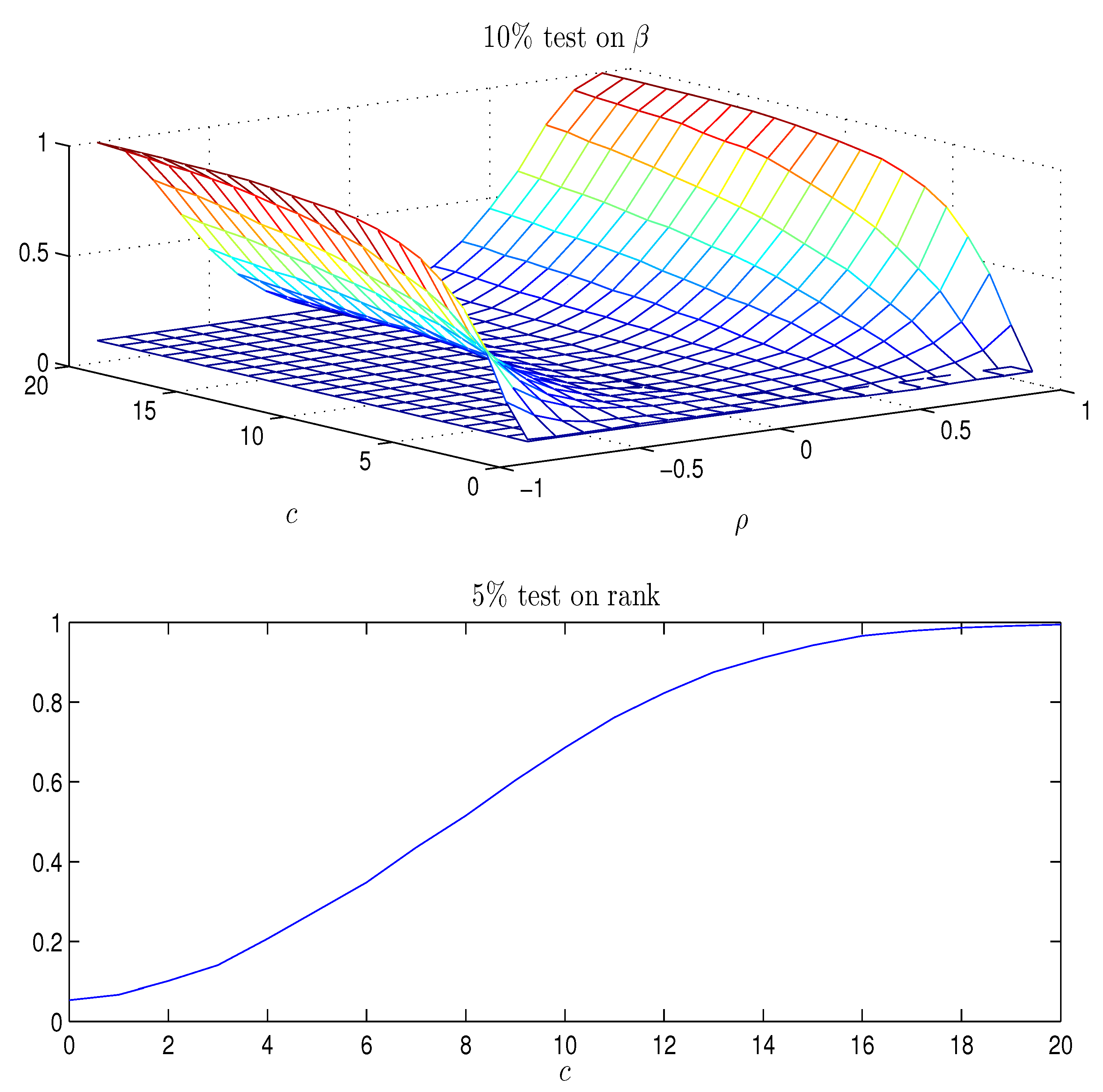
Top panel of
Figure A1 shows the rejection probabilities of the test
as a function of
, using the asymptotic critical value,
for a nominal rejection probability of
. The rejection probability increases with
and with
c. When
(corresponding to an autoregressive coefficient of
) and
, the size of the test
is around
, as found in
Elliott (1998). The results are analogous across models with an unrestricted constant term, or with a constant restricted to the cointegrating space. In the paper by
Elliott (1998) a number of tests are analyzed, and it was found that they were quite similar in their performance and similar to the above likelihood ratio test
from the CVAR with rank equal to 1.
3.4. Results with Bonferroni Quantiles and Adjusted Bonferroni Quantiles for
Data are simulated as above and first the rank test statistic,
, see
Johansen (
1996, chp. 11) for rank equal to 1, is calculated. The rejection probabilities for a 5% test using
are given in the bottom panel of
Figure A1 and they show that for
the hypothesis that the rank is 1, is practically certain to be rejected. If
the probability of rejecting that the rank is 1 is around
, so that plotting the rejection probabilities for
covers the relevant values, see
Figure A3.
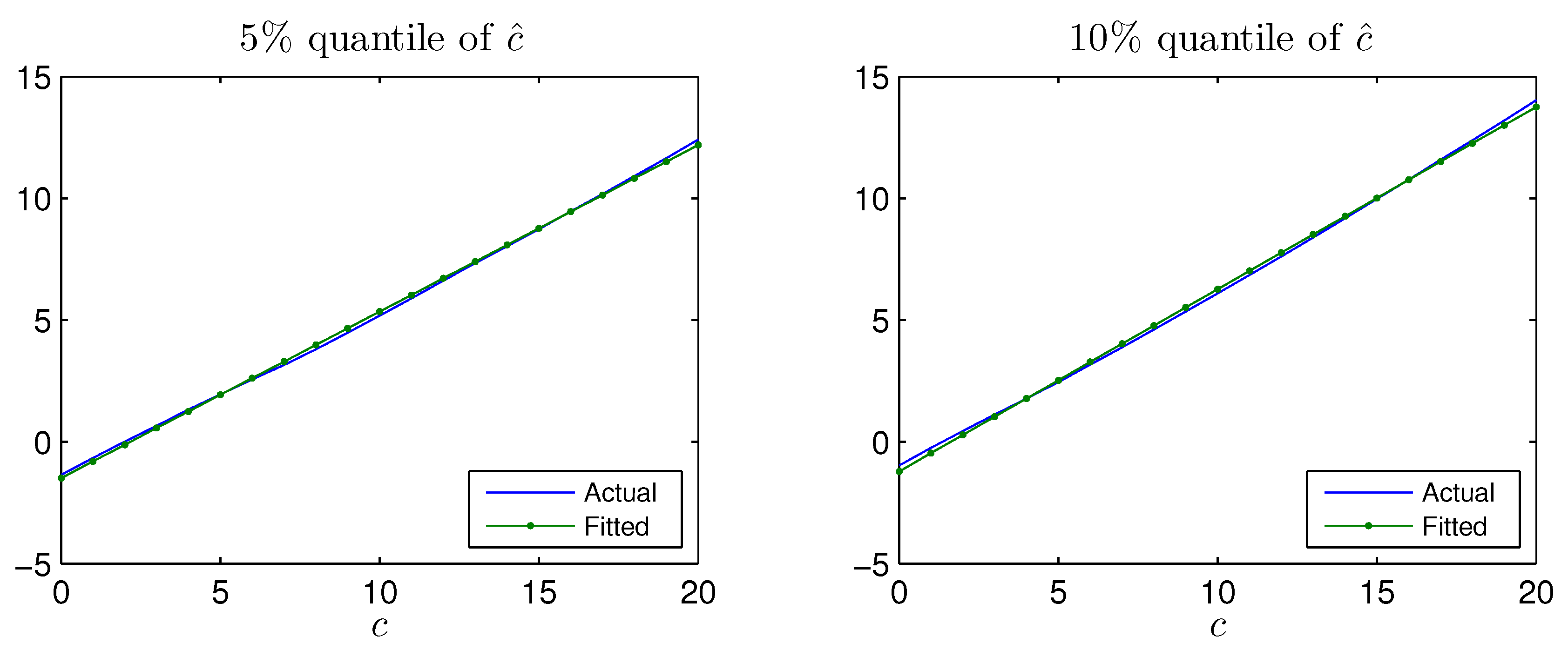
For
and
the quantiles
of
are reported in
Figure A2 as a function of
c. The quantiles
are nearly linear in
and they are approximated by
where the coefficients
depend on
, which is used to construct the upper confidence limit in (
14) as
For
and
the quantiles
of
are reported in
Figure A2 as function of
c for four values of
. It is seen that for given
, the quantiles
are monotone and quadratic in
c, for relevant values of
and hence they can be approximated by
where the coefficients
depend on
and
. The modified critical value is then constructed replacing
by
in (
19), and thus one finds the adjusted critical value
which depends on estimated values,
and
, and on discretionary values,
and
.
The adjusted Bonferroni quantile is explained in
Section 3.2. Simulations show that
is linear in
and the solution of the equation
where
is the nominal size of the test, determines
; the adjusted Bonferroni
q-quantile is then found like (
20) as
where
.
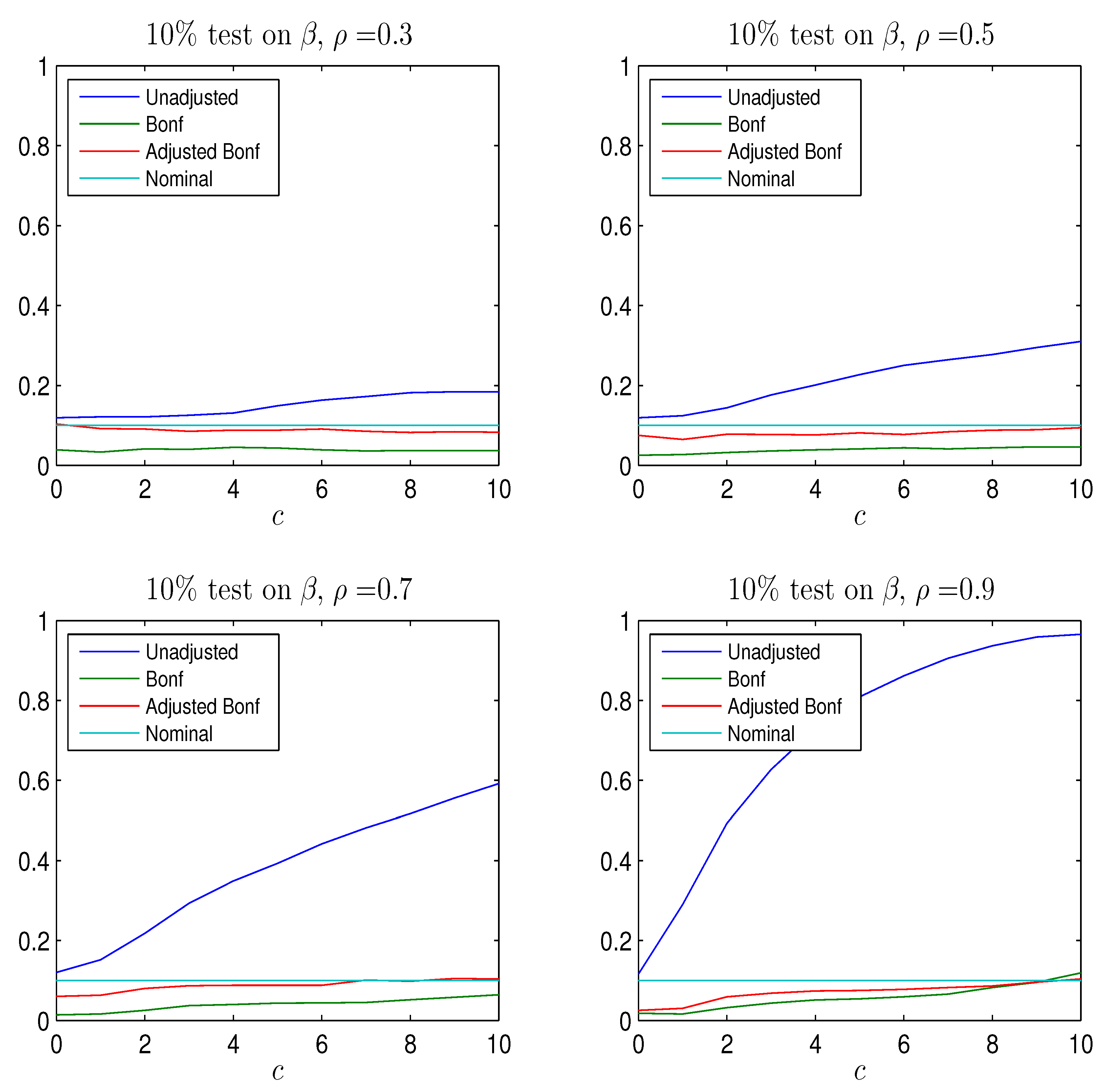
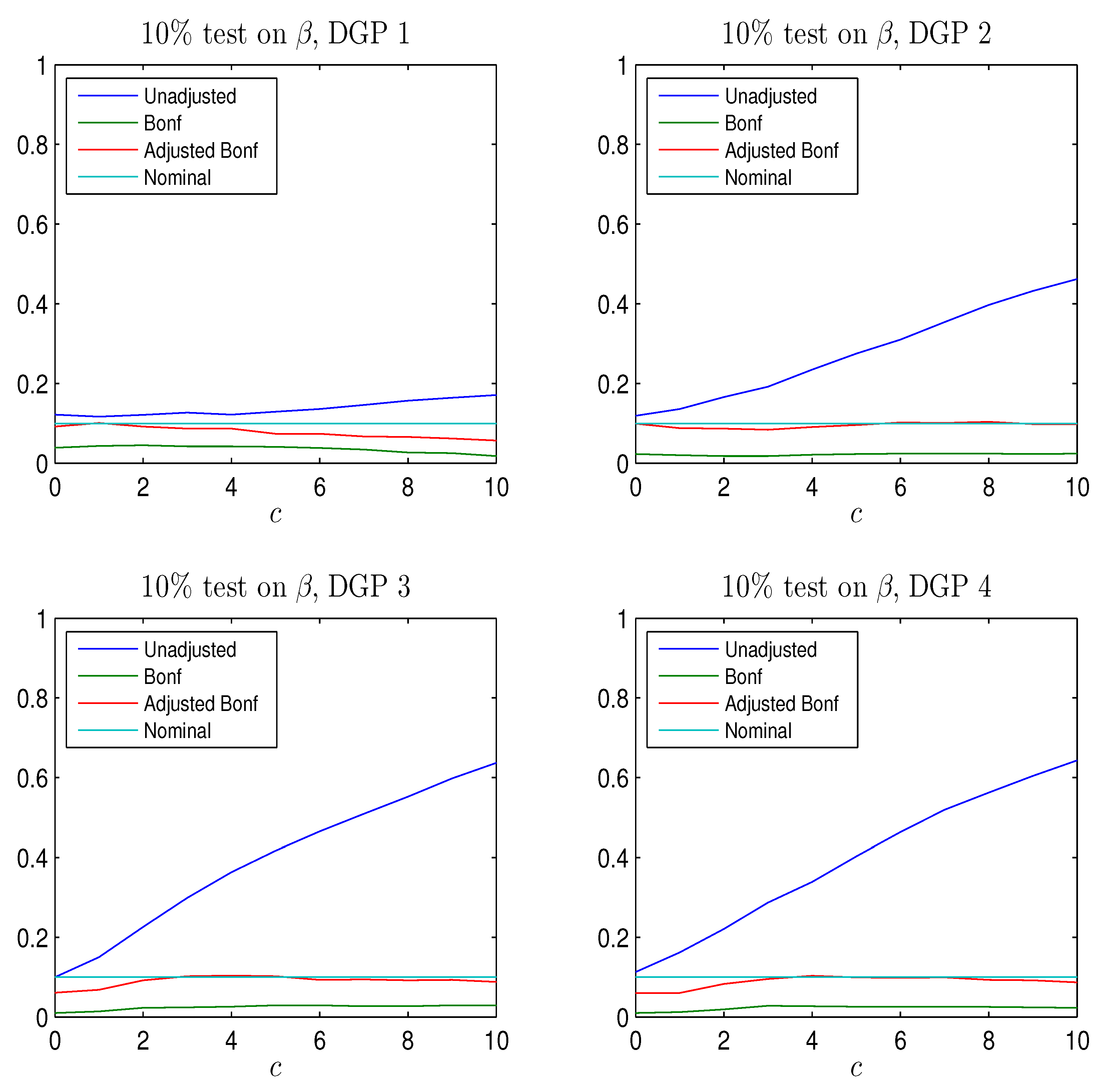
The rejection frequency of
the test for
calculated using the
quantile, the Bonferroni quantile in (
20) for
and
and the adjusted Bonferroni quantile in (
21) for
is reported as a function of
c for four values of
in
Figure A3. For both corrections the rejection frequency is below the nominal size of
; hence both procedures are able to eliminate the serious size-distortions of the
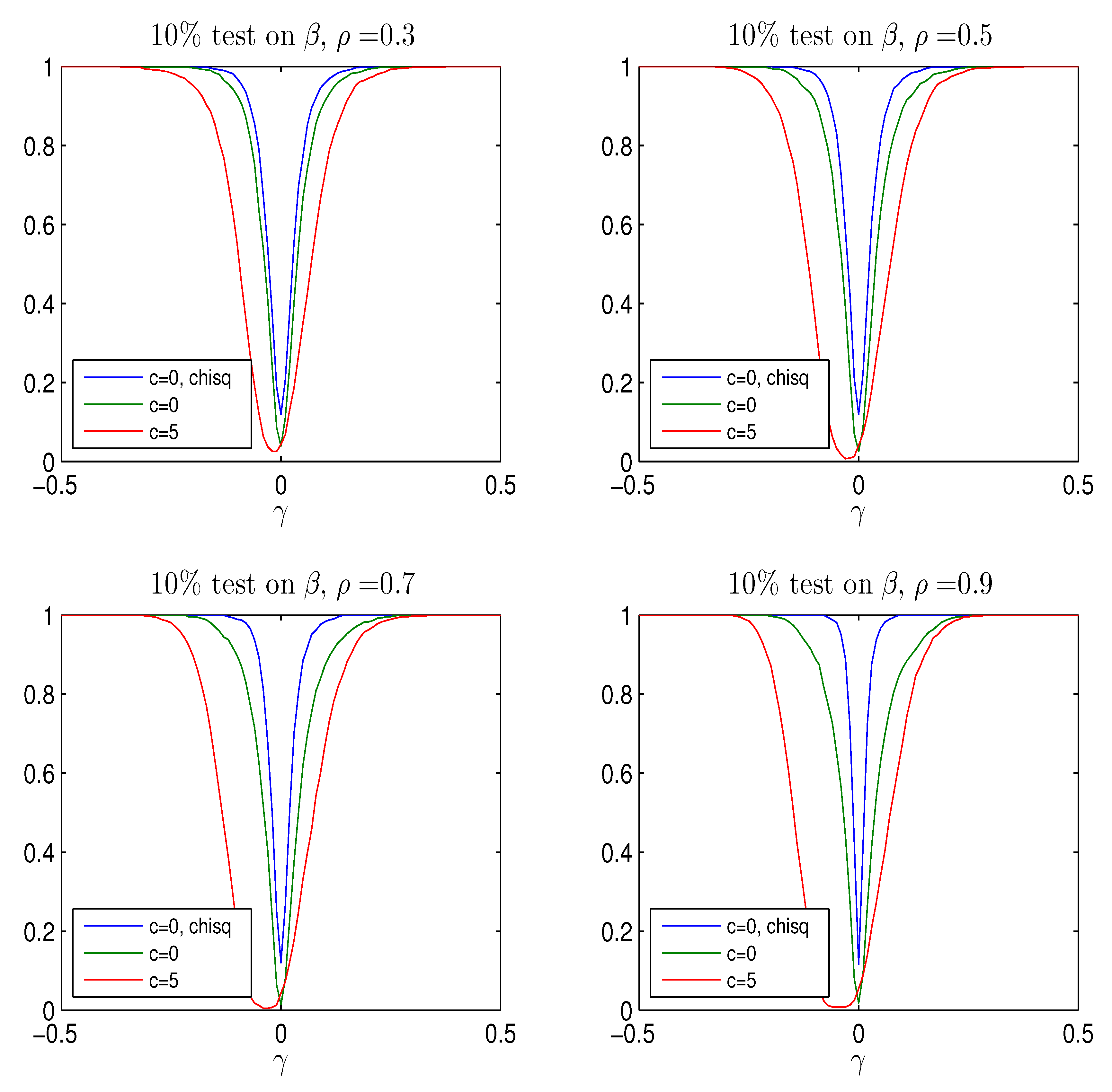
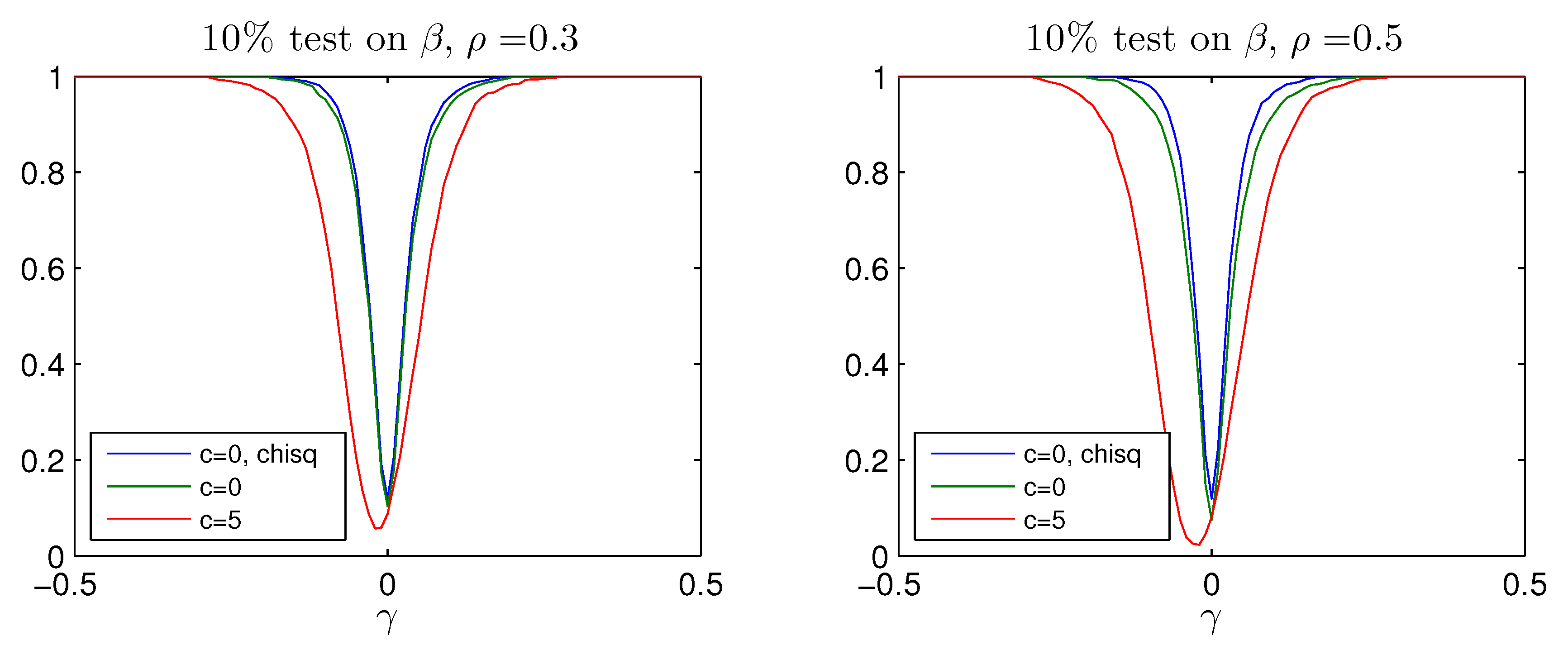
test. While the Bonferroni adjustment leads to rather conservative test with rejection frequency well below the nominal size, the adjusted Bonferroni procedure is closer to the nominal value. The power of the two procedures is shown in
Figure A4 and
Figure A5 for values of
It is seen that the better rejection probabilities in
Figure A3 are achieved together with a reasonable power for
where the probability of rejecting the hypothesis of
is around
, see bottom panel of
Figure A1. Notice that both tests become slightly biased, that is, the power functions are not flat around the null
.
In conclusion, the simulations indicate that the adjusted Bonferroni procedure works better than the simple Bonferroni, the reason being that the former relies on the joint distribution of and .
3.5. A Few Examples of Other DGPs
Four other data generating processes are defined in
Table 1, to investigate the role of different choices of
and
for the results on improving the rejection probabilities for test on
under the null and alternative. The DGPs all have
. The vectors
and
are chosen to investigate different positions of the near unit root in the DGP.
The choice of DGP turns out to be important also for the test, for In fact the probability of rejecting is around for DGP 1 if , for DGP 2 if , whereas for DGP 3 and 4 the value value is 8.
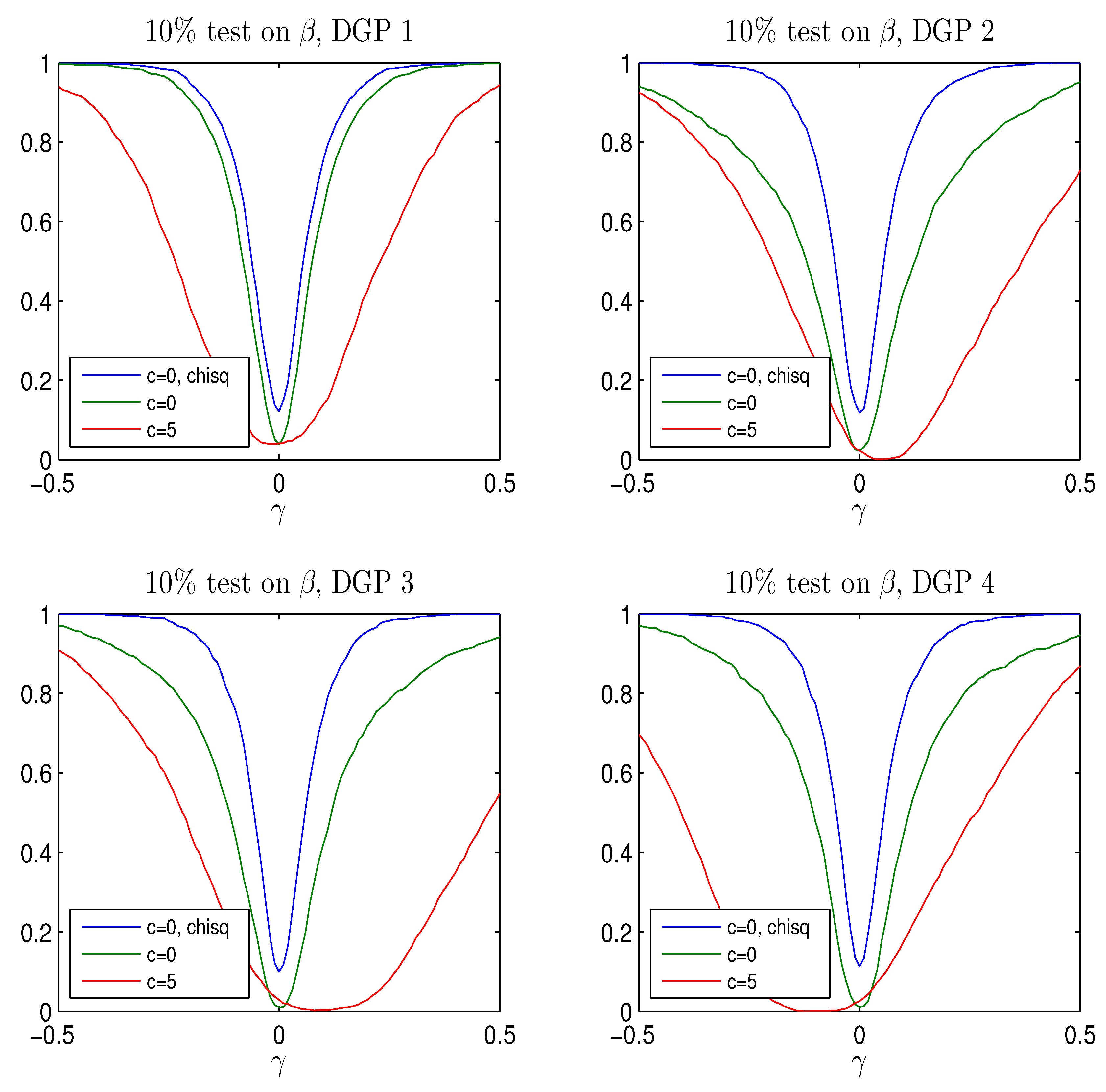
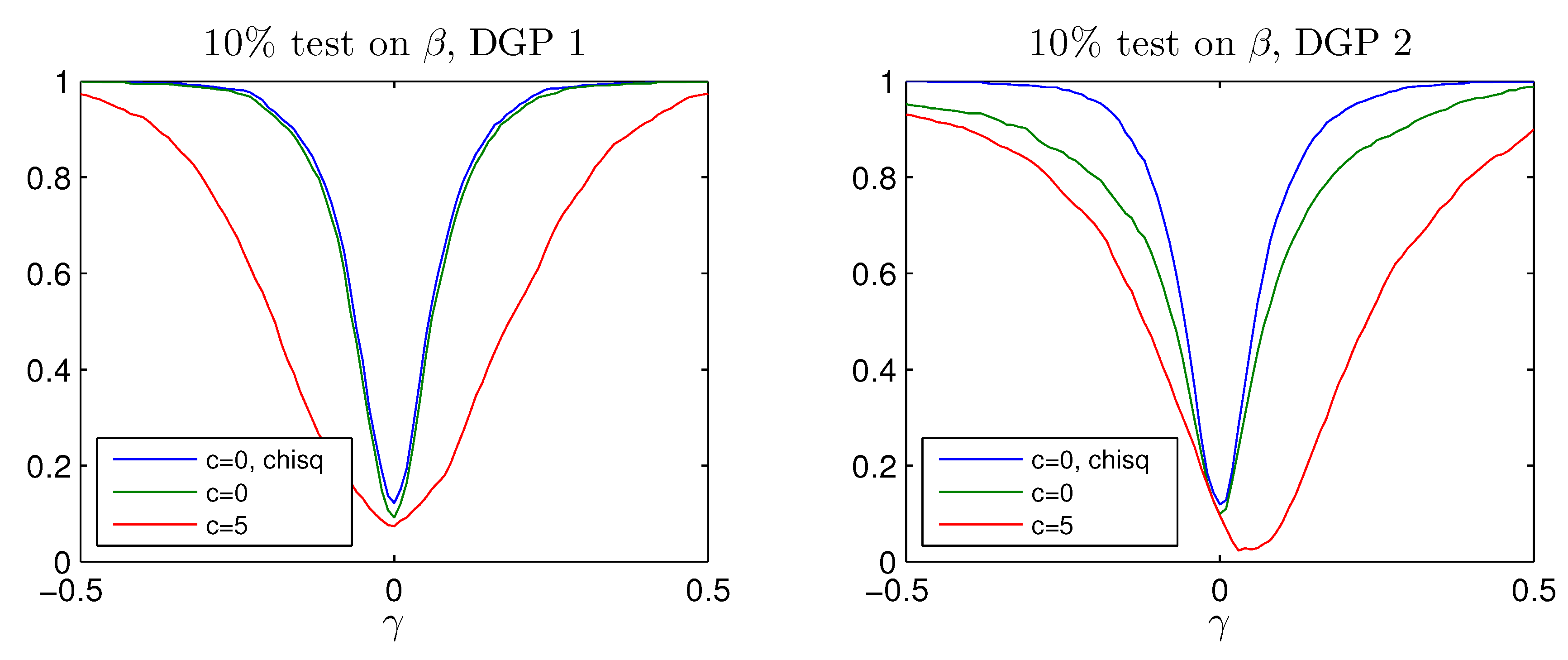
The rejection probabilities in
Figure A6 are plotted for
to cover the most relevant values.
The results are summarized in
Figure A6,
Figure A7 and
Figure A8. It is seen that the conclusions from the study of the DGP analyzed by Elliott seem to be valid also for other DGPs. For moderate values of
using the Bonferroni quantiles gives a rather conservative test while the adjusted Bonferroni procedure is closer to the nominal size and the power curves look reasonable for
although the tests are slightly biased, except for DGP 1. For this DGP,
such that
which means that the asymptotic distribution of
is
see Theorem 3, despite the near unit root. It is seen from
Figure A6, there is only moderate distortion of the rejection probability in this case and in
Figure A7 and
Figure A8, the power curves are symmetric around
so the tests are approximately unbiased.