Sustainable Financial Obligations and Crisis Cycles
Abstract
:1. Introduction
2. Data
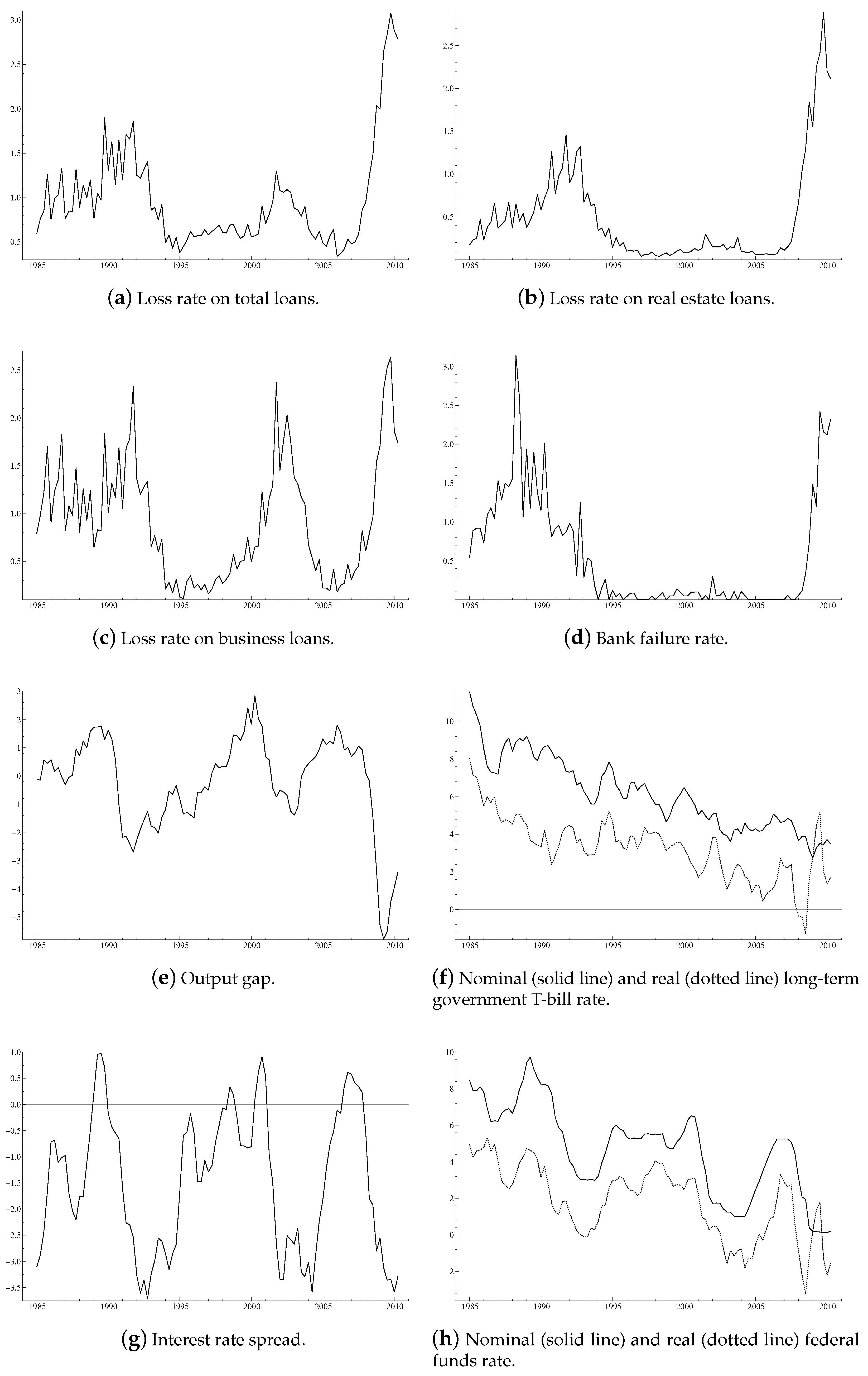
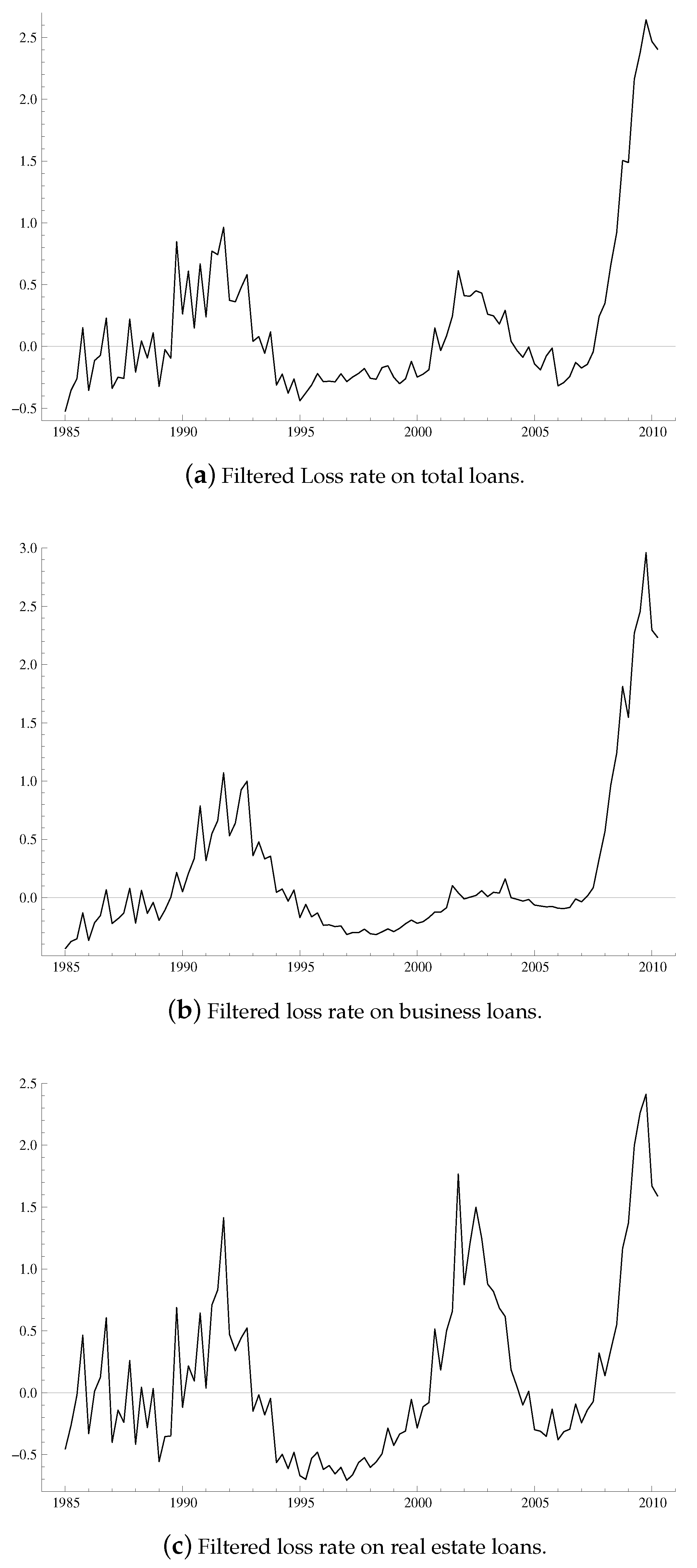
2.1. Credit Losses and Business Cycle Indicators
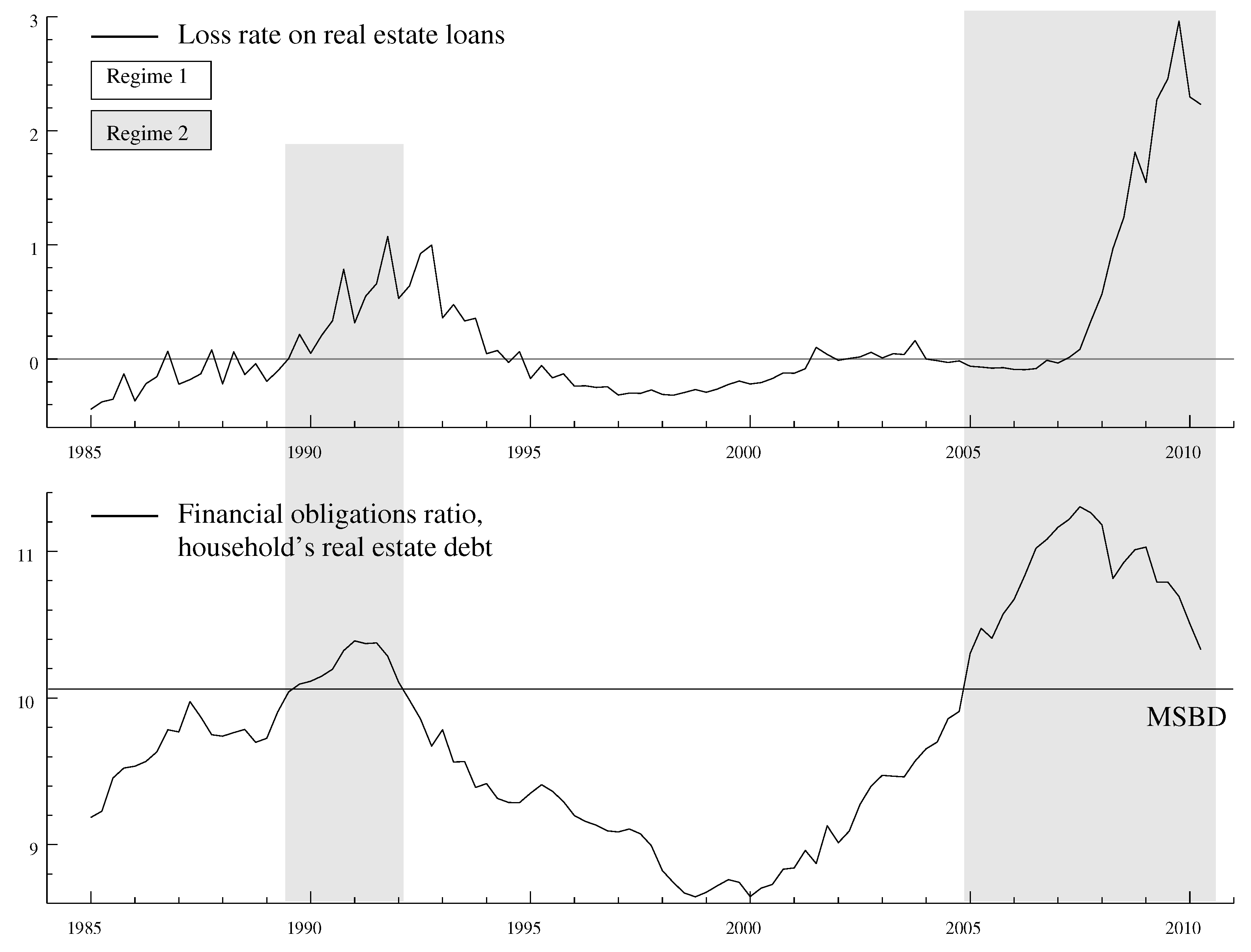
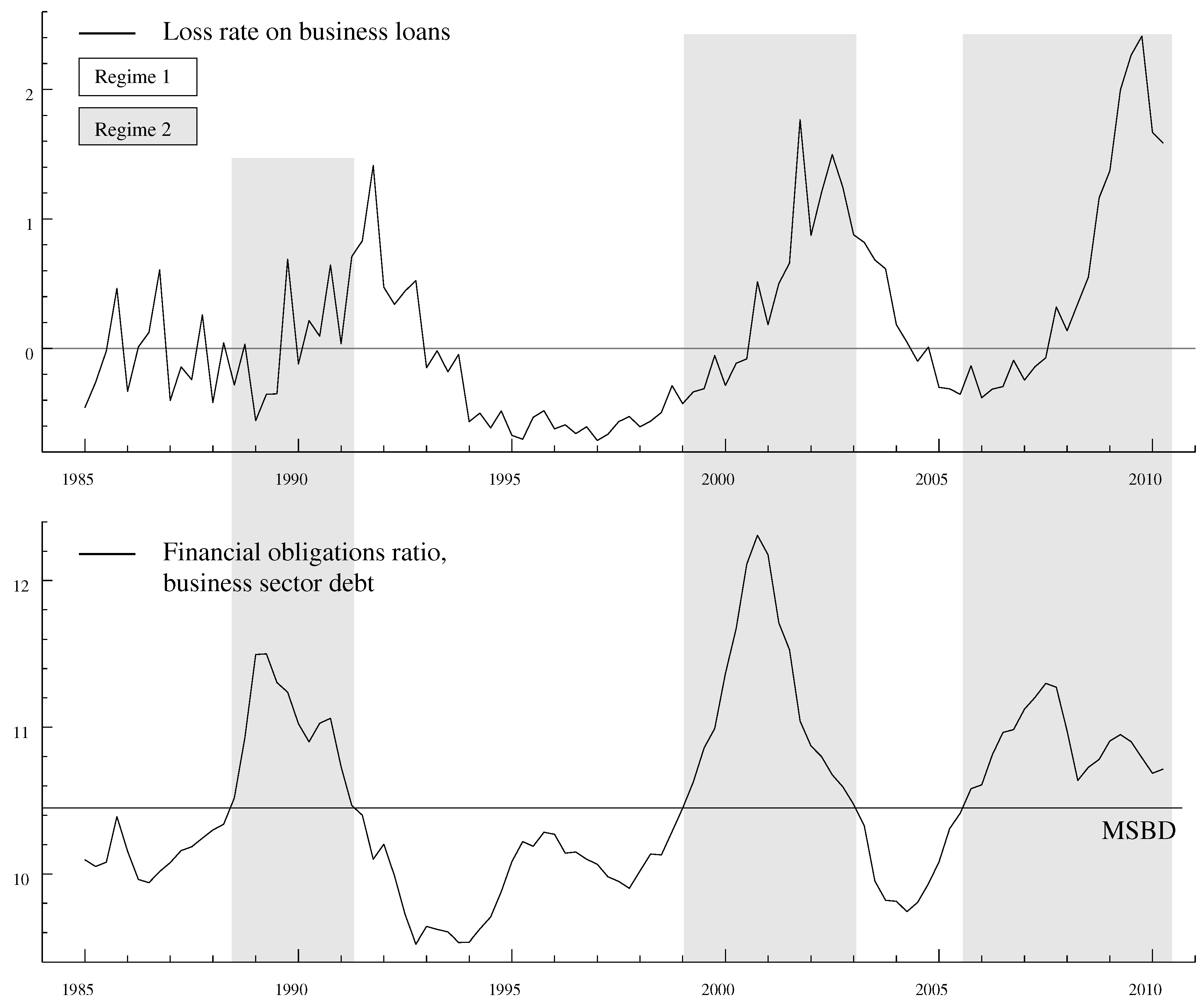
2.2. Leverage vs. Financial Obligations
3. Methodology
3.1. Statistical Models
4. Results
4.1. Linearity vs. Regime Shifts
4.2. Leverage vs. Financial Obligations
4.3. Explaining Credit Losses
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Data and Definitions | |
|---|---|
| Variable: | Definition: |
| Net charge-off rate on loans, all insured US commercial banks. h = TL (total loans), RL (real estate loans), and BL (business loans). Source: FRS (Bank Assets & Liabilities) | |
| Debt-to-income ratio (in %). (households’), B (Nonfarm nonfinancial corporate business). (total loans), (real estate loans). Household income: total wages and salaries. Business income: Value added in non farm business. Sources: FRS (Flow of Funds Accounts) and BEA (National Economic Accounts). | |
| Financial obligations ratio. i and j are as above. For the series are taken from the FRS (Household Finance). For the definition is . | |
| Effective federal fund rate (3-month average). Source: FRS (Interest Rates) | |
| Yield on 10-year Treasury securities. Source: FRS (Interest Rates) | |
| , where is log real output and is the OECD production function | |
| based level of potential output. Source: OECD. | |
Appendix B
| Dynamic STR Estimates | |||
|---|---|---|---|
| Model | |||
| Explained: | |||
| Parameters | |||
| – | |||
| – | |||
| Misspecification | |||
| AR | |||
| ARCH | |||
| Normality | |||
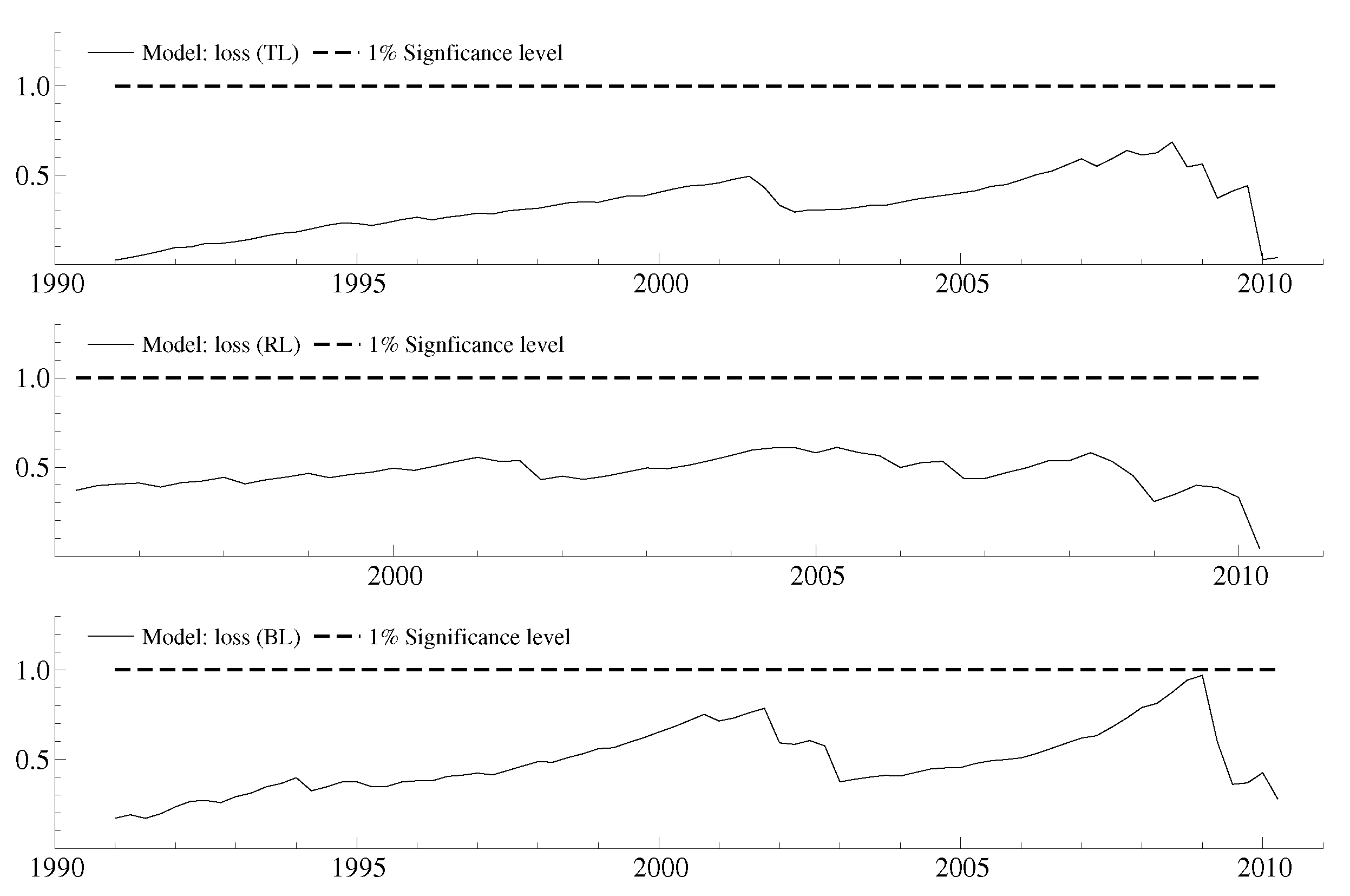
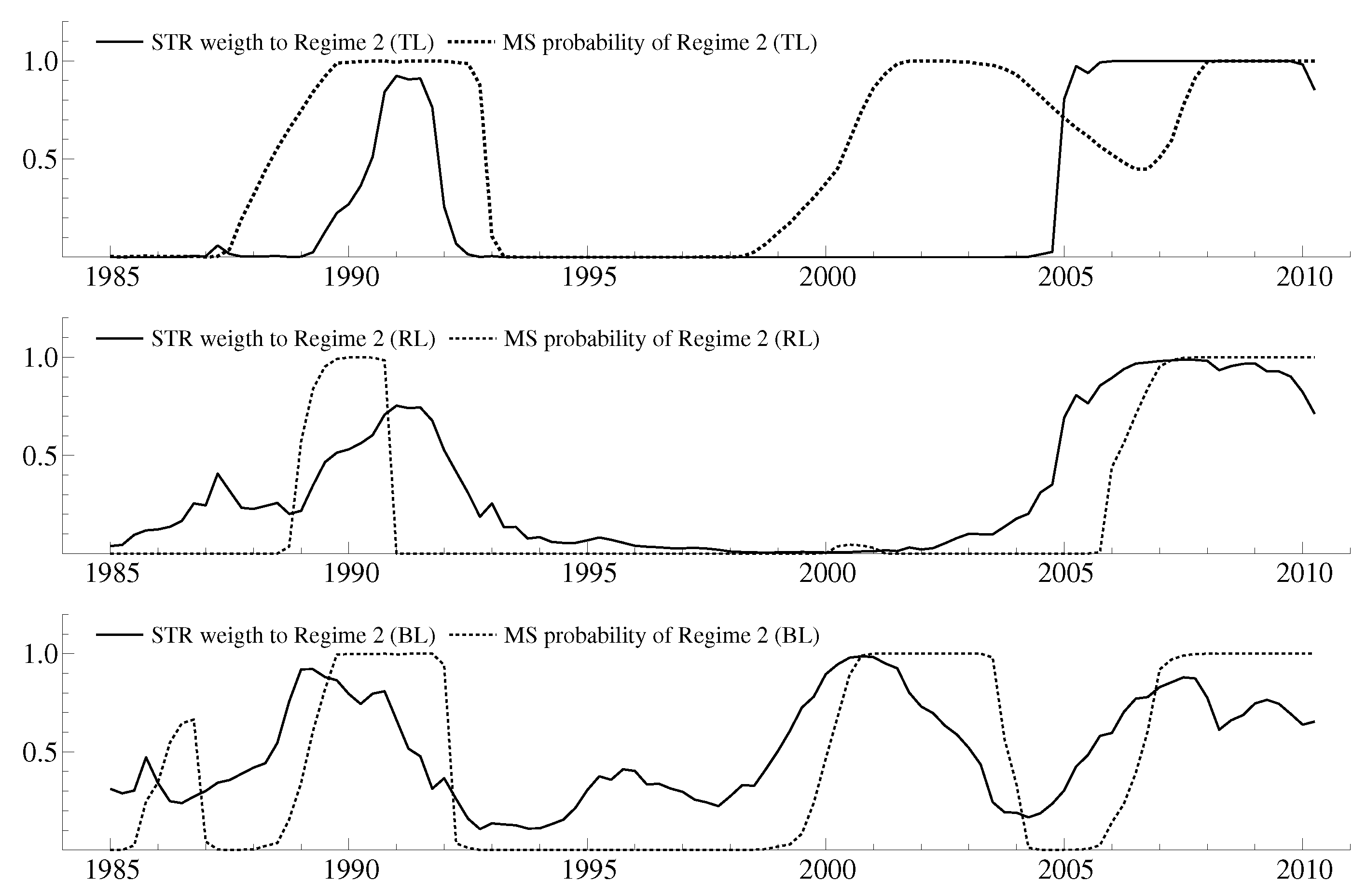
References
- Altunbas, Yener, Leonardo Gambacorta, and David Marques-Ibanez. 2010. Does Monetary Policy Affect Bank Risk-Taking? BIS Working Papers. No. 298. Available online: http://www.bis.org/publ/work298.htm (accessed on 6 November 2012).
- Berger, Allen N., Marco A. Espinosa-Vega, Nathan H. Miller, and W. Scott Frame. 2005. Debt maturity, risk, and asymmetric information. The Journal of Finance 60: 2895–923. [Google Scholar] [CrossRef]
- Bernanke, Ben S., Mark Gertler, and Simon Gilchrist. 1999. The financial accelerator in a quantitative business cycle framework. In Handbook of Macroeconomics. Edited by John B. Taylor and Michael Woodford. Amsterdam: North-Holland, vol. 1. [Google Scholar]
- Borio, Claudio. 2009. Implementing the macroprudential approach to financial regulation and supervision. Banque de France Financial Stability Review 13: 31–41. [Google Scholar]
- Borio, Claudio, and Mathias Drehmann. 2009. Assessing the risk of banking crises-revisited. BIS Quarterly Review. March. Available online: http://www.bis.org/publ/qtrpdf/r_qt0903e.htm (accessed on 6 November 2012).
- Borio, Claudio, and Philip Lowe. 2002. Asset prices, financial and monetary stability: Exploring the nexus. BIS Working Papers. No. 114. Available online: http://www.bis.org/publ/work114.htm (accessed on 6 November 2012).
- Burnside, Craig, Martin Eichenbaum, and Sergio Rebelo. 2016. Understanding booms and busts in housing markets. Journal of Political Economy 124, 4: 1088–147. [Google Scholar] [CrossRef]
- Caballero, Ricardo J., Emmanuel Farhi, and Pierre-Olivier Gourinchas. 2008. An equilibrium model of "global imbalances" and low interest rates. American Economic Review 98: 358–93. [Google Scholar] [CrossRef]
- Campello, Murillo, John R. Graham, and Campbell R. Harvey. 2010. The real effects of financial constraints: Evidence from a financial crisis. Journal of Financial Economics 97: 470–87. [Google Scholar] [CrossRef]
- Choi, In, and Pentti Saikkonen. 2004. Testing linearity in cointegrating smooth transition regressions. Econometrics Journal 7: 341–65. [Google Scholar] [CrossRef]
- Dell’Ariccia, Giovanni, and Robert Marquez. 2006. Lending booms and lending standards. The Journal of Finance 61: 2511–46. [Google Scholar] [CrossRef]
- Drehmann, Mathias, Claudio Borio, Leonardo Gambacorta, Gabriel Jiménez, and Carlos Trucharte. 2010. Countercyclical capital buffers: Exploring options. BIS Working Papers. No. 317. Available online: http://www.bis.org/publ/work317.htm (accessed on 6 November 2012).
- Drehmann, Mathias, and Mikael Juselius. 2012. Do debt service costs affect macroeconomic and financial stability? BIS Quarterly Review. September. Available online: http://www.bis.org/publ/qtrpdf/r_qt1209e.htm (accessed on 6 November 2012).
- Dynan, Karen, Kathleen Johnson, and Karen Pence. 2003. Recent changes to a measure of US household debt service. Federal Reserve Bulletin 89: 417–26. [Google Scholar]
- Frydman, Roman, and Michael D. Goldberg. 2009. Financial markets and the state: Price swings, risk, and the scope of regulation. Capitalism and Society 4: 1–43. [Google Scholar] [CrossRef]
- Gai, Prasanna, Sujit Kapadia, Stephen Millard, and Ander Perez. 2008. Financial innovation, macroeconomic stability and systemic crises. The Economic Journal 118: 401–26. [Google Scholar] [CrossRef]
- Gertler, Mark, and Cara S. Lown. 1999. The information in the high-yield bond spread for the business cycle: Evidence and some implications. Oxford Review of Economic Policy 15: 132–50. [Google Scholar] [CrossRef]
- Gilchrist, Simon, Vladimir Yankov, and Egon Zakrajšek. 2009. Credit market shocks and economic fluctuations: Evidence from corporate bond and stock markets. Journal of Monetary Economics 56: 471–93. [Google Scholar] [CrossRef]
- Hall, Robert. 2011. The long slump. American Economic Review 101, 2: 431–69. [Google Scholar] [CrossRef]
- Iacoviello, Matteo. 2005. House prices, borrowing constraints, and monetary policy in the business cycle. American Economic Review 95: 739–64. [Google Scholar] [CrossRef]
- Johansen, Søren. 1996. Likelihood-Based Inference in Cointegrated Vector Auto-Regressive Models. Oxford: Oxford University Press. [Google Scholar]
- King, Mervyn. 1994. Debt deflation: Theory and evidence. European Economic Review 38: 419–55. [Google Scholar] [CrossRef]
- Kiyotaki, Nobuhiro, and Mark Gertler. 2010. Financial intermediation and credit policy in business cycle analysis. In Handbook of Monetary Economics. Edited by Benjamin M. Friedman and Michael Woodford. Amsterdam: Elsevier. [Google Scholar]
- Kiyotaki, Nobuhiro, and John Moore. 1997. Credit cycles. Journal of Political Economy 105: 211–48. [Google Scholar] [CrossRef]
- Leybourne, Stephen, Paul Newbold, and Dimitrios Vougas. 1998. Unit roots and smooth transitions. Journal of Time Series Analysis 19: 83–97. [Google Scholar] [CrossRef]
- Lorenzoni, Guido. 2008. Inefficient credit booms. Review of Economic Studies 78: 809–33. [Google Scholar] [CrossRef]
- Meier, Andre, and Gernot J. Müller. 2006. Fleshing out the monetary transmission mechanism: Output composition and the role of financial frictions. Journal of Money, Credit, and Banking 38: 2099–133. [Google Scholar] [CrossRef]
- Mian, Atif, and Amir Sufi. 2010. The great recession: Lessons from microeconomic data. American Economic Review 100: 1–10. [Google Scholar] [CrossRef]
- Miller, Marcus, and Joseph E. Stiglitz. 2010. Leverage and asset bubbles: Averting armageddon with chapter 11? The Economic Journal 120: 500–18. [Google Scholar] [CrossRef]
- Nelson, Charles R., Jeremy Piger, and Eric Zivot. 2001. Markov regime switching and unit-root tests. Journal of Business & Economic Statistics 19: 404–15. [Google Scholar]
- Repullo, Rafael, Jesus Saurina, and Carlos Trucharte. 2010. Mitigating the pro-cyclicality of Basel II. Economic Policy 25: 659–702. [Google Scholar] [CrossRef]
- Ruckes, Martin. 2004. Bank competition and credit standards. The Review of Financial Studies 17: 1073–102. [Google Scholar] [CrossRef]
- Saikkonen, Pentti, and In Choi. 2004. Cointegration smooth transition regressions. Econometric Theory 20: 301–40. [Google Scholar] [CrossRef]
- Saikkonen, Pentti, and In Choi. 2010. Tests for nonlinear cointegration. Econometric Theory 26: 682–709. [Google Scholar]
- Stein, Jerome L. 2006. Stochastic Optimal Control, International Finance, and Debt Crises. Oxford: Oxford University Press. [Google Scholar]
- Stohs, Mark Hoven, and David C. Mauer. 1996. The determinants of corporate debt maturity structure. The Journal of Business 69: 279–312. [Google Scholar] [CrossRef]
- Van Dijk, Dick, Timo Teräsvirta, and Philip Hans Franses. 2002. Smooth transition autoregressive models—A survey of recent developments. Econometric Reviews 21: 1–47. [Google Scholar] [CrossRef]
| 1. | Several empirical studies also attempt to quantify the relative importance of the financial accelerator for output fluctuations. See for instance, Gertler and Lown (1999), Meier and Müller (2006), Gilchrist et al. (2009), and references therein. |
| 2. | The temporal association between credit losses and output losses is very strong as can be seen by comparing panels (a) and (e) of Figure 1. |
| 3. | This conjecture has recently been corroborated in a subsequent paper by Drehmann and Juselius (2012), who construct debt service ratios, a more narrow counterpart to the financial obligations ratio, for 27 countries. They find that the debt service ratio produce more accurate early warning signals than other extant measures 1–2 years ahead of systemic banking crises, whereas the credit-to-GDP gap have superior performance at longer horizons. |
| 4. | See the Federal Financial Institutions Examination Council’s “Instructions for Preparation of Consolidated Reports of Condition and Income (FFIEC 031 and 041)” and the Generally Accepted Accounting Principles (GAAP). |
| 5. | In the empirical analysis, we also control for a number of other variables including real house prices, deviations from a standard Taylor’s rule, the real exchange rate, the unemployment rate, and the inflation rate. |
| 6. | The numerator also includes rent payments on tenant-occupied property, auto lease payments, homeowners’ insurance, and property tax payments. |
| 7. | This value lies between the average maturities on firms’ bank loans reported in Stohs and Mauer (1996) and Berger et al. (2005). We checked robustness of the results below by assuming 2 and 4 years maturities. The results did not change significantly and are available upon request. |
| 8. | The precision with which the critical thresholds can be estimated depends more on the relative number of observations in each regime than the number of transitions between regimes. For instance, while our sample contains only two episodes of severe household sector financial distress, the number of observations associated with these events is 34, i.e., approximately one third of the entire sample. |
| 9. | Both the output gap and the term structure should be stationary. Moreover, credit losses reduce the credit aggregates so that even if they affect output debt to GDP ratios would not move too much. |
| 10. | See Saikkonen and Choi (2004) for a discussion of this model. |
| 11. | We also tried the other variables in , as well as real house prices. None, of these variables produced superior results in the sense discussed in Section 4.2. |
| 12. | The only exception is the financial obligations ratio on total business loans which is found to be stationary. These results are available upon request. |
| 13. | These results are omitted for brevity, but are available upon request. We also tried per capita GDP, the inflation rate, the unemployment rate, and the real exchange rate. None of these were found to be both cointegrated and weakly exogenous with respect to the credit loss rates. |
| 14. | This is statistically justified if the federal funds rate is strongly exogenous and the Hodrick-Prescott filtered trend provides an accurate estimate of the underlying trend in the federal funds rate. We found some evidence in favor of strong exogeneity for the federal funds rate by testing additional restrictions on the short-term dynamics. While there is no guarantee that the Hodrick-Prescott trend is an accurate estimate of the underlying trend, we checked robustness by estimating (2) with on the left hand side and added to the right hand side. This does not change the results below to any significant degree. |
| 15. | This does not, however, imply that such shifts are not present in the pre-crisis sample, but rather that the resulting dynamics are of a lesser magnitude and, hence, not likely to be confused with long-run movements in the credit loss rates. |
| 16. | Applying a more appropriate test, such as the one in Saikkonen and Choi (2010) which is based on the KPSS test, is left for future work. |
| 17. | It is more difficult to conduct a similar test for the household sector, as the Federal Reserve does not record financial obligations ratios before 1985. |

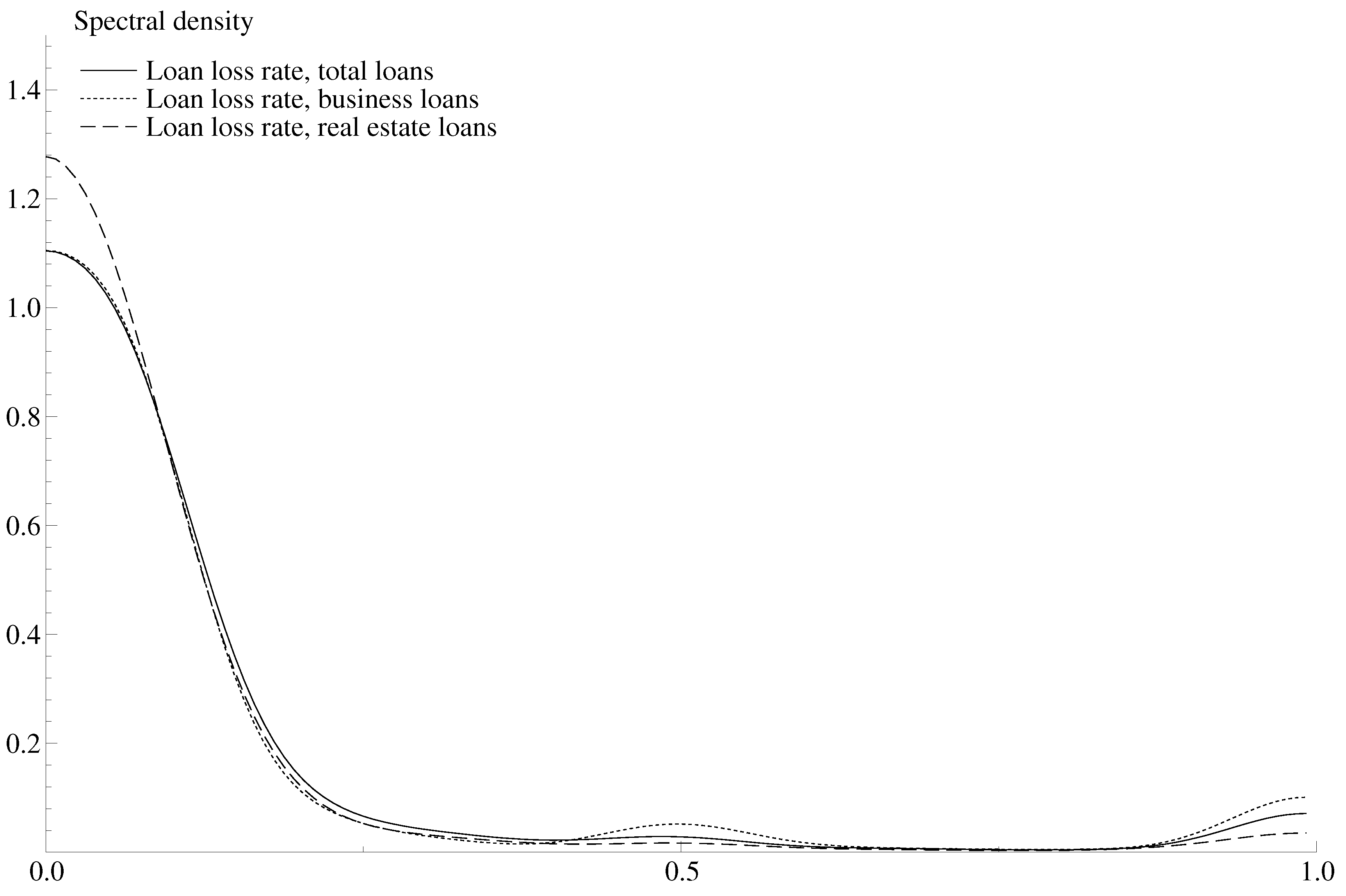
| Linear Cointegration Results | ||||
|---|---|---|---|---|
| 1985Q1–2006Q4 | ||||
| 0.00 | 0.38 | 0.00 | 0.42 | |
| 0.01 | 0.79 | 0.00 | 0.13 | |
| 0.00 | 0.19 | 0.00 | 0.54 | |
| 1985Q1–2010Q2 | ||||
| 0.96 | 0.98 | – | – | |
| 0.95 | 0.94 | – | – | |
| 0.27 | 0.29 | – | – | |
| Tests of Linearity vs. Regime Shifts | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1985Q1–2006Q2 | ||||||||
| 0.828 | 0.719 | 0.535 | 0.419 | 0.963 | 0.406 | 0.780 | 0.570 | |
| 0.363 | 0.597 | 0.489 | 0.688 | 0.108 | 0.085 | 0.221 | 0.583 | |
| 0.370 | 0.408 | 0.072 | 0.256 | 0.132 | 0.929 | 0.141 | 0.420 | |
| 1985Q1–2010Q2 | ||||||||
| 0.016 | 0.013 | 0.011 | 0.012 | 0.181 | 0.041 | 0.411 | 0.037 | |
| 0.059 | 0.042 | 0.052 | 0.021 | 0.738 | 0.018 | 0.940 | 0.054 | |
| 0.048 | 0.049 | 0.006 | 0.029 | 0.058 | 0.151 | 0.021 | 0.064 | |
| Unit-Root and Stationarity Tests | ||||||||
|---|---|---|---|---|---|---|---|---|
| Explained Variable: | ||||||||
| −3.55 | – | −4.84 | – | −3.49 | ||||
| – | – | |||||||
| Explained Variable: | ||||||||
| – | – | – | −4.31 | – | – | |||
| – | 0.63 | – | 0.52 | – | – | – | ||
| Explained Variable: | ||||||||
| – | – | – | ||||||
| – | – | – | ||||||
| STR Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Transition Parameters | Regime 1 | Regime 2 | |||||
| Equ. | |||||||
| – | – | ||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juselius, M.; Kim, M. Sustainable Financial Obligations and Crisis Cycles. Econometrics 2017, 5, 27. https://doi.org/10.3390/econometrics5020027
Juselius M, Kim M. Sustainable Financial Obligations and Crisis Cycles. Econometrics. 2017; 5(2):27. https://doi.org/10.3390/econometrics5020027
Chicago/Turabian StyleJuselius, Mikael, and Moshe Kim. 2017. "Sustainable Financial Obligations and Crisis Cycles" Econometrics 5, no. 2: 27. https://doi.org/10.3390/econometrics5020027
APA StyleJuselius, M., & Kim, M. (2017). Sustainable Financial Obligations and Crisis Cycles. Econometrics, 5(2), 27. https://doi.org/10.3390/econometrics5020027





