1. Introduction
An initiative to improve accessibility to health care and to rationalize the use of existing resources was carried out by the Portuguese Health Ministry through the creation of a national health line, LS24, in April 2007 (
Portal of the National Portuguese Health Service 2015). These objectives are accomplished by the LS24 service which directs users to the most appropriate institutions of the national public health service or by counseling self-care home measures.
This study analyses the number of calls to LS24 at a municipal level, as the location attribute for LS24 data is an important source of information to describe its use, with a view to a future development of decision support indicators in a hospital context based on the economic impact of the use of LS24 rather than on the criterion of hospital urgency. As space is an important feature of these data, ignoring it results in a poorer analysis (
Anselin et al. 1996;
Cressie 1993).
To model the number of calls to LS24 in each municipality with spatial models, given the discrete nature of data (counts), an alternative is to use a hierarchical Bayesian model with covariates (
Banerjee et al. 2004). This approach allows data to have any distribution where, in this case, the Poisson is the obvious choice. The spatial structure assumed for the risk of what is being counted is included, in the first level of the hierarchy, through a prior distribution of spatially structured random effects. In addition, some non-spatially structured random effects to account for risk variation not as yet explained can be considered. These models are better considered under the Bayesian paradigm and their inference needs to be based on simulation methods, namely the Markov Chain Monte Carlo (MCMC) method (
Doucet et al. 2001).
For the hierarchical approach spatial autocorrelation is accounted for in the disturbances and not in the observed responses, as happens with spatial autoregressive approaches. The latter is a different modelling strategy common in spatial econometrics literature that may also be considered for these data. It is plausible to think that the number of calls to LS24 in one municipality is related to the number of calls in the municipalities of its neighbourhood, driven by effects of covariates such as the number of hospitals in one municipality, which may certainly have an impact on the number of calls to LS24 in a neighbouring municipality, or others not considered in the modelling (
Lesage and Pace 2009). Hierarchical and autoregressive modelling perspectives have already been used to model the same data sets (
Bivand et al. 2014a;
Goméz-Rubio et al. 2014;
Quddus 2008).
Traditional spatial econometric models, such as the spatial lag autoregressive model (slm) and the spatial error model (sem), rely however on the gaussian assumption of the response variable (
Lesage and Pace 2009), which no longer holds true for the number of calls (counts). Consequently their usage for count data, such as the number of calls, demands data transformation to meet the assumptions of the models. Nevertheless in the scope of these spatial autoregressive models there are alternatives for modelling counts that we explore here. A spatial lag autoregressive component is incorporated in the model for counts, under a Bayesian paradigm and using Integrated Nested Laplace Approximations (INLA) methodology (
Rue et al. 2009), taking into consideration a standard spatial lag model, as recently developed within a new class of latent models defined in INLA by
Goméz-Rubio et al. (
2015) and also taking into account a spatial autoregressive lag model of counts developed by
Lambert et al. (
2010), under a classical perspective. The model is implemented in R-INLA. Combining the two referred models results in a spatial lag Poisson model, a proposed alternative to do Bayesian inference in spatial econometric models for count data.
Both hierarchical and autoregressive approaches are not yet much explored for spatial econometric models for non-Gaussian data, but they are surely more adequate for these, avoiding data transformation and corresponding to more realistic models.
Regarding the study of the number of calls to LS24, firstly standard spatial econometric techniques are used to look for spatial dependence in the number of calls to LS24 in each municipality, considering a neighbourhood contiguity structure, as well as in the residuals of a baseline log-Poisson model with covariates. The number of calls is further analysed, on one hand, through different hierarchical log-Poisson models, and on the other hand, through a spatial lag Poisson model, implementing different econometric approaches to model spatial structure in data. The results of this study are intended to be used in the near future in cooperation with the Portuguese Directorate-General of Health to analyse, test, implement and predict consequences of different government management policies at hospital level under distinct scenarios. The savings from the correct use the LS24 will avoid unnecessary urgent care in hospitals that can then be channeled towards other needy areas.
This work is organised as follows:
Section 2 is divided into two parts: (a) elaboration of some exploratory spatial techniques to look for spatial correlation and (b) description of Bayesian hierarchical models and Bayesian autoregressive models, both for Poisson count data. These methodologies are used in the following section for modelling the number of calls to LS24 in each municipality in 2014.
Section 4 discusses the main results as well as some perspectives for future work.
3. Results
3.1. The LS24 Data
The data considered in this study were provided by the Support Unit of the Call Center of the National Health Service of the Portuguese Directorate-General of Health. It is a comprehensive data set of the calls recorded by the LS24 health line in the year 2014 and includes information such as user’s gender, residence, age, call’s day of the week, together with the health problem specification.
The LS24 has two call centres and offers various services such as Triage, counseling and routing in disease situations (TAE); Therapeutic counseling (AT) to clarify issues relating to medication; Assistance in Public Health (LSP) in specific topics such as flu, heat, poisoning etc.; General Health Information (IGS), such as the location of public health units, pharmacies, among others. The LS24 service is provided by qualified nurses, trained to give the best advice or, when appropriate, to assist citizens in solving the situation by themselves. The service is available to the beneficiaries of all different kinds of health sub-systems. The LS24 incorporates approximately 300 nurses and 16 clinical supervisors.
Most of the calls answered by LS24, approximately 92%, are catalogued as TAE. These are the calls analyzed in this work where a description of the health problem and the original intention of the user about how to solve it (go to an urgency room, for example) are recorded, and then a decision algorithm follows. The final disposition is determined by this algorithm and by the evaluation of the nurse.
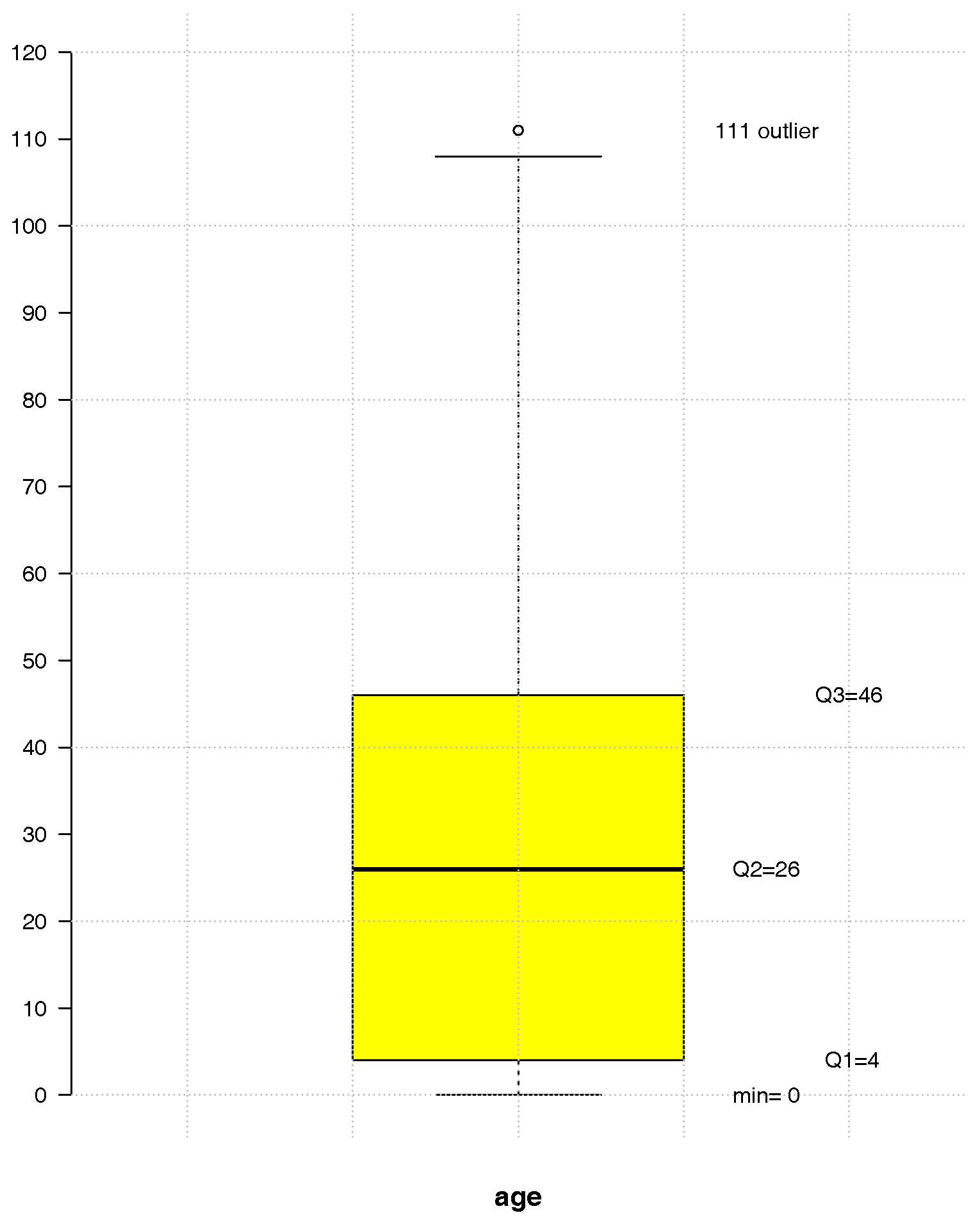
This work focuses on the number of TAE calls to LS24 in 2014 at a municipality level, in Continental Portugal. For this year, 50% of the users were aged between 4 and 46, with a median of 26 years and a range of 111 years—see
Figure 1.
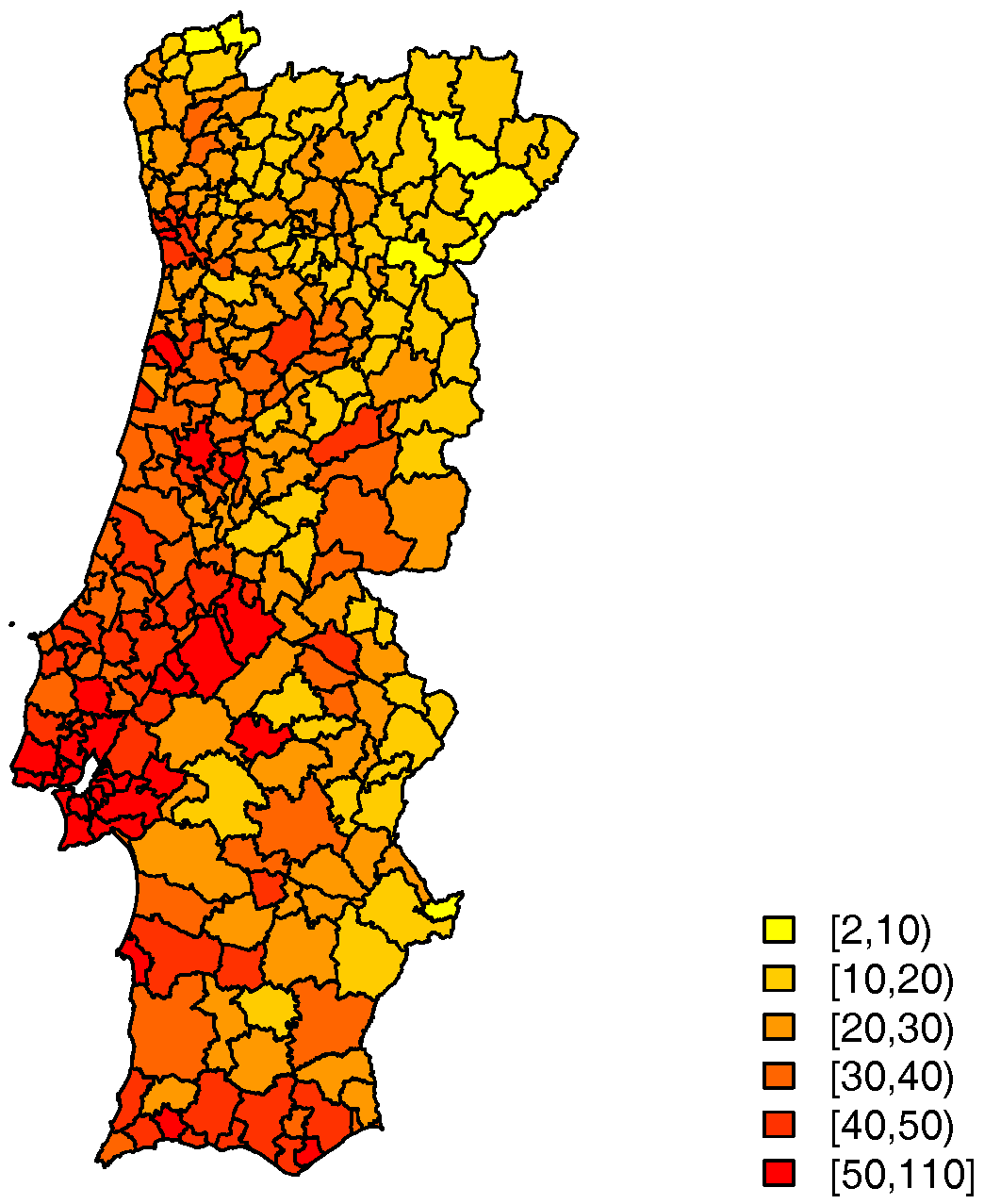
The distribution of the number of TAE calls to LS24, by municipality in 2014, is mapped in
Figure 2. The average raw call rate by municipality is 32 per 1000 inhabitants.
3.2. Non-Spatial Modelling, the Log-Poisson Regression Model
The number of TAE calls to LS24 in each of the 278 municipalities of Continental Portugal were first modelled via a log-Poisson regression model before considering the need of a spatial analysis.
An indirect standardization of these numbers has been carried out, applied to the resident population of each municipality in terms of age groups, namely 0–9, 10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70–79 and >80. This method considers standard age rates
with
the number of cases (calls) and
the at risk population (resident population), in municipality
i and age group
j,
,
, in order to obtain
,
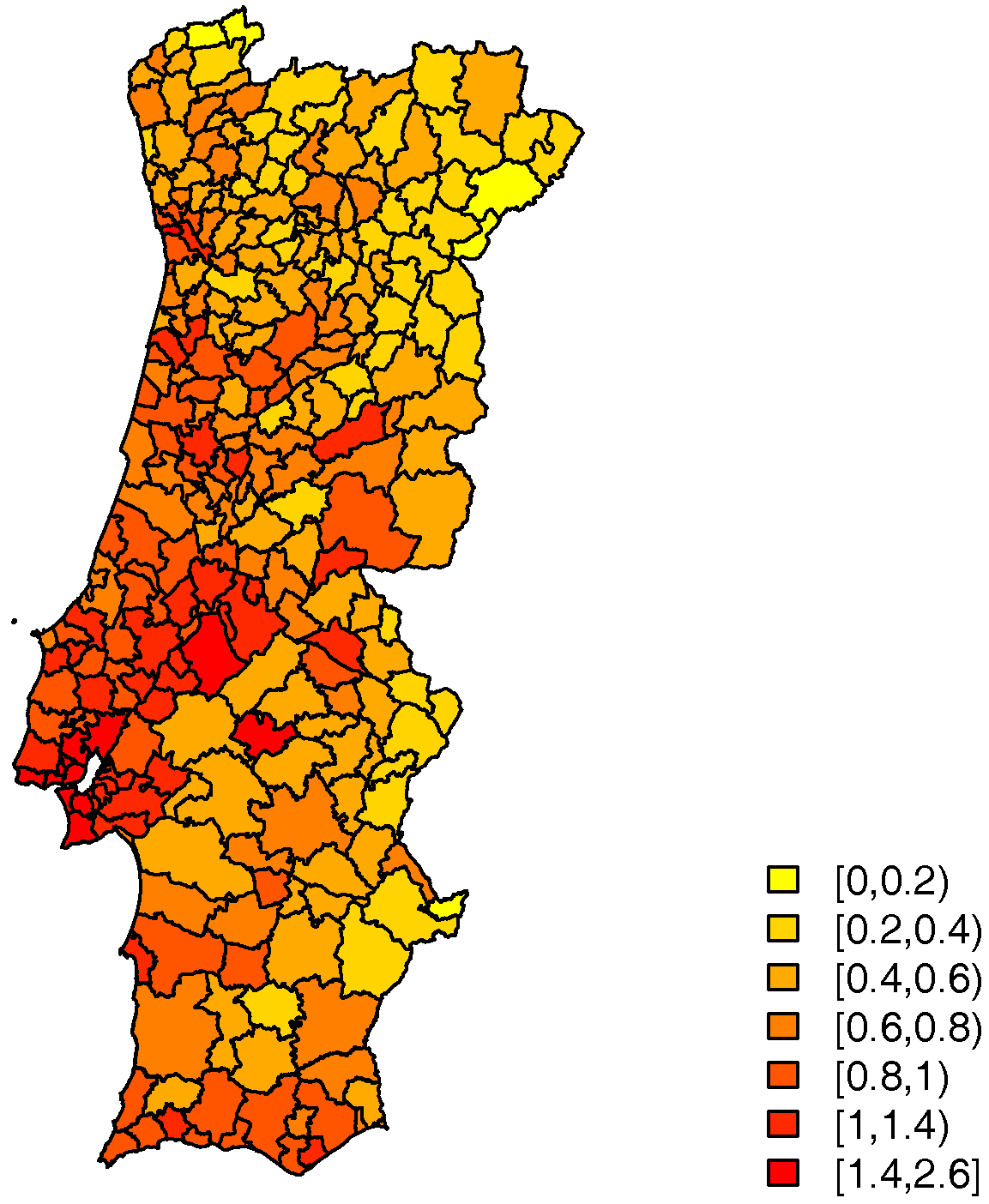
, the expected number of calls in each municipality, that is included in the model as an offset. So that, in fact, what is modelled is the relative call risk, which can be roughly estimated by the Standard Call Rate (SCR) mapped in
Figure 3. This ratio is calculated from the observed number of cases and the expected number of cases, allowing comparisons across different populations. The resident population of each municipality in terms of age groups was obtained from Census 2011 data and adjusted for subsequent years (
PORDATA-Database of Contemporary Portugal 2014).
Demographic and socio-economic information, development indicators as well as characteristics of the Portuguese health system at the municipal level, were investigated as possible covariates for modelling the TAE call counts in order to understand if the inclusion of certain covariates obviated the need for a spatial model. Using the Stepwise methodology of
Rawlings et al. (
1998) for selecting covariates, under different scenarios, the two best cases of the most significant sets of explanatory variables are:
Case 1: The average number of years of schooling, the proportion of elderly residents, the unemployment rate, the rurality index, the number of hospitals and health centres per 1000 inhabitants and the proportion of women in each municipality (AIC: 29530);
Case 2: The monthly average income, the proportion of children, the unemployment rate, the rurality index, the number of hospital and health centres (both per 1000 inhabitants), and the proportion of women in each municipality (AIC: 36980).
From these variables, the average number of years of schooling and the monthly average income are the ones that show a stronger positive correlation with the response variable (0.67 and 0.61, respectively), followed by the proportion of children (0.49). The rurality index and the proportion of elderly residents are negatively correlated with the response (−0.45 and −0.35, respectively).
Over-dispersion in these Poisson data is expected, as we suspect space to be an important feature for their modelling. If we ignore this over-dispersion, the standard errors of the covariate effects are underestimated, resulting in an incorrect assessment of the significance of individual regression parameters. Therefore, instead, we have opted to fit a quasi-Poisson model to account for the over-dispersion, realizing that the significant covariates under this approach were in fact different from the ones of the Poisson model (although the estimated effects are, of course, the same).
Table 1 and
Table 2 depict the estimated coefficients of the considered quasi-Poisson log-regression models for these analyses, with
where
is the relative risk in the
ith municipality. For case 1, the unemployment rate turned out to be not significant after all, and for case 2, the same happened with the rurality index, the number of hospital and health centres.
3.3. Spatial Correlation
In this subsection standard spatial techniques are used to look for spatial dependence in the number of TAE calls, considering a contiguity neighbourhood structure, and also in the residuals of the log-Poisson regression models fitted before.
For the considered contiguity neighbourhood structure, the first order queen neighbourhood, there are 1.9% non-zero weights and the average number of neighbours is 5.3. Taking the corresponding queen neighbourhood matrix, and using Moran’s I statistics (
1), for two sided test, both under normality (
,
) or considering a randomized distribution of the statistics (
,
), resulted in a clear rejection of the spatial independence hypothesis of the number of TAE calls, suggesting that there is a positive spatial correlation among these.
The spatial autocorrelation in the residuals of the log-Poisson regression models fitted in
Section 3.2 was further investigated, using a randomized distribution of the statistic and a two sided test, having
(
) for model 1 and
(
) for model 2. The results suggest a high positive spatial autocorrelation in the residuals. With spatially correlated residuals, the fitted models may be providing biased estimates of the parameters, leading to incorrect interpretations and misleading conclusions (
Lesage 1999). It is then clear that space is an important feature of these data and that must be considered in the modelling.
3.4. Spatial Modelling
3.4.1. Spatial Hierarchical Log-Poisson Regression Model
In order to capture and model data spatial variability, the number of TAE calls in each municipality is now analysed through different hierarchical log-Poisson regression models. The residual autocorrelation of the log-Poisson regression model considered before can be explained, in a Bayesian setting, adding to the model’s predictor a set of spatially structured (
) random effects, considering the contiguity neighbourhood structure mentioned before. Additional unstructured random effects (
) can be considered, if needed. The prior distributions of the random effects define their structure, as described in
Section 2.2.
The estimates were obtained via MCMC, implemented in R-package CARBayes (
Lee 2013). A MCMC run of 1,000,000 iterations was made, discarding 50,000 burn-in iterations and thinning by 100, in order to reduce autocorrelation, resulting in 100,000 sample points.
Two models were considered differing on the way the random effects are included.
Model A: BYM model
The BYM CAR prior model, applied to both cases 1 and 2 in
Section 3.2, is a log-Poisson regression model with the covariates considered significant before plus unstructured (
) and spatially structured random effects (
). The results are summarised in
Table 3 and
Table 4.
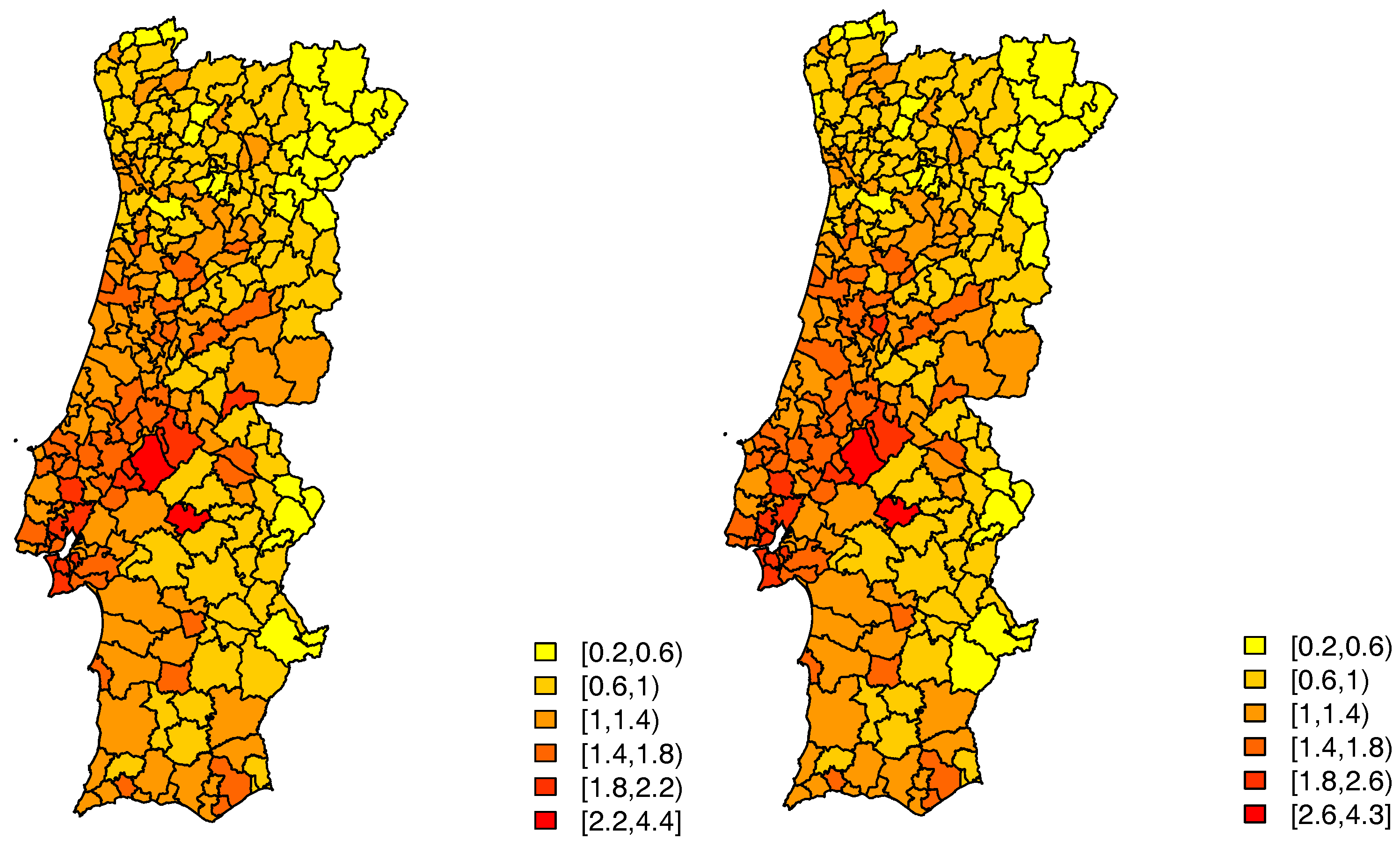
For case 1 only one of the covariates, the average number of years of schooling, proof to be significant, whereas in case 2 it was the monthly average income. The estimated random effects, given by
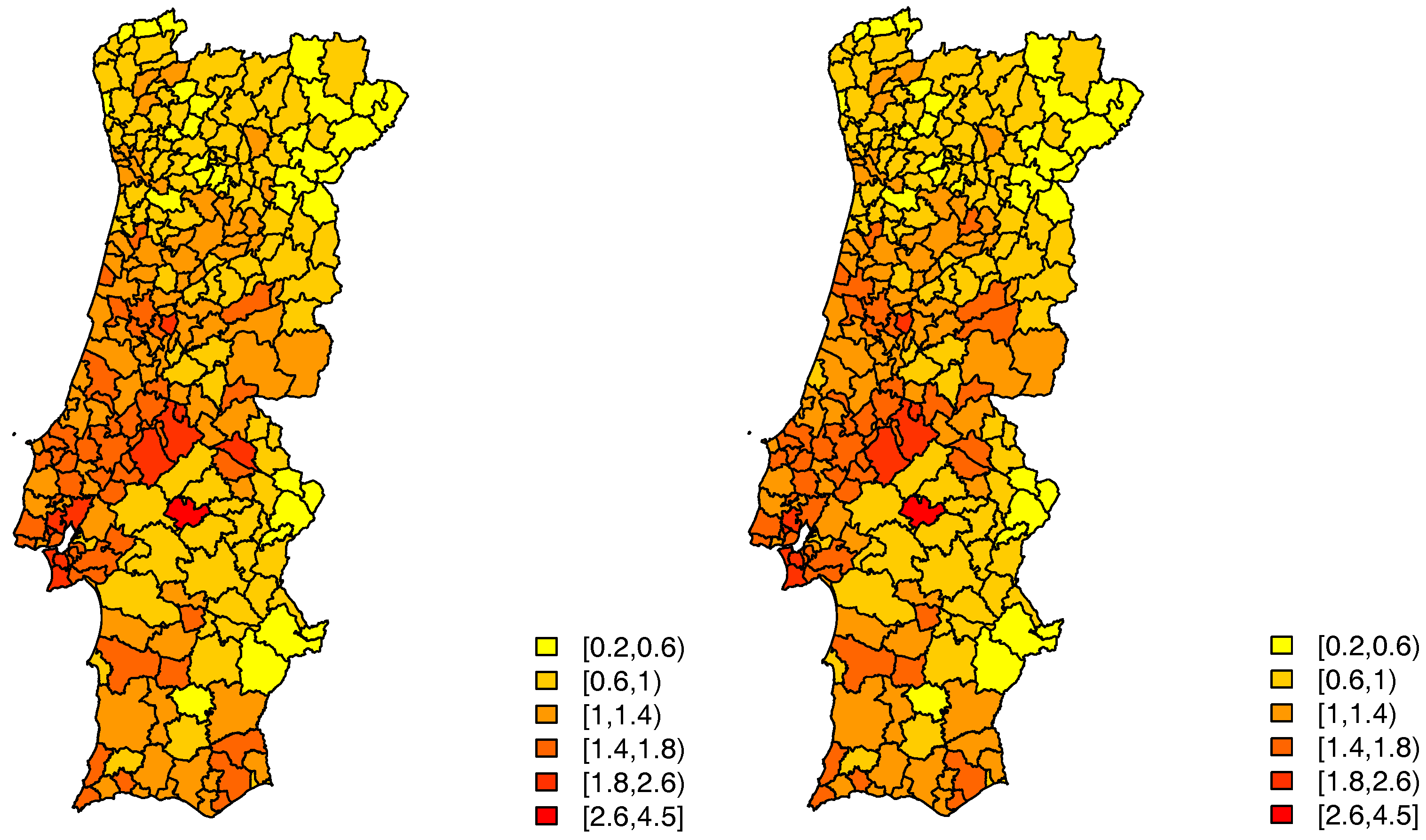
, still display some patterns for both cases—left panels of
Figure 4 and
Figure 5.
Model B: Leroux model
This is a log-Poisson regression model with the covariates previously considered significant plus the random effects (Leroux CAR prior). The results are displayed in
Table 5 for case 1 and in
Table 6 for case 2.
In this model, for the first case, only one of the initial covariates proved to be significant, the average number of years of schooling. The estimates of the random effects, given by
, seem to indicate that there still is spatial variability in these data—right panel of
Figure 4, which is strongly confirmed by an estimated value of
of
.
Considering this model, for the second case, also only one of the initial covariates proved to be significant, the monthly average income. This model has an estimated value of
of
, and the estimates of the random effects seem to indicate that there still is spatial variability—right panel of
Figure 5.
3.4.2. The Spatial Lag Poisson Model
A modelling alternative is to account for spatial autocorrelation in the observed responses instead of the disturbances, as before, using an autoregressive perspective. This approach may also be considered for these data, given that it is plausible to think that the number of TAE calls to LS24 in one municipality is related to the number of calls in the municipalities of its neighbourhood, driven by effects of covariates such as the number of hospitals in one municipality, which may certainly have an impact on the number of calls to LS24 in a neighbour municipality, or others not considered in the modelling. Additionally, the considered covariates themselves display a high spatial dependency. Therefore, the response variable in a given area is most certainly a good predictor of the response variable in its neighbourhood areas.
Here, the TAE number of calls in each municipality is then analysed through the spatial lag Poisson model where a spatial autocorrelation lag is incorporated in the econometric model of counts. The estimates were obtained via INLA methodology, in terms of the “splmINLA” model, in R-package R-INLA, according to the R-code presented in
Appendix B.
Model C: Spatial lag Poisson model
This is the spatial lag Poisson Bayesian autoregressive model with the covariates initially considered significant.
Table 7 and
Table 8 summarize the parameter estimates for case 1 and case 2, respectively.
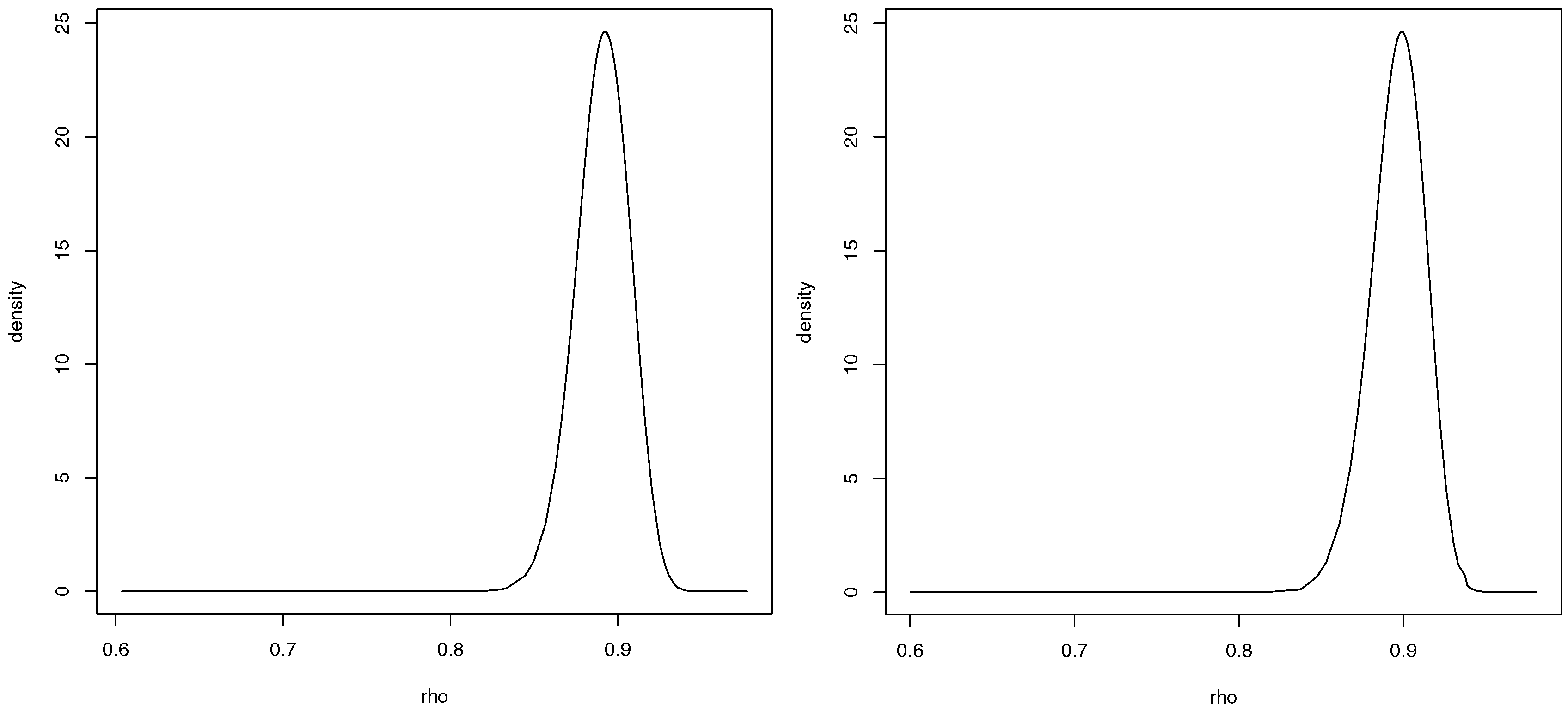
For case 1 only one of the previous covariates proved to be significant, the average number of years of schooling. This model has an estimated value of
of
. As for the second case, only the monthly average income is significant. This second model has an estimated value of
of
. The posterior marginal distribution of the spatial autocorrelation parameter, for both cases, is presented in
Figure 6.
3.5. Comparison of Results
In the various spatial fits, the covariates considered important for explaining the number of calls and the corresponding effects where the same. These fits were further compared by means of their predictive accuracy, using the DIC measure and the WAIC measure. See
Table 9 for case 1 and
Table 10 for case 2. The
Relative Root Mean Square Error (RRMSE) was also considered to measure goodness-of-fit. Results are displayed in
Table 11 and
Table 12.
In terms of spatial hierarchical log-Poisson regression models, the model with smaller DIC (preferred model) is the one including the covariates and the spatially structured random effects through Leroux CAR prior. This was confirmed by the RRMSE values. For the sake of comparison, the fit measures for the baseline log-Poisson regression model without random effects, also fitted by MCMC, are further displayed in the first line of the tables. The log-Poisson regression model was also fitted, including only covariates and unstructured random effects (results not shown here), which performed worse, indicating that spatial random effects are indeed necessary in the models. This might indicate that there are possibly some relevant covariates that are not yet being included in the model. There is a spatial asymmetry that is not explained by the variables. Similar conclusions were reached when the autoregressive perspective was considered in terms of the spatial lag Bayesian Poisson model.
In order to compare both hierarchical and autoregressive model fits, WAIC measure was used, as it is more appropriate for comparing different model structures. The autoregressive model reveals better performance, according to this measure. As for the RRMSE values, they are very similar although they are somewhat smaller for the hierarchical Leroux model.
4. Discussion
This study combines insights from classical spatial econometrics and the analysis of spatial data in order to handle spatial count data, both in a spatial hierarchical and in a spatial autoregressive perspectives. The approach applied here allows the limitations of the classical econometrics methods to be circumvented. In terms of the practical application, it represents a work in progress and this paper displays the first results of the proposed study.
Within the scope of the spatial econometric methods and also resorting to Bayesian hierarchical and autoregressive methodology, their application to study of the number of TAE calls to the national health line, LS24, revealed spatial-correlation and the addition of spatial structure in the models improved estimation.
In this study, the count data were first analysed with a log-Poisson regression model and then the inclusion of spatial random effects in a hierarchical Bayesian setting, proved to be relevant, as expected, although the modelling may perhaps be improved by considering some other more adequate covariates. Furthermore a recent alternative for doing Bayesian inference using INLA (
Rue et al. 2009) for spatial econometric models, the slmINLA recently developed by
Goméz-Rubio et al. (
2015) and implemented in R-INLA, was explored. Subsequently, considering a multiplicative spatial autoregressive lag model for counts developed by
Lambert et al. (
2010), combined with the slmINLA model, a spatial lag Poisson model was developed, an alternative to do Bayesian inference for spatial econometric models for count data. Similar conclusions were drawn when both the hierarchical and the autoregressive perspectives were considered.
The average number of years of schooling for case 1 of the analysis and the average monthly income for case 2 stand out as being important in explaining the use of LS24. Additionally, the spatial component for both cases was quite relevant, which was confirmed by the high values of the estimates of the spatial autocorrelation parameter.
For the future it is the intention to proceed with the study of the LS24 data set, maybe considering some other possible relevant covariates and to carry out analyses under other possible scenarios in order to be able to describe and evaluate in which municipalities the use of LS24 should be encouraged, as well as detecting those regions that most contribute to the economic success of the good use of the line for future assessment of hospital savings (
Hughes and McGuire 2003).
Additionally, this analysis should be extended to include available data for previous years between 2010 and 2014, fitting some spatio-temporal models (
Cressie and Wikle 2011) under an econometric approach and developing and implementing the temporal effects on Bayesian hierarchical models (
Banerjee et al. 2004;
Lee et al. 2015), or on Bayesian autoregressive models (
Blangiardo and Cameletti 2015), for count data, trending towards a spatio-temporal Bayesian econometric approach for processing count data. It is expected that analyses like the one considered here for the LS24 data contribute, in general, to the improvement of management policies in several areas of activity, the hospital domain in this case, or in others such as education or road safety.